结构稳定理论与设计4修改
桥梁结构稳定理论重要性及其发展

1
1 2[11.33(e0 )2 ]
rw
式中:为与砌体砂浆有关的系数,对于5号、2.5号、1号砂浆, 分
别采用0.002、0.0025、0.004;对混凝土通常采用0.002
l0 hw
l0 rw
对矩形截面 非矩形截面
l0 =0.36s 无铰拱
f
H N
cosm
N j ARaj / m
式中:Nj为按式(1-2-124)左边计算的平均轴力,其中荷载在 结构上产生的效应可采用在计算荷载下的评均轴向力,即:
其中
N H / cosm
cosm
1 1 4( f )2
l
N j= s0 (1.2Nd 1.4Nh )
自重产生轴力 汽车产生轴力
为受压构件的纵向弯曲系数,中心受压构件的纵向弯曲系数按公路桥
•当主拱圈宽度较大(如小于跨度的1/20),则可不验算拱的横向 稳定性 •随拱桥所用材料性能的改善和施工技术的提高,拱桥跨径不断增大, 主拱的长细比越来越大,施工和成桥运营状态稳定问题非常突出。
(二)稳定性验算
拱桥的稳定性验算,主要是针对以受压为主的 拱圈或拱肋进行的
若拱的长细比较大,则当其承受的荷载达到某 一临界值时,拱的稳定平衡状态将不能保持:
竖平面内轴线可能离开原来的稳定位置(纵向失稳) 或者轴线可能侧倾离开原竖平面(横向失稳)
上述两种离开原来稳定平衡状态而丧失承载能 力的现象,称为第一类稳定(失稳)问题
如果随着荷载逐步增大,拱(偏心受压)的变 形将沿着初始方向从接近线性到非线性的规律 逐渐发展,直至最后丧失承载能力
那么,上述平衡状态不发生变化的承载能力丧 失问题,称为第二类稳定(失稳)问题
钢结构稳定理论与设计-1详解

§1-2 稳定问题分类
2021年4月28日星期三
1)按平衡状态分
❖ 理想轴压或压弯构件或结构的稳定(perfect)
钢结构稳定理论
2021年4月28日星期三
又称:分岔失稳或第一类稳定问题(bifurcation instability) 定义:由原来的平衡状态变为一种新的微弯(或微扭)
18号普通工字钢 焊接H型钢
钢结构稳定理论
轻型热轧H型钢
2021年4月28日星期三
具有火焰切割边的 厚板焊接H型钢 焊接H型钢
焊接箱形截面
钢结构稳定理论
2021年4月28日星期三
等边角钢
钢结构稳定理论
焊接T形截面
2021年4月28日星期三
焊接圆管半个圆周截面纵向和沿壁厚环向残余应力
钢结构稳定理论
破坏原因:波纹拱的畸变屈曲没有给予很好的考虑。
钢结构稳定理论
破坏后
2021年4月28日星期三
钢结构稳定理论
2021年4月28日星期三
❖ 宁波某轻钢门式刚架施工阶段倒塌。 破坏原因:施工顺序不当、未设置必要的支撑等。
钢结构稳定理论
2021年4月28日星期三
我国其它一些地方的门式刚架也发生过倒塌事故,从设计、 制作、到安装阶段都有可能出现问题。
2、陈绍蕃,钢结构稳定设计指南,中国建筑工业出版 社,2004.
3、吕烈武、沈世钊、沈祖炎、胡学仁,钢结构构件稳 定理论,中国建筑工业出版社,1983.
4、钟善桐,钢结构稳定设计,中国建筑工业出版社, 1991.
钢结构稳定理论
2021年4月28日星期三
基础知识:
1、材料力学 2、结构力学(静力、动力、稳定) 3、钢结构/钢结构设计原理
结构稳定理论(第2版)

2022年3月7日,《结构稳定理论(第2版)》由高等教育出版社出版发行。
内容简介
《结构稳定理论(第2版)》共计9章,第1章介绍结构稳定问题概述,第2章介绍结构稳定计算的能量法,第 3章介绍轴心受压杆件的整体稳定,第4章和第5章介绍杆件的扭转与梁的弯扭屈曲、受压杆件的扭转屈曲与弯扭 屈曲,第6章和第7章介绍压弯杆件在弯矩作用平面内的稳定、刚架的稳定,第8章和第9章介绍拱的平面内屈曲以 及薄板的屈曲等内容。
郑宏,男,哈尔滨人,工学博士,长安大学建筑工程学院教授,研究生导师。研究领域:钢结构基本理论及 其应用、结构稳定理论、结构抗震及减震。
石宇,工学博士,重庆大学土木工程学院教授,硕士生、博士生导师。研究方向:钢结构基本原理及其应用、 钢—混凝土组合结构。
感谢观看
教材目录
(注:目录排版顺序为从左列至右列)
教学资源
《结构稳定理论(第2版)》的数字课程与纸质教材一体化设计,内容涵盖教学课件、动画、失稳案例分析、 练习题及答案等。
《结构稳定理论(第2版)》配有数字化资源。
作者简介
周绪红,男,1956年9月出生,汉族,湖南南县人,工学博士,中国工程院院士,日本工程院外籍院士,重 庆大学钢结构工程研究中心主任,重庆大学土木工程学院教授。研究方向:钢结构、钢-混凝土混合结构、高层结 构、大跨结构、桥梁结构、风电结构。
结构稳定理论(第2版)
3月高等教育出版社出版的图书
01 成书过程
03 教材目录 05 作者简介
目录
02 内容简介 04 教学资源
《结构稳定理论(第2版)》是由周绪红主编,高等教育出版社于2022年3月7日出版的“十二五”普通高等 教育本科国家级规划教材,新世纪土木工程系列教材。该教材可作为高等学校土木工程专业高年级本科生及相关 专业研究生教材,也可供相关专业教师和工程技术人员参考。
新课标苏教版高中通用技术技术与设计2结构与稳定性教学设计

新课标苏教版高中通用技术《技术与设计2》第一单元第二节《结构与稳定性》教学设计一、教材分析本课题是《技术与设计2》第一单元第二节第1部分的教学内容,计划用1课时进行教学。
“结构与稳定性”安排在学生学习了“常见结构的认识”之后,这样安排符合学生的认知规律,从浅到深由易到难。
“结构与稳定性”是“结构与设计”这单元的一个重要组成部分,同时也是后面学习“结构与强度”的基础,有着承上启下的作用。
并且“结构与稳定性”和生活实际联系密切。
所以,这部分内容是本单元的重点。
本课教学对象是我校高二年级学生。
学生们已经有一定的生活经验,并且经过技术与设计1模块的学习后,也具备了一定的分析问题能力。
但动手能力较差,不能很好地将理论知识与实践相结合。
所以在教学过程中,我注意创设情境,采取多种形式的教学方法吸引学生的注意力,激发学生的学习兴趣和热情,挖掘学生的创造潜能,从而达到本课的教学目标。
二、教学目标根据课标要求结合本节教材及学生已有的认知水平,我确定本节课的教学目标如下:(1)知识与技能:通过技术试验,使学生了解影响结构稳定性的主要因素;培养学生的观察分析能力,运用本节知识分析解决实际问题的能力。
(2)过程与方法:通过技术试验及试验分析、讨论等方法引导学生综合运用相关的理论知识,提高学生的知识迁移能力。
(3)情感与价值:通过本节教材内容的学习,提高学生对结构稳定性设计的意识,激发他们的学习兴趣,促进学生之间的相互交流与合作。
三、教学重点难点:重点:通过技术试验,引导学生分析影响结构稳定性的主要因素。
难点:运用影响结构稳定性的主要因素解决生活实际问题。
四、教法“教无定法,贵在得法”,选择有效的教学方法是取得良好教学效果的保证。
根据课标要求结合本节教学内容与学情分析,我采取以下教学方法:1.情境创设:通过播放视频和做演示试验,引导学生观察、分析、交流、探讨影响结构稳定性的主要因素。
2.引导发现:在学生参与演示实验的过程中,激发学生对技术理论知识掌握和学习的兴趣。
结构稳定理论第四章
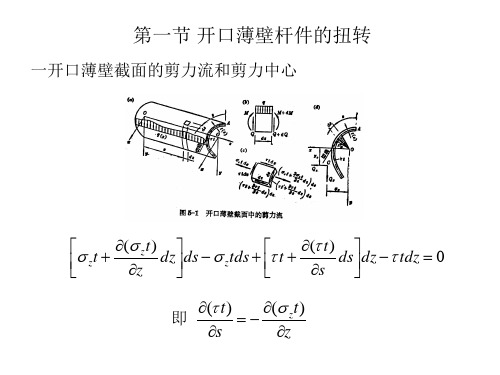
u BB1 sin BC sin tg ( y y0 ) v BB1 cos BC costg ( x x0 )
( y y0 ) cos ( x x0 ) sin c (4 8)
2. 假定约束扭转时,杆件中面的剪应变为零
2 b 2 h 2t e th 2 h b 2 h 2t 2bt e 4I x Ix 4I x 2 12
剪心坐标也可利用(4-4)时求得:建立以形心O为极点, 以下翼缘自由端点1为起始点(称为扇性零点)的扇性坐标 0图
下翼缘(bs0) s s h h 12 0 ds ds s 0 0 2 2 点2(s=b) bh 2 2 腹板(b+hsb) b h s bh 24 ds eds ( s b)e 0 2 b 2
0 0 ds — 称为s点的扇性坐标, 又称单位翘曲
0
s
I 0 x和I0 y — 称为扇性惯性积,又称 翘曲惯性积
例4-1 槽形截面在Qy作用下截面上的剪力流和剪力中心位置
解 1.剪力流 选下翼缘端点1作为曲线坐标s的起始点 下翼缘(bs0)
h ht S12 ytds tds s 0 0 2 2 Qy S x htQy t s Ix 2I x bht t bhtQy S2 点2(s=b) 2I x 2
将 z Mx y Ix M y x I y
Qy dMx dz
Qx dM y dz
代入上式得截面上的剪力流为: Qy s Qy S x Qx S y Qx s t ytds xtds Ix 0 Iy 0 Ix Iy 式中:
(4 1)
结构稳定理论与设计-2(110303)

7 23 U V 4EIa l Pa1 l 3
2 1
2.1 轴心受压构件的弯曲失稳
2.1.1 理想轴心受压构件的弹性弯曲失稳 能量法: 用里兹法求解图示轴心受压构件 的临界荷载Pcr。 d 0 由势能驻值原理 da1
4EIl 1.714EI P 3 cr 3 7l l 2 级数、 三角函数! 1.358EI Pcr 精确解 2 l 例题图 无限自由度轴心压杆
切线模量理论采用如下假定: ①杆件是挺直的; ②杆件两端铰接,荷载沿杆轴 线作用; ③杆件产生微小的弯曲变形 (小变形假定); ④弯曲前的平截面弯曲变形后 仍为平面; ⑤弯曲变形时全截面没有出现 反号应变?
Pt
2 Et I
l0
2
2 Et t 2
2.1 轴心受压构件的弯曲失稳
2.1.2 理想轴心受压构件的非弹性弯曲失稳 2.双模量理论
挠曲线方程成为:
y A sin kz Cz
z l 由 ; y 0
z l 得 y 0
A sin kl Cl 0 Ak cos kl C 0
为一关于A、C 的线形齐次方程组,为使其有非零解
(否则 y 0),则必有其系数行列式等于零,即:
2.1.1 理想轴心受压构件的弹性弯曲失稳
静力法:
2) 柱的高阶微分方程(对其他支承及荷载情况)
考虑图示杆件承受一组竖向力系, 由脱离体的平衡可得:
EIy Fy M A Vz
对上式求导两次可消去 等式右端的杆端约束力:
EIy Fy 0
2.1 轴心受压构件的弯曲失稳
sin kl
l
k cos kl 1
结构稳定理论
1.理想压杆:受压杆件两端铰支荷载作用于形心轴,杆轴线沿杆长完全平直,横截面双轴对称且沿杆长均匀不变,杆件无初应力,材料符合胡=胡克定律2.极限状态:承载能力极限状态和正常使用极限状态。
3.保守力:如果力在它作用的任意可能位移上所做的功与力作用点移动路径无关,只依赖与移动的起点和终点。
4.势能驻值原理与最小势能的区别:势能驻值原理方法比较简单,但从教学角度δp=0只是平衡条件,它不表示从稳定平衡过度到不稳定平衡的临界条件,而最小势能原理方法更加严密。
(势能驻值原理:虚位移,基本条件δp=0)5.伽辽金法瑞利-里兹法的区别:①瑞利里兹法只需要满足几何边界条件即可,而伽辽金法需要满足几何边界条件,力学边界条件;②伽辽金法直接与微分方程相联系,而瑞利里兹法需要写出体系的总势能。
6.计算长度系数μ,将非两端铰支的理想轴心压杆构件,临界荷载公式换算成相当于两端铰支理想轴心压杆构件,求解临界荷载的形式的所利用的计算长度,几何意义:杆件绕由曲线上两反弯点的间距7.自由度:用来表示约束条件允许的体系,可能变形时所必须的独立几何参数的数目。
8.柱子曲线:临界应力δcr与长细比的关系曲线,可作为轴心受压构件设计的依据。
9.残余应力:降低比例极限,使柱子提前出现弹塑性屈曲,当超过比例极限后,残余应力使杆件应力应变曲线,同时减小了截面的有效面积和有效惯性矩,从而降低了刚度和稳定性。
10.翘曲:非圆形截面的杆件扭转时,截面处绕杆件轴线转动外,截面上个点还会发生不同的轴向位移而使截面出现凹凸,不像圆截面杆件那样扭转后不保持平面。
11.影响弯曲荷载Mor的因素:①截面的形状,尺寸。
②截面的残余应力。
③初始几何缺陷。
④荷载类型及其作用特点。
⑤构件端部和侧向支撑条件。
12.梁的弯曲屈曲5个假设:①构件为各向同性完全弹性体,②弯曲和扭转时,构件截面形状不变,③小变形(侧面)。
④构件为等截面无截面。
⑤主弯矩作用平面内刚度很大,屈曲前变形对弯扭屈曲的影响的忽略。
结构稳定理论
遵循弹性规律。又因为E>Et,且弯曲拉、压应力平衡,所以中 和轴向受拉一侧移动。
令: I1为弯曲受拉一侧截面(退降 Ncr,r 区)对中和轴的惯性矩;
形心轴 中和轴
σcr
l
dσ1
I2为弯曲受压一侧截面对中 和轴的惯性矩;
dσ2
且忽略剪切变形的影响,由
x
内、外弯矩平衡得:
y
E 1 E I tI 2y N y Ncr,r
▪ 6、残余应力、结构物的弹塑性化及大挠度非线性 问题等
▪ 7、60年代出现了一门称为突变理论的新学科,正 在被用来描述渐变力产生突变效应的现象,其中也 包括结构失稳现象。
▪ 上述经典理论研究S.P.铁木辛柯(一译铁 摩辛柯)等在1907~1934年间进行了全面的 总结,所著《弹性稳定理论》成为结构稳定 理论的经典著作。
1
2EA
1 2
G A
通常剪切变形的影响较小,可忽略不计,即得欧 拉临界力和临界应力:
N c rl2 2 E I2 E 2A 2 E
c r2
上述推导过程中,假定E为常量(材料满足虎克定 律),所以σcr不应大于材料的比例极限fp,即:
cr
2E 2
fp
或 长 细 比 :
p
E fP
第14章
WTr(外力的功) UTr
若UTr ,则原体系处于稳定 。平衡 若UTr ,则原体系处于不衡稳。定平 若 UTr,则原体系处 ,于 利随 用遇 此平 条 荷衡 件 载
▪ 2、结构失稳的两种基本形式
▪ 1)第一类失稳(分支点失稳):结构变形
产生了性质上的突变,带有突然性。
P
P>Pc r
P
C
D
l
掘进巷道顶板管理规定
掘进巷道顶板管理办法各矿、各煤炭子公司:为提高集团公司掘进顶板管理水平,有效预防顶板事故发生,保障煤矿安全生产,根据《矿山安全法》、《安全生产法》、《煤矿安全规程》、《山西省煤矿顶板安全管理规定》、《煤矿巷道锚杆支护技术规范》(GB/T35056-2018)等安全生产相关法律、法规、技术政策,特制定《XX煤矿集团掘进巷道顶板管理办法》(简称“管理办法”),现将“管理办法”印发给你们,望各相关单位认真组织学习,遵照本办法严格执行。
附件:XX煤矿集团掘进巷道顶板管理办法XX煤矿集团掘进巷道顶板管理办法第一章总则第一条为提高集团公司掘进顶板管理水平,有效预防顶板事故发生,保障煤矿安全生产,根据《矿山安全法》、《安全生产法》、《煤矿安全规程》、《山西省煤矿顶板安全管理规定》、《煤矿巷道锚杆支护技术规范》(GB/T35056-2018)等安全生产相关法律、法规、技术政策,制定本办法。
第二条本办法适用于大同煤矿集团公司所属矿井。
第三条各矿(公司)、子公司,必须参照本规定制定相应顶板管理办法。
第二章基础管理第四条矿井主要负责人是顶板安全管理工作的第一责任人,对顶板管理工作负总责,负责建立健全顶板管理机构、配备相应管理人员、制定顶板管理制度和顶板管理年度计划;分管副矿长(副总经理)、总工程师具体负责本单位顶板管理、技术管理工作。
第五条建立健全技术管理体系,建立矿压观测、顶板隐患排查治理、工程质量验收、设备检修、技术档案管理等制度和台账。
同时要明确矿领导、科室及区队三级岗位职责与分工。
第六条掘进巷道作业规程编制前,地质部门应提供经矿总工程师批准的地质说明书,说明煤层赋存状况、顶底板岩性以及影响巷道施工的地质构造、应力状况,上下层对照关系、四周开采及水、火、瓦斯、煤尘等情况。
第七条作业规程必须包含顶板管理相关内容,由矿总工程师组织会审并签字后贯彻执行。
遇到地质条件发生变化时,应及时修改作业规程或补充制定安全技术措施。
第4讲 结构稳定与分支(岔)现象
当 mgl 2ka 2时,只有一个平衡点
如果m 选作为参量,平衡位置的 x 值记为 ,则临界参量为 2 m* 图4.5a 。2ka /( gl )
) 4.5b。 如果选 k 作为参量,则临界的参量为 k mgl /(2a ,图
* 2
图4.5参量变化与平 衡点∶a. 参量为 m; b. 参量为 k 。
1 x e 2 t 1 x
e 2 t 1 t x e2t 1 tht = th 2 1 2 t y x sech 2 2
4.1 一个大范围的结构稳定性定理
此时 ;当 t , y 0, x ;当 H1 1 4
t , y 0, x。这样的分型 1
方程(a)的首次积分为
x x H x
1 2 2 1 2 2 1 4
4
(c)
对应平衡点的首次积分值为 当
H1 0, H2,3 1 4
(d)
时,方程(a)的解可写为 H1 4 x asn(t , m)
4.1 一个大范围的结构稳定性定理
这里
2 2 2 2 2 , 1 1 a , m a /(2 a ) 2
考虑下列的扰动系统
dx dy (4.2) x, y2 dt dt 0 其中 是实参数。当 0 时没有奇点;当 时,奇点为 (0,0); 时,奇点 0 ) 为 (0, ), (0, 。这说明无论 多么小,系统 (4.2) 和对应的未扰动系统
则平衡点和其稳定性如图4.7所示。
图 4.6 例 4.4 装置
图 4.7 参量 变化与平衡点的稳定性
4.3
Hopf分支
我们考虑定理4.1中条件A遭到破坏的另一种形式∶系统奇点处的线性部分矩阵的 特征值不为零,但为一对纯虚数(图3.6中的情形)。 例4.5 考虑系统 及其扰动系统
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章 压弯构件的稳定 概述
压弯构件—同时承受轴向压力和弯矩的构件,亦称 Beam-Columns。本章仅讨论弯矩作用在一个主平面(单向) 的压弯构件。
压弯构件弯矩的产生 主要分三大类:
(1)压力偏心 (2)杆端弯矩 (3)横向荷载
1
作用在压弯构件上的压力和弯矩不一定由相同荷载引起,
0l
0
l
20 l
(1)式成为:
EIv2 4 Pv2 2 2qvl
U V 4l3
4l
结构处于平衡状态时,有:
(U V ) v
EIv 2l 3
4
Pv 2l
2
2ql
0
即跨中挠度
vmax
4ql 4
1
EI 4 P 2l 2
或
vmax
5ql 4 1536EI
384EI
5 5
1
EI Pl 2 / 2
矩表达式得最大弯矩为:
M max
M1 cos kz
M1
(M 2 / M1)2 2(M 2 / M1) cos kl 1 sin2 kl
M1
讨论:
(1)若z 0 或 z l,最大弯矩发生在端部,即 M max M1
(2)若 0 z (l 条件:M 2 / M1 cos kl ),系数 1.0
2(1 cos kl)
M max M eq
sin2 kl
M eq M1
(M
2
/
M1)2 2(M 2 / M1) 2(1 cos kl)
cos
kl
1
mM1
等效弯矩
8
1. 端弯矩作用下的压弯构件
将“非纯弯+轴压” 按最大弯矩相等原则转化成
纯弯+轴压 “标准受力状态”
?
m
(M 2 / M1)2 2(M 2 / M1) cos kl 1 2(1 cos kl)
M
M1
sin kz sin kl
M2
sin k(l sin kl
z)
6
最大弯矩截面位置的确定,由
dM
cos kz
cos k(l z)
dz M1k sin kl M2k sin kl 0
或 M1 cos kz M 2 cos(l z) 0
设M1>M2,可解得最大弯矩截面的位置为 z ,代入上述弯
a
c
M
c
2
当采用不同的 计算理论和力学模 型时,压弯构件的 荷载-挠度曲线差别 很大:
a. 理想轴压柱; b. 考虑初偏心的二
阶弹性分析; c. 考虑初偏心的二
阶弹塑性分析(有 下降段); e. 考虑初偏心的一 阶弹性分析。
3
4.1 压弯构件平面内失稳
对压弯构件,当弯矩作用平面外有足够多支撑可以 避免发生弯扭失稳时,其失稳则只可能发生弯矩作用平面 内——弯曲失稳。
我国钢结构设计
规范亦采用此式,
但新规范已取消
m 0.4 的限制。 10
2 横向均布荷载作用下的压弯构件
采用瑞利-里兹法(能量法),
U 1 l EI (y)2 dz
20
V 1
l P( y)2 dz q
l
ydz
20
0
U V 1 l EI ( y)2 dz
20
1
l P( y)2 dz q
等效弯矩系数
M eq M1
(M
2
/
M1)2 2(M 2 / M1) 2(1 cos kl)
cos
kl
1
mM1
9
等效弯矩系数代表了等效弯矩Meq与较大端弯矩M1的比
值,可画出 m与
端弯矩及Pcr的关 系曲线,Austin
建议用两段直线
代替,即取:
m
0.6
0.4
M2 M1
但限制 m 0.4 。
M max M1
7
(3)若两端弯矩相等,即M1=M2=Meq,最大弯矩为: 2(1 cos kl)
M max M eq sin2 kl
取Meq为等效弯矩,以替代端弯矩 的作用,使替代后杆件的Mmax相等。
例:当 M2 / M1 cos kl 时
M max M1
(M 2 / M1)2 2(M 2 / M1) cos kl 1 sin )
ql 2 8
[1
0.028P / Pcr 1 (P / Pcr )
]
令
M0
ql 2 8
,上式得
M max
M0
1 0.028P / Pcr 1 (P / Pcr )
M 0
这里 称为弯矩放大系数 1 (P / Pcr )
1 (P / Pcr ) 对均布荷载作用的压弯构件:
l
ydz
20
0
假设挠曲线(满足边界条件):
y v sin z
l
U
V
EIv2 2l 4
4
l 0
sin2
z l
dz
Pv 2 2l 2
2
l cos2 z dz qv l sin2 z dz
0
l
0l
(1)
11
l sin2 z dz l cos2 z dz l ;
l z 2l
sin dz
即压力和弯矩不一定按比例增加,是两个独立的变量,可能
有不同的加载过程。
a 比例加载 偏心受压;
b 先加 P 后加 M 框架柱、高耸结构;
c 先加 M后加 P。
弹性阶段:构件受力与加
P
载过程无关,只与最终的 P与
b
M值有关;
弹塑性阶段:构件
b
的受力不但与P和M的值有关,
还取决于加载历史,分析较困
难,需采用一些近似假定。
近似得
=1530
vmax
5ql 4 384EI
1
v0
1 (P / Pcr ) 1 (P /
; Pcr )
v0
5ql 4 384EI
12
最大弯矩截面在跨中:
M max
ql2 8
Pvmax
ql 2 8
5Pql 4 384EI
1 1 (P / Pcr )
Pcr
2
l
EI
2
或
M max
ql 2 8
[1
由高阶微分方程的通解
y Asin kz B cos kz Cz D 代入边界条件
z 0: z l :
y 0, y 0,
EIy M 2 EIy M1
得 y M1 sin kz z
P sin kl l
M2 [sin k(l z) (l z)]
P sin kl
l
由 M EIy 得任意点的弯矩:
1 0.028P / Pcr
与等效杆端弯矩作用的压弯杆比较可得等效弯矩系数:
m
1
1 0.234(P
/
Pcr
)
13
3 跨中集中力作用下的压弯构件
4
4.1 压弯构件平面内失稳
4.1.1 压弯构件弯矩作用平面内的弹性弯曲失稳
1. 端弯矩作用下的压弯构件 由高阶微分方程的通解
y Asin kz B cos kz Cz D 代入边界条件求解!
M
EIvIV Pv 0
M
M
M
5
4.1 压弯构件平面内失稳
4.1.1 压弯构件弯矩作用平面内的弹性弯曲失稳 1. 端弯矩作用下的压弯构件
