第五讲定积分的几何应用
高等数学第五章定积分及其应用

⾼等数学第五章定积分及其应⽤第五章定积分及其应⽤第⼀节定积分概念1、内容分布图⽰★曲边梯形★曲边梯形的⾯积★变速直线运动的路程★变⼒沿直线所作功★定积分的定义★定积分存在定理★定积分的⼏何意义★定积分的物理意义★例1 ★定积分的近似计算★例2★内容⼩结★课堂练习★习题5-1 ★返回2、讲解注意:3、重点难点:4、例题选讲:例1利⽤定积分的定义计算积分01dx x 2?.讲解注意:例2的近似值.⽤矩形法和梯形法计算积分-102dx ex讲解注意:第⼆节定积分的性质1、内容分布图⽰★性质1-4★性质5及其推论★例1★性质6★例2★例3★性质7★例4★函数的平均值★例5★内容⼩结★课堂练习★习题5-2★返回2、讲解注意:例1⽐较积分值dx e x ?-2和dx x ?-2的⼤⼩.讲解注意:例2估计积分dx xπ+03sin 31的值.讲解注意:例3估计积分dx xxππ/2/4sin 的值.讲解注意:例4设)(x f 可导1)(lim =+∞→x f x 求且,,dt t f tt x x x ?++∞→2)(3sin lim .讲解注意:例5计算纯电阻电路中正弦交流电t I i m ωsin =在⼀个周期上的()功率的平均值简称平均功率.讲解注意:第三节微积分基本公式1、内容分布图⽰★引例★积分上限函数★积分上限函数的导数★例1-2★例3★例4★例5★例6★例7-8 ★例9★例10★例11★例12★例13★例14★内容⼩结★课堂练习★习题5-3★返回2、讲解注意:3、重点难点:4、例题选讲:例1?x tdt dxd 02cos 求[].讲解注意:例2dt e dxdx t ?321求[].讲解注意:例3.)()((3);)()((2);)((1).,)(00sin cos )(?-===x x x x t f dt t x f x F dt t xf x F dt e x F x f 试求以下各函数的导数是连续函数设讲解注意:例4求.1cos 02x dte x t x ?-→讲解注意:设)(x f 在),(+∞-∞内连续0)(>x f .证明函数且,??=xxdtt f dtt t x F 00)()()(在),0(+∞内为单调增加函数.f 例5讲解注意:例6],1[)ln 21()(1上的最⼤值与最⼩在求函数e dt t t x I x ?+=.值讲解注意:例7求.dx x ?12讲解注意:例8求.1dxx ?--12讲解注意:例9设求??≤<≤≤=215102)(x x x x f ?2讲解注意:例10.|12|10-dx x 计算讲解注意:.cos 1/3/22?--ππdx x 计算例11讲解注意:例12求.},max{222?-dx x x讲解注意:例13计算由曲线x y sin =在,0π之间及x .轴所围成的图形的⾯积x =x =A讲解注意:例14?,./5.,362了多少距离问从开始刹车到停车刹车汽车以等加速度到某处需要减速停车速度⾏驶汽车以每⼩时s m a km -=汽车驶过设讲解注意:第四节换元法积分法和分部积分法1、内容分布图⽰★定积分换元积分法★例1★例2★例3★例4★定积分的分部积分法★内容⼩结★课堂练习★习题5-4★返回★例5★例6★例7★例16★例17★例182、讲解注意:3、重点难点:4、例题选讲:例1计算.sin cos /25?πxdx x讲解注意:例2?a0dx 计算.0a >)(-2x 2a讲解注意:例3计算.sin sin 053?π-dx x x讲解注意:例4计算定积分dx x x ++412.2?讲解注意:例5当)(x f 在],[a a -上连续,,,)(x f 为偶函数当当有(1)(2)则 ??-=aaadx x f dx x f 0)(2)()(x f 为奇函数有?-=aa dx x f 0)(.;讲解注意:例6.--+dx e x x x 计算讲解注意:例7计算.11cos 21122?--++dx x xx x讲解注意:例8若)(x f 在]1,0[上连续证明,(1)?=00)(cos )(sin dx x f dx x f ;(2)πππ=)(sin 2)(sin dx x f dx x xf ,由此计算?π+02cos 1sin dx x x x ./2π/2π讲解注意:例9计算.arcsin 0?xdx 1/2讲解注意:例10计算.2cos 10+x xdx/4π讲解注意:例11计算.sin 0?xdx /2π2x讲解注意:例12.1dx e x 计算1/2讲解注意:例13.1)1ln(102++dx x x 求定积分讲解注意:例14-22ln e e dx x x求.讲解注意:例15.,612ln 2x e dt xt 求已知?=-π讲解注意:例16).(,)(13)()(1022x f dx x f x x x f x f 求满⾜⽅程已知? --=讲解注意:例17证明定积分公式xdx I n n n 0--?-??--?-=n n n n n n n n n n ,3254231,22143231π为正偶数.为⼤于1的正奇数./2π/2π??讲解注意:例18?π05.2cos dx x 求讲解注意:第五节定积分的⼏何应⽤1、内容分布图⽰★平⾯图形的⾯积A ★例1 ★例2 ★平⾯图形的⾯积B ★例3 ★例4 ★平⾯图形的⾯积C ★例5 ★平⾯图形的⾯积D★例6 ★例7 ★例8 旋转体★圆锥★圆柱★旋转体★旋转体的体积★例9 ★例 10 ★例 11 ★平⾏截⾯⾯积为已知的⽴体的体积★例 12 ★例 13 ★内容⼩结★课堂练习★习题5-5 ★返回2、讲解注意:3、重点难点:4、例题选讲:例1]1,1[]1,0[2之间的⾯积.和轴上⽅在下⽅与分别求曲线-∈∈=x x x x y讲解注意:例2],1[ln 之间的⾯积.轴上⽅在下⽅与求e x x y =讲解注意:例3.1,1,03所围图形⾯积与直线求=-===x x y x y讲解注意:例44,0,042所围图形⾯积.和直线求由曲线===-=x x y x y讲解注意:例5.2所围成平⾯图形的⾯积与求由抛物线x y x y ==讲解注意:例642,2,所围成图形的⾯积.求由三条直线=-=+=y x y x x y422围成图形的⾯积与求+-==x y x y讲解注意:例8.0cos sin 之间所围图与在和求由曲线π====x x x y x y 形的⾯积讲解注意:例9r 圆锥体的直线、h x =及x 轴围直线连接坐标原点O 及点),(r h P 成⼀个直⾓三⾓形.x 轴旋转构成⼀个底半径为计算圆锥体的体积.h ,将它绕⾼为,的讲解注意:例10.12222y x V V y x by a x 和积轴旋转所得的旋转体体轴和分别绕求椭圆=+讲解注意:例112,22轴旋转⽽成的旋转体的体积.轴和所围成的图形分别绕求由曲线y x x y x y -==讲解注意:例12⼀平⾯经过半径为R 的圆柱体的底圆中⼼计算这平⾯截圆柱体所得⽴体的体积.并与底⾯交成,,⾓讲解注意:例13.的正劈锥体的体积的圆为底、求以半径为h R ⾼位平⾏且等于底圆直径的线段为顶、讲解注意:第六节积分在经济分析中的应⽤1、内容分布图⽰★由边际函数求原经济函数★需求函数★例1★总成本函数★例2★总收⼊函数★例3★利润函数★例4由边际函数求最优问题★例5★例6其它经济应⽤★例7⼴告策略★消费者剩余★例8★国民收⼊分配★例9★返回2、讲解注意:3、重点难点:4、例题选讲:例1),80,(80,4) (,==-='q pp qp格的函数关系.时即该商品的最⼤需求量为且边际需求的函数已知对某商品的需求量是价格求需求量与价讲解注意:例2, 90,2)(0.2 ==ceqCq 求总成本函数.固定成本的函数若⼀企业⽣产某产品的边际成本是产量讲解注意:例310,40),/(2100)(个单位时单位时的总收⼊及平均收⼊求⽣产单位元单位时的边际收⼊为已知⽣产某产品-='q q R q 并求再增加⽣产所增加的总收⼊.讲解注意:例45,10,413)(,225)(0==-='-='q c q q C q q R 时的⽑利和纯利.求当固定成本为边际成本已知某产品的边际收⼊讲解注意:例5吨产品时的边际成本为某企业⽣产q )/30501)(吨元q q C +='(?,900试求产量为多少时平均成本最低元且固定成本为讲解注意:例6q q q C q q R ,1(3)?(2);54(1)),/(/44)(),/(9)(+='-='求总成本函数和利润函数.万元已知固定成本为当产量为多少时利润最⼤万台时利润的变化量万台增加到试求当产量由其中产量万台万元成本函数为万台万元假设某产品的边际收⼊函数为以万台为单位.边际讲解注意:例70.02,10%,,100000,130000)(,.10%,1000000t e t 则决如果新增销售额产⽣的利润超过⼴告投资的美元的⼴告活动对于超过按惯例⾏⼀次类似的总成本为以⽉为单位下式的增长曲线⼴告宣传期间⽉销售额的变化率近似服从如根据公司以往的经验平均利润是销售额的美元某出⼝公司每⽉销售额是美元的⼴告活动.试问该公司按惯例是否应该做此⼴告.1000000公司现在需要决定是否举定做⼴告讲解注意:8例.2,318)(-=CS q q D 并已知需求量为如果需求曲线为个单位试求消费者剩余,表⽰某国某年国民收⼊在国民之间分配的劳伦茨曲线可近似地由讲解注意:第七节⼴义积分1、内容分布图⽰★⽆穷限的⼴义积分★⽆穷限的⼴义积分⼏何解释★例1★例2★例3★例4★例5★例6★⽆界函数的⼴义积分例7★例8★例9★例10★例11★例12★例13★内容⼩结★课堂练习★习题5-7★返回★2、讲解注意:3、重点难点:4、例题选讲:例1?∞+-0.dx e x 计算⽆穷积分讲解注意:例2.sin 0的收敛性判断⽆穷积分∞+xdx讲解注意:例312?∞+∞-+x dx计算⼴义积分讲解注意:例4计算⼴义积分.1sin 12∞+dx x x 2/π讲解注意:例5计算⼴义积分∞+-pt dt e 且0>p 时收敛p 是常数,(). t 0讲解注意:例6证明⼴义积分∞+11dxx p当1>p 时收敛当1≤p 时发散.,讲解注意:例7计算⼴义积分).0(022>-?a x a dxa讲解注意:例8证明⼴义积分11dx x q当1""讲解注意:例9计算⼴义积分.ln 21x dx讲解注意:例10计算⼴义积分.30dx1=x 瑕点)1(2/3-x .讲解注意:例11计算⼴义积分?∞+03+x x dx1().讲解注意:例12.)1(arcsin 10-dx x x x计算⼴义积分讲解注意:例13.11105?∞+++x x x dx 计算⼴义积分讲解注意:。
高等数学第05章 定积分及其应用习题详解

0
x 1 sin tdt 0dt 1 , 2
b a
f ( x)dx 在 几 何 上 表 示 由 曲 线 y f ( x) , 直 线
x a, x b 及 x 轴所围成平面图形的面积. 若 x a, b时,f ( x) 0, 则 b f ( x)dx 在几何 a
上表示由曲线 y f ( x) ,直线 x a, x b 及 x 轴所围平面图形面积的负值. (1)由下图(1)所示, 1 xdx ( A1 ) A1 0 .
n
2
i
i 1
n
2
1 1 1 1 1 n(n 1)(2n 1) = (1 )(2 ) 3 n 6 6 n n 1 1 2 当 0时 (即 n 时 ) ,由定积分的定义得: x d x = . 0 3
= 5. 利用定积分的估值公式,估计定积分
4 3
1 1
(4 x 4 2 x 3 5) dx 的值.
上任取一点 i 作乘积 f ( i ) xi 的和式:
n
f ( i ) xi c ( xi xi1 ) c(b a) ,
i 1 i 1
n
n
记 max{xi } , 则
1i n
b a
cdx lim f ( i ) xi lim c(b a) c(b a) .
x
0
(t 1)dt ,求 y 的极小值
解: 当 y x 1 0 ,得驻点 x 1 , y '' 1 0. x 1 为极小值点, 极小值 y (1)
( x 1)dx - 2
定积分的几何应用

定积分的几何应用定积分是微积分中的重要概念,它有着广泛的应用。
其中之一就是在几何学中的应用。
本文将探讨定积分在几何学中的具体应用,并解释其背后的原理和意义。
一、平面图形的面积通过定积分,我们可以计算出复杂平面图形的面积。
假设有一个曲线方程y=f(x),该曲线与x轴所围成的图形为A。
我们可以将A分解成无限个极小的矩形条,然后通过求和的方式来逼近A的面积。
具体而言,我们可以将横轴x划分为n个小区间,每个小区间的宽度为Δx。
然后,在每个小区间中,选择一个x值作为代表点,记作xi。
根据代表点xi和函数f(x)的值,我们可以计算出相应小矩形的高度为f(xi)。
由于每个小矩形的宽度Δx非常小,因此在计算总面积时,可以通过求和的方式逼近。
即可以得到如下的定积分表达式:A = ∫[a,b] f(x) dx其中[a,b]表示x的取值范围。
通过对上述定积分进行求解,即可得到图形A的面积。
二、曲线的弧长除了计算平面图形的面积外,定积分还可以用来计算曲线的弧长。
假设有一个曲线L,其方程为y=f(x)。
我们希望计算出曲线L的弧长。
与计算面积类似,我们同样可以将曲线L分解为无限个极小的线段,然后通过求和的方式来逼近曲线L的弧长。
具体而言,我们可以将横轴x划分为n个小区间,每个小区间的宽度为Δx。
然后,在每个小区间中,选择一个x值作为代表点,记作xi。
根据代表点xi和函数f(x)的值,我们可以计算出相应线段的长度为Δs。
同样地,由于每个小线段的长度Δs非常小,因此在计算总弧长时,可以通过求和的方式逼近。
即可以得到如下的定积分表达式:L = ∫[a,b] √(1 + [f'(x)]^2) dx其中[a,b]表示x的取值范围,f'(x)表示函数f(x)的导数。
通过对上述定积分进行求解,即可得到曲线L的弧长。
三、体积与质量除了平面图形的面积和曲线的弧长外,定积分还可以用来计算体积和质量。
当我们需要计算一个曲线绕某个轴旋转一周所形成的立体的体积时,定积分就派上用场了。
定积分的几何应用课件

电场中的电势
总结词
定积分可计算电场中的电势
详细描述
在静电场中,电势差与电场强度成正比。通过定积分可以计算出 某一点处的电势,即对电场强度进行积分。
公式表示
电势 = ∫E·dl
05
定积分的近似计算
方法
矩形法
总结词
矩形法是一种简单直观的定积分近似计算方法,通过将积分 区间划分为若干个小的矩形,然后求和来逼近定积分。
详细描述
辛普森法则是梯形法的一种改进,它考虑了函数在积分区间的整体变化趋势,将 积分区间分成若干个小的子区间,然后在每个子区间上应用梯形法来逼近定积分 。辛普森法则的精度比矩形法和梯形法更高,但计算量也相对较大。
THANKS
感谢您的观看
3
曲边三角形面积的近似计算
在无法直接计算定积分的情况下,可以使用近似 方法计算曲边三角形的面积,如矩形法、梯形法 等。
任意图形的面积
任意图形面积的计算
01
通过定积分计算任意图形的面积,首先需要找到图形的边界曲
线表达式,然后确定上下限,最后计算定积分。
任意图形面积的几何意义
02
任意图形面积表示的是边界曲线围成的平面区域面积。
详细描述
矩形法的基本思想是将积分区间分成若干个小的矩形,每个 矩形的宽度为小区间的宽度,高度为函数在相应小区间的平 均值。然后,将这些矩形的面积加起来,得到的就是定积分 的近似值。
梯形法
总结词
梯形法是一种基于几何直观的定积分近似计算方法,通过将积分区间划分为若干个小的梯形,然后求 和来逼近定积分。
围绕旋转轴旋转的平面图形被称为 旋转面。
旋转体的体积公式
圆柱的体积公式
V = πr²h,其中r是底面半径,h是高。
定积分在几何上的应用

定积分在几何上的应用
定积分就是求函数f(X)在区间[a,b]中图线下包围的面积。
即由y=0,x=a,x=b,y=f(X)所围成图形的面积。
这个图形称为曲边梯形,特例是曲边三角形。
绕x轴旋转体体积公式是V=π∫[a,b]f(x)^2dx。
绕y轴旋转体积公式同理,将x,y互换即可,
V=π∫[a,b]φ(y)^2dy。
或者是V=2π∫[a,b]y*f(y)dy,也是绕x轴旋转体积。
绕x轴旋转体的侧面积为A=2π∫[a,b]y*(1+y'^2)^0.5dx,其中y'^2是y对x的导数的平方。
若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。
一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
几何,就是研究空间结构及性质的一门学科。
它是数学中最基本的研究内容之一,与分析、代数等等具有同样重要的地位,并且关系极为密切。
几何学发展历史悠长,内容丰富。
它和代数、分析、数论等等关系极其密切。
第五章 定积分的几何应用

) ( r r
d
例 5
求双纽线 a cos 2 所围平面图形
2 2
的面积.
解 由对称性知总面 积=4倍第一象限 部分面积
A 4A1
y x
2 a 2 cos 2
A 40
4
1 2 a cos 2d a 2 . 2
例 6 求心形线r a(1 cos )所围平面图形的 面积 (a 0).
小结
求在直角坐标系下、参数方程形式 下、极坐标系下平面图形的面积. 求旋转体的体积
(注意恰当的选择积分变量有助于简化 积分运算)
思考题
1. 设 曲 线 y f ( x ) 过 原 点 及 点( 2,3) , 且 f ( x ) 为单调函数,并具有连续导数,今在曲线 上任取一点作两坐标轴的平行线,其中一条平 行线与 x 轴和曲线 y f ( x ) 围成的面积是另一 条平行线与 y 轴和曲线 y f ( x ) 围成的面积的 两倍,求曲线方程.
练习题答案 32 一、1、1; 2、 ; 3、2; 3 1 1 4、y ; 5、 e 2 ; 6、 . e 2 3 7 2 二、1、 ln 2 ; 2、 ; 3、 a ; 2 6 5 3 2 2 4、3a ; 5、 ; 6、 a . 2 4 9 e 8 2 三、 . 四、 . 五、 a . 4 2 3
其上相应的窄条左、右曲边分别为 1 2 x y ,x y4 2 4 1 2 A ( y 4 y )dy 18 2 2
由此可见在面积计算中应根据平面区域的具体 特征恰当地选择积分变量找出相应的面积微元可使 计算简化
上述问题的一般情况是
d
y
x ( y)
定积分在几何中的应用
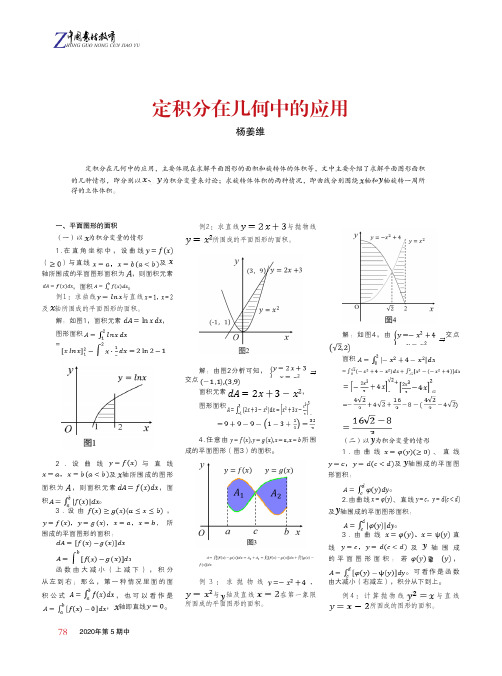
782020年第 5 期中定积分在几何中的应用杨姜维一、平面图形的面积(一)以为积分变量的情形1.在直角坐标中,设曲线()与直线及轴所围成的平面图形面积为,则面积元素,面积。
例1:求曲线与直线及轴所围成的平面图形的面积。
解:如图1,面积元素,图形面积=2.设曲线与直线及轴所围成的图形面积为,则面积元素,面积。
3.设由,所围成的平面图形的面积:函数由大减小(上减下),积分从左到右;那么,第一种情况里面的面积公式,也可以看作是,轴即直线。
例2:求直线与抛物线所围成的平面图形的面积。
解:由图2分析可知,交点面积元素,图形面积4.任意由所围成的平面图形(图3)的面积。
例3:求抛物线,与轴及直线在第一象限所围成的平面图形的面积。
解:如图4,由交点面积+(二)以为积分变量的情形1.由曲线、直线及轴围成的平面图形面积:。
2.由曲线、直线及轴围成的平面图形面积:。
3.由曲线直线及轴围成的平面图形面积:若,。
可看作是函数由大减小(右减左),积分从下到上。
例4:计算抛物线与直线所围成的图形的面积。
定积分在几何中的应用,主要体现在求解平面图形的面积和旋转体的体积等,文中主要介绍了求解平面图形面积的几种情形,即分别以为积分变量来讨论;求旋转体体积的两种情况,即曲线分别围绕轴和轴旋转一周所得的立体体积。
JIAO HAI TAN HANG/教海探航解:如图5,由交点为方便计算,选取为积分变量,则有4.任意由曲线直线及轴围成的平面图形面积:。
二、旋转体的体积一个平面图形围绕其所在平面上的一条直线旋转一周而成的立体即为旋转体,常见的旋转体有圆柱体、圆锥、圆台、球体等,这些都有对应的体积公式,面对日常生活中所用到的水杯、花瓶等立体物件,求解体积时可考虑以下情况:(一)曲线绕轴旋转的情形由连续曲线与直线及轴所围成的曲边梯形绕轴旋转一周而成的立体,选为积分变量,该旋转体的体积元素,体积为。
(二)曲线绕轴旋转的情形由曲线、直线及轴围成的平面图形绕轴旋转一周所得的立体,选为积分变量,该旋转体的体积元素,体积为。
定积分在几何计算中的应用

定积分在几何计算中的应用定积分是高等数学中的一个重要概念,它在几何计算中有着广泛的应用。
在几何学中,定积分可以用来计算曲线的长度、曲面的面积、体积等等。
下面我们就来看看定积分在几何计算中的应用。
定积分可以用来计算曲线的长度。
对于一条曲线,我们可以将其分成无数个小段,然后对每个小段的长度进行求和,最终得到整条曲线的长度。
这个过程可以用定积分来表示,即:L = ∫a^b √(1+(dy/dx)^2) dx其中,a和b分别表示曲线的起点和终点,dy/dx表示曲线在每个点的斜率。
这个式子的意义是,将曲线分成无数个小段,每个小段的长度为√(1+(dy/dx)^2) dx,然后对所有小段的长度进行求和,最终得到整条曲线的长度。
定积分可以用来计算曲面的面积。
对于一个曲面,我们可以将其分成无数个小面元,然后对每个小面元的面积进行求和,最终得到整个曲面的面积。
这个过程可以用定积分来表示,即:S = ∫∫D √(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy其中,D表示曲面的投影区域,z表示曲面在每个点的高度,∂z/∂x和∂z/∂y分别表示曲面在每个点在x和y方向上的斜率。
这个式子的意义是,将曲面分成无数个小面元,每个小面元的面积为√(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy,然后对所有小面元的面积进行求和,最终得到整个曲面的面积。
定积分可以用来计算体积。
对于一个立体图形,我们可以将其分成无数个小体元,然后对每个小体元的体积进行求和,最终得到整个立体图形的体积。
这个过程可以用定积分来表示,即:V = ∫∫∫E dxdydz其中,E表示立体图形的空间区域。
这个式子的意义是,将立体图形分成无数个小体元,每个小体元的体积为dxdydz,然后对所有小体元的体积进行求和,最终得到整个立体图形的体积。
定积分在几何计算中有着广泛的应用,可以用来计算曲线的长度、曲面的面积、体积等等。
这些应用不仅在数学中有着重要的意义,也在实际生活中有着广泛的应用,例如在建筑设计、工程计算等领域中都有着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五讲 定积分的几何应用教学目的要求:基本掌握定积分的元素法,会用定积分计算平面图形的面积,两类特殊 几何体的体积以及平面曲线的弧长。
知识点:定积分的元素法;平面图形面积的计算;旋转体体积的计算;截面面积已知的 几何体体积的计算;平面曲线弧长的计算。
教学重点:定积分的元素法;平面图形面积的计算,旋转体体积的计算。
教学难点: 定积分的元素法; 截面面积已知的几何体体积的计算; 平面曲线弧长的计算。
教学方式:讲授、演示、练习教学思路:先讲授定积分的元素法,由此导出平面图形的面积、两种特殊几何体体积以 及平面曲线弧长等积分计算公式,再以实例说明公式的运用。
教学过程:一、复习1.定积分的几何意义;2.定积分的定义。
二、新授(一)定积分的元素法一般地,如果某一实际问题中的所求量U 符合下列条件:(1)U 是与一个变量x 的变化区间[a , b ]有关的量;(2)U 对于区间[a , b ]具有可加性,即,如果把区间[a ,b ]分成许多部分区间,则U 相应 地分成许多部分量,而 U 等于所有部分量之和;(3)部分量 i U D 的近似值可表示为 () i i f x x D ;那么,就可考虑用定积分来表示这个量 U ,通常用如下方法(微元法或元素法)来建立 所求量 U 的积分式:(1)根据问题的具体情况,选取一个变量作积分变量,并确定其变化区间[a , b ];(2) 在区间[a , b ]上任取一个小区间[,] x x dx + , 并求出相应于这个小区间的部分量 U D 的近似值。
如果 U D 的近似值可以表示成某连续函数在x 处的值 () f x与dx 的乘积,就把 () f x dx 称为 U 的元素(或微元),且记作 dU ,即 () dU f x dx = ;(3)在整个区间[a , b ]上以U 的元素(或微元) () f x dx 为被积表达式求积分,就得所 求的量: () ba U f x dx = ò 。
(二)平面图形的面积1.直角坐标系中平面图形的面积设 () f x , () g x 均为[a , b ]上的连续函数, 且 ()() f x g x £ , 则由曲线 () y f x = , () y g x = , x a = ,x b = 所围成的平面图形面积(由元素法推出)为(()()) b aA g x f x dx =- ò 一般,若去掉 ()() f x g x £ 的条件,则应有 ()() ba A f x g x dx =- ò 。
类似地,若平面图形由曲线, () x y j = , () x y y = , y c = , y d = 围成,则其面积为()() dc A y y dy j y =- ò 例 1 求由曲线 2 y x = , y x = 所围成的面积。
解:作图 3 如右,易求出两曲线交点坐标为 O (0,0)及 P (1,1),由上述公式知,所求面积为 1 2 0 1 () 3A x x dx =-= ò 。
例 2 求由抛物线 2 2 y x = 和曲线 4 y x =- 所围成的面积。
解: 2 2 y x = 与 4 y x =- 的交点坐标为 P (2,-2)及 Q (8,4)。
取 y 为积分变量,则所求面积为 242 [4]18 2 y A y dy - =+-= ò 。
若取x 为积分变量,则 2802 [2(2)][2(4)]18 A x x dx x x dx =--+--= òò 计算较繁。
这说明,应适当选择积分变量,使计算简单。
例 3 求椭圆 2222 1 x y a b+= 所围成的图形的面积 解:因为椭圆关于坐标轴都对称(图 5),所以所求面积等于图中阴影部分面积的 4倍,即有 0 aA ydx = ò ,利用椭圆的参数方程 cos sin x a t y b t = ì í = î ,代入上式中相当于作变量代换。
此时 sin dx a tdt =- ,当 0 x = 时, 2 t p =;当x a = 时, 0 t = ,所以 0 2sin (sin )A b t a t dt ab p p =-= ò 一般地,当曲边梯形面积为 () b a A f x dx = ò 时,若 () y f x = 的参数方程为 ()() x t y t j y = ì í = î,且 (),() a b j a j b == ,则 ()() A t t dt ba y j ¢ = ò 。
2.极坐标系中平面图形的面积设曲线由极坐标方程 () r r q = 表示,求由此曲线 () r r q = 及两射线q a = ,q b = 所围图 形的面积(图 6),其中 () r q 在[,] a b 上连续,且 ()0 r q ³ 。
用元素法,在[,] a b 中任取一个小角区间[,] d q q q + 。
与这个小区间d q 对应的那部分 面积记为dA (图中阴影部分)。
dA 近似地用半径 () r r q = ,中心角为d q 的扇形面积代替, 即 2 1 () 2dA r d q q = 从而有 2 1 () 2 A dA r d b b a aq q == òò 。
例 4 求心形线 (1cos ) r a q =+ 所围成的面积。
解:如图 7 所示,此图形关于极轴对称,用 A 1 表示极轴上方那部分面积(图中阴影部 分),则所求面积为222 1 0 13 22(1cos ) 22A A a d a p q q p ==×+= ò 例 5 求由圆 2sin r q = 和双纽线 2 cos2 r q = 所围成的公共部分的面积A (图 8)。
解:由对称性,只需求出第一象限部分OBPCO 的面积。
由 2sin r q = 及 2 cos2 r q = 得 6 p q = ,故得两曲线在第一象限的交点 P 的极坐标是 2 (,) 26P p ,于是 2 64 0 6 11 22sin cos2 22 1 (333) 6A d d p p p q q q q p æö =+ ç÷ èø=+- òò (三)立体的体积1.旋转体的体积(1)旋转体的概念:一个平面图形绕这平面内一条直线旋转一周而成的立体。
这条直 线叫做旋转轴。
(2)旋转体体积公式:由微元法推出,由连续曲线 () y f x = ,直线 , x a x b == (a b < ) 及x 轴所围成的曲边梯形绕x 轴旋转一周而成的立体的体积为2 () b a V f x dx p = ò (*)而由 () x g y = ,y c = ,y d = (c d < )及 y 轴围成的曲边梯形绕 y 轴旋转一周而成的 立体体积为2 () d cV g y dy p = ò (**) 曲边梯形绕y 轴旋转而形成的几体体积为2 b a A xydx p = ò (***)例 6 求由椭圆 2222 1 x y a b+= 所围成的图形分别绕x 轴及y 轴旋转而成的旋转体的体积。
解:先计算绕 x 轴旋转所得的体积V 1,该体积可以看成是由上半椭圆 22b y a x a=- 及 x 轴围成的图形绕 x 轴旋转而成的立体,由公式(*)得2222 1 4 () 3a ab V a x dx ab a p p - =-= ò 再计算绕y 轴旋转而成的体积 V 2。
右半椭圆的方程为 22 a x b y b =- ,由公式(**)得 2222 1 4 () 3bb a V b y dy a b b p p - =-= ò 例 7 计算由摆线 (sin ) x a t t =- , (1cos ) y a t =- 的一拱及 0 y = 所围成的图形分别绕x 轴、y 轴旋转而成的旋转体体积。
解:由公式(*),所述图形绕x 轴旋转而成的立体体积为22 22223 1 00 (1cos )(1cos )5 a V y dx a t a t dt a p p p p p ==-×-= òò 由公式(***)所述图形绕y 轴旋转而成的立体体积为 22 33 2 0022(sin )(1cos )(1cos )6 a V xydx a t t a t a t dt a p p p p p ==-×-×-= òò 2.平行截面面积为已知的立体体积设某立体夹在过点x a = ,x b = 且垂直于x 轴的两个平面之间(a b < )(图 12),又设 过点 x 且垂直于x 轴的截面面积为 A (x ), [,] x a b Î ,取 x 为积分变量,其变化区间为[a ,b ], 立体中相应于任一小区间[,] x x dx + 的薄片的体积,近似于 () A x dx ,即 () dA A x dx = ,所以 整个立体体积为 () ba A A x dx = ò 。
例 8 求以半径 R 的圆为底,平行底面且等于底圆直径的线段为顶,高为 h 的正劈锥体 的体积。
解:取底圆所在的平面为xOy 平面,圆心 O 为原点,并使x 轴与正劈锥体的顶平行, 底圆的方程为 222 x y R += ,过x 轴上的点x ( R x R -££ )作垂直于x 轴的平面,截正劈 锥体得等腰三角形的截面。
这截面的面积为 22 () A x h y h R x =×=- ,于是所求正劈锥体体 积为 2 22 () 2R R R R R h V A x dx h R x dx p -- ==-= òò 。
例 9 一平面经过半径为 R 的圆柱体的底圆中心,且与底面的夹角为a ,计算这平面截 圆柱体所得立体的体积。
解:取这平面与圆柱体的底面的交线为x 轴,底面上过圆心,且垂直于x 轴的直线为y 轴。
那么,底圆的方程为 222 x y R += ,立体中过点 x 且垂直于 x 轴的截面是一个直角三角 形,它的两条直角边的长度分别为 y 及 tan y a ,即 22 R x - 及 22 tan R x a - ,因而截面面 积为 22 1 ()()tan 2A x R x a =-× ,所求立体体积为 223 12 ()tan tan 23 RR A R x dx R a a - =-= ò(四)平面曲线的弧长1.平面曲线弧长的概念 设 A ,B 是曲线弧上的两个端点在弧 » AB 上任取分点 A =M 0,M 1,…,M n 1,M n =B ,并 依次连接相邻的分点得一内接折线,当分点的个数无限增加且每个小弧段都缩向一点时,如果此折线的长 1 1 , ni i i M M - = å 的极限存在,则称此极限为曲线弧 » AB 的弧长,并称此曲线弧 » AB是可求长的。
