[工学]第四章 杆单元和梁单元
有限元单元的选择

单元类型的选择单元类型的选择,跟你要解决的问题本身密切相关。
在选择单元类型前,首先你要对问题本身有非常明确的认识,然后,对于每一种单元类型,每个节点有多少个自由度,它包含哪些特性,能够在哪些条件下使用,在ANSYS的帮助文档中都有非常详细的描述,要结合自己的问题,对照帮助文档里面的单元描述来选择恰当的单元类型。
1.该选杆单元(Link)还是梁单元(Beam)?这个比较容易理解。
杆单元只能承受沿着杆件方向的拉力或者压力,杆单元不能承受弯矩,这是杆单元的基本特点。
梁单元则既可以承受拉,压,还可以承受弯矩。
如果你的结构中要承受弯矩,肯定不能选杆单元。
对于梁单元,常用的有beam3,beam4,beam188这三种,他们的区别在于:1)beam3是2D的梁单元,只能解决2维的问题。
2)beam4是3D的梁单元,可以解决3维的空间梁问题。
3)beam188是3D梁单元,可以根据需要自定义梁的截面形状。
2.对于薄壁结构,是选实体单元还是壳单元?对于薄壁结构,最好是选用shell单元,shell单元可以减少计算量,如果你非要用实体单元,也是可以的,但是这样计算量就大大增加了。
而且,如果选实体单元,薄壁结构承受弯矩的时候,如果在厚度方向的单元层数太少,有时候计算结果误差比较大,反而不如shell 单元计算准确。
实际工程中常用的shell单元有shell63,shell93。
shell63是四节点的shell单元(可以退化为三角形),shell93是带中间节点的四边形shell单元(可以退化为三角形),shell93单元由于带有中间节点,计算精度比shell63更高,但是由于节点数目比shell63多,计算量会增大。
对于一般的问题,选用shell63就足够了。
除了shell63,shell93之外,还有很多其他的shell单元,譬如shell91,shell131,shell163等等,这些单元有的是用于多层铺层材料的,有的是用于结构显示动力学分析的,一般新手很少涉及到。
杆单元和梁单元

(3)形函数矩阵的推导 由单元的节点条件, 两个节点坐标为x1、x2,两个节点位移 u 为u( x) |x x u1, ( x) |xx u2 ,代入上式插值模式公式得: a1 a2 x1 u1
1
2
a1 a2 x2 u2
求解得到
a1 u1 x1 (u1 u2 ) /( x1 x2 ) a2 (u1 u2 ) /( x1 x2 )
u dN ( x) u1 1 ( x) e x dx u2 l u1 1 u1 B e l u2 u2
(4.6)
(4.7)
(5)应力 由弹性力学的物理方程知:
Ee ( x) E e B ( x) δ e S ( x) δ e e l E e u1 e u2 l
δ (1)
u1 u2
K
(1)
E (1) A(1) (1) l
1 1 1 1
P
(1)
R1 R2
4.1 杆件系统的有限2)
u2 u3
(1) (2)
K
(2)
E (2) A(2) l (2)
u 2 , u3
(9)建立系统弹性方程
u2
u3
E (1) A(1) E (2) A(2) l (1) l (2) R2 = F3 E (2) A(2) (2) l
E (2) A(2) (2) u2 l (2) (2) E A u3 l (2)
u1
1 单元1 2
E2 , A2 , l2
u2
单元2 3
岩土工程数值分析试卷试题及参考(附答案)

岩土工程数值分析试题一、简答题(40分)1.简述梁单元、杆单元、连续梁单元、平面三角形常量单元和四边形等参单元的特点(10分)。
答:1)梁单元是由两个节点组成,每一个节点都具有三个方向的线性移动位移和三个方向的旋转位移,因而每个节点具有6个自由度,梁单元具有拉,压,剪,弯,扭的变形刚度。
计算理论成熟,建模方便,计算量小,在工程结构有限元分析中得到广泛的应用,适用于各种截面形式的杆件分析。
2)由有限个构件以一定方式连接起来所形成的结构,在同一平面内的杆系结构,其所受的外力作用线位于该平面内,在杆系中,每一个杆件可视为一个单元,每个单元的端点成为结点。
3)对于每跨各自等截面的连续梁,以每跨为一个单元。
结点编号和单元编号一般是从连续梁的左端顺序编到右端。
由于连续梁各单元的轴线方向一致,各单元坐标系与结构坐标系的方向相同,因此在矩阵位移法的计算过程中无须进行坐标变换,在单元坐标系和结构坐标系中单元刚度矩阵的表达式是相同的。
4) 平面三角形单元具有适应性强的优点,较容易进行网络划分和逼近边界形状,应用比较灵活。
其缺点是它的位移模式是线性函数,单元应力和应变都是常数,精度不够理想。
5) 四边形等参单元能更好地反映物体内的应力变化,适应曲线边界,常使用于弹性力学平平面问题的分析。
八结点单元一共有16个已知的结点位移分量。
2.除有限单元法外,岩土工程常用到哪些数值方法,并对比其优缺点(10分)。
答:岩土工程常用的数值方法包括:有限差分法、边界元法、离散元法、颗粒元法、不连续变形分析法、流形元法、模糊数学方法、概率论与可靠度分析方法、灰色系统理论、人工智能与专家系统、神经网络方法、时间序列分析法。
有限单元法的优缺点:有限单元法的理论基础是虚功原理和基于最小势能的变分原理,它将研究域离散化,对位移场和应力场的连续性进行物理近似。
有限单元法适用性广泛,从理论上讲对任何问题都适用,但计算速度相对较慢。
即,物理概念清晰、灵活、通用、计算速度叫慢。
杆梁结构有限元分析
3.1 杆梁结构的直接解法
机械分社
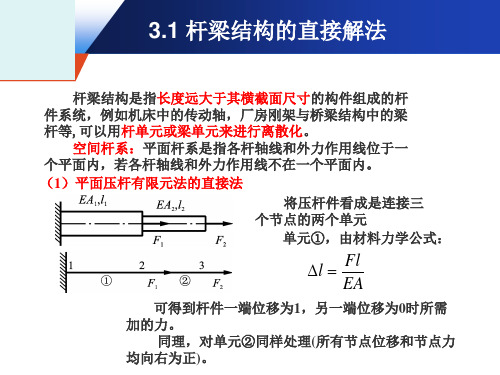
(1)平面压杆有限元法的直接法
由节点平衡有: 即有:
U1(1)u1 U1(1)u2 N1
U
u (1)
21
(U
(2 2
)
U
(1) 2
)u2
U
(2 2
)u3
F1
U
(2 3
)
u2
U
(2 3
)
u3
F2
EA1 l1
u1
EA1 l1
u2
N1
EA1 l1
u1
( EA1 l1
3.1 杆梁结构的直接解法
机械分社
杆梁结构是指长度远大于其横截面尺寸的构件组成的杆 件系统,例如机床中的传动轴,厂房刚架与桥梁结构中的梁 杆等,可以用杆单元或梁单元来进行离散化。
空间杆系:平面杆系是指各杆轴线和外力作用线位于一 个平面内,若各杆轴线和外力作用线不在一个平面内。 (1)平面压杆有限元法的直接法
单元刚度矩阵每一列元素表示一组平衡力系,对于平面 问题,每列元素之和为零。
3.1 杆梁结构的直接解法
机械分社
(2)平面梁单元有限元法的直接法 2)节点位移与节点力之间的关系
Ui
Vi
k11
k21
M i U j
k31
k41
V
j
M j
k51
k61
他们在轴和轴的投影之和等于零:
vi
6EI l2
i
12EI l3
vj
6EI l2
j
M
j
6EI l2
vi
2EI l
i
6EI l2
vj
4EI l
梁单元定义

关于LSDYNA中离散梁(discrete beam)使用的一些说明一个离散梁(6号梁单元)最多有6 个自由度,而弹簧单元(*element_discrete)只有一个自由度,离散梁单元的内力在局部坐标系(r,s,t)中输出,包括在d3plot,d3thdt和elout文件中。
离散量单元可以是0长的也可以是非0长的。
必须指定一个非0值的体积(通过*SECTION_DISCRETE中的VOL参数),离散量的重量和它的长度没有关系,而只是体积VOL和材料密度的乘积。
INER是梁关于它三个轴的质量矩,如果它的任意一个旋转自由度被激活就必须指定一个非0的INER值。
CA和OFFSET仅针对索(使用材料*MAT_CABLE_DISCRETE_BEAM)。
当使用970v6763(或者后继版本)时,索的体积在VOL 设置为0的时候会自动计算为长度与*CABLE 面积的乘积。
可使用的材料类型为:*MAT_USER_DEFINED_MATERIAL_MODELS*MAT_66 (*MAT_LINEAR_ELASTIC_DISCRETE_BEAM)*MAT_67 (*MAT_NONLINEAR_ELASTIC_DISCRETE_BEAM)*MAT_68 (*MAT_NONLINEAR_PLASTIC_DISCRETE_BEAM)*MAT_69 (*MAT_SID_DAMPER_DISCRETE_BEAM)*MAT_70 (*MAT_HYDRAULIC_GAS_DAMPER_DISCRETE_BEAM)*MAT_71 (*MAT_CABLE_DISCRETE_BEAM)最新添加的类型有:*MAT_74 (*MAT_ELASTIC_SPRING_DISCRETE_BEAM)(注)*MAT_93 (*MAT_ELASTIC_6DOF_SPRING_DISCRETE_BEAM)<-- 同时需要*MAT_74*MAT_94 (*MAT_INELASTIC_SPRING_DISCRETE_BEAM)*MAT_95 (*MAT_INELASTIC_6DOF_SPRING_DISCRETE_BEAM) <-- 同时需要o*MAT_94*MAT_97 (*MAT_GENERAL_JOINT_DISCRETE_BEAM) <--同时需要任意6 DOF类型*MAT_119 (*MAT_GENERAL_NONLINEAR_6DOF_DISCRETE_BEAM)*MAT_121 (*MAT_GENERAL_NONLINEAR_1DOF_DISCRETE_BEAM)*MAT_146 (*MAT_1DOF_GENERALIZED_SPRING) <-- 使用*ELEMENT_BEAM中的SCALAR 或者SCALR 选项*MAT_196 (*MAT_general_spring_discrete_beam) <-- 也可选*MAT_74,93,94,95中任一种,包含单独的拉伸和压缩失效准则。
《杆单元和梁单元》课件

当前研究的主要成果
经过多年的研究,杆单元和梁单元在理论建模、数值计算和实验验证等方面取得了许多重 要成果,为工程实际提供了有力支持。
面临的主要挑战
尽管杆单元和梁单元的研究已经取得了很大进展,但仍存在一些挑战,如提高计算精度、 处理复杂边界条件和适应大规模计算等。
动力响应
研究杆件在受到瞬态或周期性动力作用下的响应,如地震、风载等 自然灾害作用下的结构动力响应。
杆单元的稳定性分析
失稳判据
根据不同的失稳形式,如弯曲失 稳、剪切失稳等,采用相应的失 稳判据进行稳定性分析。
临界荷载
求解使杆件达到临界状态的荷载 ,即临界荷载,用于评估结构的 稳定性。
稳定性设计
根据稳定性分析结果,采取相应 的设计措施,如增加支撑、改变 截面形状等,以提高结构的稳定 性。
平衡方程
根据力的平衡原理,建立梁单元的平衡方程。
弯曲变形
考虑梁的弯曲变形,根据挠曲线近似法或能量法求解弯曲变形。
剪切变形
考虑梁的剪切变形,根据剪切力与剪切位移的关系求解剪切变形。
梁单元的动力分析
运动方程
根据牛顿第二定律和动力学基本原理,建立梁单元的 运动方程。
振动分析
分析梁的自由振动和受迫振动,求解振幅、频率和阻 尼等参数。
杆单元在桥梁工程中的应用
总结词
桥梁工程中广泛应用
详细描述
在桥梁工程中,杆单元被广泛应用于构建桥梁的支撑体系,如钢拱桥的拱肋、 斜拉桥的拉索等。杆单元能够承受拉压、弯曲等多种载荷,提供稳定的支撑作 用,确保桥梁的安全性和稳定性。
梁单元在建筑结构中的应用
总结词
杆梁结构的有限元分析原理
杆梁结构的有限元分析原理杆梁结构是工程中常用的一种结构形式,它由多个杆件或梁组成,用于承担载荷和传递力量。
有限元分析是一种通过将结构离散为许多小单元,利用数学方法对结构进行分析的技术。
下面将详细介绍杆梁结构的有限元分析原理。
一、杆件离散化在有限元分析中,首先需要将杆梁结构离散化为一组子结构,即离散化为一组离散的杆件。
离散后的每个杆件可以看作是一个子系统,每个子系统由两个节点组成,节点之间以杆件连接。
通过节点与杆件的连接方式,能够模拟出整个杆梁结构的受力特点。
离散化的过程中,需要确定杆件的几何形状、截面以及材料特性等参数,并根据实际情况设置合适的杆件单元数目。
通常,单元数目越多,离散程度越高,结果越接近真实情况,但计算成本也会增加。
二、有限元法的基本原理有限元方法的基本原理是将结构分成许多小的单元,每个单元内的行为可以用简单的数学函数来表示。
对于杆梁结构,常用的单元有梁单元和杆单元。
梁单元适用于承受弯曲强度较大的杆件,而杆单元适用于承受轴向载荷的杆件。
通过将结构分成小单元后,可以建立一个与原结构相似的离散模型,并在每个单元上建立相应的方程。
三、应力应变关系在进行有限元分析时,需要获得每个杆件的应变和应力。
应变与杆件的变形有关,而应力与应变之间的关系则与材料的本构关系有关。
对于线弹性材料,应力与应变之间可以通过胡克定律来描述。
胡克定律表明,应力与应变之间成线性关系,材料的弹性模量E、泊松比ν以及应变关系能够决定应力。
应根据结构中不同材料的应变特性来选择相应的材料模型。
四、施加边界条件在进行有限元分析前,需要施加适当的边界条件。
边界条件用于模拟实际情况中的约束和限制。
常见的边界条件有固定边界、弹性边界和施工阶段边界。
五、求解位移和应力当离散化杆梁结构、建立了位移和应变关系、施加了边界条件之后,可以通过数值求解方法,例如有限元法中的坐标变形法,计算得到结构的位移和应力。
坐标变形法能够基于得到的位移结果,进一步计算应力。
杆件系统有限单元法
(3)单元应力场的表达 由弹性力学中物理方程有:
σ e ( x ) = E eε e ( x ) = E e B e ( x ) ⋅ δ e = S e ( x ) ⋅ δ e
其中Se为单元的应力函数矩阵:
⎡ E S ( x) = E B ( x) = ⎢ − ⎣ l
e e e
e
E ⎤ ⎥ l ⎦
平面梁单元的节点位移δe和节点力Fe为:
δ =⎡ ⎣ui vi θi u j v j θ j ⎤ ⎦
e e
T
F =⎡ ⎣ FNi FQi M i FNj FQj M j ⎤ ⎦
相应的刚度方程为:
T
K e ⋅δ e = F e
将杆单元刚度矩阵与纯弯梁单元刚度矩阵进行组 合,可得到平面梁单元的刚度矩阵:
可以写出节点位移向量和节点力向量:
δ =⎡ ⎣ui u j ⎤ ⎦
e
e
T
T ⎡ ⎤ F = ⎣ FNi FNj ⎦
(1)单元位移模式的表达 由于每个节点只有一个轴向位移,即一个单元共有 两个自由度,因此可假设该单元的位移模式为具有 两个待定系数的函数模式:
u ( x ) = a 0 + a1 x
e
第三章
杆件结构的有限元分析 (FEA)
在杆件系统中根据单元受力的特点,我们可以 把它们分成两大类:杆和梁。为了以后描述的 方便,我们把两端铰接,只受轴向力的基本结 构称为杆单元,而受轴向力和弯矩、扭矩、剪 力共同作用的基本结构称为梁单元。
3.1 平面杆单元
局部坐标系中的杆单元描述
设有一任意的杆单元如图所示,i 和j 为单元的两 个结点,x 为该单元的局部坐标,其原点设在单 元的i 结点。设两个结点在x 方向的位移为 u i 和 u j ,它们的正方向如图3-1 所示,与它们相应的 结点力 FN δ e
有限单元法课件第四章 杆件系统的有限元法
(a)
(b)
由杆件组成的结构体系称为杆系,如起重机,桥梁等。
由桁杆组成的杆系称为桁架。
由梁组成的杆系成为刚架。
若杆系和作用力均位于同一平面内,则称为平面桁架 或平面刚架,否则称为空间桁架或空间刚架。
由于杆件结构采用一维单元进行离散,所以杆系的网 格划分容易用半自动方法实现。当采用自动网格划 分方法时,杆系的几何模型是由杆件轴线构成的线框 模型。
R
e P
RiP R jP
R
lP
R
R
e F
RiF R jF
Rlx Rly NlT l R l
lF T l
Px dx (l i, j ) Py
e T
Bj dx
kii k ji
kij k jj
其中矩阵元素为
kst D Bt dx B as 0 EA 0 at 0 0 0 bs dx 0 EI 0 bt ct 0 cs 0 0 EAas at dx 0 EIb b EIb c s t s t EIcs bt EIcs ct 0
e
du dx e x 2 B Bi q x d v dx 2
Bj q
e
其中
ai 0 0 Bi 0 b c i i a j 0 0 Bj 0 b c j j 1 12 6 ai a j bi b j 3 x 2 l l l 4 6 2 6 ci 2 x cj 2 x l l l l
《杆单元和梁单元》课件
2 力学模型
介绍了梁单元的力学模型和计算方法。
3 数学表达式
解释了梁单元的数学表示方法和计算公式。
4 应用案例
展示了梁单元在桥梁、悬臂梁、梁柱结构等 工程中的应用案例。
杆梁单元
1 适用条件
探讨了杆梁单元适用于哪些结构特点的力学 问题。
2 力学模型
介绍了杆梁单元的力学案例
解释了杆梁单元的数学表示方法和计算公式。
展示了杆梁单元在混凝土框架结构、钢结构 等工程中的应用案例。
总结
1 杆单元和梁单元的比 2 杆梁单元的优势和局 3 杆梁单元的应用前景
较
限性
展望了杆梁单元在未来工
总结了杆单元和梁单元的
分析了杆梁单元在工程设
程设计中的应用前景和发
优缺点和适用范围。
计中的优势和限制。
杆单元
1 适用条件
探讨了杆单元适用于哪些结构特点的力学问 题。
2 力学模型
详细描述了杆单元的简化力学模型和假设。
3 数学表达式
解释了杆单元的数学表示方法和计算公式。
4 应用案例
展示了杆单元在桥梁、塔桅、高层建筑等工 程项目中的应用实例。
梁单元
1 适用条件
讨论了梁单元适用于哪些结构特点的力学问 题。
展趋势。
参考资料
提供相关文献和资料的引用以供进一步学习和研究。
《杆单元和梁单元》PPT 课件
本课件介绍了杆单元和梁单元的基本概念和力学模型,以及它们在工程设计 中的应用案例。通过本课件,您将更好地了解这两种单元在结构分析中起到 的作用。
简介
1 杆单元和梁单元是什么?
介绍了杆单元和梁单元的基本定义、特点和用途。
2 力学问题的适用范围
指明了杆单元和梁单元在解决哪些实际力学问题中起到关键作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 单元1 2
u2
E2 , A2 , l2
单元2 3
F3 10N
x
图 4-1 杆件结构
(1)确定坐标系、单元离散,确定位移变量, 外载荷及边界 条件。
4.1 杆件系统的有限元分析方法
要建立两种坐标系:单元坐标系(局部坐标系)、整体坐 标系。根据自然离散, 坐标系建立成一维, 单元划分为两个, 给出相应的节点1、2、3以及相应的坐标值(见图4-1)。在 局部坐标系中,取杆单元的左端点为坐标原点,图4-2为任取 的一个杆单元。
(4.3)
1
导出
1 u1 a1 1 x1 u1 u ( x) [1 x] 1 x N ( x) u2 a2 1 x2 u2 =
得到形函数矩阵(shape function matrix)
x N ( x) (1 ) x2 x1 x x2 x1
δ (1)
u1 u2
K
(1)
E (1) A(1) (1) l
1 1 1 1
P
(1)
R1 R2
4.1 杆件系统的有限元分析方法
第二个单元:
δ
(2)
u2 u3
(1) (2)
K
(2)
E (2) A(2) l (2)
E e u1 e u l 2
(4.8)
(6)利用最小势能原理导出单元刚度矩阵
单元的势能表达式:
4.1 杆件系统的有限元分析方法
e U e W e 1 1 e ( x) ( x)d P 1 2 2 u1 P2 u2 u1 P2 u2
第4章 杆单元和梁单元
本章主要介绍利用杆单元及梁单元进行结构静力学的有限 元分析原理。首先介绍了杆单元的分析方法,详细给出了采用 杆单元进行有限元分析的整个过程;紧接着介绍了平面梁单元 ,以一个平面悬臂梁力学模型为分析实例,分别采用材料力学 、弹性力学解析计算以及有限元法进行了分析与求解,以加深 读者对有限元 ( S ( x)δ ( x)) ( B ( x)δ ( x))A dx P 1 2 0 2 1 eT l e T e e e 1 eT e δ B E BA dxδ P δ 0 2 2
上式记作如下矩阵形式:
1 eT e e 1 eT e δ K δ P δ 2 2
4.1 杆件系统的有限元分析方法
这样,u( x) a1 a2 x 可以写成如下矩阵形式
a1 u ( x) [1 x] a2
u1 1 x1 a1 a u 1 x 2 2 2
a1 1 x1 u1 u a 1 x 2 2 2
P 1 , u1
E,A,l 1
图 4-2 杆单元
P2 , u2
2
对于两个节点的杆单元,存在如下节点力和节点位移的关 系式 u P 1 e 1 (4.1) k
P2
u2
其中, k e 称为单元刚度矩阵
4.1 杆件系统的有限元分析方法
(2)确定位移模式
2 假设单元位移场: u( x) a1 a2 x a3 x a2 可由节点位移 u1、u2确定,称为位 取其线性部分,系数 a1、 移插值模式(interpolation model). (4.2) u( x) a1 a2 x
e
(4.9)
其中,单元刚度矩阵(element stiffness matrix),或称单 元特性矩阵(element characteristic matrix) le E e Ae 1 1 e T e e K B E BA dx e (4.10) 0 l 1 1
(3)形函数矩阵的推导 由单元的节点条件, 两个节点坐标为x1、x2,两个节点位移 u( x) |xx u2 ,代入上式插值模式公式得: 为u( x) |x x u1, a1 a2 x1 u1
1
2
a1 a2 x2 u2
求解得到
a1 u1 x1 (u1 u2 ) /( x1 x2 ) a2 (u1 u2 ) /( x1 x2 )
(4.4)
记节点位移矢量 (nodal displacement vector) 是 u1 e (4.5) δ u 2
4.1 杆件系统的有限元分析方法
因此,用形函数矩阵表达的单元内任一点的位移函数是
u( x) N ( x)δe
(4)应变 由弹性力学的几何方程知1维杆单元满足
4.1 杆件系统的有限元分析方法
杆件只承受轴向力,可以视为一种特殊的梁单元,本节将采 用有限元法来分析杆件系统,以下给出规范的有限元法中关于杆 单元的推导过程,以及整个杆系的求解过程。 如图4-1所示的杆件结构,左端铰支,右端作用一个集中力, 相关参数如图。具体求解过程如下:
E1 , A1 , l1
u dN ( x) u1 1 ( x) e x dx u2 l u1 1 u1 B e l u2 u2
(4.6)
(4.7)
(5)应力 由弹性力学的物理方程知:
e E ( x) E e B ( x) δ e S ( x) δ e e l
4.1 杆件系统的有限元分析方法
根据最小势能原理, e 0 ,得
K e δe P e
其中节点载荷矩阵为
e
(4.11)
P 1 P P2 (7)把所有单元按结构形状进行组集(assembly of discrete elements)
对于图4.1所示结构 第一个单元:
