§3-4转动中的功和能
刚体的定轴转动

J
1 2 m( R12 R2 ) 2
1 mR 2 2 若R1 R2 R, J mR 2
16
例:求长度为L,质量为m的均匀细棒AB的转动惯量。 (1)对于通过棒的一端与棒垂直的轴。 (2)对于通过棒的中心与棒垂直的轴。 m 解(1)细杆为线质量分布,单位长度的质量为: l L 1 3 2 2 dm A B J A x dm x dx L o 0 3 x
2 0
2
0
dm MR
2
绕圆环质心轴的转动惯量为
M
o
R
பைடு நூலகம்dm
J MR
2
讨论:若圆环绕其直径轴转动,再求此圆环的转动 惯量。
14
例: 一质量为m,半径为R的均匀圆盘,求对通过盘 中心并与盘面垂直的轴的转动惯量。
m 解: σ πR 2
dm σ 2π rdr
dJ r dm 2πσ r dr
5
匀变速圆周运动的基本公式
p
1 2 0 0t t 2
0 t
s
R
o
p
x
2 2 0 2 ( 0 )
定轴转动刚体上任一点的速度和加速度 s R 路程与角位移之间的关系:
v R 线速度与角速度的关系:
加速度与角量的关系: 2 dv d v at R R , an 2 R, dt dt R
1
柱壳形状的质元 ,其长为l半径为r厚度为dr, 则该质元的质量为 dm dV ( 2 rdr )l
R2
R2
l
J r dm 2lr dr
2 3 m R1
l
2
初中物理功与能解析

初中物理功与能解析物理学中有两个基本概念,即功和能量。
功被定义为力在物体上所做的功率与位移的乘积,常用符号是W。
能量则是物体或系统在运动中所拥有的做功能力,常用符号是E。
理解和应用功与能的概念对于初中物理学习非常重要。
在本文中,我将对功与能的概念进行解析,并说明其在日常生活中的应用。
一、功的概念和计算公式功定义了力对于位移的作用。
当力F作用于一个物体,使其在线性方向上发生位移s时,力所做的功可以用公式W = F × s来计算。
功的单位是焦耳(J)或牛顿·米(Nm)。
例如,一个力为5牛顿的物体,沿着直线方向移动2米,则所做的功为W = 5 × 2 = 10J。
二、能的概念和种类能量是物体或系统所拥有的做工能力。
在物理学中,能分为多种形式,包括机械能、热能、电能、化学能等。
1. 机械能机械能是物体或系统在运动中所拥有的能量。
它包括动能和势能两种形式。
- 动能:动能是指物体由于其运动而具有的能量。
动能的大小与物体的质量和速度相关,可以用公式K.E. = 1/2mv²来计算,其中m为物体质量,v为物体速度。
动能的单位也是焦耳(J)。
- 势能:势能是指物体由于其位置而具有的能量。
常见的势能包括重力势能和弹性势能。
重力势能可以用公式P.E. = mgh来计算,其中m为物体质量,g为重力加速度,h为物体相对于参考点的高度。
弹性势能可以用公式P.E. = 1/2kx²来计算,其中k为弹簧常量,x为弹簧伸长或压缩的长度。
2. 热能热能是物体或系统内分子运动的能量。
热能的传递是由高温处向低温处通过热传导、热对流或热辐射的方式进行的。
热能的单位也是焦耳(J)。
3. 电能电能是由电荷所携带的能量。
电能主要在电路中以电流的形式进行传输。
电能的单位是焦耳(J)。
4. 化学能化学能是指物质在化学反应过程中所释放或吸收的能量。
当化学键形成或断裂时,会释放或吸收能量。
三、功与能的转化和守恒定律功和能之间存在着转化关系和守恒定律。
刚体的定轴转动

第3章 刚体的定轴转动刚体定轴转动所遵从的力学规律,实际上是质点运动的基本概念和原理在刚体中的应用。
重要的概念有转动惯量和力矩。
刚体的动能和角动量都有其特殊的表达式,但守恒定律同样适用于包括刚体的系统。
§1 刚体的运动一 刚体刚体是固体物件的理想化模型。
实际的固体在受力作用时总是要发生或大或小的形状和体积的改变。
如果在讨论一个固体的运动时,这种形状或体积的改变可以忽略,我们就把这个固体当做刚体处理。
这就是说,刚体是受力时不改变形状和体积的物体。
刚体可以看成由许多质点组成,每一个质点叫做刚体的一个质元,刚体这个质点系的特点是,在外力作用下各质元之间的相对位置保持不变。
既然是一个质点系。
所以关于质点系的基本定律就都可以应用。
当然,由于刚体这一质点系有其特点,所以这些基本定律就表现为更适合于研究刚体运动的特殊形式。
二 刚体的运动形式刚体的运动可以是平动、转动或二者的结合。
如果刚体在运动中,连结体内两点的直线在空间的指向总保持平行,这样的运动就叫平动。
在平动时,刚体内各质元的运动轨迹都一样,而且在同一时刻的速度和加速度都相等。
因此在描述刚体的平动时,就可以用一点的运动来代表,通常就用刚体质心的运动来代表整个刚体的平动。
平动是刚体的基本运动形式之一。
转动也是刚体的基本运动形式之一,它又可分为定轴转动和定点转动。
定轴转动:运动中各质元均做圆周运动,且各圆心都在同一条固定的直线(转轴)上。
定点转动:运动中刚体上只有一点固定不动,整个刚体绕过该定点的某一瞬时轴线转动。
刚体不受任何限制的的任意运动。
它可分解为以下两种刚体的基本运动:随基点(可任选)的平动,绕通过基点的瞬时轴的定点转动。
三 刚体定轴转动的运动学描述刚体的定轴转动是最简单的转动情况。
在这种运动中各质元均做圆周运动,而且各圆的圆心都在一条固定不动的直线上,这条直线叫转轴。
刚体绕某一固定转轴转动时,各质元作圆周运动的轨道半径不同,所以各质元的线速度、加速度一般是不同的。
转动惯量

z
y
J z J x J y
例:
o
1 2 J x J y mR 4
1 2 J x J y 2 J x mR 2
1 J Z mR 2 2
x
四. 转动定律的应用
解题要点
1)受力分析
质点 :根据牛顿第二定律 : F ma 2)列方程: 刚体 :根据转动定律 : M J 无滑动条件 : a R
i i i i
i
i i
i
i
2
i i
M J
--转动定律
三. 转动惯量
1. 转动惯量的物理意义:刚体转动惯性大小的量度。
2. 转动惯量的计算
J mi ri
连续体:
2
J r dm
2
转动惯量与刚体的质量、形状及转动轴有关。
例3-1 计算质量为 m ,长为 l 的细棒绕通过其端点 的垂直轴的转动惯量。 z
E Ek E p C
1 2 质点: E k mv ,E p mgh 2
1 刚体: Ek J 2 ,E p MghC 2
例 3-5 如图,质量为 m,长为 l 的均匀细棒绕过 O 点 的转轴自水平位置以零角速度自由下摆。 ( 1)求细棒 运动到与水平夹角为时的角加速度和角速度; ( 2) 此 时细棒末端 A 的速度和加速度。
R
O r
dm 2 rdr
J 2 r dr
3 0
R
dr
R
2
4
1 2 mR 2
3. 平行轴定理与垂直轴定理
平行轴定理:
Jz
2
J z J c md
例:
Jc
动能定理【高中物理】
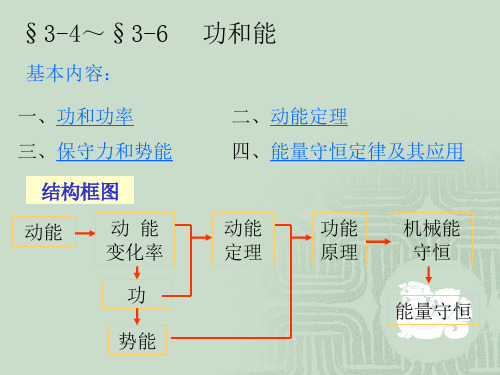
v v0 adt
0
t
0
t
0
F dt m
12t dt 3t 2 0 2
t
W
3
0
12 t 3t 2 dt
3
0
36 t 3 dt 9t 4 729 J
作业:P104 3-13
s’
b
F
④ 合力的功为各分力的功的代数和。 3、功率 力在单位时间内所作的功
dW ( Fi ) d r ( Fi d r ) dWi
W 平均功率: P t
W dW 瞬时功率: P lim t 0 t dt dr dW F d r P F F v dt
当弹簧在水平方向不受外力作用时,它将不 发生形变,此时物体位于点0(即位于x=0处), 这个位置叫做平衡位置 现以平衡位置0为坐标原点,向右为x轴正向。
F kxi
W
k
m
x2
x1
kxdx
1 1 2 2 ( kx2 kx1 ) 2 2
o k F m o x1 m k o F x2
单位:W或Js-1 量纲:ML2T-3
【瓦特(Wate)】
功的其它单位:1eV=1.6×10-19J
例1、一陨石从距地面高为h处由静止开始落向地 面,忽略空气阻力,求陨石下落过程中,万有引 力的功是多少? a 解:取地心为原点,引力与矢径方 h F b 向相反 R R W F dr r Rh
保守力:某些力对质点做功的大小只与质点的始末 位置有关,而与路径无关。这种力称为保守力。
力学第5章刚体的转动

3 g sinθ
L
解二:
M = J
=M
=
mg
L
2
cosθ
J
1 3
mL2
θ
L2
mg L 2
=
3
g cosθ 2L
=
dω
dt
=
dω
dθ
dθ dt
=ω
dω
dθ
ωω
0
dω
=
θβ 0
dθ
= θ 3gcosθ
0 2L
dθ
ω
=
3 g sinθ L
例某冲床上飞轮的转动惯量4.00×103kg·m2.当
它的转速达到 30 r/min时,它的转动动能是多少?
T 1=
m
1(2
m
2
+
m
2
m 1+m 2 +
m
2
)g
T 2=
m
2(2
m
1
+
m
2
m 1+m 2
+
m
2
)g
mr
T1
T2
m1
m2
提问:
若将m2g换成外力 F,且F=m2g,左边的 四个量还是同样的结 果吗?
§4 定轴转动中的功能关系= Fds cos
= Frdθ sinφ
r
F2
r ×F1 只能引起轴的
变形,对转动无贡献。
在定轴动问题中,如不加说明,所指的力 矩是指力在转动平面内的分力对转轴的力矩
二、转动定律
0
Fi 外力, f i 内力 ω
对Δ m i 质点应用牛二律:
fi
ri θ i Δ mi
刚体定轴转动的功和能

(解毕 )
· 10 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
五、刚体的机械能守恒
当系统中只有保守力作功,系统的机械能守恒:
E0 E
其中 E
m ,l
l 2
1 mv 2 1 J 2 2 2
C
mgh 1 kx 2 2
滑轮(R, M),m从静止开始下落,求下落 h 时物体的速 度及加速度。 系统 = 弹簧 + 滑轮 + 物体 + 地球: 提示: 机械能守恒
k
M ,R
2mgh kh 2 答案: v m M / 2
m
2(mg kh) a 2m M
ቤተ መጻሕፍቲ ባይዱ
减速、加速?
h
· 13 ·
Chapter 4. 刚体的转动
三、刚体绕定轴转动的动能定理
W Md
0
M J J d dt
d ω 0 J dt d 0 J d
·4 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
1 1 2 2 积分得: W J J 0 2 2
1 2 [定义] 刚体转动动能: E k J 2 1 1 2 2 W J J 0 E k E k 0 E k 2 2
mg
前例 已知:匀质细杆 (m,l ),光滑轴,从竖直位置静 止摆下,求细杆摆到θ 位置时的角速度。
· 11 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
解:以杆、地球为一系统,则系统机械能守恒:
3-3转动中的功与能,3-4
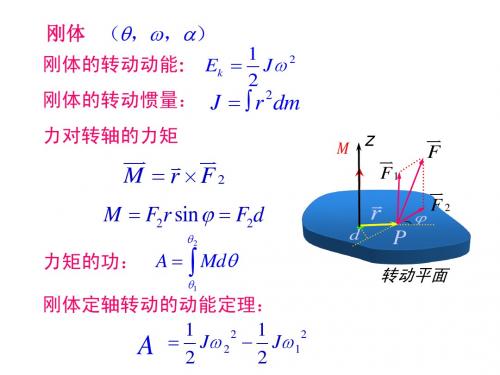
一、角动量定理的微分形式
M z J J d dt d ( J ) dt dLz dt
刚体所受到的对某给定轴的总外力矩等于刚体对该轴的 角动量的时间变化率。 系统对转轴的角动量为: Lz J ii
i
d Mz J ii dt dt i dLz
7
2
3r / s
由于中子星的致密性和极快的自转角速度,在星体周围 形成极强的磁场,并沿着磁轴的方向发出很强的无线电波、 光或X射线。当这个辐射束扫过地球时,就能检测到脉冲信号 ,由此,中子星又叫脉冲星。目前已探测到的脉冲星超过300 个。
质点的运动
机械能守恒定律 动量
F
P mv
有质量为 m1和 m2的物体1和2,且m1 m2。设滑轮的质量 为m,半径为r,所受的摩擦阻力矩为 M r 。绳与滑轮之间 无相对滑动。试求物体的加速度和绳的张力。 解:滑轮具有一定的转动惯量。 在转动中受到阻力矩的作用, 两边的张力不再相等, T '1
T '1 T '2
m e R
2
M
2 3
mg R
根据定轴转动定律
2 3
mgR J
1 2
mR
2
d dt
设圆盘经过时间t停止转动,则有
2 3
g 0 dt
t
1 2
R d
0
0
由此求得
t
3 R 4 g
0
§3-3、定轴转动刚体的角动量定理 和角动量守恒定律
刚体对转轴的角动量: L J
刚体定轴转动的动能定理:
2
1
Md
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 3
m l ma )
2 2
a
v
m
'
m 'l
3m va
2
3 ma
2
太原理工大学物理系
m 'l
3m va
2
3 ma
2
射入竿后,以子弹、细杆和地球为系统 , 机械能守恒 .
1 1 l 2 ma ( m 2 3
2
)
2
l 2 (1 cos 30 )
mga (1 cos 30 ) m g
§3-4 转动中的功和能
一、力矩的功 刚体转过d 角,外力作的元功为
dA F ds F t r d
dA M d
力矩的功
d
v Ft
F
A
力矩的r
ds
x
M d
dW M d M
P
dt dt 太原理工大学物理系
二、 刚体绕定轴转动的动能定理
当刚体在外力矩作用下,从1转到2 时所作 的功为:
A
2
1
M d
d dt
1 2 J 2
2
1
J
1
d
1 2
2
1
J d
A
J1
2
太原理工大学物理系
转动动能
1 2
J
2
转动动能定理:合外力矩对刚体所作的功,等 于刚体转动动能的增量。 使用中应注意: 1)转动动能是相对量; 2)转动动能定理的表达式为标量式。
v g (2
l 2 ma )( m l 2 3 ma 2 ) 6 ma 3 )( m
太原理工大学物理系
F dt P P
0
M dt L L
0
太原理工大学物理系
例1 一长为l , 质量为m的竿可绕支点O自由转动 . 一质量为m´速率为v的子弹射入竿内距支点为a处, 使竿的偏转角为30º. 问子弹的初速率
解 把子弹和竿看作一个系统 .子弹 射入竿的过程系统角动量守恒
o
30
m va (
直线运动与定轴转动规律对照
质点的直线运动 刚体的定轴转动
v
dx dt
a
dv dt
d x dt
2
2
d dt
d dt
1 2
d
2
dt
J
2
2
P mv E K
F
1 2
mv
2
L J
M
EK
J
m
d A F d x F dt
d A M d M d t
M J
F ma
3)应用该定理时只需分析始态与末态。
太原理工大学物理系
三、机械能守恒定律 刚体的势能等于刚体全部质量集中于质心 时的重力势能.
设地面为零势面,刚体的质心离地面的高度 为 hc 则 E p mgh c 只有保守力作功时,机械能守恒,即 常数 太原理工大学物理系
讨论 子细 弹绳 击质 入量 沙不 袋计
o
v
子 弹 击 入 杆
v
o
圆 锥 摆
m
p
o
T
'
o
v
R
以子弹和沙袋为系统 以子弹和杆为系统 动量守恒; 动量不守恒; 角动量守恒; 角动量守恒; 机械能不守恒 . 机械能不守恒 . 太原理工大学物理系
圆锥摆系统 动量不守恒; 角动量守恒; 机械能守恒 .
定轴转动刚体的角动量守恒定律
