8.刚体定轴转动的功和能
yyf--刚体功与能

J
B
2
B
1 2
J
A
JB
2
1.32 104 J
21
经典力学小结(一~三章)
1、运动学
位矢,位移(路程),速度(平均速度,瞬时 速度,平均速率,瞬时速率),加速度(平均, 瞬时);切向加速度与法向加速度(曲线运动中 自然坐标系下),圆周运动角量描述,线量与角 量关系,直线运动与圆周运动的运动学方程(匀 变速与一般变速),相对运动变换式(坐标,速 度,加速度)
解: 这个问题可分三个阶段进
O
行分析。第一阶段是棒自由摆落
的过程。只有重力做功,机械能 C
守恒。我们把棒在竖直位置时质
心所在处取为势能零点,用表
示棒这时的角速度:
mg
l 2
1 2
J2=1 21 ml 322(1)
15
定轴转动刚体的角动量守恒定律
第二阶段是碰撞过程。因
碰撞时间极短,冲力极大,
O
地面摩擦力可忽略。棒与物
M d t L L0
F
d
x
1 2
mv2
1 2
mv02
M
d
1 J 2
2
1 2
J02
9
例题1: 一根质量为m、长为 L的均匀细棒OA(如 图),可绕通过其一端的光滑轴O在竖直平面内转 动,今使棒从水平位置开始自由下摆,求细棒摆到 竖直位置时其中点C和端点A的速度。
解 先对细棒OA所受的力作 O
一分析;重力 G作用在棒的
22
2、动力学 牛顿三定律,牛顿方程应用(变力)
伽利略相对性原理,惯性力(非惯性系中形式地 运用牛顿方程)
时间累积效应:冲量,动量,动量定理(质点, 质点系),动量守恒;质心,质心运动规律
定轴转动刚体的功能原理

l l
c hc
m
ho
h’
h=3h0/2
a
b
解:碰撞前单摆摆锤的速度为 v0 2gh0 7
令碰撞后直杆的角速度为,摆锤的速度为v'。
由角动量守恒,有:
ml (v0
v)
J ,式中J
1 ml 2 3
①
在弹性碰撞过程中机械能也是守恒的:
1 2
m(v02
v2 )
1 2
J
2
②
二式联立解得:
v v0 , 3v0
2
2l
按机械能守恒,碰撞后摆锤达到的高度显然为 h h0
而杆的质心达到的高度满足
1 2
J 2
mghc
4
由此得
h 2hc
3h0 2
8
解 : 作用于杆的力有重力及 轴对杆的支承力 N , N过O点,
其力矩为零 .重力矩为 mg l sin .
2
dA mg l sin d
2
A m mg l sin d
0
2
mg
l 2
(1
cos
m
)
N
o
m c
将h l(1 cosm )代入上式得
A 1 mgh 2
矩的总功也必为零。
二、刚体的动能
质点动能:
Ek
1 mv2 2
刚体上所有质元的动能之和为:
v2
v3 r3 m3
r2
m2 v1
o r1 m1
Ek
1 2
mi vi 2
刚体定轴转动的动能定理 ppt课件

dt 12
dt
考虑到 t
dr g cost 7lg cos(12 v0 t)ຫໍສະໝຸດ dt 224 v0
7l
上页 下页 返回 结束
第七章 刚体力学 作业: P256 7.4.2 7.5.1
上页 下页 返回 结束
O
上页 下页 返回 结束
第七章 刚体力学
[解](1)由机械能守恒得
m ghc
1 2
I 2
hc
1 2
l
I 1 ml2 3
联立得
3g
l
O Ep=0 C
v l 3gl
上页 下页 返回 结束
(2)根据质心运动定理
FN W mac
分量式
FNn
m
g
m
vc2 rc
mvM
l 2
I
2mu
l 2
1 ml 2
12
1 2
ml 2
解得
mvMl 2
ml 2 12 ml 2 2
6m(2gh)1 2 (m 6m)l
M
N
C
B
l
h A
l/2
上页 下页 返回 结束
第七章 刚体力学 演员N以u起跳,达到的高度,由机械能守恒:
h u 2 l 2 2 ( 3m )2 h
第七章 刚体力学
角动量守恒条件:
M 0
刚体所受的合外力矩为零
若I不变,ω不变; 若I变,ω也变,但 L I 不变.
内力矩不改变系统的角动量.
在冲击等问题中,因内力矩远大于外力矩 ,此时, 角动量守恒。
刚体定轴转动转动定理、功与能
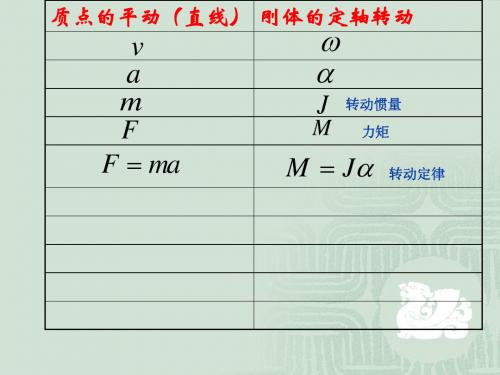
已知:均匀直杆质量为m,长为l, 光滑, 光滑 例. 已知:均匀直杆质量为 ,长为 ,轴o光滑, 0
A
θ
l /4 C
l,m B
初始静止在水平位置。 AO = l / 4 初始静止在水平位置。 角时, 求: 杆下摆到 θ 角时, 角速度 ω ?
【解】
ω
“杆+地球”系统, 杆 地球 系统, 地球”
只有重力作功, 只有重力作功,
E 守恒。 守恒。 (1) (2)
1 l 2 J 0ω − mg sin θ = 0 2 4
1 l 2 7 2 J 0 = ml + m ( ) = ml 2 12 4 48
课堂练习
研究对象是杆,显然本题中杆不可视为质点,不可用牛二; N 研究对象是杆,显然本题中杆不可视为质点,不可用牛二;杆应抽 象为刚体模型,这里就是刚体定轴转动问题, 象为刚体模型,这里就是刚体定轴转动问题,使用转动定理
o
θ
【解】 杆做定轴转动由转动定律有
mg
l 1 2 m cosθ = Jα = m α g L 2 3 3g 得 α= cos θ 2l
r dr
α
r Fபைடு நூலகம்
φ
r r d A = F ⋅ dr r = F d r cos α
P
A= ∫ M dθ
θ1 θ2
= F (rd θ ) sin φ = (Fr sin φ ) d θ = M dθ
此式称为力矩的功 实质上仍然是力的功)。 (实质上仍然是力的功)。
(对比
r r A = ∫ F ⋅d r)
R
设绳轻, 轴上的摩擦力矩为 Mf(设绳轻, 且不伸长,与滑轮无相对滑动)。 且不伸长 与滑轮无相对滑动)。 与滑轮无相对滑动
刚体定轴转动的功和能

(解毕 )
· 10 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
五、刚体的机械能守恒
当系统中只有保守力作功,系统的机械能守恒:
E0 E
其中 E
m ,l
l 2
1 mv 2 1 J 2 2 2
C
mgh 1 kx 2 2
滑轮(R, M),m从静止开始下落,求下落 h 时物体的速 度及加速度。 系统 = 弹簧 + 滑轮 + 物体 + 地球: 提示: 机械能守恒
k
M ,R
2mgh kh 2 答案: v m M / 2
m
2(mg kh) a 2m M
ቤተ መጻሕፍቲ ባይዱ
减速、加速?
h
· 13 ·
Chapter 4. 刚体的转动
三、刚体绕定轴转动的动能定理
W Md
0
M J J d dt
d ω 0 J dt d 0 J d
·4 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
1 1 2 2 积分得: W J J 0 2 2
1 2 [定义] 刚体转动动能: E k J 2 1 1 2 2 W J J 0 E k E k 0 E k 2 2
mg
前例 已知:匀质细杆 (m,l ),光滑轴,从竖直位置静 止摆下,求细杆摆到θ 位置时的角速度。
· 11 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
解:以杆、地球为一系统,则系统机械能守恒:
大学物理复习笔记

⼤学物理复习笔记刚体1 定轴转动定律(转动惯量如:滑轮问题J =1/2MR^2)常⽤列⽅程组解题M=Jα;F=Ma;a=rα2 刚体定轴转动的功和能E=1/2 Jw^2例棒⼦质量M,⼩球质量m1/2(mglsinθ)=1/2(Jw^2)J=1/12(ML^2)+m(L/2)^23 转动惯量J(会判断谁⼤谁⼩)4 ⾓动量守恒(例如圆盘与⼦弹考虑圆盘与⼦弹同向与反向同向时,L增⼤但J也增⼤,不好判断⾓速度变⼤还是变⼩,反向时⼀定变⼩创新实验:⾓动量合成,⼤⼩⽅向,旋转转轮的⾓动量合成实验室有⼏个⾓动量演⽰仪,这是其中⼀个。
两边的圆盘分别可以逆时针或顺时针转动,上⾯的⼿柄可以将圆盘拉起来。
这⾥只介绍其中⼀种转动情况,其他情况可以类⽐。
假设两侧转盘都逆时针转动,则当转盘的⽅向是斜向下时,他们的合⾓动量是向下的,由于系统所受的合外⼒矩为零,所以系统⾓动量守恒。
故从空中俯看,会看到整个装置逆时针转动。
当⽤⼿柄将转盘拉起时,转盘的合⾓动量为向上,整个装置会顺时针转。
当转盘⽔平时,整个装置不转动。
其他的装置也是利⽤⾓动量守恒的原理,可以去看下振动1 简谐振动表达式x=Acos(wt+φ) 会判断运动⽅向,(旋转圆⽮量法)2 相位相位差3 振动的合成(已知A和φ)画图法波动1 写波函数y(x,t)=Acos [w(t-x/u)+ φ]=Acos[wt-2πx/λ+φ]、某⼀点的振动表达式;速度(对t求偏导,把对应t,x带⼊)2 介质元的能量特征平衡位置,动能最⼤势能最⼤,且⼀样⼤作业第四章⼆第5条3 波动图像(给出波动图像判断初相时要注意波的传播⽅向)静电场1 场强E (导体球(电荷表⾯分布),带点球壳,球体)⾼斯定理2 电势U⽆限⼤带电平板,沿垂直于平板⽅向的场强分布,电势分布电势(0电势定在板的位置)场强3 平板电容器板间作⽤⼒F=σq/(2ε。
)σ为⾯电荷密度板间场强E=σ/(2ε。
)C=Q/U =εs/d4 两个带电体电场⼒电势能例如:两带电体,⼀个带点球壳电量为Q,⼀导体细棒,延长线过球⼼,电荷线密度为λ细棒端和尾离圆⼼分别为r1 r2 求电场⼒电势能dF =Edq; dq=λdr;dF =EλdrF=对dF的积分(r1到r2)dW=Uλdr5 电场的能量W=Q^2/(2c)=cU^2/2:有介质时W=DE/2=εE^ 2/2 (另外,page 215 还有充介质的情况,充两层呢(关于计算单位体积的能量;能量的密度)6 探索实验带电乒乓(这是静电乒乓。
刚体定轴转动动能定理公式

刚体定轴转动动能定理公式刚体定轴转动动能定理是描述刚体绕某一固定轴转动时动能变化的物理定理。
在物理学中,刚体定轴转动动能定理是非常重要的定理之一,它能够帮助我们更好地理解物体在转动时的能量变化规律。
我们需要了解一下刚体的概念。
刚体是指在运动或者受力作用下不会发生形变的物体,也就是说,在运动或者受力作用下,刚体的形状和大小都不会发生任何改变。
我们可以将刚体分为两种类型,一种是平面刚体,另一种是空间刚体。
平面刚体指的是只有面积,没有厚度的物体,空间刚体指的是有一定大小和形状的物体。
接下来,我们来了解一下刚体定轴转动动能定理。
刚体定轴转动动能定理的表达式是:E = 1/2 * I * ω²,其中E表示刚体定轴转动的动能,I表示刚体对于轴的转动惯量,ω表示刚体绕轴的角速度。
从这个公式中,我们可以看出,刚体定轴转动动能与刚体的转动惯量和角速度的平方成正比。
那么,什么是转动惯量呢?转动惯量是描述物体转动惯性的物理量,它表示物体绕着某一轴旋转时所具有的旋转惯性。
不同形状的刚体,其转动惯量也是不同的。
例如,对于一个质量均匀分布的球体,其转动惯量为2/5 * m * r²,其中m表示球体的质量,r表示球体的半径。
刚体定轴转动动能定理的应用非常广泛。
例如,在机械制造和工程设计中,我们可以通过刚体定轴转动动能定理来计算物体旋转时所需要的能量和功率。
同时,在运动学和动力学研究中,刚体定轴转动动能定理也是非常重要的工具。
刚体定轴转动动能定理是描述刚体绕某一固定轴转动时动能变化的重要定理。
通过刚体定轴转动动能定理,我们可以更好地理解物体在转动时的能量变化规律,这对于物理学的研究和应用都具有非常重要的意义。
刚体的能量定轴转动的动能定理
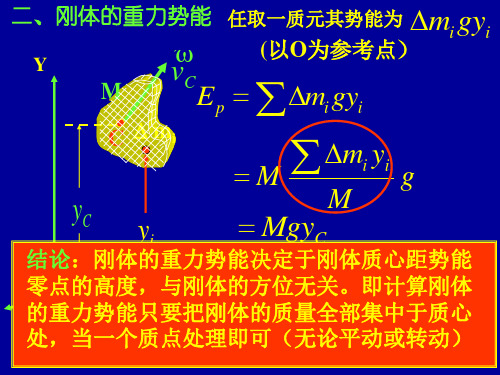
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ,则该质元动能:
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能:
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程,设
在力矩作用下,刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用,力矩越 大,在空间转过的角度越大,作的功就越大。 这种力矩对空间的积累作用的规律是什么呢?
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例)设一细杆的质量为m,长为L,一端支以
枢轴而能自由旋转,设此杆自水平静止释放。
求: 当杆过铅直位置时的角速度:
N
YZ
XO
r
mg
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《大学物理》练习题 No.8 刚体定轴转动的功和能
班级 ___________ 学号 __________ 姓名 _________ 成绩 ________
基本要求: (1) 掌握力矩的功、转动动能、动能定理、含刚体的机械能守恒定律及应用
内容提要: 1. 力矩的功:
⎰=θ
Md A
2 转动动能:刚体的转动惯量与角速度平方乘积的一半。
22
1
ωJ E k =
3 刚体定轴转动的动能定理:合外力矩对定轴转动刚体所做的功等于刚体转动动能的增
量
21222
121ωωJ J A -=
若在刚体转动过程中,只有重力做功,其他非保守内力不做功,则刚体在重力场中机械能守恒.
常量=+=
C mgh J E 2
2
1ω
一、选择题
1. 如图8.1所示, 一匀质细杆可绕通过其一端的水平光滑轴在竖直平面内自由转动. 杆长 l = (5/3)m,今使杆从与竖直方向成60°角的位置由静止释放(g 取10m/s 2), 则杆的最大角速度为
[ ] (A) 3rad/s.
(B) π rad/s (C) 9 rad/s.
(D)
3rad/s.
2.一人站在旋转平台的中央,两臂侧平举,整个系统以2π rad/s 的角速度旋转,转动惯量为6.0kgm 2.如果将双臂收回则系统的转动惯量变为2.0kgm 2.此时系统的转动动能与原来的转动动能之比E k / E k0为 [ ] (A)2.
(B) 2. (C) 3. (D)
3.
图8.1
3.如图8.2所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴旋转,初始状态为静止悬挂。
现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统 [ ] (A) 只有机械能守恒.
(B) 只有动量守恒.
(C) 只有对转轴O 的角动量守恒.
(D) 机械能、动量角和动量均守恒.
二.填空题
1.一匀质细杆AB,长为l ,质量为m . A 端挂在一光滑的固定水平轴上, 细杆可以在竖直平
面内自由摆动.杆从水平位置由静止释放开始下摆,当下摆θ 时,杆的角速度为 .
2.将一质量为m 的小球, 系于轻绳的一端, 绳的另一端穿过光滑水平桌面上的小孔用手拉住, 先使小球以角速度ω 1 在桌面上做半径为r 1的园周运动, 然后缓慢将绳下拉, 使半径缩小为r 2, 在此过程中小球的动能增量是 .
三.计算题
1.有一质量为m 1、长为l 的均匀细棒,静止平放在滑动摩擦系数为μ的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动. 另有一水平运动的质量为m 2的小滑块,从侧面垂直于棒与棒的另一端A 相撞,设碰撞时间极短,已知小滑块在碰撞前后的速度分别为v 1和v 2,如图8.3所示. 求碰撞后从细棒开始转动到停止转动的过程所需的时间 (以知棒绕O 点的转动惯量J=m 1l 2/3).
图8.2
2 (图8.3
2.一长l=0.4m 的均匀木棒,质量M=1.0kg ,可绕水平轴O 在竖直内转动,开始时棒自然地竖直悬垂,今有质量m=8g 的子弹以s m v 200=地速率从A 点射入棒中,假定A 点与O 点的距离为43l ,求: (1)、棒开始运动时的角速度; (2)、棒的最大偏转角。
No, 8 参考答案 一、选择题
1. (A), 提示:杆下摆过程,根据机械能守恒22
1
)cos 1(21ωθJ Mgl =-可得杆在竖直放置时的最大转动角速度为s rad /3=ω;
2. (C ),提示:在手臂收回的过程中,角动量是守恒的:2211ωωJ J =,可得s rad /62πω=,
所以前后的能量比
31
2
121
2222
112
1
=⋅=ωωJ J E E k k ; 3. (C ) 二.填空题 1. l g θωsin 3=
,杆下摆过程,机械能守恒,2
2
1sin 21ωθJ mgl =,可得; 4
l
O A
2. )(2122
2
2212121r r
r mr E k -=∆ω,由于绳子上的拉力通过了转轴,故没有力矩,角动量守恒,
但此拉力是要做功的,2
22
22
12
1ωωmr mr =,得12
1
2ωωr r =
,所以动能的增量为212222
121ωωJ J E k -=
∆; 三.计算题
1. 解:由角动量守恒可以得到 )(212v v l m J +=ω
碰后,由于摩擦产生的阻力矩为:
l
gm dr gr gdm r M rdF
M l
⎰⎰⎰====012
1
μρμμ 由角动量定理,ωJ Mt =
得到,碰撞后从细棒开始转动到停止转动的过程所需的时间
g
m v v m t 1212)
(2μ+=
2. 解:(1)、碰撞瞬间由角动量守恒可以得到 43,)(2
l d J md mdv =+=ω 所以: )(88.81
-⋅=s rad ω
(2)、子弹与棒一同偏转的过程中只受重力矩作用,所以 系统机械能守恒:
)cos 1)(4
3
2()169(2122θω-+=+l mg l Mg ml J
所以:,
5294
=θ。
