03-01简谐近似和简正坐标
固体物理第四章总结1
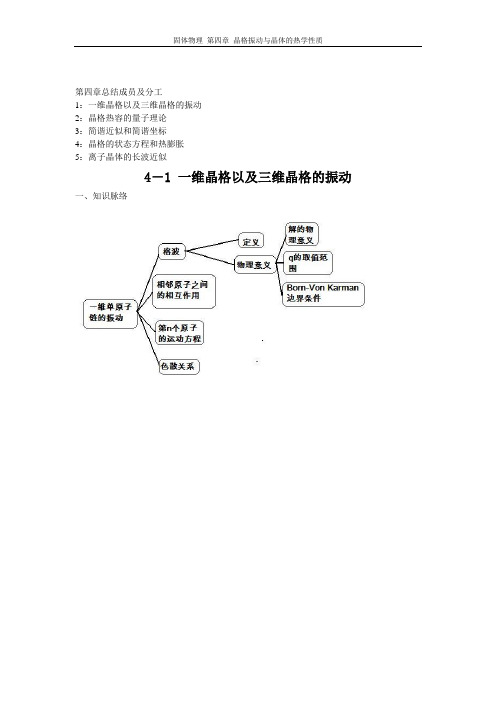
第四章总结成员及分工1:一维晶格以及三维晶格的振动2:晶格热容的量子理论3:简谐近似和简谐坐标4:晶格的状态方程和热膨胀5:离子晶体的长波近似4-1 一维晶格以及三维晶格的振动一、知识脉络二、重点1.格波的概念和“格波”解的物理意义(1)定义:晶格原子在平衡位置附近作振动时,将以前进波的形式在晶体中传播,这种波称为格波。
(2)物理意义:一个格波解表示所有原子同时做频率为ω的振动,不同原子之间有位相差。
相邻原子之间的位相差为aq 。
(3) q 的取值范围:-(π/a)<q ≤(π/a)这个范围以外的值,不能提供其它不同的波。
q 的取值及范围常称为布里渊区(Brillouin zones )。
(4) Born-Von Karman 边界条件: 1)(=-Naq i e h Naq ⨯=π22.一维单原子链的色散关系22241[1cos ]sin ()2aq aq m m ββω=-=把 ω 与q 之间的关系称为色散关系(disperse relation),也称为振动频谱或振动谱。
3.一维单原子链的运动方程相邻原子之间的相互作用βδδ-≈-=d dvF ad v d ⎪⎪⎭⎫ ⎝⎛=22δβ 第n 个原子的运动方程11()(2)n n n n i t naq nq m Ae ωμβμμμμ∙∙+--=+-=4.一维双原子链中两种原子的运动方程及其解(1)运动方程( equation))2(2221212n n n n M μμμβμ---=+++∙∙ )2(2221212n n n n M μμμβμ---=+++∙∙(2)方程的解(solution)])2([2q na t i n Ae -=ωμ ])12([12aq n t i n Be +-+=ωμ5.声学波与光学波的概念与物理意义(1)声学波与光学波的定义}]sin )(41[1{2/1222aq M m mM mM M m +-++=+βω }]sin )(41[1{2/1222aq M m mMmM M m +--+=-βω ω+对应的格波称为光学波(optic wave )或光学支(optic branch) ;ω-对应的格波称为声学波(acoustic wave)或声学支(acoustic branch )(2)两种格波的振幅比aq m A B cos 222ββω--=⎪⎭⎫⎝⎛++aq m A B cos 222ββω--=⎪⎭⎫⎝⎛--(3)ω+ 与ω- 都是q 的周期函数)()(q aq --=+ωπω)()(q aq ++=+ωπω其中aq a22ππ≤〈-6.对色散关系的讨论(1)一维单原子链与一维双原子链的格波解的差异一维单原子链只有一支格波(一个波矢对应一个格波)— 声学波;而一维双原子链则有两支格波(一个波矢对应两个格波)— 声学波和光学波,两支格波的频率各有一定的范围:0)0()(min ==--ωω Maβπωω2)2()(max ==-- m aβπωω2)2()(min ==++ mMM m )(2)0()(max +==++βωω 在ω-max 与ω+min 之间有一频率间隙,说明这种频率的格波不能被激发。
简谐近似和简正坐标

N个原子的位移矢量 N个原子体系的势能函数在平衡位置按泰勒级数展开
取
平衡位置
—— 不计高阶项
系统的势能函数
V
1 2
i
3N , j1
(
2V
i
j
)0
i
j
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
系统的势能函数
系统的动能函数
系统的哈密顿量
H
1 2
3N i1
mi i 2
1 3N 2V (
只考察某一个振动模
系统能量本征值计算
i
aij mi
Qj
aij mi
Asin( jt )
正则动量算符
系统薛定谔方程
(1
2
3N i1
pi2
1 2
3N
i2Qi2 ) (Q1, Q3N )
i1
E (Q1,
Q3N )
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
任意一个简正坐标
(
)
—— 一个简正坐标对应一个谐振子方程,波函数是以简正 坐标为宗量的谐振子波函数
声子 —— 晶格振动的能量量子;或格波的能量量子
一个格波是一种振动模,称为一种声子,能量为
当这种振动模处于
时,说明有 个声子
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
晶格振动 —— 声子体系 —— 声子是一种元激发,可与电子或光子发生作用 —— 声子具有能量_动量,看作是准粒子 —— 晶格振动的问题 声子系统问题的研究 —— 每个振动模式在简谐近似条件下都是独立的 —— 声子系宗是无相互作用的声子气组成的系统
2 i, j1 i j
固体物理 晶体振动

3.2 晶格振动的量子化-声子参考黄昆书3.1节(p79-82)及p88-92Kittel 书 4.3和4.4 两节一. 简谐近似和简正坐标二. 晶格振动的量子化三. 声子一.简谐近似和简正坐标:从经典力学的观点看,晶格振动是一个典型的小振动问题,由于质点间的相互作用,多自由度体系的振动使用拉格朗日方程处理比上节中使用的牛顿方程要简单明了。
本节采用简正坐标重新处理。
(见黄昆书p79-82)N 个原子组成的晶体,平衡位置为,偏离平衡位置的位移矢量为:'()()n n n R t R u t =+n R ()n u t 所以原子的位置表示为:晶体中原子间的耦合振动,在简谐近似下也可以用3nN 个简正坐标下的谐振子运动来描述。
由于简正坐标Q是各原子位移量的某种线性组合,所以一个简正i振动并不是表示一个原子的振动,而是整个晶体所有原子都参与的运动。
由简正坐标所代表的体系中所有原子一起参与的共同振动常被称作晶体的一个振动模。
N个原胞,每个原胞n个原子的晶体总共有3nN种振动模。
或说可以用3nN种简谐振子的运动来表述。
引入简正坐标后,我们可以方便地转入用量子力学的观点来理解晶格振动问题,这才是最为重要的。
显然,一旦找到了简正坐标,就可以直接过渡到量子理论。
每一个简正坐标,对应一个谐振子方程,波函数是以简正坐标为宗量的谐振子波函数,其能量本征值是量子化的,所以把量子力学的基本结论应用到晶格振动上才揭示出了晶格振动的最基本的特征。
从量子力学的观点看,表征原子集体运动的简谐振子的能量是量子化的,每个振动模式能量的最小单位被称为声子(Phonon )。
这是晶格振动量子理论最重要的结论。
在经典理论中,势能函数是连续的,量子理论修正了这个错误,而保留了经典理论中原子振动要用集体运动方式描述的观点,因而按经典力学求出的色散关系是正确的,量子理论并没有改变其结论,只是对各模式振幅的取值做了量子化的规定。
i ω声子概念引入后给我们处理具有强相互作用的原子集体--晶体带来了极大方便,而且生动地反映了晶格振动能量量子化的特点。
4-3 简谐近似和

2)化简系统的动能和势能
动能
1 T m 2
n
2 n
1 1 m 2 Nm
1 2
n q
Q ( q )e inaq
q'
Q ( q ' )e inaq'
qq '
1 Q ( q ) Q ( q ' ) N
Department of Physics, Northwest University
Solid State Physics
由(5)式知,当只考察某一个 Qi 的振动时,(5)式可以化为
i
aij mi
A sin( it )
(12)
这表明,一般地说,一个简正振动并不是表示某一个原子的振动,而是表示 整个晶体所有原子都参与的振动,而且它们的振动频率都相同。由简正坐标所代 表的,体系中所有原子一起参与的共同振动,常称为一个振动模或简正模 (normal mode)。 由量子力学我们知道,用(9)式可以直接写出哈密顿算符和薛定谔方程
1 2 2 2 [ i Qi ] (Qi ) i (Qi ) 2 2 Qi
(14)
Department of Physics, Northwest University
Solid State Physics
谐振子方程的解为
i (ni )i
ni (Qi )
i 2l N
0
说明声子不是动量的携带者。
Department of Physics, Northwest University
1 e
Solid State Physics
4-3 简谐近似和

一、 简谐近似和非谐作用 (harmonic approximation and an-harmonic interaction) )
晶格振动是一个小振动问题。对于此类问题常采用简谐近似。 晶格振动是一个小振动问题。对于此类问题常采用简谐近似。 假设晶体包含N个原子, 假设晶体包含 个原子,平衡位置为 个原子 偏离平衡位置的位移矢量为 µn (t )
i =1
3N
•
Qi
2
(6) )
1 V= 2
∑
i =1
3N
ω i 2Qi 2
(7) )
其中仅有简正坐标的平方项之和,而没有了坐标的交叉项。 其中仅有简正坐标的平方项之和,而没有了坐标的交叉项。
Department of Physics, Northwest University
Solid State Physics
∑
(3) )
体系的势能函数只保留至µ 的二次方程,称为简谐近似 简谐近似( 体系的势能函数只保留至 i的二次方程,称为简谐近似(harmonic approximation)。要考虑到高阶作用的则称为非谐作用(an-harmonic 非谐作用( ) 要考虑到高阶作用的则称为非谐作用 interaction)。
Department of Physics, Northwest University
Solid State Physics
将N个原子体系的势能函数在平衡位置附近展开成泰勒级数 个原子体系的势能函数在平衡位置附近展开成泰勒级数
∂V 1 3 N ∂ 2V V = V0 + ( ) 0 µi + ( )0 µi µ+高阶项 j ∂µi 2 i , j =1 ∂µi ∂µ j i =1
03_01简谐近似和简正坐标

n=0,1,2…… (3-57)
这表明谐振子处于不连续的能量状态。
1 ,称为零点能。 当n=0时,它处于基态,E0= 2
相邻状态的能量差为,它是谐振子的能量量子, 称它为声子 ,正如人们把电磁辐射的能量量子称 为光子一样。 3NS个格波与3NS个量子谐振子一一对应,因此式 (3-57)也是一个频率为ω的格波的能量。频率 为ωi(q)的格波被激发的程度,用该格波所具有的 能量为ωi (q)的声子数n的多少来表征。
2.声子是一种准粒子
声子与声子,声子与其它粒子、准粒子互作用, 满足能量守恒。 不具有通常意义下的动量,常把q称为声子的
粒子数不守恒,例如温度升高后声子数增加。
准动量。
3.准动量选择定则
准动量的确定只能准确到可以附加任何 一个倒格矢Gh
ω(q)= ω(q+ Gh) Ex: 二声子作用 q1+q2=q3+Gh q1+q2=q3+Gh
系统的势能函数
系统的动能函数
系统的哈密顿量 H
1 1 V 2 i ( mi ) 0 i j 2 i 1 2 i , j 1 i j
3N 3N 2
—— 含有坐标的交叉项
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
引入简正坐标
—— 原子的坐标和简正坐标通过正交变换联系起来 假设存在线性变换
1 能量本征值 i ( ni ) i 2
本征态函数
—— 谐振子方程
n (Qi ) iຫໍສະໝຸດ iexp(
2
2
) H ni ( )
— 厄密多项式
§3-1 简谐近似和简正坐标 ——
晶格振动与晶体的热学性质
简谐震动简正坐标(0301)

在声学领域,声音的传播和辐射都 可以看作是简谐震动的叠加,因此 简谐震动理论也是声学研究的重要 基础。
02
简正坐标的概念
什么是简正坐标
• 简正坐标是一种描述系统振动的坐标方式,它将复 杂的振动问题简化为简单的数学模型,以便于分析 和求解。在简正坐标下,系统的振动形式被分解为 一系列正弦和余弦函数,每个函数代表一种独立的 振动模式。
简谐震动
简谐震动是物理学中一个基本而重要的概念,它描述的是一个振动系统在平衡 位置附近做周期性的往复运动。简谐震动可以用数学公式表示,其运动规律具 有特定的周期性和振幅。
简正坐标
简正坐标是用来描述简谐震动的坐标系,它能够将复杂的振动问题简化,方便 分析和计算。简正坐标系的选择取决于系统的具体形式和物理特性。
实例二:单摆的简谐震动
总结词
单摆在摆角较小的情况下,做近似于简谐振动的往复运动。
详细描述
单摆由一根长度为摆长的细线悬挂着一个质量块组成,在重 力作用下产生往复运动。当摆角较小(小于5度)时,单摆的 运动可以近似看作是简谐振动。在简正坐标系下,单摆的振 动形式可以表示为正弦或余弦函数。
实例三:电磁振荡器的简谐震动
教育教学
在高等教育中,简谐震动和简正坐标是物理学、工程学等专业的重要教学内容。通过深入 学习和理解简谐震动和简正坐标的理论基础,可以培养学生的逻辑思维和分析能力,提高 他们的科学素养。
THANKS
感谢观看
简正坐标的应用
1. 振动分析
简正坐标广泛应用于振动分析 领域,用于研究系统的振动特
性和响应。
2. 结构优化
在结构优化设计中,简正坐标 可以帮助分析结构的振动模态 和频率,从而优化结构的设计 。
3. 声学研究
固体物理总复习

gap
2 )q 一维双原子链的长声学波 ( a mM B 长声学波中相邻原子的振动 ( A ) 1
光学波 长波极限
2
mM B m , ( ) - mM A M
§3.4
1. 三维复式格子
三维晶格的振动
l i [ t R l k q ] 格波的一般形式 A e k k
ab c
§5 晶体的宏观对称性
点对称操作 1. 绕轴旋转 2.旋转-反演(反演,镜面) 对称操作
1. 绕轴旋转
2.旋转-反演 3.空间平移
晶体的宏观对称性只有8种独立的对称操作: 1,2,3,4,6, 1 ( i ),
2 (m)
和
4
能证明为何晶体中没有5次对称性?
第二章
• 晶体结合的类型? • 晶体结合的物理本质? • 固体结合的类型与固体性质之间的联系?
T —— 电子对比热的贡献, 即电子热容
AT 3—— 晶格振动对比热的贡献, 即晶格热容
温度不太低时,可以忽略电子的贡献 爱因斯坦模型与德拜模型 爱因斯坦温度和德拜温度
§3.9 晶格振动模式密度
晶格振动模式密度 —— 单位频率间隔的振动模式数目
n g ( ) lim 0
在q空间,晶格振动模是均匀分布的,状态密度
本课程的主要内容
晶格动力学
原子核的运动规律 核外电子的运动规律
固体物理
固体电子论
晶格动力学
1. 晶体结构 2. 固体的结合 3. 晶格振动和热学性质
固体电子论
4. 能带理论 5. 外场中电子的运动 6. 金属电子论
第一章 摘
§1-1 §1-2 §1-3 §1-4 §1-5 §1-6 §1-7 §1-8 §1-9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
—— 不计高阶项 取 平衡位置
西 南 科 技 大 学
系统的势能函数
简谐近似
固 体 物 理
Solid State Physics
系统的势能函数
系统的动能函数
系统的哈密顿量
西 南 科 技 大 学
—— 含有坐标的交叉项
固 体 物 理
Solid State Physics
引入简正坐标
—— 原子的坐标和简正坐标通过正交变换联系起来 假设存在线性变换: 系统的哈密顿量
西 南 科 技 大 学
固体的热学性质
1. 2. 固体比热容的爱因斯坦模型 固体比热容的德拜模型
固 体 物 理
Solid State Physics
固体中的热现象
热的本质?
热质说:认为热是一种物质,不生不灭。可以在火中 存在,也可以流动到别的物质中。使之发热。 但是,热 质说不能解释摩擦生热的现象。
在18世纪以后,渐渐有另一种观点来解释热现象,即 认为热不是一种流质,而是物质运动的一种表现。
西 南 科 技 大 学
1842年,德国医生迈尔(Julius Robert Mayer) 提 出了能量守恒学说,认为热是一种能量,可以和机械能互 相转换。
固 体 物 理
Solid State Physics
简谐近似 —— 只考虑最近邻原子之间的相互作用
研究对象 —— 由N个质量为m的原子组成的晶体
第n个原子的平衡位置 偏离平衡位置的位移矢量
西 南 科 技 大 学
原子的位置 3个方向上的分量
原子位移宗量
固 体 物 理
Solid State Physics
N个原子的位移矢量 —— 体系的势能函数在平衡位置按泰勒级数展开
固 体 物 理
Solid State Physics
晶格振动 ——原子在格点附近的振动 —— 研究固体宏观性质和微观过程的重要基础 晶格振动
—— 晶体的热学性质、电学性质、光学性质、
西 南 科 技 大 学
超导电性、磁性、结构相变有密切关系
固 体 物 理
Solid State Physics
§3.1 简谐近似和简正坐标
任意一个简正坐标
西 南 科 技 大 学
—— 谐振子方程
固 体 物 理
Solid State Physics
任意一个简正坐标
—— 谐振子方程 能量本征值: 本征态函数:
西 南 科 技 大 学
— 厄密多项式
固 体 物 理
Solid State Physics
N个原子组成的晶体
系统薛定谔方程
系统能量本征值:
固 体 物 理
Solid State Physics
杜隆-珀替经验规律: 一摩尔固体有N个原子,有3N个振动自由度,按 能量均分定律,每个自由度平均热能为kT 总的内能 摩尔热容量
摩尔热容量:
西 南 科 技 大 学
—— 与温度无关 —— 杜隆-珀替经验规律
—— 实验表明较低温度下,热容量随着温度 的降低而下降
西 南 科 技 大 学
固 体 物 理
Solid State Physics
系统的哈密顿量:
拉格朗日函数
正则动量
正则方程
西 南 科 技 大 学
系统的哈密顿量:
固 体 物 理
Solid State Physics
系统的哈密顿量
正则方程
正则动量
西 南 科 技 大 学
—— 3N个独立无关的方程 简正坐标方程解
热的本质
19世纪中叶,焦耳(James Prescott Joule)研究 多种能量形式的转换,为能量守恒和转换定律提供了试 验基础。
热的本质:热是构成物质系统的大量微观粒 子无规则混乱运动的宏观表现。
西 南 科 技 大 学
晶格振动的研究 —— 晶体的热学性质 固体热容量 —— 热运动是晶体宏观性质的表现
固 体 物 理
Solid State Physics
简正坐标方程解: 简正振动 —— 所有原子参与的振动,振动频率相同 振动模 —— 简正坐标代表所有原子共同参与的一个 振动
西 南 科 技 大 学
只考察某一个振动模:
固 体 物 理
Solid State Physics
系统能量本征值计算
正则动量算符 系统薛定谔方程
系统本征态函数:
西 南 科 技 大 学
固 体 物 理
Solid State Physics
固体物理 Solid State Physics
第三章 晶格振动
§ 3.1 简谐近似和简正坐标
西 南 科 技 大 学
固 体 物 理
Solid State Physics
第三章 晶格振动与晶体的热学性质
ቤተ መጻሕፍቲ ባይዱ
固体中热现象的研究历史 晶格动力学
1. 2. 3. 4. 5. 简谐近似 一维单原子链 一维双原子链 三维晶格振动 确定晶格振动谱的试验方法
