天体运动突破
专题天体运动的三大难点破解剖析宇宙中的双星三星模型讲义

二、重难点提示:重点:1.根据万有引力定律求解双星、三星模型的周期,线速度等物理量;2. 双星、三星两种模型的特点。
难点:双星、三星模型的向心力来源。
一、双星模型绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示,双星系统模型有以下特点:(1)各自需要的向心力由彼此间的万有引力相互提供即221LmGm=m1ω21r1,221LmGm=m2ω22r2;(2)两颗星的周期及角速度都相同即T 1=T 2,ω1=ω2;(3)两颗星的半径与它们之间的距离关系为r 1+r 2=L ;(4)两颗星到圆心的距离r 1、r 2与星体质量成反比即1221r r m m =; (5)双星的运动周期T =2π)(213m m G L +;(6)双星的总质量公式m 1+m 2=GT L 2324π。
二、三星模型第一种情况:三颗星连在同一直线上,两颗星围绕中央的星(静止不动)在同一半径为R 的圆轨道上运行。
特点:1. 周期相同; 2. 三星质量相同; 3. 三星间距相等;4. 两颗星做圆周运动的向心力相等。
原理:A 、C 对B 的引力充当向心力,即:,可得:GmR T 543π=,同理可得线速度:R GmR 25。
第二种情况:三颗星位于等边三角形的三个顶点上,并沿等边三角形的外接圆轨道运行。
特点:1. 运行周期相同; 2. 半径相同; 3. 质量相同; 4. 所需向心力相等。
原理:B 、C 对A 的引力的合力充当向心力,即:r Tm R Gm F 2222430cos 2π==︒合,其中R r 33=,可得:运行周期GmRRT 32π=。
例题1 如图,质量分别为m 和M 的两颗星球A 和B 在引力作用下都绕O 点做匀速圆周运动,星球A 和B 两者中心之间距离为L 。
已知A 、B 的中心和O 三点始终共线,A 和B 分别在O 的两侧。
引力常数为G 。
(1)求两星球做圆周运动的周期。
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A 和B ,月球绕其轨道中心运行的周期记为T 1。
2018高考物理总复习专题天体运动的三大难点破解1深度剖析卫星的变轨讲义
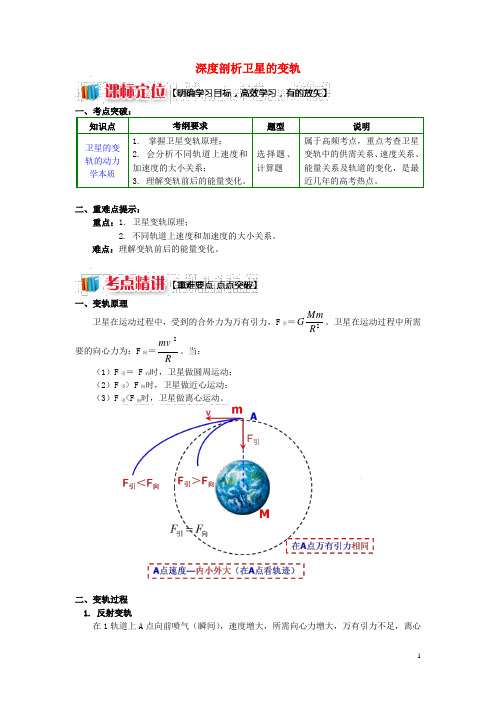
深度剖析卫星的变轨一、考点突破:知识点 考纲要求题型说明卫星的变轨的动力学本质 1. 掌握卫星变轨原理; 2. 会分析不同轨道上速度和加速度的大小关系;3. 理解变轨前后的能量变化。
选择题、计算题 属于高频考点,重点考查卫星变轨中的供需关系、速度关系、能量关系及轨道的变化,是最近几年的高考热点。
二、重难点提示:重点:1. 卫星变轨原理;2. 不同轨道上速度和加速度的大小关系。
难点:理解变轨前后的能量变化。
一、变轨原理卫星在运动过程中,受到的合外力为万有引力,F 引=2R MmG 。
卫星在运动过程中所需要的向心力为:F 向=Rmv 2。
当:(1)F 引= F 向时,卫星做圆周运动; (2)F 引> F 向时,卫星做近心运动; (3)F 引<F 向时,卫星做离心运动。
二、变轨过程 1. 反射变轨在1轨道上A 点向前喷气(瞬间),速度增大,所需向心力增大,万有引力不足,离心运动进入轨道2沿椭圆轨道运动,此过程为离心运动;到达B点,万有引力过剩,供大于求做近心运动,故在轨道2上供需不平衡,轨迹为椭圆,若在B点向后喷气,增大速度可使飞船沿轨道3运动,此轨道供需平衡。
2. 回收变轨在B点向前喷气减速,供大于需,近心运动由3轨道进入椭圆轨道,在A点再次向前喷气减速,进入圆轨道1,实现变轨,在1轨道再次减速返回地球。
三、卫星变轨中的能量问题1. 由低轨道到高轨道向后喷气,卫星加速,但在上升过程中,动能减小,势能增加,增加的势能大于减小的动能,故机械能增加。
2. 由高轨道到低轨道向前喷气,卫星减速,但在下降过程中,动能增加,势能减小,增加的动能小于减小的势能,故机械能减小。
注意:变轨时喷气只是一瞬间,目的是破坏供需关系,使卫星变轨。
变轨后稳定运行的过程中机械能是守恒的,其速度大小仅取决于卫星所在轨道高度。
3. 卫星变轨中的切点问题【误区点拨】近地点加速只能提高远地点高度,不能抬高近地点,切点在近地点;远地点加速可提高近地点高度,切点在远地点。
物理实验技术中对天体运动的测量方法

物理实验技术中对天体运动的测量方法天体运动一直以来都是人类探索的对象之一。
为了更好地理解宇宙的奥秘和运行机制,物理学家们致力于发展各种测量方法来研究天体运动。
在物理实验技术领域,有许多精密的设备和仪器被设计出来,用于测量天体运动的各个方面,从而揭示宇宙的奥秘。
一种常见的测量天体运动的方法是角度测量。
角度测量是通过观察天体在天空中的位置变化来确定其运动状态。
此方法通常使用望远镜和天文学坐标系统。
望远镜可以放大天体,并提供更清晰的观测。
而天文学坐标系统则是用来描述天体位置的一种标准。
常见的天文学坐标系统包括赤道坐标系统和黄道坐标系统。
通过观测天体在赤道或黄道上的角度变化,可以计算出它的位置、速度和运动轨迹。
这种方法常用于观测行星、恒星和其他天体的运动。
天体运动的速度测量也是物理实验技术中的重要任务。
为了测量天体的速度,物理学家们使用了多种技术和仪器。
其中一种常用的方法是多普勒效应。
多普勒效应是指当一个物体相对于观察者运动时,它所发出的波的频率会发生改变。
在天文学中,多普勒效应可用来测量天体的径向速度。
通过观测天体发出的光谱线的频移,可以计算出它离我们的距离和径向速度。
这种方法被应用于研究星系的演化、宇宙膨胀以及恒星的自转等问题。
除了角度和速度测量,物理实验技术还涉及距离和质量的测量。
测量天体的距离是了解宇宙结构和演化的重要手段。
传统的天文学中,通过观测天体的视差来测量其距离。
视差是指当观察者的位置发生变化时,同一个物体在不同位置上的位置差别。
然而,当天体距离较远时,视差非常小,很难直接测量。
为了解决这个问题,物理学家发展了一种被称为“标准烛光”的方法。
标准烛光是指在宇宙中有已知亮度的物体,通过观测天体的亮度,可以推算出其距离。
常见的标准烛光包括新星、超新星和巨星等。
此外,物理实验技术还包括质量的测量。
测量天体的质量对于研究引力和宇宙的结构非常重要。
质量测量通常需要通过观测天体的运动轨迹来进行推算。
例如,对于双星系统,可以通过观测它们的轨道运动和周期来测量质量。
中国在天体运行方面的科技创新

中国在天体运行方面的科技创新示例回答如下1:China has made significant advancements in the field of celestial mechanics and space technology. Over the past few decades, the country has invested heavily in research and development, leading to numerous breakthroughs and innovations.One of the notable achievements in China's space technology is the successful launch and operation of the Chang'e lunar exploration program. The program, named after the Chinese moon goddess, has seen the deployment of several lunar missions, including the Chang'e 3 and Chang'e 4 missions. These missions have successfully landed on the moon's surface, conducting scientific experiments and collecting valuable data.China has also made significant strides in satellite technology. The country has developed and launched a series of remote sensing satellites, such as the Gaofen series, which provides high-resolution images for various applications, including land and resource management, disaster monitoring, and environmental protection. These satellites have greatlycontributed to China's ability to monitor and manage its vast territory.Furthermore, China has been actively involved in space exploration beyond Earth's orbit. The country has plans for a Mars mission, with the aim of sending a rover to the red planet to study its geology and search for signs of past or present life. Additionally, China has expressed interest in building a space station and sending astronauts to the moon in the near future.In terms of technological innovation, China has made significant progress in the development of rocket systems. The Long March series of rockets, developed by the China Aerospace Science and Technology Corporation, has become a reliable workhorse for launching satellites into space. The Long March 5, for instance, has a payload capacity of 25 tons to low Earth orbit, making it one of the most powerful rockets in operation.China's advancements in space technology have not only had scientific implications but also economic and geopolitical significance. The country has become a major player in theglobal space industry, offering commercial satellite launches and services to other countries. This has not only generated revenue but also fostered international collaboration and cooperation in space exploration and research.中国在天体运行方面的科技创新取得了重大突破。
高考物理总复习 专题 天体运动的三大难点破解2 赤道物体、近地卫星、同步卫星参量比较讲义

赤道物体、近地卫星、同步卫星参量比较一、考点突破:二、重难点提示:重点:赤道物体、近地卫星、同步卫星区别和联系。
难点:赤道物体、近地卫星、同步卫星向心力来源。
一、同步卫星、近地卫星与赤道物体的相同点1. 三者都在绕地轴做匀速圆周运动,向心力都与地球的万有引力有关;2. 同步卫星与赤道上物体的运行周期相同:T=24h;3. 近地卫星与赤道上物体的运行轨道半径相同:r=R0(R0为地球半径)。
二、同步卫星、近地卫星与赤道物体的不同点1. 轨道半径不同如图所示,同步卫星的轨道半径同r=R0+h,h为同步卫星离地面的高度,大约为36000千米,近地卫星与赤道物体的轨道半径近似相同,都是R0,半径大小关系为:赤近同rrr=>;2. 向心力不同同步卫星和近地卫星绕地球运行的向心力完全由地球对它们的万有引力来提供,赤道物体的向心力由万有引力的一个分力来提供,万有引力的另一个分力提供赤道物体的重力;考点考纲要求备注赤道物体、近地卫星、同步卫星参量比较1. 理解赤道物体、近地卫星、同步卫星向心力来源;2. 掌握赤道物体、近地卫星、同步卫星参数的比较。
本知识点是难点,但在高考中属于高频考点,主要考查赤道物体、近地卫星、同步卫星参量的大小比较,同时加强了三种情况的区别和联系的考查,题型:选择题。
3. 向心加速度不同 由ma r Mm G=2得:2rGMa =,又近同r r >,所以:近同a a <;由ma Tmr =224π得:r T a 224π=,又赤同r r >,所以:赤同a a >;向心加速度的大小关系为:赤同近a a a >>;4. 周期不同近地卫星的周期由224T mR mg π=得:==gR T 02πmin 84;同步卫星和赤道物体的周期都为24h ,周期的大小关系为:近赤同T T T >=;5. 线速度不同由r m r Mm G 22υ=得:rGM =υ,又近同r r >,所以:近同υυ<;由T r πυ2=和赤同r r >得:赤同υυ>,故线速度的大小关系为:赤同近υυυ>>;6. 角速度不同 由22ωmr r Mm G =得:3rGM=ω,又近同r r >,所以:近同ωω<;由赤同T T =得:赤同ωω=,从而角速度的大小关系为:近赤同ωωω<=。
必修2 第四章 专题突破 天体运动中的“三大难点”

专题突破天体运动中的“三大难点”突破一近地卫星、同步卫星及赤道上物体的运行问题如图1所示,a为近地卫星,半径为r1;b为地球同步卫星,半径为r2;c为赤道上随地球自转的物体,半径为r3。
图1近地卫星(r1、ω1、v1、a1)同步卫星(r2、ω2、v2、a2)赤道上随地球自转的物体(r3、ω3、v3、a3)向心力万有引力万有引力万有引力的一个分力轨道半径r2>r3=r1角速度由GMmr2=mω2r得ω=GMr3,故ω1>ω2同步卫星的角速度与地球自转角速度相同,故ω2=ω3ω1>ω2=ω3线速度由GMmr2=m v2r得v=GMr,故v1>v2由v=rω得v2>v3v1>v2>v3向心加速度由GMmr2=ma得a=GMr2,故a1>a2由a=ω2r得a2>a3a1>a2>a3【例1】 (2018·青海西宁三校联考)如图2所示,a 为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b 为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径约等于地球半径),c 为地球的同步卫星。
下列关于a 、b 、c 的说法中正确的是( )图2A.b 卫星转动线速度大于7.9 km/sB.a 、b 、c 做匀速圆周运动的向心加速度大小关系为a a >a b >a cC.a 、b 、c 做匀速圆周运动的周期关系为T c >T b >T aD.在b 、c 中,b 的速度大解析 b 为沿地球表面附近做匀速圆周运动的人造卫星,根据万有引力定律有G Mm R 2=m v 2R ,解得v =GMR ,代入数据得v =7.9 km/s ,故A 错误;地球赤道上的物体与同步卫星具有相同的角速度,所以ωa =ωc ,根据a =rω2知,c 的向心加速度大于a 的向心加速度,根据a =GM r 2得b 的向心加速度大于c 的向心加速度,即a b >a c >a a ,故B 错误;卫星c 为同步卫星,所以T a =T c ,根据T =2πr 3GM 得c 的周期大于b 的周期,即T a =T c >T b ,故C 错误;在b 、c 中,根据v =GM r ,可知b 的速度比c 的速度大,故D 正确。
高考一轮复习 专题4 天体运动的“两类热点”问题

专题四 天体运动的“两类热点”问题考点突破热点一 赤道上的物体、同步卫星和近地卫星师生共研1.同步卫星和近地卫星比较二者都是由万有引力提供向心力⎝ ⎛⎭⎪⎫GMm r 2=mv2r =m ω2r ,是轨道半径不同的两个地球卫星,应根据卫星运行参量的变化规律比较各物理量.2.同步卫星和赤道上的物体比较二者的角速度相同,即周期相等,半径不同,由此比较其他物理量.注意:赤道上的物体由万有引力和支持力的合力提供向心力,G Mm r 2=m v2r 不适用,不能按照卫星运行参量的变化规律判断.3.近地卫星和赤道上的物体比较先将近地卫星和赤道上物体分别与同步卫星比较,然后再对比二者的各物理量.例1 [2021·广州一模]如图所示,A 是地球的同步卫星,B 是地球的近地卫星,C 是地面上的物体,A 、B 、C 质量相等,均在赤道平面上绕地心做匀速圆周运动.设A 、B 、C 做圆周运动的向心加速度为a A 、a B 、a C ,周期分别为T A 、T B 、T C ,A 、B 、C 做圆周运动的动能分别为E kA 、E kB 、E kC .下列关系式正确的是( )A .aB =aC >a A B .a B >a A >a C C .T A =T B <T CD .E kA <E kB =E kC练1 国务院批复,自2016年起将4月24日设立为“中国航天日”.1970年4月24日我国首次成功发射的人造卫星东方红一号,目前仍然在椭圆轨道上运行,其轨道近地点高度约为440 km ,远地点高度约为2 060 km ;1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km 的地球同步轨道上.设东方红一号在远地点的加速度为a 1,东方红二号的加速度为a 2,固定在地球赤道上的物体随地球自转的加速度为a 3,则a 1、a 2、a 3的大小关系为( )A .a 2>a 1>a 3B .a 3>a 2>a 1C .a 3>a 1>a 2D .a 1>a 2>a 3练2 (多选)如图所示,同步卫星与地心的距离为r ,运行速率为v 1,向心加速度为a 1;地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则下列比值正确的是( )A.a1a2=rRB.a1a2=⎝⎛⎭⎪⎫Rr2 C.v1v2=rRD.v1v2=Rr题后反思赤道上的物体(A)、近地卫星(B)和地球同步卫星(C)之间常见的运动学物理量比较如下:半径r A<r B<r C周期T A=T C>T B角速度ωA=ωC<ωB线速度v A<v C<v B向心加速度a A<a C<a B热点二卫星(航天器)的变轨及对接问题多维探究题型1|卫星变轨问题1.卫星变轨的实质两类变轨离心运动近心运动变轨起因卫星速度突然增大卫星速度突然减小受力分析G<m G>m变轨结果变为椭圆轨道运动或在较大半径圆轨道上运动变为椭圆轨道运动或在较小半径圆轨道上运动2.人造卫星的发射过程,如图所示.(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.(2)在A点(近地点)点火加速,由于速度变大,万有引力不足以提供向心力,卫星做离心运动进入椭圆轨道Ⅱ.(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ.例2 近年来,我国的航天事业飞速发展,“嫦娥奔月”掀起高潮.“嫦娥四号”进行人类历史上的第一次月球背面登陆.若“嫦娥四号”在月球附近轨道上运行的示意图如图所示,“嫦娥四号”先在圆轨道上做圆周运动,运动到A点时变轨为椭圆轨道,B点是近月点,则下列有关“嫦娥四号”的说法正确的是( ) A.“嫦娥四号”的发射速度应大于地球的第二宇宙速度B.“嫦娥四号”要想从圆轨道进入椭圆轨道必须在A点加速C.“嫦娥四号”在椭圆轨道上运行的周期比圆轨道上运行的周期要长D.“嫦娥四号”运行至B点时的速率大于月球的第一宇宙速度题型2|卫星的对接问题在低轨道运行的卫星,加速后可以与高轨道的卫星对接.同一轨道的卫星,不论加速或减速都不能对接.例3 [2021·南宁一模]我国是少数几个掌握飞船对接技术的国家之一,为了实现神舟飞船与天宫号空间站顺利对接,具体操作应为( )A.飞船与空间站在同一轨道上且沿相反方向做圆周运动接触后对接B.空间站在前、飞船在后且两者沿同一方向在同一轨道做圆周运动,在合适的位置飞船加速追上空间站后对接C.空间站在高轨道,飞船在低轨道且两者同向飞行,在合适的位置飞船加速追上空间站后对接D.飞船在前、空间站在后且两者在同一轨道同向飞行,在合适的位置飞船减速然后与空间站对接题型3|变轨前、后各物理量的变化规律4 2020年10月6日,诺贝尔物理学奖的一半颁给了给出黑洞形成理论证明的罗杰·彭罗斯,引起世界轰动.黑洞是近代引力理论所预言的宇宙中的一种特殊天体,在黑洞引力范围内,任何物体都不能脱离它的束缚,甚至连光也不能射出,欧洲航天局由卫星观察发现银河系中心存在一个超大型黑洞,假设银河系中心仅存一个黑洞,太阳系绕银河系中心做匀速圆周运动,则根据下列哪组数据可以估算出该黑洞的质量(引力常量为已知)( )A.太阳系的质量和太阳系绕该黑洞公转的周期B.太阳系的质量和太阳系到该黑洞的距离C.太阳系的运行速度和该黑洞的半径D.太阳系绕该黑洞公转的周期和轨道的半径题后反思航天器变轨的问题“四个判断”(1)判断速度①在两轨道切点处,外轨道的速度大于内轨道的速度.②在同一椭圆轨道上,越靠近椭圆焦点速度越大.③对于两个圆轨道,半径越大速度越小.(2)判断加速度①根据a =,判断航天器的加速度.②公式a =对椭圆不适用,不要盲目套用.(3)判断机械能①在同一轨道上,航天器的机械能守恒.②在不同轨道上,轨道半径越大,机械能一定越大.(4)判断周期:根据开普勒第三定律,行星轨道的半长轴(半径)越大周期越长.题型4|卫星的追及相遇问题行星A和B围绕恒星O做匀速圆周运动,周期分别为T A和T B.设t=0时刻,A、B和O三者共线,则三者再次共线所需要的最少时间t满足以下条件:情境图若A、B公转方向相同若A、B公转方向相反t0=0时,A、B在O同侧(A、B再次在O同侧)⎝⎛⎭⎪⎫2πT B-2πT At=2πtT B-tT A=1(A、B再次在O同侧)⎝⎛⎭⎪⎫2πT A+2πT Bt=2πtT A+tT B=1t0=0时,A、B在O异侧⎝⎛⎭⎪⎫2πT B-2πT At=πtT B-tT A=12⎝⎛⎭⎪⎫2πT A+2πT Bt=πtT A+tT B=12例5 火星冲日现象即火星、地球和太阳刚好在一条直线上,如图所示.已知火星轨道半径为地球轨道半径的1.5倍,地球和火星绕太阳运行的轨道都视为圆且两行星的公转方向相同,则( ) A.火星与地球绕太阳运行的线速度大小之比为2:3B.火星与地球绕太阳运行的加速度大小之比为4:9C.火星与地球的公转周期之比为:D.2021年10月13日前有可能再次发生火星冲日现象练3 [2021·湖南怀化一模]随着嫦娥奔月梦想的实现,我国不断刷新深空探测的“中国高度”.“嫦娥”卫星整个飞行过程可分为三个轨道段:绕地飞行调相轨道段、地月转移轨道段、绕月飞行轨道段.我们用如图所示的模型来简化描绘“嫦娥”卫星飞行过程,假设调相轨道和绕月轨道的半长轴分别为a、b,公转周期分别为T1、T2.关于“嫦娥”卫星的飞行过程,下列说法正确的是( )A.=B.“嫦娥”卫星在地月转移轨道上运行的速度应大于11.2 km/sC.从调相轨道切入到地月转移轨道时,卫星在P点必须减速D.从地月转移轨道切入到绕月轨道时,卫星在Q点必须减速练4 [2021·成都七中二诊](多选)2020年3月9日我国成功发射第54颗北斗导航卫星,意味着北斗全球组网仅差一步之遥.人造卫星的发射过程要经过多次变轨方可到达预定轨道,如图所示,在发射地球同步卫星的过程中,卫星从近地圆轨道Ⅰ的A点先变轨到椭圆轨道Ⅱ,然后在B点变轨进入地球同步轨道Ⅲ,则( )A.卫星在同步轨道Ⅲ上的运行速度小于7.9 km/sB.卫星在轨道Ⅱ稳定运行时,经过A点时的速率比过B点时小C.若卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行的周期分别为T1、T2、T3,则T1<T2<T3D.现欲将卫星由轨道Ⅱ变轨进入轨道Ⅲ,则需在B点通过点火减速来实现思维拓展卫星通信中的“阴影区”问题在卫星的通信、观测星体问题中,由于另一个星体的遮挡出现“阴影区”,解决此类问题的基本方法是:(1)建立几何模型:通过构建平面几何画图,找出被星体挡的“阴影区”.(2)建立几何关系:关键是找出两个星体转动角度之间的几何关系.例1 [2020·福州二模]有一颗绕地球做匀速圆周运动的卫星,其运行周期是地球近地卫星的2倍,卫星圆形轨道平面与地球赤道平面重合,卫星上有太阳能收集板可以把光能转化为电能,已知地球表面重力加速度为g,地球半径为R,忽略地球公转,此时太阳处于赤道平面上,近似认为太阳光是平行光,则卫星绕地球一周,太阳能收集板的工作时间为( )A. B. C. D.例2 侦察卫星对国家有极高的战略意义,尤其是极地侦察卫星.极地侦察卫星在通过地球两极的圆轨道上运行,由于与地球自转方向垂直,所以理论上可以观察到地球上任何一处.假如它的运行轨道距地面高度为h,要使卫星在一天的时间内将地面上赤道各处在日照条件的情况下全都拍摄下来,在卫星通过赤道上空时,卫星上的摄像机至少应拍摄地面上赤道圆周的弧长是多少?(设地球半径为R,地面处的重力加速度为g,地球自转的周期为T)专题四天体运动的“两类热点”问题考点突破例1 解析:C与A的角速度相同,根据a=ω2r,可知a C<a A;根据卫星的加速度a=,可知a A<a B;所以a C<a A<a B,故A项错误,B项正确;对卫星A、B,由开普勒第三定律=k,知T A>T B,卫星A是地球的同步卫星,则T A=T C,所以T A=T C>T B,故C项错误;对于卫得A、B,由v=分析知v A<v B.由于卫星A、C角速度相等,由v=ωr分析知v C<v A,所以v C<v A<v B,卫星的动能为:E k=mv2可得:E kC<E kA<E kB,故D项错误.答案:B练1 解析:由于东方红二号卫星是同步卫星,则其角速度和赤道上的物体角速度相等,根据a=ω2r,r2>r3,则a2>a3;由万有引力定律和牛顿第二定律得,G=ma,由题目中数据可以得出,r1<r2,则;综合以上分析有,a1>a2>a3,选项D正确.答案:D练2 解析:对于卫星,其共同特点是由万有引力提供向心力,有G=m,故=.对于同步卫星和地球赤道上的物体,其共同特点是角速度相等,有a=ω2r,故=.答案:AD例2 解析:“嫦娥四号”的发射速度应大于地球的第一宇宙速度7.9 km/s,小于地球的第二宇宙速度11.2 km/s,故A错误;“嫦娥四号”要想从圆轨道变轨到椭圆轨道,必须在A点进行减速,故B错误;由开普勒第三定律知=,由题图可知,圆轨道的半径r大于椭圆轨道的半长轴a,故“嫦娥四号”在圆轨道上运行的周期T1大于在椭圆轨道上运行的周期T2,所以C错误;“嫦娥四号”要想实现软着陆,运行至B点时必须减速才能变为环月轨道,故在B点时的速率大于在环月轨道上运行的最大速率,即大于月球的第一宇宙速度,故D正确.答案:D例3 解析:飞船在轨道上高速运动,如果在同一轨道上沿相反方向运动,则最终会撞击而不是成功对接,故A项错误;两者在同一轨道上,飞船加速后做离心运动,则飞船的轨道抬升,故不能采取同一轨道加速对接,故B项错误;飞船在低轨道加速做离心运动,在合适的位置,飞船追上空间站实现对接,故C项正确;两者在同一轨道飞行时,飞船突然减速做近心运动,飞船的轨道高度要降低,故不可能与同一轨道的空间站实现对接,故D项错误.答案:C例4 解析:太阳系绕银河系中心的黑洞做匀速圆周运动,万有引力提供向心力,则有G=mr=m=mω2r=mωv,分析可知,要计算黑洞的质量M,需知道太阳系的公转周期T与轨道半径r,或者线速度v与轨道半径r,或者轨道半径r与角速度ω,或者角速度ω、线速度v与轨道半径r,选项A、B、C 错误,D正确.答案:D例5 解析:火星和地球绕太阳做圆周运动,万有引力提供向心力,有G=m=ma=m r,得v=,a=,T=2π.由v=可知v∝,则火星与地球的公转线速度大小之比为,选项A错误;由a=可知a∝,则火星与地球的向心加速度大小之比为4∶9,选项B正确;由T=2π可知T∝,则火星与地球公转周期之比为3∶2,选项C错误;再次相距最近时,地球比火星多转动一周,则据此有t=2π,其中T火∶T地=3∶2,解得t≈2.2年,故下一次发生火星冲日现象的时间为2022年10月13日前后,选项D错误.答案:B练3 解析:根据开普勒第三定律,调相轨道与绕月轨道的中心天体分别对应地球和月球,故它们轨道半长轴的三次方与周期的二次方比值不相等,故A错误;11.2 km/s是第二宇宙速度,是地球上发射脱离地球束缚的卫星的最小发射速度,由于嫦娥卫星没有脱离地球束缚,故其速度小于11.2 km/s,故B错误;从调相轨道切入到地月转移轨道时,卫星的轨道将持续增大,故卫星需要在P点做离心运动,故在P 点需要加速,故C错误;从地月转移轨道切入到绕月轨道时,卫星相对月球而言,轨道半径减小,需要在Q点开始做近心运动,故卫星需在Q点减速,故D正确.答案:D练4 解析:卫星绕地球做匀速圆周运动,万有引力提供向心力,有=,得v=.可知卫星运动半径r越大,运行速度v越小,所以卫星绕近地轨道运行时速度最大,即地球的最大的环绕速度(7.9 km/s),则卫星在同步轨道Ⅲ上的运行速度小于7.9 km/s,选项A正确.卫星在轨道Ⅱ上从A向B运动过程中,万有引力对卫星做负功,动能逐渐减小,速率也逐渐减小,所以卫星在轨道Ⅱ上过A点的速率比卫星在轨道Ⅱ上过B点的速率大,选项B错误.设卫星在轨道Ⅰ上运行的轨道半径为r1、轨道Ⅱ的半长轴为r2、在轨道Ⅲ上运行的轨道半径为r3.根据图中几何关系可知r1<r2<r3,又由开普勒第三定律有=k,可得T1<T2<T3,选项C正确.卫星在B点要进入Ⅲ必须加速做离心运动,所以卫星在B点通过点火加速可实现由轨道Ⅱ进入轨道Ⅲ,选项D错误.答案:AC思维拓展典例1 解析:地球近地卫星做匀速圆周运动,根据牛顿第二定律:mg=mR T=2π,此卫星运行周期是地球近地卫星的2倍,所以该卫星运行周期T′=4π,由=m′r,=m′g,得r=2R.如图,当卫星在阴影区时不能接受阳光,据几何关系:∠AOB=∠COD=,卫星绕地球一周,太阳能收集板工作时间为:t=T′=.答案:C典例2 解析:设卫星运行周期为T1,则有G=(h+R)物体处于地面上时有G=m0g解得T1=在一天内卫星绕地球转过的圈数为,即在一天中有次经过赤道上空,所以每次摄像机拍摄的赤道弧长为s==T1,将T1代入,可得s=.答案:。
浅析“天体运动”考题的破题技巧

浅析“天体运动”考题的破题技巧天体运动是物理学和天文学中一个非常重要的概念,也是考试中经常会涉及到的一个知识点。
在考试中,天体运动的题目往往是一些较为复杂和抽象的问题,需要考生具备一定的物理和数学知识,才能正确解答。
所以,掌握破解天体运动考题的技巧对于考生来说是非常重要的。
下面将从几个方面来浅析破解天体运动考题的技巧。
一、掌握天体运动的基本概念要想破解天体运动的考题,首先必须要掌握天体运动的基本概念。
天体运动是指天体在宇宙空间中的运动规律,包括行星的公转和自转、月球的公转和自转等。
还有一些特殊的天体运动现象,如日食、月食、日月飨交食等。
了解这些基本概念,对于解答天体运动的考题至关重要。
二、掌握一定的数学和物理知识天体运动考题往往伴随着一定的数学和物理知识,考生在破解这类考题时,必须要掌握一定的数学和物理知识。
比如要了解行星的轨道是椭圆形的,需要用到椭圆的相关知识;要分析行星的自转和公转,需要用到角度、速度、加速度等物理知识。
只有掌握了相关的数学和物理知识,才能更好地解答天体运动的考题。
三、善于运用逻辑思维解答天体运动的考题需要善于运用逻辑思维。
因为这类考题往往比较复杂,需要通过分析问题,找出其中的逻辑关系,然后运用相关的知识来解决。
比如在分析一个行星的轨道的时候,可以先根据已知的条件,推导出不同的结果,再根据不同的结果来分析行星的轨道特征。
只有善于运用逻辑思维,才能更加容易地解答这类考题。
四、多做题多练习五、了解常见的考题类型在解答天体运动的考题时,需要了解一些常见的考题类型。
比如有关行星轨道的计算、行星自转和公转的关系、天体运动的定律等。
只有了解了常见的考题类型,才能更好地有针对性地进行准备。
六、注意题目中的关键词解答天体运动的考题时,需要特别注意题目中的关键词。
因为这些关键词往往能够帮助我们更好地理解题目,从而更准确地进行解答。
比如有些题目中可能会出现“质点”、“轨道”、“角速度”等关键词,只有在理解了这些关键词的含义后,才能更好地解答问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理三轮复习难点绝对突破7-万有引力定律专题万有引力定律与牛顿三定律,并称经典力学四大定律,可见万有引力定律的重要性。
万有引力定律定律已成为高考和各地模拟试卷命题的热点。
此部分内容在《考纲》中列为Ⅱ级要求。
有关题目立意越来越新,但解题涉及的知识,难度不大,规律性较强。
特别是随着我国载人飞船升空和对空间研究的深入,高考对这部分内容的考查将会越来越强。
一、对万有定律的理解1.万有引力定律发现的思路、方法开普勒解决了行星绕太阳在椭圆轨道上运行的规律,但没能揭示出行星按此规律运动的原因.英国物理学家牛顿(公元1642~1727)对该问题进行了艰苦的探索,取得了重大突破.首先,牛顿论证了行星的运行必定受到一种指向太阳的引力.其次,牛顿进一步论证了行星沿椭圆轨道运行时受到太阳的引力,与它们的距离的二次方成反比.为了在中学阶段较简便地说明推理过程,课本中是将椭圆轨道简化为圆形轨道论证的.第三,牛顿从物体间作用的相互性出发,大胆假设并实验验证了行星受太阳的引力亦跟太阳的质量成正比.因此得出:太阳对行星的行力跟两者质量之积成正比.最后,牛顿做了著名的“月一地”检验,将引力合理推广到宇宙中任何两物体,使万有引力规律赋予普遍性.2.万有引力定律的检验牛顿通过对月球运动的验证,得出万有引力定律,开始时还只能是一个假设,在其后的一百多年问,由于不断被实践所证实,才真正成为一种理论.其中,最有效的实验验证有以下四方面.⑴.地球形状的预测.牛顿根据引力理论计算后断定,地球的赤道部分应该隆起,形状像个橘子.而笛卡尔根据旋涡假设作出的预言,地球应该是两极伸长的扁球体,像个柠檬.1735年,法国科学院派出两个测量队分赴亦道地区的秘鲁(纬度φ=20°)和高纬度处的拉普兰德(φ=66°),分别测得两地1°纬度之长为:赤道处是110600m,两极处是111900m.后来,又测得法国附近纬度1°的长度和地球的扁率.大地测量基本证实了牛顿的预言,从此,这场“橘子与柠檬”之争才得以平息.⑵.哈雷彗星的预报.英国天文学家哈雷通过对彗星轨道的对照后认为,1682年出现的大彗星与1607年、1531年出现的大彗星实际上是同一颗彗星,并根据万有引力算出这个彗星的轨道,其周期是76年.哈雷预言,1758年这颗彗星将再次光临地球.于是,预报彗星的回归又一次作为对牛顿引力理论的严峻考验.后来,彗星按时回归,成为当时破天荒的奇观,牛顿理论又一次被得到证实.⑶.海王星的发现.⑷.万有引力常量的测定.由此可见,一个新的学说决不是一蹴而就的,也只有通过反复的验证,才能被人们所普遍接受.3.万有引力定律的适用条件例1、如下图所示,在半径R=20cm、质量M=168kg的均匀铜球中,挖去一球形空穴,空穴的半径为要,并且跟铜球相切,在铜球外有一质量m=1kg、体积可忽略不计的小球,这个小球位于连接铜球球心跟空穴中心的直线上,并且在空穴一边,两球心相距是d=2m,试求它们之间的相互吸引力.解: 完整的铜球跟小球m 之间的相互吸引力为2dMm GF =这个力F 是铜球M 的所有质点和小球m 的所有质点之间引力的总合力,它应该等于被挖掉球穴后的剩余部分与半径为娄的铜球对小球m 的吸引力 F=F 1+F 2.式中F 1是挖掉球穴后的剩余部分对m 的吸引力,F 2是半径为R /2的小铜球对m 的吸引力。
因为22)2(8R d m MGF -=,所以挖掉球穴后的剩余部分对小球的引力为F 1=F -F 2=2.41×10-9N例2、深入地球内部时物体所受的引力 假设地球为正球体,各处密度均匀.计算它对球外物体的引力,可把整个质量集中于球心.如果物体深入地球内部,如何计算它所受的引力?如右图所示,设一个质量为m 的物体(可视为质点)在地层内离地心为r 的A 处.为了计算地球对它的引力,把地球分成许多薄层.设过A 点的对顶锥面上两小块体积分别为△V 1、△V 2.当△V 1和△V 2很小时,可以近似看成圆台.已知圆台的体积公式)(31212221R R R R H V ++=π式中R 1和R 2分别是上、下两底面的半径.当圆台很小很薄时,且H << a ,H << b 时,R 1≈R 2≈R .那么V=πHR 2根据万有引力定律 θρπθρπ2222211sinsinH Gm aa m Gam m GF ==∆=∆θρπθρπ222222sinsin2H Gm bb m Gbm m GF ==∆=∆所以21F F ∆=∆,即两小块体积的物体对A 处质点的引力大小相等,且方向相反,它们的合力为零.当把地球分成许多薄层后,可以看到,位于A 点以外的这一圈地层(右图中用斜线表示)对物体的引力互相平衡,相当于对A 处物体不产生引力,对A 处物体的引力完全由半径为r 的这部分球体产生.引力大小为:m r G rmr Grm M GF r r ρπρπ22323434=∙==即与离地心的距离成正比.当物体位于球心时,r=0,则F r =O .它完全不受地球的引力. 所以,当一个质量为m 的物体从球心(r =0)逐渐移到球外时,它所受地球的引力F 随r的变化关系如右图所示.即先随r 的增大正比例地增大;后随r 的增大,按平方反比规律减小;当r =R 0(地球半径)时,引力20R Mm GF =.4.注意领会卡文迪许实验设计的巧妙方法. 由万有引力定律表达式221rm m GF =可知,212m m FrG =,要测定引力常量G ,只需测出两物体m 1、m 2间距离r 及它们间万有引力F 即可.由于一般物体间的万有引力F 非常小,很难用实验的方法显示并测量出来,所以在万有引力定律发现后的百余年间,一直没有测出引力常量的准确数值.卡文迪许巧妙的扭秤实验通过多次“放大”的办法解决了这一问题.图是卡文迪许实验装置的俯视图.首先,图中固定两个小球m 的r 形架,可使m 、m’之间微小的万有引力产生较大的力矩,使金属丝产生一定角度的偏转臼,这是一次“放大”效应.其次,为了使金属丝的微小形变加以“放大”,卡文迪许用从1发出的光线射到平面镜M 上,在平面镜偏转θ角时,反射光线偏转2θ角,可以得出光点在刻度尺上移动的弧长s =2θR ,增大小平面镜M 到刻度尺的距离R ,光点在刻度尺上移动的弧长S 就相应增大,这又是一次“放大”效应.由于多次巧妙“放大”,才使微小的万有引力显示并测量出来.除“放大法”外,物理上观察实验效果的方法,还包括“转换法”、“对比法”等.深刻认识卡文迪许实验的意义(1)卡文迪许通过改变质量和距离,证实了万有引力的存在及万有引力定律的正确性. (2)第一次测出了引力常量,使万有定律能进行定量计算,显示出真正的实用价值. (3)标志着力学实验精密程度的提高,开创了测量弱力的新时代. (4)表明:任何规律的发现总是经过理论上的推理和实验上的反复验证才能完成.5.物体在地面上所受的引力与重力的区别和联系地球对物体的引力是物体具有重力的根本原因.但重力又不完全等于引力.这是因为地球在不停地自转,地球上的一切物体都随着地球自转而绕地轴做匀速圆周运动,这就需要向心力.这个向心力的方向是垂直指向地轴的,它的大小是2ωr m f =,式中的r 是物体与地轴的距离,ω是地球自转的角速度.这个向心力来自哪里?只能来自地球对物体的引力F ,它是引力F 的一个分力如右图,引力F 的另一个分力才是物体的重力mg .在不同纬度的地方,物体做匀速圆周运动的角速度ω相同,而圆周的半径r 不同,这个半径在赤道处最大,在两极最小(等于零).纬度为α处的物体随地球自转所需的向心力αωcos 2R m f = (R 为地球半径),由公式可见,随着纬度升高,向心力将减小,在两极处Rcos α=0,f =0.作为引力的另一个分量,即重力则随纬度升高而增大.在赤道上,物体的重力等于引力与向心力之差.即.2RMm Gmg =.在两极,引力就是重力.但由于地球的角速度很小,仅为10-5rad /s 数量级,所以mg 与F 的差别并不很大.在不考虑地球自转的条件下,地球表面物体的重力.RMmG mg 2=这是一个很有用的结论.从图中还可以看出重力mg 一般并不指向地心,只有在南北两极和赤道上重力mg 才能向地心.同样,根据万有引力定律知道,在同一纬度,物体的重力和重力加速度g 的数值,还随着物体离地面高度的增加而减小.若不考虑地球自转,地球表面处有.2RMm Gmg =,可以得出地球表面处的重力加速度.2RM Gg =.在距地表高度为h 的高空处,万有引力引起的重力加速度为g ',由牛顿第二定律可得:2)(h R Mm Gg m +=' 即g h R Rh R M Gg 222)()(+=+='如果在h =R处,则g '=g /4.在月球轨道处,由于r =60R,所以重力加速度: g '= g /3600.重力加速度随高度增加而减小这一结论对其他星球也适用.例3、某行星自转一周所需时间为地球上的6h ,在这行星上用弹簧秤测某物体的重量,在该行量赤道上称得物重是两极时测得读数的90%,已知万有引力恒量G =6.67×10-11N·m 2/kg 2,若该行星能看做球体,则它的平均密度为多少?[解析]在两极,由万有引力定律得 .2RMm Gmg = ①在赤道R Tmg m RMm G 2224π+'= ②依题意mg '=O.9m g ③由式①②③和球体积公式联立解得332/1003.31.03m kg GT⨯==πρ二、万有引力定律在天文学上的应用1. 万有引力定律提供天体做圆周运动的向心力⑴人造地球卫星的绕行速度、角速度、周期与半径的关系 ①由rvmrMm G22=得r GM v =r 越大,v 越小②由22ωmr rMm G=得3rGM =ω r 越大,ω越小③由r TmrMm G2224π=得GMr T 324π=r 越大,T 越大例4、土星外层上有一个环。
为了判断它是土星的一部分还是土星的卫星群,可以测量环中各层的线速度a 与该l 层到土星中心的距离R 之间的关系来判断: ( AD )A .若v ∝R ,则该层是土星的一部分;B .若v 2∝R ,则该层是土星的卫星群C .若v ∝1/R ,则该层是土星的一部分D .若v 2∝1/R ,则该层是土星的卫星群 ⑵求天体质量、密度由r TmrMm G2224π= 334R M πρ= 即可求得注意天体半径与卫星轨迹半径区别⑶人造地球卫星的离心向心问题例5、在地球大气层外有很多太空垃圾绕地球做匀速圆周运动,每到太阳活动期,由于受太阳的影响,地球大气层的厚度开始增加,从而使得部分垃圾进入大气层,开始做靠近地球的向心运动,产生这一结果的原因是 ( C ) A .由于太空垃圾受到地球引力减小而导致的向心运动 B .由于太空垃圾受到地球引力增大而导致的向心运动 C .由于太空垃圾受到空气阻力而导致的向心运动D .地球引力提供了太空垃圾做圆周运动所需的向心力,故产生向心运动的结果与空气阻力无关例6、宇宙飞船要与轨道空间站对接,飞船为了追上轨道空间站 ( A ) A .只能从较低轨道上加速 B .只能从较高轨道上加速C .只能从同空间站同一高度轨道上加速D .无论在什么轨道上,只要加速都行 2. 人造地球卫星⑴宇宙速度第一宇宙速度s m v /109.731⨯=,是地球卫星的最小发射速度,也是地球卫星在近地轨道上运行时的速度. 由mgRvmRMm G==22得sm gR RGM v /109.73⨯===.例7、1990年3月,紫金山天文台将1965年9月20日发现的第2752号小行星命名为吴健雄星,其直径为32 km ,如该小行星的密度和地球相同,则其第一宇宙速度为 m /s ,已知地球半径R=6400km ,地球的第一宇宙速度为8 km /s .(20m /s ) 第二宇宙速度的计算如果人造卫星进入地面附近的轨道速度等于或大于1l.2km /s ,就会脱离地球的引力,这个速度称为第二宇宙速度.为了用初等数学方法计算第二宇宙速度,设想从地球表面至无穷远处的距离分成无数小段ab 、bc 、…,等分点对应的半径为r 1、r 2…,如下图所示.由于每一小段ab 、bc 、cd…极小,这一小段上的引力可以认为不变.因此把卫星从地表a 送到b 时,外力克服引力做功)11()()(111121r RGMm R r r R Mm GR r RMm GW -=-∙=-=同理,卫星从地表移到无穷远过程中,各小段上外力做的功分别为)11(212r r GMm W -=)11(323r r GMm W -=…)11(1n n n r r GMm W -=-)11(∞∞-=r r GMm W n把卫星送至无穷远处所做的总功 RMm G W W W W W W n =+++++=∞ 321为了挣脱地球的引力卫星必须具有的动能为RMm GW mv ==2221所以s km gR RGM v /2.11222===第三宇宙速度的推算脱离太阳引力的速度称为第三宇宙速度.因为地球绕太阳运行的速度为v 地=30km/s ,根据推导第二宇宙速度得到的脱离引力束缚的速度等于在引力作用下环绕速度的2倍,即s km s km v /4.42/3022=⨯=地因为人造天体是在地球上,所以只要沿地球运动轨道的方向增加△v =12.4km /s 即可,即需增加动能2)(21v m ∆.所以人造天体需具有的总能量为 2322221)(2121mv v m mv E =∆+=得第三宇宙速度s km v /7.163=。
