一次函数解析式的求法
一次函数解析式快速求法(一秒出答案)
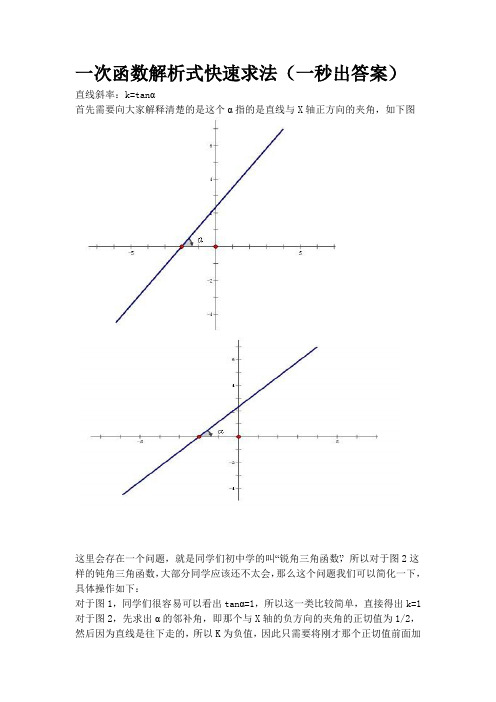
一次函数解析式快速求法（一秒出答案）直线斜率：k=tanα首先需要向大家解释清楚的是这个α指的是直线与X轴正方向的夹角，如下图这里会存在一个问题，就是同学们初中学的叫“锐角三角函数”，所以对于图2这样的钝角三角函数，大部分同学应该还不太会，那么这个问题我们可以简化一下，具体操作如下：对于图1，同学们很容易可以看出tanα=1，所以这一类比较简单，直接得出k=1 对于图2，先求出α的邻补角，即那个与X轴的负方向的夹角的正切值为1/2，然后因为直线是往下走的，所以K为负值，因此只需要将刚才那个正切值前面加上“－”号就可以了，即K=tanα=－1/2。
它在求一次函数的解析式的时候能减少计算量，节省考试时间。
举例说明：已知直线过A(-1，5)， B(1，-1)两点，求直线的解析式。
常规方法是将这两点代入y=kx+b，然后解二元一次方程组，那么同学们可以这样操作：首先可以简单画个草图，然后像我这样构造一个直角三角形，tan∠ABC=3,又因为直线往下走，所以k=-3，于是直线解析式为y=－3x+b,再将(1，-1)代入，可口算出b=2，所以直线解析式为y=－3x+2。
肯定有同学认为这样做学校老师不会给分的，那么我教大家一个可以拿分的办法：考试的时候试卷上这样写：“将A,B两点坐标代入y=kx+b，解得k=-3,b=2。
”所有老师都希望学生通过解二元一次方程组来求这个直线解析式，但事实上我们可以偷偷使用我教的这个方法，但是卷面上可以假装解了一个二元一次方程组，老师不会看具体计算过程，因此这样写老师是会给分的。
一次函数解析式练习题一次函数及其图像是初中代数的重要内容，也是高中解析几何的基石，更是中考的重点考查内容。
其中求一次函数解析式就是一类常见题型。
例1. 已知函数y m x m=-+-()3328是一次函数，求其解析式。
例2. 已知一次函数y kx =-3的图像过点（2，－1），求这个函数的解析式。
例3. 已知某个一次函数的图像与x 轴、y 轴的交点坐标分别是（－2，0）、（0，4），求这个函数的解析式。
一次函数解析式的求法
2021/5/27
3. 若直线y=3x+b与两坐标轴 所围成的三角形的面积是6个 面积单位，求b的值.
15
2021/5/27
4.一次函数的图象与直线x+y6=0交于A(5,m)点，且与直线 y=2x-3无交点，求一次函数的 解析式。
16
2021/5/27
6、已知直线y=kx+b经过点 （2.5，0），且与坐标轴所围 成的三角形的面积为6.25，求 该直线的解析式。 7、已知直线y=2x-4向左平移4 个单位后的解析式 8、判断点A(3，2)、B(-3，1)、 C(1，1)是否在一直线上？
为y_＝__2_x_+__1___.
11
你会用所学知识解决生活中的问2021/5题/27 吗?
(4)生物学家研究表明： 某种蛇的长度y(cm)是其尾长x(cm)的一次函数； 当蛇的尾长为 14cm时, 蛇的长为105.5cm; 当蛇的尾长为6 cm时, 蛇的长为45.5 cm； 当蛇的尾长为10 cm时,这条蛇的长度是多少?
x -2 -1 0 1
y3
10
其中有一格不慎被墨汁遮住了,想想看， 该空格里原来填的数是多少？
13
2021/5/27
1、一次函数的图象经过点(0,2),且与 两坐标轴形成的三角形面积等于1.求 出一次函数的解析式. 2、一次函数y=2x-2（1）向下平移4 个单位得到的解析式（2）向右平移2 个单位后的解析式（3）直线l与一次 函数y=2x-2直线关于x轴对称,求解析 式。
3
1．用待定系数法求一次函数的解析式 (1)先设出函数解析式，再根据条件确定解析式中未知数的 ___系__数___，从而具体写出这个式子的方法，叫做待__定__系__数__法__． (2)探究：已知一次函数的图象经过(2,5)和(－4,2)，求这个 一次函数的解析式．
函数解析式的常用求解方法函数解析式的求解九种方式函数解析式有几种形式
一、函数解析式的常用求解方法（1）待定系数法：（已知函数类型如：一次、二次函数、反比例函数等）：若已知f（x）的结构时，可设出含参数的表达式，再根据已知条件，列方程或方程组，从而求出待定的参数，求得f（x）的表达式。
待定系数法是一种重要的数学方法，它只适用于已知所求函数的类型求其解析式。
（2）换元法（注意新元的取值范围）：已知f（g（x））的表达式，欲求f（x），我们常设t=g（x），从而求得，然后代入f（g （x））的表达式，从而得到f（t）的表达式，即为f（x）的表达式。
（3）配凑法（整体代换法）：若已知f（g（x））的表达式，欲求f（x）的表达式，用换元法有困难时，（如g（x）不存在反函数）可把g（x）看成一个整体，把右边变为由g（x）组成的式子，再换元求出f （x）的式子。
（4）消元法（如自变量互为倒数、已知f（x）为奇函数且g（x）为偶函数等）：若已知以函数为元的方程形式，若能设法构造另一个方程，组成方程组，再解这个方程组，求出函数元，称这个方法为消元法。
（5）赋值法（特殊值代入法）：在求某些函数的表达式或求某些函数值时，有时把已知条件中的某些变量赋值，使问题简单明了，从而易于求出函数的表达式。
二、函数解析式的求解九种方式：1.代入法：已知f(x)的解析式,求f[g(x)] 的解析式.[例1] 若f(x)=2x＋1,g(x)=x－1, 求f[g(x)],g[f(x)].2. 换元法已知f[g(x)]=h(x), 求f(x)的解析式.令g(x)=tx=(t),则f(t)=h[(t)],再将t换成x即可.但要注意换元前后变量的等价性。
[例2] 已知f( +1)= x+2 ,求f(x),f(x+1).3.配凑法已知f[g(x)]=h(x), 求f(x)的解析式。
若能将h(x)用g(x)表示, 然后用x去代换g(x),则就可以得到f(x)的解析式。
[例3] 已知f(x+ )= x3 + , 求f(x)，f(x+1).4.待定系数法根据已知函数的类型或者特征,求函数解析式。
一次函数解析式求法
斜率 $k$ 的意义
截距 $b$ 的意义
解析式求法
表示函数图像的倾斜程度，$k > 0$ 时图像上升，$k < 0$ 时图像下降。
表示函数图像与 $y$ 轴交点的纵坐标。
通过已知的两个点坐标，利用两点式或点斜式求出一次函数的解析式。
关键知识点总结
忽视斜率 $k neq 0$ 的条件，将常数函数误认为一次函数。
已知斜率和一点坐标求解析式
已知一次函数的图像经过点 $(2, 3)$ 和 $(-1, -2)$，求这个一次函数的解析式。
例题
设一次函数解析式为 $y = kx + b$，根据已知条件列方程组
解
实际应用举例
$$begin{cases}
3 = 2k + b
2 = -k + b
实际应用举例
end{cases}$$
将求得的待定系数代回原解析式后，必须验证是否满足已知条件。
误区提示：常见的误区有以下几点
注意事项与误区提示
忽略了已知条件对解析式的限制；
在列方程或方程组时出现了错误；
在解方程或方程组时出现了计算错误；
没有验证求得的解析式是否满足已知条件。
01
02
03
04
注意事项与误区提示
04
解析式求法之图像法
创新思维在求解过程中运用
逆向思维
从问题的结论出发，逆向推导问题的条件，从而找到解决问题的新思路。
类比思维
将问题与其他类似问题进行类比，借鉴其他问题的解决方法，以启发新的解题思路。
转化思维
将问题转化为另一种形式或模型，以便利用已知的知识和方法进行求解。
06
总结回顾与拓展延伸
一次函数解析式23招经典解法
一次函数表达式的方法解法（23招）求一次函数的表达式基本解法1、待定系数法（1）图象过原点：函数为正比例函数，可设表达式为y=kx ，再找图象上除原点外的一个点的坐标代入表达式，即可求出k.（2）图象不过原点：函数为一般的一次函数，可设表达式为y=kx+b ，再找图象上的两个点的坐标代入表达式，即可求出k ，b 。
例：已知一次函数y=kx+b （k ，b 为常数且0≠k ）的图象经过点A （0，－2）和点B （1，0），则k=______，b=______.答案：k=2，b=-2例：已知正比例函数)0(≠=k kx y 的图象经过点（1，－2），则这个正比例函数的表达式为______.答案：y=-2x常见解法：1、定义式例：已知函数3)3(82+-=-mx m y 是一次函数，求其解析式。
解析：该函数是一次函数， ∴182=-m解得m=±3,又m≠3∴m=-3故解析式为y=-6x+32、点斜式要点：如何求k ？（1）公式：1212x x y y k --=，（2）图象（比值）：|k |=BCAB (两直角边的比） （3）增量：V （速度）、P （电功率）（4）平移变换：k 值相等（5）垂直变换：121-=k k（6）对称变换：|k|、|b|不变（7）相似比：(略)（8）正切值：tanα（斜率）（9）旋转变换：（略）例：已知一次函数y=kx-3的图象过点（2，-1），求这个函数解析式。
解析：方法一：（代入法）将点（2,-1）代入y=kx-3得，-1=2k-3，解得k=1.故解析式为y=x-3方法二：（一点式）解析：一次函数y=kx-3的图象过点（2，-1），∴可令y=k(x-2)-1=kx-2k-1，∴-2k-1=-3,解得k=1，∴这个函数解析式为y=x-3.3、两点式例：一次函数经过（-2，0)、(0，4),求此函数的解析式。
解析：方法一：（构建方程组）令解析式为y=kx+b,过（-2,0)、(0,4)，则⎩⎨⎧=+-=b b k 420 解得k=2，b=4 故解析式为y=2x+4. 方法二：由点斜式，得)2(0041212---=--=x x y y k =2 再一点式，得y=2(x+2)+0=2x+4方法三：由斜截式，得y=2x+4方法四：由数形结合，得y=2x+4(k=直角边的比）方法五：（纯一点式）y=k(x+2)=k(x+0)+4⇒k=24、一点式：例：过（2,5）的一次函数解析式为_____。
函数解析式的求法
函数解析式的求法1.待定系数法例1.求一次函数y=f(x)解析式，使f(f(x))=4x+3.解：设f(x)=ax+b(a≠0).∴f(f(x))==af(x)+b=a(ax+b)+b=a^2x+ab+b∴a^2x+ab+b=4x+3∴a^2=4,ab+b=3解得a=2,b=1或a=-2,b=-3.∴f(x)=2x+1或f(x)=-2x-3.总结：当已知函数类型时，求函数解析式，常用待定系数法。
其基本步骤：设出函数的一般式，代入已知条件通过解方程（组）确定未知系数。
2.换元法换元法就是引进一个或几个新的变量来替换原来的某些量的解题方法，它的目的是化繁为简、化难为易，以快速的实现从未知向已知的转换，从而达到顺利解题的目的。
常见换元法是多种多样的，如局部换元、整体换元、分母换元、平均换元等，应用极为广泛。
例2.已知f(1-√x)=x.求f(x).解：设1-√x=t,则x=(1-t)^2∵x≥0,∴t≤1,∴f(t)=(1-t)^2(t≤1)∴f(x)=(1-x)^2(x≤1)(函数变量的无关性)总结：(1)利用换元法解题时，要注意在换元时易引起定义域的变化，所以最后的结果要注意所求函数的定义域。
(2)函数变量的无关性，变量无论是用x还是用t表示，都无关紧要，函数依然成立。
3.配凑法例3.已知f(3x+1)=9x^2-6x+5,求f(x).解：∵f(3x+1)=9x^2-6x+5=(3x+1)^2-12x+4=(3x+1)^2-4(3x+1)+8∴f(x)=x^2-4x+8总结：当已知函数表达式比较简单时，可直接应用配凑法，即根据具体的解析式凑出复合变量的形式，从而求出函数解析式。
4.消元法（又叫解方程组法）例4.已知函数f(x)满足条件：f(x)+2f(1/x)=x,求f(x).分析：用1/x代替条件方程中的x得：f(1/x)+2f(x)=1/x.把它与原条件式联立。
用消元法消去f(1/x),即得f(x)的解析式。
一次函数解析式快速求法(一秒出答案)
一次函数解析式快速求法（一秒出答案）
直线斜率：k=tanα
首先需要向大家解释清楚的是这个α指的是直线与X轴正方向的夹角，如下图
这里会存在一个问题，就是同学们初中学的叫“锐角三角函数”，所以对于图2这样的钝角三角函数，大部分同学应该还不太会，那么这个问题我们可以简化一下，具体操作如下：
对于图1，同学们很容易可以看出tanα=1，所以这一类比较简单，直接得出k= 1
对于图2，先求出α的邻补角，即那个与X轴的负方向的夹角的正切值为1/2，
然后因为直线是往下走的，所以K为负值，因此只需要将刚才那个正切值前面加上“－”号就可以了，即K=tanα=－1/2。
它在求一次函数的解析式的时候能减少计算量，节省考试时间。
举例说明：已知直线过A(-1，5)， B(1，-1)两点，求直线的解析式。
常规方法是将这两点代入y=kx+b，然后解
二元一次方程组，那么同学们可以这样操作：
首先可以简单画个草图，然后像我这样构造一个直角三角形，tan∠ABC=3,又因为直线往下走，所以k=-3，于是直线解析式为y=－3x+b,再将(1，-1)代入，可口算出b=2，所以直线解析式为y=－3x+2。
肯定有同学认为这样做学校老师不会给分的，那么我教大家一个可以拿分的办法：
考试的时候试卷上这样写：“将A,B两点坐标代入y=kx+b，解得k=-3,b=2。
”
所有老师都希望学生通过解二元一次方程组来求这个直线解析式，但事实上我们可以偷偷使用我教的这个方法，但是卷面上可以假装解了一个二元一次方程组，老师不会看具体计算过程，因此这样写老师是会给分的。
友情提示：本资料代表个人观点，如有帮助请下载，谢谢您的浏览！。
七种求法求函数解析式
七种求法求函数解析式七种求函数解析式的方法一、待定系数法：已知函数的解析式时，可以使用待定系数法构造函数。
例如，设$f(x)$是一次函数，且$f[f(x)]=4x+3$，求$f(x)$的解析式。
设$f(x)=ax+b(a\neq0)$，则$f[f(x)]=af(x)+b=a(ax+b)+b=a^2x+ab+b$。
根据题意，有$a^2=4$，解得$a=2$或$a=-2$。
再代入$f[f(x)]=4x+3$中，解得$b=1$或$b=3$。
因此，$f(x)=2x+1$或$f(x)=-2x+3$。
二、配凑法：已知复合函数$f[g(x)]$的表达式，求$f(x)$的解析式，可以使用配凑法。
但需要注意所求函数$f(x)$的定义域不是原复合函数的定义域，而是$g(x)$的值域。
例如，已知$f(x+1)=(x+1)^2-2$，求$f(x)$的解析式。
将$x$换成$x-1$，得$f(x)=(x-1)^2-2(x\geq2)$。
三、换元法：已知复合函数$f[g(x)]$的表达式时，可以使用换元法求$f(x)$的解析式。
与配凑法类似，需要注意所换元的定义域的变化。
例如，已知$f(x+1)=x+2x$，求$f(x)$的解析式。
令$t=x+1$，则$t\geq1$，$x=(t-1)$，$f(t)=(t-1)^2+2(t-1)=t^2-1$，因此$f(x)=x^2-1(x\geq1)$。
四、代入法：求已知函数关于某点或者某条直线的对称函数时，一般使用代入法。
例如，已知函数$y=x+\sqrt{x}$与$y=g(x)$的图像关于点$(-2,3)$对称，求$g(x)$的解析式。
设$M(x,y)$为$y=g(x)$上任一点，且$M'(x',y')$为$M(x,y)$关于点$(-2,3)$的对称点，则$x'+x=-4$，$y'+y=6$，解得$y=-x-7+\sqrt{x+4}$，因此$g(x)=-x^2-7x-6$。
求一次函数的解析式的方法
求一次函数的解析式的方法
一次函数是形如y=ax+b的函数，其中a和b为常数。
求一次函数的解析式的方法如下：
1.通过已知的点求解析式
如果已知一次函数经过某个点(x1, y1)，那么可以将这个点代入函数中，得到一个方程：y1=ax1+b，其中a和b为未知数。
此时可以再通过另一个点(x2, y2)来构建另一个方程：y2=ax2+b。
解这个方程组即可得到a和b的值。
2.通过斜率和截距求解析式
一次函数的斜率就是a，截距就是b。
如果已知斜率和截距，那么可以将它们代入y=ax+b中，得到函数的解析式。
3.通过两个点的坐标差求解析式
如果已知一次函数经过两个点(x1, y1)和(x2, y2)，那么可以求出两点的坐标差Δx和Δy。
由于a表示函数的斜率，因此有a=Δy/Δx。
将a和其中一个点的坐标代入y=ax+b中，再解出b的值，即可得到函数的解析式。
总之，求一次函数的解析式需要从已知条件入手，通过方程求解的方法得到函数的斜率和截距，进而得到函数的解析式。
- 1 -。
函数解析式的七种求法
函 数 解 析 式 的 七 种 求 法一、 待定系数法：在已知函数解析式的构造时，可用待定系数法。
例1 设)(x f 是一次函数，且34)]([+=x x f f ，求)(x f解：设b ax x f +=)( )0(≠a ，则b ab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 练习1. 已知x 2x )1x (f +=+，求)x (f 。
解：因为)1x (1x )x (f ,11x ,1]1)x [(x 2x )1x (f 22≥-=≥+-+=+=+所以二、 配凑法：已知复合函数[()]f g x 的表达式，求()f x 的解析式，[()]f g x 的表达式容易配成()g x 的运算形式时，常用配凑法。
但要注意所求函数()f x 的定义域不是原复合函数的定义域，而是()g x 的值域。
例2 已知221)1(xx x x f +=+ )0(>x ，求 ()f x 的解析式 解：2)1()1(2-+=+x x x x f ， 21≥+xx 2)(2-=∴x x f )2(≥x 三、换元法：已知复合函数[()]f g x 的表达式时，还可以用换元法求()f x 的解析式。
与配凑法一样，要注意所换元的定义域的变化。
例3 已知x x x f 2)1(+=+，求)1(+x f解：令1+=x t ，则1≥t ，2)1(-=t x x x x f 2)1(+=+∴,1)1(2)1()(22-=-+-=t t t t f1)(2-=∴x x f )1(≥x x x x x f 21)1()1(22+=-+=+∴ )0(≥x 练习3：已知f(3x+1)=4x+3, 求f(x)的解析式.令t=3x+1， x=31-t 354)(3314)(-=⇒+-⨯=⇒t t f t t f 354)(-=⇒x x f四、构造方程组法：若已知的函数关系较为抽象简约，则可以对变量进行置换，设法构造方程组，通过解方程组求得函数解析式。
求一次函数解析式
-k+b=0 b=3
解得 k=3
b=3
∴这个一次函数的解析式为y=3x+3
Page 10
2. 利用图像求函数关系式 例3 ：求下图中直线的函数表达式
解：设这个一次函数的解析式为y=kx+b.
∵y=kx+b的图象过点（0，3）与（1，0）.
Page 21
巩固拓展 知识升华 1.利用点的坐标求函数解析式
已知一条直线与x轴交点的横坐 标为-1，与y轴交点的纵坐标为 -3，求这条直线的解析式.
Page 22
∴ k=2 ∴ y=2x+b ∵ y=2x+b 的图象过点（2，-1）.
∴ -1=2×2 - b 解得 b=-5 ∴这个一次函数的解析式为y=2x-5
Page 8
变式3.利用点的坐标求函数解析式
已知一条直线与x轴交点的横坐 标为-1，与y轴交点的纵坐标为 -3，求这条直线的解析式.
Page 9
解：设这条直线的解析式y=kx=b(kǂ0)
解：把 y=xk=x1+时b（，kyǂ=01）和中当，x=得2时，y=3.代入
k+b=1 解得 k=2
2k+b=3
b=-1
∴这个一次函数的解析式为y=2x-1
Page 5
例2：已知一次函数的图象经过点(3,5)与 （－4，－9）.求这个一次函数的解析式．
解:设这个一次函数的解析式为y=kx+b(k≠0)
Page 3
1.利用点的坐标求函数解析式
例1、已知一次函数y=kx-2(k≠0) ， 且过点(1,3)，求函数解析式
解： 把(1,3)代入一次函数y=kx-2（ k≠0 ）中， 得 k-2=3 解得，k=5
一次函数解析式的求法
第14讲确定一次函数表达式(Ａ)【知识回顾】1、一次函数的形式：（其中k、b是常数，）；当b=0时，一次函数 ( )叫做正比例函数；正比例函数是特殊的一次函数.2、一次函数的图像是一条。
正比例函数的图像是必定过的一条直线.3、一次函数（），如果几个一次函数的k相同b不同则这几个一次函数的图像（直线）；如果几个一次函数的k不同b相同则这几个一次函数的图像（直线）与轴相交于同一点（，）【基础知识精讲】一、待定系数法：1、我们要画出一次函数的图像只要知道2个点的坐标就可以确定，利用一次函数关系式可以求出来；反过来如果知道一次函数y=kx+b的2个点的坐标或者2组x和y 的值，那么就可以用待定系数法求解出一次函数关系式。
2、待定系数法：先设待求函数关系式（其中含有未知常数系数），再根据条件列出方程或方程组，求出未知系数，从而得到所求结果的方法。
例1：一次函数的图象经过点（3，3）和（1，-1）.求它的函数关系式3、用待定系数法求函数的步骤：（1）设：设出函数一般形式；（2）列：代入特殊点的坐标，列出方程（组）（3）解：解方程（组），求出待定系数（4）写：写出函数关系式。
练习、1、一次函数的图像经过了点（2，3），并且与y轴相交于（0，6）。
求此一次函数的关系式。
2：一次函数的图像经过了点（2，3），并且与x轴相交于（6，0）。
求此一次函数的关系式。
二、直线的平移:函数y=kx+b由正比例函数y=kx上下平移得到【例2】1、把直线向上平移3个单位，就得到直线，它经过象限2、一次函数的图象过点（，），且与直线平行，则其解析式为（）、、、、变式训练：把一次函数向平移个单位得到；【例3】、一次函数图像过点（3，7），并且与正比例函数y=2x图像平行，求一次函数关系式。
三、交点问题例4、1.直线与直线的交点在第象限。
2.若直线经过一次函数的交点，则的值是；3.一次函数图像与函数平行,并且与的交点是（，）,请确定一次函数的函数关系式。
求一次函数解析式的方法
依题意得 ：
解 得
－
点． 求 ， ． ｂ
’
．
４
பைடு நூலகம்
．
｛ ＋ ． ｒ一 ２ １胖 ｋ ２ Ｏ ｂ６ ， ｋ ＝０ ＝ ． ：９ ￣ ：。 ， ９
／ －２ Ｄ
‘ ． ．
所 求 的解 析式 为 ： ２ ４ ｙ＝ ｘ＋ ．
６ 验证． ．
方法四 利用平行求解析式．
ｔ 秘 糖
解 巧与 法 罅 题技 方 鞋５ ８臻 ≥ 魂
§～
函数
◎ 罗全 文 （ 江西 省 南 昌市 西 湖 区抚 生路 学校 ３０ ２ ） ３ ０ ５
方 法 一 给 出一 次 函数 上 的 两点 坐 标 求 函数 的解析 式 ． 例 １ 已知 一 次 函数 Ｙ ｘ ＝ｋ ＋ｂ的 图像 经过 点 Ａ（ ， １ ， ２一 ）
同理
．
・ ． ．
直 线 解 析 式 为 ： ＝一 ｘ＋５或 ｙ ｘ一５ ｙ ２ ＝２ ．
解 设 ｈ＝ｋ ｄ＋ｂ 依题 意得 ： ，
数学 学 习与 研 究 ２ ０ ． ０ ９９
Ｂ（ ４， ３ ． 一 一１ ） 求这 个 函数 的解 析 式． 解 依题意得 ：
ｆ ＋ １ｆ ｛９ ２ ｂ６ｉ ｋ， ０ ＝０ ｂ ｋ ， ＝ ￣
． ．
ｈ与 ｄ之 间 的 函数 关 系 式 为 ： ｈ＝９ ｄ一２ ． ０
｛＋：。 得 ； ２ｂ 一 解 ： 一＋－ ． ｆ ． ｋ ＝ ４ １ ，
／
方法 五
通 过 表 格求 解 析 式．
例 ５ 大拇 指 与 小拇 指 尽 量 张 开 时 ，两 指 尖 的 距 离 称
解由 意 ： Ｉ５ 孚， 图２ 题 得１ ＝
函数解析式的8种求法
函 数 解 析 式 的 八 种 求 法一．待定系数法：（已知函数类型如：一次、二次函数、反比例函数等）若已知)(x f 的结构时，可设出含参数的表达式，再根据已知条件，列方程或方程组，从而求出待定的参数，求得)(x f 的表达式。
【例1】已知函数f(x)是一次函数，且满足关系式3f(x+1)-2f(x -1)=2x +17，求f(x )的解析式。
分析：所求的函数类型已定，是一次函数。
设f(x)=ax+b(a≠0)则f(x+1)=?，f(x-1)=?解：设f(x)=ax+b(a≠0)，由条件得：3[a(x+1)+b]-2[a(x-1)+b]=ax+5a+b=2x+17，∴f(x)=2x+7 【例2】求一个一次函数f(x)，使得f{f[f(x)]}=8x+7分析：所求的函数类型已定，是一次函数。
设f(x)=ax+b(a≠0)则f{f[f(x)]}=f{f[ax+b]}=f[a(ax+b)+b]=? 解：设f(x)=ax+b （a≠0)，依题意有a[a(ax+b)+b]+b=8x+7 ∴x a 3+b(2a +a+1)=8x+7，∴f(x)=2x+1例 设)(x f 是一次函数，且34)]([+=x x f f ，求)(x f 解：设bax x f +=)( )0(≠a ，则bab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 例、已知二次函数)(x f y =满足),2()2(--=-x f x f 且图象在y 轴上的截距为1，被x 轴截得的线段长为22，求函数)(x f y =的解析式。
分析：二次函数的解析式有三种形式： ① 一般式：)0()(2≠++=a c bx ax x f② 顶点式：()为函数的顶点点其中k h a kh x a x f ,,0)()(2≠++=③ 双根式：的两根是方程与其中0)(,0))(()(2121=≠--=x f x x a x x x x a x f解法1：设)0()(2≠++=a cbx ax x f ，则由y 轴上的截距为1知：1)0(=f ，即c=1 ① ∴ 1)(2++=bx ax x f由)2()2(--=-x f x f 知：1)2()2(1)2()2(22+--+--=+-+-x b x a x b x a 整理得：0)4(=-x b a , 即： 04=-b a ②由被x 轴截得的线段长为22知，22||21=-x x ， 即84)()(21221221=-+=-x x x x x x . 得:814)(2=--aab .整理得： 2284a a b =- ③ 由②③得： 2,21==b a , ∴ 1221)(2++=x x x f .解法2：由)2()2(--=-x f x f 知：二次函数对称轴为2-=x ，所以设)0()2()(2≠++=a kx a x f ；以下从略。
一次函数解析式求法
数学教学案例——一次函数解析式的求法大木初中张礼军在上八年级上《一次函数》这章内容时，常常要求一次函数解析式，根据不同的题型，结合本人的教学经验，现将一次函数解析式的求法归纳如下：一. 定义型（根据定义列方程或不等式组）例1. 已知函数是一次函数，求其解析式。
解：由一次函数定义知，故一次函数的解析式为注意：利用定义求一次函数解析式时，要保证。
如本例中应保证二. 一点型（只含一个待定系数）例2. 已知一次函数的图像过点（2，－1），求这个函数的解析式。
解：一次函数的图像过点（2，－1），即故这个一次函数的解析式为变式问法：已知一次函数，当时，y＝－1，求这个函数的解析式。
三. 两点型（含有两个待定系数）已知某个一次函数的图像与x轴、y轴的交点坐标分别是（－2，0）、（0，4），则这个函数的解析式为_____________。
解：设一次函数解析式为由题意得故这个一次函数的解析式为四. 图像型（数型结合思想的运用）例4. 已知某个一次函数的图像如图所示，则该函数的解析式为__________。
解：设一次函数解析式为由图可知一次函数的图像过点（1，0）、（0，2）有故这个一次函数的解析式为五. 平行型（两直线平行，k的值相等，b的值不等）例5. 已知直线与直线平行，且在y轴上的截距为2，则直线的解析式为___________。
解析：两条直线：；：。
当，时，直线与直线平行，。
又直线在y轴上的截距为2，故直线的解析式为六. 平移型（平移得到的直线与原直线平行，但b的值发生变化）例6. 把直线向下平移2个单位得到的图像解析式为___________。
解析：设函数解析式为，直线向下平移2个单位得到的直线与直线平行直线在y轴上的截距为，故图像解析式为七. 实际应用型（一定要考虑自变量范围）例7. 某油箱中存油20升，油从管道中匀速流出，流速为0.2升/分钟，则油箱中剩油量Q （升）与流出时间t（分钟）的函数关系式为___________。
一次函数解析式过程
一次函数解析式过程
嘿，小伙伴们！今天咱们来讲讲一次函数解析式的求解过程呀。
这事儿吧，乍一听可能有点唬人，但其实没那么难啦。
首先呢，我们得知道一次函数的一般形式是y = kx + b（这里的k和b是常数，k还不能等于0哦）。
那怎么求出这个k和b呢？这就开始有趣咯。
通常题目会给我们一些条件。
比如说，它可能会告诉我们函数图像经过哪两个点。
那这个时候呢，我们就把这两个点的坐标代入到y = kx + b里面去。
比如说，一个点是（x1，y1），另一个是（x2，y2），那就有y1 = kx1 + b和y2 = kx2 + b 啦。
接下来呢，这就变成了一个方程组。
解这个方程组就能得到k和b的值咯。
不过呢，我觉得这一步可以更灵活一点哦。
有时候我们可以先观察一下这两个方程，看看有没有什么简便的方法来求解。
像如果其中一个方程里b的值比较容易求出来，那我们就可以先把b求出来，再代入另一个方程求k。
根据经验，这样做效果会更好呢！
还有一种情况题目可能会给我们函数的斜率k，然后再给一个点的坐标。
那这个时候就简单多了。
我们直接把k的值，还有那个点的坐标代入y = kx + b，就可以求出b的值啦。
这一步要特别注意！别把数字代错咯。
有时候刚开始做这个求解一次函数解析式的时候，可能会觉得麻烦，但习惯了就好了。
为什么要这么仔细地求k和b呢？因为这两个值确定了，这个一次函数就完全确定了呀！你看，是不是还挺好玩的呢？
哎这个求解过程就是这样啦。
希望大家都能顺利掌握哦！要是在做的过程中遇到啥问题，再回来看看这篇小文章呀。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
y
8 7 6 5 4 3 2 1
画函数y=x+3的图象
y=x+3
(3，6)
(0，3)
1 2 3 4 5 6 7 8 x
பைடு நூலகம்
0
从数到形 函数解 选取 满足条 画出 一次函 数的图 析式 件的两 象 y=kx+b 解出 点(x1,y1) 选取 (k≠0) 与(x2,y2) 直线
从形到数
数学的思想方法：数形结合
求一次函数的解析式
学习目标：
1.了解待定系数法的思维方式与特点。 2.会根据所给信息用待定系数法求一次函 数解析式，发展解决问题的能力。 3.进一步体验并初步形成“数形结合”的思 想方法。
（1）若点A（-1，1）在函数Y=KX的图象上则 K= . （2）在一次函数Y=KX-3中，当X=3时Y=6则K= .
(3)若小李 5 月份上网费用为 75 元，则他在该月份的上网时间
35 是__________ ．
再见
解：设这个一次函数的解析式为y=kx+b.依题意得
14k+b=105.5 解之得 6k+b=45.5
K=7.5
b=0.5
∴函数的解析式为y=7.5x+0.5 当X=10时 y=7.5×10+0.5=75.5 答:当一条蛇的尾长为10 cm时,这条蛇的长度是75.5cm
小明根据某个一次函数关系式填写了下表:
4、已知一个正比例函数和一个一次函数，它们 的图象都经过点P （-2，1），且一次函数图象与 y轴交于点Q（0，3）。
（1）求出这两个函数的解析式；
用待定系数法求一次函数的解析式(重点) 例 1：直线 y＝kx＋b 在坐标系中的图象如图 1，则(
2 A．k＝3，b＝－2 2 B．k＝－3，b＝2 2 C．k＝－1，b＝－3 2 D．k＝－2，b＝3
)
图1
思路导引：根据待定系数法求出一次函数的解析式中未知
数的系数．
解析：根据图象知，直线过点(3,0)和(0,2)，
k 2 0 3k b 3. 代入 y＝kx＋b 得 ，解得 2b b2
答案：B
【规律总结】用待定系数法求一次函数的解析式，要根据
解题的步骤: 1.设一次函数的一般形式y=kx+b(k≠0) ; 2.根据已知条件列出关于k , b 的二元一次方程 组 3.解这个方程组,求出k, b ; 4 .据求出的 k, b的值，写出所求的解析式.
象刚才这样先设待求的函数关系式(其中含有 未知的系数)，再根据条件列出方程或方程组，求 出未知系数，从而具体写出关系式的方法,叫做待
定系数法.
2．分段函数 在一个变化过程中，函数 y 随自变量 x 变化的函数解析式 有时要分成几部分，这样在确定函数解析式或函数图象时，要
根据自变量的取值范围分段描述．这种函数通常称为分段函数．
分段函数的解析式
例 2：从广州市向北京市打长途电话，按时间收费，3 分钟内 收费 2.4 元，每加 1 分钟收费 0.5 元，求时间 t(分)与电话费 y(元)
3．某市推出电脑上网包月制，每月收取费用 y(元)与上网时间
x(小时)的函数关系如图 4，其中 BA 是线段，且 BA∥x 轴，AC 是
射线．
图4
y＝3x－30 ； (1)当 x≥30 时，y 与 x 之间的函数解析式为______________ 60 元上网费用； (2)若小李 4 月份上网 20 小时，他应付________
(2，5) , _______ (1，3) 代入所设解析式 把点_______ 得 2 k+b＝ 5
1 解得,
k+b ＝
3
k＝_____ 2
b＝_____ 1
把k=1，b=2代入y=kx+b中，得一次函数解析式 y__________. ＝2x+1 为
你会用所学知识解决生活中的问题吗? (4)生物学家研究表明： 某种蛇的长度y(cm)是其尾长x(cm)的一次函数； 当蛇的尾长为 14cm时, 蛇的长为105.5cm; 当蛇的尾长为6 cm时, 蛇的长为45.5 cm； 当蛇的尾长为10 cm时,这条蛇的长度是多少?
点拨：(1)当 x≥30 时，设函数解析式为 y＝kx＋b，
30k b 60 k 3 则 ，解得 .所以 y＝3x－30. 40k b 90 b 30
(2)当 0≤x<30 时，y＝60， 所以 4 月份上网 20 小时，应付上网费 60 元． (3)由 75＝3x－30，解得 x＝35， 所以 5 月份小李上网 35 小时．
x y -2 -1 0 1
3
1
0
其中有一格不慎被墨汁遮住了,想想看， 该空格里原来填的数是多少？
1、一次函数的图象经过点(0,2),且与 两坐标轴形成的三角形面积等于1.求 出一次函数的解析式. 2、一次函数y=2x-2（1）向下平移4 个单位得到的解析式（2）向右平移2 个单位后的解析式（3）直线l与一次 函数y=2x-2直线关于x轴对称,求解析 式。
↓
↓
:物理课扰乱课堂，并把校服的字洗掉！ 代入求得函数解析式为________．
1 2
2、已知一次函数 的自变量x=3时，函数值y=5； 当 x=-4时，y=-9。根据解决上面问题的经验，你 能写出这个一次函数的解析式吗？ 3、 已知直线 y=kx+b 经过点（9，10）和点 （24，20），求k与b。
（3）一次函数Y=3X-B过A（-2，1）则B=
,。
1．用待定系数法求一次函数的解析式 (1)先设出函数解析式，再根据条件确定解析式中未知数的 系数 ，从而具体写出这个式子的方法，叫做待定系数法 ________ __________． (2)探究：已知一次函数的图象经过(2,5)和(－4,2)，求这个 一次函数的解析式．
1．已知一次函数，当 x＝－2 时，y＝－3；当 x＝1 时， y＝2x＋1 ． y＝3，则这个一次函数的解析式为____________ 2．在图 3 中，将直线 OA 向上平移 1 个单位，得到一个一 y＝2x＋1 ． 次函数的图象，那么这个一次函数的解析式是____________
图3
已知:一次函数的图象经过点(2，5) 和点(1，3),求出一次函数的解析式. y＝kx+b 解： 设一次函数的解析式为_______________
题意找出函数上的已知两点坐标．
1、一次函数y=kx+5与直线y=2x-1交于点 P(2，m)，求k、m的值 2、已知函数y=kx+b的图象与另一个一次 函数y=-2x-1的图象相交于y轴上的点A， 且x轴下方的一点B(3，n)在一次函数 y=kx+b的图象上，n满足关系n2=9.求这 个函数的解析式. 3、若直线y=kx+b平行直线y=-3x+2，且 在y轴上的的截距为-5，则k= ， b= 。
解：设一次函数的解析式为 y＝kx＋b， ↓
____________________ ____________________
5＝2k＋b ， 2＝－4k＋b
←代入点(2,5)和(－4,2)
1 k ________ 2 ，←解方程组，求出 k、b 的值 4 b ________
3. 若直线y=3x+b与两坐标轴 所围成的三角形的面积是6个 面积单位，求b的值.
4.一次函数的图象与直线x+y6=0交于A(5,m)点，且与直线 y=2x-3无交点，求一次函数的 解析式。
6、已知直线y=kx+b经过点 （2.5，0），且与坐标轴所围 成的三角形的面积为6.25，求 该直线的解析式。 7、已知直线y=2x-4向左平移4 个单位后的解析式 8、判断点A(3，2)、B(-3，1)、 C(1，1)是否在一直线上？
之间的函数解析式，并画出函数的图象． 思路导引：分段函数要根据自变量的取值范围分段描述．
解：当 0＜t≤3 时，y＝2.4； 当 t＞3 时，y＝2.4＋0.5(t－3)＝0.5t＋0.9. 函数图象由一条线段和一条射线组成，如图 2：
图2
【规律总结】分段函数是一个函数而不是多个函数，求出的分
段函数解析式必须写出自变量的取值范围．