第十七章 平面图及图的着色
图论中的平面图与染色问题

图论中的平面图与染色问题图论是数学的一个分支,研究的是图的性质和图之间的关系。
在图论中,平面图与染色问题是重要的研究方向。
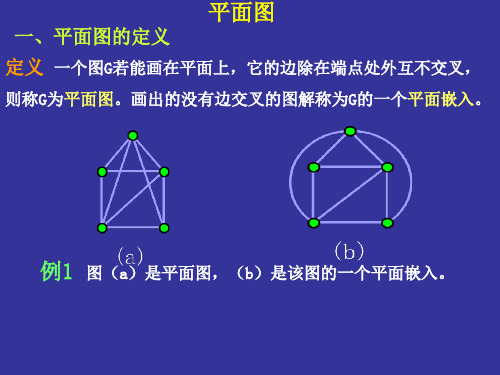
一、平面图平面图是指可以在平面上画出的图,其中任意两条边都不相交,任意两个顶点之间都只有一条边相连。
平面图可以用来描述许多实际问题,如地图、电路等。
在平面图中,有一个重要的定理,即欧拉定理。
欧拉定理是数学家欧拉在1736年提出并证明的,它给出了平面图中顶点数、边数和面数的关系。
根据欧拉定理,对于连通的平面图,满足公式:V - E + F = 2,其中V表示顶点数,E表示边数,F表示面数。
二、染色问题染色问题是图论中的一个经典问题,即给定一个图,如何用有限种颜色对图的各个顶点进行染色,使得相邻的顶点之间的颜色不相同。
这是一种常见的应用问题,如地图着色、课程表安排等。
在染色问题中,有一个重要的定理,即四色定理。
四色定理是染色问题中的一个著名定理,它指出任何平面图都可以用至多四种颜色对其顶点进行染色,使得相邻的顶点颜色不同。
三、平面图与染色问题的关系平面图与染色问题之间有着紧密的联系。
通过合理的染色方案,可以将一个平面图的顶点进行染色,满足相邻顶点颜色不同的要求。
同时,染色问题的解法与平面图的结构和性质也有关系。
在研究平面图与染色问题时,可以通过绘制平面图的平面嵌入图来分析和求解染色问题。
平面嵌入图是平面图在平面上的一种表示形式,可以把平面图的顶点和边绘制在平面上,形成一种更加直观的图形。
在解决染色问题时,可以借助平面嵌入图的结构和特性,通过一定的算法进行染色。
例如,可以利用贪心算法对顶点进行依次染色,确保相邻顶点染不同的颜色。
四、应用举例平面图与染色问题在实际中有广泛的应用。
一个典型的例子是地图着色问题。
在地图上,每个国家或地区可以用一个顶点表示,国家或地区之间的边表示它们的相邻关系。
通过对地图进行染色,可以实现相邻国家或地区的颜色不同,从而更加方便地辨认。
另一个例子是课程表安排问题。
第17章桥隧涵工程图

根 长
数
共
长
一
柱全
桥
总
质
量
1号
Ⅱ -Ⅱ
Ⅱ
净
6
Ⅱ
2号
-
1:60
焊
接
说
明
:
1.本
图
尺
寸
除
钢
筋
直
径
以
毫
米
(
焊
接
(cm)为
单
位
。
将构件化整为零,分别对各个构件独立进行配筋, 平
均
2.主
筋
N5和
N1、
N2接
头
均
采
用
对
素砼段
3.图
中
加
强
钢
筋
N4、
N5在
钢
筋
笼
施工时,再采用集零为整,将所有构件的钢筋配置好后, 焊
%
土木工程制图—桥隧涵工程图 制作:姚晓琴、林国华
(2)桩基一般构造图
防震挡块
H外
半立面 半平面
5×5
支座支承线
桥墩混凝土数量表 (单位:m )
盖梁(棱柱体) 方向 墩号 墩帽
柱
系梁
桩
H内
九峰
至
富岭
墩桥 中 身(圆柱体)
富岭 至
心
九峰
线
全桥合计
系梁(H1 长方体)
桩身(圆柱体)
说明: 1.盖梁构造见另图。 2.图中尺寸除注明外余均以厘米(cm)为单位。 3.图中比例 1:100。
说明: 1.本图尺寸均以厘米(cm)为单位,标高以米(m)为单位。 2. 本桥位于平曲线的主曲线内,R=1300m。 3. 钻孔灌注桩单桩容许承载力桥墩应大于 2840kN, 桥台应大于 1920kN。 4. 图中比例 1:300。
17,18平面图及图的着色

(3)设m=k(k≥1)时成立,当m=k+1时,对G进行如下讨论。 设 = 时成立, 进行如下讨论。 时成立 = 时 进行如下讨论 是树, 是非平凡的, 中至少有两片树叶。 若G是树,则G是非平凡的,因而 中至少有两片树叶。 是树 是非平凡的 因而G中至少有两片树叶 为树叶, 仍然是连通图, 设v为树叶,令G'=G-v,则G'仍然是连通图,且G'的边数 为树叶 , 仍然是连通图 的边数 m'=m-1=k,n'=n-1,r'=r。 , , 。 由假设可知 n'-m'+r'=2,式中n',m',r'分别为 的顶点数, ,式中 , , 分别为G'的顶点数, 分别为 的顶点数 边数和面数。 边数和面数。 于是n-m+r=(n'+1)-(m'+1)+r'=n'-m'+r'=2 于是 不是树, 中含圈。 若G不是树,则G中含圈。 不是树 中含圈 设边e在 中某个圈上 中某个圈上, 仍连通且m'=m-1=k 设边 在G中某个圈上,令G'=G-e,则G'仍连通且 , 仍连通且 , n'=n,r'=r-1。 , 。 由假设有 n'-m'+r'=2。 。 于是 n-m+r=n'-(m'+1)-(r'+1)=n'-m'+r'=2
定理16.9 对于具有k(k≥2)个连通分支的平面图 ,有 个连通分支的平面图G, 定理16.9 对于具有 个连通分支的平面图 n-m+r = k+1 其中n, 分别为G的顶点数 其中 ,m,r分别为 的顶点数,边数和面数。 分别为 的顶点数,边数和面数。
离散数学中的图的平面图与平面图的着色

图是离散数学中的重要概念,而平面图和平面图的着色是图论中的两个关键概念。
平面图是指在平面上绘制的图形,使得图中的边不会相交。
平面图的着色是指对平面图中的顶点进行染色,且相邻的顶点不会被染成相同的颜色。
平面图的概念最早由欧拉在1736年提出。
他发现,如果一个图是可以在平面上绘制而不会边相交的,那么这个图是一个平面图。
欧拉还引入了一个重要的公式,即欧拉定理,它描述了平面图中的顶点、边和面的关系:V - E + F = 2,其中V代表顶点数,E代表边数,F代表面数。
对于平面图的着色问题,四色定理是一个非常重要的结果。
四色定理指出,任何一个平面图,在不考虑多重边和自环的情况下,最多只需要使用四种颜色就能够对图的顶点进行染色,使得相邻的顶点不会有相同的颜色。
这个定理在1976年被由英国数学家Tomás Oliveira e Silva使用计算机辅助证明,被认为是图论史上的一大突破。
对于平面图的着色,有一种特殊的染色方法叫做四色标号。
四色标号是指对于任意一个平面图,都可以给图中的每个顶点赋予一个自然数,使得相邻的顶点之间的差值不超过3。
这种染色方法保证了相邻的顶点不会被染成相同的颜色,同时最多只需要使用四种颜色。
平面图的着色不仅在图论中有着重要的应用,同时在现实生活中也有很多实际的应用。
比如,考虑地图上的城市,如果我们希望将城市标记成不同的颜色,以表示它们的关系,那么可以利用平面图的着色来实现。
另外,平面图的着色还有很多其他的实际应用,比如在工程规划中用于规划电路的布线、在计算机科学中用于处理图像等等。
总之,离散数学中的图的平面图与平面图的着色是图论中的两个重要概念。
平面图是指在平面上绘制的图形,使得边不会相交;平面图的着色是指对平面图中的顶点进行染色,且相邻的顶点不会被染成相同的颜色。
四色定理是平面图着色的重要结果,它指出任意一个平面图可以使用最多四种颜色进行着色。
平面图的着色在现实生活中有着广泛的应用,是离散数学中的一个重要研究领域。
平面图

17.4 平面图的对偶图
实线边图为平面图,虚线边图为其对偶图。
17.4 平面图的对偶图
从定义不难看出G的对偶图G*有以下性质: G*是平面图,而且是平面嵌入。 G*是连通图。 若边 e 为 G中的环,则 G*与 e对应的边 e* 为桥,若 e 为桥, 则G*中与e对应的边e*为环。 在多数情况下,G*为多重图(含平行边的图)。
i 1 i 1 k k
(17.1)
由于每个Gi 有一个外部面,而G只有一个外部面,所以G的面数 k r ri k 1
i 1
于是,对(17.1)的两边同时求和得
2k (ni mi ri ) ni mi ri n m r k 1
17.3 平面图的判断
例17.1 证明彼得松图不是平面图。
证 明
将彼得松图顶点标顺序,见图 (1)所示。 在图中将边(a,f), (b,g), (c,h), (d,i), (e,j)收缩,
所得图为图 (2)所示,它是K5,
由定理17.1彼得松图,令 G'=G-{(j,g),(c,d)} G‘如图 (3)所示,易知它与K3,3同胚, 由定理17.15可知,G为非平面图。
17.4 平面图的对偶图
一、对偶图的定义 定义17.6 设G是某平面图的某个平面嵌入,构造G的对偶图 G*如下: 在G的面Ri中放置G*的顶点vi* 。
设e为G的任意一条边,
若 e 在 G 的面 Ri 与 Rj 的公共边界上,做 G* 的边 e* 与 e 相交, 且e*关联G*的位于Ri与Rj中的顶点vi*与vj*,即e*=(vi*,vj*) ,e*不与其它任何边相交。 若e为G中的桥且在面Ri的边界上,则e*是以Ri中G*的顶点 vi*为端点的环,即e*=(vi*,vi*)。
第十七章 平面图及图的着色
注意观察K5与K3,3的特点!
K5 的特点每三个点构成一个面! 而K3,3每四个点构成一个面
4.库拉托斯基定理判别法
定义
如果两个图G1和G2是同构的,或者通过反复插入或删
除度为2的结点,它们能变成同构的图,则称G1 和G2 在度为2的结
点内同构(同胚)。
K3,3与K5称为库拉托夫斯基(Kuratowski)图, 它们有
例5
利用定理判别图G是否非平面图。
解法一与 K3,3同胚
图G 去掉图G中边:{a,c},{a,d},{d,e},{b,e},与 K3,3同胚
可以去边吗?
边少时非平面图,边多时更不是平面图
解法二 去掉图中边{d,f}和{e,g},为K5
练习
1.用简单、直观判别法判断下图所给出的两个图a,b是否平面图。
3. 欧拉公式判断法
定义设G是一个连通平面图,G的边将G所在的平面划分成若干个区
面积有限的区域称为有限面。包围每个面的所有边构成的回路称为 面的边界。它的长度称为面的度(次数)(degree)。
域,每一个区域称为G的一个面。其中面积无限的区域称为无限面。
例3
定理 一个有限平面图,面的次数之和等于其边数的两倍. 证明:因为任何一条边,或者是二个面的公共边,或者在 一个面中作为边界被重复计算两次,故面的次数之和等于 其边数的两倍。 如右图中,
若v1 和v3 同属于一个G(RY)的连通分支,那么从v1到v3 必有一 条通路,其各顶点被红、黄两色相间着色。这条通路连同v0便构 成回路: C:v0, v1,…, v3, v0,
C把BW分成两部分,一部分在回路C之外,一部分在C之内。 于是,BW生成的G的子图也被分成了两个互不连通的部分,一 部分在C外,一部分在C内,这就使v2,v4 处于BW生成的G的子 图的两个不同连通分支,同上将v2所在分支作颜色对换,以便给 v0着上白色,完成对G的5-着色。
平面图与图的着色

2020/4/12
3
4.1 平面图
e6 F4
v 1 F1 e4 v4
e1
e5 F3
F2
e3
v2 e2 v3 (b)
F1= v1 e1 v2 e6 v4 e4 v1 边界为:{e1 , e6 , e4 }
F3= v1 e1 v2 e2 v3 e5 v1 边界为:{e1 , e2 , e5 }
F2= v1 e5 v3 e3 v4 e4 v1 边界为:{e5 , e3 , e4 }
2020/4/12
不是极大平面图
15
4.2 极大平面图
v1
v2
v5
v3
v4
2020/4/12
16
4.2 极大平面图
设有n个结点和m条边的极大平面图G具有以下性质: 性质1. G是连通的。 性质2. G不存在割边。 性质3. G的每个域的边界数都是3(极大平面图也称为
平面三角剖分)。 性质4. 3d=2m。
e3
i3 i4
dj
i5
e4
e1 e2 i2 i1
e3 i3i4
dj
i5
e4
2020/4/12
19
4.2 极大平面图
性质3. G的每个域的边界数都是3。
证明:这时,在域dj之外不可能存在边(i2, i4 ) 。 亦即i2和 i4 不相邻,但在域dj内加入边(i2, i4 )并 不影响G的平面性,得到矛盾。
F4= v2 e2 v3 e3 v4 e6 v2 边界为:{e2 , e3 , e6 }
2020/4/12
4
4.1 平面图
v1
e1e6FF13ve4F42e3e5 F4
v2
e2
F17平面图及图的着色

插入或消去 2 度顶点不影响图的可 平面性: 同胚的图有相同的可平面性.
u
插 入
u
† 就可平面性而言, 2 度顶点是“多余的”
w 消
点.
v去v
同胚: 同构或者反复插入或消去 2 度顶点后同构.
插入/insertion,消去/elimination, 同胚的/homeomorphic
081离散数学(60). W&M.
该面次数为6 悬挂边算两次
边界/boundary, 次数/degree
081离散数学(60). W&M. §17.1平面图的基本概念
定理 平面图中面的次数之和是边数的2倍: deg(R) = 2|E|. 证 每条边对次数的贡献都是 2: 割边,非割边.
R0 R1
R3 R2
面 次数
R0
§17.1平面图的基本概念
K5
第十七章 平面图及图的着色
§17.1平面图的基本概念 §17.2 欧拉公式 §17.3平面图的判断 §17.4平面图的对偶图 §17.5图中顶点的着色 §17.6地图的着色与平面图的点着色 §17.7边着色
081离散数学(60学时). W&M.
欧拉多面体公式 对任何一个凸多面体有
点的最小度为 . 由握手定理和定理17.12知,
整理得
n d(v) = 2m 2(3n – 6).
6 – 12/n 5. QED
†事实上, n 阶 (n 4) 简单平面图至少有 4 个顶点的 度不大于 5.
081离散数学(60). W&M.
§17.2 欧拉公式
maximal planar graph.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若e为G中的桥且在面Ri 的边界上,则e*是以Ri 中G*的顶点v*i为端点的环,即e*=(v*i,v*i).
下图实线边图为平面图,虚线边图为其对偶图.
练习:求下图的对偶图
二、平面图与对偶图的阶数、边数与面数之间 的关系. 定理17.17 设G*是连通平面图G的对偶图,n*, m*, r*和n, m, r分别为G*和G的顶点数、边数和 面数,则 (1)n*= r (2)m*=m (3)r*=n ( 4 ) 设 G* 的 顶 点 v*i 位 于 G 的 面 Ri 中 , 则 dG*(v*i)=deg(Ri)
例:
图(2),(3)都是图(1)的平面嵌入,图(2)中, R0)=3,图(3)中,deg(R0) =4,它们虽然形 状不同,但都与(1)同构。
定理17.4 平面图各面次数之和等于边数的两倍.
证明: 因为任何一条边,或者是两个面的公 共边,或者在一个面中作为边界被重复计算两 次,故面的次数之和等于其边数的两倍。
R2的边界:v1v2v3v1 ,deg(R2)=3 ;
R0 的边界为复杂回路: v1v2v3v4v5v6v5v4v1, deg(R0)=8 。
注意: (1) 一个平面图的无限面只有一个。 (2) 同一个平面图可以有不同形状的平面 嵌入 (互相同构)。 (3) 不同的平面嵌入可能将某个有限面变 成无限面,而将无限面变成有限面。
定理17.12:设G是n(n≥3)阶m条边的简单平面 图,则m≤3n-6
证明:设G有k个连通分支。若G为树或森林, 因为(3n-6)-(n-k)=2n-6+k ≥0,所以m=n-k ≤3n-6 (n≥3)。若G不是树也不是森林,则G中必含圈, 又因为G为简单图,所以各圈的长度均大于或 等于3,因各面的次数至少为l,又
1、韦尔奇· 鲍威尔法(Welch Powell)
⑴将图G的顶点按照度数的递减次序进行排列。 (这种排列可能并不是唯一的,因为有些点有 相同的度数)。 ⑵用第一种颜色对第一点进行着色,并且按排 列次序,对前面着色点不邻接的每一点着上同 样的颜色。 ⑶用第二种颜色对尚未着色的点重复⑵,用第 三种颜色继续这种做法,直到所有的点全部着 上色为止。
三、自对偶图
定义17.8 设G*是平面图G的对偶图,若G*G,则 称G为自对偶图。
四、着色问题
从对偶图的概念,可以看到,对于地图的着色问题, 可以归纳为对于平面图的顶点着色问题,因此四色 问题可以归结为要证明对于任何一个平面图,一定 可以用四种颜色,对于它的顶点进行着色,使得邻 接的顶点都有不同的颜色。 着色数 x(G):对图G着色时,需要的最少颜色数。
3 10 (5 2 ) 9 3 2
这是个矛盾,所以K5不是平面图. 同理,若K3,3 是平面图,由于K3,3 中圈的长度 l≥4,所以边数9应满足
4 9 ( 6 2) 8 42
这是个矛盾,所以K3,3不是平面图.
定理17.11 :设G是有k个连通分支的平面图, 各面的次数至少为l(l≥3),则边数m与结点数n 应满足如下关系:
l 2
证明:由于平面图各面次数之和等于边数的两 倍,所以 2m r deg( R ) l r (1)
i 1
i
由欧拉公式可知 r=2+m-n (2) 将 (2)代入(1)得2m≥l(2+m-n) 整理得:
l m ( n 2) l 2
推论 K5, K3,3不是平面图.
证明:若K5是平面图,由于K5中无环和平行边, 所以每个面的次数均大于或等于l≥3,根据定理 17.10可知边数10应满足
l m ( n k 1) l 2
证明:由于平面图各面次数之和等于边数的两 r 倍,所以 2m deg( R ) l r (1)
i 1
i
由欧拉公式的推广可知 r=k+1+m-n (2) 将 (2)代入(1)得2m≥l(k+1+m-n) 整理得:
l m ( n k 1) l 2
例: 用韦尔奇· 鲍威尔法对下图着色
解: ⑴根据递减次序排列各点A5,A3,A7,A1, A2,A4,A6,A8。 ⑵第一种颜色对A5着色,并对不相邻的结点A1 也着第一种颜色。 ⑶对A3结点和它不相邻的结点A4,A8着第二种 颜色。 ⑷对A7结点和它不相邻的结点A2,A6着第三种 颜色。 因此图G是三色的。所以x(G)=3。
(2)无限面或外部面:(可用R0表示)面积无限的面。
(3)有限面或内部面(可用R1, R2, …, Rk等表示):面 积有限的面 。 (4)面Ri的边界:包围Ri的回路组。
(5)面Ri的次数:Ri边界的长度,用deg(Ri)表示 。
例:
v1 R1
v4
v6 R0
R2
v2 v3
v5
此平面图,共有3 个面:R0,R1,R2 ; R1 的边界: v1v3v4v1,deg(R1) =3;
定义:设G为简单平面图,若在G的任意不相 邻的结点u,v之间加边(u,v),所得图为非平 面图,则称G为极大平面图。 例:K1,K2,K3,K4,K5-e都是极大平面图。 定理17.5:极大平面图是连通的。 定理17.6:设G为n(n≥3)阶极大平面图,则G 中不可能存在割点和桥。 定理17.7:设G为n(n≥3)阶简单连通的平面图, 极大平面图当且仅当G的每个面的次数均为3。
(2)是(1)的平面嵌入;
(1)
(2)
例:
(1)即K4 图,(2)是(1)的平面嵌入,故(1)是平面图. (4)是(3)的平面嵌入,故(3)是平面图。 (5)即K5 图,无论怎样画,都不可能将交叉的边 全去掉,(6)是(5)的一种画法。 (7)即K3,3 图,无论怎样画,也不可能将交叉的 边全去掉;(8)是(7)的一种画法。 故 K5和 K3,3都不是平面图。 注意: 有些图形从表面上看有几条边是相交的,但不 能就此肯定它不是平面图。
若G不是树,则G中含有圈,设边e在G的某个圈 上,令G’=G-e,则G’仍连通,且m’=m-1=k, 由归纳假设有n’-m’+r’=2,而n’=n,r’=r-1,于 是 n-m+r=n’-(m’+1)+(r’+1)= n’-m’+r’=2
定理17.9 (欧拉公式的推广)设G是具有k(k2) 个连通分支的平面图,则nm+r=k+1 。 证明:设G的连通分支分别为G1,G2,…,Gk ,并 设 Gi 的 结 点 数 , 边 数 和 面 数 分 别 为 ni,mi,ri,i=1,2,…,k。由欧拉公式可知 ni-mi+ri=2 (1) 又m=∑mi, n=∑ni,由于每个Gi有一个外部面, 而G只有一个外部面,所以
若G是树,则G是非平凡的,因而G中至少有2 片树叶,设v为树叶,令G’=G-v,则G’仍然连 通,且G’的边数m’=m-1=k,由归纳假设可知 n’-m’+r’=2 ( n,m’,r ‘分别为G’的结点数、 边数和面数),所以 n-m+r=(n’+1)-(m’+1)+r’= n’-m’+r’=2 。
第十七章 平面图及图的着色
在一张纸上画几何模型时常常会发 现,不仅需要允许各边在结点处相交, 而且还应该允许各边在某些非结点处相 交。但是,有些图形是不允许边交叉的, 例如大家熟悉的印制电路,除了结点外, 它的导线是不允许交叉的,这就是本章 要学习的平面图。
本章的主要内容
平面图的基本概念
欧拉公式
2、相关结论
定理:对于n个结点的完全图Kn,有 x(Kn)=n。 定理:任意平面图G至多是5-色的。
例:某大学计算机专业三年级学生总共 选n门选修课,期末考试前必须提前将这 n门选修课程考完。要求每天每人在下午 考一门课,问至少需要几天考完这n门课? 若设n=5,并且课程1与2,1与3,1与4, 2与5,3与4,3与5均有人同时选,问至 少需要几天考完这5门课程?
f
g
h
证明:在左图中将边(a,f), b (b,g),(c,h),(d,i),(e,j)收缩 所得的图为K5,由于K5不是 平面图,所以彼得松图不是 平面图。
c
17.2 图的着色
问题的提出:这个问题最早起源于地图的着色,一个 地图的相邻的两个国家着于不同的颜色,那么最少需 用多少种颜色?一百多年前,英国格色里(Guthrie)提 出了用四种颜色即可对地图着色的猜想,1879年肯普 (Kempe)提出了这个猜想的第一个证明,但到1890年希 伍德(Hewood)发现肯普的证明是错误的,但他指出肯 普的方法,虽不能证明地图着色用四种颜色就够了, 但可证明用五种颜色就够了。此后四色猜想一直成为 数学家感兴趣而未能解决的难题。直到1976年美国数 学家阿佩尔和黑肯宣布:他们用电子计算机证明了四 色猜想是成立的。所以从1976年以后就把四色猜想这 个名词改为“四色定理”了。
平面图的判断
平面图的对偶图 图的着色
17.1 平面图
一、关于平面图的一些基本概念
1. 平面图的定义(定义17.1 ) (2)G是可平面图或平面图——G可嵌入平面。 (3)平面嵌入——画出的无边相交的平面图。
(1)G可嵌入曲面S:若能将G除顶点外无边相交地画在S上。
(4)非平面图——无平面嵌入的无向图。
4、两个判定定理 定理17.15 G是平面图 G中不含与K5或K3,3同胚 的子图. 定理17.16 G是平面图 G中无可收缩为K5或K3,3 的子图
例: 证明下图所示二图均为非平面图.
两个图的子图如下,分别与K3,3, K5同胚.
例:证明彼得松(Prterson)图不是平面图。
a
e
j i d
l 2 1 l2 l2
在l=3时达到最大值3,由定理17.11知
l m (n k 1) 3( n 2) 3n 6 l 2
定理17.13:设G是n(n≥3)阶m条边的极大平 面图,则m=3n-6。
