13.2.2 用坐标表示轴对称
13.2.2用坐标表示轴对称

二、用坐标表示轴对称的应用: 7、已知△ABC的三个顶点的坐标分别为
A(-3,5),B(- 4,1),C(-1,3y),
作出△ABC关于y轴对称的图形. ·y
A
5
4
3
B
C2
1
-4 -3 -2 -1-01
-2 -3
1 2 3 4 5x
-4
8、作出△ABC关于y轴的轴对称图形 y
ABO来自xC课堂小结
对称点
D′
y
规律:
E
F
(4,0) (0,-2)
E'(4,0) F'(0,2)
A C′
在平面直角坐标系中, 关于x轴对称的点的
B F′
横坐标 不变 , 纵坐标 互___为__相__反__数__; 即点(x,y)关于x轴对
O B ′F
E′ x
称的点的坐标为
A′
( x , -y )
D
C
已知点 A
B
C
D
(2,4) (-1,2) (3,-5) (-6, -5)
4、点A(m+2,3)、B(-5,n+6)关 于y轴对称,则m n = -9 。
5、P(a,3)和P1(2,b)关于x轴对称, 则a+b= -1 。
6、已知点A(2m+1,m-3)关于y轴的对称
点在第四象限,则m的取值范围是
m<-
1 2
,
【例 】 如图,四边形ABCD的四个顶点的坐
标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),
13.2.2用坐标表示轴对称
导入新课
如图,是一幅老北京城 的示意图,其中西直门 和东直门是关于中轴线 对称的.如果以天安门 为原点,分别以长安街 和中轴线为x轴和y轴建 立平面直角坐标系.根 据如图所示的东直门的 坐标,你能说出西直门 的坐标吗?
13.2。2用坐标表示轴对称
Ⅱ.讲授新课[活动2]在如图所示的平面坐标系中,画出下列已知点及其对称点,并把坐标填入表格中.看看每对对称点的坐标有怎样的规律.再和同学讨论一下.已知点A (2,-3),B (-1,2),C (-6,-5),D (,1),E (4,0). 关于x 轴的对称点A ′(____,____)B ′(_____,______)C ′( _____, _____) D ′(____,_____)E ′(_____,_____).关于y 轴的对称点A ″(_____,____)B ″(_____,______)C ″( _____, _____) D ″(____,_____)E ″(_____,_____).设计意图:通过学生动手操作,分别作A ,B ,C ,D ,E 关于x 轴、y 轴的对称点A ′,B ′,C ′,D ′,E ′;A ″,B ″,C ″,D ″,E ″,并且求出它们的坐标,观察,归纳它们坐标之间的关系.师生行为:教师引导,学生自主探索发现关于x 轴、y 轴对称的每组对称点坐标的规律.[生]如图,我们先在直角坐标系中描出A (2,-3),B (-1,2),C (-6,-5),D (,1),E (4,0)点.我们先在坐标系中作出A 点关于x 轴的对称点,即过A 作x 轴的垂线交x 轴于M 点, M 点的坐标为(2,0).在AM 的延长线上截A ′M=AM ,则A ′就是A 点关于x 轴的对称点,所以A ′在第一象限,因为A ′M=AM ,所以A ′的纵坐标为3,因为AA ′⊥x 轴,即AA ′∥y 轴, 所以A ′的横坐标为2,即A ′的坐标为(2,3).同理可求得B ,C ,D ,E 关于x 轴的对称点B ′,C ′,D ′,E ′的坐标分别为B ′(-1, -2),C ′(-6,5),D ′(,-1),E ′(4,0).列表如下: 121212C / .。
13.2.2 用坐标表示轴对称

B
B′
O
顶点C的对称点的坐标为( 2 ,5 )
A′
x
顶点D的对称点的坐标为( 5 ,4 )
描出这四个点并依次连接即可.
应用新知
小结:在坐标系中作已知图形关于坐标轴对称的图形:
一求:求已知图形的一些特殊点的对称点的坐标;
二描:在坐标系中描出这些对称点;
三连:顺次连接这些对称点得到对称图形.
应用新知
(2)若点A、B关于y轴对称,求a、b的值.
a = −1
a−b = 2
ቊ
解:(1)由题可得 ቊ
,解得 b = −3
b = −3
a=1
a−b
=
−2
(2)由题可得 ቊ
,解得 ቊ
b=3
b=3
应用新知
例3. 已知点P(a+1,2a-1 )关于x轴的对称点在
第一象限,求a的取值范围.
解:由题可得,点P关于x轴的对称点为(a+1, 1−2a )
关于y轴 A′(-3.5 ,4)
的对称点
B′( 4 ,2)
C′(-3 , -3)
规律:关于y轴对称的两个点,
横坐标互为相反数,纵坐标相等。
公式:P(a,b)
关于y轴对称
P′ (-a,b)
探究新知
y
P′ (-a,b)
=
=
-a
P
┌
┌
关
于
y
轴
对
称
P′
b
┌
为什么?
P(a,b)
O
a
x
探究新知
y
A (3.5,4)
13.2.2 用坐标表示轴对称
要点回顾
1.作点的轴对称图形:如果直线MN外有一点A,那么怎样
13.2.2用坐标表示轴对称2

用坐标表示轴对称
用坐标表示轴对称
快乐大解密
一名游客在天安 门广场向小明问 西直门的位置, 但他只知道东直 门的位置,可是 聪明的小明想了 想,就准确的告 诉了她,你知道 原因吗?
西直门?? y
4
A
3
2
1
-4
-3
-2
-1
0 -1
-2
-3
-4
东直门 (3.5,4) C
1234x
B
③依次连接各对称点就可以 A”
·B”
得到这个图形的轴对称图形.
·C”
C’
··A’ ·B’
已知点 P(-2,3) M(-1,探1) 究N(三-3,-2)
关对关对称 称于于类P坐,点点xxM比标==,1-N研之1 关究间PP’”于有:((40直,什(,33线)么拓) MMx关展=’”(1(系提3-的,11,吗高对)1))?称NN如点”’(图(51,,,-你,-2分2))能别发作现出它点们
探究一
探究1:关于y轴对称的点的坐标与已知点的 坐标具有怎样的关系?
已知点 关于x轴 对称点
y
C’(-2,3) 4 C (2,3)
A (-4, 2) 3
2
A(-4,2) A’ (4, 2)
1
A’ (4, 2)
B(3,-4) B’(-3, -4) C(2, 3) C’(-2, 3)
-4 -3 -2 -1-10 -2
1 2 3 4 5x
·
N”(1,-2) N’(5,-2)
类似的:
点A(x, y)关于直线y=1对称 的点的坐标为 (x, -y+2)
点A (x, y)关于直线y= -1对 称的点的坐标为 (x, -y-2)
13.2.2 用坐标表示轴对称

13.2.2 用坐标表示轴对称教学目标:1、能理解平面直角坐标系中,与已知点关于x 轴或y 轴对称点的坐标的规律;2、能作出与一个图形关于x 轴或y 轴对称的图形。
3、通过现实情景的创设,使学生体验到数学就在我们身边,从而培养审美情趣。
教学重点:用坐标表示点关于坐标轴对称的点的坐标。
教学难点:找对称点的坐标之间的关系、规律。
教学设计:一、创设情境 承上启下(一)动手画一画:已知点A 和一条直线MN ,你能画出这个点关于已知直线的对称点吗?(二)、图片导入 有关用坐标表示的生活中的轴对称图例:一幅老北京城的示意图,其中西直门和东直门是关于中轴线为x 轴和y 轴建立平面直角坐标系,对应于如图所示的东直门的坐标,你能说出西直门的坐标吗?二、探索新知1、在平面直角坐标系中画出下列已知点。
A (2,-3);B (-1,2);C (-6,-5);D (3,5);E (4,0);F (0,-3)。
2、画出这些点分别关于x 轴、y 轴对称的点。
并填写表格。
3、请你仔细观察点的坐标,你能发现关于坐标轴对称的点的坐标有什么规律吗?4、尝试再找几个点,分别画出它们的对称点。
5、小组合作,总结规律在平面直角坐标系中:关于x 轴对称的点横坐标相等,纵坐标互为相反数;·· A MN关于y 轴对称的点横坐标互为相反数,纵坐标相等.即:点(x, y )关于x 轴对称的点的坐标为(x, - y);点(x, y )关于y 轴对称的点的坐标为(- x, y)。
三、巩固新知1、说出下列各点关于x 轴、y 轴对称的点的坐标:(2,-3);(-1,2);(-6,-5);(0,-1.6); (4,0)。
2、如下图,△ABC 关于x 轴对称,点A 的坐标为(1,-2),说出点B 的坐标。
3、四边形ABCD 的四个顶点的坐标分别为A (-5,1)、B (-2,1)、 C (-2,5) 、D (-5,4),分别作出四边形关于x 轴与y 轴对称的图形。
人教版数学八年级上册13.2.2 用坐标表示轴对称教案

第2课时用坐标表示轴对称●情景导入十一黄金周,北京吸引了许多游客.一天,小红在天安门广场玩,一位外国友人问小红西直门的位置,可小红只知道东直门的位置,不过,小红想了想,就准确地告诉了他.你知道为什么吗?如图是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,各个地点的地理位置就可以用坐标表示出来.提问:根据如图所示的东直门的坐标,你能说出西直门的坐标吗?对称点的坐标与已知点的坐标有怎样的关系?这节课将学习用坐标表示轴对称.【教学与建议】教学:以老北京地图为例引入新课,让学生感受到用坐标描述对称的重要性.建议:在教学时,先出示老北京地图,让学生进行观察,感受各个位置之间的关系,然后建立平面直角坐标系.●归纳导入 1.如图①:(1)图中两个圆脸有什么关系?(2)已知右边圆脸上右眼的坐标为B(4,3),左眼的坐标为A(2,3),嘴角两个端点的坐标分别为C(4,1),D(2,1).你能根据轴对称的性质写出左边圆脸上左眼、右眼及嘴角两端点的坐标吗?图①图②2.在平面直角坐标系中,将坐标分别为(2,2),(4,2),(4,4),(2,4)的点用线段依次连接起来形成一个图案(如图②).(1)将各个点的纵坐标不变,横坐标分别乘-1,再将所得的各个点用线段依次连接起来,所得的图案与原图案相比有何变化?(2)将各个点的横坐标不变,纵坐标分别乘-1,再将所得的各个点用线段依次连接起来,所得的图案与原图案相比有何变化?如图②,师生共同归纳:(1)将各个点的纵坐标不变,横坐标乘-1,得到相应的四个点分别为A1(-2,2),B1(-4,2),C1(-4,4),D1(-2,4).顺次连接各点所得到的图案和原图案比较.归纳:它们是关于__y轴__对称的,且横坐标__互为相反数__,纵坐标__不变__.(2)将各个点的横坐标不变,纵坐标乘-1,得到相应的四个点分别为A2(2,-2),B2(4,-2),C2(4,-4),D2(2,-4).顺次连接各点所得到的图案和原图案比较,归纳:它们是关于__x轴__对称的,且纵坐标__互为相反数__,横坐标不变.【教学与建议】教学:通过轴对称图形的研究,激发学生探究坐标特点,归纳在坐标的变化中掌握坐标规律.建议:教学中注意渗透数形结合思想.命题角度1 求已知点关于x 轴、y 轴对称的点的坐标两点关于x 轴对称,横坐标相等,纵坐标互为相反数;两点关于y 轴对称,纵坐标相等,横坐标互为相反数.【例1】在平面直角坐标系中,点A (3,4)与点B 关于y 轴对称,则点B 的坐标为(A) A .(-3,4) B .(-3,-4) C .(3,-4) D .(3,4)【例2】在平面直角坐标系中,点A 的坐标是(-3,1),作点A 关于y 轴的对称点,得到点A ′,再将点A ′向下平移2个单位长度,得到点A ″,则点A ″的坐标是(__3__,__-1__).【例3】如图,在平面直角坐标系中,对△ABC 进行循环往复的轴对称变换,若原来点A 的坐标是(a ,b ),则经过2 023次变换后所得的图形中点A 的对应点的坐标是__(-a ,b )__.――→第1次关于x 轴对称――→第2次关于y 轴对称 ――→第3次关于x 轴对称 ――→第4次关于y 轴对称命题角度2 根据轴对称的点的坐标特征确定字母的取值在平面直角坐标系中,若成轴对称的两个点的坐标中包含字母,则先根据轴对称的坐标特征确定字母的值,再求含有字母的式子的值.【例4】点P (1,2)关于y 轴对称的点的坐标是P ′(a ,b ),则a -b =__-3__. 【例5】若点M (a ,-3)与点N (-4,b )关于x 轴对称,则a =__-4__,b =__3__;若这两点关于y 轴对称,则a =__4__,b =__-3__.命题角度3 作规则图形关于坐标轴的对称图形(1)计算已知图形中的一些特殊点的对称点的坐标;(2)根据对称点的坐标描点;(3)依次连接所描各点得到对称图形.【例6】如图,已知△ABC 的三个顶点的坐标分别是A (-1,5),B (-5,3),C (-3,-1).作出△ABC 关于x 轴、y 轴的对称图形.解:如图所示,△A 1B 1C 1和△A 2B 2C 2即为所求作的图形.命题角度4 作规则图形关于直线x =m (或y =n )(m ,n 为常数)对称的图形推广轴对称的点的坐标特征,可得:对于点A (x 1,y 1)与点B (x 2,y 2),如果它们关于直线x =m 对称,那么x 1+x 2=2m ,y 1=y 2;如果它们关于直线y =n 对称,那么x 1=x 2,y 1+y 2=2n .【例7】在平面直角坐标系中,直线l 是经过点(1,0)且平行于y 轴的直线,点A (m -1,3)与点B (2,n -1)关于直线l 对称,则(m +n )2 023的值为(D)A .0B .1C .32 023D .52 023【例8】若点P (-2,1)与点Q (a ,b )关于直线l :y =-1对称,则a +b =__-5__.高效课堂 教学设计1.在平面直角坐标系中,探索并掌握关于x 轴、y 轴对称的点的坐标规律. 2.利用关于x 轴、y 轴对称的点的坐标规律,作出关于x 轴、y 轴对称的图形.▲重点利用坐标的变化规律在平面直角坐标系中画出一些简单的关于x 轴和y 轴对称的图形. ▲难点能根据平面直角坐标系中轴对称点的坐标特点解决实际问题.◆活动1 新课导入用多媒体展示北京城风光图片及北京城形象地图.老北京的地图(教材P 69图13.2-3)中,西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x 轴和y 轴建立平面直角坐标系,对应于如教材图13.2-3所示的东直门的坐标,你能找到西直门的位置和坐标吗?学生指出西直门的位置或坐标,由此指出用坐标表示轴对称,能够很方便确定一个地方的位置. ◆活动2 探究新知1.教材P 69 思考下面的内容. 提出问题:(1)你能完成下表吗?已知点 A (2,-3) B (-1,2) C (-6,-5) D ()12,1 E (4,0) 关于x 轴的对称点 A ′(__2__,__3__) B ′(__-1__,__-2__) C ′(__-6__,__5__) D ′(__12 __,__-1__)E ′(_4_,_0_) 关于y 轴的对称点A ″(__-2__,__-3__)B ″(__1__,__2__)C ″(__6__,__-5__)D ″(__-12__,__1__)E ″(_-4_,_0_)(2)根据上面的表格,你发现关于x 轴的对称点的坐标有什么规律? (3)关于y 轴的对称点的坐标有什么规律? 学生完成并交流展示. ◆活动3 知识归纳1.点(x ,y )关于x 轴对称的点的坐标为__(x ,-y )__. 2.点(x ,y )关于y 轴对称的点的坐标为__(-x ,y )__. ◆活动4 例题与练习 例1 教材P 70 例2.例2 已知点A (a ,4-b )与点B (1-b ,2a ). (1)若点A ,B 关于x 轴对称,求a ,b 的值; (2)若点A ,B 关于y 轴对称,求a ,b 的值.解:(1)由题意,得{a =1-b ,4-b =-2a ,解得{a =-1,b =2; (2)由题意,得{-a =1-b ,4-b =2a ,解得{a =1,b =2. 例3 △ABC 在平面直角坐标系中的位置如图所示. (1)画出△ABC 关于y 轴对称的△A 1B 1C 1;(2)将△ABC 向右平移6个单位长度,作出平移后的△A 2B 2C 2,并写出△A 2B 2C 2各顶点的坐标; (3)观察△A 1B 1C 1和△A 2B 2C 2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.解:(1)△A 1B 1C 1如图所示;(2)∵△ABC 向右平移6个单位长度,∴A ,B ,C 三点的横坐标加6,纵坐标不变,作出△A 2B 2C 2如图所示,A 2(6,4),B 2(4,2),C 2(5,1);(3)△A 1B 1C 1和△A 2B 2C 2关于图中直线l :x =3对称. 练习1.教材P 70~71 练习第1,2,3题. 2.下列判断正确的是(C )A .点(-3,4)与(3,4)关于x 轴对称B .点(3,-4)与点(-3,4)关于y 轴对称C .点(3,4)与点(3,-4)关于x 轴对称D .点(4,-3)与点(4,3)关于y 轴对称3.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是(B )A .(-2,1)B .(-1,1)C .(1,-2)D .(-1,-2)(第3题图)(第4题图)4.如图,以长方形ABCD的中心为原点建立平面直角坐标系,点A的坐标是(3,2),则点B的坐标是__(3,-2)__,点C的坐标是__(-3,-2)__,点D的坐标是__(-3,2)__.◆活动5课堂小结1.关于x轴、y轴对称的点的坐标之间的关系.2.在坐标系中,作关于x轴(或y轴)的轴对称图形.1.作业布置(1)教材P71~72习题13.2第2,3,4,5,7题;(2)对应课时练习.2.教学反思。
13.2.2 用坐标表示轴对称 (课件)

纵轴
y 5
4 第一象限
第二象限
3 2 1
-4
-3
-2 原点
-1
0 -1 -2 -3
1
2
3
4
5
x
横轴
第三象限
第四象限
-4
注
意:坐标轴上的点不属于任何象限。
纵轴
y
5
4
A点在x 轴上的坐标为3 A点在y 轴上的坐标为2 A点在平面直角坐标系中的坐标为(3, 2)
B( - 4 ,1)2
B
3
记作:A(3,2) X轴上的坐标 A
课后作业 1.从课后习题中选取;
2.完成练习册本课时的习题。B B′′ O1 Nhomakorabea1
B′ A′x
D′′
C′′
归纳画一个图形关于x 轴或y 轴对称 的图形的方法和步骤. 先求出已知图形中一些特殊点(多边形的 顶点)的对称点的坐标,描出并连接这些点, 就可以得到这个图形的轴对称图形. 步骤简述为: (1)求特殊点的对称点的坐标;(2)描点; (3)连线.
练习2 如图, △ABO关于x轴对称,点 A的坐标为(1,-2),写出点B的坐标。
3 2 1 B(1,2)
-3 -2 -1 O -1 -2 -3
1 2
3
A(1,-2)
练习3 如图,利用关于坐标轴对称的 点的坐标的特点,分别画出与△ABC关于x 轴和y轴对称的图形。 A(-4,1) B(-1,-1) C(-3,2)
B
A 3 2 1
-4 -3 -2 -1 O C -1 -2 -3
1 2 3
方法二:∵点A(3x-1,2x+5)关于y 轴对称的点在第一象限. ∴点A(3x-1,2x+5)在第二象限. ∴3x-1<0,2x+5>0,解得 -52<x<13. 综上所述,x的取值范围:-52<x<13.
13.2.2用坐标表示轴对称

活动一
轴对称关系(关于y轴对称)
5 4
1.观察图中两张圆脸有 什么关系?
y
· · C D · ·
B1
1
A1
3 2
1 0 -1 -2 -3 -4 1
1
· · D C · ·
A
2 3 4 5
B
-4
-3
-2
-1
x
活 动 二
你能根据 轴对称的 性质写出 左边圆脸 的眼睛和 嘴角的坐 标吗?
2.已知右边圆脸中眼睛A的坐标 (4,3)嘴角 ) 为( C的 (2,3)B的坐标为( (2,1)。 ) 坐标为( (4 4,1)D的坐标为(
探究1:如图,在平面直角坐标系中你能画出 点A关于x轴的对称点吗?
y
想一想
5 4 3 2 1
·
1 2
A (2,3)
-4
-3
-2
-1 0 -1
-2 -3
3
4
5
x
-4
· A′(2,-3)
你能说出 点A与点A′ 坐标的关 系吗?
想一想
在平面直角坐标系中画出下列各点关于x 轴的对称点. y 思考:关于x轴对 5 C′(3, 4) 称的点的坐标具 4 B (-4, 2) 有怎样的关系? 3
·
·
2
1
1 2 3 4 5
-4 -3 -2 -1 0 -1 -2 B′ (-4, -2) -3
x
·
-4
· C(3, -4)
归纳
关于x轴对称的点的坐标的特点是: 横坐标相等,纵坐标互为相反数.
练习
1.点P(-5, 6)与点Q关于x轴对称,则点Q的坐标 (- 5 , -6 ) 为__________. 2.点M(a, -5)与点N(-2, b)关于x轴对称,则 a=_____, 5 -2 b =_____.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.2.2 用坐标表示轴对称
一、学习目标
1、能够经过探索利用坐标来表示轴对称;
2、掌握关于x 轴、y 轴对称的点的坐标特点。
二、温故知新
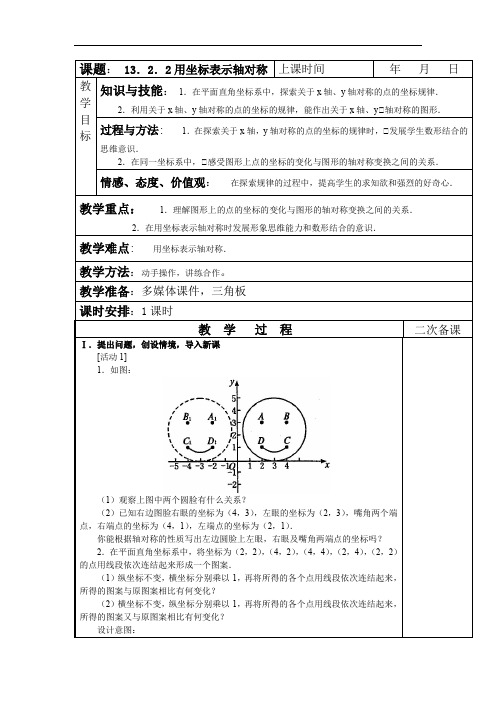
如图:(1)观察图(1)中两个圆脸有什么关系?
(2)若已知图(1)中圆脸右眼的坐标为(4,3),左眼 的坐标为(2,3),嘴角两个端点,右端点的坐标为(4,1), 左端点的坐标为(2,1).你能根据轴对称的性质写出左边圆 脸上左眼,右眼及嘴角两端点的坐标吗?
三、自主探究 合作展示
探究(一)
1、 在如图(2)所示平面直角坐标系内画出下列已知点以及对称点,并把坐标填在表格中,
你能发现坐标间有什么规律?
2、归纳:点(x ,y )关于x 轴对称的点的坐标是 ;
点(x ,y )关于y 轴对称的点的坐标是
探究(二)
图(2) 图(3)
图(1)
例题:
如图(3),四边形ABCD 的四个顶点的坐标分别为A (-5,1),B (-2,1),C (-2,5),D (-5,4),分别作出四边形ABCD 关于y 轴和x 轴对称的图形。
(在教材中完成)
例题反思:
四、双基检测
1、分别写出下列各点关于x 轴和y 轴对称的点的坐标。
2、已知点P (2a+b,-3a)与点'
P (8,b+2).(1)若点P 与点'
P 关于x 轴对称,则a=_____;b=_______.
(2)若点P 与点'
P 关于y 轴对称,则a=_____;b=_______.
3、如图(4),△AOB 关于x 轴对称,点A 的坐标为(1,-2),标出点B 的坐标.
3、如图(5),利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC 关于x 轴和y 轴对称的图形.
图(5)
图(4)
五、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
