饮酒驾车问题模型
饮酒驾车问题

8
C (t )
k1Q (e k2t e k1t ) C0e k2t V0 (k1 k2 )
5.2.2 具体模型二的求解
模型二求解:根据题设,我们取 T 2 。
Q dy (t ) k1 y (t ), 2 由 dt k1 y (t ),
3 模型假设
(1) 体液总体积保持不变 (2) 在较短时间内喝酒的情况下,酒精量是瞬间进入到胃里的。 (3) 体液的总体积不变。 (4) 酒精在血液中的含量与在体液中的含量大至相同。 (5) 不管喝的是什么酒,只以涉入的酒精总量纳入计算。 (6) 假设整体过程中人没有摄入任何影响代谢的药类物质和作剧烈性运 动。 (7) 人的吸收速率和代谢速率是恒定的。 (8) 忽略不同人对酒精代谢能力的差异。
5.1.3 具体模型二(慢速饮酒)
针对具体模型二:该模型针对长期饮酒效应,可将其近似认为在持续饮酒的 过程中酒精是匀速进入肠胃的,参照模型一可有 y (0) 0 ,在此我们引入函数
f 1 (t ) 来表示酒精进入肠胃的速率(单位:毫克/小时), T 表示饮酒时的持续总
时间,则酒精进入肠胃的速率与整个过程中喝入的酒精量有如下关系:
5.2 模型求解 5.2.1 具体模型一的求解
模型一求解:根据具体模型一得:
dy (t ) k1 y (t ) dt f (t ) k1 y (t )
将其整理并带入一般模型中求解得到 C (t ) 与 t 的关系:
dC (t ) aC0 k1t e k2C (t ) dt V0
关键词:房室模型 微分方程组
Ct 驻点法 吸收和代谢
饮酒驾车的微分方程模型

二 、 模 假 设 建
1 饮 酒 后 , 精经 胃逐 步 扩散 到 血液 中 . 被 血 液 中 的酶 逐 渐 . 酒 冉
分解 。
由( ) ( ) 看出 :( ) , + y t 是 以 e 为 公 比的等 比序 8÷ 9可 , 一 ) ( ) ( 列, 故有 :( - ( ) r y t = ) y 0 + , 0 1e ) y £) ( ’, y £ y t + q ( ) (】- ( ) 1 )( (I・ep ) ( = ) 对 七式 两边求 和得 :
( , 各 时段 均 定作 常 数 T 并将 时 段 分 点记 成 t i l2 3 t 将 ) , i= , , ……)则 ( , 上 式化 为 :( - ( ) y t =2 p Wi y t 『, y £ y t + () [ae 'q ( )r ) -
整 理 为 :( ) ( + q ( )2 e 8 f } ) T y t = 1’ _ ・ 亦 有 :( - ( + y t = a e 。 y £ yt ( ) H) ) 2p・ 。 () 8 ( 9)
q- p
() 6
8 8 7 6 6 5 2 2 7 8 8 8 9 1 1 1 1 1 o 1 2 3 4 2 2 1 1 1 1 8 5 8 5 2 o
5 5 4 1 0 1 1 1 5 6 7 7 4
所求 的血 液 中酒 精浓 度 随时 间变化 的 函数 :
巾图 分类 号: 7 O15
一
文 献标 识码 : A
文章编 号 : 9 83 (00 0— 14 0 10- 6 12 1 )8 03— 2
() ^ t t= p () () 】
、
前 言
饮 酒肇 事 , 所周 知 , 众 本模 型 给 出了如下 建模依 据 : 饮 洒 、 ① 醉酒
微分方程模型--饮酒驾车

– 在建模仿真中的应用 – ……
MATLAB 的保留常量
特殊变量 ans pi eps flops inf NaN i,j nargin nargout realmin realmax 取 值 用于结果的缺省变量名 圆周率 计算机的最小数,当和 1 相加就产生一个比 1 大的数 浮点运算数 无穷大,如 1/0 不定量,如 0/0 i=j= − 1 所用函数的输入变量数目 所用函数的输出变量数目 最小可用正实数 最大可用正实数
人把酒喝入体内后,酒精进入血液需要有一个吸收的过程,故可认为有一 酒精向体外排泄速率与人体体液中酒精的含量成正比; 个吸收室,且酒精被完全吸收。把肠胃作为Ⅰ室,人体体液作为Ⅱ室,酒 2、仅考虑所喝酒中的酒精全部进入血液,不考虑其他因素的影响; 精被吸收后进入Ⅱ室,并最终由Ⅱ室分解并排除,其运动过程如图:
体重约70kg的某人在短时间内喝下2瓶啤酒后,隔一定时间测量他 的血液中酒精含量(毫克/百毫升),得到数据如下:
时间(小时) 酒精含量 时间(小时) 酒精含量
0.25 30 6 38
0.5 68 7 35
0.75 75 8 28
1 82 9 25
1.5 82 10 18
2 77 11 15
2.5 68 12 12
4 51 15 7
4.5 50 16 4
5 41
30
时间(小时) 6 酒精含量
38
人把酒喝入体内后,酒精进入血液需要有一个吸收的过程,故可认为有一 酒精向体外排泄速率与人体体液中酒精的含量成正比; 个吸收室,且酒精被完全吸收。把肠胃作为Ⅰ室,人体体液作为Ⅱ室,酒 2、仅考虑所喝酒中的酒精全部进入血液,不考虑其他因素的影响; 精被吸收后进入Ⅱ室,并最终由Ⅱ室分解并排除,其运动过程如图:
“饮酒驾车的药物注射模型”求解

实验6.8“饮酒驾车的药物注射模型”求解一·实验目的运用药物注射模型,使用曲线拟合方法,解释饮酒驾车的一些实际问题二·实验原理由于酒精不需要进入肠道即可被吸收,且胃对其吸收速率也非常快,本题应采用“快速静脉注射模型”。
酒精主要存在于血液中,故本例应计算吸收室的血药浓度c1(t)=A1*e^(-αt)+B1*e(-βt)相关系数可以通过拟合法求解。
三·实验代码>> t=[0.25,0.5,0.75,1,1.5,2,2.5,3,3.5,4,4.5,5,6,7,8,9,10,11,12,13,14,15,16];>> y=[30,68,75,82,84,77,70,68,58,51,50,41,38,35,28,25,18,15,12,10,7,7,4];>> ft=fittype('A1*exp(-a*x)+B1*exp(-b*x)');>> options=fitoptions('Method','NonlinearLeastSquares');>> options.StartPoint=[0 -1000 0 0];>> cfit=fit(t',y',ft,options);>> plot(cfit,t',y','o');//拟合曲线1>> A1=cfit.A1>> B1=cfit.B1>> a=cfit.a>> b=cfit.b>> t1=6;>> c1=(A1*exp(-a*t1)+B1*exp(-b*t1))/2>> t2=13.2;>> c2=(A1*exp(-a*t2)+B1*exp(-b*t2))/2>> t3=7.2;>> c3=(A1*exp(-a*t3)+B1*exp(-b*t3))/2>> t2=0.2:0.1:24;>> for i=1:239c2(i)=(A1*exp(-a*t2(i))+B1*exp(-b*t2(i)))/2;end>> plot(t2,c2,t2,20);>> plot(cfit,t',y','o');//拟合曲线2>> t4=0.2:0.1:72>> for i=1:length(t4)c4(i)=(A1*exp(-a*t4(i))+B1*exp(-b*t4(i)))*1.5;end>> for i=121:length(t4)c42(i)=(A1*exp(-a*t4(i-120))+B1*exp(-b*t4(i-120)))*1.5;end>> for i=241:length(t4)c43(i)=(A1*exp(-a*t4(i-240))+B1*exp(-b*t4(i-240)))*1.5;end>> for i=361:length(t4)c44(i)=(A1*exp(-a*t4(i-360))+B1*exp(-b*t4(i-360)))*1.5;end>> for i=481:length(t4)c45(i)=(A1*exp(-a*t4(i-480))+B1*exp(-b*t4(i-480)))*1.5;end>> for i=1:length(t4)c4A1(i)=c4(i)+c42(i)+c43(i)+c44(i)+c45(i);c4A2(i)=c4(i)+c43(i)+c45(i);end>> plot(t4,c4A1,t4,20);//拟合曲线3>> plot(t4,c4A2,t4,20);//拟合曲线4四·代码结果1.问题:根据表格数据拟合求解相关系数A1=110.55B1=-151.46a=0.17949b=2.8243拟合曲线如下2.问题:某人中午12点喝了一瓶啤酒,下午6点检查合格,晚饭又喝了一瓶,次日凌晨2点检查未通过,请解释此情况。
饮酒驾车问题的微分方程模型

口
可 酒 在 的 谢 成 出 过 用( 】 ( 把 精 体内 代 看 进与 的 程, 鲁 鲁L 和
分别表示酒精输入速率和酒精输 出速率 ,这样 问题可简化 为血液
由图可知在饮酒后 的 1 时内驾车都违反 交通 规则 ,其 中 2小 03 _ . .5 45 h内属于醉酒驾车。根据 医学知识 :一 次进酒后 ,4小时 “ 2 基本全部排泄完 , 2 即 4小时之后就可 以认为血液 中的酒精含量约
善 ■
短时间饮酒是一次饮入 , 中间时差不计 。 酒精在血液与体液 中 含量相同。 酒精进人体 内后不受其他因素对酒精 的分解 , 不考虑个
体差异。 转移过程为 , 胃一体液一 体外 。 的体液 占人体重的 6% 人 5 至 7 %, 0 血液 占体重的 7 %左右 ; 而酒精在血液与体液 中的含量是
问题 1 . 饮酒后 多长时间后血液中含酒精量最大 。 问题 2某 人在早上 8点喝 了一瓶 啤酒 , . 下午 2点检查 时符 合
新 的驾车 标准 , 他在 I 9点吃晚饭 时又喝 了一瓶啤酒 , 了 6小 时 过 后驾车 回家 , 又一次遭遇检查时却被定为饮酒驾车 , 这让他 陷入 困 惑, 为什 么喝同样多的酒 , 两次检查结果会不一样 呢?过六 小时后 再 喝一瓶 , 过多长时间才可 以驾 车。 问题 3 . 一次喝 3瓶啤酒多长时间可以驾车。
可以看 出, 当
。”酒精 含量最大 得 , 解 :
,
,
。
时 c) (达到最大值。 【 五、 问题 的回答 1饮酒后多长时间后血 液中含酒精量最大 。根据 以上数 据拟 . 合出参数 k. f o的值分别为 k= . 7 ,2O -k, Y 1连 , 并成 了处理形形色色的实际问题 的有效工具 , 本文 应用微分方程的基本理论 建立 的模型 ,很好 的描述 了酒后体内酒 精 含量 的变化规律 ,司机 可根据这个关 系来判断饮酒 后安全驾车
饮酒驾车的数学模型

饮酒驾车的数学模型(CUMCM-2004C题)一、摘要本题是关于一个饮酒驾车的数学模型。
因为酒精在一个房呈均匀分布,从吸收室到中央室按照一定的规律进行吸收和排除。
所以根据不同时刻的吸收与排除情况,为了研究酒精的吸收和排除的动态过程,我们对市场上酒的分析调查为参考资料。
以传统的常微分方程理论来建立控制饮酒驾车模型方程与曲线拟合的模型,近似于房室模型来解决.通过matlab数学软件求解模型,得到相关结果。
最后从模型方程跟实际对比分析中找出实际与理论的差异。
关健词:常微分方程曲线拟合房室模型二、问题的提出在2003年全国道路交通事故死亡数字的10.4372万中饮酒所造成的事故占着相当大的比例。
针对这一比例所造成的事故国家质量验检局与2004年5月31日发布的新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准规定了驾驶人员血液中的酒精含量。
新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫升为饮酒驾车(原标准是小于100毫克/百毫升),血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车(原标准是大于或等于100毫克/百毫升)。
为了减少和预防事故发生,保证人民的生命财产的安全,我们建立模型对饮酒驾车进行分析,为政府提供一些相关资料的参考。
三、问题的分析与假设(一) 问题分析因为在1个小时以内酒精未达到机体最大消除力时,假设在吸收过程仍符合一级动力方式消除。
因为按酒精的一般规律,酒精的清除符合零级动力学方式,所以我们可以假设在一开始喝酒的过程时,酒精的排除符合零级动力方学方式。
另一种情况就是酒在长时间内喝的,近似于口服药液。
根据表格数据我们可知,酒精在血液中的浓度随时间的变化而变化(二)问题假设1.假设在酒精的吸收收速率及排除速率,与该室的酒精浓度成正比。
2.假设机体分为中心室和吸收室(如图1),且两个室的容积在过程中保持不变。
3.假设当酒精进入中心室时,吸收和排除的数量相比,吸收可以忽略。
饮酒驾车模型

五,饮酒驾车问题分析酒精摄入体内直接进入胃中,再由胃中进入体液,由体液排除,不考虑人体其他代谢方式产生的酒精。
他第一次检验时体液中的酒精含量小于20毫克/百毫升,第二次却大于或等于20毫克/百毫升,小于80毫克/百毫升,判断大李第二次检查时中午12点摄入体内的酒精还未代谢完,因而此次检查体液中的酒精含量是两次之和。
所以根据已知条件建立微分方程,得到饮酒后血液中酒精含量m(t)随时间{ EMBED Equation.DSMT4 |t的变化规律,将大李从饮酒到检查的时间间隔代入其中,检验此刻酒精含量是否符合新标准,便可解释大李碰到的情况。
设如下变量:1.,胃和体液的酒精含量;2.:胃和体液的酒精浓度;3.:酒精进入体液的速率;4.:引入的酒精总量5.:胃和体液的体积;6.:酒精从胃进入体液的速率;7.:.酒精从体液排出体外的速率。
模型假设一、酒精从体外进入胃,单向渗入体液,从体液排出体外;二、胃和体液的容积不变;三、酒精在体液的转移速率及向体外排出的速率与体液酒精浓度成正比;模型的建立饮酒者喝酒后,酒精进入胃,单向渗入体液,从体液排出体外,在胃和体液的转移速率和排出速率均不同,所以可得:胃:(1)体液:(2)模型求解与结果分析方程组(1)解得,方程组(2)运用数学软件MATLAB,解得:在现实中每瓶啤酒体积:640ml;啤酒酒精度数:3.6%4.2%;啤酒酒精密度:800mg/l。
取啤酒酒精度数为4%,可得每瓶啤酒酒精含量为20480mg。
人的体液占人的体重的65%至70%,人体体液密度约为mg/100ml,酒精在血液中的含量与在体液中的含量大体一致,体重约为70kg的人在短时间内喝下2瓶啤酒,则为40960mg,(百毫升)。
编写程序如下t=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16];c=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4];k0=[3,0.5];k=lsqcurvefit('test',k0,t,c)Optimization terminated: relative function valuechanging by less than OPTIONS.TolFun.k =2.68580.1474plot(t,c,'*')tt=0:0.1:16;cc=test(k,tt);holdCurrent plot heldplot(tt,cc,'r')拟合图示如下:下面来求解问题我们认为:(1)大李在两次喝酒直到检查时没有服用任何影响体内酒精含量的药物;(2)大李吃晚饭时间为20:00。
饮酒驾车问题模型
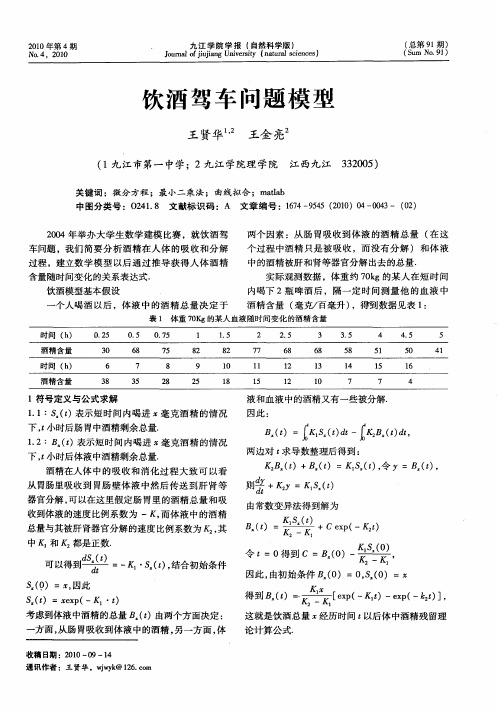
%所求含参非线性函数 B t ()=c 血 一 , I ‘ c e e
F= X ( ) . ep ( ( ) 1 x X 2. () 1 . ep ( ( ) x X 3 . x a ) dt ; a x a ) +x dt a
23在命 令窗 口中输 入 :Nh . ie
为了得到 的结果更精确 ,我们 把每次运算的
B ()+B ()=K S()令 Y =B () t t t , t,
则 +K y =K S () 2 1 由常数 变异 法得 到解 为 = +c e p x ( )
可 得 一 st结 初 条 因此 , 始条 件 B O =0, ( ) = 以到安 : , 始 件 .( 合 ) 由初 () 0
20 04年举 办 大学 生数 学 建模 比赛 ,就饮 酒 驾 车问题 ,我 们 简要 分 析 酒 精 在 人体 的 吸 收和 分 解 过程 ,建立 数 学模 型 以后 通 过 推 导获 得 人 体 酒 精
含量 随时 间变化 的关 系表 达式 . 饮酒模 型基本假 设
一
两 个 因素 :从 肠 胃吸 收到 体 液 的酒 精 总量 ( 这 在 个 过程 中酒 精 只是 被 吸 收 ,而 没有 分 解 ) 和 体 液
( )= , 9 因此
s t I () =x x ( 1・ ) , e p 一K £
令
得到 c
( )一 o
,
得 ( 一 [p一 ) e(尼), 到 t. )乏 e( x £一x 一:] p f
这就 是饮 酒 总量 经历时 间 t 以后 体 中酒 精 残 留理
论计 算公 式.
表 1 体重 7 l O( g的某人血液随时间变化 的酒精含 量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
饮酒驾车的优化问题摘要近年来因饮酒驾车引起的交通伤亡事故频频发生,为维持良好的道路交通情况,更好的保障广大行人人身安全。
国家质量监督检验检疫局对此出台了更为严格的酒驾国家标准,本文针对饮酒驾车问题,主要研究了酒精浓度在人体内吸收与分解随时间的变化规律,并针对不同饮酒方式和饮酒量时血液酒精浓度随时间变化规律的不同进行了比较研究。
针对问题一本文利用药物代谢动力学分析方法,模拟了人体吸收与分解酒精的过程,采用二室房室模型把肠胃和体液模拟成两个封闭的空间——吸收室与中心室,基于“体内酒精含量=现有量+吸收量-分解量”的原理,分别建立吸收室与中心室的酒精含量变化与时间t 的微分方程,并运用MATLAB 求解得到中心室酒精含量与时间t 的关系式,并通过111v c x ⨯= ,最终得到体液中酒精浓度随时间t 的变化关系式())(46.4014c 1474.06853.21t t e e t ---=。
求得大李第一次检查时血液中酒精浓度为14.2695 mg/dml ,没有超标。
第二次检查时血液中酒精浓度为20.1622 mg/dml ,结果了超标。
针对问题二,对于快速饮酒,会很快达到最大。
然而对于长时间喝酒,则是可以看成分割的瞬时饮酒的之和,所以仍用本文的瞬时饮酒模型进行求解。
对快速饮酒而言,经过计算,在饮酒13.1629小时内血液中酒精浓度大于20mg/dml ,违反标准;在饮酒3.7574小时内血液中酒精浓度大于80mg/dml ,属于醉酒驾车。
对长时间饮酒而言,经过计算在14.0113小时内血液中酒精浓度大于20mg/dml.属于违规。
在饮酒4.6051小时内血液中酒精浓度大于80mg/dml ,属于醉酒驾车。
针对问题三无论是快速饮酒或较长时间内喝酒,酒精向体液渗透和体液中酒精分解的速度会随着时间变化而增大,而当体液分解酒精的速度等于肠胃内酒精向体液渗透的速度时,体液中的酒精浓度达到最大。
本文用lingo 软件对非线性约束())(46.4014c 1474.06853.21t t e e t ---=求极大值可知,体液中酒精浓度达到最大的时刻为:1.1015小时。
针对问题四如果天天喝酒,且饮过量的酒,由前面三问结论可知,不论饮酒时间长短,血液酒精浓度均不能在很长一个时间内恢复到安全驾驶标准。
即使长时间内均匀的喝少量的酒,人体血液中的酒精的含量也会积少成多,天天喝酒必定超过安全驾驶标准。
所以如果天天喝酒,就不能开车。
针对问题五中在新的酒驾国家标准下,想喝一点酒的司机需要开车时,切记不要饮酒过量,不要马上驾车。
保护自己与他人的安全。
关键词:饮酒驾车 酒精浓度 微分方程 拟合1 问题重述安全驾驶不仅有助于维持良好的道路交通情况,也是广大行人人身安全的重要保障。
而因饮酒驾车引起的道路交通伤亡事故所占比例较高,饮酒驾车引起的交通安全问题越来越受到全社会的高度关注,国家质量监督检验检疫局对此也发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫升为饮酒驾车(原标准是小于100毫克/百毫升),血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车(原标准是大于或等于100毫克/百毫升)。
新标准中关于酒驾的界定有了更为严格的规定。
司机大李中午12点喝了一瓶啤酒,下午6点检查时符合新的驾车标准,紧接着他在吃晚饭时又喝了一瓶啤酒,凌晨2点驾车回家遭遇检查时却被定为饮酒驾车,喝同样多的酒,两次检查结果却不一样。
他既懊恼又困惑。
可参考以下数据:建立饮酒后血液中酒精含量的数学模型,并讨论以下问题:1. 对大李碰到的情况做出解释;2. 在喝了3瓶啤酒或者半斤低度白酒后多长时间内驾车就会违反上述标准,并考虑不 同饮酒方式和饮酒量,比如酒是在很短时间内喝的或酒是在较长段时间(比如2小时)内喝的。
3. 怎样估计血液中的酒精含量在什么时间最高。
4. 根据你的模型论证:如果天天喝酒,是否还能开车?5. 根据血液酒精浓度随时间变化的规律,给想喝一点酒的司机如何驾车提出建议。
避免酒后驾车时酒精超标而引起不必要的交通事故,创造和谐的交通环境。
时间(小时)0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 酒精含量 30 68 75 82 82 77 68 68 58 51 50 41 时间(小时) 6 7 8 9 10 11 12 13 14 15 16 酒精含量 38 35 28 25 18 15 12 10 7 7 42 问题分析要解释大李的困惑,就必须找出影响血液中的酒精含量的因素,即血液中酒精含量随时间,饮酒量和饮酒方式的变化关系。
大李两次喝相同份量的啤酒,接受检查的时间间隔相差不多,检查结果却不一样。
原因在于两次接受检查前的血液中酒精初始浓度不同。
第二次接受检查前血液中的酒精浓度高于第一次接啤酒受检查前血液中的酒精浓度,因为第二次凌晨2点接受检查时血液中含有第一次12点喝啤酒时留存的酒精,所以第一次检查合格,第二次检查不合格。
可知血液中酒精含量与原有的酒精含量同进来的酒精含量和出去的酒精含量均有关系。
而血液中酒精含量的变化与不同饮酒方式和饮酒量及时间长短等因素有关。
故本文主要考虑了饮酒的时间和饮酒量的变化对体血液中酒精浓度的影响.找出血液中酒精浓度的变化规律,找出饮酒后安全的驾车时间。
3 模型假设1. 假设喝啤酒后,啤酒的酒精全部进入胃肠(含肝脏),然后经过胃肠渗透到体液中。
2. 假设酒精从胃肠向体液的转移速度,与胃肠中的酒精浓度(或含量)成正比。
3. 假设体液的酒精消耗(向外排出、分解)的速度,与体液中的酒精浓度(或含量)成正比。
4. 假设大李两次喝酒时都是将酒瞬时喝下去并立即进入胃肠中,没有时间耽搁。
5. 假设人体喝入的酒精最终会被人体全部吸收。
6. 假设在较长时间饮酒的情况下,这个持续的饮酒过程中酒精是匀速均匀的进入肠胃的。
4 符号说明 符号 符号说明单位 )(0t x 吸收室的酒精含量毫克 )(1t x 中心室的酒精含量毫克 01k 吸收室向中心室的酒精转移比率 k 中心室的酒精分解比率 1c 体液中的酒精浓度毫克/百毫升 1v 人体的体液体积百毫升 0D 饮入的酒精量毫克 )(1t c血液中的酒精浓度 毫克/百毫升5 模型的建立与求解5.1 问题一的模型5.1.1 模型建立针对问题一,对于短时间内饮入酒的情况我们可以建立下述模型我们用吸收室代表胃,用中心室代表体液。
首先我们对吸收室建立微分方程,考虑到酒在短时间内进入吸收室,可得, 0()dx t =-01k )(0t x )(0t x =0D 解此微分方程得,)(0t x =0D t k e 01- (一) 对中心室创建微分方程,并将公式(一)带入,可得,1()dx t =01k )(0t x -k)(1t x 1(0)x =0 (二) 考虑到,1x =1c 1v解此微分方程得 )(1t c =)()(01011010t k kt e e k k v k D ---- (01k ≠k ) (三) 接下来,我们通过题中所给实验数据来非线性拟和求出两个系数,01k ,k每瓶啤酒的体积为640毫升,啤酒的酒精度约为4%,酒精的密度为800毫克/毫升,所以可以计算得到每瓶啤酒中含有酒精为20480毫克。
体液约占体重的65%-70%,体液的密度约为51005.1⨯毫克/百毫升。
可以计算70公斤的人体液约为467百毫升。
所以对于题中实验数据,可以确定(代表0D 饮入两瓶的饮酒量,单位为毫克)等于40960毫克,1v (人体的体液的体积,单位为百毫升)467百毫升。
又体液中酒精浓度和血液中酒精浓度相同。
)(0t x 吸收室 )(1t x 中心室 K 01 k用函数)(1t c =)()(01011010t k kt e e k k v k D ----拟和题中实验数据得图形如下: 02468101214160102030405060708090401k =2.6853 k =0.1474所以得到拟和函数:)(1t c =)(92.80291474.06853.2t t e e --- ,y 轴表示酒精血液浓度,x 表示时间。
程序见附录一 6、模型求解下面对问题一用模型做出解答(1)首先给出快速饮酒一瓶时血液中酒精浓度的函数)(1t c =)(46.4014 1474.06853.2t t e e ---做出图象:大李中午12点饮酒一瓶啤酒经过六小时,血液中酒精浓度19.1620mg/dml ,所以六小时后大李通过了检查。
大李凌晨2点再一次检查时血液中的酒精含量应为两部分组成,第一部分是中午12点喝的酒经过了14个小时后在血液中的残量,应为5.8927 mg/dml ,它属于一直分解后的残量,第二部分是晚上6点又喝了一瓶酒后经过吸收和分解的过程,在过了八小时后在血液中的浓度为:14.2695 mg/dml ,所以血液中的酒精总浓度为20.1622 mg/dml ,大于20 mg/dml ,所以没通过检查。
(以上数据均为通过模型精确计算得到)。
针对问题二(一),给出快速喝进3瓶啤酒后的血液酒精浓度随时间变化的函数:)(1t c =)(139.2042 1474.06853.2t t e e ---,图象为:经过计算,在饮酒13.1629小时内血液中酒精浓度大于20mg/dml,违反标准。
在饮酒3.7574小时内血液中酒精浓度大于80mg/dml,属于醉酒驾车。
(二),如果酒是在较长一段时间内(2小时)喝的,我们可以认为酒是匀速饮入,我们对时间进行分割,然后在每个小时间段内看成是快速饮入定量的酒。
在每个小时间段内用模型模拟,如果我们把时间分为6等份,也就是每20分喝半瓶啤酒,每次饮酒看成是快速饮酒,用快速饮酒模型分别模拟得图象:(下图:3瓶啤酒六次速饮各曲线)在每个时间点把每个函数值相加就得到在这一时刻,血液中酒精的浓度,经过计算在14.0113小时内血液中酒精浓度大于20mg/dml.属于违规。
在饮酒4.6051小时内血液中酒精浓度大于80mg/dml,属于醉酒驾车。
针对问题三:分别讨论快速饮酒和较长时间内喝完酒两种情况对于快速饮酒,无论饮酒量为多少(如下图),酒会在很短的时间内进入到胃中,这时胃中的酒精浓度会短时间内达到很高,这时酒精高速渗透向体液,随着时间的增加,体液中排出酒的速度会增加,而当体液排出酒精的速度等于胃向体液渗透的速度时,体液中的酒精浓度达到最大,对于快速饮酒,会很快达到最大。
经过计算,体液中酒精浓度达到最大的时刻均为1.1015小时。
对于在较长时间内喝完酒,因为酒可看成是匀速饮入,酒精渗入体液的速度相对增加较慢,相对于快速饮酒,血液中酒精浓度达到最大值的时间要靠后,经过计算对于上述2小时喝三瓶酒达到最大的时间为:2.3416小时。
