学而思三年级数学寒假1-6讲课程讲义201802
第01讲 等差数列基础 学而思三年级春季超常班讲义

第一讲等差数列基础关于第一讲等差数列,是中年级学习的一个重点。
高年级的很多题虽不是直接考察等差数列,但往往中间的某一步需要用到等差数列的知识。
等差数列这讲公式繁多,但希望孩子们千万不要死记硬背这些公式,一定要理解着记忆。
死记硬背公式不易记牢,往往容易出错,考试中一旦出现,背错公式,分数就得不到了;在在我总结的知识点解析里每个公式,我都讲了理解的方法。
可以在做题时反复理解几次,就不容易出错了。
关于计算这里,再啰嗦几句。
很多孩子的计算基本功不过关,所以往往上课时算式列出来了,但不会算,算得慢或算不准,这样就太可惜了。
所以希望孩子们能够每天坚持练几道大数乘除法。
乘法可以按照三位数×一位数,两位数×两位数,三位数×两位数,四位数×两位数,三位数×三位数,四位数×三位数。
除法可以从三位数÷一位数,四位数÷一位数,三位数÷两位数,四位数÷一位数,五位数÷一位数,五位数÷三位数等等这样的顺序练起。
一、通项公式知识点解析:⒈第n项=首项+(n-1)×公差理解方法:可以对比植树问题来理解等差数列,第二项比第一项多一个公差,第三项比第一项多两个公差,……第n项比第一项多(n-1)个公差。
辅助练习:等差数列5、8、11……求这个数列的第2011项是多少?答:5+(2011-1)×3=6035这个公式含有四个量首项,第n项,项数n,公差,这四个其实是知三求一的。
⒉首项=第n项-(n-1)×公差理解方法:同1,第n项比第一项多(n-1)个公差,用第n项剪去多出的即可。
辅助练习:等差数列……91,95,99共17项,求第一项是多少?分析:已知第17项是99,项数n为17,公差95-91=4答:99-(17-1)×4=35(此公式本讲没有涉及)⒊项数n=(第n项-首项)÷公差+1理解方法:对比植树问题,第n个数与第一个数之间共差了第n项-首项,那么间隔数应为(第n项-首项)÷公差,项数n应该比间隔数多1,所以,项数n=(第n项-首项)÷公差+1此公式为求和公式的基础,往往一道题第一步需要孩子判断一下共有多少项,第二步利用求和公式求和。
学而思小学奥数个精彩讲座总汇全

第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 18262 13581333416⨯+⨯-÷【分析与解】原式=7123723174612241488128131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×.具体过程如下:原式=5919(3 5.22)19930.41.6910()52719950.5199519(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143.计算:1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少【分析与解】方法一:1118x68114x112x7111+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25.方法二:有11131118821x4+==+++,所以18222133x4+==++;所以13x42+=,那么x=.5.求944,43,443,...,44 (43)个这10个数的和.【分析与解】方法一:944+43+443...44 (43)++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44 (49)++++-个=1094(999999...999...9)99⨯++++-个=1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个=914111.1009=49382715919⨯-个.方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=;再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=;再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=;再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=;再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=;再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=;再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=;再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4.所以,这10个数的和为91.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少【分析与解】因为每个端点均有三条线段通过,所以这6条线段的长度之和为:1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○=○=.符号“△”表示选择两数中较小数的运算,例如:△=△=.请计算:23155 (0.625)(0.4)33384 1235(0.3)( 2.25) 3104⨯+【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如.那么在所有这种数中。
学而思奥数三年级讲义-《长方形与正方形》
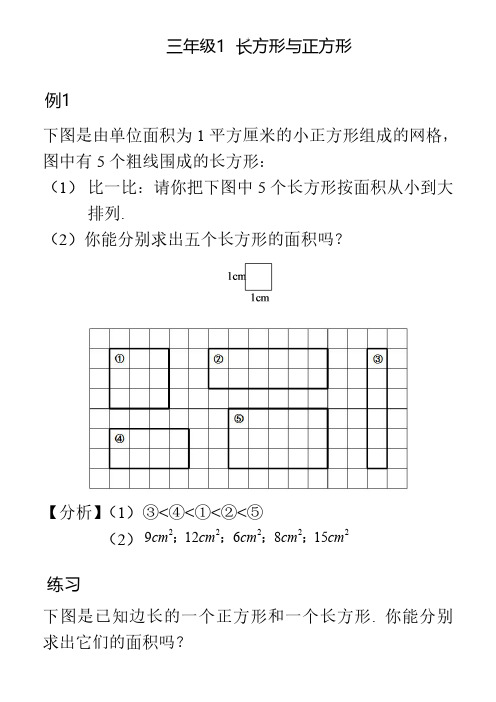
排列. (2)你能分别求出五个长方形的面积吗?
【分析】(1)③<④<①<②<⑤ (2) 9cm2;12cm2;6cm2;8cm2;15cm2
例4
算一算: (1)一个长方形长 12 米,宽 8 米,如果它的长增加 2 米, 宽不变,这个长方形的面积增加多少平方米? (2)一个长方形如果宽不变,长增加 8 米,面积增加 72
平方米;如果长不变,宽减少 4 米,面积减少 48 平方米,
这个长方形原来的面积是多少?
【分析】(1)增加部分的面积: 2 ×8 =16 (平方米)(2)
(2)5m²=( )dm²
3dm²=( )cm²
(3)7 平方米=( )平方分米=( )平方厘米
(4)( )m²=800dm²=( )cm²
(5)10 公顷=( )m²
(6) 6 平方千米=( )公顷=( )平方米
【分析】(1)200 厘米=20 分米=2 米
(2)5 m²=500 dm²
3dm²=300 cm²
(3)7 平方米=700 平方分米=70000 平方厘米 (4)8 m²=800 dm²=80000 cm ² (5)10 公顷=100000 m² (6)6 平方千米=600 公顷=6000000 平方米
练习
选用合适的度量单位填入空白处.
黑板面的面积约 3(
) 一间教室长约 8(
)
一幢楼高约 50(
6
根 据 公 式 可 知 , 空 白 处 面 积 黄 绿 红
三年级学而思数学讲义

三年级学而思数学讲义第一章 - 加法与减法1.1 加法- 加法是一种基本的数学运算,用于将两个或多个数字相加。
- 如何进行加法运算的步骤如下:1. 对齐数位,从最右边的数位开始相加。
2. 如果相加的结果超过9,我们将进位到更高位。
3. 继续相加剩余的数位,直到所有数位都相加完毕。
4. 最后的结果就是两个数的和。
1.2 减法- 减法是一种用于求两个数之差的运算。
- 如何进行减法运算的步骤如下:1. 对齐数位,从最右边的数位开始相减。
2. 如果相减的结果小于0,我们将向更高位借位。
3. 继续相减剩余的数位,直到所有数位都相减完毕。
4. 最后的结果就是两个数的差。
第二章 - 乘法与除法2.1 乘法- 乘法是一种基本的数学运算,用于将两个或多个数字相乘。
- 如何进行乘法运算的步骤如下:1. 对齐数位,从最右边的数位开始相乘。
2. 按照乘法的规则进行计算,并将进位到更高位。
3. 继续相乘剩余的数位,直到所有数位都相乘完毕。
4. 最后的结果就是两个数的乘积。
2.2 除法- 除法是一种用于求两个数之商的运算。
- 如何进行除法运算的步骤如下:1. 对齐数位,从最高位开始进行整除。
2. 根据除法的规则进行计算,并将余数带下一位进行除法运算。
3. 继续进行剩余的数位的除法运算,直到所有的数位都被除完。
4. 最后的结果就是两个数的商和余数。
第三章 - 数学问题解决方法3.1 理解问题- 在解决数学问题时,首先要理解问题的要求和条件。
- 仔细阅读问题,并提取出关键信息。
- 可以通过画图、列出方程等方法来帮助理解问题。
3.2 探索解决方法- 根据问题的要求和条件,可以尝试不同的解决方法。
- 可以使用已知的数学知识和技巧来解决问题。
- 如果找到了一个解决方法,可以尝试将其应用到问题上。
3.3 验证答案- 在解决数学问题后,应该验证答案的正确性。
- 可以进行逆向计算或使用其他方法来验证答案。
- 如果验证结果与问题的要求一致,则可以确认答案的正确性。
三年级奥数寒假大纲(盛)11

LOGO
例题: 例题: 第四届《小数报》决赛) (第四届《小数报》决赛) 有一大一小两个正方形, 有一大一小两个正方形,它 们的周长相差20厘米 厘米, 们的周长相差 厘米,面积 相差55平方厘米 平方厘米. 相差 平方厘米.小正方形 的面积是多少平方厘米? 的面积是多少平方厘米?
Page 10
例题: 例题: 果园里有桃树、梨树、苹果树共552 552棵 果园里有桃树、梨树、苹果树共552棵.桃树比梨 树的2倍多12 12棵 苹果树比梨树少20 20棵 求桃树、 树的2倍多12棵,苹果树比梨树少20棵,求桃树、 梨树和苹果树各有多少棵? 梨树和苹果树各有多少棵?
Page 5
三年级奥数寒假课程设置 第3讲:简单图形的面积计算 长方形、正方形; 1、长方形、正方形; 三角形、梯形; 2、三角形、梯形; 图形分割法。 3、图形分割法。
LOGO
学而思三年级奥数寒假大纲
主讲: 主讲:盛老师
LOGO
小学关键的 第二阶段
三位一体抓 学习习惯
寒假
速算与巧算 图形面积计算 余数问题 集中时间学 习效果明显
Page 2
三年级寒假我们学什么?
LOGO
知识点 速算与巧算之四则运算 和差倍综合运用 简单图形的面积计算 间隔与方阵 有趣的余数问题 乘除法竖式填空格 杯赛真题串讲
三年级奥数寒假课程设置 第4讲:间隔与方阵 植树问题(直线型、封闭型); 1、植树问题(直线型、封闭型); 方阵(实心、空心); 2、方阵(实心、空心); 三角形阵、正六边形阵等等。 3、三角形阵、正六边形阵等等。
LOGOΒιβλιοθήκη 例题: 例题: 有一队学生排成一个中空方阵,最外层共有52 52人 有一队学生排成一个中空方阵,最外层共有52人, 最内层共有20 20人 问这个方阵中有学生多少人? 最内层共有20人,问这个方阵中有学生多少人?
学而思-数学-三年级-期末复习知识点汇总复习课程

三春十五讲知识点总结第一讲巧填算符1.注意读题,分清数字之间和适当位置的区别。
2.方法:倒推法(从后向前一步一步推)凑数法(可合并数的问题先凑个和结果相近的数)分组固定搭配(能够出1或0的重点考虑)和差法(全加减法,假设全是+,再换成-)3.括号位置影响结果,剧烈变化多考虑乘除,其次加减。
4.二十四点多利用固定搭配考虑,如3×8,4×6,2×12,18+6,16+8等。
第二讲有余数除法1.重要特征,余数重要考察点:除数>余数2.余数性质(除数相同时):和的余数=余数的和;差的余数=余数的差(除法算式除数相同可以相加减)注意余数保证比除数小。
第三讲平行四边形与梯形1.理解高的含义。
2.面积计算:①平行四边形:底×高②梯形:(上底+下底)×高÷2梯形面积已知后倒推其他条件注意灵活运用。
第四讲小数的认识1.注意数位含义:十分位(几个0.1),百分位(几个0.01),千分位(几个0.001)……2.比较大小从左到右按照数位依次比较。
3.小数点的移动:×10,×100……向右移动,0有几个移动几个数位;÷10,÷100……向左移动,0有几个移动几个数位。
4.加减法:和自然数相同,只需要注意小数点先对齐再算,小数部分缺位补0.第五讲年龄问题1.基本特征:你长我也长,年龄差永不变。
2.涉及到的类型:和差倍,变倍,当当型。
借助画图,利用年龄差永不变来算。
第六讲简单统计1.统计图优势:清晰明了,可根据图进行对比。
2.平均数:总和÷个数3.中位数:大小排序后最中间的数4.众数:出现次数最多的数据。
5.注意此类问题开放问题多,需要根据题目给出的数据进行合理化分析。
第七讲标数法1.注意适用题型:最短路线。
2.方法:每个点的方法数等于前一步所有点的方法数之和。
3.步骤:定起点,终点,确定最短路线的方向,从起点开始一步步每个点都标数。
小学三年级奥数精品讲义1-34讲全

小学三年级奥数精品讲义目录第一讲加减法的巧算(一)第二讲加减法的巧算(二)第三讲乘法的巧算第四讲配对求和:第五讲找简单的数列规律第六讲图形的排列规律第七讲数图形第八讲分类枚举第九讲填符号组算式第十讲填数游戏第十一讲算式谜(一)第十二讲算式谜(二)^第十三讲火柴棒游戏(一)第十四讲火柴棒游戏(二)第十五讲从数量的变化中找规律第十六讲数阵中的规律第十七讲时间与日期第十八讲推理第十九讲循环第二十讲最大和最小¥第二十一讲最短路线第二十二讲图形的分与合第二十三讲格点与面积第二十四讲一笔画第二十五讲移多补少与求平均数第二十六讲上楼梯与植树第二十七讲简单的倍数问题第二十八讲年龄问题)第二十九讲鸡兔同笼问题第三十讲盈亏问题第三十一讲还原问题第三十二讲周长的计算第三十三讲等量代换第三十四讲一题多解第三十五讲总复习(第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
:观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小熊不禁问:“白兔弟弟,你这么快就算出了答案,有什么决窍吗”小白兔说:“比如2号选手是93、95、98、96、88、89、87、91、93、91,去掉最高分98,去掉最低分87,剩下的都接近90为基准数,超过90的表示成90+‘零头数’,不足90的表示成90-‘零头数’。
于是(93+95+96+88+89+91+93+91)÷8=90+(3+5+6―2―1+1+3+1)÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做,果然既快又对。
学而思三年级第六讲巧求周长

第六讲 三年级奥数巧求周长1、 周长:围成一个图形的所有边长的总和就是这个图形的周长。
2、长方形周长 (长 宽) 2,如果 C 表示长方形的周长, a 表示长方形的长, b 表示 长方形的宽,则长方形的周长可以写成 C (a b ) 2 . 3、正方形的周长 =边长 4,如果用 C 表示正方形的周长, a 表示正方形的边长,则正方形的周长可以写成 C a 4.4、 正方形四条边都相等,长方形对边相等。
类型一:不规则图形——平移】2 厘米的正方形拼成的,你能算出这个图形的周长是多少变式 1:计算下面各图的周长。
(单位:厘米)9 厘米、 8 厘米和 7 厘米的 4 个正方形按从大到小的顺序排 成一行(如图) ,排成的图形周长是( )厘米。
变式 2:求下列图形的周长. ( 单位:米 )3020801015134013例 2】把边长分别是 10 厘米、6 个边长都是 1008变式 1:下图是一座楼房的平面图 , 图中不同字母表示长度不同的各条边 . 已知 b 50 米,c 30米, g 10米, 这座楼房平面的周长是米。
变式 3:一个长为 12厘米, 宽为 10厘米的长方形, 挖去一个边长为 4 厘米的正方形补在另 边上(如图) 。
所得图形的周长为 _ 厘米。
【例 3】将 19张边长为 1分米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候, 要求后摆的纸片必须有一个顶点与前一张纸片的中心重合 (图中表示已经摆好的 5 张),地板 上摆好后图形的周长是多少?变式: 李明将 5 张扑克牌像下图那样摆放,已知扑克牌的长是 86 毫米,宽 56 毫米,那么这 个摆成后的图形的周长是多少?b 8 厘米,c 3 厘米,图形的周长为( )厘米。
a 10 厘米,类型二:等量代换】例1】8 个同样的小长方形拼成一个大长方形,大长方形的周长是84厘米,小长方形的周长是多少厘米?变式1:由9 个相等的小长方形拼成的大长方形,已知小长方形的宽是12厘米,求大长方形的周长是多少厘米?变式2:下图是由三个同样的长方形拼成的,求周长是多少?变式3:李明从A走到B再走到C再到 D ,走了38米,马力从B到C再到D再到A走了31 米,问此长方形的水池ABCD 的周长是多少米?【类型三:规则图形的变化】【例1】如图,一个正方形被分成 6 个大小、形状完全一样的长方形,每个长方形的周长都是14 厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学而思三年级数学寒假1-6讲课程讲义
第1讲角的认识
模块2:角度计算
例3:
(1)若∠A和∠B的和为150°,且∠A是∠B的4倍,那么∠A=.
(2)若∠A+∠B+∠C=160°,其中∠C是直角,那么∠B=.
例4:
如图所示,已知∠1的度数是∠2度数的2倍,求∠1、∠2、∠3、∠4分别是多少度?
练一练
如图所示,已知∠3=30°,求∠2、∠1、∠4分别是多少度?3
1
2
3
1
2
作业2:
10点整的时候,钟面上时针与分针所成的角是度。
作业3:
已知∠1=35°,求∠1的补角是度,余角是是度。
作业4:
(1)若∠A+∠B+∠C=120°,其中∠A=28°,∠C=60°,那么∠B=°。
第2讲四则运算
模块1:加减法巧算
例1:
计算
(1)63+294+37+54+6(2)261-43+83-157+39
==
(3)19+199+1999+19999(4)81+85+78+87+79 ==
模块2:乘法的巧算
例2:
计算
(1)33×15÷5(2)1800÷25÷4
==
(3)125×(8÷10)(4)(36×21)÷(6×7)
==
练一练
(1)36×25(2)32×125
==
(3)25÷(10÷8)(4)37000÷125÷8
==
计算:
(1)34×36;78×72(2)13×17;31×39 (3)43×63;87×27(4)25×25;56×56
模块3:提取公因数
例4:
计算:
(1)67×66+67×35-67(2)80×15+15×22-30 (3)33×34+34×35+68×66(4)12×38+12×34+24×14
(1)76×25-50+25×26(2)60×29+60×33+40×62
作业1:
(1)736+49+264+24+11(2)653-249-151
作业2:
(1)240÷100×5(2)2800÷(25×7)
作业3:
35×20+70+35×78
67×46+54×33+34×54
第3讲数列中的秘密
模块1:求通项与项数
例1:
(1)等差数列3,7,11,15,……,第26项是。
例2:
(1)等差数列4,7,10,13,……70,这个数列共有项。
(2)等差数列2,6,10,14,……,其中42是这个数列的第项。
练一练
在一个等差数列中,首项为15,第7项为57,公差是多少,第10项是多少?
模块2:求数列和例3:
(1)3+6+9+12+15+18+21+24+27
(2)5+9+13+17+21+25+29+33
例4:
(1)1+2+3+…+61+62+63
(2)5+9+13+…+57+61+65
(3)37+34+31+…+7+4
5+10+15+…+55
第4讲和、差、倍
模块1:和差问题
例1:
(1)小猴和小熊到动物商店一共买了30块糖,小猴把买的糖给了小熊五块,给完后他们的糖一样多(小猴比小熊多10块),请问原来小猴和小熊够买几块糖?
模块2:和倍问题
例2:
(1)现在未来服装店里有129件衣服,男装是童装的两倍。
女装是男装的两倍多三件。
请问三种服饰各有多少件?
养殖场有鸡鸭鹅300只。
鸡是鹅的3倍少6只。
鸭是鹅的五倍多18只。
求鸡鸭鹅各有多少只?
模块3:差倍问题
例3:
甲班的图书数量是乙班的6倍,如果甲班给乙班20本图书,那么甲班比乙班还多5本。
甲班和乙班原来各有多少本图书?
例4:
甲乙两个书架,从甲书架取30本放入乙书架,则两书架的书本数一样。
如果从乙书架取30本放到甲书架,则甲书架上的书是乙书架的3倍。
两书架原来有书多少本?
有两筐苹果,如果从第一筐拿出9个放进第二筐,两筐苹果数相等。
如果从第二筐拿出12个放进第一筐,那么第一筐是第二筐的4倍。
原来各有多少个苹果?
作业1:
企鹅出版社出版了一套《天才的智慧》丛书。
出版社为这套丛书设计了一个漂亮的书盒。
这套丛书连同书盒售价280元。
书店允许顾客只买书而不买书盒。
如果书价比书盒贵230元。
那么书盒价为多少元?
作业2:
某交通协管员7月份开出78张罚单。
这些罚单分为2种,一种是违章停车,另一种是闯红灯。
违章停车的罚单较多,比闯红灯罚单数量的4倍还多3张。
违章停车的罚单有多少张?
作业3:
玩具厂生产红、黄、白气球共141,其中红气球的个数是黄气球的3倍。
黄气球是白气球的两倍少3个。
所以红气球生产了多少个?
作业4:
甲的积分卡数量是乙的五倍,现在甲拿出20张积分卡给乙。
给完之后两人积分卡数量一样多。
甲原来有多少张积分卡?
第5讲倒推与图示
模块1:单个量的还原问题
例1:
(1)猜猜年龄:一位程序员设置了以下一个程序。
请输入您的年龄乘2减去2除以2输出结
果
一位老婆婆输入自己的年龄后,最后输出的结果是80,聪明的小朋友们,你能猜出老婆的年龄吗?
练一练
牛老师带着37名同学到野外春游。
休息时,小强问牛老师:“您今年多少岁啦?”牛老师有趣地回答:“我的年龄乘2,减去16后,再除以2,加上8,结果恰好是我们今天参加活动的总人数。
”小朋友们,你知道牛老师今年多少岁吗?
例2:
(1)有一个人非常喜欢喝酒,他每经过一个酒店都要买酒喝。
这个人出门带了一个酒葫芦,看到一个酒店,就把酒葫芦中的酒加一倍,然后喝下去八两酒。
这天他一共遇到两家酒店。
在第二家酒店喝完酒后,葫芦里的酒刚好喝完。
问原来酒壶里有多少两酒?
(1)三个等等,吃一棵树上的桃子。
等等一号吃了所有的一半还多两个,等等2号吃了剩下的一半少十个,等等3号吃了15个,这时树上刚好还有9个桃子,那么原来树上一共有多少个桃子?
练一练
电工组买来一捆电线,工人们第一天用去全长的一半多五米,第二天用去余下的一半少8米,第三天又用去14米,最后还剩十米,请问这捆电线原来有多少米?
模块2:多个量的还原问题
例4:
(1)有甲乙两堆棋子,其中甲堆棋子多于一堆。
现在按如下方法移动棋子,第一次从甲堆中拿出和乙堆一样多的棋子放到乙堆,第二次从乙堆中拿出和甲堆剩下的同样多的棋子放到甲堆,第三次又从甲堆拿出和乙堆同样多的棋子放到乙堆,照此移动,移动完三次后,甲、乙两堆棋子数恰好都是32个,请问甲乙两堆棋子原来各有多少个?
有一捆电线,第一次用去全长的一半,第二次又用去余下的一半,第三次用去15米,最后还剩7米,请问这捆电线原来有多少米?
作业2
山顶上有棵桃树,一只猴子偷吃桃子,第一天偷吃了总数的一半多两个,第二天又偷吃了剩下的一半多两个,这时还剩1个,请问树上原来有多少个桃子?
作业3
玩具店的玩具每卖出一半就补充20个,到第二次卖出一半后,恰好剩下20个,请问,玩具店原来有玩具多少个?
第6讲方阵
模块1:实心方阵
例1:
(1)一个实心方阵,最外一层每边18人,那么整个方阵一共有人?最外面一层有人?从外向内数,第二层每边有人?第二层一共有人?如果这个方阵,横竖各增加一排,成为一个大一点的实心方阵,那么需要增加人?
例2:
(1)对一块空地进行种树绿化,要把树种成实心方阵的样子,最外面一周有60棵树,问这个方阵外边外层每边有多少棵树?这块空地一共需要多少棵树?
练一练
学校图书馆前摆了一个方正花坛,这个花坛的最外层摆了100盆花,请问这个花坛最外层每边摆了多少盆花?这个花坛一共摆了多少盆花?
模块2:空心方阵
例3:
大家要用盆花在空地上摆一个空心的方阵花坛,最外面的一层每边摆12盆花,一共3层,请问一共要多少盆花?
练一练
有一队学生排成一个中空方阵,最外层人数共52人,最内层人数共28人,这对学生共有多少人?
例4:
用64枚棋子摆成一个两层中空方阵,如果想在最外面再增加一层,请问需要增加多少枚棋子?
四年级一班同学参加了广播操比赛,排成每行8人、每列8人的实心方阵,方阵中共有多少个学生?
作业2
三年级学生排成一个实心方阵进行体操表演,最外一层的人数为32人,所以这个方阵最外层每边有多少人?这个方阵共有三年级学生多少人?
作业3
小小爱好围棋,他用棋子在棋盘上摆了一个两层的空心方阵,外层每边有14枚棋子,他一共用了多少枚棋子?
用152枚棋子摆成一个两层中空方阵,如果想在最外面再增加一层,需要增加多少枚棋子。
