3.3二阶系统
合集下载
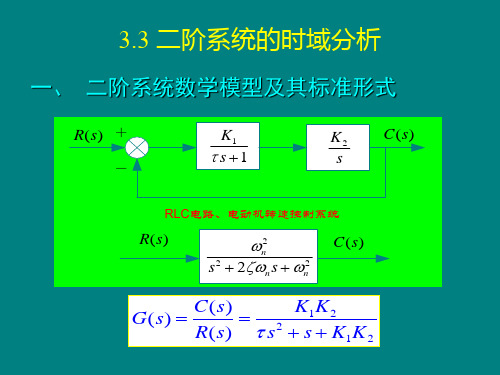
3.3 二阶系统分析

tr
d
,其中 d
n
1 2, arccos
3.3 二阶系统的时域分析
峰值时间tp
c(t) 1
1
1 2
e nt sin(d t )
c(tp)=cmax
dc(tp)/dt=0
1
1 2
e nt sin(d t p ) 0
sin d t p 0, d t p k , k
解: k 6,n 2.45, 0.408
ts
4
n
4
M p 22%
k 12,n 3.46, 0.289
ts
4
n
4
M p 40%
K增大,系统的上升时间减小,超调量增大。 系统的响应速度加快,但振荡幅度增大、频率加快
3.3 二阶系统的时域分析
例题3.3 已知某系统的结构和单位阶跃响应的Mp<5%, tS<4秒,求系统的参数。
n n
2
1
,..T2
n
1
n
,
2 1
C(s)
n2
1
(s 1/ T1)(s 1/ T2 ) s
t
t
c(t) 1 e T1
e T2
T2 / T1 1 T1 / T2 1
1 / T2 1/ T1
3.3 二阶系统的时域分析
T1
1
n n
n
K
3.3.6 改善二阶系统性能的措施
1. 比例—微分控制
(1) 方法的思路
r(t)
1
c(t)01
R(s) E(s)
U(s
ωn2
大学自动控制原理_3.3二阶系统时间响应

1s 5% ts 1.33 2%
例2 如图所示的机械系统,在质量块上 施加9.8牛顿阶跃力后,m的时间响应 如图曲线,试求系统的 m、k 、c 。
Fi (t )
xo (t )
m c
k
解:根据牛顿第二定律,得
Fi (t ) Fk Fc Mo (t ) x Fk kxo (t ) Fc cxo (t )
即:
e
nt 2
1
1 1 1
2
解得: t s
n
ln
4 ln
若 0.02
1 1
2
则t s
n
3 ln
1 1
2
若 0.05
则t s
n
4
0.02) ( 若0 0.7时 ts n ts 32、源自阻尼状态( 0)2
1 X o (s) 2 2 s s n
1 s s s 2 n2
n
xo (t ) 1 cos nt
曲 线 特 点 : 等 幅 振 荡
3、临界阻尼状态
1 X o (s) 2 s (s n )
( 1)
n
5、振荡次数N
在调整时间内响应曲线振荡的次数
ts ts N T 2
d
0 0.7时,
0.02时,t s 0.05时,t s 4
n
3
N N
2 1
2
1. 5 1
2
n
振荡次数N随着 而 。
( 2 1) nt ( 2 1) n t e e 2 2 1
3.3 二阶系统的时域分析

=
由
e
ζω nts
1 1ζ
=
2
e
ζω nt
sin(ω d t + β ) ≤
e
ζω nt
1ζ 2
1ζ 2
得
ts =
1
ζω n
(ln
1
+ ln
1 1ζ
2
)
15
当0.4<ζ≤0.8时,可 以采用下面的近似公式 3.5 = 0.05 tS ≤
= 0.02 tS ≤
ts =
1
ζω n
(ln
1
+ ln
18
�
ωd
ζ一定,即β一定, ωn↑ → tr↓,响应速度越快; ωn一定, ζ ↓ → tr ↓ ,响应速度越慢.
12
h(t ) = 1
1 1ζ 2
e ζω nt sin(ω d t + β )
(t ≥ 0)
(2) 峰值时间tp 根据峰值时间的定义,在峰值处,h(t)的导数为零,故 ζω nt p ζω e ωd dh(t ) ζω t = n sin(ω d t + β ) e n p cos(ω d t + β ) = 0 dt t =t p 1ζ 2 1ζ 2
R C R 实际阻尼系数 ζ= = = 2 L Rc 临界阻尼系数
2
故ζ 称为相对阻尼系数或阻尼比.
一,二阶系统的数学模型
R(s)
2 ωn
C(s)
开环传递函数
2 ωn G(s) = s ( s + 2ζω n )
-
s( s + 2ζω n )
图 3-13 典型二阶系统结构图
闭环传递函数
3-3二阶系统的时域分析

二阶系统的闭环极点分布
j
特征根: s1, 2 n n 2 1
j
n 1 2
j
n
n 1 2
n
0
n 1 2
0
1
0
n 1 2
0 1
1 0
j
s1 s 2 n 0
1
1
C1 C2 C3 L C1e S t C2 e S t C3 ( s s1 ) ( s s2 ) s
1
1 2
其中
C1
n2
( s1 s2 ) s1
; C2
n2
( s1 s2 ) s2
; C3 1
而s1,s2是ζ和ωn的函数,显然c(t)只与ζ ,ωn有关,即ζ ,ωn决
第三章 时域分析法
第三节 二阶系统时域分析
第三节 二阶系统的时域分析
项目
教学目的
内容
掌握二阶系统的数学模型和时域响应的特点。 能够计算欠阻尼时域性能指标。
欠阻尼时域性能指标的计算。阻尼系数和自 然频率对系输出的影响。
教学重点
教学难点 阻尼 系数 和自然频率 对系统输出 的影响 。 及 其 处 理 MATLAB作图、对比、总结。
①
环节;
比例+微分(引入零点):在前向通路中串一个PD控制
② 采用测速反馈控制。 3) PD控制与测速反馈控制两种方案比较 (见下页附表)
附表: PD控制与测速反馈控制两种方案比较
性能指标
PD控制
方
案
测速反馈控制 增 大 降 低
阻尼比 自然频率 开环增益 稳态误差 超调量 性能 适用场合
3.3二阶系统
tp d 1 2 n
(6)最大超调量的计算:
p
c(t p ) c() c ( )
n t p
100%
1 2
2
e
e
(cos d t p
sin d t p ) 100%
n t p
(cos
1
sin ) 100%
dc(t ) / dt 0
则
故
n e
nt p
sin(d t p ) d e
tan(d t p )
nt p
cos(d t p ) 0
2
1
tan
到达第一个峰值时应有
d t p 0, , 2 ,3
d t p
s1 , s2 jn 是一对共轭纯虚数根。
三、二阶系统的单位阶跃响应
对于单位阶跃输入
r (t ) 1(t )
1 R( s) s
于是
2 n 1 C ( s) 2 2 s 2n s n s
由拉氏反变换可以得到二阶系统的单位阶跃响应为
c(t ) L1[C ( s)] 下面按阻尼比分别讨论。
欠阻尼系统单位阶跃响应为
c(t ) 1 e nt cos d t
n t e sin d t d
n
1 e nt (cos d t
1
2
sin d t )
(t 0)
或写为
c(t ) 1 e nt 1
2
( 1
解得 t 1/ n 。 整个暂态过程中,临界阻尼系统阶跃响应都是单调 增长的没有超调。如以达到稳态值的 95% 所经历的时 间做为调整时间,则
欠阻尼二阶系统动态过程分析
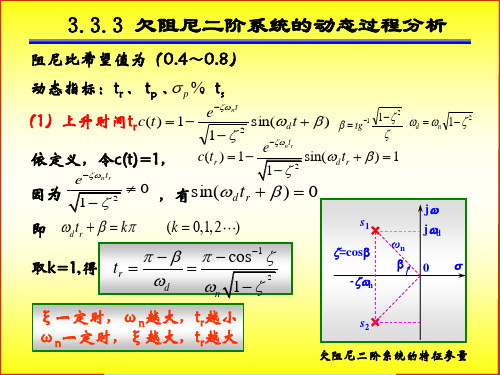
3.3.3 欠阻尼二阶系统的动态过程分析
阻尼比希望值为(0.4~0.8)
动态指标:tr 、 tp 、 p %、ts
(1)上升时间trc(t) 1
e nt
1 2
s in( d t
)
tg1
1 2
d n
1 2
依定义,令c(t)=1, c(tr ) 1
因为
entr
1 2
0
,有s in( d t
r
若 lim c(t) 0 t
(渐近)稳定
若 lim c(t)
t
系统不稳定
若 lim c(t) A
t
临界稳定
非零常数
设若n阶全系部统特表征达根式有为负实部,则
(sl)im t
CcR(((tss)))
0ba00ssmn
b1s m 1 a1s n 1
( 渐 近bamn)11ss 稳 ab定mn
(2)K=16,T=0.25,得
0.25 n 8
将n 、 代入动态性能指标公式得
tr
d
0.24(s)
p % e / 1 2 100% 44%
tp
d
0.41(s)
ts
3.5
n
1.75(s)
( 0.05)
例3.7 系统及阶跃响应曲线如图 示,求K1、K2和a。
R(s) k1 _
有
e nt
1
2
sin(d t
)
(t ts )
所以
ent
1 2
sin(d t
)
ent
1 2
即
取 =0.707得
因为ts
3.5
snin((d t=5% ))
阻尼比希望值为(0.4~0.8)
动态指标:tr 、 tp 、 p %、ts
(1)上升时间trc(t) 1
e nt
1 2
s in( d t
)
tg1
1 2
d n
1 2
依定义,令c(t)=1, c(tr ) 1
因为
entr
1 2
0
,有s in( d t
r
若 lim c(t) 0 t
(渐近)稳定
若 lim c(t)
t
系统不稳定
若 lim c(t) A
t
临界稳定
非零常数
设若n阶全系部统特表征达根式有为负实部,则
(sl)im t
CcR(((tss)))
0ba00ssmn
b1s m 1 a1s n 1
( 渐 近bamn)11ss 稳 ab定mn
(2)K=16,T=0.25,得
0.25 n 8
将n 、 代入动态性能指标公式得
tr
d
0.24(s)
p % e / 1 2 100% 44%
tp
d
0.41(s)
ts
3.5
n
1.75(s)
( 0.05)
例3.7 系统及阶跃响应曲线如图 示,求K1、K2和a。
R(s) k1 _
有
e nt
1
2
sin(d t
)
(t ts )
所以
ent
1 2
sin(d t
)
ent
1 2
即
取 =0.707得
因为ts
3.5
snin((d t=5% ))
自动控制原理3.3~3.4 二阶系统时域分析

闭环特征方程: D( s ) s 2 2 s 2 0 n n 闭环特征根: s1, 2 n n
2
1
二、二阶系统单位阶跃响应
单位阶跃输入r(t)=1(t)时,其二阶系统的输出的拉氏变换为
2 2 n n 1 C ( s ) ( s ) R( s ) 2 2 s 2 n s n s s( s s1 )(s s2 )
e
(ζ ζ 2 1 ) n t
ζ 2 1 ) n t
c(t ) 1
1
2 ζ 2 1 (ζ ζ 2 1) 1 (ζ e 2 ζ 2 1 (ζ ζ 2 1)
e
(ζ ζ 2 1 ) n t
ζ 2 1 ) n t
c(t)
1
0 t
单调上升过程
2.0 1.8 1.6 1.4 1.2 c(t) 1.0 0.8 0.6 0.4 0.2 0
=0
0.4 0.5 0.6 0.7 0.8
0.1 0.2 0.3
1.0 2.0
1
2
3
4
5
• 在0<<1, 越小,超调量越大,平稳性越差,调节时间ts长; • =0.7,调节时间短,而超调量%<5%,平稳性也好,故称 ζ=0.7为最佳阻尼比。工程希望=0.4~0.8为宜; •在≥1 , 越大,系统响应速度慢,调节时间ts也长。
例题:设角度随动系统如图所示,T=0.1为伺服电机时间常数, 若要求系统的单位阶跃响应无超调,且调节时间ts≤1s,问K应 取多大?此时上升时间等于多少?
Θi(s)
_
K s(Ts 1)
Θo(s)
解:闭环传递函数为
K K K /T s (Ts 1) (s) 2 2 K Ts s K s s / T K / T 1 s (Ts 1)
3.3二阶系统的动态性能(上)解析

s 2n 1 s [( s n ) jd )][( s n ) jd ]
s 2n 1 s 2n 1 s ( s n )2 ( jd )2 s ( s n )2 d 2
at
s n n 1 s (s n )2 d 2 (s n )2 d 2 n 1 2 1 s n 1 2 2 s ( s n ) d ( s n )2 d 2
5.84 n ts 4.75 n
4、稳态误差为0,说明典型二阶系统跟踪阶跃输入信号时,无稳态误差, 系统为无静差系统。
4.过阻尼(ζ>1)状态
闭环特征方程
特征根
2 s 2 2n s n 0
s1 n n 2 1
s2 n n 2 1
nt
d
L[e at cos t ]
上式取拉氏反变换,得
y(t ) 1 e
1 1
cos d t
1
2
sa ( s a)2 2 L[e at sin t ] ( s a)2 2
ent sin d t
e nt 1 2 e
Δ 2 Δ 5
4T1 1.25 ts 3T 1
Δ 2 Δ 5
1.34
3、稳态误差为0,说明典型二阶系统跟踪阶跃输入信号时,无稳态误 Y(t) 差,系统为无静差系统。
2
4、需要说明的是,对于临界阻尼和过阻 尼的二阶系统,其单位阶跃响应都没有 振荡和超调,系统的调节时间随ζ的增加 而变大,在所有无超调的二阶系统中, 临界阻尼时,响应速度最快。
2 n 1 1 s Y ( s ) ( s ) R( s ) 2 2 2 s n s s s 2 n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若允许误差带是±Δ(如±2%),可以认为调整时间 就是包络线衰减到± Δ区域所需的时间,则有
e n ts 1
2
解得
ts
1
n
1
(ln
1 1 ln ) 2 1
当Δ=5%时,
当Δ=2%时, 当 0 0.8时,
ts ts
n
1
(3 ln (4 ln
• 典型二阶系统是一个前向通道为惯性环节和积分 环节串联的单位负反馈系统。
• 令
K1 K 2 1
2 n
2n
则二阶系统传递函数的标准形式为
2 n C (s) G( s) 2 2 R( s ) s 2n s n
其中ζ称为阻尼比,τ为时间常数,ωn为系统的自然 振荡角频率(无阻尼自振角频率)。
e
nt p
100%
1 2
p e
100%
p
越小, p 越大(只与ζ有关)
(7)调整时间ts的计算:
欠阻尼二阶系统的单位阶跃响应曲线位于一对曲线
y (t ) 1 e nt 1
2
以内,这对曲线称为响应曲线 的包络线。
可以采用包络线代替实际响应曲线估算调整时间,所 得结果一般略偏大。
解得 t 1/ n 。 整个暂态过程中,临界阻尼系统阶跃响应都是单调 增长的没有超调。如以达到稳态值的 95% 所经历的时 间做为调整时间,则
t s 4.7 1
n
临界阻尼二阶系统多在记录仪表中使用。
3. 欠阻尼(0<ζ<1)
此时,系统具有一对共轭复数极点,则
2 n C ( s) 2 s ( s 2 2n s n )
1 c() lim sG( s) R( s) lim s 1; s 0 s 0 ( s s1 )( s s2 ) s
2
e( ) 0
过渡过程时间(按近似后一阶系统求出)
ts (3 ~ 4)
1 ( 2 1)n
单调上升,无振荡,过渡过程时间长,无稳态误差。
d n 1 2
(2)振荡周期为
Td 2
d
2
n 1 2
(3)ζ 越大,振幅衰减越快,振荡周期越长(频率越 低)。
(4)上升时间tr的计算:
c(tr ) 1 e
n tr
(cos d tr
1
2
sin d tr ) 1
或
即 所以
cos d tr
2 A2 C ( s )( s ) n s n n
单位阶跃响应为
c(t ) 1 ent (1 n t )
临界阻尼系统单位阶跃响应的误差及终值
e(t ) r (t ) c(t ) ent (1 n t )
单位阶跃响应的变化率为:
R( s)
+ -
K s( s 1)
1 K As
C (s)
得
4. 无阻尼(ζ=0)
无阻尼情况下系统的阶跃响应是等幅正(余)弦
振荡曲线,振荡角频率是 n
c(t ) 1 cos nt
2.0 1.8 1.6 1.4 1.2 c(t) 1.0 0.8 0.6 0.4 0.2
=0
2
d
2
n 1
2
2t p
1
n
(3 ln
)
ts ts N Td 2t p
设计二阶系统时,可先由超调量确定阻尼比,再 由其他指标(如调整时间)和已确定的阻尼比给 出自然振荡角频率。
• 例3-2:设一个带速度反馈的伺服系统,其结 构图如图所示。要求系统的性能指标为 σp=20%, tp=1s. 试确定系统的 K 和 KA 值,并计 算性能指标tr、ts和N.
欠阻尼系统单位阶跃响应为
c(t ) 1 e nt cos d t
n t e sin d t d
n
1 e nt (cos d t
1
2
sin d t )
(t 0)
或写为
c(t ) 1 e nt 1
2
( 1
为阻尼振荡
欠阻尼二阶系统单位阶跃响应性能指标计算公式
arctan( 1 2 ) tr 2 d n 1 n 1 2
tp d n 1 2
p e
ts
1 2
100%
1 1
2
Td
2
cos d t sin d t )
1
e nt 1
2
sin(d t )
(t 0)
arctan( 1 2 )
d n 1 2
讨论: (1)欠阻尼情况下,二阶系统的单位阶跃响应是衰减的 正弦振荡曲线。衰减速度取决于特征根实部的绝对值 ζωn 的大小,振荡角频率是特征根虚部的绝对值,即 有阻尼自振角频率ωd,
注意:
• 控制工程中,二阶系统的典型应用极为普
遍; • 为数众多的高阶系统在一定条件下可近似 为二阶系统。
二、二阶系统的特征根(极点)分布
求解二阶系统特征方程,
2 s2 2n s n 0
可得两个特征根(极点)
s1 , s2 n n 1
2
( 1) ( <1)
n jn 1 2
j
j
[s]
2
j
[s]
s1
j n 1
n 0
2
s1 s 2
n
0
s2
j n 1
(a) 0 1
j
(b) 1
[s]
j
[s]
s1
s1
s2
n
0
s2
0
(c) 1
(d) 0
1 1 1 1
2 2
) )
n
ts
3
n
( 5%)
ts
4Leabharlann n( 2%)设计二阶系统时,常取 0.707 为最佳阻尼比。
(8).振荡次数
振荡次数是指在调节时间内, xc (t ) 振荡的次 数。根据这一定义,可得振荡次数为
ts tf
tf 式中, d n 1 2 的周期时间。 2 2
惯性环节来近似原来的二阶系统。即有
n n 2 1 s1 C ( s) R( s ) s n n 2 1 s s1
• 近似原则:用其中一个惯性环节近似原二
阶系统,需要保证近似前后初值和终值相 等,并且要用到待定系数法!
过阻尼系统稳态值和最终误差
tp d 1 2 n
(6)最大超调量的计算:
p
c(t p ) c() c ( )
n t p
100%
1 2
2
e
e
(cos d t p
sin d t p ) 100%
n t p
(cos
1
sin ) 100%
s n n 1 2 2 2 2 2 2 s ( s n ) (1 )n ( s n ) (1 )n
s n n d 1 2 2 2 s ( s n ) d d ( s n ) 2 d
s1 , s2 jn 是一对共轭纯虚数根。
三、二阶系统的单位阶跃响应
对于单位阶跃输入
r (t ) 1(t )
1 R( s) s
于是
2 n 1 C ( s) 2 2 s 2n s n s
由拉氏反变换可以得到二阶系统的单位阶跃响应为
c(t ) L1[C ( s)] 下面按阻尼比分别讨论。
1.
过阻尼(ζ>1)
n n 2 1
这种情况下,系统存在两个不等的负实根,则
2 2 n n C (s) 2 2 s ( s 2n s n ) s ( s s1 )( s s2 )
A0 A1 A2 s s s1 s s2
A0 C (s)s s 0 1
tan d tr
1
2
sin d t r 0
tan( )
1 2
arctan( 1 2 ) tr 2 d n 1 n 1 2
(5)峰值时间tp的计算:
出现峰值时,阶跃响应随时间的变化率为0,即
0.4 0.5 0.6 0.7 0.8
0.1 0.2 0.3
1.0
2.0
0
1
2
3
4
5
6 nt
7
8
9
10 11 12
不同ζ下,二阶系统的单位阶跃响应曲线图
几点结论:
1)二阶系统的阻尼比ζ决定了其振荡特性:
ζ< 0 时,阶跃响应发散, 系统不稳定(负阻尼) ζ= 0时,出现等幅振荡 0<ζ<1 时 , 有 振 荡 , ζ 愈 小,振荡愈严重,但响 应愈快 ζ≥1 时,无振荡、无超调, 过渡过程长
t 0 t 0
所以,整个暂态过程中, 阶跃响应都是单调增长的 .
2. 临界阻尼(ζ=1)
此时,系统具有二重负实极点,则
2 n A0 A1 A2 C ( s) 2 s ( s n ) s s n ( s n ) 2
A0 1
d 2 A1 C ( s )( s ) 1 n ds s n
