北理工贾云德《计算机视觉》chapter15三维运动估计
北理工贾云德《计算机视觉》chapter12标定

第12章 标定本章将讨论各种摄象机系统及深度成像系统的标定方法.在摄影测量学领域中,已经建立了大量的摄象机和测距传感器标定方法.这些方法可以用来确定摄象机或测距传感器在场景中的位置和方向以及与场景坐标之间的关系.在摄影测量学中有以下四个标定问题:(1) 绝对定位:通过标定点确定两个坐标系在绝对坐标系统中的变换关系,或确定测距传感器在绝对坐标系中的位置和方向.(2) 相对定位:通过场景中的标定点投影确定两个摄象机之间的相对位置和方向.(3) 外部定位:通过场景中的标定点投影确定摄象机在绝对坐标系中的位置和方向.(4) 内部定位:确定摄象机内部几何参数,包括摄象机常数,主点的位置以及透镜变形的修正量.这些标定问题主要起源于高空摄影技术,是摄影测量中的经典问题.除了以上四个标定问题外,摄影测量学还解决以下两个问题:一是通过双目立体视差确定点在场景中的实际位置,二是对立体图像对进行校正变换,使得立体图像对的外极线与图像的行平行以便简化后续处理(见第十一章).摄象机标定过程中涉及到以下几种坐标,场景坐标、摄象机坐标、图像坐标和像素坐标等,这些坐标已经在1.7中介绍成像基础知识时引入.确定这些坐标之间的关系就是本章所要讨论的各种标定问题的目的.12.1 刚体变换物体位置和方向的任意变化都可以认为是刚体变换,因为物体的移动只改变其位置和方向,并不改变其形状和大小.假定通过两个处于不同位置的摄像机均可看到θ点,p 点在两个摄像机坐标系中的坐标分别是和()2222,,z y x =p .显然两个摄象机位置之间的变换是刚体运动,因此,p 点在第一个视场中的坐标p 1可以通过旋转和平移变换到第二个视场中的坐标2p ,t Rp p +=12(12.1)其中矩阵R 是一个33⨯的正交方阵,用于旋转变换:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=zz zy zx yz yy yxxz xy xx r r r r r r r r r R (12.2) 矢量T z y x t t t ),,(=t 表示平移,或者说点t 是第一个坐标系原点在第二个坐标系上的坐标,如图12.1所示.图12.1 两个摄像机坐标系方程12.1可以认为是计算一个点经过旋转和平移以后的新坐标,或是计算空间中同一个点在不同坐标系中的坐标 .前者用于刚体力学:在物体移动到一个新的位置以后,计算物体上一点的新坐标;后者用于标定问题:同一点在不同观察位置上观察将会得到不同的坐标,这种不同可以由刚体变换确定,而标定问题就是来确定这种刚体变换.例如,考虑两个具有不同位置和姿态的摄象机观察场景中同一点,由于观察角度不同,这一点在两个摄像机坐标系中的坐标是不同的.设想旋转第一个摄象机,使其方向与第二个摄象机的方向相同;再设想将第一摄象机平移到第二摄象机的位置上,则两个摄象机坐标系完全重合. 12.1.1旋转矩阵空间角可用直角坐标系中的欧拉角描述:绕x 轴旋转角θ,绕新的y 轴旋转角ψ,绕新的z 轴旋转角φ,角θ是光轴的俯仰角(pitch),也叫垂直角,角ψ是光轴的偏航角(yaw)(水平角),角φ表示光轴滚动角(roll)或扭转角(twist).无转动(三个角都等于零)指的是两个坐标系统完全对正.各角度旋转正方向为从坐标系原点沿各轴正方向观察时的逆时针旋转方向.用这些角表示方程12.2定义的旋转矩阵各元素如下:ψθψθψφθφψθφθφψθφψφθφψθφθφψθφψcos cos cos sin sin cos sin sin sin cos cos cos sin sin sin sin cos sin sin cos sin cos sin cos cos sin sin cos cos ==-=-=+==+=-==zz zy zx yz yy yx xz xy xx r r r r r r r r r(12.3)用欧拉角的形式来确定坐标系的旋转会引起数值解不稳定,因为欧拉角很小的变化可能对应很大的旋转变化.因此,标定算法或者求解旋转矩阵的各元素常使用其它形式的旋转角表达式,如,四元数等.旋转矩阵是一个正交矩阵:I R R =T (12.4)其中I 表示单位矩阵.由上述公式不难得到旋转矩阵的逆就是该矩阵的转置.标定算法会在坐标系之间产生刚体变换;例如,从坐标系1到坐标系2,我们有212t Rp p += (12.5)刚体变换的逆变换就是将坐标系2的坐标变为坐标系1的坐标:12221)(t p R t p R p +=-=T T (12.6)这里的i t 表示坐标系上的i 点是另一个坐标系的原点.注意平移变换的逆变换并不是简单的等于2t 必须乘以旋转变换的逆变换,因为2t 表示在坐标系2上的平移,其逆变换一定要表示到与坐标系1同一个方位的坐标系中 .图12.2 欧拉角或俯仰角、偏航角和滚动角示意图12.1.2旋转轴旋转也可以规定为逆时针(右手坐标系)绕由单位矢量(,,)ωωωx y z 表示的轴的旋转.这是一种观察旋转的非常直观方法,但是它在数值计算上也有和欧拉角一样的问题.旋转轴和旋转角度表达式可以转换成矩阵表达式(方程12.1),以作为刚体变换的公式.当然,如果能直接使用旋转轴和旋转角表达式来产生满意的数值解,将是最好不过的了.在这种思路的基础上产生了旋转四元数,这也是将四元数用于旋转表示的原因之一.12.1.3 四元数四元数是一个四元矢量()432,1,,q q q q q =,可用来表示坐标旋转.实践证明,对于定位求解问题,四元数表示可以给出很好的数值解.为了理解四元数是如何对旋转进行表示的,我们首先想象在二维平面x y -上的一个单位圆,单位圆上的任何一个位置都只对应于一个旋转角.如图所示.图12.3 单位圆上一点),(y x 只能对应一个旋转角θ再考虑三维空间中的单位球:x y z 2221++= (12.7)在单位球上的任意一点只对应绕x 轴和y 轴旋转的两个角θ和ψ,无法表示绕z 轴旋转的第三个角φ.显然,再增加一个自由度就可以表示所有三个旋转角.四维空间单位球定义如下:x y z 22221+++=ω (12.8)三维空间中所有三个旋转角可以通过四维单位球上的点来表示.由单位四元数表示的旋转公式如下:q q q q 021222321+++= (12.9)每一个单位四元数和其反极点(antipole)-=----q (,,,)q q q q 0123都表示三维空间中的旋转.用单位四元数表示刚体变换的旋转矩阵:()()()⎢⎢⎢⎣⎡-+--+=203130212322212022q q q q q q q q q q q q q R ()()103223212220302122q q q q q q q q q q q q +--+- ()()222123201032203122q q q q q q q q q q q q --+-+⎤⎦⎥⎥⎥ (12.10) 在计算出单位四元数之后,就可利用上式计算旋转矩阵.单位四元数与上节描述的旋转角和旋转轴有密切关系.旋转可以用旋转量θ和旋转轴方向()ωωωx y z ,,的组合来表示,即四元数由一个与旋转量有关的标量和一个旋转轴矢量组成 .设旋转轴的单位矢量为()ωωωx y z ,,,使用i ,j 和k 表示坐标轴,则旋转轴单位矢可以表示为: ωωωx y z i j k ++(12.11)绕该轴逆时针旋转θ角的单位四元数为: ()k j i k j i z y x z y x q q q q q +++=+++=02sin 2cos ωωωθθ (12.12)上式的第一项为四元数的标量(实)部分,其余项为矢量(虚)部分.空间点p =(x,y,z)的四元数r 实际上只有矢量部分(虚部),该矢量就是空间点p 的矢量表示.k j i r z y x ++=(12.13)设'p 是点p 通过矩阵()R q 旋转得到, ()p q p R =' (12.14)若r 是点p 的四元数表示,那么对旋转后点的四元数表示'r 可以由四元数q 直接计算:'=*r qrq (12.15)这里的()q *=---q q q q x y z 0,,,,是q 的共轭四元数:四元数乘法定义如下: ),,,(00000000q r q r q r q r q r q r q r q r q r q r q r q r q r q r q r q r z x y y x z x z y z x y y z z y x x z z y y x x +-+++--++---=rq (12.16) 刚体变换可以很方便地用七个元素()6543210,,,,,,q q q q q q q 表示,前四个量是单位四元数,后三个量是平移量.在这一表达式中,若用R(q)表示对应于单位四元数的旋转矩阵,则刚体变换式为:()()T q q q R 65412,,+=p q p (12.17)12.2 绝对定位绝对定位问题是确定两个坐标系之间的刚体变换问题.求解绝对定位问题在机器视觉中有着许多应用,其中的一个应用是确定测距成像系统或双目立体视觉系统与定义在场景中的绝对坐标系之间的关系,这样可以将所有的测量值均表示在一个公共的坐标系里.若()c c c c z y x ,,=p 表示点在摄象机坐标系中的坐标,()a a a a z y x ,,=p 表示点在绝对坐标系中的坐标,则绝对坐标定位问题的输入就是一个共轭对组:),{(1,1,a c p p ,),(2,2,a c p p ,...,)},(,,n a n c p p .为了求解绝对定位问题,我们把刚体变换方程展开,以便说明旋转矩阵中各项的作用.设c p 是摄象机坐标系内的点,p a 是绝对坐标系内的点,从p c 到p a 的刚体变换公式为:zc zz c zy c zx a y c yz c yy c yx a xc xz c xy c xx a t z r y r x r z t z r y r x r y t z r y r x r x +++=+++=+++=(12.18)其中12个未知参数中有9个是旋转矩阵参数r ,3个是平移参数t .每个共轭对),(a c p p 对应有三个等式,则至少需要四个共轭对产生12个方程才能解出12个未知数.在实际应用过程中,常常使用大量的共轭对(这些共轭对通常是空间标定点在不同坐标系中的表示)来提高计算精度.在解线性系统方程时,如果旋转矩阵R 没有正交标准化,则可能得不到有效的旋转矩阵.使用非标准正交矩阵作为旋转矩阵可能会产生意想不到的结果,如不能保证矩阵转置一定等于矩阵逆,并且共轭对的测量误差会严重地影响计算结果,从而不能产生刚体变换的最佳逼近.有些方法是在每一步迭代过程之后对矩阵进行正交化,但仍不能保证正交化的矩阵是旋转矩阵的最佳逼近.一种替代的方法是求解旋转角而不是矩阵的各项元素.旋转角最一般的表示方法是欧拉角,不过使用欧拉角会导致非线性方程,从而产生数值计算上的困难.在摄影测量中,通常的做法是对非线性方程线性化并求解,以便得到名义值的修正值.这种线性化算法的成功与否很大程度上取决于初始预估值好坏.下面讨论用单位四元数表示方法求刚体变换.设)(q R 是对应于单位四元数q 的旋转矩阵,则摄象机坐标系上的每一点坐标转换成绝对坐标的刚体变换公式如下:()c i c i a R t p q p +=,, (12.19)其中c t 是摄象机原点在绝对坐标系中的位置.现在的回归问题有七个参数:表示旋转的单位四元数的四个参数加上平移矢量的三个参数.正如前面所指出的,绝对定位问题的输入是共轭对集合:),{(1,1,a c p p ,),(2,2,a c p p ,…,)},(,,n a n c p p .考虑一组点的两种集合表示,在摄象机坐标系中的点集{}n a p p p p ,2,1,,,,Λa a a =和绝对坐标系中的点集{}n p p p p ,2,1,,,,c c c c Λ=.绝对定位问题就是在空间中将这两个点群对正.下面计算每个点集的矩中心: ∑==ni i a a n 1,1p p (12.20) ∑==ni i c c n 1,1p p (12.21)用矩中心与每一个点相减得: r p p a i a i a ,,=-(12.22) r p p c i c i c ,,=-(12.23)若已知旋转矩阵)(q R ,则平移表达式可表示为: ()c c p q R p t a -= (12.24)下面将讨论求解旋转矩阵,使得这两簇射线对正.在推导旋转矩阵时,将点表示为从矩中心出发的射线,这样所有坐标都将是射线坐标.由于射线束是由共轭对集合推导的,因此,我们可以知道在摄象机射线束中的某一条射线对应于绝对坐标射线的那一条射线.当两组射线对正后,每一对对应射线将会重合.换句话说,每一对射线位于同一条直线上,并指向同一方向.若不考虑测量误差的影响,则每对射线之间的夹角应为0,夹角的余弦为1.测量误差导致射线束不能完全对正.但可以在最小方差的意义上,通过求解旋转矩阵R ()q 束得到最佳对正结果,其中旋转矩阵的求解是求每对射线标量积的极大值:()χ21=⋅=∑r q a i c i i n R r ,, (12.25)在四元数中,上面的和式可以表示为:()()rqr q qr qr a i c i i n c i a i i n ,,,,⋅=⋅==∑∑11 (12.26)上式可以变成二次表达式:()()()()q q q q q q q q q q q r qr N N N N N N N N T n i i T n i i a T i c T ni i a T i c T n i i a T i c n i i a i c =⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛===⋅∑∑∑∑∑=====11,,1,,1,,1,, (12.27) 假设q 对应一个列向量.则使二次式取极大值的单位四元数是对应于最大正特征值的特征向量.特征根可以利用[Horn 1987]给出的公式求解四阶多项式来确定,也可以利用标准数值方法[Press 1988]计算特征向量和特征值.矩阵N c i ,和N a i ,是由每个射线元素构成.设()r x y z c i c i c i c i ,,,,,=,()r x y z a i a i a i a i ,,,,,,=,那么:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------=0000,,,,,,,,,,,,,i c i c i c i c i c i c i c i c i c i c i c i c j c x y z x z y y z x z y x N (12.28) ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------=0000,,,,,,,,,,,,,i a i a i a i a i a i a i a i a i a i a i a i a j a x y z x z y y z x z y x N (12.29) 矩阵N 为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+--++-+-+-+-++------++=zz yy xx zy yz xz zx yx xy zy yz zz yy xx yx xy xz zx xz zx yx xy zz yy xx zy yz yx xy zy zx zy yz zz yy xx S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S N (12.30) 式中的和式S 是由摄象机坐标系和绝对坐标系的射线坐标元构成.其中,S kl 是求所有共轭对的摄象机坐标点的坐标k 坐标和在绝对坐标点的坐标l 坐标的乘积和:S kl kl c i a i i n ==∑,,1 (12.31)上述计算的结果是一个单位四元法,表示校准射线束的旋转变换.刚体变换可以作用于测距摄象机,双目立体视觉系统或任何其它深度测量系统产生的测量坐标值,以便把这是测量值变换到绝对坐标系统的测量坐标值 .12.3 相对定位相对定位问题是指用场景点在两个图像平面上的投影来确定两个摄象机坐标系之间的关系.相对定位问题是双目立体视觉系统标定的第一步.我们曾在第十一章讨论了沿极线匹配特征的双目立体视觉算法.为了简化表示,假定左、右图像平面上的外极线皆与图像阵列的行线重合,且对应的左、右图像阵列的行标号也相同.设场景点p 在左、右两个摄象机的视场范围内(见图11.1).点p 在左摄象机坐标系用),,(l l l l z y x =p 表示,在右摄象机坐标系内用),,(r r r r z y x =p 表示.点p 在左摄象机图像平面上的投影为'=''p l l l x y (,),在右摄象机图像平面上的投影为'=''p r (,)x y rr 设左右摄像机智的焦距分别为r l F F ,.由透视投影得到公式:l l l l z x F x =' ll l l z y F y =' (12.32) r r r r z x F x =' rr r r z y F y =' (12.33) 将左摄象机坐标系转换为右摄象机坐标系的刚体变换方程如下:zl zz l zy l zx r y l yz l yy l xy r xl xz l xy l xx r t z r y r x r z t z r y r x r y t z r y r x r x +++=+++=+++= (12.34)从透视投影方程()和()求出x y x l l r ,,和y r ,并将它们代入上面的刚体变换方程,得到一组共轭对投影之间的关系方程:rl l r r l l z l zz l zy l xz r l l r r l l yl yz l yy l xy r l l r r l l xl xz l xy l xx F F z z x z F t z r y r x r F F z z x z F t z r y r x r F F z z x z F t z r y r x r '=+'+'+''=+'+'+''=+'+'+' (12.35) 变换方程的旋转部分改变左摄象机的方位使之与右摄象机方位相同.而平移部分就是两个摄象机之间的基线.平移变量和深度变量在等式中以比值的形式出现,分别表示基线的长度和深度可任意缩放.例如,可以将摄象机分离两倍的距离,并将场景中的点移远两倍的距离而不改变透视几何关系.仅通过标定点的投影是不可能确定基线长度,但这并不是一个严重的问题,和确定比例系数一样,基线长度可以通过其它的方法确定.现在,假定摄象机之间的平移量是单位矢量.求解相对定位问题可以得到旋转的三个参数和表示基线方向的单位矢量的两个参数.双目立体深度测量值是以基线长度为计量单位的.假定单位基线长度,意味着双目立体测量值可以用任意计量单位表示.在这个单位基线长度假设下得到的测量值是正确的,但仍未确定比例系数.点之间的相对距离是正确的.这些任意设置的计量单位值乘以基线长度可以得到真实计量单位值.12.7节将介绍如何确定基线距离,这也是求解绝对定位问题的一个部分.求解绝对定位问题得到绝对坐标变换.使用绝对坐标变换,任意计量单位立体测量值到真实计量单位的转换和点在观察者坐标系到绝对坐标系的变换可以同步进行.方程组()含有12个相对位置参数和2个与场景点有关的未知数,因此若有n 个标定点,则有122+n 个未知量,旋转矩阵是正交矩阵,由此可以产生6个约束,另一个约束是基线距离取单位值的约束。
北理工贾云德《计算机视觉》chapter08纹理

第八章纹理8.1 引言纹理是以象素的邻域灰度空间分布为特征的,因此无法用点来定义.纹理尺度与图像分辨率有关,例如,从远距离观测由地板砖构成的地板时,我们看到的是地板砖块构成的纹理,而没有看到地板砖本身的纹理模式,当在近距离(只能看到几块砖的距离)观测同样的场景时,我们开始察觉到每一块砖上的详细模式,如图8.1所示.关于图像纹理的精确定义迄今还没有一个统一的认识.一般地来说,纹理是指图像强度局部变化的重复模式.纹理形成的机理是图像局部模式变化太小,一般无法在给定的分辨率下把不同的物体或区域分开.这样,在一个图像区域中重复出现满足给定灰度特性的一个连通像素集合构成了一个纹理区域.最简单的例子是在白色背景下黑点的重复模式.打印在白纸上的一行行字符也构成了纹理,其中的每一个灰度级基元是由表示每一个字符的连通像素集合构成;把一个个字符放在一行,把一行行字放在一页,就得到一个纹理.(a) 远距离观察时的纹理图像(b) 近距离观察时的纹理图像图8.1 由地板砖构成的地板纹理示意图实际上,对纹理的研究有两个目的,一种是研究纹理的观赏特性,即如何设计具有特定效果的纹理,使之具有一定美学价值或自然逼真效果,这是计算机图形学所研究的主要目标.另一种是研究纹理图像的特性,即纹理分析,以便分类和识别场景,这是机器视觉追求的目标.也就是说,对机器视觉来说,纹理是为了分割和识别场景或物体表面类型而产生的一种视觉标记.纹理分析包含有三个主要的问题:纹理分类、纹理分割和从纹理恢复形状.在纹理分类中,问题变成了从给定的一组纹理集中识别给定的纹理区域.例如,一幅特定的航空照片可能属于海洋、陆地或是城区,每一类都对应着唯一的纹理特征.对于每一类纹理,还可以精细划分,比如,根据纹理的粗细特征划分纹理.在海洋波浪方面,波浪的波长越长,图像的纹理越粗.由于波长与浪高有密切的关系,浪高信息也可以从纹理中获得.在土地纹理方面,森林比灌木林的纹理细,湿地和沼泽比森林和灌木林的纹理更细.用于纹理分析的算法很多,这些方法可大致分为统计分析和结构分析两大类.统计方法被广泛地用于纹理分析中.为了强化分类,可以从灰度图像计算灰度同现(co-occurrence) 矩阵、对比度(contrast)、熵(entropy)以及均匀度(homogeneity)等纹理特性.当纹理基元很小并成为微纹理时,统计方法特别有用;相反,当纹理基元很大时,应使用结构化方法,即首先确定基元的形状和性质,然后,再确定控制这些基元位置的规则,这样就形成了宏纹理.另一种自底而上的纹理特性分析方法是基于模型的方法,这种方法首先假定一个纹理模型,然后通过图像区域估计模型参数。
北理工贾云德《计算机视觉》chapter11深度图

135 第十一章 深度图获取场景中各点相对于摄象机的距离是计算机视觉系统的重要任务之一.场景中各点相对于摄象机的距离可以用深度图(Depth Map)来表示,即深度图中的每一个像素值表示场景中某一点与摄像机之间的距离.机器视觉系统获取场景深度图技术可分为被动测距传感和主动深度传感两大类.被动测距传感是指视觉系统接收来自场景发射或反射的光能量,形成有关场景光能量分布函数,即灰度图像,然后在这些图像的基础上恢复场景的深度信息.最一般的方法是使用两个相隔一定距离的摄像机同时获取场景图像来生成深度图.与此方法相类似的另一种方法是一个摄象机在不同空间位置上获取两幅或两幅以上图像,通过多幅图像的灰度信息和成象几何来生成深度图.深度信息还可以使用灰度图像的明暗特征、纹理特征、运动特征间接地估算.主动测距传感是指视觉系统首先向场景发射能量,然后接收场景对所发射能量的反射能量.主动测距传感系统也称为测距成象系统(Rangefinder).雷达测距系统和三角测距系统是两种最常用的两种主动测距传感系统.因此,主动测距传感和被动测距传感的主要区别在于视觉系统是否是通过增收自身发射的能量来测距。
另外,我们还接触过两个概念:主动视觉和被动视觉。
主动视觉是一种理论框架,与主动测距传感完全是两回事。
主动视觉主要是研究通过主动地控制摄象机位置、方向、焦距、缩放、光圈、聚散度等参数,或广义地说,通过视觉和行为的结合来获得稳定的、实时的感知。
我们将在最后一节介绍主动视觉。
11.1 立体成象最基本的双目立体几何关系如图11.1(a)所示,它是由两个完全相同的摄象机构成,两个图像平面位于一个平面上,两个摄像机的坐标轴相互平行,且x 轴重合,摄像机之间在x 方向上的间距为基线距离b .在这个模型中,场景中同一个特征点在两个摄象机图像平面上的成象位置是不同的.我们将场景中同一点在两个不同图像中的投影点称为共轭对,其中的一个投影点是另一个投影点的对应(correspondence),求共轭对就是求解对应性问题.两幅图像重叠时的共轭对点的位置之差(共轭对点之间的距离)称为视差(disparity),通过两个摄象机中心并且通过场景特征点的平面称为外极(epipolar)平面,外极平面与图像平面的交线称为外极线.在图11.1 中,场景点P 在左、右图像平面中的投影点分为p l 和p r .不失一般性,假设坐标系原点与左透镜中心重合.比较相似三角形PMC l 和p LC l l ,可得到下式:Fx z x l '= (11.1) 同理,从相似三角形PNC r 和p RC l r ,可得到下式:Fx z B x r '=- (11.2) 合并以上两式,可得:rl x x BF z '-'= (11.3) 其中F 是焦距,B 是基线距离。
北理工贾云德《计算机视觉》chapter06边缘检测

第六章边缘检测边缘(edge)是指图像局部强度变化最显著的部分.边缘主要存在于目标与目标、目标与背景、区域与区域(包括不同色彩)之间,是图像分割、纹理特征和形状特征等图像分析的重要基础.图像分析和理解的第一步常常是边缘检测(edge detection).由于边缘检测十分重要,因此成为机器视觉研究领域最活跃的课题之一.本章主要讨论边缘检测和定位的基本概念,并使用几种常用的边缘检测器来说明边缘检测的基本问题.图像中的边缘通常与图像强度或图像强度的一阶导数的不连续性有关.图像强度的不连续可分为:(1) 阶跃不连续,即图像强度在不连续处的两边的像素灰度值有着显著的差异;(2) 线条不连续,即图像强度突然从一个值变化到另一个值,保持一个较小的行程后又返回到原来的值.在实际中,阶跃和线条边缘图像是很少见的,由于大多数传感元件具有低频特性,使得阶跃边缘变成斜坡型边缘,线条边缘变成屋顶形边缘,其中的强度变化不是瞬间的,而是跨越一定的距离,这些边缘如图6.1所示.(a)(b)图6.1 两种常见的边缘,(a) 阶跃函数,(b) 线条函数.其中第一排为理想信号,第二排对应实际信号对一个边缘来说,有可能同时具有阶跃和线条边缘特性.例如在一个表面上,由一个平面变化到法线方向不同的另一个平面就会产生阶跃边缘;如果这一表面具有镜面反射特性且两平面形成的棱角比较圆滑,则当棱角圆滑表面的法线经过镜面反射角时,由于镜面反射分量,在棱角圆滑表面上会产生明亮光条,这样的边缘看起来象在阶跃边缘上叠加了一个线条边缘.由于边缘可能与场景中物体的重要特征对应,所以它是很重要的图像特征。
比如,一个物体的轮廓通常产生阶跃边缘,因为物体的图像强度不同于背景的图像强度.在讨论边缘算子之前,首先给出一些术语的定义:边缘点:图像中具有坐标],[j i 且处在强度显著变化的位置上的点.边缘段:对应于边缘点坐标],[j i 及其方位θ,边缘的方位可能是梯度角.边缘检测器:从图像中抽取边缘(边缘点和边缘段)集合的算法.轮廓:边缘列表,或是一条表示边缘列表的拟合曲线.边缘连接:从无序边缘表形成有序边缘表的过程.习惯上边缘的表示采用顺时针方向来排序.边缘跟踪:一个用来确定轮廊的图像(指滤波后的图像)搜索过程.边缘点的坐标可以是边缘位置像素点的行、列整数标号,也可以在子像素分辨率水平上表示.边缘坐标可以在原始图像坐标系上表示,但大多数情况下是在边缘检测滤波器的输出图像的坐标系上表示,因为滤波过程可能导致图像坐标平移或缩放.边缘段可以用像素点尺寸大小的小线段定义,或用具有方位属性的一个点定义.请注意,在实际中,边缘点和边缘段都被称为边缘.由边缘检测器生成的边缘集可以分成两个子集:真边缘集和假边缘集.真边缘集对应场景中的边缘,假边缘集不是场景中的边缘.还有一个边缘子集,即场景中漏检的边缘集.假边缘集称之为假阳性(false Positive ),而漏掉的边缘集则称之为假阴性(false Negative ). 边缘连接和边缘跟踪之间的区别在于:边缘连接是把边缘检测器产生的无序边缘集作为输入,输出一个有序边缘集;边缘跟踪则是将一幅图像作为输入,输出一个有序边缘集.另外,边缘检测使用局部信息来决定边缘,而边缘跟踪使用整个图像信息来决定一个像素点是不是边缘.6.1 梯度边缘检测是检测图像局部显著变化的最基本运算.在一维情况下,阶跃边缘同图像的一阶导数局部峰值有关.梯度是函数变化的一种度量,而一幅图像可以看作是图像强度连续函数的取样点阵列.因此,同一维情况类似,图像灰度值的显著变化可用梯度的离散逼近函数来检测.梯度是一阶导数的二维等效式,定义为向量⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=f x f y x G G y x G ∂∂∂),((6.1)有两个重要的性质与梯度有关:(1) 向量),(y x G 的方向就是函数),(y x f 增大时的最大变化率方向;(2) 梯度的幅值由下式给出:22|),(|y x G G y x G += (6.2)在实际应用中,通常用绝对值来近似梯度幅值:y x G G y x G +=|),(| (6.3)或),max(|),(|y x G G y x G ≈ (6.4)由向量分析可知,梯度的方向定义为)/arctan(),(x y G G y x a = (6.5)其中α角是相对x 轴的角度.注意梯度的幅值实际上与边缘的方向无关,这样的算子称为各向同性算子(isotropic operators).对于数字图像,方程6.1的导数可用差分来近似.最简单的梯度近似表达式为],1[],[],[]1,[j i f j i f G j i f j i f G y x +-=-+= (6.6)请注意j 对应于x 轴方向,而i 对应于负y 轴方向.这些计算可用下面的简单卷积模板来完成 11-=x G 11-=y G (6.7) 在计算梯度时,计算空间同一位置x 和y 处的真实偏导数是至关重要的.然而采用上面公式计算的梯度近似值x G 和y G 并不位于同一位置,x G 实际上是内插点 [,/]i j +12处的梯度近似值,y G 是内插点],2/1[j i +处的梯度近似值.由于这个缘故,人们常常使用22⨯一阶差分模板(而不用21⨯或 12⨯模板)来求x 和y 的偏导数:1111--=x G 1111--=y G (6.8) 用上式计算x 和y 方向梯度的位置是相同的,这一点位于内插点]2/1,2/1[++j i 处,即在22⨯邻域的所有四个像素点之间.不过这种计算可能会导致一些混淆,所以,通常用33⨯邻域计算梯度值.这一方法将在下一节讨论.6.2 边缘检测算法边缘检测算法有如下四个步骤:滤波:边缘检测算法主要是基于图像强度的一阶和二阶导数,但导数的计算对噪声很敏感,因此必须使用滤波器来改善与噪声有关的边缘检测器的性能.需要指出,大多数滤波器在降低噪声的同时也导致了边缘强度的损失,因此,增强边缘和降低噪声之间需要折衷.增强:增强边缘的基础是确定图像各点邻域强度的变化值.增强算法可以将邻域(或局部)强度值有显著变化的点突显出来.边缘增强一般是通过计算梯度幅值来完成的.检测:在图像中有许多点的梯度幅值比较大,而这些点在特定的应用领域中并不都是边缘,所以应该用某种方法来确定哪些点是边缘点.最简单的边缘检测判据是梯度幅值阈值判据.定位:如果某一应用场合要求确定边缘位置,则边缘的位置可在子像素分辨率上来估计,边缘的方位也可以被估计出来.在边缘检测算法中,前三个步骤用得十分普遍。
北理工贾云德《计算机视觉》第十三章 三维场景表示

第十三章 三维场景表示
x = rx cos s1 ϕ cos s2 θ y = ry cos s1 ϕ sin s2 θ z = rz sin s1 ϕ
−π / 2 ≤ ϕ ≤ π / 2 −π ≤θ ≤ π
渐变s1和s2值可生成形状渐变的超圆球 这些及其它超二次曲面形状的可以生成很 复杂的形状,如家具、闪电和其它金属构 成。
13.2.4 超二次曲面
由二次方程添加参数可生成超二次曲面 通过调整参数可以改变物体的形状。 增加的参数数目等同于物体的维数 (1)超椭圆 在超椭圆方程中,当x和y项的指数视 为变量时,笛卡儿超椭圆方程表示:
x y ( ) +( ) =1 rx ry
2 s 2 s
超椭圆参数方程:
x = rx cos s θ y = ry sin θ
]
⎡v3 ⎤ ⎢ 2⎥ ⎢v ⎥ ⎢v⎥ ⎢ ⎥ ⎢1⎥ ⎣ ⎦
其中, ai是三元行矢量 bj是三元列矢量 Ai,bj的积 是各 坐标系数的双积
该系数曲面为:
P(u,v)=UTMV
其中,
M是4×4矩阵,其元素是参数曲面的每一个坐标系数的矢 量. 张量积曲面是两曲线的积:一条曲线以u为坐标,另一条 以v为坐标.任何平行于坐标轴的平面和张量积三次多项式曲 面的交线都是三次多项式曲线.
场景分割 是将表示场景的网面分割成若干
部分,每一部分表示一个物体或一个特定 的区域,这样有利于物体识别、曲面精确 估计等后处理算法的实现.
北理工贾云德《计算机视觉》chapter07轮廓表示

第七章 轮廓表示把边缘连接起来就成为轮廓(contour).轮廓可以是断开的,也可以是封闭的.封闭轮廓对应于区域的边界,而区域内的像素可以通过填充算法来填满.断开的轮廓可能是区域边界的一部分,也可能是图像线条特征,如手写体笔画、图画中的线条等.区域之间的对比度太弱或边缘检测阈值设置太高都有可能产生间断的轮廓.轮廓可以用边缘序列表或曲线来表示.曲线通常称为轮廓的数学模型.曲线表示包括线段、二次曲线、三次样条曲线等.下面是几种轮廓表示的评价标准:高效:轮廓应该是一种简单和紧凑的表示.精确:轮廓应能精确地逼近图像特征.有效:轮廓应适合于后处理阶段的计算.轮廓表示的精确性由以下三个方面因素决定:① 用于轮廓建模的曲线形式;② 曲线拟合算法的性能;③ 边缘位置估计的精确度.轮廓的最简单表示形式是边缘有序表.这种表示的精确度就是边缘估计的精确度,但其表示的紧凑性是最差的,因此不是一种有效的后续图像分析表示方法.用适当的曲线模型来拟合边缘会提高精确度,这是因为曲线模型拟合边缘时往往具有均值化效应,因而可以减少边缘位置误差.曲线模型也会提高轮廓表示的经济性,为后处理提供了一种更适合、更紧凑的表示,例如,一条直线上的边缘集用一直线来拟合是表示这些边缘的最简单和最有效的方法,这一表示也简化了后续处理(如确定线的长度和方向);另外,由于估计直线与真实直线的均值方差小于真实直线与任何其它边缘之间的均值方差,因此可以说这种表示也增加了精确度.轮廓曲线拟合通常采用内插曲线或逼近曲线来实现.已知一组称为控制点的坐标点,内插是指一条曲线拟合这组控制点,使得曲线通过所有的控制点;逼近是指一条曲线拟合这组这组控制点,使得这条曲线非常接近这些控制点而无需一定通过这些点.在下面几节中,假定由边缘检测器得到的边缘十分准确,并使用内插值方法进行边缘曲线拟合. 定义7.1 边缘表是边缘点或边缘段的有序集合.定义7.2 轮廓是边缘表或用于表示边缘表的曲线.定义7.3 边界是包围一个区域的封闭轮廓.在无特别说明的情况下,边缘通常是指边缘点.对大多数曲线拟合算法来说,只需要边缘的位置信息。
北理工贾云德《计算机视觉》第十五章 三维运动估计

′ y k +1
′ ⎛ xk ⎞ ⎜ ⎟ ′ 1)E⎜ y k ⎟ = 0 ⎜1⎟ ⎝ ⎠
外极线 方程
⎛ e00 ⎞ ⎜ ⎟ ⎜ e01 ⎟ ⎜e ⎟ ⎜ 02 ⎟ ⎜ e10 ⎟ ⎜ ⎟ e11 ⎟ = 0 ⎜ ⎜ e12 ⎟ ⎜ ⎟ e 20 ⎟ ⎜ ⎜e ⎟ ⎜ 21 ⎟ ⎜ 1 ⎟ ⎝ ⎠
′ ′ (x k +1 x k
rxz和ryz缩小α,zk放大α,方程仍然成立,因此产 生多义性。三帧或三帧以上图象上的四点就可以克服 这个问题。
15.1.2 基于正交投影的运动估计
将(15.2)小角度旋转矩阵代入(15.1),得到如下的正交投 影模型:
′ ′ ′ xk +1 = xk − φy k + ψz k + t x ′ ′ ′ y k +1 = φxk + y k − θz k + t y
15.1.3 透视投影模型
设空间点(x,y,z)在图象平面上的投影(x’,y’)。如果成象 模型为透视投影,则 x y
x′ = F z
y′ = F
z
根据(15.1)式有
⎛ x k +1 ⎞ ⎡ rxx ⎜ ⎟ ⎢ ⎜ y k +1 ⎟ = ⎢ ryx ⎜ z ⎟ ⎢r ⎝ k +1 ⎠ ⎣ zx rxy ryy rzy rxz ⎤ ⎛ x k ⎞ ⎛ t x ⎞ ⎛ xk ⎞ ⎜ ⎟ ⎥⎜ ⎟ ⎜ ⎟ ryz ⎥ ⎜ y k ⎟ + ⎜ t y ⎟ = R k ⎜ y k ⎟ + Tk ⎜z ⎟ rzz ⎥ ⎜ z k ⎟ ⎜ t z ⎟ ⎝ k⎠ ⎦⎝ ⎠ ⎝ ⎠
2n个方程,通 过最小二乘法 来求解
2.根据1得到的运动参数估计值,再对深度值{zi,k}进行估计。 将式(15.7)重新写为(15.8)
《计算机视觉》知识要点总结终极
1、、。
;视觉是人类观察世界、认知世界的重要功能手段。
人类从外界获得信息约有80%来自视觉系统。
2、计算机视觉是指用计算机实现人类的视觉功能,即对客观世界中三维场景的感知、加工和理解。
计算机视觉的研究方法只有有两种:一种是仿生学的方法,参照人类视觉系统的结构原理,建立相应的处理模块完成类似的功能和工作;另一种是工程的方法,即从分析人类视觉过程的功能着手,并不刻意模拟人,视觉系统内部结构,而仅考虑系统的输入和输出,并采用任何现有的手段来实现系统的功能。
计算机视觉主要研究目标有两个:一是建立计算机视觉系统来完成各种视觉任务;二是把该研究作为探索人脑视觉工作机理的手段,即生物学机理。
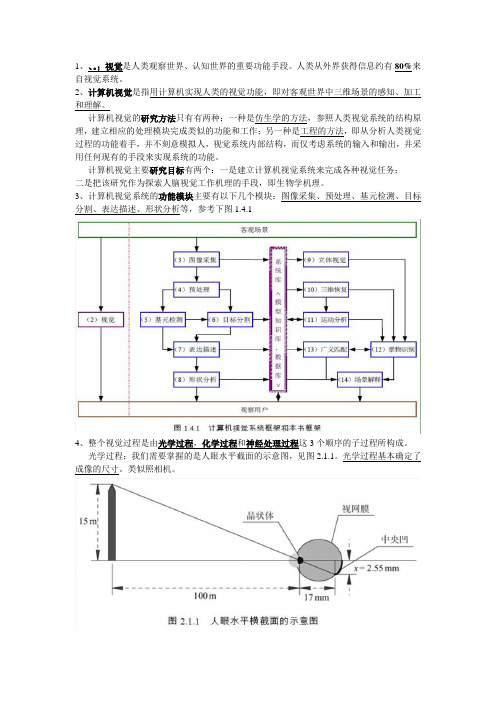
3、计算机视觉系统的功能模块主要有以下几个模块:图像采集、预处理、基元检测、目标分割、表达描述、形状分析等,参考下图1.4.14、整个视觉过程是由光学过程,化学过程和神经处理过程这3个顺序的子过程所构成。
光学过程:我们需要掌握的是人眼水平截面的示意图,见图2.1.1。
光学过程基本确定了成像的尺寸。
类似照相机。
化学过程:视网膜表面的光接收细胞可分为:锥细胞(亮视觉)和柱细胞(暗视觉)。
化学过程,基本确定了成像的亮度或颜色。
神经处理过程:将对光的感觉转换为对景物的知觉。
视觉处理过程流图2.1,2如下:5、形状知觉是对景物各部分相对关系的知觉,也与视野中各种空间关系的知觉有关。
6、轮廓(封闭的边界)是形状知觉中最基本的概念,人在知觉一个形状以前一定先看到轮廓。
轮廓的构成如果用数学语言来说就是轮廓对应亮度的二阶导数。
轮廓与形状又有区别,轮廓不等于形状。
轮廓在帮助构成形状时还有“方向性”。
轮廓通常倾向于对它所包围的空间发生影响,即轮廓一般是向内部而不是向外部发挥构成形状的作用。
7、主观轮廓:在没有直接刺激作用下产生的轮廓知觉。
主观轮廓的形成是在一定感觉信息的基础上进行知觉假设的结果8、空间知觉的问题本质是一个深度感知的问题。
人对空间场景的深度感知主要依靠双目视觉实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
211第十五章 三维运动估计三维运动估计是指从二维图象序列来估计物体三维运动参数以及三维结构。
具体地说,假定三维物体上一点M 相对于摄象机坐标系从时刻k t 的位置),,(k k k z y x 运动到时刻1+k t 的位置),,(111+++k k k z y x ,它在二维图象平面上的投影从),(k ky x ''运动到),(11++''k k y x ,然后,通过分析二维运动来恢复物体的三维运动及物体上感兴趣点的深度值。
这一点类似于立体视觉的深度恢复,不过立体视觉是从立体图象对来恢复深度值,而三维运动分析是从图象序列中恢复参数。
三维运动估计有着广泛的应用,如机器人视觉,自主导航,目标跟踪,图象监控,智能车辆高速公路系统,基于物体的图象压缩等。
三维运动估计仍然是一个不适定问题,必须增加适当的约束才能得到有效解。
三维运动估计和分析也可以是基于场景的深度图像序列,其方法与基于二维图像序列完全不同。
基于深度图像序列的三维运动估计是一个适定问题,求解方法要比基于二维图像序列要简单一些,主要问题是数据量十分巨大,因此许多研究人员一开始就以实现大规模集成电路(VLSI )作为三维场景估计的基础。
我们将不讨论深度图像序列运动估计问题,感兴趣的读者可以查阅有关文献[Wheeler 1996,Jiar 1996].15.1 基于成象模型的对应点估计首先回顾一下第十二章引入的三维刚体运动方程。
假定三维场景中有一个刚性物体,其上一点M 从时刻k t 的位置),,(k k k z y x 经过旋转和平移,运动到时刻1+k t 的位置),,(111+++k k k z y x 。
设旋转矩阵和平移向量分别是k R 和k T ,则三维刚体运动模型重新表示为k k k k k z y x k k k zz zyzxyz yy yx xz xy xx k k k z y x t t t z y x r r r r r r r r r z y x T R +⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎪⎪⎭⎫ ⎝⎛+++111 (15.1)用欧拉角的形式表示上述旋转矩阵(见式(12.2),(12.3)),并假定旋转角较小,则旋转矩阵可以表示为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=111θψθφψφk R(15.2)其中θ,ψ,φ分别表示绕z y x ,, 轴逆时针旋转小角位移。
15.1.1 正交投影模型当物体深度变化范围不大时,正交投影是透视投影的一个很好的逼近。
其它逼近方法还有弱透视投影,超透视投影,正交透视投影等[Dementhon 1992]。
设空间点),,(z y x 在图象平面上的投影为),(y x ''。
如果成象模型为正交投影(参见图1.8),则有x x =' y y =' (15.3) 所以,式(15.1) 可表示为)()(1111y k yz k yy k yx kk x k xz k xy k xx kk t z r y r x r y y t z r y r x r x x ++'+'='=++'+'='=++++ (15.4)上述方程包含有6个参数,即xx r ,xy r ,yy r ,yx r ,)(x k xz t z r +和)(y k yz t z r +,表示第k 帧212图象像素),(k k y x ''到第1+k 帧图象像素),(11++''k k y x 的仿射映射关系。
显然,正交投影模型是无法确定物体点到成象平面的距离,因为垂直于图像平面的一条直线,其上的所有点都将投影到该图象平面上一点(见图1.8)。
但是,如果在物体上选择一个参考点,并设该点的深度值为ref z ,则通过上式有可能估计出物体上其它点相对于这个参考点在垂直图像平面方向上的距离rel z 。
实际上,我们无法得到真实的相对深度值,只能得到关于一个尺度系数α的相对深度值,即rel ref z z z α+= (15.5)从方程15.4中,我们看到xz r 和yz r 缩小α,k z 放大α,方程仍然成立,因此产生多义性。
文献[Ull79]证明三帧或三帧以上图象上的四点就可以克服这个问题。
15.1.2 基于正交投影的运动估计将(15.2)小角度旋转矩阵代入(15.1),得到如下的正交投影模型:y k k k kx k k k kt z y x y t z y x x +-'+'='++'-'='++θφψφ11 (15.6)在该方程中,对于每一个给定的对应点),(k ky x ''和),(11++''k k y x ,共有6个未知参数,其中5个是全局运动参数φ,ψ,θ,x t ,y t ,一个是深度参数k z 。
另外,这个方程是一个双线性方程,因为k z 与未知参数ϕ和θ是乘积关系。
理论上,给定三点,就可以根据(15.6)列出6个方程,从而解出六个未知参数。
但实际上,由于数值计算误差,常常需要多个点,这样有可能得到较好的结果。
文献[Aizawa 1989] 基于上述正交投影模型提出了基于两帧图象的两步迭代法:首先,根据上一次迭代得到的深度估计值,确定运动参数,然后再使用新的运动参数更新深度估计值。
具体实现见算法15.1算法15.1 基于两帧图像的运动估计两步迭代算法① 给定n 个对应点坐标对)},{(,,k i k i y x '')},{(1,1,++''k i k i y x 和深度估计值}{,k i z ,n i ,,2,1 =,且3≥n ,这样方程(15.6)可重新写为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛'-'-=⎪⎪⎭⎫ ⎝⎛'-''-'++y x kkkk k k k k t t x zy z y y x x φψθ10001011 (15.7) n 个对应点对应着n 2个方程,而未知参数仅有5个,因此,可以通过最小二乘法来求解这5个运动参数。
深度参数的初始估计值可以根据场景的先验模型来设置,深度估计值应在预先设定的范围内选定,这主要是为了避免解的不唯一性。
② 根据①得到的运动参数估计值,再对深度值}{,k i z 进行估计。
将式(15.7)重新写为()k y k k k x k k k z t x y y t y x x ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-'-'-'-'+'-'++θψφφ11 (15.8) 由于每一个深度值对应两个方程,即方程(15.8)是一个超定方程,因此,可以用最小二乘法来求解。
③ 重复上述两步,直到两次迭代值之差小于给定的某一个阈值。
请注意,在上述算法中,运动估计误差和深度估计误差有着密切的关系。
由方程(15.7)和(15.8)可知,深度估计的随机误差会重复反馈到运动估计上。
因此,当深度估计不够准确或深度的初始值设置不当时,都可能导致迭代算法的错误收敛或收敛在一个局部最小值。
为了避免这种错误的收敛,[Bozdagi 1994]提出了改进的算法,该算法的基本思想是在每一次修正后,在深度估计值上加一个随机扰动。
改进的算法如算法15.1所示。
213算法15.2 基于两帧图像运动估计扰动迭代算法:① 初始化深度值}{,k i z ,n i ,,2,1 =,置迭代计数器0=m 。
② 在给定深度值下根据式(15.6)估计运动参数③ 根据当前的运动估计和深度参数,由公式(15.6)计算对应点的坐标),()(1,)(1,m k i m k i y x ++''④ 计算预估误差:∑==ni i m e n E 11 (15.9)其中2)(1,1,2)(1,1,)()(m k i k i m k i k i i y y x x e ++++'-'+'-'=,1,+'k i x 和1,+'k i y 是已知的对应点真实坐标。
⑤ 如果m E 小于预定的误差阈值T E ,即T m E E <,则终止迭代,否则,置1+=m m 。
⑥ 给深度参数赋一个扰动值)()1(,)(,m i im ki m k i ze z z ∆+∂∂-←-αβ (15.10) 其中α和β是常系数,),0()(2)(m i i m i N σ=∆是零均值高斯分布函数,其方差i m i e =)(2σ。
⑦ 回到第②步实验证明,这种改进的迭代算法在初始深度值有50%的误差的情况下,也能很好地收敛到正确的运动参数值。
15.1.3 透视投影模型设空间点),,(z y x 在图象平面上的投影为),(y x ''。
如果成象模型为透视投影,则z x F x =' zyF y =' (15.11) 根据(15.1)式有zk zz k zy k zx yk yz k yy k yx k k kz k zz k zy k zx x k xz k xy k xx k k kt z r y r x r t z r y r x r F z y F y t z r y r x r t z r y r x r F z x F x ++++++=='++++++=='++++++111111 (15.12)由于成象系统的焦距是一个常数,因此,不乏一般性,取1=F ,即规范化透视投影。
上式右边分子分母同除以k z ,得到图象平面坐标表示式:k z zz k zy kzx k y yz k yy kyx kk z zz k zy kzx k x xz k xy kxx k z t r y r x r z t r y r x r y z t r y r x r z t r y r x r x ////11++'+'++'+'='+'+'+'++'+'='++ (15.13)按照图像平面坐标,透视投影模型(15.13)是一个非线性方程。
因为每一点对应的深度值z是一个自由参数,因此,这个模型适合于任意表面形状三维物体的运动估计。
15.1.4 外极线方程和基本矩阵由方程(15.13)可见,在透视投影情况下,运动和结构参数之间的关系是非线性的。
早期人们使用迭代方法求解运动参数,但迭代过程往往不收敛,比如两步迭代法。
[Huang 1986]证明,使用八个对应点或更多对应点来求取外极线约束方程并估计运动参数是可以改进两步迭代法的收敛性能。
