9_对数线性模型分析
计量经济学实验一 一元回归模型
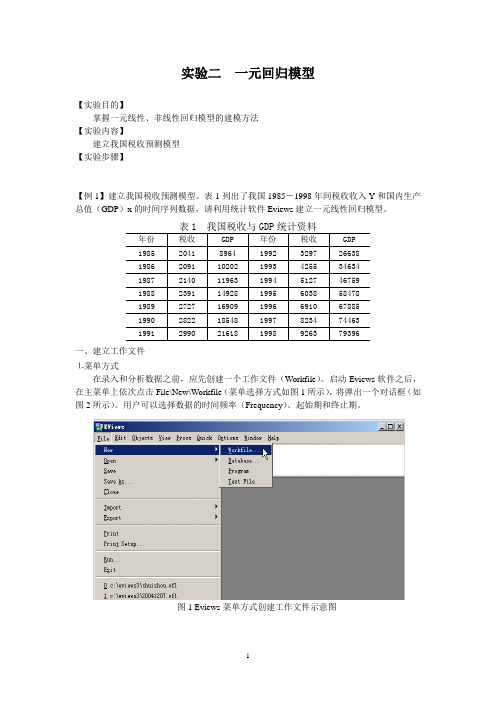
实验二一元回归模型【实验目的】掌握一元线性、非线性回归模型的建模方法【实验内容】建立我国税收预测模型【实验步骤】【例1】建立我国税收预测模型。
表1列出了我国1985-1998年间税收收入Y和国内生产总值(GDP)x的时间序列数据,请利用统计软件Eviews建立一元线性回归模型。
一、建立工作文件⒈菜单方式在录入和分析数据之前,应先创建一个工作文件(Workfile)。
启动Eviews软件之后,在主菜单上依次点击File\New\Workfile(菜单选择方式如图1所示),将弹出一个对话框(如图2所示)。
用户可以选择数据的时间频率(Frequency)、起始期和终止期。
图1 Eviews菜单方式创建工作文件示意图图2 工作文件定义对话框本例中选择时间频率为Annual(年度数据),在起始栏和终止栏分别输入相应的日期85和98。
然后点击OK,在Eviews软件的主显示窗口将显示相应的工作文件窗口(如图3所示)。
图3 Eviews工作文件窗口一个新建的工作文件窗口内只有2个对象(Object),分别为c(系数向量)和resid(残差)。
它们当前的取值分别是0和NA(空值)。
可以通过鼠标左键双击对象名打开该对象查看其数据,也可以用相同的方法查看工作文件窗口中其它对象的数值。
⒉命令方式还可以用输入命令的方式建立工作文件。
在Eviews软件的命令窗口中直接键入CREATE命令,其格式为:CREATE 时间频率类型起始期终止期本例应为:CREATE A 85 98二、输入数据在Eviews软件的命令窗口中键入数据输入/编辑命令:DA TA Y X此时将显示一个数组窗口(如图4所示),即可以输入每个变量的数值图4 Eviews数组窗口三、图形分析借助图形分析可以直观地观察经济变量的变动规律和相关关系,以便合理地确定模型的数学形式。
⒈趋势图分析命令格式:PLOT 变量1 变量2 ……变量K作用:⑴分析经济变量的发展变化趋势⑵观察是否存在异常值本例为:PLOT Y X⒉相关图分析命令格式:SCAT 变量1 变量2作用:⑴观察变量之间的相关程度⑵观察变量之间的相关类型,即为线性相关还是曲线相关,曲线相关时大致是哪种类型的曲线说明:⑴SCAT命令中,第一个变量为横轴变量,一般取为解释变量;第二个变量为纵轴变量,一般取为被解释变量⑵SCAT命令每次只能显示两个变量之间的相关图,若模型中含有多个解释变量,可以逐个进行分析⑶通过改变图形的类型,可以将趋势图转变为相关图本例为:SCA T Y X图5 税收与GDP趋势图图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。
对数线性模型

对于分类数据的分析,最简单也是最广泛使用的是卡方检验,但卡方检验在处理分类数据时,有两个局限:1.卡方检验只能简单描述变量间的相关关系,而无法分析出具体的因果关系或变量间相互作用(效应)大小2.卡方检验通常用于2*2列联表,而对于高维列联表,则无法系统的评价变量间的关系,而对数线性模型则是分析高维列联表的常用方法。
基于以上问题,我们除了可以使用Logistic模型之外,还可以使用对数线性模型进行分析。
对数线性模型的结构类似于方差分析,思想也和方差分析一样,不同的是方差分析用于连续变量,而对数线性模型用于分类变量。
在方差分析中,观测值y 的变异由各因素的主效应、各因素之间的交互效应、随机误差三者之和组成。
而对于分类变量也可以采用这种方法进行分解,只不过此时的观测值y为频数而不是实际的观测值,最终观测值变异的组成也不是相加关系,而是乘积关系。
以两个分类变量α、β为例:M ij代表第i行第j列的频数αi代表变量α的主效应βj代表变量β的主效应(αβ)ij代表变量αβ的交互作用εij代表随机误差分类数据的频数分布一般分为多项式分布、二项式分布、泊松分布,取值在0—+∞之间,因此等式两边都取其对数ln,这样可以使期望频数取值在-∞—+∞,这就是所谓的对数线性模型。
模型的独立参数和自由度:独立参数个数=分类数-限制条件数数据提供的信息量=列联表中网格的数量模型自由度=信息量-独立参数个数对数线性模型的一个假设前提是:每个分类变量各水平的效应之和等于0========================================== ===对数线性模型的统计检验:对数线性模型的假设检验都是基于Pearson卡方检验和似然比卡方检验L2,当样本规模较大时,这两个统计值很接近,但似然比卡方更加稳健1.对模型的整体检验也就是拟合优度检验,两种卡方的零假设是:检验模型的频数估计与观测频数无差异,也就是拟合度良好2.分层效应检验类似于逐步回归的筛选自变量,分层效应检验就是逐步筛选交互作用,每剔除一种交互作用,就检验一次,主要是:某一阶及更高阶所有交互作用项的集体检验,检验是否显著表明这一阶及更高阶中是否至少有一项分类的效应是有意义的。
线性与对数模型比较分析

实验报告——线性模型与对数模型举例分析一、实验目的本实验的目的在于研究GNP 与货币是否有关系,若有关系有怎样的数量关系,用哪种模型来描述二者之间关系较为合适。
二、下面根据GNP/货币供给数据,得到的回归结果(Y=GNP ,X=货币供给):年 GNP (10亿美元) Μ2 年 GNP (10亿美元) Μ2 1973 1359.3 861.0 1981 3052.6 1795.5 1974 1472.8 908.5 1982 3166.0 1954.0 1975 1598.4 1023.2 1983 3405.7 2185.2 1976 1782.8 1163.7 1984 3772.2 2363.6 1977 1990.5 1286.7 1985 4014.9 2562.6 1978 2249.7 1389.0 1986 4240.3 2807.7 1979 2508.2 1500.2 1987 4526.7 2901.0 1980 2732.0 1633.1 平均值 2791.47 1755.70模型 截距 斜率2r双对数 0.5531 0.9882 0.9926t=(3.1652) 41.889 对数-线性 6.8616 0.00057 0.9493 (增长模型) t=(100.05) 15.597 线性-对数 -16329.0 2584.8 0.9832t=(-23.494) 27.549 线性 101.20 1.5323 0.9915 (LIV 模型) t=(1.369) 38.867a. 解释每个模型斜率的意义。
1. 双对数模型中斜率0.9882表示,货币供给每提高1个百分点,GNP 平均增加约0.98个百分点。
2. 对数―线性模型中的斜率0.00057表示,货币供给每增加1(10亿)美元,GNP 将以0.057%的速度增长。
3. 线性―对数模型中的斜率2584.8表示,货币供给每提高1个百分点,GNP 将增加25.848(10亿)美元。
计量经济学练习题

计量经济学试题1一 名词解释(每题5分,共10分) 1. 经典线性回归模型 2. 加权最小二乘法(WLS ) 二 填空(每空格1分,共10分)1.经典线性回归模型Y i = B 0 + B 1X i + µi 的最小二乘估计量b 1满足E ( b 1 ) = B 1,这表示估计量b 1具备 性。
2.广义差分法适用于估计存在 问题的经济计量模型。
3.在区间预测中,在其它条件不变的情况下,预测的置信概率越高,预测的精度越 。
4.普通最小二乘法估计回归参数的基本准则是使 达到最小。
5.以X 为解释变量,Y 为被解释变量,将X 、Y 的观测值分别取对数,如果这些对数值描成的散点图近似形成为一条直线,则适宜配合 模型。
6.当杜宾-瓦尔森统计量d = 4时,ρˆ= ,说明 。
7.对于模型i i i X Y μββ++=10,为了考虑“地区”因素(北方、南方两种状态)引入2个虚拟变量,则会产生 现象。
8. 半对数模型LnY i = B 0 + B 1X i + µI 又称为 模型。
9.经典线性回归模型Y i = B 0 + B 1X i + µi 的最小二乘估计量b 0、b 1的关系可用数学式子表示为 。
三 单项选择题(每个1分,共20分)1.截面数据是指--------------------------------------------------------------( )A .同一时点上不同统计单位相同统计指标组成的数据。
B .同一时点上相同统计单位相同统计指标组成的数据。
C .同一时点上相同统计单位不同统计指标组成的数据。
D .同一时点上不同统计单位不同统计指标组成的数据。
2.参数估计量βˆ具备有效性是指------------------------------------------( ) A .0)ˆ(=βar V B.)ˆ(βar V 为最小 C .0)ˆ(=-ββD.)ˆ(ββ-为最小 3.如果两个经济变量间的关系近似地表现为:当X 发生一个绝对量(X ∆)变动时,Y 以一个固定的相对量(YY /∆)变动,则适宜配合的回归模型是------------------------------------------------------------------------------------------- ( )A .i i i X Y μβα++= B.i i i X Y μβα++=ln C .i ii X Y μβα++=1D.i i i X Y μβα++=ln ln 4.在一元线性回归模型中,不可能用到的假设检验是----------( ) A .置信区间检验 B.t 检验 C.F 检验 D.游程检验5.如果戈里瑟检验表明 ,普通最小二乘估计的残差项有显著的如下性质:24.025.1i i X e +=,则用加权最小二乘法估计模型时,权数应选择-------( )A .i X 1 B. 21i X C.24.025.11iX + D.24.025.11i X +6.对于i i i i X X Y μβββ+++=22110,利用30组样本观察值估计后得56.827/)ˆ(2/)ˆ(2=-∑-∑=iiiY Y Y Y F ,而理论分布值F 0.05(2,27)=3.35,,则可以判断( )A . 01=β成立 B. 02=β成立C.021==ββ成立 D. 021==ββ不成立7.为描述单位固定成本(Y )依产量(X )变化的相关关系,适宜配合的回归模型是:A .i i i X Y μβα++= B.i i i X Y μβα++=ln C .i ii X Y μβα++=1D.i i i X Y μβα++=ln ln 8.根据一个n=30的样本估计ii i e X Y ++=10ˆˆββ后计算得d=1.4,已知在95%的置信度下,35.1=L d ,49.1=U d ,则认为原模型------------------------( )A .存在正的一阶线性自相关 B.存在负的一阶线性自相关 C .不存在一阶线性自相关 D.无法判断是否存在一阶线性自相关9.对于ii i e X Y ++=10ˆˆββ,判定系数为0.8是指--------------------( ) A .说明X 与Y 之间为正相关 B. 说明X 与Y 之间为负相关 C .Y 变异的80%能由回归直线作出解释 D .有80%的样本点落在回归直线上10. 线性模型i i i i X X Y μβββ+++=22110不满足下列哪一假定,称为异方差现象-------------------------------------------------------------------------------( )A .0)(=j i ov C μμ B.2)(σμ=i ar V (常数)C .0),(=i i ov X C μ D.0),(21=i i ov X X C11.设消费函数i i i X D Y μβαα+++=10,其中虚拟变量⎩⎨⎧=南方北方01D ,如果统计检验表明1α统计显著,则北方的消费函数与南方的消费函数是--( )A .相互平行的 B.相互垂直的 C.相互交叉的 D.相互重叠的12. 在建立虚拟变量模型时,如果一个质的变量有m 种特征或状态,则一般引入几个虚拟变量:----------------------------------------------------------------( )A .m B.m+1 C.m -1 D.前三项均可 13. 在模型i i iX Y μββ++=ln ln ln 10中,1β为---------------------( )A .X 关于Y 的弹性 B.X 变动一个绝对量时Y 变动的相对量 C .Y 关于X 的弹性 D.Y 变动一个绝对量时X 变动的相对量14.对于i i i e X Y ++=10ˆˆββ,以S 表示估计标准误差,iY ˆ表示回归值,则-------------------------------------------------------------------------------------------( )A .S=0时,0)ˆ(=-∑ti Y Y B.S=0时,∑==-ni i i Y Y 120)ˆ( C .S=0时,)ˆ(ii Y Y -∑为最小 D.S=0时,∑=-ni i i Y Y 12)ˆ(为最小 15.经济计量分析工作的基本工作步骤是-----------------------------( )A .设定理论模型→收集样本资料→估计模型参数→检验模型B .设定模型→估计参数→检验模型→应用模型C .理论分析→数据收集→计算模拟→修正模型D .确定模型导向→确定变量及方程式→应用模型16.产量(X ,台)与单位产品成本(Y ,元/台)之间的回归方程为:X Y5.1356ˆ-=,这说明-----------------------------------------------------------( )A .产量每增加一台,单位产品成本平均减少1.5个百分点B .产量每增加一台,单位产品成本减少1.5元C .产量每增加一台,单位产品成本减少1.5个百分点D .产量每增加一台,单位产品成本平均减少1.5元17.下列各回归方程中,哪一个必定是错误的------------------------( )A .8.02.030ˆ=+=XY i i r X Y B. 91.05.175ˆ=+-=XY ii r X YC .78.01.25ˆ=-=XY i i r X Y D. 96.05.312ˆ-=--=XY ii r X Y18.用一组有28个观测值的样本估计模型i i i X Y μββ++=10后,在0.05的显著性水平下对1β的显著性作t 检验,则1β显著地不等于0的条件是统计量t 大于-------------------------------------------------------------------------------------( )A .t 0.025(28) B. t 0.05(28) C. t 0.025(26) D. t 0.05(26)19.下列哪种形式的序列相关可用DW 统计量来检验(V t 为具有零均值、常数方差,且不存在序列相关的随机变量)---------------------------------( )A .t t t V +=-1ρμμ B.t t t t V +⋅⋅⋅++=--121μρρμμ C.t t V ρμ= D. ⋅⋅⋅++=-12t t t V V ρρμ20.对于原模型t t t X Y μββ++=10,一阶差分模型是指------------( )A .)()()(1)(1t tt t t t t X f X f X X f X f Y μββ++=B .t t t X Y μβ∆+∆=∆1C .t t t X Y μββ∆+∆+=∆10D .)()()1(11101----+-+-=-t t t t t t X X Y Y ρμμρβρβρ四 多项选择题(每个2分,共10分)1.以Y 表示实际值,Y ˆ表示回归值,ie 表示残差项,最小二乘直线满足------------------------------------------------------------------------------------------( )A .通用样本均值点(Y X ,) B.ii Y Y ˆ∑=∑ C .0),ˆ(=i i ov e Y C D.0)ˆ(2=-∑ii Y Y E .0)ˆ(=-∑Y Y i 2.剩余变差(RSS )是指--------------------------------------------------( )A .随机因素影响所引起的被解释变量的变差B .解释变量变动所引起的被解释变量的变差C .被解释变量的变差中,回归方程不能作出解释的部分D .被解释变量的总变差与解释变量之差E .被解释变量的实际值与回归值的离差平方和3. 对于经典线性回归模型,0LS 估计量具备------------------------( ) A .无偏性 B.线性特性 C.正确性 D.有效性 E.可知性4. 异方差的检验方法有---------------------------------------------------( ) A .残差的图形检验 B.游程检验 C.White 检验D.帕克检验E.方差膨胀因子检验5. 多重共线性的补救有---------------------------------------------------()A.从模型中删掉不重要的解释变量 B.获取额外的数据或者新的样本 C.重新考虑模型D.利用先验信息E. 广义差分法五简答计算题(4题,共50分)1.简述F检验的意图及其与t检验的关系。
对数线性模型

双向无序列联表; 单向有序列联表; 双向有序且属性不同的列联表; 双向有序且属性相同的列联表
3、列联表的优势
约束条件少 清晰 可以快速准确进行判断
4、列联表的劣势:对于多关系变量 两个以上 研究:不能被清晰解读
失去了对多变量之间的交互联系的分析 进行两变量间关联分析时缺乏统计控制 不能准确定量描述一个变量对另一个变量的作用幅度
密度函数和似然函数 带着参数的密度函数 是相同的,但前者视参数是固定的且数据时变化的,后者视参数变化的且数据时固定的。 1 写出似然函数; 2 对似然函数取对数,并整理; 3 求导数 ; 4 解似然方程
三、对数线性模型的假设检验
1、假设检验的作用 统计推论中包括参数估计与假设检验两部分,上面我们已经介绍了参数估计,那估计的可信度有多少,还要经过假设检验。不经过统计检验,研究者便不能肯定得到的参数估计是不是仅仅源于抽样误差,因而不能肯定在总体中是否存在相同情况。所有结论只能限于这个样本之内,不能肯定再抽一个样本能否得到类似结果。
上两式的数学变换使各种效应项相乘的关系被转换成相加的关系,使各项效应独立化了。 常数效应; A因素效应; B因素效应; 主效应 A、B两因素的交互效应;
主效应和多元交互列表涉及因素数量相等; 交互效应的总数则为所有因素各阶组合数之和。 对数线性模型有一个限制条件: 模型中每一项效应的各类参数之和等于0; 如果每项效应中只有一类的参数未知,那么可以由已知参数推算出来。
5、对数线性模型:多维度列联表解决之道,以及模型自身特点
通过数学方法 方差分析+逻辑变换 来描述多元频数分布。 综合性:同时囊括多个变量于一个模型之中。 控制性:可以在控制其他变量的条件下研究两个分类变量之间的关联。 饱和性:将多元频数分布分解成具体的各项主效应和各项交互效应,以及高阶效应,不会漏项。 饱和模型与不饱和模型 定量性:以发生比的形式来表示自变量的类型不同反映在因变量频数分布上的差异。 可检验性:不仅可以对所有参数估计进行检验,使抽样数据可以推论总体,且能够通过不同模型的统计检验结果,对备选模型进行筛选和评价,进而确定具有最大解释能力且最简单的模型。 消除抽样波动所带来的明显的不规则性
《SPSS数据分析与应用》线性回归分析

“票房”直方图
对数线性回归模型结果解读
变量
截距项 类型=主旋律
类型=儿童 类型=动作 类型=动画 类型=励志 类型=历史剧情 类型=喜剧 类型=家庭伦理 类型=悬疑 类型=惊悚 类型=灾难 类型=警匪 类型=魔幻
回归系数
5.490 0.278 -0.110 0.150 0.176 0.454 0.096 0.072 -0.432 1.008 -0.276 0.807 0.345 0.820
=黄金2档, 年=2011, 类型=动作, 宣发方=G, 导演得奖情况=1.0, 类型=历史剧情, 类型=动画, 时长, 年=2013, 类型=主旋律, 档期=暑期
档, 宣发方=L
R表示拟合优度(goodness of fit), 是用来衡量估计的模型对观测值的拟合程度。它的值 越接近1说明模型越好。调整后的 考虑了模型的复杂程度,也就是自变量的个数,其含义与 非常类似,更多的被用于不同模型拟合优度的比较(因变量必须相同)。在本案例中,调整后 为 0.376,表示自变量可以解释因变量37.6%的变化。当然,在实际项目中,不建议一味地追 求 ,这不是建模的目标。
第 7 章 线性回归分析
学习目标
1.掌握回归分析的基本原理及步骤。 2.掌握线性回归分析模型的SPSS实现与解读方法。 3.掌握对数线性回归分析模型的SPSS实现与解读方法。 4.熟悉线性回归分析报告的撰写方法。
引导案例
近年来,得益于国民经济的持续快速增长以及国家对文化产业的支持,整体电影 文化与产业环境持续改善。作为文化娱乐市场重要组成部分的电影市场已连续多年实 现电影票房的快速增长,同时,也吸引了各类社会资本积极进军电影行业,从而进一 步推动了电影行业的良性快速发展。
对数线性回归模型的具体实现方法与线性回归模型的实现方法一致,这里就不再 一一赘述了。但是对于回归结果的解读,对数线性回归模型结果的解读与线性回归模 型结果的解读还是有不同的地方需要注意。
各种对数线性模型

第九章对数线性模型第一节 General过程9.1.1 主要功能9.1.2 实例操作第二节 Hierarchical过程9.2.1 主要功能9.2.2 实例操作第三节 Logit过程9.3.1 主要功能9.3.2 实例操作对数线性模型是用于离散型数据或整理成列联表格式的计数资料的统计分析工具。
在对数线性模型中,所有用作的分类的因素均为独立变量,列联表各单元中的例数为应变量。
对于列联表资料,通常作χ 2 检验,但χ 2 检验无法系统地评价变量间的联系,也无法估计变量间相互作用的大小,而对数线性模型是处理这些问题的最佳方法。
第一节 General过程9.1.1 主要功能调用该过程可对一个或多个二维列联表资料进行非层次对数线性分析。
它只能拟合全饱和模型,即分类变量各自效应及其相互间效应均包含在对数线性模型中。
返回目录返回全书目录9.1.2 实例操作[例9-1]在住院病人中,研究其受教育程度与对保健服务满意程度的关系,资料整理成列联表后如下所示。
按一般情形作χ2检验,结果显示不同受教育程度的住院病人其对保健服务满意程度无差别。
但从百分比分析中可见,随受教育程度的提高,满意程度有下降的趋势;且我们还想了解受教育程度与满意程度有无交互作用和交互作用的大小。
对此,必须采用对数线性模型加以分析。
9.1.2.1 数据准备激活数据管理窗口,定义变量名:实际观察频数的变量名为freq,受教育程度和满意程度作为行、列分类变量(即独立变量),变量名分别为educ、care。
输入原始数据,结果如图9.1所示。
如同第四章Crosstab过程中所述,为使列联表的频数有效,应选Data 菜单的Weight Cases...项,弹出Weight Cases对话框(图9.2),激活Weight cases by 项,从变量列表中选freq点击 钮使之进入Frequency Variable框,点击OK钮即可。
图9.1 原始数据的输入图9.2 频数的加权定义9.1.2.2 统计分析激活Statistics菜单选Loglinear中的General...项,弹出General Loglinear Analysis对话框(图9.3)。
对数线性模型

B
25
2、统计量
似然卡方比,根据相关计算,看原假设是否成立。 贝叶斯信息标准,不同模型而言越小的BIC越好。
B
26
3、对数线性模型的统计 检验
四种主要检验: 1、对于假设模型的整体检验; 2、分层效应的检验; 3、单项效应的检验; 4、单个参数估计的检验。
B
27
对数线性模型的统计检验
1、对于假设模型的整体检验 采用似然比卡方检验(likelihood-ratio chi-square test,标
B
17
通过上组式子,我们可以计算出线性模型等式右侧的所有参数值。 A因素效应是行平均值与总平均值之差 B因素效应是列平均值与总平均值之差 交互效应计算结果表示在除去所有其他分布效应之后两个因素之间
的净关联。
B
18
常数项只受样本规模和交互单元数的影响;
主效应项反映的是各因素内部类别频数分布的特征,是 在总平均频数基础上的“补差”;
B
31
对数线性模型的统计检验
举例说明:
由图可知,自由度变为1,L2由0增大到10.284,显著性水平α为0.01(P)(拒绝原假设), 说明简略模型和饱和模型存在十分显著的差异,即拟合程度受到很大影响。
显著=不能剔除该交互因素 在因素很多的复杂饱和模型中,通过此方法删减多个不显著效应项来形成简略模型。
极大似然估计所要解决的问题是:选择参数Ɵ,使已知 数据在某种意义下最可能出现。某种意义指的是似然函 数最大,此处似然函数就是概率密度函数。也就是经常 提到的“模型已知,参数未定”。
B
22
二者的区别就是,后者需要知道概率密度函数。最小二 乘法要的是求出最优的那个参数,而极大似然要求出概 率最大(最可能出现的)参数。举个例子,生活中我们 一个着眼最合理是哪一个,一个着眼于最可能的是哪一 个(极大似然法)当总体服从正态分布时,二者是一样 的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
28
【结果解释】
① 所有分类变量的一维频数分布表,它包含了各变量的类别 数以及类别的排列顺序。 ② 最大似然估计法的主要分析结果,包括参数的自由度, Wald-卡方值和p-值,以及似然比统计量,它用来检验模型的
拟和优度。即,比较特定的模型和无限制模型(unrestricted
model),即,仅含常数的模型。p-值越大,模型拟越好。 从②可以得知,该模型拟和数据较好(p=0.7651)。并且可以得 出结论:采用不同手术是导致术后并发症不同严重程度的根 本原因(TRT*SEV:p=0.0502),至于病人在哪家医院接受手
自变量之间的交互效应就很繁杂,可能需要
建立很多哑变量。
16
3、对数线性模型:可以直接分析各种类型的分 类变量,对于名义变量,也不需要事先建立哑变
量,可以直接分析变量的主效应和交互效应。对
数线性模型不仅可以解决卡方分析中常遇到的高
维列联表的“压缩”问题,又可以解决logistic回
归分析中多个自变量的交互效应问题。
术与术后并发症的严重程度并无关系(HP*SEV:p=0.5563)。
29
总 结
• Logistic回归分析和卡方分析的优缺点是什么? • 对数合独立模型 和完全
独立模型?
• 在什么情况下可以压缩变量?
30
结 束
31
19
3)用对数线性模型来分析这组数据。 A:护理地点 B:护理量 C:婴儿存活情况
20
4)用Logistic回归模型来分析这组数据。 A:护理地点 (自变量) B:护理量 (自变量) C:婴儿存活情况(因变量)
21
对数线性模型的缺点: 1)对数线性模型更强调的是变量之间的交互 效应,它不能直接将因变量用自变量的函 数表示出来。 2)对数线性模型抽象复杂,特别是高维模型,
对数线性模型分析
Log-linear Model Analysis
流行病与卫生统计学系
1
分类变量的主要统计分析方法
卡方分析
Logistic回归分析
对数线性模型分析
2
变量的模型分析比较
多元线性回归分析: Y 是数值型变量
X 是任意变量 Logistic回归分析: Y 是分类型变量 X 是任意变量 对数线性模型分析: Y 是分类型变量 X 是分类型变量
24
其中,变量HP 表示医院(hospital:1,2,3,4) ,变量 TRT 表示手术处理方法(treatment:A,B,C,D) , 变量SEV表示术后并发症的严重程度(severity:0= 没有,1=轻度,2=中度) ,变量WT表示频数。
25
【SAS程序】 data eg9_3; input hp trt $ sev wt @@ ; cards; 1 A 0 23 1 A 1 7 1 A 2 2 …… 4 D 0 13 4 D 1 6 4 D 2 4 run; proc catmod; weight wt; model hp*trt*sev=_response_/oneway; loglin hp|trt hp|sev trt|sev ; run;
17
【例9-2】为研究产前护理量多少对婴儿死亡率的影 响,收集了甲乙两个诊所的资料,数据列在下表中。 试用卡方检验,对数线性模型分析和logistic回归分析 来分析这组数据。
孕妇在两个诊所接受产前护理量与婴儿的存活情
18
解:1)先用卡方检验分别分析两个诊所中产前
护理量多少对婴儿死亡率的影响。
2)把这两个诊所的资料合并起来,消除护理 地点这个变量。
交互效应AB
M i j 为第 i 行第 j 列网格频数X i j 的理论值 或期望频数值(expected ferquency)
5
限制条件:
6
二维对数线性模型的分类: 1、一阶交互效应模型
2、完全独立模型
7
三维对数线性模型:
总均值
主效应A,B,C, 交互效应AB,AC,BC,ABC
M i j k为第 i 行第 j 列第k层网格频数X i jk 的理论值
27
② MAXIMUM-LIKELIHOOD ANALYSIS-OF-VARIANCE TABLE Source DF Chi-Square Prob -------------------------------------------------HP 3 16.63 0.0008 TRT 3 5.03 0.1694 HP*TRT 9 1.10 0.9992 SEV 2 93.62 0.0000 HP*SEV 6 4.90 0.5563 TRT*SEV 6 12.58 0.0502 LIKELIHOOD RATIO 18 13.43 0.7651 --------------------------------------------------
3
第一节 对数线性模型的基本概念
一、频数分布:
1、列联表 (contingency table)
2、 维数 (dimension)
3、行(row)、列(column)、层(layer)变量
4、网格频数 (cell frequency)
4
第二节 对数线性模型
二维对数线性模型:
总均值
主效应A 主效应B
不如线性回归模型易理解。
22
建议:
1)在变量类别较少,特别是二类的情况下,
建议还是用logistic回归分析。
2)在变量较多或变量水平较多的情况下,可
以先用对数线性模型分析主效应和交互效
应,对没有统计意义的变量或水平作适当
的维数或水平的压缩,将数据简化后再用
logistic回归分析拟和模型。
23
【例9-3】四家医院对同一病症采用四种不同手术, 手术后病人出现并发症,其严重性分成三级。数 据例在下表中。
26
【SAS 主要输出结果】 CATMOD PROCEDURE ① ONE-WAY FREQUENCIES Variable Value Frequency -------------------------HP 1 148 2 115 3 74 4 90 TRT A 96 B 107 C 113 D 111 SEV 0 240 1 129 2 58
的对数表示为各变量及其交互效应的线性模型,
然后运用类似方差分析的基本思想检验各变量
及其交互效应的作用大小。
10
模型的独立参数和自由度:
独立参数的个数 = 分类数 - 限制条件数
数据提供的信息量=列联表中网格的数目
模型的自由度= 信息量 - 独立参数个数
11
饱和模型和非饱和模型 饱和模型:独立参数的个数=列联表的网格数 非饱和模型:独立参数的个数< 列联表的网格数
14
第五节 对数线性模型在医学中的应用
比较三种分析方法的优缺点:
1、卡方检验:简单易学,不需要确定因变量 和自变量。但是,卡方检验对三维和三维以 上列联表资料的分析有一定困难,即对混杂 变量的控制较难。
15
2、Logistic回归分析:解决了对混杂变量的控 制的问题,而且,它能将因变量与自变量的 关系用模型表示出来,清晰易理解。 但是,当模型中自变量较多,特别是名义 变量较多,或名义变量的类别较多时,分析
或期望频数值。
8
三维对数线性模型的分类:
1、二阶交互效应模型 --- (9-8)
2、无二阶交互效应模型 --- (9-22)
3、条件独立模型 ---(9-23)
4、联合独立模型 ---(9-24)
5、完全独立模型 ---(9-25)
9
什么是对数线性模型分析?
对数线性模型分析是把列联表资料的网格频数
分层模型
如果一个高阶效应出现在模型中,那么组成这个 高阶效应的所有低阶效应也必须出现在模型中。
12
第三节 对数线性模型分析的方法步骤
一、参数的估计和假设检验
二、模型的拟和优度检验
三、模型参数的意义解释
13
第四节 对数线性模型的选择
原则:
1、应当包含尽可能少的参数;每个参数 要 有显著意义(p<0.05); 2、模型总体拟和度高(p>0.05)。
