计量经济学第九章异方差
计量经济学Stata软件应用4-【Stata软件之异方差】-1次课

e 2 0 1 X 1 2 X 2 3 X 3 4 X 1 2 5 X 2 2 6 X 3 2 7 X 1 X 2 8 X 1 X 3 a 9 X 2 X 3
H 0 :12 a 9 0
原假设实际上是对模型进行回归总体显著性检验 (F检验),
如果拒绝原假设,则存在异方差,如果不能拒绝原假设,
P>|t|
-.2244643 -.1118717 -.0010955
.0033752 -3.51e-07
.0009005 -.0001233
-.000147 .6133288
[95% Conf. Interval]
-.081382 .0003771 .0052239 .0085688 1.60e-06 .0076082 .0000182 .0000395 1.726195
则不存在异方差。
容易看出,用于怀特一般检验的模型会包含很多解释变量;
例如如果原模型有3个解释变量,那么怀特一般检验的模型
将包含9个解释变量,而如果原模型有6个解释变量,那么怀
特一般检验的模型将包含27个解释变量。这样对于样本容量
不大的数据,使用怀特一般检验会使得估计的时候自由度偏
少。
为此,怀特特殊检验使用了一个节省自由度的回归模型,即:
Stata软件操作实例
实验 1 工资方程中异方差的检验和修正
本例使用“工资方程1.dta”数据文件介绍异方差的检验和修 正。
1、打开数据文件。直接双击“工资方程1.dta”文件;或者点
击Stata窗口工具栏最左侧的Open键,然后选择“工资方程
1.dta”即可;
2、估计工资方程: l n w a g e 0 1 e d u 2 e x p 3 e x p s q + u ( 2 )
计量经济学
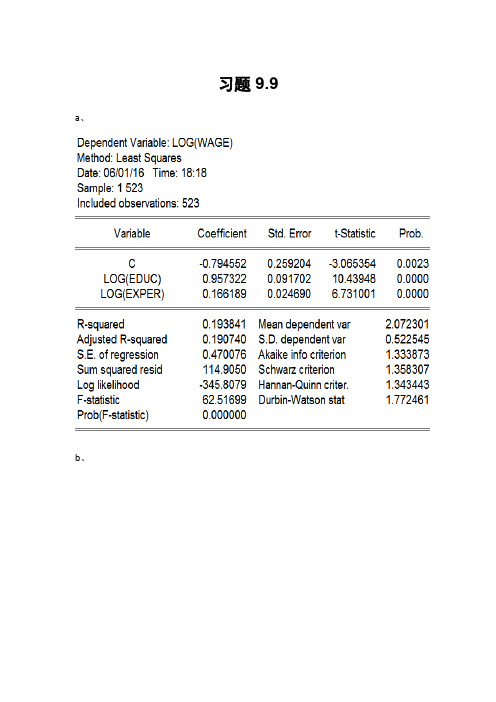
习题9.9 a、b、两者均可能存在异方差。
C、帕克检验三种帕克检验的p值都大于0.05,因此不拒绝原假设,即没有证据表明自变量系数为0;实质上帕克检验表明的是残差的平方并不体现出所假定的变化模式,残差的平方仍然可能存在其他形式的变化模型。
所以尚不能肯定一定不存在异方差。
格莱泽检验模型:ln(ei 2)=B1+B2ln(ln(educ))+vi格莱泽检验的第三种形式:残差的绝对值和1/educ显著相关,可能存在异方差问题。
怀特检验P=0.0004,拒绝原假设,即可能存在异方差问题。
帕克检验和格莱泽检验对异方差的形式要做出特殊的假定,要对不同的函数形式进行多次尝试,即便是自变量的系数不显著,也不態断定一定不存在异方差问题,因为可能是假定的函数形式不正确。
而怀特一般异方差检验采用了最为全面的函数形式,建议采用怀特一般异方差检验。
d、使用加权最小二乘法,选择权重是首要解决的问题。
权重选择得不恰当,异方差问题仍然会存在。
事实上,加权最小二乘法在使用过程中,需要经过多次尝试,多次检验,才可能找到一个合适的权重,因此在运用中这是比较不方便的。
本题样本容量为523,是个大样本,适合用怀特异方差校正。
其结果如下:e、选择不存在异方差的模型,即双对数模型。
因为异方差的存在会导致OLS估计量不再有效,其方差通常也会出现有偏性,在这种情况下,常用的假设检验都不再可靠,有可能出现错误的结论。
f、不能,因为两个模型的因变量形式不同。
习题9.28a、回归结果表明:小轿车的最高时速每提高1个百分点,耗油量平均下降1.27个百分点;马力每提高1个百分点,耗油量平均上升0.39个百分点;车重每提高1个百分点,耗油量平均下降1.90个百分点。
b、因为这是关于轿车耗油量的截面数据,因此预计存在异方差问题。
c、p值近似等于0,则拒绝原假设,即可能存在异方差问题。
d、校正后的值与OLS的结果比较发现:两者的估计系数的值是相同的,但是他们的方差和标准误差是不同的。
异方差性的概念、类型、后果、检验及其修正方法含案例

Yi和Xi分别为第i个家庭的储蓄额和可支配收入。
在该模型中,i的同方差假定往往不符合实际情况。对高收 入家庭来说,储蓄的差异较大;低收入家庭的储蓄则更有规律 性(如为某一特定目的而储蓄),差异较小。
因此,i的方差往往随Xi的增加而增加,呈单调递增型变化 。
– 在选项中,EViews提供了包含交叉项的怀特检验“White Heteroskedasticity(cross terms)”和没有交叉项的怀特检 验“White Heteroskedasticity(no cross terms)” 这样两个 选择。
• 软件输出结果:最上方显示两个检验统计量:F统计 量和White统计量nR2;下方则显示以OLS的残差平 方为被解释变量的辅助回归方程的回归结果。
随机误差项具有不同的方差,那么: 检验异方差性,也就是检验随机误差项的方差与解
释变量观测值之间的相关性及其相关的“形式”。 • 各种检验方法正是在这个共同思路下发展起来的。
路漫漫其修远兮, 吾将上下而求索
问题在于:用什么来表示随机误差项的方差? 一般的处理方法:
路漫漫其修远兮, 吾将上下而求索
2.图示检验法
路漫漫其修远兮, 吾将上下而求索
3.模型的预测失效
一方面,由于上述后果,使得模型不具有良好的统计性质;
【书上这句话有点问题】
其中 所以,当模型出现异方差性时,Y预测区间的建立将发生困 难,它的预测功能失效。
路漫漫其修远兮, 吾将上下而求索
三、异方差性的检验(教材P111)
1.检验方法的共同思路 • 既然异方差性就是相对于不同的解释变量观测值,
(注意:其中的2完全可以是1)
第九章 模型设定误差 《计量经济学》PPT课件

n
(ei ei1)2
d i2 n
ei2
i 1
(9.3.2)
3. 给定显著性水平,查DW表,若统计量显示为正
自相关,则拒绝原假设,首先考虑存在模型设定
误差。
• 例9.1 我们来看一个教学例子。表9.1给出了一个 总成本(Y)和产出(X)的数据,现在来建立总成 本函数模型
• 对于模型一,DW=2.7002,n=10,k′=3,给定显著
性水平5%,查表得临界值为dL=0.525和dU=2.016。 DW落在[4-dU,4-dL]=[1.984,3.475]区域,表明残 差中不存在显著的正相关。从而可以判断模型没
有遗漏的变量。
(三)拉姆齐的RESET检验
拉姆齐(Ramsey)于1969年提出了回归设定误 差检验(regression specification error test, RESET),它是一般性设定误差检验(test for general mis-specification)。
(一)残差图示法
进行OLS回归,得到残差序列ei,并做其与时间t 或某解释变量X的散点图,从图形上来考察残差序 列ei是否有规律地变动,以此来判断模型是否有遗 漏变量或函数形式设定的错误。
(二)DW检验
确定模型存在遗漏有关变量(非纯自相关)还是 模型真的存在自相关(纯自相关)。
假如真实模型为:
Yi 1 2 X 2i 3 X3i ui(9.2.1)
RESET检验的具体步骤:
1. 对所选模型
u)
(9.2.14)
从而,在满足经典假定条件下
计量经济学(数字教材版)教案第九章

1.根据数据频率和时间范围,创建Stata数据文件。2.录入数据,进行初步统计分析。根据要求绘制图形。3.分别计算MO/GDP、M1/GDP、M2/GDP,并绘制图形。
4.对GDP和GDP的组成部分数据,分别以1978年不变价格和2000年不变价格调整数据。对调整后的数据绘制时间序列图形。
课程名称:计量经济学
课程性质:专业基础课
授课内容:第九章计量经济学综合ห้องสมุดไป่ตู้验
授课对象:全校经管类二(三)年级本科生
教学内容
第九章计量经济学综合实验
教学说明
教学实践表明,为了更好地帮助学生提高和掌握运用计量模型的能力,培养学生的科研实践能力,实验教学也是非常重要和有效的一部分。特别是一些项目式和研讨式的实验非常有效,可以调动学生的学习热情并快速地在实践中提高科研水平。本章从已发表的前沿文献和优秀学生论文中,结合经济现实和热点,设立了若干项目式和研讨式的综合实验,帮助学生在学习计量经济学后将论文写作水平提高到更高的档次。
课后任务
1.搜集查找教材实验四、实验五的数据;
2.给出实验四、实验五的实验结果;
3.对实验结果进行解释并给出相应的经济学对策或建议。
(2)授课教师根据学生在操作中中出现的问题,在班级进行筛选讲解。
(3)请各个小组各派一个同学对模型的结果解释以及操作中的感想或者注意点进行讲解,教师打分。
总结提高
在学生实验操作结束,授课教师进行分组,根据学生的实验结果以及研究的问题意义及时设疑,设置思考题(P239-P241),加深学生对于计量经济学模型理论的理解。要想更深入地思考,要更好地估计模型,还需温习和加深课程的理论知识,让学生对课程充满期待,激发自主完成课题的探究欲望。
计量经济学讲义——线性回归模型的异方差问题1

Gleiser检验与Park检验存在同样的弱点。
(9.3) (9.4) (9.5)
9.4 异方差的诊断-方法4:怀特(White)检验法
Yi = B1 + B 2 X 2 i + B3 X 3 i + u i
2、做如下辅助回归: (9.6) (9.7)
1、首先用普通最小二乘法估计方程(9.6),获得残差ei
E(Y|X)=α+β*X Y
+u +u -u -u -u +u
0
同方差(homoscedasticity)
X 0
E(Y|X)=α+β*X
异方差(heteroscedasticity)
X
一元线性回归分析-回归的假定条件
假定5 无自相关假定,即两个误差项之间不相关。 Cov(ui,uj) = 0。
ui
9.2 异方差的性质
例9.1 美国创新研究:销售对研究与开发的影响 ^ R&D = 266.2575 + 0.030878*Sales se=(1002.963) (0.008347) t =(0.265471) (3.699508) p =(0.7940) R2 = 0.461032 从回归结果可以看出: (1)随着销售额的增加,R&D也逐渐增加,即销售 额每增加一百万美元,研发相应的增加3.1 万美元。 (2)随着销售额的增加,R&D支出围绕样本回归线 的波动也逐渐变大,表现出异方差性。 (0.0019)
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解-第9章 模型设定和数据问题的深入探讨【圣才出

(c)
来检验模型
y 0 1x1 2 x2 u
(d)
或者把这两个模型反过来。然而,它们是非嵌套模型,所以不能仅使用标准的 F 检验。
(1)综合模型的 F 检验
构造一个综合模型,将每个模型都作为一个特殊情形而包含其中,然后检验导致每个模
型的约束。在目前的例子中,综合模型为:
y 0 1x1 2 x2 3 log x1 4 log x2 u
y 0 1x1 2 x2 3 x3 u
但有 x3 的一个代理变量,并称之为 x3
x3 0 3 x3 v3
其中,v3 是因 x3 与 x3 并非完全相关所导致的误差。参数 3 度量了 x3 与 x3 之间的关系。 x3 和 x3 正相关,所以 δ3 0 。如果 δ3 0 ,则 x3 不是 x3 合适的代理变量。截距 δ0 ,是容许 x3
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 9 章 模型设定和数据问题的深入探讨
9.1 复习笔记
一、函数形式设误 1.函数形式设误的概念 遗漏一个关键变量能导致误差与某些解释变量之间的相关,从而通常导致所有的 OLS 估计量都是偏误和不一致的。在遗漏的变量是模型中一个解释变量的函数的特殊情形下,模 型就存在函数形式误设的问题。遗漏自变量的函数并不是模型出现函数形式误设的唯一方 式。
②用戴维森—麦金农检验拒绝了式(d),这并不意味着式(c)就是正确的模型。模型 (d)可能会因多种误设的函数形式而被拒绝。
③在比较因变量不同那么就不能得到上面的综合嵌套模型。
二、对无法观测解释变量使用代理变量 1.代理变量 代理变量就是某种与我们在分析中试图控制而又无法观测的变量相关的东西。例如,人 的能力无法观测,可以使用 IQ 得分作为能力的一个代理变量。 (1)遗漏变量问题的植入解 假设在有 3 个自变量的模型中,其中有两个自变量是可以观测的,解释变量 x3 观测不 到:
计量经济学--异方差性讲解

图1:我国税收和GDP
图2:1998年我国制造工业和利润
X-GDP Y-税收
X-销售收入 Y-销售利润
两个散点图有共同的特征,随着自变量增加,因变量也 增加,但是图2中,当X比较小时,数据点相对集中,随 着X增大,数据点变得相对分散。而图1中数据分布却没 有出现这一特征。
异方差的性质
➢经典线形回归模型的一个重要假定是同方差性:
PRF的干扰项 u i 是同方差的(homoscedastic)
即: E(ui2) 2
i 1, 2, , n (3.3.1)
➢异方差性是指,ui 的条件方差(= Yi 的条件方差)
随着X的变化而变化,用符号表示为:
E (ui2
)
2 i
(3.3.2)
Var(Yi ) Var(ui )
异方差产生的主要原因
——这就是GLS方法,得到的是GLS估计量
•模型函数形式存在设定误差 •模型中遗漏了一些重要的解释变量 •随机因素本身的影响
异方差较之 同方差更为
常见
7
异方差的具体理由
➢按照边错边改学习模型(error—learning models),人 们的行为误差随时间而减少。
➢随着收入的增长,人们在支出和储蓄中有更大的灵活
性。在做储蓄对收入的回归中, i2与收入俱增
此时如果仍采用
计算斜率参数的方差,将会
产生估计偏误,偏误的大小取决与因子值的大小。
17
3.t检验的可靠性降低
由于异方差的存在,无法正确估计参数的方差和标 志误差,因此也影响到t检验的效果
4.模型的预测误差增大
模型的预测区间和随机误差项的方差有着紧密联 系,随着随机误差项方差的增大,模型的预测区 间也随之增大,模型的预测误差也会相应增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、异方差的补救措施
(一)加权最小二乘法 1.当 2i已知时: 考虑双变量PRF,
Y i B 1 B 2 X i ui (7)
var(ui ) i2
其中,Y为被解释变量,X为解释变量。假设误差方差 对模型(7)考虑如下变换:
i
Yi B 1(
是已知的。
i
1
) B2 (
ln ei2 B1 B2 ln X i vi
2
(3)
(4)检验零假设 B 0 ,即不存在异方差。如果 ln X i 和 ln ei2 之 间是统计显著的,则拒绝零假设:不存在异方差。
例子:利用方程(2)来说明帕克检验。把从该回归方程中得到的残差 用于模型(3),得到如下结果:
ln ei2 3.412 0.938 ln salesi se (4.972)
三、异方差的诊断
与多重共线性的情况一样,并没有诊断异方差的确定办法,只能借助一 些诊断工具判断异方差的存在。主要有:
1.根据问题的性质 2.残差的图形检验
(1)残差图可以是关于观察值与残差的散点图,也可以是残 ˆ 的散点图。这些图可以帮 差与解释变量,残差与估计值 Y i 助我们判断同方差假设或者是CLRM其他假设是否满足。 例子可参见美国行业利润,销售量和R&D支出。 由该例中关于观察值与残差的散点图可以得出结论,该模 型存在异方差。 2 e (2)此外,还可以利用残差的平方 i 与观察值或解释变量或 ei2 估计值的散点图来判断是否存在异方差。一般来说, 与变量 X 之间的散点图主要有如下样式。(见下一页) 图a到图c中,图a中残差平方与X之间没有可识别的系统模 式,所以不存在异方差;而图b到图e中两者都呈现出系统 关系,所以都可能存在异方差。
假定要了解研究与发展与销售的关系,有如下模型:
R & Di B1 B2 Salesi ui (1)
该模型的最小二乘回归结果如下:
R & Di 266.19 0.0309 Salesi se (1002.96) (0.008)
t (0.27) (3.70) R 0.46
t (0.686) (0.452) (2.075) R
2
0.2119
(4)
在5%的显著水平下(单边检验),估计的斜率系数是统 计不显著的。所以接受原假设:原始模型中不存在异方差。 但可惜的是,帕克检验本身也存在比较严重的问题,那就 是在回归方程(3)中,误差项本身也可能存在异方差。所 以除了进行帕克检验外,还应该用其他检验方法进行判断。 4.格莱泽检验(Glej下残差图(如下)。
从图中可以看到,残差的绝对值随销售额的增加而增加。因为残差可以 近似地看作随机误差项,所以可以得出结论,该模型存在异方差。 由于观察值是按照销售额升序排列的,这就等同于间接地将残差对销售额 作图
1988年美国研究与发展支出费用(百万美元)
二、异方差的后果
如果CLRM其他假设保持不变,放松同方差假定,异方差则有 如下后果:
1.OLS估计量仍是线性无偏估计量。 2.异方差情况下,OLS估计量不再有效。 ˆ 2 即 ei2 / d. f . , 3.OLS估计量的方差通常是有偏的。偏差的产生是由于 2 不再是真实 的无偏估计量。 4.建立在t分布和F分布之上的置信区间和假设检验不再可靠。如果沿用 传统的假设检验方法,则很可能得出错误的结论。
(6)
(3)求辅助回归方程(6)的 R 2 值。在不存在异方差(即式(6) 中所有斜率系数都为零)的零假设下,怀特证明了从方程 2 (6)中得到的 R 2 值与样本容量的积服从 分布,自由度等 于方程(6)中解释变量的个数(不包括截距项)。 2 n R2 k 1 (4)如果从方程(5)中得到的 值超过了所选显著水平下的 2 临界值,或者说计算 值的p值很低,则拒绝零假设。否 则,不能拒绝零假设。
第九章 异方差
上海立信会计学院
主要内容: 1.异方差的性质 2.异方差的后果 3.异方差的诊断 4.异方差的补救措施
总体回归函数中随着解释变量的变化,随机误差项的方差不变,这
称为同方差性。而如果随着解释变量的变化,随机误差项的取值不同, 则称为异方差性。
一、异方差
异方差可以表示为:
Var (ui ) i2 常数
假设的 ei2 模式
3.帕克检验 假如存在异方差,而且方差可能与一个或者多个解释变量 系统相关,那么可以用帕克检验对是否存在异方差做出判 断,帕克检验的步骤如下: (1)在不考虑异方差的情况下,做原模型的最小二乘回归。 (2)从原始回归方程中求得残差 ei ,并求其平方,再取对数 形式。 (3)利用原始模型中的一个解释变量作如下形式的回归,如 果有多个解释变量,则对每一个解释变量作形如下式的回 ˆ 的回归。 归,或者做 ei2 对Y的估计值 Y i
格莱泽检验实质上与帕克检验类似。从原始模型获得残差后,格莱泽 建议做 ei 的绝对值 ei 对X的回归。其具体回归函数如下:
ei B1 B2
X i vi
ei B 1 B 2 Xi v i
ei B1 B2 (
1 ) vi Xi
每种情形下的零假设都为:H0:B2=0。如果拒绝零假设, 则表明可能存在异方差。 例子:如研发支出 但应注意的是,格莱泽检验同帕克检验存在同样的缺陷。 5.怀特一般异方差检验
例如:在一个双变量线性回归模型中,应变量Y是个人储蓄,解释变量 X是个人可支配收入或税后收入(PDI)。画出Y的方差如下图:
图a 同方差
图b 异方差
注意:研究发现,异方差问题多存在于截面数据(cross-
sectional data)而非时间序列数据。 例子:美国行业利润,销售量和R&D支出
下表给出了美国18个行业1988年的销售、利润和研究与发展(R&D)支出的 数据。(见本章ppt第6页)
假定有如下模型:
Yi B1 B2 X 2i B3 X 3i ui (5)
怀特检验步骤如下: (1)首先用普通最小二乘法估计回归模型(5),获得残差。 (2)然后做如下辅助回归,
2 2 e2 A A X A X A X A X 1 2 2i 3 3i 4 2i 5 3i A 6 X 2i X 3i vi
Yi u 1 B1 ( ) B2 ( i ) Xi Xi Xi B1 ( 1 ) B2 vi Xi
很容易证明,以上变换后的方程的随机误差项是同方差的,因 此,可以用OLS法估计以上方程。
误差方差与 X 成比例的图示
2
(二)重新设定模型 有时候,我们也可以通过重新选择一个新的函数形式来 消除异方差。比较常用的是改变原来的变量线性模型(LIV), 而改为对数线性模型形式。比如原来的方程形式是如方程(7) 的变量线性形式,那么可以变换成如下的对数线性形式,
i
Xi
)
i
ui
(8)
令
vi
i
ui
可以证明,新的随机误差项 vi是同方差的。因此,变换后的模型(8) 不存在异方差问题,因而可以用常规OLS方法估计。
注意:此方法称为加权最小二乘法(WLS)
2.当 i2 未知时 实践中很难获得真实误差方差的信息。因此,要使用WLS法, i2 必须对 进行特殊、合理的假设,通过对原始模型变换,使 得变化后的模型满足同方差假定,然后运用OLS法。 以双变量模型为例,对这个未知的误差方差作如下假设, 然后运用WLS法。 (1)误差方差与 X i 成比例
用OLS方法估计模型后,把回归的残差对解释变量X作图,如果观察到图 形与下图相似,则表明误差方差与解释变量X线性相关,即 Var (ui ) E(ui2 ) 2 X i 那么,对方程(7)做如下变换
Yi Xi B1 B1 1 B2 Xi 1 B2 Xi Xi Xi ui Xi (9)
ln Yi B1 B2 ln X i ui 这种变换可以在一定程度上消除异方差。因为对数变换压缩 了变量的度量程度,把两个变量值间的10倍差异缩小为2倍 差异。
X i vi
误差方差与X成比例的图示
很容易证明变形后回归方程的随机误差项是同方差的,因此, 可以应用OLS法估计式(9)。 (2)误差方差与 X 成比例 如果估计的残差呈现类似下图的模型,则表明误差方差与X 之间呈现如下关系: E (ui2 ) 2 X i2
2 i
在这种情况下,把方程两边同除以 X i ,变换如下:
