列联表的对数线性模型
第7章对数线性模型-原理及软件实现

loglin(table7.3,list("A","B"),fit=TRUE,param=TRUE)
#等价于上条命令
loglin(table7.3,list(1,2,c(1,2)),fit=TRUE,param=TRUE) #拟合包含主效应及交互效应的对数 线性模型
loglin(table7.3,list("A","B",c("A","B")),fit=TRUE,param=TRUE) #等价于上条命令
chisq.test:卡方检验
Loglin:拟合对数线性模型
?loglin(table, margin, start = rep(1, length(table)), fit = FALSE, eps = 0.1, iter = 20, param = FALSE, print = TRUE)
Hale Waihona Puke 交互效应。二维列联表的对数线性模型
【例】对给出的二维列联表(表7.3),构建对数线性模型。
SPSS:Loglinear->General:主效应、输出估计
• 注:SPSS的约束条件设置为最后一类参数为0,所以此处结果不同于 P195的结果
R:Xtabs、loglin
初始数据为三列变量csv格式,采用read.csv读入数据,数据形式为
table7.3=xtabs(N~A+B) #构造二维表,N作为单元格数目
summary(table7.3)
#对A,B进行卡方独立性检验
#拟合仅含有A和B的主效应的对数线性
对数线性模型剖析

极大似然法与最小二乘法的区别于联系
最小二乘法所要解决的问题是:为了选出似的模型输出 与系统输出尽可能接近的参数估计,用误差平方和即离 差平方和的大小来表示接近程度。使离差平方和最小的 参数值即为估计值。简单来说,已知点,自己拟合模型 也即分布函数(概率密度函数的积分),进行预测。
极大似然估计所要解决的问题是:选择参数Ɵ,使已知 数据在某种意义下最可能出现。某种意义指的是似然函 数最大,此处似然函数就是概率密度函数。也就是经常 提到的“模型已知,参数未定”。
对数线性模型的统计检验
举例说明:
由图可知,自由度变为1,L2由0增大到10.284,显著性水平α为0.01(P)(拒绝原假设), 说明简略模型和饱和模型存在十分显著的差异,即拟合程度受到很大影响。 显著=不能剔除该交互因素 在因素很多的复杂饱和模型中,通过此方法删减多个不显著效应项来形成简略模型。
上两式的数学变换使各种效应项相乘的关系被转换成相 加的关系,使各项效应独立化了。
常数效应;
A因素效应;
B因素效应;(主效应)
A、B两因素的交互效应;
主效应和多元交互列表涉及因素数量相等;
交互效应的总数则为所有因素各阶组合数之和。
对数线性模型有一个限制条件:
模型中每一项效应的各类参数之和等于0; 如果每项效应中只有一类的参数未知,那么可以由已知参数推 算出来。
ɯ1=π12/π11
ɯ2=π22/π21
同理我们可以测量两个两个类别间的比值,称作比数比。
Ɵ= ɯ1/ ɯ2=π22π21/π12π21=F11 F22/ F12 F21 一个大于1 的比数比意味着行变量和列变量的第二个(或者第一个) 存在正相关;等于1无关;小于1负相关。
第5章列联表分析与对数线性模型
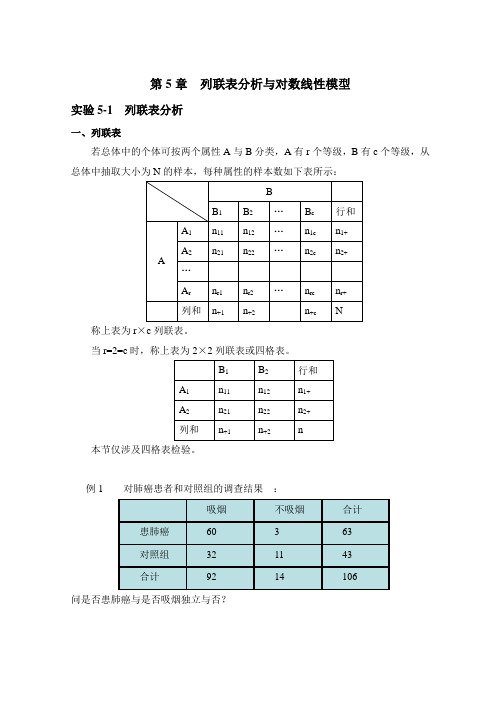
第5章列联表分析与对数线性模型实验5-1 列联表分析一、列联表若总体中的个体可按两个属性A与B分类,A有r个等级,B有c个等级,从总体中抽取大小为N的样本,每种属性的样本数如下表所示:称上表为r×c列联表。
当r=2=c时,称上表为2×2列联表或四格表。
本节仅涉及四格表检验。
例1 对肺癌患者和对照组的调查结果:问是否患肺癌与是否吸烟独立与否?例2 1976年至1977年美国佛罗里达州29个区的凶杀案件中凶手的肤色和是否被判死刑的326个犯人的情况如下,问是否存在种族歧视与审判不公?二、实验内容数据来源:wushujiance.sav某防疫站观察当地一个污水排放口在高温和低温季节中伤寒病菌检出情况。
其中高温和低温季节各观测12次,数据有24个观测样本,有两个属性变量degree 和test,degree有1(高温季节)和2(低温季节)两个等级;test有1(+)和2(-)两个等级。
问:两个季节的伤寒菌检出率有无差别?数据如下图所示:意为:Degree1(高温) 2(低温) 合计 test1(检出)17 8 2(没有检出) 115 16合计121224设A :高温季节;A :低温季节;B :检出;B :没有检出。
记)|(1A B P p =,2p =)|(A B P 此处欲检验0H :21p p =1H ↔:21p p ≠检验统计量:Pearson 卡方统计量=21212211222112)(++++-=n n n n n n n n n χ~)(12χ (渐进)称此检验为卡方检验。
此外,可以证明:卡方检验等价于独立性检验(A 属性与B 属性独立),即:0H :21p p =1H ↔:21p p ≠等价于0H :j i ij p p p ⋅⋅=1H ↔:j i ij p p p ••≠,.2,1,=j i其中nn p ij ij =,nn p i i +•=,n n p j j +•=,.2,1,=j i实验过程:(1)打开数据文件;(2)分析->描述统计->交叉表;相依系数:其数值在0~1之间,但不能达到1,是行变量和列变量相关性的度量指标。
08列联表卡方检验和对数线性模型

R
交互作用 高维表
例1.2 (性别,观点和收入)
6
8.4 Poisson对数线性模型
Poisson 对数线性模型
每个格子出现的频数服从Poisson分布 例8.1(acc2.sav/txt) 模型 广义线性模型(Generalized Linear Model)
自变量:Y 解释变量:X 联系函数(Link Function)
u=E(Y) g(u)
7
一些例子
线性回归:g(u)=u Logistic 回归:g(u)=log[u/(1-u)] Poisson 对数线性模型:g(u)=log(u)
软件实现
SPSS
Data Weight Cases Do not weight cases Analyze Generalized Linear Models
30度
8.2 二维列联表的检验
观点和收入) 例1.2 (观点和收入) 零假设
这两个变量不相关,ห้องสมุดไป่ตู้立
检验统计量
Pearson 卡方检验 似然比卡方检验 Fisher 精确检验:超几何分布
3
软件实现
SPSS
Analyze Descriptive Statistics Crosstabs
Opinion Row(s) Income Column(s) Exact Exact Statistics Chi-square
R
8
讨论
Poisson 分布 模型诊断
拟和优度(Goodness-of-fit) 残差分析(Residual analysis)
模型选择
层次模型(Hierarchical model)
饱和模型(Saturated model ) 简约模型(Parsimonious models )
对数线性模型

由比数计算而来。那么什么叫做比数呢?比数 是一个事件发生的概率与其不发生概率之比,测 量了一个事件发生的可能性。这个数值越高说 明结果2相对于结果1发生的可能性就越高。
• F, ji)j代有表关某的模期型望fij的概期率望值,令πij 代表与单元格(i • 上表可转化为
互效应就很繁杂,可 以解决logistic回归分
能需要建立很多哑变 析中多个自变量的交
量
互效应问题
2、列联表的四种类型
• 双向无序列联表; • 单向有序列联表; • 双向有序且属性不同的列联表; • 双向有序且属性相同的列联表
3、列联表的优势
• 约束条件少 • 清晰 • 可以快速准确进行判断
4、列联表的劣势:对于多关系变量(两个 以上)研究:不能被清晰解读
对数多元线社会性统计分回析 归
一、对数线性模型简介
• 1、对数线性模型基本思想
• 对数线性模型分析是把列联表资料的网格频数
的对数表示为各变量及其交互效应的线性模型 ,然后运用类似方差分析的基本思想,以及逻 辑变换来检验各变量及其交互效应的作用大小
区别
方法
作用
优缺点
列联表
逻辑回归
对数线性模型
分析定类变量和定类 分析尺度变量(也可 综合运用方差分析和
联。
• 饱和性:将多元频数分布分解成具体的各项主效应和各项交互效应
,以及高阶效应,不会漏项。(饱和模型与不饱和模型)
• 定量性:以发生比的形式来表示自变量的类型不同反映在因变量频
数分布上的差异。
• 可检验性:不仅可以对所有参数估计进行检验,使抽样数据可以推
对数线性模型

B
25
2、统计量
似然卡方比,根据相关计算,看原假设是否成立。 贝叶斯信息标准,不同模型而言越小的BIC越好。
B
26
3、对数线性模型的统计 检验
四种主要检验: 1、对于假设模型的整体检验; 2、分层效应的检验; 3、单项效应的检验; 4、单个参数估计的检验。
B
27
对数线性模型的统计检验
1、对于假设模型的整体检验 采用似然比卡方检验(likelihood-ratio chi-square test,标
B
17
通过上组式子,我们可以计算出线性模型等式右侧的所有参数值。 A因素效应是行平均值与总平均值之差 B因素效应是列平均值与总平均值之差 交互效应计算结果表示在除去所有其他分布效应之后两个因素之间
的净关联。
B
18
常数项只受样本规模和交互单元数的影响;
主效应项反映的是各因素内部类别频数分布的特征,是 在总平均频数基础上的“补差”;
B
31
对数线性模型的统计检验
举例说明:
由图可知,自由度变为1,L2由0增大到10.284,显著性水平α为0.01(P)(拒绝原假设), 说明简略模型和饱和模型存在十分显著的差异,即拟合程度受到很大影响。
显著=不能剔除该交互因素 在因素很多的复杂饱和模型中,通过此方法删减多个不显著效应项来形成简略模型。
极大似然估计所要解决的问题是:选择参数Ɵ,使已知 数据在某种意义下最可能出现。某种意义指的是似然函 数最大,此处似然函数就是概率密度函数。也就是经常 提到的“模型已知,参数未定”。
B
22
二者的区别就是,后者需要知道概率密度函数。最小二 乘法要的是求出最优的那个参数,而极大似然要求出概 率最大(最可能出现的)参数。举个例子,生活中我们 一个着眼最合理是哪一个,一个着眼于最可能的是哪一 个(极大似然法)当总体服从正态分布时,二者是一样 的。
对数线性模型

对数线性模型的统计检验
案例
二阶以上 (简略模型)
一阶以上
一阶 二阶
对数线性模型的统计检验
分层检验提供了模型L2的分解。
第一种分层检验中,一阶及以上所有效应都从模型中删 除,就会使简略模型的L2增加到13.142,而第二种分层 检验告诉我们,这个L2的增量是一阶效应L2 2.858与二 阶效应L2 10.284之和。
2、比数比
比数比是对数线性模型的基础,而比数比又是由比数计 算而来。那么什么叫做比数呢?比数是一个事件发生的 概率与其不发生概率之比,测量了一个事件发生的可能 性。这个数值越高说明结果2相对于结果1发生的可能性 就越高。
Fij代表某模型fij的期望值,令πij 代表与单元格(i , j)有 关的期望概率 上表可转化为
对数线性模型的统计检验
公式:
其中
为估计交互频数。
原假设:检验模型的频数估计与观测频数无差异,也可 以理解为检验模型和饱和模型无差异。(无关假设)
对数线性模型的统计检验
饱和对数线性模型可以完美无缺的再现观测频数,因此 不需要对饱和模型进行整体性检验。
DF等于0,意味着所检验的模型与饱和模型之间的效应 项目没有差别。
6、对数线性模型的缺点
对数线性模型更强调的是变量之间的交互效应,它不能 直接将因变量用自变量的函数表示出来。
对数线性模型抽象复杂,特别是高维模型,不如线性回 归模型易理解
二、对数线性模型的基本原理
1、与方差分析相关的
在多元方差分析中,以二元方差为例:每一个观测值 yij=µ +Ai的效果+Bj的效果+(AB)ij交互作用+Ɛij
通过上组式子,我们可以计算出线性模型等式右侧的所有参数值。 A因素效应是行平均值与总平均值之差 B因素效应是列平均值与总平均值之差 交互效应计算结果表示在除去所有其他分布效应之后两个因素之间 的净关联。
列联表

注 • 二维列联表的Pearson c2检验是关于 两个分类变量是否相关的检验。但是 对于两个连续变量之间的检验则需要 另外和Pearson相关系数有关的检验。 • 这里的检验是关于二维列联表的。对 于高维列联表,需要使用下面要介绍 的对数线性模型来研究。
注
注
• 实际上,各种软件不仅仅输出输出Pearson c2检 验统计量的值和相关的p值,也输出似然比检验 (likelihood ratio test或lrt)统计量的值和相关的p 值。这两个检验是渐近等价的。它们近似地有 相同自由度的c2分布。 列联表除了 Pearson和似然比检验(有近似的 c2 分布)之外,还有一种精确检验,称为Fisher检 验(如果列联表距阵为y可以在R中用 fisher.test(y) 施行)。但由于 Fisher 检验使用超 几何分布,计算量很大,在总频数大的时候, 或者计算机内存不够时,则无法计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
列联表的对数线性模型理堑/壁窭对数线性模型■孙凤一,问题的提出我们在进行属性数据处理时,常常运用列联表反映变量之间的联合分布.当列联表中包含个变时,被称作二维列联表;列联表中包含二个变量时,则被称作二维列联表.__维或高维列联表亦可称作多维列联表.无论是简单的列联表还足复杂的列联表,其中所自'频数之间分布的关联都町以分解为两种效应:一种反映了变量自身的频数分布影响,称之为卞效应;另一种反映变量之间关联所产牛的效应,称之为交互效应.对于两个属性变节构成的频数列联表是一张二维列联表,其主效应有两个,交效应只有一个.当变最数增加时,交互的维数就会增加,相当于多张=维列联表;同样当变鼍中的分类数增加时,每一张■维列联表也会变大.但是不论变_早=数怎样增加或变最中的分类数怎样增加,仍然町以将整个频数分布分解为主效臆和交互效应,只不过两类效麻各自的项数有所增加而已,尤其是交钉效应的项数会增加得更快.常规频数表统计方法通常只分析I埘个变量之间的联系,如受教育程度与生活满意度的列联表,我们以直接从列联表的分布中读取主效应和交互效应.然而,进行多个变世的属性分析时,常规统汁力法就尢法把握变量之间的关系了在实际研究中,研究者通常采用一次H分析两个变量之问的交且表,经过多个两交互分析,氽图}=I}拼接成多个分类变量之I1_lJ复杂关系的帑体.尽管这种做法d土能得到?些信息,然而止如多个简单同IJ]并能代替多元回归一样,这种缺乏综合性的分析方式足不可能以多个个另IJ分析叠加出整怵的多尤联系的.特别足由于整个频数分布被分成多张二维交互表,只能大致分析每一张二维交互表的主效幢祠】交且效应,更多变量之i'nI的联合交互效应(或岛阶交q作)将无法分析,然而,正是联合交1f.效嘘才真正反映变世之川的关联.IJ(】g—linear模犁是一种有效处理列联丧信息I的统汁t万法,令文运用耍例埘该方法的由此uJ推算:譬,和俭怯及常用F1J=点(2)的模型形式作一讨论.IH二,L.gliar模型式(2)意味着任何单元格中的预期l诎立性检验频数是由之相关的边际次数决定的.首先以一个例子来理解议.logli一倘若HO为真,则表中的条件次数应是模型的基本要素.表1是英国19721预期次数(1),但表中的实际次数却是f.年的职业流动表,其中行变黄为父亲的这里我们把全部的"f-F"相加起来,取平职业,列变量为儿子的职业.通过职业流方和,以避免正负值相互抵f肖的问题.×动表我们町以J,解一个社会职业上下流越大,原似设正确的可能性越小,也即在动的渠道是甭通畅,这也是考察礼会运I总体中RC越uf能是相关的,反之1行机制足否正常的重要指标..I则反是.我们以R表示行变量(父亲的职2.1oglinear模型的参数估计业),C表示列变量(儿子的职).R的以组频数作为因变错,行和列的分下标为i,j:1,2…I;C的下标为j'j_l,2J类作虚拟自变龟所建立的回归模型即为…J.通常R代表解释变请,C代表结果jxII数线性回归模型,亦称泊松回力'程:1变量.c.代表第i行第J列的观察频数FlIlog(Fii)13o+13Rt+13R+.''+B4c4代表预期频数.所谓预期次数足指存总埘数线性模型有一套专用符号系j体If1两个变情没有关系的前提下,表l统,上式可以表示为:中每单元格所应有的次数10g(F?)=h+h,"++(3)独性检验统汁量为X2,对于二变其中Fii代表预期频数,i=1,2,……,节总体来随,原假没是R-L.iC不相关;;j=1,2,……J.是总均值,是行边缘备择假设足R与C相关,公式如下:l(r0wmargina1)效应,是列边缘(∞l一一,,umnmargina1)效应,"是行列交互作x''(1)用,交可作用反映的是行与列之间的相自由度df_(I-1I)fJ一11关.其巾f是实际7欠数,F是预期次数.{如何反映行边缘效应和列边缘效应{倘若R与c确实是不相关的,则由.个l及其交互作用呢?首先需要对变量进行i 随机样本中所得的条件次数,理应显示『虚拟化处理n对于对数线性模型,常常采Rc足不相关的;也就是说F和F.用0总合限制,办称为方差编码,如B1十所占的比例膻该相同,而I.12l和F所占p2=O,则p1-B2.如:的比例也卡H同n邮:∑.hill-∑,.∑,∑.lIl:oF::—;f+.n{"有(卜1)个参数;有卜1个参:岛:!数;,有(I一1)x(J-1)个参数f+-nf.z这样我ffJ就可以运用(3)I毫一——j:兰些堕查……——式仙汁"变,列变量交_———十]—_『T—_一F]作用对分组频数的影响.———_r-]—_『—厂—]…i]丽fI:州_,j_姒H.lJ.IJ々!i238Il59『59I36f13l505从表2可以发现,I一0g一2r『J铷f34If456J313I】9622f1328linear模与线性回归模:}领"引.j").61}60j有很大的不川,突出表现为fjif术i261i499l【们l33i26875649g2234776"iI'-I冈变IIHI运:农I1I1l;Ii6uI"}'】甜~止互二叵『]亘工j_互工:工:堕曼r果变量,这意味着结果变贳和数据来坪于李沛~(20o01J《社会研究的统计应用》,社会科学文献解释变同时出现在loglin—df版社,I)32522缱纠楗镶表2英国1972年职业流动方差编码分组频率父职业子职业I{lR2R3R4ClC2C3C4jll1lJIJUl【JUlJ34l2l0l0(JlOl1O3373l00l0lO002614l0(】OllO00645l—1一l—l—JlO0015912l0O00l0045622Ol00Ol005lO320Ol0Ol0fJ49942OO0l0l009852—l—l一l—l0l005913l000O0l03l3230l0000l0l06l3300l0()Ol0959430O0l(】0l02l153一l—l一l—l0【】lO36l4l000O00ll96240l00O00l6023400lO000l93544OO0I00Ol23454一1—I一l—l000ll315ll0nll—1—l22250OO0—l—l—1一1433500lf】—l—l一ll3345000l—l—l—l—ll6955一l一l一l—l—l—l一1—l ear模型中,这就使得研究者能够从模型参数推断出■者之问的关系;Loglinear 模型经常包含许多参数,研究者可将其分为有意义和无意义的参数,在实际应用中,大量有意义的参数都是变量有交互作用的参数.如何解释参数的影响作用呢?我们需要借助发生比率来反映.发生比率是指交]彳去同两行}l'不㈣列的比率之比如层白领之子和_尢技术监领之子成为上层[j领或无技术蓝领之发生比率是:0-暑=2?.6836/935fI/…如果单就交互表言,横向或纵向可分比受制r行列合汁之分布,不其町比性.如表1单看代上层白领的流入率,会发现其很多来自蓝领背景;但从行合计可看到,这是由于父代蓝领远多f白领之故.以上的发生比是运用观察值计算出来的,而理沦或模型的发,卜比则需耍用交互作用参数箅出,例如0={l_:一:cpfl】:+44"一『4:一r)(4)程(4)是饱和模型,即观察频数与期望频数完全一样,观察和理论的发尘比相等.们对非饱干『I模噩!』言,沦的发生比有着更蕈耍的作用.可以说,对数线性分析的主要用途在于检验和清除经验发牛比中的杂音.除饱和模型外,还有许多非饱和模型.这里介绍常见的几种:(1)独模型由假定交互作用为0得到:Log(Fi.)=+.+(5)即当衍变量列变量独立时,类别频数只取决于行合汁与列_△计的分布(■者的乘积).(2)准独立模型(quasi—independence) Log(1',i.J=+."+."+8(6)其中{j是埘角线各类的参数.我们观察表2的英田职业流动数据,可以发现对角线的单元格的数值是比较大的,这数值反映了"继承"的特点,人们希将这种特征分离出束,进一步讨论其中所包含的信息,因此假定除了丰对角线以外的行变量和硎变摄是独立的,我们称其为准独立模3.参数估计与拟台优废枪验l,oglinear模型的参数估汁足非线性模,这类模犁进行参数估汁的最好力法足檄大似然估计运用极大似然估汁法的核心是需要lr解样奉的分布特征我们这里时论的列联表建模,主要集中在二:J_!j!分布,泊松分布和多项式分布23统计%决策,;理论{…一2006年第12期(总第227期)埘数线性模型的统汁检验包括两种主要检验:(1)埘于假设模的整休检验;(2)单个参数估计的检验.对于假设模型的整体拟合优度检验包括对数似然比f÷力'和皮尔逊卡方检验.对数似然比卡方检验崽想是指对数线性模型常以饱和模型的对数似然比为基准,计算埘数似然比,衡量非饱和模型的拟合优度(或劣度).加入用Is表示饱和模础的似然,IIr表示非饱和模型的似然,那么对数似然比卡方就足:lJ(F=-21.g():2(∑∑Fiilog(F=-21Fii(1i7(p)og()=2(l((p)L.i;Ij=IU 当交叉表的数据不稀疏(审格少HT-均组频最好不小于7),这个统汁量符合卡方分布.自由度是交叉表的分组数减参数数目.如此定义的对数似然比,反映模型与数据的差距,当然越小越好.单个参数估汁的检验,有单项效应检验和单个参数估汁的检验.项敏应检验反映的足如果从模型中撤销…个效应以后时似然比的影响,称为偏关联检验(to.slsofPARTIAIassocia—tions)埘r单个参数估计的榆验我们用标准正态分布检验z.(作者单位/清华大学社会学系)(责任编辑/李友平)。
