中考数学解答题常见类型(2020年整理).pptx
中考数学材料阅读题专题练习(2020年整理).pptx

阅读理解(二)(24题)
例 1、进位制是一种记数方式,可以用有限的数字符号代表所有的数值,使用数字符号的数 目称为基数,基数为 n,即可称 n 进制.现在最常用的是十进制,通常使用 10 个阿拉伯数
字 0~9 进行记数,特点是逢十进一.对于任意一个用n n 10 进制表示的数,通常使用n 个
a b 2 m2 2n2 2mn 2 .
∴ a m2 2n2 , b 2mn .这样小明就找到了一种把类似a b 2 的式子化为平方式的
方法. 请你仿照小明的方法探索并解决下列问题:
若有 5 个连续整数:102+112+316252+132+142=2;
若有 7 个连续整数:212+222+232+2204320+252+262+272 =2; … 由此获得启发,若存在 n(7<n<11)个连续正整数也满足上述规律,求这n 个数.
例5、观察下列等式: 12×231=132×21 , 14×451=154×41, 32×253=352×23, 34×473=374×43 ,45×594=495×54,…… 以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字 之 间具有相同规律,我们称这类等式为“数字对称等式”.
例 3、如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数大
1,那么我们把这样的自然数叫做“妙数”.例如:321, 6543 , 98数的153 倍,则这个“妙数”为;
2
证明:任意一个四位“妙数”减去任意一个两位“妙数”之差再加上1得到的结果
1 根据上述各式反映的规律填空,使式子成为“数字对称等式”:
中考专题训练 阿氏圆(2020年整理).pptx
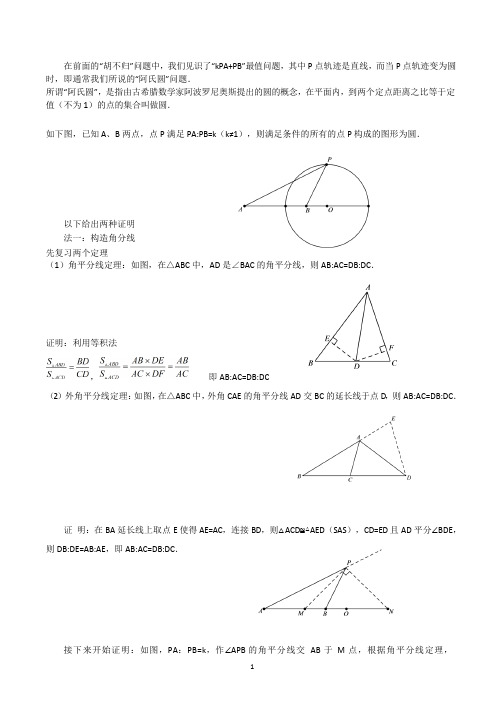
证 明:在 BA 延长线上取点 E 使得 AE=AC,连接 BD,则△ACD≌△AED(SAS),CD=ED 且 AD 平分∠BDE, 则 DB:DE=AB:AE,即 AB:AC=DB:DC.
接下来开始证明:如图,PA:PB=k,作∠APB 的角平分线交 AB 于 M 点,根据角平分线定理,
1
MA:MB=PA:PB=k,故 M 点为定点,即∠APB 的角平分线交 AB 于定点;
2
4.如图 1,抛物线 y=ax2+(a+3)x+3(a≠0)与 x 轴交于点 A(4,0),与 y 轴交于点 B,在 x 轴上有一动点 E(m, 0)(0<m<4),过点 E 作 x 轴的垂线交直线AB 于点N,交抛物线于点 P,过点 P 作 PM⊥AB 于点 M.
(1)求 a 的值和直线 AB 的函数表达式;
在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中 P 点轨迹是直线,而当 P 点轨迹变为圆 时,即通常我们所说的“阿氏圆”问题. 所谓“阿氏圆”,是指由古希腊数学家阿波罗尼奥斯提出的圆的概念,在平面内,到两个定点距离之比等于定 值(不为 1)的点的集合叫做圆.
如下图,已知 A、B 两点,点 P 满足 PA:PB=k(k≠1),则满足条件的所有的点 P 构成的图形为圆.
一动点,且∠BPA=135°,则 2PD+PC 的最小值是
.
5.已知⊙O 半径为 1,AC、BD 为切线,AC=1,BD=2,P 为弧 AB 上一动点, 试求 2 PC PD 的最小值. 2
4
巩固练习:
1.如图,在△ABC 中,∠B﹦90°,AB﹦CB﹦2,以点 B 为圆心作⊙B 与 AC 相切,点 P 为圆 B 上任一动点,
2020年中考数学应用类二阅读理解型问题课件 (共25张PPT)

解:应用:①若 PB=PC,连接 PB,则∠PCB=∠PBC,∵CD 为等边三角形的高,∴ AD=BD,∠PCB=30°.∴∠PBD=∠PBC=30°,∴PD= 33DB= 63AB.与已知 PD=12AB 矛盾,∴PB≠PC.②若 PA=PC,连接 PA,同理可得 PA≠PC.
③若 PA=PB,由 PD=12AB,得 PD=AD=BD,∴∠APD=∠BPD=45°.∴∠APB =90°.
(2)∵经过三次折叠,∠BAC是△ABC的好角,∴第三次折叠时, ∠A2B2C=∠C,如图所示.∵∠ABB1=∠AA1B1,∠AA1B1=∠A1B1C +∠C,又∵∠A1B1C=∠A1A2B2,∠A1A2B2=∠A2B2C+∠C,∴∠ABB1 =∠A1B1C+∠C=∠A2B2C+∠C+∠C=3∠C.由上面的探索发现,若 ∠BAC是△ABC的好角,折叠一次重合,有∠B=∠C;折叠两次重合 ,有∠B=2∠C;折叠三次重合,有∠B=3∠C;由此可猜想若经过n 次折叠,∠BAC是△ABC的好角,则∠B=n∠C;
小俊的证明思路是:如图②,过点P作PG⊥CF,垂足为G,可以证得: PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图③,当点P在BC延长线上时,其余条件不变,求证: PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下题:
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C 落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE,PH⊥BC,垂 足分别为G,H,若AD=8,CF=3,求PG+PH的值.
中考数学应用类问题三
阅读理解型问题
阅读理解型问题,一般篇幅较长,涉及内容丰富,构思新颖别致.这类 问题,主要考查解题者的心理素质,自学能力和阅读理解能力,考查解题 者的观察分析能力、判辩是非能力、类比操作能力、抽象概括能力、数学 归纳能力以及数学语言表达能力.
2020中考数学各类经典题型汇总

2020中考数学各类经典题型汇总1.中点①中线:D为BC中点,AD为BC边上的中线()有全等平行线中有中点,容易是斜边的一半直角三角形的斜边中线,可得使得到延长.6.5BDAD2cb.4CDEABDDEADEAD.3SS.2CDBD.12222ACDABD+=+∆≅∆===∆∆1.例.如图,在菱形ABCD中,tan∠ABC=,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则的值为()A. B.C.D.2.角平分线②角平分线:AE平分∠BAC有等腰三角形平行线间有角平分线易作全等三角形有相同角有公共边极易.5.4.3.2BAE.1CEBEACABDFDECAE==∠=∠3.高线③垂线:AF ⊥BC角形多个直角,易有相似三充分利用求高线可用等面积法即.4Rt .3.290AFC BC AF .1∆︒=∠⊥②直角三角形:AD 为中线AE 为垂线∆︒︒︒•=•==+•=•====︒=∠+∠∆Rt AE BC AB AC S BC CD ABC ,构造充分利用特殊角;勾股定理:等面积法::斜边中线为斜边的一半两角互余:,60,45305.BC CE AC BC BE AB BC AB AC .42121.321BD AD .290C B .1222224.函数坐标公式公式1:两点求斜率k2121x x y y k AB --=113531203330360145-=︒-=︒=︒=︒=︒k x k x k x k x k x 时,轴正方向夹角为⑤与时,轴正方向夹角为④与时,轴正方向夹角为③与时,轴正方向夹角为②与时,轴正方向夹角为①与公式2:两点之间距离221221)()(AB y y x x -+-=应用:弦长公式公式3:中点公式)2,3(ABC )2,2(AB 3213212121y y y x x x y y x x ++++=∆++=重心中点 应用:求中点坐标公式4:两直线平行与垂直1//21212121-=•⇔⊥=⇔k k l l k k l l ②①应用:①平行与垂直②直角三角形5.相似中的特殊角βαβαβαtan tan 1tan tan tan -+=+)(6.将军引马7.旋转8.对称9.反比例函数看坐标求面积对称反比例函数关于系直线与反比例交点的关坐标点的表示的关系面积与.5x y .4.3.2k .110.二次函数最值二次函数中的三种线段与铅垂高二次函数当中的水平长二次函数的移动不等式二次函数与二次方程或关系对称轴与顶点及三大表达式及转化.6.5.4.3c.b.a.2.111.圆 扇形的面积与弧长弧度,圆心角,圆周角弦长,弦心距,弧长,园中的对称与翻折内心外心,内切圆外接圆与弧度园中的圆周角,圆心角园中的内接四边形园中的两个等腰三角形园中的三个直角三角形.8.7.6--.5.4.3.2.112规律题圆14应用题。
2020年全国各地中考数学解析汇编1 有理数.doc

2020年全国各地中考数学解析汇编1 有理数1.1 正数和负数1.(2020浙江丽水3分,1题)如果零上2℃记作+2℃,那么零下3℃记作( )A.-3℃B.-2℃C.+3℃D.+2℃【解析】根据相反意义的量可知,零上2℃记作“+2℃”,则零下3℃记作“-3℃”,故选A.【答案】A【点评】本题考查相反意义的量.2.(2020山东德州中考,9,4,)-1, 0, 0.2,71 , 3 中正数一共有 个. 【解析】由题意知2,17,3是正数,共有三个. 【答案】3.【点评】有理数的分类方法有2种:①正有理数、0、负有理数;②整数和分数.3.(2020安徽,1,4分)下面的数中,与-3的和为0的是 ( ) A.3 B.-3 C.31 D.31- 【解析】根据有理数的运算法则,可以把选项中的数字和-3相加,进行筛选只有选项A 符合,也可以利用相反数的性质,根据互为相反数的两数和为0,必选-3的相反数3.【答案】A .【点评】本题考查了有理数的运算、及其概念,理解有关概念,掌握运算法则,是解答此类题目的基础.4.(2020山东泰安,1,3分)下列各数比-3小的数是( )A. 0B. 1C.-4D.-1【解析】根据正数大于0,0大于负数,两个负数绝对值大的反而小可得,比-3小的数是-4.【答案】C【点评】本题考查了实数大小的比较.要掌握实数大小的比较:正数大于0,负数小于0,正数大于负数;数轴上表示的两个数,右边的比左边的大.5.(2020浙江省衢州,1,3分)下列四个数中,最小的数是( )A.2B.-2C.0D. 21- 【解析】根据有理数比较大小的法则进行判断,有-2<12-<0<2. 【答案】B【点评】本题考查了有理数大小的比较,①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.6.(2020重庆,1,4分)在一3,一1,0,2这四个数中,最小的数是()A.一3 B.一1 C.0 D.2【解析】正数大于0,负数小于0,两个负数绝对值大的反而小。
2020年中考数学--实数ppt(习题含答案)

10 、 我 们 知 道 , 无 限 循 环 小 数 都 可 以 转 化 为 分 数 . 例 如 : 将 转 化 为 分
数时,可设
, 则 x 0.3 1 x , 解 得 x 1 , 即
A、2.5 B、2 2 C、 3
D、 5
B 5、若 x, y 为实数,且 x 2 与 y 2 互为相反数,则 ( x ) 2015 的值为(
)
y
A、1 B、-1 C、2
D、-2
6、一列数
a1
,
a2
,
a3
, a4
……其中 a1
=
1 2
,
a
2
=
1
1 a1
2 3
…… an
1 1 a n1
D ( n 为大于 2 的整数),则 a5 的值为( )
A、 5 8
B、 8 5
二、填空题
C、 13 8
D、 8 13
7、 1 的倒数是 -2
2
0.05 8、用四舍五入法时 0.05049 取近似值,精确到百分位的结果是
。
9、PM 2.5 是 指 大 气 中 直 径 小 于 或 等 于 2.5 m(1m 0.000001m )的 颗 粒 物 .也
称 为 可 入 肺 颗 粒 物 ,它 们 含 有 大 量 的 有 毒 、有 害 物 质 ,对 人 体 健 康 和 大
点 P37 所表示的数用科学记数法表示为 3.7×10-6.
一、 解答题 14、在数轴上,N 点与原点的距离是 N 点与 30 所对应点之间的 4 倍,那么 N 点所 表示的数是多少?
2020年中考数学3轮专题复习课件-第43讲解答题(一)专题PPT课件

9.(2019·宁夏)解方程:x+2 2+1=x-x 1.
解:方程两边同乘(x+2)(x-1),得 2(x-1)+(x+2)(x-1)=x(x+2),解得 x=4. 经检验,x=4 是原方程的解, ∴原方程的解为 x=4.
10.(2019·江苏无锡)解方程:x2-2x-5=0.
解:∵a=1,b=-2,c=-5,
对角线. (1)用直尺和圆规作出线段 AC 的垂直平分线,与 AD
相交于点 E,连接 CE(保留作图迹,不写作法);解:如答图,CE 即为所求.
(2)在(1)的条件下,若 AB=3,BC=5,求△ DCE 的 周长.
解:∵四边形 ABCD 为平行四边形, ∴AD=BC=5,CD=AB=3. ∵点 E 在线段 AC 的垂直平分线上,∴EA=EC. ∴△DCE 的周长为 CE+DE+CD=EA+DE+CD =AD+CD=5+3=8.
x-3(x-2)≥-4, 12.(2019·山东菏泽)解不等式组:x-1<2x+ 3 1.
解:解不等式 x-3(x-2)≥-4,得 x≤5. 解不等式 x-1<2x3+1,得 x<4. ∴不等式组的解集为 x<4.
(D)尺规作图 13.如图,AB∥CD. (1)在图中,用尺规作∠ACD 的平分线交 AB 于点 E(不要求写作法,保留作图痕迹);
代入 x=1,y=-2,得原式=-1+8=7.
5 . (2019·黑 龙 江 佳 木 斯 ) 先 化 简 , 再 求 值 : x+1 1-xx2--21÷x+1 1,其中 x=2sin 30°+1.
解:原式=(x+1x)-(1x-1)-(x+1x)-(2x-1) ÷x+1 1=(x+1)1(x-1)·(x+1)=x-1 1.
∴Δ=4-4×1×(-5)=24>0,
2020年九年级中考数学应用类一 情境应用型问题课件(共24张ppt)

七巧板拼图 趣题巧解 数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)比赛后,甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四个项
目得分分别按 10%,40%,20%,30%折算记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为 80 分以上(包含 80 分)的学生获一等
探索延伸: 如图②,若在四边形 ABCD 中,AB=AD,∠B+∠D=180°.E,F 分别是 BC,CD 上的点,且∠EAF=12∠BAD,上述结论是否仍然成立,并说明理由; 实际应用: 如图③,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西 30°的 A 处, 舰艇乙在指挥中心南偏东 70°的 B 处,并且两舰艇到指挥中心的距离相等,接 到行动指令后,舰艇甲向正东方向以 60 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 80 海里/小时的速度前进.1.5 小时后,指挥中心观测到甲、乙两舰 艇分别到达 E,F 处,且两舰艇之间的夹角为 70°,试求此时两舰艇之间的距离.
(2)当用水量为 30 吨时,水费为:17×3+13×5=116 元,∵9200×2%= 184 元,116<184,∴小王家六月份的用水量可以超过 30 吨.设小王家六月份 用水量为 x 吨,由题意,得 17×3+13×5+6.8(x-30)≤184,6.8(x-30)≤68, 解得 x≤40.答:小王家六月份最多能用水 40 吨.
【点评】本题考查了列二元一次方程组解实际问题的运用、加权平均 数的运用,在解答时建立方程组求出趣题巧解和数学运用的百分比是解答 本题的关键.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题 3.为了增强环境保护意识,6 月 5 日“世界环境日”当天,在环保局工作人员指导下,若干名“
环 保小卫士”组成的“控制噪声污染”课题学习研究小组,抽样调查了全市 40 个噪声测量点在某
时刻 的噪声声级(单位:dB),将调查的数据进行处理(设所测数据是正整数),得频数分布表如下
说明理由.
例题 2.今年 3 月 5 日,花溪中学组织全体学生参加了“走出校门,服务社会”的活动。九年级一班高 伟同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图 和 扇形统计图。请根据高伟同学所作的两个图形,解答:
1 九年级一班有多少名学生? 2补全直方图的空缺部分;并 求出 “去敬老院服务”的扇形的圆 心
2 搅均后从中一把模出两个球,请通过列表或树状图求两个球都是白球的概率;
(3)搅均后从中任意模出一个球,要使模出红球的概率为 2 ,应如何添加红球? 3
例题 6.小明和小颖做掷骰子的游戏,规则如下:
①游戏前,每人选一个数字;②每次同时掷两枚均匀骰子;
③如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜 .
(1)在下表中列出同时掷第两2 枚枚骰均子匀骰子所有可能出现的结果。
第 1 枚骰子 掷得的点数
1
2
3
4
5
6
掷得的点数
1
2
3
4
5
6
3
(2)小明选的数字是 5,小颖选的数字是 6.如果你也加入游戏,你会选什么数字,使自己获胜的概 率比他们大?请说明理由. 四、解直角三角形的应用题 主要类型有:(1)在直角三角形中,已知两个元素,求其它未知元素(可直接利用三角函数来求解); 在直角三角形中,只知一个元素,求其它未知元素。(可通过设未知数,利用已知角的三角函数来列 方程求解)
:
组别
噪声声级分组
频数
频率
1
44.5————74.5
a
0.2
3
74.5——89.5
10
0.25
4
89.5——104.5
b
c
5
104.5——119.5
6
0.15
合计
40
1.00
根据表中提供的信息解答下列问题:
2
1 频数分布表中的 a =
,b=
,c =
;
2 补充完整频数分布直方图; 3 如果全市共有 200 个测量点,那么在这一时刻噪声 声级 小于 75dB 的测量点约有多少个?
2x 1 3
并把解集在数轴上表示出来.
1
三、统计与概率题 统计题要求会从图表提供的信息中来求平均数(加权平均数)、众数、中位数、频率与频数、极
差与方差、扇形图中的百分比和圆心角度数;会利用样本的结果来估算总体的结果。
概率题要求会利用树形图或列表法来求事件发生的概率。 例题 1.某校八年级(1)班 50 名学生参加 2008 年北海市数学质量监控考试,全班学生的成绩统计如 下表:
中考解答题常见类型
一、计算题
包括有:(1)实数的混合计算;(2)整式的计算;(3)分式的计算;(4)分解因式。
例如:1.计算:
(1) 27 (3.14 )0 3 tan 30 ( 1)1
3
(2) (1) 2009 (1)2 2 cos 450 4 18 2
2.先化简,再求值: (3x 2)(3x 2) 5x(x 1) (2x 1)2 ,其中x 1 . 3
二、解方程(组)或不等式(组)
包括有:(1)解一元二次方程;(2)解分式方程;(3)解二元一次方程组;(4)解不等式组
1. 解方程: x2 3x 1 0
2. 解方程: 2 4x 1 x 1 1 x2 x 1
3.解方程组:
2x 3x
y 3 5y 11
2 x 0,
4. 解不等式组5x211≥
例题 1.如图,一只运载火箭从地面 L 处发射,当卫星到达 A 点时,从位于地面 R 处的雷达站测得 AR 的距离是 6km,仰角为 450,2s 后,火箭到达 B 点,此时测得仰角为 600,这个火箭从 A 到 B 的平 均速度是多少?
例题 2.海中有一个小岛 P,它的周围 18 海里内有暗礁,渔船跟踪鱼群由西向东航行,在点 A 测 得小岛 P 在北偏东 60°方向上,航行 12 海里到达 B 点,这时测得小岛 P 在北偏东 45°方向上.如 果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
3
4
0
乙队(人数) 2
1
1
2 甲队队员身高的平均数为
厘米,中位数是
厘米,众数是 厘米。
乙队队员身高的平均数为
厘米;
3 学校要从中挑一支队伍去参加校庆表演,你认为选哪支队伍更合适?简要说明理由 .
例题 5.一只不透明的袋子中,装有 2 个白球和 1 个红球,这些球除颜色外者都相同。 1小明认为,搅均后从中任意摸出一个球,不是白球就是红球,因此模出白球和模出红球是等可 能 的。你同意他的说法吗?为什么?
例题3.如图6,在气象站台A 的正西方向240km 的 B 处有一台风中心,该台风中心以每小时20km 的速度沿北偏东60o 的 BD 方向移动,在距离台风中心130km 内的地方都要受到其影响。
成绩(分 71 74 78 80 82 83 85 86 88 90 91 92 94 )
请根据表人中数提供的信1 息解2答下列3问题:5 4 5 3 7 8 4 3 3 2
1 该班学生考试成绩的平均分是
,众数是
.
2 该班学生考试成绩的中位数是
.
3该班张华同学在这次考试中的成绩是 83 分,能不能说张华同学的成绩处于全班中游偏上水平 ?试
例题 4. 甲、乙两支仪仗队队员的身高(单位:厘米)如下: 甲队:178,177,179,178,177,178,177,179,178,179; 乙队:178,179,176,178,180,178,176,178,177,180;
(1)将下表填完整:
身高(厘米) 176
177
178
179
180
甲队(人数)
3.(1) 先化简,再求值: x 3 (x 2 5 ) ,其中 x=-4.
x 2
x 2
(2)先化简,再求值:( x 2 x 1 ) x2 16 ,其中 x= 2 2 . x 2 2x x2 4x 4 x2 4x
4. 分解因式:(1)3x3 12x
(2) 6xy 2 9x 2 y y 3
