最新全国各地中考数学解答题压轴题解析4
2024广东中考数学压轴题

2024广东中考数学压轴题一、在直角坐标系中,抛物线y = ax2 + bx + c与x轴交于点A(-3,0)和B(1,0),且与y 轴交于点C(0,3)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 抛物线的对称轴是直线x = -1(答案:D)二、已知三角形ABC的三边长为a,b,c,且满足a2 + b2 + c2 = 10a + 6b + 8c - 50。
则下列判断三角形ABC的形状中,正确的是:A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形(答案:D)三、函数y = (x - 1)/(x + 2)中,当x的值增大时,y的值会:A. 一直增大B. 一直减小C. 在某个区间内增大,在另一个区间内减小D. 保持不变(答案:C)四、已知四边形ABCD是平行四边形,且AB = 6,BC = 8,对角线AC与BD相交于点O,则下列关于O点到AB和BC的距离d1和d2的说法正确的是:A. d1 + d2 = 14B. d1 × d2 = 24C. d1/d2 = AB/BCD. d12 + d22 = AB2 + BC2(答案:B)五、圆O的半径为5,点P在圆O外,且OP = 8。
过点P作圆O的两条切线,分别与圆O 相切于点A和B。
则弦AB的长度为:A. 6B. 4√3C. 5√2D. 2√15(答案:A)六、在数轴上,点A表示的数为-2,点B表示的数为3。
若点C表示的数为x,且满足AC + BC = 8,则x的值为:A. -3或4B. -4或3C. -3或-1D. 2或-5(答案:B)七、已知二次函数y = ax2 + bx + c的图像经过点(1,0),(2,0)和(3,4)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 函数的顶点在x轴上(答案:A)八、正方形ABCD的边长为4,点E在边AB上,且AE = 1。
全国各地中考数学压轴题精选(含详细答案)

12.(黄冈)已知:如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系 ,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点, 动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为t秒. (1)求直线BC的解析式; (2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积的 ; (3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S 与t的函数关系式,并指出自变量t的取值范围;
8
点F重合时,梯形ABCD停止移动.观察得知:在梯形ABCD移动过程中,其腰BC始终经过坐 标原点O.(如图2) ①设点A的坐标为(a,b),梯形ABCD与梯形OEFG重合部分的面积为S,试求a与何值时, S的值恰好等于梯形OEFG面积的 ;
②当点A在EF上滑动时,设AD与x轴的交点为M,试问:在y轴上是否存在点P,使得△PAM 是底角为30°的等腰三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在, 请说明理由.(利用图3进行探索)
2020年中考数学10道压轴题(附答案)(4)

2020年中考数学10道压轴题(附答案)1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D. (1) 求该抛物线的解析式;(2) 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3) △AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22)2. 如图,在Rt ABC △中,90A ∠=o ,6AB =,8AC =,D E ,分别是边AB AC ,的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作QR BA ∥交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,QR y =.(1)求点D 到BC 的距离DH 的长;(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围); (3)是否存在点P ,使PQR△为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.3在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN ∥BC 交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM =x .(1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切? (3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?4.如图1,在平面直角坐标系中,己知ΔAOB 是等边三角形,点A 的坐标是(0,4),点B 在第一象限,点P 是x 轴上的一个动点,连结AP ,并把ΔAOP 绕着点A 按逆时针方向A BCD ERP H QA BCM N P图 3OABC MND图 2OACMNP图 1O旋转.使边AO与AB重合.得到ΔABD.(1)求直线AB的解析式;(2)当点P运动到点(3,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于3,若存在,请求出符合条件的点P的坐标;若不存在,4请说明理由.5如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.(1)求证:△BDE≌△BCF;(2)判断△BEF的形状,并说明理由;(3)设△BEF的面积为S,求S的取值范围.6如图,抛物线21:23L y x x =--+交x 轴于A 、B 两点,交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ,2L 交x 轴于C 、D 两点.(1)求抛物线2L 对应的函数表达式;(2)抛物线1L 或2L 在x 轴上方的部分是否存在点N ,使以A ,C ,M ,N 为顶点的四边形是平行四边形.若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点P 是抛物线1L 上的一个动点(P 不与点A 、B 重合),那么点P 关于原点的对称点Q 是否在抛物线2L 上,请说明理由.7.如图,在梯形ABCD 中,AB ∥CD ,AB =7,CD =1,AD =BC =5.点M ,N 分别在边AD ,BC 上运动,并保持MN ∥AB ,ME ⊥AB ,NF ⊥AB ,垂足分别为E ,F .(1)求梯形ABCD 的面积; (2)求四边形MEFN 面积的最大值.(3)试判断四边形MEFN 能否为正方形,若能, 求出正方形MEFN 的面积;若不能,请说明理由.8.如图,点A (m ,m +1),B (m +3,m -1)都在反比例函数xk y 的图象上.(1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点,以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式.(3)选做题:在平面直角坐标系中,点P 的坐标为(5,0),点Q 的坐标为(0,3),把线段PQ 向右平 移4个单位,然后再向上平移2个单位,得到线段P 1Q 1, 则点P 1的坐标为 ,点Q 1的坐标为 .C D A BE F NMxO yAB 友情提示:本大题第(1)小题4分,第(2)小题7分.对完成第(2)小题有困难的同学可以做下面的(3)选做题.选做题2分,所得分数计入总分.但第(2)、(3)小题都做的,第(3)小题的得分不重复计入总分.x O y 123 1 QP 2 P 1Q 19.如图16,在平面直角坐标系中,直线33y x =--与x 轴交于点A ,与y 轴交于点C ,抛物线223(0)3y ax x c a =-+≠经过A B C ,,三点. (1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标; (2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由;(3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.10.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,3OB =,矩形ABOC绕点O 按顺时针方向旋转60o 后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,.(1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;A OxyBFC(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.11.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?y xOD EC FA B12.在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C若C的坐标为(0,2),AB=5, A,B两点的横坐标X A,X B是关于X的方程2(2)10-++-=的两根:x m x n(1)求m,n的值(2)若∠ACB的平分线所在的直线l交x轴于点D,试求直线l对应的一次函数的解析式(3)过点D任作一直线`l分别交射线CA,CB(点C除外)于点M,N,则11+的值是否为定值,若是,求出定值,若不CM CN是,请说明理由13.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D. (1)求该抛物线的解析式;(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3)△AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a bac a b 44,22)14.已知抛物线c bx ax y ++=232,ACO BNDML`(Ⅰ)若1==b a ,1-=c ,求该抛物线与x 轴公共点的坐标;(Ⅱ)若1==b a ,且当11<<-x 时,抛物线与x 轴有且只有一个公共点,求c 的取值范围;(Ⅲ)若0=++c b a ,且01=x 时,对应的01>y ;12=x 时,对应的02>y ,试判断当10<<x 时,抛物线与x 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.15.已知:如图①,在Rt △ACB 中,∠C =90°,AC =4cm ,BC =3cm ,点P 由B 出发沿BA 方向向点A 匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为t (s )(0<t <2),解答下列问题:(1)当t 为何值时,PQ ∥BC ?(2)设△AQP 的面积为y (2cm ),求y 与t 之间的函数关系式; (3)是否存在某一时刻t ,使线段PQ 恰好把Rt △ACB 的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;(4)如图②,连接PC ,并把△PQC 沿QC 翻折,得到四边形PQP ′C ,那么是否存在某一时刻t ,使四边形PQP ′C 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.图②A Q CPB图①QP16.已知双曲线k y x =与直线14y x =相交于A 、B 两点.第一象限上的点M (m ,n )(在A 点左侧)是双曲线k y x=上的动点.过点B 作BD ∥y 轴于点D.过N (0,-n )作NC ∥x 轴交双曲线k y x=于点E ,交BD 于点C.(1)若点D 坐标是(-8,0),求A 、B 两点坐标及k 的值. (2)若B 是CD 的中点,四边形OBCE 的面积为4,求直线CM 的解析式.(3)设直线AM 、BM 分别与y 轴相交于P 、Q 两点,且MA =pMP ,MB =qMQ ,求p -q 的值.压轴题答案1. 解:( 1)由已知得:310c b c =⎧⎨--+=⎩解得c=3,b=2∴抛物线的线的解析式为2y x =-+(2)4)所以对称轴为x=1,A,E 关于称,所以E(3,0)D BCE NO A Myx设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9 (3)相似如图,2222112BG DG +=+=22223332BO OE +=+= 22222425DF EF ++=所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且2AO BO BD BE ==所以AOB DBE ∆∆:.2 解:(1)Q Rt A ∠=∠,6AB =,8AC =,10BC ∴=.Q 点D 为AB 中点,132BD AB ∴==. 90DHB A ∠=∠=o Q ,B B ∠=∠.BHD BAC ∴△∽△, DH BD AC BC ∴=,3128105BD DH AC BC ∴==⨯=g . (2)QR AB Q ∥,90QRC A ∴∠=∠=o .C C ∠=∠Q ,RQC ABC ∴△∽△, RQ QCAB BC∴=,10610y x-∴=,即y 关于x 的函数关系式为:365y x =-+. (3)存在,分三种情况:①当PQ PR =时,过点P 作PM QR ⊥于M ,则QM RM =.1290∠+∠=o Q ,290C ∠+∠=o ,1C ∴∠=∠.84cos 1cos 105C ∴∠===,45QM QP ∴=, 1364251255x ⎛⎫-+ ⎪⎝⎭∴=,185x ∴=. ②当PQ RQ =时,312655x -+=, 6x ∴=.③当PR QR =时,则R 为PQ 中垂线上的点, 于是点R 为EC 的中点,11224CR CE AC ∴===.tan QR BAC CR CA ==Q , 366528x -+∴=,152x ∴=.综上所述,当x 为185或6或152时,PQR △为等腰三角形. 3解:(1)∵MN ∥BC ,∴∠AMN =∠B ,∠ANM =∠C . ∴ △AMN ∽ △ABC .∴AM AN AB AC=,即43x AN =. ∴ AN =43x . (2)分ABCD ERP H QM 21 A BCD E RP HQA BCD E R PHQACM NP 图 1O∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=.(0<x <4) ……………3分(2)如图2,设直线BC 与⊙O 相切于点D ,连结AO ,OD ,则AO =OD =21MN .在Rt △ABC 中,BC =22AB AC +=5.由(1)知 △AMN ∽ △ABC .∴AM MN AB BC=,即45x MN=.∴ 54MN x =, ∴58OD x =. (5)分过M 点作MQ ⊥BC 于Q ,则58MQ OD x ==. 在Rt △BMQ 与Rt △BCA 中,∠B 是公共角, ∴ △BMQ ∽△BCA . ∴ BM QMBC AC=.∴55258324xBM x ⨯==,25424AB BM MA x x =+=+=. ∴ x =4996. ∴ 当x =4996时,⊙O 与直线B C 相切. (7)分(3)随点M 的运动,当P 点落在直线BC 上时,连结AP ,则O 点为AP 的中点.∵ MN ∥BC ,∴ ∠AMN =∠B ,∠AOM =∠APC . ∴ △AMO ∽ △ABP . ∴12AM AO AB AP ==. AM =MB =2. ABCMND图 2O QAC MNP图 3O故以下分两种情况讨论: ① 当0<x ≤2时,2Δ83x S y PMN ==.∴ 当x=2时,2332.82y =⨯=最大 (8)分② 当2<x <4时,设PM ,PN 分别交BC 于E ,F .∵ 四边形AMPN 是矩形, ∴ PN ∥AM ,PN =AM =x . 又∵ MN ∥BC ,∴ 四边形MBFN 是平行四边形. ∴ FN =BM =4-x . ∴ ()424PF x x x =--=-. 又△PEF ∽ △ACB . ∴2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭.∴ ()2322PEF S x ∆=-. (9)分MNP PEF y S S ∆∆=-=()222339266828x x x x --=-+-.……………………1分当2<x <4时,29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭. ∴当83x =时,满足2<x<4,2y =最大. (11)分综上所述,当83x =时,y 值最大,最大值是ABCMN图 4OEF2. …………………………12分4 解:(1)作BE ⊥OA ,∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23B(3∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-,以直线AB 的解析式为343y x =-+ (2)由旋转知,AP=AD, ∠PAD=60o , ∴ΔAPD 是等边三角形,PD=PA=2219AO OP +如图,作BE ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30° ∴GD=12BD=33+3=53,∴GB=32BD=32,OH=OE+HE=OE+BG=37222+= ∴D(532,72) (3)设OP=x,则由(2)可得D(323,22x x +)若ΔOPD 的面积为:133(2)2x x +=g 解得:2321x -±=所以2321-±,0) yxH G E DBA OP567解:(1)分别过D ,C 两点作DG ⊥AB 于点G ,CH ⊥AB 于点H . ……………1分 ∵ AB ∥CD ,∴ DG =CH ,DG ∥CH .∴ 四边形DGHC 为矩形,GH =CD =1.∵ DG =CH ,AD =BC ,∠AGD =∠BHC =90°, ∴ △AGD ≌△BHC (HL ).∴ AG =BH =2172-=-GH AB =3. ………2分 ∵ 在Rt △AGD 中,AG =3,AD =5, ∴ DG =4.C D ABE F NMG H∴()174162ABCD S +⨯==梯形. ………………………………………………3分(2)∵ MN ∥AB ,ME ⊥AB ,NF ⊥AB , ∴ ME =NF ,ME ∥NF . ∴ 四边形MEFN 为矩形. ∵ AB ∥CD ,AD =BC , ∴ ∠A =∠B .∵ ME =NF ,∠MEA =∠NFB =90°, ∴ △MEA ≌△NFB (AAS ).∴ AE =BF . ……………………4分 设AE =x ,则EF =7-2x . ……………5分 ∵ ∠A =∠A ,∠MEA =∠DGA =90°, ∴ △MEA ∽△DGA . ∴ DGMEAG AE =.∴ME =x 34. …………………………………………………………6分 ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形. (8)分当x =47时,ME =37<4,∴四边形MEFN 面积的最大值为649.……………9分(3)C D E FNMG H能. ……………………………………………………………………10分由(2)可知,设AE =x ,则EF =7-2x ,ME =x 34.若四边形MEFN 为正方形,则ME =EF . 即=34x 7-2x .解,得1021=x . ……………………………………………11分∴ EF =21147272105x -=-⨯=<4.∴ 四边形MEFN 能为正方形,其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形.8解:(1)由题意可知,()()()131-+=+m m m m .解,得 m =3. ………………………………3分∴ A (3,4),B (6,2);∴ k =4×3=12. ……………………………4分 (2)存在两种情况,如图:①当M 点在x 轴的正半轴上,N 点在y 轴的正半轴 上时,设M 1点坐标为(x 1,0),N 1点坐标为(0,y 1).∵ 四边形AN 1M 1B 为平行四边形,∴ 线段N 1M 1可看作由线段AB 向左平移3个单位, 再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).由(1)知A 点坐标为(3,4),B 点坐标为(6,2), ∴ N 1点坐标为(0,4-2),即N 1(0,2); ………………………………5分xO yAB M 1N 1M 2 N 2M 1点坐标为(6-3,0),即M 1(3,0). ………………………………6分设直线M 1N 1的函数表达式为21+=x k y ,把x =3,y =0代入,解得321-=k .∴ 直线M 1N 1的函数表达式为232+-=x y . (8)分②当M 点在x 轴的负半轴上,N 点在y 轴的负半轴上时,设M 2点坐标为(x 2,0),N 2点坐标为(0,y 2).∵ AB ∥N 1M 1,AB ∥M 2N 2,AB =N 1M 1,AB =M 2N 2, ∴ N 1M 1∥M 2N 2,N 1M 1=M 2N 2.∴ 线段M 2N 2与线段N 1M 1关于原点O 成中心对称. ∴ M 2点坐标为(-3,0),N 2点坐标为(0,-2). ………………………9分设直线M 2N 2的函数表达式为22-=x k y ,把x =-3,y =0代入,解得322-=k ,∴ 直线M 2N 2的函数表达式为232--=x y .所以,直线MN 的函数表达式为232+-=x y 或232--=x y . (11)分(3)选做题:(9,2),(4,5). ………………………………………………2分 9解:(1)Q 直线33y x =-x 轴交于点A ,与y 轴交于点C .(10)A ∴-,,(03)C -, ········································· 1分Q 点A C ,都在抛物线上,23033a c c ⎧=++⎪∴⎨⎪-=⎩ 333a c ⎧=⎪∴⎨⎪=-⎩ ∴抛物线的解析式为2323333y x x =-- ····················· 3分 ∴顶点4313F ⎛⎫- ⎪ ⎪⎝⎭, ··········································· 4分(2)存在 ················································ 5分 1(03)P -, ··················································· 7分 2(23)P -, ··················································9分(3)存在 ·············································· 10分 理由: 解法一:延长BC 到点B ',使B C BC '=,连接B F '交直线AC 于点M ,则点M 就是所求的点.······························· 11分 过点B '作B H AB '⊥于点H .B Q 点在抛物线2323333y x x =--上,(30)B ∴, 在Rt BOC △中,3tan 3OBC ∠=,30OBC ∴∠=o ,23BC =,在Rt BB H '△中,1232B H BB ''==,36BH B H '==,3OH ∴=,(323)B '∴--, (12)分设直线B F '的解析式为y kx b =+A O xyBFC HBM233433k b k b ⎧-=-+⎪∴⎨-=+⎪⎩ 解得36332k b ⎧=⎪⎪⎨⎪=-⎪⎩33362y x ∴=- ············································ 13分3333362y x y x ⎧=--⎪∴⎨=-⎪⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩,310377M ⎛⎫∴- ⎪ ⎪⎝⎭, ∴在直线AC上存在点M ,使得MBF △的周长最小,此时310377M ⎛⎫- ⎪ ⎪⎝⎭,. ··········································· 14分解法二:过点F 作AC 的垂线交y 轴于点H ,则点H 为点F 关于直线AC 的对称点.连接BH 交AC 于点M ,则点M 即为所求. 11分过点F 作FG y ⊥轴于点G ,则OB FG ∥,BC FH ∥.90BOC FGH ∴∠=∠=o ,BCO FHG ∠=∠HFG CBO ∴∠=∠同方法一可求得(30)B ,. 在Rt BOC △中,3tan 3OBC ∠=,30OBC ∴∠=o ,可求得33GH GC ==,GF ∴为线段CH 的垂直平分线,可证得CFH △为等边三角形, AC ∴垂直平分FH .即点H 为点F 关于AC 的对称点.5303H ⎛⎫∴- ⎪ ⎪⎝⎭, ············· 12分设直线BH 的解析式为y kx b =+,由题意得A OxyBF C HM G03533k b b =+⎧⎪⎨=⎪⎩ 解得539533k b ⎧=⎪⎪⎨⎪=⎪⎩553393y ∴=··········································· 13分55339333y x y x ⎧=⎪∴⎨⎪=⎩ 解得37103x y ⎧=⎪⎪⎨⎪=⎪⎩310377M ⎛∴- ⎝⎭, ∴在直线AC上存在点M ,使得MBF △的周长最小,此时31037M ⎛ ⎝⎭. 110解:(1)点E 在y 轴上 ·································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =Q ,3BO =,2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠=o 由题意可知:60AOE ∠=o306090BOE AOB AOE ∴∠=∠+∠=+=o o oQ 点B 在x 轴上,∴点E 在y 轴上. (3)分(2)过点D 作DM x ⊥轴于点M1OD =Q ,30DOM ∠=o∴在Rt DOM △中,12DM =,32OM =Q 点D 在第一象限,∴点D 的坐标为3122⎛⎫⎪ ⎪⎝⎭, ····································· 5分由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A 的坐标为(31), ······································ 6分Q 抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(31)A ,,312D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得 3321331242a b a ⎧+=⎪⎨+=⎪⎩ 解得8953a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:285329y x x =-+ (9)分(3)存在符合条件的点P ,点Q . ······················ 10分 理由如下:Q 矩形ABOC 的面积3AB BO ==g ∴以O B P Q ,,,为顶点的平行四边形面积为3由题意可知OB 为此平行四边形一边, 又3OB =QOB ∴边上的高为2 ······································· 11分依题意设点P 的坐标为(2)m ,Q 点P 在抛物线285329y x x =-+上 2853229m ∴-+= 解得,10m =,2538m =-1(02)P ∴,,25328P ⎛⎫- ⎪ ⎪⎝⎭,Q 以O B P Q ,,,为顶点的四边形是平行四边形,PQ OB ∴∥,3PQ OB ==, ∴当点1P 的坐标为(02),时,点Q 的坐标分别为1(32)Q -,,2(32)Q ,;当点2P 的坐标为5328⎛⎫- ⎪ ⎪⎝⎭,时,点Q 的坐标分别为313328Q ⎛⎫-⎪ ⎪⎝⎭,,43328Q ⎛⎫⎪ ⎪⎝⎭,. ·············· 14分(以上答案仅供参考,如有其它做法,可参照给分) 11解:(1)在2334y x =-+中,令0y =23304x ∴-+= 12x ∴=,22x =-(20)A ∴-,,(20)B , ······················ 1分又Q 点B 在34y x b =-+上 302b ∴=-+ 32b = BC ∴的解析式为3342y x =-+ ·································2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ···················· 4分914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,y xO D EC FA B Mx yA B CE M D P N O4AB ∴=,94CD = ··········································· 5分 1994242ABCS ∴=⨯⨯=△ ·········································6分(3)过点N 作NP MB ⊥于点PEO MB ⊥Q NP EO ∴∥BNP BEO ∴△∽△ ············································7分 BN NPBE EO∴=················································· 8分由直线3342y x =-+可得:302E ⎛⎫ ⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP∴=,65NP t ∴= ········································ 9分 16(4)25S t t ∴=-g g2312(04)55S t t t =-+<< ······································ 10分2312(2)55S t =--+ ·········································· 11分Q 此抛物线开口向下,∴当2t =时,125S =最大∴当点M 运动2秒时,MNB △的面积达到最大,最大为125.12解: (1)m=-5,n=-3 (2)y=43x+2(3)是定值.因为点D 为∠ACB 的平分线,所以可设点D 到边AC,BC 的距离均为h ,设△ABC AB 边上的高为H, 则利用面积法可得:222CM h CN h MN H⋅⋅⋅+=(CM+CN )h=MN ﹒HCM CN MNH h+=又 H=CM CNMN⋅化简可得 (CM+CN)﹒1MN CM CN h=⋅故 111CM CN h+=13解:( 1)由已知得:310c b c =⎧⎨--+=⎩解得 c=3,b=2∴抛物线的线的解析式为223y x x =-++ (2)由顶点坐标公式得顶点坐标为(1,4)所以对称轴为x=1,A,E 关于x=1设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9 (3)相似如图,2222112BG DG +=+=yxDEA BFOG22223332BO OE +=+= 22222425DF EF ++=所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且22AO BO BD BE ==所以AOB DBE ∆∆:.14解(Ⅰ)当1==b a ,1-=c 时,抛物线为1232-+=x x y , 方程01232=-+x x 的两个根为11-=x ,312=x .∴该抛物线与x 轴公共点的坐标是()10-,和103⎛⎫⎪⎝⎭,. ········· 2分(Ⅱ)当1==b a 时,抛物线为c x x y ++=232,且与x 轴有公共点. 对于方程0232=++c x x ,判别式c 124-=∆≥0,有c ≤31. ······ 3分①当31=c 时,由方程031232=++x x ,解得3121-==x x .此时抛物线为31232++=x x y 与x 轴只有一个公共点103⎛⎫-⎪⎝⎭,. · 4分②当31<c 时,11-=x 时,c c y +=+-=1231, 12=x 时,c c y +=++=5232.由已知11<<-x 时,该抛物线与x 轴有且只有一个公共点,考虑其对称轴为31-=x ,应有1200.y y ⎧⎨>⎩≤, 即1050.c c +⎧⎨+>⎩≤,解得51c -<-≤.综上,31=c 或51c -<-≤. ······························ 6分(Ⅲ)对于二次函数c bx ax y ++=232,由已知01=x 时,01>=c y ;12=x 时,0232>++=c b a y , 又0=++c b a ,∴b a b a c b a c b a +=++++=++22)(23. 于是02>+b a .而c a b --=,∴02>--c a a ,即0>-c a .∴0>>c a . ············································· 7分 ∵关于x 的一元二次方程0232=++c bx ax 的判别式0])[(412)(4124222>+-=-+=-=∆ac c a ac c a ac b ,∴抛物线c bx ax y ++=232与x 轴有两个公共点,顶点在x 轴下方.8分 又该抛物线的对称轴abx 3-=,由0=++c b a ,0>c ,02>+b a , 得a b a -<<-2, ∴32331<-<a b . 又由已知01=x 时,01>y ;12=x 时,02>y ,观察图象,可知在10<<x 范围内,该抛物线与x 轴有两个公共点. ··· 10分15 解:(1)由题意:BP =tcm ,AQ =2tcm ,则CQ =(4-2t)cm , ∵∠C =90°,AC =4cm ,BC =3cm ,∴AB =5cm ∴AP =(5-t )cm ,x∵PQ ∥BC ,∴△APQ ∽△ABC ,∴AP ∶AB =AQ ∶AC ,即(5-t )∶5=2t ∶4,解得:t =107∴当t 为107秒时,PQ ∥BC ………………2分(2)过点Q 作QD ⊥AB 于点D ,则易证△AQD ∽△ABC ∴AQ ∶QD =AB ∶BC ∴2t ∶DQ =5∶3,∴DQ =65t∴△APQ 的面积:12×AP ×QD =12(5-t )×65t ∴y 与t 之间的函数关系式为:y =2335t t -………………5分(3)由题意:当面积被平分时有:2335t t -=12×12×3×4,解得:t 55± 当周长被平分时:(5-t )+2t =t +(4-2t )+3,解得:t =1∴不存在这样t 的值………………8分(4)过点P 作PE ⊥BC 于E易证:△PAE ∽△ABC ,当PE =12QC 时,△PQC 为等腰三角形,此时△QCP ′为菱形∵△PAE ∽△ABC ,∴PE ∶PB =AC ∶AB ,∴PE ∶t =4∶5,解得:PE =45t∵QC =4-2t ,∴2×45t =4-2t,解得:t =109∴当t =109时,四边形PQP ′C 为菱形 此时,PE =89,BE =23,∴CE =73………………10分在Rt △CPE 中,根据勾股定理可知:PC 22PE CE +2287()()93+=5059505cm ………………12分16 解:(1)∵D (-8,0),∴B 点的横坐标为-8,代入14y x =中,得y =-2.∴B 点坐标为(-8,-2).而A 、B 两点关于原点对称,∴A (8,2)从而k =8×2=16(2)∵N (0,-n ),B 是CD 的中点,A ,B ,M ,E 四点均在双曲线上,∴mn =k ,B (-2m ,-2n),C (-2m ,-n ),E (-m ,-n )DCNO S 矩形=2mn =2k ,DBO S △=12mn =12k ,OEN S △=12mn =12k.∴OBCE S 矩形=DCNO S 矩形―DBO S △―OEN S △=k.∴k =4.由直线14y x =及双曲线4y x=,得A (4,1),B (-4,-1) ∴C (-4,-2),M (2,2)设直线CM 的解析式是y ax b =+,由C 、M 两点在这条直线上,得4222a b a b -+=-⎧⎨+=⎩,解得a =b =23∴直线CM 的解析式是y =23x +23.(3)如图,分别作AA 1⊥x 轴,MM 1⊥x 轴,垂足分别为A 1,M设A 点的横坐标为a ,则B 点的横坐标为-a.于是111A M MA a mp MP M O m-===, 同理MB m aq MQ m+== ∴p -q =a m m --m am+=-2D B CE N O A My xQ A 1M 1。
24湖南中考数学压轴题

24湖南中考数学压轴题以下是根据2024年湖南中考数学可能考察的知识点和难度水平,原创设计的8道压轴选择题。
每道题都包含了题目描述、选项、答案以及解析。
一、在平面直角坐标系中,点A的坐标为(1,2),点B的坐标为(4,6),若点C在直线AB上,且AC的长度是AB长度的三分之一,则点C的坐标可能为:A. (2,3)B. (3,4)C. (2,5)D. (3,5)(答案)B解析:首先计算AB的长度,使用距离公式得到AB=√[(4-1)²+(6-2)²]=5。
然后,根据题意,AC=AB/3=5/3。
设点C的坐标为(x,y),由于C在AB上,可以根据A、B的坐标求出直线AB 的方程,再联立AC的长度公式,解出x和y的值。
经过计算,可以得到点C的坐标为(2,3)或(3,4),但考虑到C可能在A和B之间,也可能在B的延长线上,结合题意和选项,只有(3,4)满足条件。
二、若关于x的一元二次方程x²+2(m-1)x+m²-1=0有两个相等的实数根,则m的值为:A. 0B. 1C. 2D. -1(答案)B解析:一元二次方程有两个相等的实数根,即判别式Δ=0。
将方程的系数代入判别式,得到[2(m-1)]²-4(m²-1)=0,化简后得到m=1。
三、如图,在矩形ABCD中,AB=6,BC=8,点E在边AD上,且AE=2,点F在边BC上,连接EF,将△AEF沿EF翻折,使得点A落在点G处,连接GF,若GF⊥BC,则GF的长度为:A. 4B. 5C. 6D. 8(答案)C解析:由于GF⊥BC,且ABCD是矩形,所以GF∥AB。
设GF与EF交于点H,由于△AEF翻折得到△GEF,所以AE=GE=2,且∠AEF=∠GEF。
又因为AD∥BC,所以∠AEF=∠EFC。
由此可以得到∠GEF=∠EFC,所以GF=GE=2。
再根据相似三角形的性质,可以得到GF/AB=FC/ED,设FC=x,则ED=8-x,代入得到GF/6=x/(8-x),解得x=4,所以GF=2+4=6。
中考数学28道压轴题含答案解析

中考数学选填压轴题练习一.根的判别式(共1小题)1.(2023•广州)已知关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,则的化简结果是()A.﹣1B.1C.﹣1﹣2k D.2k﹣3【分析】首先根据关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,得判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,由此可得k≤1,据此可对进行化简.【解答】解:∵关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,∴判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,整理得:﹣8k+8≥0,∴k≤1,∴k﹣1≤0,2﹣k>0,∴=﹣(k﹣1)﹣(2﹣k)=﹣1.故选:A.二.函数的图象(共1小题)2.(2023•温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.【问题】路线①③⑥⑦⑧各路段路程之和为()A.4200米B.4800米C.5200米D.5400米【分析】设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.【解答】解:由图象可知:小州游玩行走的时间为75+10﹣40=45(分钟),小温游玩行走的时间为205﹣100=105(分钟),设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米由图象可得:,解得:x+y+z=2700,∴游玩行走的速度为:(2700﹣2100)÷10=60 (米/分),由于游玩行走速度恒定,则小温游路线①④⑤⑥⑦⑧的路程为:3x+3y=105×60=6300,∴x+y=2100,∴路线①③⑥⑦⑧各路段路程之和为:2x+2y+z=x+y+z+x+y=2700+2100=4800(米).故选:B.三.动点问题的函数图象(共1小题)3.(2023•河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为()A.6B.3C.D.【分析】如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,PB=PC,AO=,易知∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,可知AO=OB=,过点O作OD⊥AB,解直角三角形可得AD=AO•cos30°,进而得出等边三角形ABC的边长.【解答】解:如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,\结合图象可知,当点P在AO上运动时,,∴PB=PC,,又∵△ABC为等边三角形,∴∠BAC=60°,AB=AC,∴△APB≌△APC(SSS),∴∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,∴OB=,即AO=OB=,∴∠BAO=∠ABO=30°,过点O作OD⊥AB,垂足为D,∴AD=BD,则AD=AO•cos30°=3,∴AB=AD+BD=6,即等边三角形ABC的边长为6.故选:A.四.反比例函数系数k的几何意义(共1小题)4.(2023•宁波)如图,点A,B分别在函数y=(a>0)图象的两支上(A在第一象限),连结AB交x 轴于点C.点D,E在函数y=(b<0,x<0)图象上,AE∥x轴,BD∥y轴,连结DE,BE.若AC =2BC,△ABE的面积为9,四边形ABDE的面积为14,则a﹣b的值为12,a的值为9.【分析】依据题意,设A(m,),再由AE∥x轴,BD∥y轴,AC=2BC,可得B(﹣2m,﹣),D (﹣2m,﹣),E(,),再结合△ABE的面积为9,四边形ABDE的面积为14,即可得解.【解答】解:设A(m,),∵AE∥x轴,且点E在函数y=上,∴E(,).∵AC=2BC,且点B在函数y=上,∴B(﹣2m,﹣).∵BD∥y轴,点D在函数y=上,∴D(﹣2m,﹣).∵△ABE的面积为9,∴S△ABE=AE×(+)=(m﹣)(+)=m••==9.∴a﹣b=12.∵△ABE的面积为9,四边形ABDE的面积为14,∴S△BDE=DB•(+2m)=(﹣+)()m=(a﹣b)••()•m=3()=5.∴a=﹣3b.又a﹣b=12.∴a=9.故答案为:12,9.五.反比例函数图象上点的坐标特征(共2小题)5.(2023•德州)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(6,3),D是OA的中点,AC,BD交于点E,函数的图象过点B.E.且经过平移后可得到一个反比例函数的图象,则该反比例函数的解析式()A.y=﹣B.C.D.【分析】先根据函数图象经过点B和点E,求出a和b,再由所得函数解析式即可解决问题.【解答】解:由题知,A(6,0),B(6,3),C(0,3),令直线AC的函数表达式为y1=k1x+b1,则,解得,所以.又因为点D为OA的中点,所以D(3,0),同理可得,直线BD的函数解析式为y2=x﹣3,由得,x=4,则y=4﹣3=1,所以点E坐标为(4,1).将B,E两点坐标代入函数解析式得,,解得.所以,则,将此函数图象向左平移3个单位长度,再向下平移4个单位长度,所得图象的函数解析式为:.故选:D.6.如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=(k>0)的图象经过斜边OB的中点C.(1)k=;(2)D为该反比例函数图象上的一点,若DB∥AC,则OB2﹣BD2的值为4.【分析】(1)根据直角三角形的性质,求出A、B两点坐标,作出辅助线,证得△OPC≌△APC(HL),利用勾股定理及待定系数法求函数解析式即可解答.(2)求出AC、BD的解析式,再联立方程组,求得点D的坐标,分两种情况讨论即可求解.【解答】解:(1)在Rt△OAB中,AB=2,∠AOB=30°,∴,∴,∵C是OB的中点,∴OC=BC=AC=2,如图,过点C作CP⊥OA于P,∴△OPC≌△APC(HL),∴,在Rt△OPC中,PC=,∴C(,1).∵反比例函数y=(k>0)的图象经过斜边OB的中点C,∴,解得k=.故答案为:.(2)设直线AC的解析式为y=k1x+b(k≠0),则,解得,∴AC的解析式为y=﹣x+2,∵AC∥BD,∴直线BD的解析式为y=﹣x+4,∵点D既在反比例函数图象上,又在直线BD上,∴联立得,解得,,当D的坐标为(2+3,)时,BD2==9+3=12,∴OB2﹣BD2=16﹣12=4;当D的坐标为(2﹣3,)时,BD2=+=9+3=12,∴OB2﹣BD2=16﹣12=4;综上,OB2﹣BD2=4.故答案为:4.六.反比例函数与一次函数的交点问题(共1小题)7.(2023•湖州)已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t,p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠﹣2),点C(t,m)和点D(t+2,n)在函数的图象上.当p﹣m与q﹣n的积为负数时,t的取值范围是()A.或B.或C.﹣3<t<﹣2或﹣1<t<0D.﹣3<t<﹣2或0<t<1【分析】将交点的横坐标1代入两个函数,令二者函数值相等,得k1=k2.令k1=k2=k,代入两个函数表达式,并分别将点A、B的坐标和点C、D的坐标代入对应函数,进而分别求出p﹣m与q﹣n的表达式,代入解不等式(p﹣m)(q﹣n)<0并求出t的取值范围即可.【解答】解:∵y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,∴k1=k2.令k1=k2=k(k>0),则y=k1x=kx,=.将点A(t,p)和点B(t+2,q)代入y=kx,得;将点C(t,m)和点D(t+2,n)代入y=,得.∴p﹣m=kt﹣=k(t﹣),q﹣n=k(t+2)﹣=k(t+2﹣),∴(p﹣m)(q﹣n)=k2(t﹣)(t+2﹣)<0,∴(t﹣)(t+2﹣)<0.∵(t﹣)(t+2﹣)=•=<0,∴<0,∴t(t﹣1)(t+2)(t+3)<0.①当t<﹣3时,t(t﹣1)(t+2)(t+3)>0,∴t<﹣3不符合要求,应舍去.②当﹣3<t<﹣2时,t(t﹣1)(t+2)(t+3)<0,∴﹣3<t<﹣2符合要求.③当﹣2<t<0时,t(t﹣1)(t+2)(t+3)>0,∴﹣2<t<0不符合要求,应舍去.④当0<t<1时,t(t﹣1)(t+2)(t+3)<0,∴0<t<1符合要求.⑤当t>1时,t(t﹣1)(t+2)(t+3)>0,∴t>1不符合要求,应舍去.综上,t的取值范围是﹣3<t<﹣2或0<t<1.故选:D.七.二次函数图象与系数的关系(共3小题)8.(2023•乐至县)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).现有以下结论:①abc<0;②5a+c=0;③对于任意实数m,都有2b+bm≤4a﹣am2;④若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,则y1<y2,其中正确的结论是()A.①②B.②③④C.①②④D.①②③④【分析】根据题意和函数图象,利用二次函数的性质,可以判断各个小题中的结论是否正确,从而可以解答本题.【解答】解:由图象可得,a>0,b>0,c<0,∴abc<0,故①正确,∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).∴﹣=﹣2,a+b+c=0,∴b=4a,∴a+b+c=a+4a+c=0,故5a+c=0,故②正确,∵当x=﹣2时,y=4a﹣2b+c取得最小值,∴am2+bm+c≥4a﹣2b+c,即2b+bm≥4a﹣am2(m为任意实数),故③错误,∵抛物线开口向上,对称轴为直线x=﹣2,若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,∴y1<y2,故④正确;故选:C.9.(2023•丹东)抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为A(﹣3,0),与y轴交于点C,点D是抛物线的顶点,对称轴为直线x=﹣1,其部分图象如图所示,则以下4个结论:①abc>0;②E(x1,y1),F(x2,y2)是抛物线y=ax2+bx(a≠0)上的两个点,若x1<x2,且x1+x2<﹣2,则y1<y2;③在x轴上有一动点P,当PC+PD的值最小时,则点P的坐标为;④若关于x的方程ax2+b(x﹣2)+c =﹣4(a≠0)无实数根,则b的取值范围是b<1.其中正确的结论有()A.1个B.2个C.3个D.4个【分析】根据所给函数图象可得出a,b,c的正负,再结合抛物线的对称性和增减性即可解决问题.【解答】解:根据所给函数图象可知,a>0,b>0,c<0,所以abc<0,故①错误.因为抛物线y=ax2+bx的图象可由抛物线y=ax2+bx+c的图象沿y轴向上平移|c|个单位长度得到,所以抛物线y=ax2+bx的增减性与抛物线y=ax2+bx+c的增减性一致.则当x<﹣1时,y随x的增大而减小,又x1<x2,且x1+x2<﹣2,若x2<﹣1,则E,F两点都在对称轴的左侧,此时y1>y2.故②错误.作点C关于x轴的对称点C′,连接C′D与x轴交于点P,连接PC,此时PC+PD的值最小.将A(﹣3,0)代入二次函数解析式得,9a﹣3b+c=0,又,即b=2a,所以9a﹣6a+c=0,则c=﹣3a.又抛物线与y轴的交点坐标为C(0,c),则点C坐标为(0,﹣3a),所以点C′坐标为(0,3a).又当x=﹣1时,y=﹣4a,即D(﹣1,﹣4a).设直线C′D的函数表达式为y=kx+3a,将点D坐标代入得,﹣k+3a=﹣4a,则k=7a,所以直线C′D的函数表达式为y=7ax+3a.将y=0代入得,x=.所以点P的坐标为(,0).故③正确.将方程ax2+b(x﹣2)+c=﹣4整理得,ax2+bx+c=2b﹣4,因为方程没有实数根,所以抛物线y=ax2+bx+c与直线y=2b﹣4没有公共点,所以2b﹣4<﹣4a,则2b﹣4<﹣2b,解得b<1,又b>0,所以0<b<1.故④错误.所以正确的有③.故选:A.10.(2023•河北)已知二次函数y=﹣x2+m2x和y=x2﹣m2(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为()A.2B.m2C.4D.2m2【分析】求出三个交点的坐标,再构建方程求解.【解答】解:令y=0,则﹣x2+m2x=0和x2﹣m2=0,∴x=0或x=m2或x=﹣m或x=m,∵这四个交点中每相邻两点间的距离都相等,若m>0,则m2=2m,∴m=2,若m<0时,则m2=﹣2m,∴m=﹣2.∵抛物线y=x2﹣m2的对称轴为直线x=0,抛物线y=﹣x2+m2x的对称轴为直线x=,∴这两个函数图象对称轴之间的距离==2.故选:A.八.二次函数图象上点的坐标特征(共1小题)11.(2023•广东)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac 的值为()A.﹣1B.﹣2C.﹣3D.﹣4【分析】过A作AH⊥x轴于H,根据正方形的性质得到∠AOB=45°,得到AH=OH,利用待定系数法求得a、c的值,即可求得结论.【解答】解:过A作AH⊥x轴于H,∵四边形ABCO是正方形,∴∠AOB=45°,∴∠AOH=45°,∴AH=OH,设A(m,m),则B(0,2m),∴,解得am=﹣1,m=,∴ac的值为﹣2,故选:B.九.二次函数与不等式(组)(共1小题)12.(2023•西宁)直线y1=ax+b和抛物线(a,b是常数,且a≠0)在同一平面直角坐标系中,直线y1=ax+b经过点(﹣4,0).下列结论:①抛物线的对称轴是直线x=﹣2;②抛物线与x轴一定有两个交点;③关于x的方程ax2+bx=ax+b有两个根x1=﹣4,x2=1;④若a >0,当x<﹣4或x>1时,y1>y2.其中正确的结论是()A.①②③④B.①②③C.②③D.①④【分析】根据直线y1=ax+b经过点(﹣4,0).得到b=4a,于是得到=ax2+4ax,求得抛物线的对称轴是直线x=﹣﹣=2;故①正确;根据Δ=16a2>0,得到抛物线与x轴一定有两个交点,故②正确;把b=4a,代入ax2+bx=ax+b得到x2+3x﹣4=0,求得x1=﹣4,x2=1;故③正确;根据a>0,得到抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,于是得到结论.【解答】解:∵直线y1=ax+b经过点(﹣4,0).∴﹣4a+b=0,∴b=4a,∴=ax2+4ax,∴抛物线的对称轴是直线x=﹣﹣=2;故①正确;∵=ax2+4ax,∴Δ=16a2>0,∴抛物线与x轴一定有两个交点,故②正确;∵b=4a,∴方程ax2+bx=ax+b为ax2+4ax=ax+4a得,整理得x2+3x﹣4=0,解得x1=﹣4,x2=1;故③正确;∵a>0,抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,∴当x<﹣4或x>1时,y1<y2.故④错误,故选:B.一十.三角形中位线定理(共1小题)13.(2023•广州)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点M是边AC上一动点,点D,E分别是AB,MB的中点,当AM=2.4时,DE的长是 1.2.若点N在边BC上,且CN=AM,点F,G分别是MN,AN的中点,当AM>2.4时,四边形DEFG面积S的取值范围是3≤S≤4.【分析】依据题意,根据三角形中位线定理可得DE=AM=1.2;设AM=x,从而DE=x,由DE∥AM,且DE=AM,又FG∥AM,FG=AM,进而DE∥FG,DE=FG,从而四边形DEFG是平行四边形,结合题意可得DE边上的高为(4﹣x),故四边形DEFG面积S=4x﹣x2,进而利用二次函数的性质可得S的取值范围.【解答】解:由题意,点D,E分别是AB,MB的中点,∴DE是三角形ABM的中位线.∴DE=AM=1.2.如图,设AM=x,∴DE=AM=x.由题意得,DE∥AM,且DE=AM,又FG∥AM,FG=AM,∴DE∥FG,DE=FG.∴四边形DEFG是平行四边形.由题意,GF到AC的距离是x,BC==8,∴DE边上的高为(4﹣x).∴四边形DEFG面积S=2x﹣x2,=﹣(x﹣4)2+4.∵2.4<x≤6,∴3≤S≤4.故答案为:1.2;3≤S≤4.一十一.矩形的性质(共2小题)14.(2023•宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连结AE,AD,设△AED,△ABE,△ACD的面积分别为S,S1,S2,若要求出S﹣S1﹣S2的值,只需知道()A.△ABE的面积B.△ACD的面积C.△ABC的面积D.矩形BCDE的面积【分析】作AG⊥ED于点G,交BC于点F,可证明四边形BFGE是矩形,AF⊥BC,可推导出S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,所以只需知道S△ABC,就可求出S﹣S1﹣S2的值,于是得到问题的答案.【解答】解:作AG⊥ED于点G,交BC于点F,∵四边形BCDE是矩形,∴∠FBE=∠BEG=∠FGE=90°,BC∥ED,BC=ED,BE=CD,∴四边形BFGE是矩形,∠AFB=∠FGE=90°,∴FG=BE=CD,AF⊥BC,∴S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,∴只需知道S△ABC,就可求出S﹣S1﹣S2的值,故选:C.15.(2023•河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为2或1+.【分析】以点D,M,N为顶点的三角形是直角三角形时,分两种情况:如图1,当∠MND=90°时,如图2,当∠NMD=90°时,根据矩形的性质和等腰直角三角形的性质即可得到结论.【解答】解:以点D,M,N为顶点的三角形是直角三角形时,分两种情况:①如图1,当∠MND=90°时,则MN⊥AD,∵四边形ABCD是矩形,∴∠A=90°,∴MN∥AB,∵M为对角线BD的中点,∴AN=DN,∵AN=AB=1,∴AD=2AN=2;如图2,当∠NMD=90°时,则MN⊥BD,∵M为对角线BD的中点,∴BM=DM,∴MN垂直平分BD,∴BN=DN,∵∠A=90°,AB=AN=1,∴BN=AB=,∴AD=AN+DN=1+,综上所述,AD的长为2或1+.故答案为:2或1+.一十二.正方形的性质(共2小题)16.如图,在边长为4的正方形ABCD中,点G是BC上的一点,且BG=3GC,DE⊥AG于点E,BF∥DE,且交AG于点F,则tan∠EDF的值为()A.B.C.D.【分析】由正方形ABCD的边长为4及BG=3CG,可求出BG的长,进而求出AG的长,证△ADE∽△GAB,利用相似三角形对应边成比例可求得AE、DE的长,证△ABF≌△DAE,得AF=DE,根据线段的和差求得EF的长即可.【解答】解:∵四边形ABCD是正方形,AB=4,∴BC=CD=DA=AB=4,∠BAD=∠ABC=90°,AD∥BC,∴∠DAE=∠AGB,∵BG=3CG,∴BG=3,∴在Rt△ABG中,AB2+BG2=AG2,∴AG=,∵DE⊥AG,∴∠DEA=∠DEF=∠ABC=90°,∴△ADE∽△GAB,∴AD:GA=AE:GB=DE:AB,∴4:5=AE:3=DE:4,∴AE=,DE=,又∵BF∥DE,∴∠AFB=∠DEF=90°,又∵AB=AD,∠DAE=∠ABF(同角的余角相等),∴△ABF≌△DAE,∴AF=DE=,∴EF=AF﹣AE=,∴tan∠EDF=,故选:A.17.(2023•湖州)如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,直角顶点E,F,G,H分别在边BF,CG,DH,AE上.(1)若EF=3cm,AE+FC=11cm,则BE的长是4cm.(2)若,则tan∠DAH的值是3.【分析】(1)将AE和FC用BE表示出来,再代入AE+FC=11cm,即可求出BE的长;(2)由已知条件可以证明∠DAH=∠CDG,从而得到tan∠DAH=tan∠CDG,设AH=x,DG=5k,GH =4k,用x和k的式子表示出CG,再利用tan∠DAH=tan∠CDG列方程,解出x,从而求出tan∠DAH 的值.【解答】解:(1)∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∵AE+FC=11cm,∴BE+BF=11cm,即BE+BE+EF=11cm,即2BE+EF=11cm,∵EF=3cm,∴2BE+3cm=11cm,∴BE=4cm,故答案为:4;(2)设AH=x,∵,∴可设DG=5k,GH=4k,∵四边形EFGH是正方形,∴HE=EF=FG=GH=4k,∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∠ABE=∠CBF=45°,∴CG=CF+GF=BF+4k=BE+8k=AH+12k=x+12k,∠ABC=∠ABE+∠CBF=45°+45°=90°,∵四边形ABCD对角互补,∴∠ADC=90°,∴∠ADH+∠CDG=90°,∵四边形EFGH是正方形,∴∠AHD=∠CGD=90°,∴∠ADH+∠DAH=90°,∴∠DAH=∠CDG,∴tan∠DAH=tan∠CDG,∴,即,整理得:x2+12kx﹣45k2=0,解得x1=3k,x2=﹣15k(舍去),∴tan∠DAH===3.故答案为:3.一十三.正多边形和圆(共1小题)18.(2023•河北)将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中:(1)∠α=30度;(2)中间正六边形的中心到直线l的距离为2(结果保留根号).【分析】(1)作图后,结合正多边形的外角的求法即可得到结论;(2)把问题转化为图形问题,首先作出图形,标出相应的字母,把正六边形的中心到直线l的距离转化为求ON=OM+BE,再根据正六边形的性质以及三角函数的定义,分别求出OM,BE即可.【解答】解:(1)作图如图所示,∵多边形是正六边形,∴∠ACB=60°,∵BC∥直线l,∴∠ABC=90°,∴α=30°;故答案为:30°;(2)取中间正六边形的中心为O,作图如图所示,由题意得,AG∥BF,AB∥GF,BF⊥AB,∴四边形ABFG为矩形,∴AB=GF,∵∠BAC=∠FGH,∠ABC=∠GFH=90°,∴△ABC≌△GFH(SAS),∴BC=FH,在Rt△PDE中,DE=1,PE=,由图1知AG=BF=2PE=2,OM=PE=,∵,∴,∴,∵,∴,∴.∴中间正六边形的中心到直线l的距离为2,故答案为:2.一十四.扇形面积的计算(共1小题)19.(2023•温州)图1是4×4方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为5.若点A,N,M在同一直线上,AB∥PN,DE=EF,则题字区域的面积为.【分析】根据不共线三点确定一个圆,根据对称性得出圆心的位置,进而垂径定理、勾股定理求得r,连接OE,取ED的中点T,连接OT,在Rt△OET中,根据勾股定理即可求解.【解答】解:如图所示,依题意,GH=2=GQ,∵过左侧的三个端点Q,K,L作圆,QH=HL=4,又NK⊥QL,∴O在KN上,连接OQ,则OQ为半径,∵OH=r﹣KH=r﹣2,在Rt△OHQ中,OH2+QH2=QO2,∴(r﹣2)2+42=r2,解得:r=5;连接OE,取ED的中点T,连接OT,交AB于点S,连接PB,AM,过点O作OU⊥AM于点U.连接OA.由△OUN∽△NPM,可得==,∴OU=.MN=2,∴NU=,∴AU==,∴AN=AU﹣NU=2,∴AN=MN,∵AB∥PN,∴AB⊥OT,∴AS=SB,∴NS∥BM,∴NS∥MP,∴M,P,B共线,又NB=NA,∴∠ABM=90°,∵MN=NB,NP⊥MP,∴MP=PB=2,∴NS=MB=2,∵KH+HN=2+4=6,∴ON=6﹣5=1,∴OS=3,∵,设EF=ST=a,则,在Rt△OET中,OE2=OT2+TE2,即,整理得5a2+12a﹣32=0,即(a+4)(5a﹣8)=0,解得:或a=﹣4,∴题字区域的面积为.故答案为:.一十五.轴对称-最短路线问题(共1小题)20.(2023•安徽)如图,E是线段AB上一点,△ADE和△BCE是位于直线AB同侧的两个等边三角形,点P,F分别是CD,AB的中点.若AB=4,则下列结论错误的是()A.P A+PB的最小值为3B.PE+PF的最小值为2C.△CDE周长的最小值为6D.四边形ABCD面积的最小值为3【分析】延长AD,BC交于M,过P作直线l∥AB,由△ADE和△BCE是等边三角形,可得四边形DECM 是平行四边形,而P为CD中点,知P为EM中点,故P在直线l上运动,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB=P A'+PB最小,即可得P A+PB 最小值A'B==2,判断选项A错误;由PM=PE,即可得当M,P,F共线时,PE+PF 最小,最小值为MF的长度,此时PE+PF的最小值为2,判断选项B正确;过D作DK⊥AB于K,过C作CT⊥AB于T,由△ADE和△BCE是等边三角形,得KT=KE+TE=AB=2,有CD≥2,故△CDE周长的最小值为6,判断选项C正确;设AE=2m,可得S四边形ABCD=(m﹣1)2+3,即知四边形ABCD面积的最小值为3,判断选项D正确.【解答】解:延长AD,BC交于M,过P作直线l∥AB,如图:∵△ADE和△BCE是等边三角形,∴∠DEA=∠MBA=60°,∠CEB=∠MAB=60°,∴DE∥BM,CE∥AM,∴四边形DECM是平行四边形,∵P为CD中点,∴P为EM中点,∵E在线段AB上运动,∴P在直线l上运动,由AB=4知等边三角形ABM的高为2,∴M到直线l的距离,P到直线AB的距离都为,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB =P A'+PB最小,此时P A+PB最小值A'B===2,故选项A错误,符合题意;∵PM=PE,∴PE+PF=PM+PF,∴当M,P,F共线时,PE+PF最小,最小值为MF的长度,∵F为AB的中点,∴MF⊥AB,∴MF为等边三角形ABM的高,∴PE+PF的最小值为2,故选项B正确,不符合题意;过D作DK⊥AB于K,过C作CT⊥AB于T,如图,∵△ADE和△BCE是等边三角形,∴KE=AE,TE=BE,∴KT=KE+TE=AB=2,∴CD≥2,∴DE+CE+CD≥AE+BE+2,即DE+CE+CD≥AB+2,∴DE+CE+CD≥6,∴△CDE周长的最小值为6,故选项C正确,不符合题意;设AE=2m,则BE=4﹣2m,∴AK=KE=m,BT=ET=2﹣m,DK=AK=m,CT=BT=2﹣m,∴S△ADK=m•m=m2,S△BCT=(2﹣m)(2﹣m)=m2﹣2m+2,S梯形DKTC =(m+2﹣m)•2=2,∴S四边形ABCD=m2+m2﹣2m+2+2=m2﹣2m+4=(m﹣1)2+3,∴当m=1时,四边形ABCD面积的最小值为3,故选项D正确,不符合题意;故选:A.一十六.翻折变换(折叠问题)(共2小题)21.(2023•乐至县)如图,在平面直角坐标系xOy中,边长为2的等边△ABC的顶点A、B分别在x轴、y 轴的正半轴上移动,将△ABC沿BC所在直线翻折得到△DBC,则OD的最大值为+1.【分析】过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,在Rt△ABO 中利用斜边中线性质求出OE,根据OE+DE≥OD确定当D、O、E三点共线时OD最大,最大值为OD =OE+DE.【解答】解:如图,过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,∵等边三角形ABC的边长为2,∴AB=2,∠ABC=60°,由翻折可知:∠DBC=∠ABC=60°,DB=AB=2,∴∠DBF=60°,∵DF⊥AB,∴∠DFB=90°,∴∠BDF=30°,∴BF=BD=1,∴DF=BF=,∵E是AB的中点,∴AE=BE=OE=AB=1,∴EF=BE+BF=2,∴DE===,∴OD≤DE+OE=+1,∴当D、E、O三点共线时OD最大,最大值为+1.故答案为:+1.22.(2023•南京)如图,在菱形纸片ABCD中,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB′⊥AD,垂足为F.若CF=4cm,FB′=1cm,则BE=cm.【分析】作EH⊥BC于点H,由CF=4cm,FB′=1cm,求得B′C=5cm,由折叠得BC=B′C=5cm,由菱形的性质得BC∥AD,DC=BC=5cm,∠B=∠D,因为CB′⊥AD于点F,所以∠BCB′=∠CFD =90°,则∠BCE=∠B′CE=45°,DF==3cm,所以∠HEC=∠BCE=45°,则CH=EH,由=sin B=sin D=,=cos B=cos D=,得CH=EH=BE,BH=BE,于是得BE+BE =5,则BE=cm.【解答】解:作EH⊥BC于点H,则∠BHE=∠CHE=90°,∵CF=4cm,FB′=1cm,∴B′C=CF+FB′=4+1=5(cm),由折叠得BC=B′C=5cm,∠BCE=∠B′CE,∵四边形ABCD是菱形,∴BC∥AD,DC=BC=5cm,∠B=∠D,∵CB′⊥AD于点F,∴∠BCB′=∠CFD=90°,∴∠BCE=∠B′CE=∠BCB′=×90°=45°,DF===3(cm),∴∠HEC=∠BCE=45°,∴CH=EH,∵=sin B=sin D==,=cos B=cos D==,∴CH=EH=BE,BH=BE,∴BE+BE=5,∴BE=cm,故答案为:.一十七.旋转的性质(共1小题)23.(2023•西宁)如图,在矩形ABCD中,点P在BC边上,连接P A,将P A绕点P顺时针旋转90°得到P A′,连接CA′,若AD=9,AB=5,CA′=2,则BP=2.【分析】过A′点作A′H⊥BC于H点,如图,根据旋转的性质得到P A=P A′,再证明△ABP≌△PHA′得到PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=4﹣x,然后在Rt△A′CH中利用勾股定理得到x2+(4﹣x)2=(2)2,于是解方程求出x即可.【解答】解:过A′点作A′H⊥BC于H点,如图,∵四边形ABCD为矩形,∴BC=AD=9,∠B=90°,∵将P A绕点P顺时针旋转90°得到P A′,∴P A=P A′,∵∠P AB+∠APB=90°,∠APB+∠A′PH=90°,∴∠P AB=∠A′PH,在△ABP和△PHA′中,,∴△ABP≌△PHA′(AAS),∴PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=9﹣x﹣5=4﹣x,在Rt△A′CH中,x2+(4﹣x)2=(2)2,解得x1=x2=2,即BP的长为2.故答案为:2.一十八.相似三角形的判定与性质(共2小题)24.(2023•杭州)如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设=k,若AD=DF,则=(结果用含k的代数式表示).【分析】方法一:先根据轴对称的性质和已知条件证明DE∥AC,再证△BDE∽△BAC,推出EC=k•AB,通过证明△ABC∽△ECF,推出CF=k2•AB,即可求出的值.方法二:证明AD=DF=BD,可得BF⊥AC,设AB=AC=1,BC=k,CF=x,则AF=1﹣x,利用勾股定理列方程求出x的值,进而可以解决问题.【解答】解:方法一:∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB,∵AD=DF,∴∠A=∠DF A,∵点B和点F关于直线DE对称,∴∠BDE=∠FDE,∵∠BDE+∠FDE=∠BDF=∠A+∠DF A,∴∠FDE=∠DF A,∴DE∥AC,∴∠C=∠DEB,∠DEF=∠EFC,∵点B和点F关于直线DE对称,∴∠DEB=∠DEF,∴∠C=∠EFC,∵AB=AC,∴∠C=∠B,∵∠ACB=∠EFC,∴△ABC∽△ECF,∴=,∵DE∥AC,∴∠BDE=∠A,∠BED=∠C,∴△BDE∽△BAC,∴==,∴EC=BC,∵=k,∴BC=k•AB,∴EC=k•AB,∴=,∴CF=k2•AB,∴====.方法二:如图,连接BF,∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB=DF,∴BF⊥AC,设AB=AC=1,则BC=k,设CF=x,则AF=1﹣x,由勾股定理得,AB2﹣AF2=BC2﹣CF2,∴12﹣(1﹣x)2=k2﹣x2,∴x=,∴AF=1﹣x=,∴=.故答案为:.25.(2023•广东)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为15.【分析】根据相似三角形的性质,利用相似比求出梯形的上底和下底,用面积公式计算即可.【解答】解:如图,∵BF∥DE,∴△ABF∽△ADE,∴=,∵AB=4,AD=4+6+10=20,DE=10,∴=,∴BF=2,∴GF=6﹣2=4,∵CK∥DE,∴△ACK∽△ADE,∴=,∵AC=4+6=10,AD=20,DE=10,∴=,∴CK=5,∴HK=6﹣5=1,∴阴影梯形的面积=(HK+GF)•GH=(1+4)×6=15.故答案为:15.一十九.相似三角形的应用(共1小题)26.(2023•南京)如图,不等臂跷跷板AB的一端A碰到地面时,另一端B到地面的高度为60cm;当AB 的一端B碰到地面时,另一端A到地面的高度为90cm,则跷跷板AB的支撑点O到地面的高度OH是()A.36cm B.40cm C.42cm D.45cm【分析】过点B作BC⊥AH,垂足为C,再证明A字模型相似△AOH∽△ABC,从而可得=,过点A作AD⊥BH,垂足为D,然后证明A字模型相似△ABD∽△OBH,从而可得=,最后进行计算即可解答.【解答】解:如图:过点B作BC⊥AH,垂足为C,∵OH⊥AC,BC⊥AC,∴∠AHO=∠ACB=90°,∵∠BAC=∠OAH,∴△AOH∽△ABC,∴=,∴=,如图:过点A作AD⊥BH,垂足为D,∵OH⊥BD,AD⊥BD,∴∠OHB=∠ADB=90°,∵∠ABD=∠OBH,∴△ABD∽△OBH,∴=,∴=,∴+=+,∴+=,∴+=1,解得:OH=36,∴跷跷板AB的支撑点O到地面的高度OH是36cm,故选:A.二十.解直角三角形(共1小题)27.(2023•丹东)如图,在平面直角坐标系中,点O是坐标原点,已知点A(3,0),B(0,4),点C在x 轴负半轴上,连接AB,BC,若tan∠ABC=2,以BC为边作等边三角形BCD,则点C的坐标为(﹣2,0);点D的坐标为(﹣1﹣2,2+)或(﹣1+2,2﹣).【分析】过点C作CE⊥AB于E,先求处AB=5,再设BE=t,由tan∠ABC=2得CE=2t,进而得BC =,由三角形的面积公式得S△ABC=AC•OB=AB•CE,即5×2t=4×(3+OC),则OC=﹣3,然后在Rt△BOC中由勾股定理得,由此解出t1=2,t2=10(不合题意,舍去),此时OC=﹣3=2,故此可得点C的坐标;设点D的坐标为(m,n),由两点间的距离公式得:BC2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,由△BCD为等边三角形得,整理:,②﹣①整理得m=3﹣2n,将m=3﹣2n代入①整理得n2﹣4n+1=0,解得n=,进而再求出m即可得点D的坐标.【解答】解:过点C作CE⊥AB于E,如图:∵点A(3,0),B(0,4),由两点间的距离公式得:AB==5,设BE=t,∵tan∠ABC=2,在Rt△BCE中,tan∠ABC=,∴=2,∴CE=2t,由勾股定理得:BC==t,∵CE⊥AB,OB⊥AC,AC=OC+OA=3+OC,∴S△ABC=AC•OB=AB•CE,即:5×2t=4×(3+OC),∴OC=﹣3,在Rt△BOC中,由勾股定理得:BC2﹣OB2=OC2,即,整理得:t2﹣12t+20=0,解得:t1=2,t2=10(不合题意,舍去),∴t=2,此时OC=﹣3=2,∴点C的坐标为(﹣2,0),设点D的坐标为(m,n),由两点间的距离公式得:BC2=(﹣2﹣0)2+(0﹣4)2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,∵△BCD为等边三角形,∵BD=CD=BC,∴,整理得:,②﹣①得:4m+8n=12,∴m=3﹣2n,将m=3﹣2n代入①得:(3﹣2n)2+n2﹣8n=4,整理得:n2﹣4n+1=0,解得:n=,当n=时,m=3﹣2n=,当n=时,m=3﹣2n=,∴点D的坐标为或.故答案为:(﹣2,0);或.二十一.解直角三角形的应用(共1小题)28.(2023•杭州)第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH 拼成的大正方形ABCD中,∠ABF>∠BAF,连接BE.设∠BAF=α,∠BEF=β,若正方形EFGH与正方形ABCD的面积之比为1:n,tanα=tan2β,则n=()A.5B.4C.3D.2【分析】设AE=a,DE=b,则BF=a,AF=b,解直角三角形可得,化简可得(b﹣a)2=ab,a2+b2=3ab,结合勾股定理及正方形的面积公式可求得S正方形EFGH;S正方形ABCD=1:3,进而可求解n的值.【解答】解:设AE=a,DE=b,则BF=a,AF=b,∵tanα=,tanβ=,tanα=tan2β,∴,∴(b﹣a)2=ab,∴a2+b2=3ab,∵a2+b2=AD2=S正方形ABCD,(b﹣a)2=S正方形EFGH,∴S正方形EFGH:S正方形ABCD=ab:3ab=1:3,∵S正方形EFGH:S正方形ABCD=1:n,∴n=3.故选:C.。
2024年中考数学压轴题重难点知识剖析及训练—求函数的取值范围

2024年中考数学压轴题重难点知识剖析及训练—求函数的取值范围通用的解题思路:第一步:先判定函数的增减性:一次函数、反比例函数看k ,二次函数看对称轴与区间的位置关系;第二步:当a x =时,min y y =;当b x =时,max y y =;所以max min y y y ≤≤.二次函数求取值范围之动轴定区间或者定轴动区间的分类方法:分对称轴在区间的左边、右边、中间三种情况。
(1)若自变量x 的取值范围为全体实数,如图①,函数在顶点处abx 2-=时,取到最值.(2)若abn x m 2-<≤≤,如图②,当m x =时,max y y =;当n x =时,min y y =.(3)若n x m ab≤≤<-2,如图③,当m x =,min y y =;当n x =,max y y =.(4)若n x m ≤≤,且n a b m ≤-≤2,m a b a b n -->+22,如图④,当a bx 2-=,min y y =;当n x =,max y y =.1.(中考真题)设a 、b 是任意两个不等实数,我们规定:满足不等式a ⩽x ⩽b 的实数x 的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x 与函数值y 满足:当m ⩽x ⩽n 时,有m ⩽y ⩽n,我们就称此函数是闭区间[m,n]上的“闭函数”。
(1)反比例函数xy 2013=是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;(3)若二次函数5754512--=x x y 是闭区间[a,b]上的“闭函数”,求实数a ,b 的值。
【解答】解:(1)反比例函数y=是闭区间[1,2013]上的“闭函数”.理由如下:反比例函数y=在第一象限,y随x的增大而减小,当x=1时,y=2013;当x=2013时,y=1,所以,当1≤x≤2013时,有1≤y≤2013,符合闭函数的定义,故反比例函数y=是闭区间[1,2013]上的“闭函数”;(2)分两种情况:k>0或k<0.①当k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=x;②当k<0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而减小,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=﹣x+m+n;(3)∵y=x2﹣x﹣=(x﹣2)2﹣,∴该二次函数的图象开口方向向上,最小值是﹣,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大;①当b≤2时,此二次函数y随x的增大而减小,则根据“闭函数”的定义知,,解得,(不合题意,舍去)或;②当a<2<b时,此时二次函数y=x2﹣x﹣的最小值是﹣=a,根据“闭函数”的定义知,b=a2﹣a﹣或b=b2﹣b﹣;a)当b=a2﹣a﹣时,由于b=(﹣)2﹣×(﹣)﹣=<2,不合题意,舍去;b)当b=b2﹣b﹣时,解得b=,由于b>2,所以b=;③当a≥2时,此二次函数y随x的增大而增大,则根据“闭函数”的定义知,,解得,,∵<0,∴舍去.综上所述,或.2.(中考真题)若关于x 的函数y ,当1122t x t -≤≤+时,函数y 的最大值为M ,最小值为N ,令函数2M N h -=,我们不妨把函数h 称之为函数y 的“共同体函数”.(1)①若函数4044y x =,当1t =时,求函数y 的“共同体函数”h 的值;②若函数y kx b =+(0k ≠,k ,b 为常数),求函数y 的“共同体函数”h 的解析式;(2)若函数21y x x=≥(),求函数y 的“共同体函数”h 的最大值;(3)若函数24y x x k =-++,是否存在实数k ,使得函数y 的最大值等于函数y 的“共同体函数”h 的最小值.若存在,求出k 的值;若不存在,请说明理由.解析:(1)解:①当1t =时,则111122x -≤≤+,即1322x ≤≤, 4044y x =,4044k =0>,y 随x 的增大而增大,314044404422202222M N h ⨯-⨯-∴===,②若函数y kx b =+,当0k >时,1122t x t -≤≤+,∴11,22M k t b N k t b ⎛⎫⎛⎫=++=-+ ⎪ ⎪⎝⎭⎝⎭,22M N k h -∴==,当0k <时,则11,22M k t b N k t b ⎛⎫⎛⎫=-+=++ ⎪ ⎪⎝⎭⎝⎭,22M N k h -∴==-,综上所述,0k >时,2k h =,0k <时,2kh =-,(2)解:对于函数()21y x x=≥, 20>,1x ≥,函数在第一象限内,y 随x 的增大而减小,112t ∴-≥,解得32t ≥,当1122t x t -≤≤+时,∴2424,11212122M N t t t t ====-+-+,()()()()()()2221221144442221212121212141t t M N h t t t t t t t +---⎛⎫∴==-=== ⎪-+-+-+-⎝⎭,∵当32t ≥时,241t -随t 的增大而增大,∴当32t =时,241t -取得最小值,此时h 取得最大值,最大值为()()4412121242h t t ===-+⨯;(3)对于函数24y x x k =-++()224x k =--++,10a =-<,抛物线开口向下,2x <时,y 随x 的增大而增大,2x >时,y 随x 的增大而减小,当2x =时,函数y 的最大值等于4k +,在1122t x t -≤≤+时,①当122t +<时,即3t 2<时,211422N t t k ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭,211422M t t k ⎛⎫⎛⎫=-++++ ⎪ ⎪⎝⎭⎝⎭,∴h =2M N -=22111114422222t t k t t k ⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫⎛⎫⎛⎫-++++---+-+⎢⎥⎨⎬ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭=2t -,∴h 的最小值为12(当32t =时),若124k =+,解得72k =-,但32t <,故72k =-不合题意,故舍去;②当122t ->时,即5t 2>时,211422M t t k ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭,211422N t t k ⎛⎫⎛⎫=-++++ ⎪ ⎪⎝⎭⎝⎭,∴h =2M N -=2t -,∴h 的最小值为12(当52t =时),若124k =+,解得72k =-,但52t >,故72k =-不合题意,故舍去③当11222t t -≤≤+时,即3522t ≤≤时,4M k =+,i )当112222t t ⎛⎫⎛⎫--≥+- ⎪ ⎪⎝⎭⎝⎭时,即322t ≤≤时,211422N t t k⎛⎫⎛⎫=--+-+ ⎪ ⎝⎭⎝⎭22114415252222228k t t k M N h t t ⎛⎫⎛⎫++---- ⎪ ⎪-⎝⎭⎝⎭===-+ 对称轴为52t =,102>,抛物线开口向上,在322t ≤≤上,当t =2时,h 有最小值18,148k ∴=+,解得318k =-;i i )当112222t t ⎛⎫⎛⎫--≤+- ⎪ ⎪⎝⎭⎝⎭时,即522t ≤≤时,4M k =+,N =211422t t k ⎛⎫⎛⎫-++++ ⎪ ⎝⎭⎝⎭,∴2211441392222228k t t kM N h t t ⎛⎫⎛⎫+++-+- ⎪ ⎪-⎝⎭⎝⎭===-+, 对称轴为32t =,102>,抛物线开口向上,在522t <≤上,当t =2时,h 有最小值18,148k ∴=+解得318k =-,综上所述,2t =时,存在318k =-.3.(中考真题)我们不妨约定:若某函数图像上至少存在不同的两点关于原点对称,则把该函数称之为“H 函数”,其图像上关于原点对称的两点叫做一对“H 点”,根据该约定,完成下列各题(1)在下列关于x 的函数中,是“H 函数”的,请在相应题目后面的括号中打“√”,不是“H 函数”的打“×”①2y x =()②my (m 0)x=≠()③31y x =-()(2)若点()1,A m 与点(),4B n -关于x 的“H 函数”()20y ax bx c a =++≠的一对“H 点”,且该函数的对称轴始终位于直线2x =的右侧,求,,a b c 的值或取值范围;(3)若关于x 的“H 函数”223y ax bx c =++(a ,b ,c 是常数)同时满足下列两个条件:①0a b c ++=,②(2)(23)0c b a c b a +-++<,求该H 函数截x 轴得到的线段长度的取值范围.【详解】(1)①2y x =是“H 函数”②my (m 0)x=≠是“H 函数”③31y x =-不是“H 函数”;故答案为:√;√;×;(2)∵A,B 是“H 点”∴A,B 关于原点对称,∴m=4,n=1∴A(1,4),B (-1,-4)代入()20y ax bx c a =++≠,得44a b c a b c ++=⎧⎨-+=-⎩,解得40b ac =⎧⎨+=⎩,又∵该函数的对称轴始终位于直线2x =的右侧,∴-2b a >2,∴-42a >2,∴-1<a <0,∵a+c=0,∴0<c <1,综上,-1<a <0,b=4,0<c <1;(3)∵223y ax bx c =++是“H 函数”,∴设H 点为(p,q )和(-p,-q ),代入得222323ap bp c qap bp c q⎧++=⎨-+=-⎩,解得ap 2+3c=0,2bp=q ,∵p 2>0,∴a,c 异号,∴ac <0,∵a+b+c=0,∴b=-a-c ,∵(2)(23)0c b a c b a +-++<,∴(2)(23)0c a c a c a c a -----+<,∴(2)(2)0c a c a -+<,∴c 2<4a 2,∴22c a<4,∴-2<c a <2,∴-2<c a <0,设t=c a ,则-2<t <0,设函数与x 轴的交点为(x 1,0)(x 2,0),∴x 1,x 2是方程223ax bx c ++=0的两根,∴12x x -=,又∵-2<t <0,∴2<12x x -<4.(2022春•芙蓉区校级期末)在y 关于x 的函数中,对于实数a ,b ,当a ≤x ≤b 且b =a +3时,函数y 有最大值y max ,最小值y min ,设h =y max ﹣y min ,则称h 为y 的“极差函数”(此函数为h 关于a 的函数);特别的,当h =y max ﹣y min 为一个常数(与a 无关)时,称y 有“极差常函数”.(1)判断下列函数是否有“极差常函数”?如果是,请在对应()内画“√”,如果不是,请在对应()内画“×”.①y =2x ();②y =﹣2x +2();③y =x 2().(2)y 关于x 的一次函数y =px +q ,它与两坐标轴围成的面积为1,且它有“极差常函数”h =3,求一次函数解析式;(3)若,当a ≤x ≤b (b =a +3)时,写出函数y =ax 2﹣bx +4的“极差函数”h ;并求4ah 的取值范围.【解答】解:(1)①∵y =2x 是一次函数,且y 随x 值的增大而增大,∴h =2(a +3)﹣2a =6,∴y =2x 是“极差常函数”,故答案为:√;②∵y =﹣2x +2是一次函数,且y 随x 值的增大而减小,∴h =﹣2a +2﹣[﹣2(a +3)+2]=6,∴y =﹣2x +2是“极差常函数”,故答案为:√;∵y =x 2是二次函数,函数的对称轴为直线x =0,当a +3≤0时,h =a 2﹣(a +3)2=﹣9﹣6a ;当a ≥0时,h =(a +3)2﹣a 2=9+6a ;∴y =x 2不是“极差常函数”,故答案为:×;(2)当x =0时,y =q ,∴函数与y 轴的交点为(0,q ),当y =0时,x =﹣,∴函数与x 轴的交点为(﹣,0),∴S =×|q |×|﹣|=1,∴=2,当p >0时,h =p (a +3)+q ﹣(pa +q )=3,∴p =1,∴q =±,∴函数的解析式为y =x ;当p <0时,h =pa +q ﹣[p (a +3)+q ]=3,∴p =﹣1,∴q =±,∴函数的解析式为y =﹣x;综上所述:函数的解析式为y =x 或y =﹣x;(3)y =ax 2﹣bx +4=a (x ﹣)2+4﹣,∴函数的对称轴为直线x =,∵b =a +3,∴x ==+,∵,∴≤+≤,≤a +3≤,∵(a +3﹣﹣)﹣(+﹣a )=2a +2﹣,∵,∴2a +2﹣>0,∴a +3到对称轴的距离,大于a 到对称轴的距离,∴当x =a +3时,y 有最大值a (a +3)2﹣(a +3)2+4,当x =时,y 有最小值4﹣=4﹣,∴h =a (a +3)2﹣(a +3)2+4﹣4+=(a +3)2(a ﹣1+),∴4ah =(2a 2+5a ﹣3)2,∵2a 2+5a ﹣3=2(a +)2﹣,,∴≤2a 2+5a ﹣3≤9,∴≤4ah ≤81.5.(雅实)若函数1y 、2y 满足12y y y =+,则称函数y 是1y 、2y 的“融合函数”.例如,一次函数121y x =+和二次函数2234y x x =+-,则1y 、2y 的“融合函数”为21253y y y x x =+=+-.(1)若反比例函数12y x=和一次函数23y kx =-,它们的“融合函数”过点()1,5,求k 的值;(2)若21y ax bx c =++为二次函数,且5a b c ++=,在x t =时取得最值,函数2y 为一次函数,且1y 、2y 的“融合函数”为224y x x =+-,当12x -≤≤时,求函数1y 的最小值(用含t 的式子表示);(3)若二次函数21y ax bx c =++与一次函数2y ax b =--,其中0a b c ++=且a b c >>,若它们的“融合函数”与x 轴交点为()1,0A x 、()2,0B x 12x -的取值范围.【解答】解:(1)由题意可得y 1、y 2的融合函数23y kx x=+-,将点()1,5代入,可得:523k =+-,解得6k =.(2)∵12y y y =+,∴()()2222124214y y y x x ax bx c a x b x c =-=+----=-+---,∵y 2为一次函数,∴20a -=,即2a =,∴212y x bx c =++在x =t 处取得最值,∴4bt =-,即4b t =-,∴5a b c ++=,即54234c t t =+-=+,∴212434y x tx t =-++,对称轴:x t =.①若1t ≤-时,即当1x =-时,min 58y t =+,②若12t -<<时,即当x t =时,2min 234y t t =-++,③若2t ≥时,即当2x =时,min 114y t =-.(3)y 1、y 2的融合函数()2y ax b a x c b =+-+-,∵与y 轴交于点()1,0A x 、()2,0B x ,∴12b a x x a -+=,12c b x x a -⋅=,∵12||x x a -==,又∵0a b c ++=,∴b a c =--,∴12x x ==,∵a b c >>∴a a c c >--<,∴122c a -<<-,当2ca=-时,12maxx x -=,当12c a =-时,12min32x x -=12x <-<.6.(立信)已知:抛物线1C :2y ax bx c =++(0a >).(1)若顶点坐标为(1,1),求b 和c 的值(用含a 的代数式表示);(2)当0c <时,求函数220221y ax bx c =-++-的最大值;(3)若不论m 为任何实数,直线()214m y m x =--与抛物线1C 有且只有一个公共点,求a ,b ,c 的值;此时,若1k x k ≤≤+时,抛物线1C 的最小值为k ,求k 的值.【解答】解:(1)∵抛物线的顶点坐标为(1,1),∴y =a (x ﹣1)2+1=ax 2﹣2ax +a +1,∴b =﹣2a ,c =a +1;(2)∵y =ax 2+bx +c ,a >0,c <0,∴Δ=b 2﹣4ac >0,∴抛物线y =ax 2+bx +c (a >0)与x 轴有两个交点,∴|ax2+bx+c|≥0,∴﹣2022|ax2+bx+c|≤0,∴﹣2022|ax2+bx+c|﹣1≤﹣1,∴函数y=﹣2022|ax2+bx+c|﹣1的最大值为﹣1;(3)∵直线与抛物线C1有且只有一个公共点,∴方程组只有一组解,∴ax2+(b﹣m)x++m+c=0有两个相等的实数根,∴Δ=0,∴(b﹣m)2﹣4a(+m+c)=0,整理得:(1﹣a)m2﹣2(2a+b)m+b2﹣4ac=0,∵不论m为任何实数,(1﹣a)m2﹣2(2a+b)m+b2﹣4ac =0恒成立,∴,∴a=1,b=﹣2,c=1.此时,抛物线解析式为y=x2﹣2x+1=(x﹣1)2,∴抛物线的对称轴为直线x=1,开口向上,∵当k≤x≤k+1时,抛物线的最小值为k,∴分三种情况:k<0或0≤k≤1或k>1,①当k<0时,k+1<1,当k≤x≤k+1时,y随着x的增大而减小,则当x=k+1时,y的最小值为k,∴(k+1﹣1)2=k,解得:k=0或1,均不符合题意,舍去;②当0≤k≤1时,当x=1时,抛物线的最小值为0,∴k=0;③当k>1时,y随着x的增大而增大,则当x=k时,y的最小值为k,∴(k﹣1)2=k,解得:k=或,∵k>1,∴k=,综上所述,若k≤x≤k+1时,抛物线的最小值为k,k的值为0或.7.(长郡)对于一个函数给出如下定义:对于函数y,若当a≤x≤b,函数值y满足m≤y≤n,且满足n﹣m=k (b﹣a),则称此函数为“k属和合函数”,例如:正比例函数y=﹣3x,当1≤x≤3时,﹣9≤y≤﹣3,则﹣3﹣(﹣9)=k(3﹣1),求得:k=3,所以函数y=﹣3x为“3属和合函数”.(1)若一次函数y=kx﹣1(1≤x≤3)为“4属和合函数”,求k的值;(2)反比例函数kyx(k>0,a≤x≤b,且0<a<b)是“k属和合函数”,且a+b=3,请求出a﹣b的值;(3)已知二次函数y=﹣x2+2ax+3,当﹣1≤x≤1时,y是“k属和合函数”,求k的取值范围.【详解】解:(1)当k >0时,y 随x 的增大而增大,∵1≤x ≤3,∴k ﹣1≤y ≤3k ﹣1,∵函数y =kx ﹣1(1≤x ≤3)为“k 属和合函数”,∴(3k ﹣1)﹣(k ﹣1)=4(3﹣1),∴k =4;当k <0时,y 随x 的增大而减小,∴3k ﹣1≤y ≤k ﹣1,∴(k ﹣1)﹣(3k ﹣1)=4(3﹣1),∴k =﹣4,综上所述,k 的值为4或﹣4;(2)∵反比例函数y =kx,k >0,∴在第一象限,y 随x 的增大而减小,当a ≤x ≤b 且0<a <b 是“k 属和合函数”,∴k a ﹣kb=k (b ﹣a ),∴ab =1,∵a +b =3,∴(a ﹣b )2=(a +b )2﹣4ab =9﹣4=5,∴a ﹣b (3)∵二次函数y =﹣x 2+2ax +3的对称轴为直线x =a ,∵当﹣1≤x ≤1时,y 是“k 属和合函数”,∴当x =﹣1时,y =2﹣2a ,当x =1时,y =2+2a ,当x =a 时,y =a 2+3,①如图1,当a ≤﹣1时,当x =﹣1时,有y 最大值=2﹣2a ,当x =1时,有y 最小值=2+2a ∴(2﹣2a )﹣(2+2a )=k •[1﹣(﹣1)]=2k ,∴k =﹣2a ,而a ≤﹣1,∴k ≥2;②如图2,当﹣1<a ≤0时,当x =a 时,有y 最大值=a 2+3,当x =1时,有y 最小值=2+2a ,∴a 2+3﹣(2+2a )=2k ,∴k =2(1)2a -,∴12≤k <2;③如图3,当0<a ≤1时,当x =a 时,有y 最大值=a 2+3,当x =﹣1时,有y 最小值=2﹣2a ,∴a 2+3﹣(2﹣2a )=2k ,∴k =2(1)2a +,∴12<k ≤2;④如图4,当a >1时,当x =1时,有y 最大值=2+2a ,当x =﹣1时,有y 最小值=2﹣2a ,∴(2+2a )﹣(2﹣2a )=2k ,∴k =2a ,∴k >2.综上所述,当﹣1≤x ≤1时,y 是“k 属和合函数”,k 的取值范围为k ≥12.8.(师大附中博才)已知a 、b 是两个不相等的实数且a b <,我们规定:满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间,表示为[],.a b 对于一个函数,如果它的自变量x 与函数值y 满足:当a x b ≤≤时,有(ta y tb t ≤≤为正数),我们就称此函数是闭区间[],a b 上的“t 倍函数”.例如:正比例函数2y x =,当13x ≤≤时,26y ≤≤,则2y x =是13x ≤≤上的“2倍函数”.(1)已知反比例函数4yx=是闭区间[],m n 上的“2倍函数”,且m n +=22m n +的值;(2)①已知正比例函数y x =是闭区间[]1,2023上的“t 倍函数”,求t ;②一次函数()0y kx b k =+≠是闭区间[],m n 上的“2倍函数”,求此函数的解析式.(3)若二次函数269y x x =--是闭区间[],a b 上的“7倍函数”,求实数a 、b 的值.【详解】(1)已知反比例函数4y x=是闭区间[],m n 上的“2倍函数”,∴当m x n ≤≤时,22m y n ≤≤,当x m =时,4y m =;当x n =时,4y n=,又40k => ,∴当0x >时,y 随x 的增大而减小,当0x <时,y随x 的增大而减小,42n m ∴=,且42m n=,24mn ∴=,又m n += ,()22222023m n m mn n ∴+=++=,2220232202342019m n mn ∴+=-=-=.(2)①已知正比例函数y x =,y 随x 的增大而增大,且当1x =时,1y =;当2023x =时,2023y =,∴当12023x ≤≤时,12023y ≤≤,y x ∴=是闭区间[]1,2023上的“1倍函数”,即1t =.② 一次函数0y kx b k =+≠()是闭区间[],m n 上的“2倍函数”,∴当m x n ≤≤时,22m y n ≤≤,若0k >时,y 随x 的增大而增大,∴当x m =,则2y km b m =+=;当x n =,则2y kn b n =+=,()()2m n k m n ∴-=-,2k ∴=,将2k =代入2km b m +=,得22m b m +=,0b ∴=.∴若0k >时,函数解析式为2y x =.若0k <时,y 随x 的增大而减小,∴当x m =时,2y km b n =+=;当x n =时,2y kn b m =+=,2k ∴=-,22b m n =+.∴若0k <时,函数解析式为()22y x m n =-++,综合以上分析,函数的解析式为2y x =或()22y x m n =-++.(3)由二次函数269y x x =--解析式可知,抛物线开口向上,对称轴3x =,∴当3x <时,y 随x 的增大而减小;当3x >时,y 随x 的增大而增大, 二次函数269y x x =--是闭区间[],a b 上的“7倍函数”,∴当a x b ≤≤时,()770a y b a ≤≤≠,若3b ≤时,根据增减性,当x a =时,2697y a a b =--=;当x b =时,2697y b b a =--=,两式相减得:226677a b a b b a --+=-,()()a b a b b a ∴+-=-,1b a ∴=--,将1b a =--代入2697a a b --=得:220a a +-=,2a ∴=-或1a =,当2a =-时,1b =;当1a =时,2b =-(舍去,a b <).若3a ≥时,当x a =时,2697y a a a =--=,解得a =a =x b =时,2697y b b b =--=.解得132b =或b =均不符合a b <,舍去.若3a <,3b >时,当3x =时,236397y a =-⨯-=,187a ∴=-,则x a =时,26396949y a a =--=,若639749b =,6393343b =<,(舍去),当x b =时,2697y b b b =--=,则b =b =综上分析,2a =-,1b =或者187a =-,b =9.(长郡)定义:在平面直角坐标系中,点P (x ,y )的横、纵坐标的绝对值的和叫做点P (x ,y )的勾股值,记为[]P x y =+.(1)已知点A (1,3),B (2-,4),C 22),直接写出[]A,[]B ,[]C 的值;(2)已知点D 是直线2y x =+上一点,且[]4D =,求点D 的坐标;(3)若抛物线21y ax bx =++与直线y x =只有一个交点M ,已知点M 在第一象限,且[]24M ≤≤.令2242022t b a =-+,试求t 的取值范围.【详解】(1)解:∵A (1,3),B (−2,4),C ),∴[A ]=|1|+|3|=4,[B ]=|-2|+|4|=6,[C ;(2)设D (m ,n ),∵D 是直线y =x +2上一点,且[D ]=4,∴42m n n m ⎧+⎨+⎩==,解得13m n =⎧⎨=⎩或31m n =-⎧⎨=-⎩,∴点D 的坐标(1,3)或(-3,-1);(3)由题意方程组21y x y ax bx =⎧⎨=++⎩只有一组实数解,消去y 得2(1)10ax b x +-+=,由题意224(1)40b ac b a -=--=,∴24(1)a b =-,∴方程可以化为()()2214140b x b x -+-+=,∴1221x x b ==-,∴22,11M b b ⎛⎫ ⎪--⎝⎭,∵[]24M ≤≤,∴2121b ≤≤-或2211b -≤≤--,解得10b -≤≤或23b ≤≤,∵点M 在第一象限,∴10b -≤≤,∵22222420222(1)202222021t b a b b b b =-+=--+=++=2(1)2020b ++,∵10b -≤≤,∴20202021t ≤≤.10.(雅礼)在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:若b′=11b ab a≥⎧⎨-⎩,,<,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).(1)①点1)的限变点的坐标是;②在点A(-2,-1),B(-1,2)中有一个点是函数y=2x图象上某一个点的限变点,这个点是;(填“A”或“B”)(2)若点P在函数y=-x+3(-2≤x≤k,k>-2)的图象上,其限变点Q的纵坐标b′的取值范围是-5≤b′≤2,求k的取值范围;(3)若点P在关于x的二次函数y=x2-2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m-n,求s关于t的函数解析式及s的取值范围.【详解】(1)①根据限变点的定义可知点1)1);②(-1,-2)限变点为(-1,2),即这个点是点B.(2)依题意,y=-x+3(x≥-2)图象上的点P的限变点必在函数y=31321x xx x-+≥⎧⎨--≤⎩,,<的图象上.∴b′≤2,即当x=1时,b′取最大值2.当b′=-2时,-2=-x+3.∴x=5.当b′=-5时,-5=x-3或-5=-x+3.∴x=-2或x=8.∵-5≤b′≤2,由图象可知,k的取值范围是5≤k≤8.(3)∵y=x2-2tx+t2+t=(x-t)2+t,∴顶点坐标为(t,t).若t<1,b′的取值范围是b′≥m或b′<n,与题意不符.若t≥1,当x≥1时,y的最小值为t,即m=t;当x<1时,y的值小于-[(1-t)2+t],即n=-[(1-t)2+t].∴s=m-n=t+(1-t)2+t=t2+1.∴s关于t的函数解析式为s=t2+1(t≥1),当t=1时,s取最小值2,∴s的取值范围是s≥2.。
2024年中考数学压轴题重难点知识剖析及训练—圆与射影定理结合型压轴题(含解析)

2024年中考数学压轴题重难点知识剖析及训练—圆与射影定理结合型压轴题(含解析)射影定理模型:射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。
射影定理是数学图形计算的重要定理,在初三各名校的数学和各地中考试题中都多次考查了这一模型的应用。
图形推导过程结论因为⎩⎨⎧∠=∠∠=∠ACDABCAA∴ABC∆∽ACD∆∴ACABADAC=①ABADAC ⋅=2;②BABDBC⋅=2;③BDADCD⋅=21.(长沙中考)如图,点P在以MN为直径的半圆上运动(点P不与M,N重合),PQ⊥MN,NE平分∠MNP,交PM于点E,交PQ于点F.(1)+=.(2)若PN2=PM•MN,则=.【解答】解:(1)∵MN 为⊙O 的直径,∴∠MPN =90°,∵PQ ⊥MN ,∴∠PQN =∠MPN =90°,∵NE 平分∠PNM ,∴∠MNE =∠PNE ,∴△PEN ∽△QFN ,∴,即①,∵∠PNQ +∠NPQ =∠PNQ +∠PMQ =90°,∴∠NPQ =∠PMQ ,∵∠PQN =∠PQM =90°,∴△NPQ ∽△PMQ ,∴②,∴①×②得,∵QF =PQ ﹣PF ,∴=1﹣,∴+=1,故答案为:1;(2)∵∠PNQ =∠MNP ,∠NQP =∠NPM ,∴由射影定理得:PN 2=QN •MN ,∵PN 2=PM •MN ,∴PM =QN ,∴,∵,∴,∴,∴NQ 2=MQ 2+MQ •NQ ,即,设,则x 2+x ﹣1=0,解得,x =,或x =﹣<0(舍去).2.(北雅)如图,点P 在以MN 为直径的半圆上运动(不与M 、N 重合),PH MN ⊥于H 点,过N 点作NQ 与PH 平行交MP 的延长线于Q 点.(1)求QPN ∠的度数;(2)求证:QN 与O 相切;(3)若2PN PM MN =⋅,求MH NH 的值.【解答】(1)解:MN 是直径,90MPN ∴∠=︒,90QPN ∴∠=︒;(2)证明:PH MN ⊥ ,90PHM ∴∠=︒,//QN PH ,90QNM PHM ∴∠=∠=︒,ON QN ∴⊥,ON 是半径,QN ∴与O 相切;(3)解:90MNP PNQ ∠+∠=︒ ,90PNQ Q ∠+∠=︒,MNP Q ∴∠=∠,MPN QPN ∠=∠ ,NPM QPN ∴∆∆∽,∴PN PM QP PN=,2PN PM QP ∴=⋅,2PN PM MN =⋅ ,QP MN ∴=,//PH QN ,∴MH MP HN PQ=,∴MH MP HN MN =,同理得,MHP MPN ∆∆∽,∴MP MH MN MP =,HN MP ∴=,设PQ MN a ==,MP b =,∴MH MP HN PQ=,∴a b b b a -=,(12a b -∴=(舍)或1)2a b =∴12MH a b HN b -==.3.(长沙中考)如图,点A ,B ,C 在O 上运动,满足222AB BC AC =+,延长AC 至点D ,使得DBC CAB ∠=∠,点E 是弦AC 上一动点(不与点A ,C 重合),过点E 作弦AB 的垂线,交AB 于点F ,交BC 的延长线于点N ,交O 于点M (点M 在劣弧 AC 上).(1)BD 是O 的切线吗?请作出你的判断并给出证明;(2)记BDC ∆,ABC ∆,ADB ∆的面积分别为1S ,2S ,S ,若212()S S S ⋅=,求2(tan )D 的值;(3)若O 的半径为1,设FM x =,FE FN y ⋅=,试求y 关于x 的函数解析式,并写出自变量x 的取值范围.【解答】解:(1)BD 是O 的切线.证明:如图,在ABC ∆中,222AB BC AC =+,90ACB ∴∠=︒.又点A ,B ,C 在O 上,AB ∴是O 的直径.90ACB ∠=︒ ,90CAB ABC ∴∠+∠=︒.又DBC CAB ∠=∠,90DBC ABC ∴∠+∠=︒.90ABD ∴∠=︒.BD ∴是O 的切线.(2)由题意得,112S BC CD =⋅,212S BC AC =⋅,12S AD BC =⋅.212()S S S ⋅= ,∴2111()222BC CD AD BC BC AC ⋅⋅⋅=⋅.2CD AD AC ∴⋅=.2()CD CD AC AC ∴+=.又90D DBC ∠+∠=︒ ,90ABC A ∠+∠=︒,DBC A ∠=∠,D ABC ∴∠=∠.tan tan BC AC D ABC CD BC∴∠==∠=.2BC CD AC ∴=.又2()CD CD AC AC +=,∴4222BC BC AC AC +=.4224BC AC BC AC ∴+⋅=.241(()AC AC BC BC ∴+=.由题意,设2(tan )D m ∠=,2(AC m BC∴=.21m m ∴+=.152m ±∴=.0m > ,152m ∴=.2(tan )D ∴∠=.(3)设A α∠=,90A ABC ABC DBC ABC N ∠+∠=∠+∠=∠+∠=︒ ,A DBC N α∴∠=∠=∠=.如图,连接OM .∴在Rt OFM ∆中,OF =.1BF BO OF ∴=+=+,1AF OA OF =-=.∴在Rt AFE ∆中,tan (1tan EF AF αα=⋅=⋅,1cos cos AF AE αα==.在Rt ABC ∆中,sin 2sin BC AB αα=⋅=.(1r = ,2AB ∴=.)cos 2cos AC AB αα=⋅=.在Rt BFN ∆中,sin BF BN α==tan BF FN α==.y FE FN ∴=⋅2x =2x =2x =21x x=⋅x =.即y x =.FM AB ⊥ ,FM ∴最大值为F 与O 重合时,即为1.01x ∴< .综上,y x =,01x <.4.(长沙中考)如图,四边形ABCD 内接于⊙O ,对角线AC 为⊙O 的直径,过点C 作AC 的垂线交AD 的延长线于点E ,点F 为CE 的中点,连接DB ,DC ,DF .(1)求∠CDE 的度数;(2)求证:DF是⊙O的切线;(3)若AC=2DE,求tan∠ABD的值.解:(1)∵对角线AC为⊙O的直径,∴∠ADC=90°,∴∠EDC=90°;(2)证明:连接DO,∵∠EDC=90°,F是EC的中点,∴DF=FC,∴∠FDC=∠FCD,∵OD=OC,∴∠OCD=∠ODC,∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线;(3)设DE=1,则AC=2,由射影定理得:AC2=AD×AE,∴20=AD(AD+1),∴AD=4或﹣5(舍去),∵DC2=AC2﹣AD2,∴DC=2,∴tan∠ABD=tan∠ACD==2;5.(青竹湖三模)如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、B、D三点,CB的延长线交⊙O于点E.(1)求证:AE=CE;(2)EF与⊙O相切于点E,交AC的延长线于点F,若CD=CF=2cm,求⊙O的直径;(3)在(2)的条件下,若CF:CD=n(n>0),求sin∠CAB.解:(1)证明:连接DE,∵∠ABC=90°∴∠ABE=90°∴AE是⊙O直径,∴∠ADE =90°∴DE ⊥AC 又∵D 是AC 的中点∴DE 是AC 的垂直平分线∴AE =CE ;(2)解:在△ADE 和△EFA 中,∵∠ADE =∠AEF =90°,由射影定理得:AE 2=AD ×AF,∴AE 2=2×6,∴AE =2cm ;(3)解:∵AE 是⊙O 直径,EF 是⊙O 的切线,∵CF:CD=n,令CD=1,则CF=n ,∵∠ADE =∠AEF =90°,由射影定理得:AE 2=AD ×AF ,∴AE 2=1×(n+2),∴AE ==CE ,∵∠CAB =∠DEC,∴sin ∠CAB =sin ∠DEC ===.6.(长郡)如图,AB 为⊙O 的直径,弦CD 与AB 相交于E ,DE =EC ,过点B 的切线与AD 的延长线交于F ,过E 作EG ⊥BC 于G ,延长GE 交AD 于H .(1)求证:AH =HD ;(2)若BFBD =,DF =9,求⊙O 的半径.【解答】(1)证明:∵AB 为⊙O 的直径,DE =EC ,∴AB ⊥CD ,∴∠C +∠CBE =90°,∵EG ⊥BC ,∴∠C +∠CEG =90°,∴∠CBE =∠CEG ,∵∠CBE =∠CDA ,∠CEG =∠DEH ,∴∠CDA =∠DEH ,∴HD =EH ,∵∠A +∠ADC =90°,∠AEH +∠DEH =90°,∴AH =EH ,∴AH =HD ;(2)解:∵∠BDF =90°,BFBD =,令BD=4x ,BF=5x ,则222)5(94x x =+)(,∴2=x ,BD=12,由射影定理得:BD 2=DF •DA ,∴144=9×DA ,∴DA=16,又由射影定理得:AB 2=AF •DA ,∴AB 2=25×16,∴AB=20,即半径为10.10.如图,AB 是O 的直径,点C 是O 上一点,AD 与过点C 的切线垂直,垂足为D ,直线DC 与AB的延长线交于点P ,弦CE 平分ACB ∠,交AB 于点F ,连接BE ,BE =.(1)求证:AC 平分DAB ∠;BC=,求阴影部分的面积;(2)若5CD=,求PC的长度(射影定理).(3)若3【解答】(1)证明:连接OC.∵OA=OC,∴∠OAC=∠OCA.∵PC是⊙O的切线,AD⊥CD,∴∠OCP=∠D=90°,∴OC∥AD.∴∠CAD=∠OCA=∠OAC.即AC平分∠DAB.(2)解:连接AE.∵∠ACE=∠BCE,∴,∴AE=BE.又∵AB是直径,∴∠AEB=90°.∴AB=BE=×5=10,∵OB=5,∴BC=OB=OC=5,即△OBC是等边三角形,=×5×=,∴∠BOC=60°,∴OH==,CH=OH=,∴S△BOCS扇形BOC=×π×52=π,∴阴影部分的面积为π﹣;(3)解:过点C作CH⊥AB垂足为点H,如图:由(2)得:OC=OB=5,(2)∵AC平分∠DAB,CH⊥AB,CD⊥AD,∴CH=CD=3,∵∠ACB=∠BHC=90°,由射影定理得:CH2=BH•AH,设BH=x,AH=10-x,∴32=x(10﹣x),解得:x=1或9(舍),又由射影定理得:CH2=O H•HP,∴32=4HP,解得:HP=.7.(雅礼)如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且AD•AO=AM•AP.(1)连接OP,证明:△ADM∽△APO;(2)证明:PD是⊙O的切线;(3)若AD=24,AM=MC,求的值.解:(1)证明:连接OD、OP、CD.∵AD•AO=AM•AP,∴=,∠A=∠A,∴△ADM∽△APO.(2)∵△ADM∽△APO,∴∠ADM=∠APO,∴MD∥PO,∴∠1=∠4,∠2=∠3,∵OD=OM,∴∠3=∠4,∴∠1=∠2,∵OP=OP,OD=OC,∴△ODP≌△OCP,∴∠ODP=∠OCP,∵BC⊥AC,∴∠OCP=90°,∴OD⊥AP,∴PD是⊙O的切线.(2)连接CD.由(1)可知:PC=PD,∵AM=MC,∴AM=2MO=2R,在Rt△AOD中,OD2+AD2=OA2,∴R2+242=9R2,∴R=6,∴OD=6,MC=12,∵==,∴DP=12,∵O是MC的中点,∴==,∴点P是BC的中点,∴BP=CP=DP=12,∵MC是⊙O的直径,∴∠BDC=∠CDM=90°,在Rt△BCM中,∵BC=2DP=24,MC=12,∴BM=12,由射影定理得:MC2=MD×MB,∴122=12×MD,∴MD=4,∴=.8.(广益)如图,已知PB与⊙O相切于点B,A是⊙O上的一点,满足PA=PB,连接PO,交AB于E,交⊙O于C,D两点,E在线段OD上,连接AD,OB。
中考数学 中考数学压轴题(讲义及答案)及解析
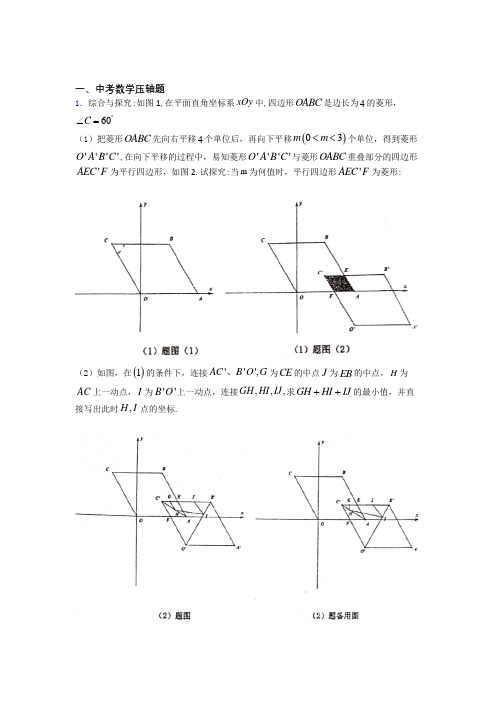
一、中考数学压轴题1.综合与探究:如图1,在平面直角坐标系xOy 中,四边形OABC 是边长为4的菱形,60C ︒∠=(1)把菱形OABC 先向右平移4个单位后,再向下平移()03m m <<个单位,得到菱形''''O A B C ,在向下平移的过程中,易知菱形''''O A B C 与菱形OABC 重叠部分的四边形'AEC F 为平行四边形,如图2.试探究:当m 为何值时,平行四边形'AEC F 为菱形:(2)如图,在()1的条件下,连接''',AC B O G 、为CE 的中点J 为EB 的中点,H 为AC 上一动点,I 为''B O 上一动点,连接,,,GH HI IJ 求GH HI IJ ++的最小值,并直接写出此时,H I 点的坐标.2.如图,已知抛物线y =2ax bx c ++与x 轴交于A 3,0-(),B 33,0()两点,与y 轴交于点C 0,3().(1)求抛物线的解析式及顶点M 坐标;(2)在抛物线的对称轴上找到点P ,使得PAC 的周长最小,并求出点P 的坐标; (3)在(2)的条件下,若点D 是线段OC 上的一个动点(不与点O 、C 重合).过点D 作DE //PC 交x 轴于点E .设CD 的长为m ,问当m 取何值时,PDE ABMC 1S S 9=四边形. 3.在平面直角坐标系中,抛物线24y mx mx n =-+(m >0)与x 轴交于A ,B 两点,点B在点A 的右侧,顶点为C ,抛物线与y 轴交于点D ,直线CA 交y 轴于E ,且:3:4∆∆=ABC BCE S S .(1)求点A ,点B 的坐标;(2)将△BCO 绕点C 逆时针旋转一定角度后,点B 与点A 重合,点O 恰好落在y 轴上, ①求直线CE 的解析式;②求抛物线的解析式.4.已知:如图,AB 为O 的直径,弦CD AB ⊥垂足为E ,点H 为弧AC 上一点.连接DH 交AB 于点F ,连接HA 、BD ,点G 为DH 上一点,连接AG ,HAG BDC ∠=∠. (1)如图1,求证:AG HD ⊥;(2)如图2,连接HC ,若HC HF =,求证:HC HA =;(3)如图3,连接HO 交AG 于点K ,若点F 为DG 的中点,HC 2HG =,求KG AK的值.5.如图1,抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),交x 轴于A 、B 两点,交y轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.(3)如图3,点M的坐标为(32,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.6.如图,在梯形ABCD中,AD//BC,AB=CD=AD=5,cos45B ,点O是边BC上的动点,以OB为半径的O与射线BA和边BC分别交于点E和点M,联结AM,作∠CMN=∠BAM,射线MN与边AD、射线CD分别交于点F、N.(1)当点E为边AB的中点时,求DF的长;(2)分别联结AN 、MD ,当AN//MD 时,求MN 的长;(3)将O 绕着点M 旋转180°得到'O ,如果以点N 为圆心的N 与'O 都内切,求O 的半径长.7.如图,在四边形ABCD 中,∠B=90°,AD//BC ,AD=16,BC=21,CD=13.(1)求直线AD 和BC 之间的距离;(2)动点P 从点B 出发,沿射线BC 以每秒2个单位长度的速度运动,动点Q 从点A 出发,在线段AD 上以每秒1个单位长度的速度运动,点P 、Q 同时出发,当点Q 运动到点D 时,两点同时停止运动,设运动时间为t 秒.试求当t 为何值时,以P 、Q 、D 、C 为顶点的四边形为平行四边形?(3)在(2)的条件下,是否存在点P ,使△PQD 为等腰三角形?若存在,请直接写出相应的t 值,若不存在,请说明理由.8.如图1,正方形CEFG 绕正方形ABCD 的顶点C 旋转,连接AF ,点M 是AF 中点. (1)当点G 在BC 上时,如图2,连接BM 、MG ,求证:BM =MG ;(2)在旋转过程中,当点B 、G 、F 三点在同一直线上,若AB =5,CE =3,则MF = ;(3)在旋转过程中,当点G 在对角线AC 上时,连接DG 、MG ,请你画出图形,探究DG 、MG 的数量关系,并说明理由.9.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,第一颗弹珠弹出后其速度1y (米/分钟)与时间x (分钟)前2分钟满足二次函数21y ax ,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.(1)求第一颗弹珠的速度1y (米/分钟)与时间x (分钟)之间的函数关系式;(2)第一颗弹珠弹出1分钟后,弹出第二颗弹珠,第二颗弹珠的运行情况与第一颗相同,直接写出第二颗弹珠的速度2y (米/分钟)与弹出第一颗弹珠后的时间x (分钟)之间的函数关系式;(3)当两颗弹珠同时在轨道上时,第____分钟末两颗弹珠的速度相差最大,最大相差______;(4)判断当两颗弹珠同时在轨道上时,是否存在某时刻速度相同?请说明理由,并指出可以通过解哪个方程求出这一时刻.10.综合与实践A纸是我们学习工作最常用的纸张之一,其长宽之比是2:1,我们定义:长宽之比是42:1的矩形纸片称为“标准纸”.操作判断:()1如图1所示,矩形纸片2=是一张“标准纸”,将纸片折叠一次,使点ABCD AD AB()AB=求CF的B与D重合,再展开,折痕EF交AD边于点,E交BC边于点F,若1,长,()2如图2,在()1的基础上,连接,BE判断四边形BD折痕EF交BD于点O,连接,BFDE的形状,并说明理由.探究发现:()3如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点A 与点C 重合,再展开,痕MN 交AD 边于点M ,BC 交边于点,N 交BD 也是点O .然后将四边形ENFM 剪下,探究纸片ENFM 是否为“标准纸”,说明理由.11.如图,在平面直角坐标中,点O 为坐标原点,ABC ∆的三个顶点坐标分别为()A O m ,,(),B m O -,(),C n O ,5AC =且OBA OAB ∠=∠,其中m ,n 满足725m n m n +=⎧⎨-=⎩.(1)求点A ,C 的坐标;(2)点P 从点A 出发,以每秒1个单位长度的速度沿y 轴负方向运动,设点P 的运动时间为t 秒.连接BP 、CP ,用含有t 的式子表示BPC ∆的面积为S (直接写出t 的取值范围);(3)在(2)的条件下,是否存在t 的值,使得ΔΔ32PAB POC S S =,若存在,请求出t 的值,并直接写出BP 中点Q 的坐标;若不存,请说明理由.12.注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.如图,将一个矩形纸片ABCD ,放置在平面直角坐标系中,()0,0A ,()4,0B ,()0,3D ,M 是边CD 上一点,将ADM 沿直线AM 折叠,得到ANM . (Ⅰ)当AN 平分MAB ∠时,求DAM ∠的度数和点M 的坐标;(Ⅱ)连接BN ,当1DM =时,求ABN 的面积;(Ⅲ)当射线BN 交线段CD 于点F 时,求DF 的最大值.(直接写出答案) 在研究第(Ⅱ)问时,师生有如下对话:师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题. 小明:我是这样想的,延长MN 与x 轴交于P 点,于是出现了Rt NAP △.小雨:我和你想的不一样,我过点N 作y 轴的平行线,出现了两个Rt NAP △.13.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a += (x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为__________________;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x=+>,请利用特征点求出该函数的最小值.14.如图①,在ABC ∆中,90C ∠=︒,10,8AB BC ==.点,D E 分别是边,AC BC 上的动点,连接DE .设CD x =(0x >),BE y =,y 与x 之间的函数关系如图②所示.(1)求出图②中线段PQ 所在直线的函数表达式;(2)将DCE 沿DE 翻折,得DME .①点M 是否可以落在ABC ∆的某条角平分线上?如果可以,求出相应x 的值;如果不可以,说明理由;②直接写出....DME 与ABC ∆重叠部分面积的最大值及相应x 的值.15.平面直角坐标系中,点A 、B 分别在x 轴正半轴、y 轴正半轴上,AO =BO ,△ABO 的面积为8.(1)求点A 的坐标;(2)点C 、D 分别在x 轴负半轴、y 轴正半轴上(D 在B 点上方),AB ⊥CD 于E ,设点D 纵坐标为t ,△BCE 的面积为S ,求S 与t 的函数关系;(3)在(2)的条件下,点F 为BE 中点,连接OF 交BC 于G ,当∠FOB +∠DAE =45°时,求点E 坐标.16.如图,在平面直角坐标系中,点(1,2)A ,(5,0)B ,抛物线22(0)y ax ax a =->交x 轴正半轴于点C ,连结AO ,AB .(1)求点C 的坐标;(2)求直线AB 的表达式;(3)设抛物线22(0)y ax ax a =->分别交边BA ,BA 延长线于点D ,E .①若2AE AO =,求抛物线表达式;②若CDB △与BOA △相似,则a 的值为 .(直接写出答案)17.已知:菱形 ABCD ,点 E 在线段 BC 上,连接 DE ,点 F 在线段 AB 上,连接 CF 、DF , CF 与 DE 交于点 G ,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.(1)求证:CD=CF ;(2)设∠CED = x ,∠DCF = y ,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围) (3)在(2)的条件下,当 x =45°时,以 CD 为底边作等腰△CDK ,顶角顶点 K 在菱形 ABCD 的内部,连接 GK ,若 GK ∥CD ,CD =4 时,求线段 KG 的长.18.在Rt ABC ∆中,6AB =,90B ∠=︒,8BC =,点P 从A 出发沿AC 方向在运动速度为3个单位/秒,点Q 从C 出发向点B 运动,速度为1个单位/秒,P 、Q 同时出发,点Q到点B 时两点同时停止运动.(1)点P 在线段AC 上运动,过P 作DP PQ ⊥交边AB 于D ,2t =时,求PD PQ 的值; (2)运动t 秒后,90BPQ ∠=︒,求此时t 的值;(3)t =________时,AQ QP =. 19.已知:AB 为⊙O 的直径,点C 为弧AB 的中点,点D 为⊙O 上一点,连接CD ,交AB 于点M ,AE 为∠DAM 的平分线,交CD 于点E .(1)如图1,连接BE ,若∠ACD=22°,求∠MBE 的度数;(2) 如图2,连接DO 并延长,交⊙O 于点F ,连接AF ,交CD 于点N .①求证:DM 2+CN 2=CM 2;②如图3,当AD=1,AB=10时,请直接写出....线段ME 的长. 20.如图,平面直角坐标系中,抛物线228y ax ax a =--与x 轴交于B 、C 两点(点B 在点C 右侧),与y 轴交于点A ,连接AB ,25AB =.(1)求抛物线的解析式;(2)点P 在第二象限的抛物线上,连接PB 交y 轴于D ,取PB 的中点E ,过点E 作EH x ⊥轴于点H ,连接DH ,设点P 的横坐标为t .ODH 的面积为S ,求S 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,作PF y ⊥轴于F ,连接CP 、CD ,CP CD =,点S 为PF 上一点,连接BS 交y 轴于点T ,连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒,在射线CS 上取点Q.连接QF ,QF RF =,求直线TQ 的解析式. 21.如图,直角梯形ABCD 中,1//,90,60,3,9,AD BC A C AD cm BC cm O ︒︒∠∠====的圆心1O 从点A 开始沿折线——A D C 以1/cm s 的速度向点C 运动,2O 的圆心2O 从点B 开始沿BA 边以3/cm s 的速度向点A 运动,1O 半径为22,cm O 的半径为4cm ,若12,O O 分别从点A 、点B 同时出发,运动的时间为ts(1)请求出2O 与腰CD 相切时t 的值;(2)在03s t s ≤<范围内,当t 为何值时,1O 与2O 外切?22.如图1,以AB 为直径作⊙O ,点C 是直径AB 上方半圆上的一点,连结AC ,BC ,过点C 作∠ACB 的平分线交⊙O 于点D ,过点D 作AB 的平行线交CB 的延长线于点E .(1)如图1,连结AD ,求证:∠ADC =∠DEC . (2)若⊙O 的半径为5,求CA •CE 的最大值. (3)如图2,连结AE ,设tan ∠ABC =x ,tan ∠AEC =y , ①求y 关于x 的函数解析式; ②若CB BE =45,求y 的值.23.在平面直角坐标系xOy 中,点A 、B 为反比例函数()4x 0xy =>的图像上两点,A 点的横坐标与B 点的纵坐标均为1,将()4x 0xy =>的图像绕原点O 顺时针旋转90°,A 点的对应点为A’,B 点的对应点为B’.(1)点A’的坐标是 ,点B’的坐标是 ;(2)在x 轴上取一点P ,使得PA+PB 的值最小,直接写出点P 的坐标. 此时在反比例函数()4x 0xy =>的图像上是否存在一点Q ,使△A’B’Q 的面积与△PAB 的面积相等,若存在,求出点Q 的横坐标;若不存在,请说明理由;(3)连接AB’,动点M 从A 点出发沿线段AB’以每秒1个单位长度的速度向终点B’运动;动点N 同时从B’点出发沿线段B’A’以每秒1个单位长度的速度向终点A’运动.当其中一个点停止运动时,另一个点也随之停止运动.设运动的时间为t 秒,试探究:是否存在使△MNB’为等腰直角三角形的t 值.若存在,求出t 的值;若不存在,说明理由.24.问题探究(1)如图1.在ABC 中,8BC =,D 为BC 上一点,6AD =.则ABC 面积的最大值是_______.(2)如图2,在ABC 中,60BAC ∠=︒,AG 为BC 边上的高,O 为ABC 的外接圆,若3AG =,试判断BC 是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.问题解决:如图3,王老先生有一块矩形地ABCD ,6212AB =,626BC =+,现在他想利用这块地建一个四边形鱼塘AMFN ,且满足点E 在CD 上,AD DE =,点F 在BC上,且6CF =,点M 在AE 上,点N 在AB 上,90MFN ∠=︒,这个四边形AMFN 的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由. 25.如图,直线y =12x ﹣2与x 轴交于点B ,与y 轴交于点A ,抛物线y =ax 2﹣32x+c 经过A ,B 两点,与x 轴的另一交点为C . (1)求抛物线的解析式;(2)M 为抛物线上一点,直线AM 与x 轴交于点N ,当32MN AN =时,求点M 的坐标; (3)P 为抛物线上的动点,连接AP ,当∠PAB 与△AOB 的一个内角相等时,直接写出点P 的坐标.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.H解析:(13221H(91413314,I(275235【解析】 【分析】(1)根据菱形性质,得到A 、B 、C 、O 四点坐标,然后根据平移得到对应点坐标,故可求得C E '和C F '的长,令它们相等可得m 的值;(2)点G 作以C A '为对称轴的点G ',交C F '于点G ',点J 作以O B ''为对称轴的点J ',交A B ''于点J ',G J ''与C A '、A B ''的交点便是点H 、I ;先利用对称的性质,求解得出点G '、J '的坐标,然后利用代入系数法求得线段对应函数解析式,最后联立方程得到点H 、I 的坐标. 【详解】(1)如下图,CB 与y 轴交于点M ,过点C 作x 轴的垂线,交x 轴于点N∵在菱形ABCO 中,∠C=60°,菱形边长为4 ∴在Rt △COM 中,CM=2,3∴O(0,0),A(4,0),B(2,3,C(-2,3∵将菱形OABC 先向右平移4个单位后,再向下平移() 03m m <<个单位,得到菱形''''O A B C∴O '(4,-m),A '(8,-m),B '(6,3m -),C '(2,3m -) ∴直线AB 的解析式为:y=343x +∵点E 的纵坐标为:3m -,代入解析式得:x=32+ ∴E(32+,3m -) 同理,F(34,0) ∵四边形AE C F '是菱形 ∴E F C C '=' E 33C m '=∵C '(2,3m -),F(34,0) ∴NF=32,∴23F 4C =-' 3234=- 解得:3(2)如下图,点G 作以C A '为对称轴的点G ',交C F '于点G ',过点C '作x 轴的垂线,交过点G '作y 轴的垂线于点K ,同样作点J '和点Q3C '(23),E(33 ∵点G 是C E '的中点,∴12C G '= ∴12C G ''=,∴14G K '=,3C K '=∴G '(94,334) 同理,J 32B J B '''== ∴34J Q '=,334QB '= ∴J '(274,3 ∴22279333214444G J ⎛⎫⎛⎫=-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭''21根据点A 、C '可得直线A C '的解析式为:35324y x =-+根据点O '、B '可得直线O B ''的解析式为:353y x =- 根据点G '、J '可得直线G J ''的解析式为:339y x = 联立G J ''和A C '得:x=914,y=13314,∴H(914,13314) 联立G J ''和O B ''得:x=275,2327523) 【点睛】本题考查了菱形的性质、一次函数与平面直角坐标系,在第(2)问中,解题关键是利用对称找出最短距离对应的点.2.C解析:(1)21y x 43=-+(,顶点M4;(2)P 2);(3)1m =2,2m =1【解析】 【分析】(1)由点C 的坐标,可求出c的值,再把()A、()B 代入解析式,即可求出a 、b 的值,即可求出抛物线的解析式,将解析式化为顶点式,即可求出顶点M 的坐标;(2)因为A 、B 关于抛物线的对称轴对称,连接BC 与抛物线对称轴交于一点,即为所求点P ,设对称轴与x 轴交于点H ,证明PHB COB ∽,即可求出PH 的长,从而求出点P 的 坐标;(3)根据点A 、B 、M 、C 的坐标,可求出ABMC S 四边形,从而求出PDES=OC =3,OB=OCB ∠=60,因为DE //PC ,推出 ODE ∠=60,从而得到OD =3m -,)OE 3m =-,根据PDEDOE PDOE SS S=-四边形,列出关于m 的方程,解方程即可. 【详解】(1)∵抛物线y =2ax bx c a 0++≠()过()A、()B ,()C 0,3三点, ∴c =3,∴3a 3027a 30⎧-+=⎪⎨++=⎪⎩,解得1a 3b 3⎧=-⎪⎪⎨⎪=⎪⎩.故抛物线的解析式为(2211y x x 3x 4333=-++=--+,故顶点M为)4.(2)如图1,∵点A 、B 关于抛物线的对称轴对称,∴连接BC 与抛物线对称轴交于一点,即为所求点P . 设对称轴与x 轴交于点H , ∵PH //y 轴, ∴PHB COB ∽. ∴PH BHCO BO=. 由题意得BH =23,CO =3,BO =33,∴PH 23333=, ∴PH =2. ∴()P3,2.(3)如图2,∵()A 3,0-、()B 33,0,()C 0,3,()M3,4,∴ABMC S 四边形=()AOC MHBCOHM 111SS S3334342393222++=⨯⨯++⨯⨯=梯形. ∵ABMC S 四边形=PDE9S ,∴PDES3=∵OC =3,OB =33∴OCB ∠=60. ∵DE //PC , ∴ODE ∠=60.∴OD =3m -,)OE 33m =-.∵PDOE S 四边形=))COE1S 33m 3m 22=⨯-=-,∴PDES=))2DOEPDOE S S3m 3m -=--=四边形20m +<<(.∴2+= 解得1m =2,2m =1. 【点睛】此题主要考查了待定系数法求二次函数解析式以及相似三角形的判定与性质和四边形面积求法等知识,熟练运用方程思想方法和转化思想是解题关键.3.A解析:(1) A (12,0) B (72,0);(2) ①33y x =-+,②2999y x x =-+【解析】 【分析】(1)根据抛物线的解析式可得对称轴为x =2,利用:3:4∆∆=ABC BCE S S 得出CA :CE =3:4,由△AOE ∽△AGC 可得13=AO AG ,进而求得OA 、OB 的长,即可求得点A 、点B 的坐标; (2)根据旋转的性质求出C 点坐标,利用C 点坐标和△AOE ∽△AGC 可求得E 点坐标,,分别利用待定系数法即可求得直线CE 和抛物线的解析式. 【详解】解:(1)∵抛物线的解析式为24(0)=-+>y mx mx n m ,∴对称轴为直线422-=-=mx m, 如图,设对称轴与x 轴交于G ,则//CG y 轴,2OG =,∴△AOE ∽△AGC , ∴=AO AEAG AC, ∵:3:4ABCBCES S=, ∴CA :CE =3:4 ,则31AE AC =, ∴13==AO AE AG AC , ∴1142==OA OG ,3342==AG OG , 则23==AB AG ,72=+=OB OA AB , ∴A (12,0), B (72,0); (2)如图,设O 旋转后落在点Q 处,过点C 作CP y ⊥轴于点P ,由旋转的性质得:△BCO ≌△ACQ , ∴BO =AQ =72,CO =CQ , ∴OQ====∵CP y ⊥轴,∴12==OP OQ ∴点C的坐标为(2,,则CG =由(1)得△AOE ∽△AGC ,13==OE AE CG AC ,∴3OE =,即点E的坐标为(0,3, ①设CE 的解析式为y kx b =+,分别代入C (2,,E 得:23k b b ⎧+=⎪⎨=⎪⎩,解得:k b ⎧=⎪⎪⎨⎪=⎪⎩, ∴CE的解析式为33y x =-+; ②将A (12,0),C (2,分别代入24y mx mx n =-+得:120448m m n m m n ⎧-+=⎪⎨⎪-+=⎩,解得:99m n ⎧=⎪⎪⎨⎪=⎪⎩,∴抛物线解析式为2999y x x =-+. 【点睛】本题考查了二次函数的综合、旋转的性质、相似三角形的性质和求一次函数的解析式,正确的理解题意,熟练运算“数形结合思想”是解题的关键.4.A解析:(1)详见解析;(2)详见解析;(3)15KG AK = 【解析】 【分析】(1)根据同弧所对的圆周角相等,进行角度计算,得90AHG HAG ∠+∠=︒,进而得到90AGH ∠=︒,即可证明AG HD ⊥;(2)连接AC 、AD 、CF ,根据同弧所对的圆周角相等,进行角度计算,得HFA HAF ∠=∠,进而得到HF HA =,再根据已知HC HF =,得到HC HA =; (3)在DH 上截取DT HC =,过点C 作CM HD ⊥于点M ,通过证明AHC ≌ATD 得到AH AT =,进而得到HG CH GD +=,再根据F 为DG 中点,得到GF DF =,通过勾股定理逆用,证明90HCF ∠=︒,再通过解ACE △得1tan 3CAB ∠=,解△CDH 得1tan 2CDF ∠=,求得OF 、OH ,逆用勾股定理证明90HOF ∠=︒,易求1tan 2KHG ∠=,1tan 3HAG ∠=,最后求得KG AK 的值. 【详解】(1)证明:如图,设HAG ∠为α,∵HAG BDC ∠=∠,∴HAG BDC α∠=∠=,∵CD AB ⊥,∴90BDC DBE ∠+∠=︒∴90DBE α∠=︒-, ∵AHG ∠与ABD ∠为同对弧AD 所对的圆周角,∴90AHG ABD α∠=∠=︒-,∴90AHG HAG ∠+∠=︒,∴18090AGH AHG HAG ∠=︒-∠-∠=︒∴AG HD ⊥(2)如图,连接AC 、AD 、CF ,∵AB 为直径,AB CD ⊥,∴CE DE =,∴AB 垂直平分CD ,∴AC AD =,FC FD =,∴ACD ADC ∠=∠,FCD FDC ∠=∠,∴ACD FCD ADC FDC ∠-∠=∠-∠,即ACF ADF ∠=∠,设FCD FDC α∠=∠=,ACF ADF β∠=∠=,∵ADH ∠与ACH ∠为同对弧AH 所对的圆周角,∴ADH ACH β∠=∠=,∴2HCF HCA ACF β∠=∠+∠=,∵HFC FCD FDC ∠=∠+∠,∴2HFC α∠=,∵HC HF =,∴HCF HFC ∠=∠,∴22αβ=,∴αβ=,∵AB 为直径,∴90ADB ∠=︒,∴90HDB β∠=︒-,∵HAB ∠与为HDB ∠同对弧BH 所对的圆周角,∴90HAB HDB β∠=∠=︒-,∵AB CD ⊥,∴9090BFD αβ∠=︒-=︒-,∵9090HFA BFD αβ∠=∠=︒-=︒-,∴HFA HAF ∠=∠,∴HF HA =,∴HC HA =;(3)如图,在DH 上截取DT HC =,∵ADH ∠与ACH ∠同对弧AH 所对的圆周角,∴ADH ACH ∠=∠,∵AB 为直径,且AB CD ⊥∴AC =AD ,∴AC AD =,∴AHC ≌ATD ,∴AH AT =,∵AG HT ⊥,∴HG TG =,∴HG CH GT DT GD +=+=,设2HG k =,则4CH k =,GD 6k =,∵F 为DG 中点,∴3GF DF k ==,∴5HF HG GF k =+=,FD =CF =3k ,在HCF 中,由勾股定理逆定理得90HCF ∠=︒,过点C 作CM HD ⊥于点M ,由△HCF 面积,可求CM =125k ,∴95MF k =, ∴1tan 2CM CM CDF MD MF FD ∠===+, 解ACE △得1tan 3CAB ∠=, 易求OF ,OH ,由勾股定理逆定理得90HOF ∠=︒, 易求1tan 2KHG ∠=,1tan 3HAG ∠=, ∴15KG AK =. 【点睛】本题考查圆与三角形综合,主要考查知识点有同弧所对的圆周角相等,垂径定理,三角形全等的判定与性质,勾股定理的逆用,解直角三角形,锐角三角函数等,知识点跨度大,计算量多;熟练掌握圆的性质和三角形相关知识是解决本题的关键.5.E解析:(1)2y x 2x 3=-++;(2)E (2,3)或(1,4);(3)P 点横坐标为【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),设抛物线的解析式为2(1)4y a x =-+,由抛物线过点B,(3,0),即可求出a 的值,即可求得解析式; (2)过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x xx -++,求出A 、D 点的坐标,得到OM=x ,则AM=x+1,由AF=2EF 得到22(1)33x AN AM +==,从而推出点F 的坐标21210(,)3333x x --+,由23FN EM =,列出关于x 的方程求解即可;(3)先根据待定系数法求出直线DM 的解析式为y=-2x+3,过点P 作PT ∥y 轴交直线DM 于点T ,过点F 作直线GH ⊥y 轴交PT 于点G ,交直线CE 于点H.证明△FGP ≌△FHQ ,得到FG=FH ,PT=45GH.设点P (m ,-m²+2m+3),则T (m ,-2m+3),则PT=m²-4m ,GH=1-m , 可得m²-4m=45(1-m ),解方程即可. 【详解】(1)∵抛物线的顶点为C (1,4),∴设抛物线的解析式为2(1)4y a x =-+,∵抛物线过点B,(3,0),∴20(31)4a =-+,解得a=-1,∴设抛物线的解析式为2(1)4y x =--+,即2y x 2x 3=-++;(2)如图,过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x x x -++,∵抛物线的解析式为2y x 2x 3=-++,当y=0时,2023x x =-++,解得x=-1或x=3,∴A (-1.0),∴点D (0,3),∴过点BD 的直线解析式为3y x =-+,点F 在直线BD 上,则OM=x ,AM=x+1,∴22(1)33xAN AM+==,∴2(1)2111333x xON AN+=-=-=-,∴21210(,)3333x xF--+,∴2210332233FNEM x xx+--++==,解得x=1或x=2,∴点E的坐标为(2,3)或(1,4);(3)设直线DM的解析式为y=kx+b,过点D(0,3),M(32,0),可得,323k bb⎧+=⎪⎨⎪=⎩,解得k=-2,b=3,∴直线DM的解析式为y=-2x+3,∴32OM=,3OD=,∴tan∠DMO=2,如图,过点P作PT∥y轴交直线DM于点T,过点F作直线GH⊥y轴交PT于点G,交直线CE于点H.∵PQ⊥MT,∴∠TFG=∠TPF,∴TG=2GF,GF=2PG,∴PT=25GF,∵PF=QF,∴△FGP≌△FHQ,∴FG=FH ,∴PT=45GH. 设点P (m ,-m²+2m+3),则T (m ,-2m+3),∴PT=m²-4m ,GH=1-m ,∴m²-4m=45(1-m ), 解得:1112018m -=,或2112018m +=(不合题意,舍去), ∴点P 的横坐标为11201-. 【点睛】本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识,解题的关键是学会用转化的思想思考问题,学会用数形结合的思想解决问题,有一定难度.6.D解析:(1)DF 的长为158;(2)MN 的长为5;(3)O 的半径长为258. 【解析】【分析】(1)作EH BM ⊥于H ,根据中位线定理得出四边形BMFA 是平行四边形,从而利用cos 45B =解直角三角形即可求算半径,再根据平行四边形的性质求FD 即可; (2)先证AMB CNM ∠=∠,再证MAD CNM ∠=∠,从而证明AFM NFD ∆~∆,得到AF MF AF DF NF MF NF DF=⇒=,再通过平行证明AFN DFM ∆~∆,从而得到AF NF AF MF NF DF DF MF=⇒=,通过两式相乘得出AF NF =再根据平行得出NF DF =, 从而得出答案.(3)通过图形得出MN 垂直平分'OO ,从而得出90BAM CMN ∠=∠=︒,再利用cos 45B =解三角函数即可得出答案. 【详解】(1)如图,作EH BM ⊥于H :∵E 为AB 中点,45,cos 5AB AD DC B ==== ∴52AE BE ==∴cos 45BH B BE == ∴2BH = ∴2253222EH ⎛⎫=-= ⎪⎝⎭设半径为r ,在Rt OEH ∆中: ()222322r r ⎛⎫=-+ ⎪⎝⎭ 解得:2516r =∵,E O 分别为,BA BM 中点 ∴BAM BEO OBE ∠=∠=∠又∵CMN BAM ∠=∠∴CMN OBE ∠=∠∴//MF AB∴四边形BMFA 是平行四边形∴2528AF BM r ===∴2515588FD AD AF =-=-= (2)如图:连接MD AN ,∵,B C BAM CMN ∠=∠∠=∠∴AMB CNM ∠=∠又∵AMB MAD ∠=∠∴MAD CNM ∠=∠又∵AFM NFD ∠=∠∴AFM NFD ∆~∆∴AF MF AF DF NF MF NF DF=⇒=① 又∵//MD AN∴AFN DFM ∆~∆ ∴AF NF AF MF NF DF DF MF=⇒=② 由①⨯②得; 22AF NF AF NF =⇒=∴NF DF =∴5MN AD ==故MN 的长为5;(3)作如图:∵圆O 与圆'O 外切且均与圆N 内切设圆N 半径为R ,圆O 半径为r∴'=NO R r NO -=∴N 在'OO 的中垂线上∴MN 垂直平分'OO∴90NMC ∠=︒∵90BAM CMN ∠=∠=︒∴A 点在圆上∴54cos 5AB B BM BM === 解得:254BM =O 的半径长为258【点睛】 本题是一道圆的综合题目,难度较大,掌握相似之间的关系转化以及相关线段角度的关系转化是解题关键.7.A解析:(1)12;(2)5s或373s;(3)163s或685s或72s【解析】【分析】(1)AD与BC之间的距离即AB的长,如下图,过点D作BC的垂线,交BC于点E,在RtDEC中可求得DE的长,即AB的长,即AD与BC间的距离;(2)四边形QDCP为平行四边形,只需QD=CP即可;(3)存在3大类情况,情况一:QP=PD,情况二:PD=QD,情况三:QP=QD,而每大类中,点P存在2种情况,一种为点P还未到达点C,另一种为点P从点C处返回.【详解】(1)如下图,过点D作BC的垂线,交BC于点E∵∠B=90°,AD∥BC∴AB⊥BC,AB⊥AD∴AB的长即为AD与BC之间的距离∵AD=16,BC=21,∴EC=5∵DC=13∴在Rt DEC中,DE=12同理,DE的长也是AD与BC之间的距离∴AD与BC之间的距离为12(2)∵AD∥BC∴只需QD=PC,则四边形QDCP是平行四边形QD=16-t,PC=21-2t或PC=2t-21∴16-t=21-2t或16-t=2t-21解得:t=5s或t=37 3s(3)情况一:QP=PD图形如下,过点P作AD的垂线,交AD于点F∵PQ=PD ,PF ⊥QD ,∴QF=FD∵AF ∥BP ,AB ∥FP ,∠B=90°∴四边形ABPF 是矩形,∴AF=BP由题意得:AQ=t ,则QD=16-t ,QF=8-2t ,AF=8+2t BP=2t 或BP=21-(2t -21)=42-2t∵AF=BP∴8+2t =2t 或8+2t =42-2t 解得:t=163或t=685情况二:PD=QD ,图形如下,过点P 作AD 的垂线,交AD 于点F同理QD=16-t ,PF=AB=12BP=2t 或21-(2t -21)=42-2t则FD=AD -AF=AD -BP=16-2t 或FD=16-(42-2t)=2t -26 ∴在Rt PFD 中,()22212162PD t =+-或()22212226PD t =+- ∵PD=QD ,∴22PD QD =∴()()22216t 12162t =+--或()()22216t 12226t =+-- 解得:2个方程都无解情况三:QP=QD ,图形如下,过点P 作AD 的垂线,交AD 于点F同理:QD=16-t ,FP=12BP=2t 或BP=42-2tQF=AF -AQ=BP -AQ=2t -t=t 或QF=42-2t -t=42-3t在Rt QFP 中,22212PQ t =+或()22212423PQ t =+- ∵PQ=QD ,∴22PQ QD =∴()22216t 12t =+-或()()22216t 12423t =+--第一个方程解得:t=72,第二个方程解得:无解 综上得:t=163或685或72 【点睛】本题考查四边形中的动点问题,用到了勾股定理、平行四边形的性质、矩形的性质,解题关键是根据点Q 运动的轨迹,得出BP 的长度. 8.D解析:(1)证明见解析;(2)29或5;(3)DG =2MG ,理由见解析.【解析】【分析】(1)连接MG 并延长交AB 于N 点,证明△ANM ≌△FGM 后得到MG=MN ,AN=CG ,进而得到BN=BG ,得到△ANG 为等腰直角三角形,即可证明MG=MB.(2)分两种情况画出图形再利用(1)中的思路结合勾股定理即可求解.(3)先画出图形,然后证明△ADG ≌△ABG ,得到DG=BG ,又△BMG 为等腰直角三角形,故而得到DG=BG=2MG.【详解】解:(1) 连接MG 并延长交AB 于N 点,如下图所示:∵GF ∥AN ,∴∠NAM=∠GFM在△ANM 和△FGM 中∠∠=⎧⎪=⎨⎪∠=∠⎩BAM GFM AM FMNMA GMF ,∴△ANM ≌△FGM(ASA)∴MG=MN ,CG=GF=AN∴AB-AN=BC-CG∴NB=GB∴△NBG 为等腰直角三角形又M 是NG 的中点∴由直角三角形斜边上的中线等于斜边的一半知:故有:MG=MB.(2)分类讨论:情况一:当B 、G 、F 三点在正方形ABCD 外同一直线上时延长MG 到N 点,并使得MG=MN ,连接AN ,BN∴∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ,∴△AMN ≌△FMG(SAS)∴AN=GF=GC ,∠NAM=∠GFM∴AN ∥GF∴∠NAB+∠ABG=180°又∠ABC=90°∴∠NAB+∠CBG=90°又在△BCG 中,∠BCG+∠CBG=90°∴∠NAB=∠BCG∴在△ABN 中和△CBG 中:∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ,∴△ABN ≌△CBG(SAS)∴BN=BG ,∠ABN=∠CBG∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形,且∠BGN=45°在Rt △BCG 中,2222=534-=-=BG BC CG过M 点作MH ⊥BG 于H 点,∴△MHB 为等腰直角三角形∴MH=BH=HG=12BG=2 在Rt △MFH 中,2222MF=2529+=+=MH HF情况二:当B 、G 、F 三点在正方形ABCD 内同一直线上时如下图所示,延长MG 到MN ,并使得MG=MN ,连接NA 、NB ,同情况一中证明思路,∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ,△AMN ≌△FMG(SAS)∴AN=GF=GC ,∠NAM=∠GFM∴AN ∥GF∴∠NAB=∠ABG又∠ABG+∠GBC=90°∠GBC+∠BIF=90°∴∠BIF=∠ABG又∠BIF=∠BCG ,∠ABC=∠NAB∴∠NAB=∠GCB∴在△ABN 中和△CBG 中:∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ,∴△ABN ≌△CBG(SAS)∴BN=BG ,∠ABN=∠CBG∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形,且∠BGN=45°在△BCG 中,2222=534-=-=BG BC CG过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形∴MH=BH=HG=12BG=2∴HF=HG-GF=2-1=1在Rt△MFH中,2222MF=215+=+=MH HF故答案为:29或 5.(3)由题意作出图形如下所示:DG、MG的数量关系为:2,理由如下:∵G点在AC上∴∠DAG=∠BAG=45°在△ADG和△ABG中:∠∠=⎧⎪=⎨⎪=⎩AD ABDAG BAGAG AG,∴△ADG≌△BAG(SAS)∴DG=BG又由(2)中的证明过程可知:△MBG为等腰直角三角形∴2MG∴2MG故答案为:2MG.【点睛】本题考查了正方形的旋转、三角形的全等、勾股定理等知识,难度很大,关键是要能正确做出图形,利用数形结合的思想,熟练的使用正方形的性质是解题的关键.9.(1)212(02)16(25)x xyxx⎧≤≤⎪=⎨≤≤⎪⎩;(2)220(01)2(1)(13)16(36)1xy x xxx⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)第2分钟末两颗弹珠速度相差最大,最大相差6米/分钟;(4)存在,理由详见解析【解析】【分析】(1)将(1,2)代入21y ax =,得2a =,从而得到212y x =,再代入2x =求出18y =,即可得到反比例函数解析式,即可得解;(2)当01x ≤≤时,第二颗弹珠未弹出,故第二颗弹珠的解析式为20y =;再分别根据(1)中的结论,即可求出当13x <≤和36x <≤时第二颗弹珠的解析式;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,则第2分钟末两颗弹珠速度相差最大,分别求出第2分钟末时两颗弹珠的速度,再相减即可的解;(4)第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟,第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同.可以根据速度相等时列方程求得时刻.【详解】(1)当02x ≤≤时,将(1,2)代入21y ax =,得2a =,212y x ∴=,∵当2x =时,18y =,∴当25x ≤≤时,116y x=, 1y ∴与x 的函数关系式为212(02)16(25)x x y x x⎧≤≤⎪=⎨≤≤⎪⎩; (2)当01x ≤≤时,第二颗弹珠未弹出,∴第二颗弹珠的解析式为20y =;当13x <≤时,第二颗弹珠的解析式为222(1)y x =-;当36x <≤时,第二颗弹珠的解析式为2161y x =-; ∴2y 与x 的函数关系式为220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,∴第2分钟末两颗弹珠速度相差最大,∵第一颗弹珠的速度为2218222y x =⨯==米/分钟,第二颗弹珠的速度为2122(1)212y x =⨯==-米/分钟,∴两颗弹珠的速度最大相差8-2=6米/分钟;(4)存在,理由如下:第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟, 第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同. 这个时刻可以通过解方程2162(1)x x =-求得. 【点睛】本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息,明确自变量的取值范围和图象所经过的点的坐标.10.(1) CF ;(2) 四边形BFDE 是菱形,理由见解析;(3) 纸片ENFM 是“标准纸",理由见解析【解析】【分析】(1)1AB =,则AD =ABCD 是矩形,得到1,CD AB BC AD ==-=FB FD =,设CF x =,则FB FD x ==,在Rt DCF △中,222+=CD CF DF ,可得)2221x x +=即可求解.(2)当顶点B 与点D 重合时,折痕EF 垂直平分BD ,可得OB OD =,90BOF DOE ∠=∠=,在矩形ABCD 中,//AD BC ,得到OBF ODE ∠=∠,在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,,可得BOF DOE ≅,OE OF =,再根据OB OD =,可得四边形BFDE 是平行四边形,最后根据EF BD ⊥,即可求证平行四边形BFDE 是菱形.(3)由()2可知,OE OF =,同理可知,OM ON =,可得四边形ENFM 是平行四边形,根据90DOE DAB ∠=∠=︒,得到DOE DAB ,再根据AD =,可得2OE AB OD AD ===,进而得到2OE OD =,2EF BD =,同理可得,2MN AC =,根据四边形ABCD 是矩形,可得AC BD =,EF MN =,四边形ENFM 是矩形,90EMF ∠=,MF OD tan FEM ME OE ∠===MF =,即可求证纸片ENFM 是“标准纸".【详解】解:()11,AB =则AD AB ==四边形ABCD 是矩形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国各地中考数学解答题压轴题解析42011年全国各地中考数学解答题压轴题解析(4) 1.(福建福州14分)已知,如图,二次函数223y ax ax a =+-(0)a ≠图象的顶点为H ,与x 轴交于A 、B 两点(B 在A 点右侧),点H 、B 关于直线l :33y x =+对称.(1)求A 、B 两点坐标,并证明点A 在直线l 上;(2)求二次函数解析式;(3)过点B 作直线BK∥AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连接HN 、NM 、MK ,求HN+NM+MK 和的最小值.【答案】解:(1)依题意,得2230ax ax a +-=(0)a ≠,解得x 1=﹣3,x 2=1, ∵B 点在A 点右侧,∴A 点坐标为(﹣3,0),B 点坐标为(1,0)。
∵直线l :33y x =+,当x =﹣3时,()3330y =+-=,∴点A 在直线l 上。
(2)∵点H 、B 关于过A 点的直线l :33y x =+对称,∴AH=AB=4。
过顶点H 作HC⊥AB 交AB 于C 点,则AC=12AB=2,HC=224223-=。
∴顶点H (-1,23)。
代入二次函数解析式,解得32a =-,∴二次函数解析式为23333y x x =--+。
(3)直线AH 的解析式为333y x =+,直线BK 的解析式为33y x =-,由33333y x y x =+=-⎧⎨⎩,解得32x y ==⎧⎨⎩。
∴K (3,32)。
则BK=4。
过点K 作直线AH 的对称点Q ,连接QK ,交直线AH 于E ,过点K 作KD⊥AB ,垂足为点D 。
∵点H 、B 关于直线AK 对称,∴HN+MN 的最小值是MB , 。
且QM=MK ,QE= KE= KD=32 ,AE⊥QK 。
∴BM+MK 的最小值是BQ ,即BQ 的长是HN+NM+MK 的最小值。
∵BK∥AH ,∴∠BKQ=∠HEQ=90°。
由勾股定理得QB=8。
∴HN+NM+MK 的最小值为8。
【考点】二次函数综合题,解一元二次方程,轴对称的性质,解二元一次方程组,待定系数法,曲线上点的坐标与方程的关系,勾股定理。
【分析】(1)解出方程2230ax ax a +-=(0)a ≠,即可得到A 点坐标和B 点坐标;把A 的坐标代入直线l 即可判断A 是否在直线上。
(2)根据点H 、B 关于过A 点的直线l :33y x =+对称,得出AH=AB=4,过顶点H 作HC⊥AB 交AB 于C 点,求出AC 和HC 的长,得出顶点H 的坐标,代入二次函数解析式,求出a ,即可得到二次函数解析式。
(3)解方程组33333y x y x =+=-⎧⎨⎩,即可求出K 的坐标,根据点H 、B 关于直线AK 对称,得出HN+MN 的最小值是MB ,过点K 作直线AH 的对称点Q ,连接QK ,交直线AH 于E ,得到BM+MK 的最小值是BQ ,即BQ 的长是HN+NM+MK 的最小值,由勾股定理得QB=8,即可得出答案。
2.(福建泉州14分)如图1,在第一象限内,直线y=mx与过点B(0,1)且平行于x轴的直线l相交于点A,半径为r的⊙Q与直线y=mx、x轴分别相切于点T、E,且与直线l分别交于不同的M、N两点.(1)当点A的坐标为(33,p)时,①填空:p=___ ,m= ___,∠AOE= ___.②如图2,连接QT、QE,QE交MN于点F,当r=2时,试说明:以T、M、E、N 为顶点的四边形是等腰梯形;(2)在图1中,连接EQ并延长交⊙Q于点D,试探索:对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值会变化吗?若不变,求出a的值;若变化.请说明理由.【答案】解:(1) 1,3,60°。
(2)如图,连接TM,ME,EN,QN,QM ,∵OE和OP是⊙Q的切线,∴QE⊥x轴,QT⊥OT,即∠QTA=90°。
而l∥x轴,∴QE⊥MN。
∴MF=NF。
又∵r=2,EF=1,∴QF=2-1=1。
∴四边形QNEM为平行四边形,即QN∥ME。
∴EN=MQ=EQ=QN,即△QEN为等边三角形。
∴∠NQE=60°,∠QNF=30°。
在四边形OEQT中,∠QTO=∠QEO=90°,∠TOE=60°,∴∠TQE=360°-90°-90°-60°=120°。
∴∠TQE+∠NQE=120°+60°=180°。
∴T、Q、N三点共线,即TN为直径。
∴∠TMN=90°。
∴TN∥ME,∴∠MTN=60°=∠TNE。
∴以T、M、E、N为顶点的四边形是等腰梯形。
(3)对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值不会变化。
理由如下:如图,连DM,ME,∵DM为直径,∴∠DME=90°。
而DM垂直平分MN,∴Rt△MFD∽Rt△EFM。
∴MF2=EF•FD。
设D(h,k),(h>0,k=2r),则过M、D、N三点的抛物线的解析式为:y=a(x-h)2+k。
又∵M、N的纵坐标都为1,当y=1时,a(x-h)2+k=1,解得x1=1kha--,x2=1kha-+。
∴MN=21ka-。
∴MF=12MN=1ka-。
∴()21k1=⋅-。
∴()1k1k1a-=⋅-。
∴a=-1。
∴对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值会变化,a=-1。
【考点】一次、二次函数综合题,曲线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值,切线的性质,平行四边形的判定和性质,等边三角形的判定和性质,多边形内角和定理,平行的判定和性质,等腰梯形的判定,垂径定理,圆周角定理,相似三角形的判定和性质。
【分析】(1)∵点A的坐标为(,p),点A在直线l:y=1上,识理 21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网21世纪教育网∴p=1,即点A坐标为(3,1)。
∵点A在直线y=mx上,∴1= 3m,解得在Rt△OBA中,OB=1,AB= ,tan∠AOB=,∴∠AOB =30°。
∴∠AOE=60°。
(2)作辅助线:连接TM,ME,EN,QN,QM,根据切线的性质得到QE⊥x轴,QT⊥OT,由QE⊥MN,得到MF=NF,而r=2,EF=1,则四边形QNEM为平行四边形,即QN∥ME;同时有△QEN为等边三角形,则∠NQE=60°,∠QNF=30°;在四边形OEQT中,∠QTO=∠QEO=90°,∠TOE=60°,可求出∠TQE=120°,于是有∠TQE+∠NQE=120°+60°=180°,即T、Q、N三点共线,得到TN为直径;得到∠TMN=90°,得到TN∥ME ,所以∠MTN=60°=∠TNE ,得到以T 、M 、E 、N 为顶点的四边形是等腰梯形。
(3)作辅助线:连接DM ,ME ,根据垂径定理和圆周定理的推论得到∠DME=90°,DM 垂直平分MN ,所以Rt△MFD∽Rt△EFM ,得到MF2=EF•FD ,设D (h ,k ),(h >0,k=2r ),则过M 、D 、N 三点的抛物线的解析式为:y=a (x-h )2+k ,令y=1,得到x1=h -x2=h +MF=12到()21k 1=⋅-),解得a=-1。
3.(福建漳州14分)如图1,抛物线y =mx2-11mx +24m (m <0) 与x 轴交于B 、C 两点(点B 在点C的左侧),抛物线另有一点A 在第一象限内,且∠BAC =90°.(1)填空:OB =_ ▲ ,OC =_ ▲ ;(2)连接OA ,将△OAC 沿x 轴翻折后得△ODC ,当四边形OACD 是菱形时,求此时抛物线的解析式;(3)如图2,设垂直于x 轴的直线l :x =n 与(2)中所求的抛物线交于点M ,与CD 交于点N ,若直线l沿x 轴方向左右平移,且交点M 始终位于抛物线上A 、C 两点之间时,试探究:当n 为何值时,四边形AMCN 的面积取得最大值,并求出这个最大值.【答案】解:(1)OB =3,OC =8。
(2)连接AD ,交OC 于点E ,∵四边形OACD 是菱形,∴AD⊥OC ,OE =EC =12×8=4。
∴BE =4-3=1。
又∵∠BAC =90°,∴△ACE∽△BAE 。
∴AE BE =CE AE。
∴AE2=BE·CE =1×4=4。
∴AE =2。
∴点A 的坐标为 (4,2) 。
把点A 的坐标 (4,2)代入抛物线y =mx2-11mx +24m ,得m =-12。
∴抛物线的解析式为y =-12x2+112x -12。
(3)∵直线x =n 与抛物线交于点M ,∴点M 的坐标为 (n ,-12n2+112n -12) 。
由(2)知,点D 的坐标为(4,-2),则由C 、D 两点的坐标求直线CD 的解析式为y =12x -4。
∴点N 的坐标为 (n ,12n -4)。
∴MN=(-12n2+112n-12)-(12n-4)=-12n2+5n-8。
∴S四边形AMCN=S△AMN+S△CMN=12MN·CE=12(-12n2+5n-8)×4=-(n-5)2+9 。
∴当n=5时,S四边形AMCN=9。
【考点】二次函数综合题,解一元二次方程,待定系数法,曲线上点的坐标与方程的关系,菱形的性质,相似三角形的判定和性质,二次函数的最值。
【分析】(1)根据二次函数与x轴交点坐标求法,由mx2-11mx+24m =0(m<0),解一元二次方程即可得出。
(2)利用菱形性质得出AD⊥OC,从而得出△ACE∽△BAE,即可得出A点坐标,从而求出二次函数解析式。
(3)用待定系数法求出过C、D两点的坐标的直线CD的解析式,从而由S四边形AMCN=S△AMN+S△CMN利用二次函数的最值求出即可。
4.(福建三明14分)在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:①tan∠PEF的值是否发生变化?请说明理由;②直接写出从开始到停止,线段EF的中点经过的路线长.【答案】解:(1)在矩形ABCD 中,∠A =∠D =90°,AP =1,CD =AB =2,则PB =5。
