静电场中的电介质(1)
大学物理(6.2.1)--静电场中的电介质

d r
P
E
0 - -+- -+- -+- -+- -+-
E E0 0 r 0 r
'
(1
1 r
)
0
,
电极化率
10/13
电介质的击穿
理想电介质中没有自由电荷,但是实际的电 介质中总是存在一定的自由电荷。可以在电场作用 下产生微弱的电流。
加在电介质上的电场强度足够大时,电介质 中的电流迅速增加,其绝缘性能被破坏,甚至电介 质可能被烧毁。这叫电介质的击穿。
热释电性:温度的变化 表面产生极化电荷
电光效应:施加电场 晶体折射率发生变化
重要应用领域:
微电子学技术、超声波技术、电子光学、激光技术 、
新材料等
3/13
※ 电介质对电场的影响
( 电介质放在电场中)
U 0 E0
+
-
+
-
+
-
+
-
+
-
+
-
+
-
σ σ
电场
U E
+++++++
- - -εr- - - -
)
0
,
Q'
εr εr
1
Q0
9/13
※ 电极化强度与电场强度的关系
充满 r 的各向同性均匀电介质的平行板电容器
P
σ
'
r 1 r
0
,
P ( r 1)0E
P (r 1)0E
大学物理 电介质

χ = εr − 1 电极化率
令 ε r = (1 + χ e ) 为相对介电常量(相对电容率)
ε = ε 0ε r ~电介质的电容率
5
四、极化电荷与自由电荷的关系
E
=
E0
−
E'=
E0 εr
E'=
εr − 1 εr
E0
d
σ'=
εr − εr
1
σ
0
Q' =
εr − εr
即 D⇒ E ⇒ P ⇒σ′ ⇒q′
9
物理意义
E
单位试验电荷 的受力
单位体积内的 P 电偶极矩的矢
量和 无物理意义, D 只有一个数学 上的定义 D = ε0E + P
= ε 0ε r E
特点
真空中关于电场的讨论都 适用于电介质:高斯定律、 电势的定义、环路定理等
各向同性均匀电介质中
P = ε0χe E ,表面束缚电荷 σ ′ = P ⋅ n ,电介质中P ≠ 0
D = (1+ χ )ε0E
ε r = (1 + χ )
ε = ε rε 0
相对电容率或相对介电常量
电容率或介电常量
D=ε0ε r E = εE
•注意: D 是辅助矢量,描写电场性质的物理量仍为 E ,V
对于真空 χ e = 0 ε r = 1 ε = ε 0 则 D = ε 0 E
3、有电介质时的高斯定理的应用
在垂直于电场方向的两个表面上,将产生极化电荷。
4.极化电荷
在外电场中,均匀介质内部各处仍呈电中性,但在介质表 面要出现电荷,这种电荷不能离开电介质到其它带电体,也不 能在电介质内部自由移动。我们称它为束缚电荷或极化电荷。 它不象导体中的自由电荷能用传导方法将其引走。
(整理)西安交通大学电介质物理姚熹、张良莹课后习题答案第一章

第一章 静电场中的电介质1-1 半径为a 的 球带电量为q ,电荷密度正比于距球心的居里。
求空间的电位和电场分布。
解: 由题意可知,可设kr =ρ再由于 ⎰=q dv ρ,代入可以求出常数k 即 ⎰=424ka krdr r ππ 所以 4a q k π= r a q 4πρ= 当 a r >.时 由高斯定理可知 024επqr E =⋅ ; 204rq E πε=⎰∞=⋅=rrq dr E U 04πε当 a r <<0时 由高斯定理可知 4042040024114aqr dr r r a q dv r E rrεππερεπ=⋅==⋅⎰⎰4024a qr E πε= dr r qr dr a qr dr E U a r ar⎰⎰⎰∞∞+=⋅=20240244πεπεaq r a a q 033404)(12πεπε+-=)4(123340r a a q -=πε1-2 电量为q 的8个点电荷分别位于边长为a 的立方体的各顶角。
求其对以下各点的电距:(1)立方体中心;(2)某一面的中心;(3)某一顶角;(4)某一棱的中点。
若8个点电荷中4个为正电荷、4个为负电荷,重新计算上述问题解 :由电矩的定义 ∑∑==ii i ii i r q r q μ(一)八个电荷均为正电荷的情形(1)立方体的在中心: 八个顶点相对于立方体中心的矢量和为∑==810i i r ,故0==∑ii i r q μ(2)某一面心: 该面的四个顶点到此面心的矢量和∑==410i i r ,对面的四个顶点到此点的矢量和∑==854i i a r故qa 4=μ;(3)某一顶角 :其余的七个顶点到此顶点的矢量和为:∑==7534i ia r故qa 34=μ;(4)某一棱的中心 ;八个顶点到此点的矢量和为∑==7524i i a r故qa 24=μ;(二)八个电荷中有四个正电荷和四个负电荷的情形与此类似; 1-3 设正、负电荷q 分别位于(0,0,l /2)、(0,0,-l /2),如图所示。
静电场中的电介质

C 与 d S 0 有关
S
C ; d C
插入介质
0S q C u A uB d
C
0 r S
d
C
(2)球形电容器 已知
设+q、-q 场强分布: E 电势差:
RB
RA RB
q
r q
B A
RA
q 4 0 r 2
q q
RB
1 1 u A uB dr ( ) 2 4 0 RA RB R A 4 0 r
f
pe
pe
3;
+ E + 外 + + + +
在外电场中有极分子的固有电 矩要受到一个力矩作用,电矩方 向趋于外电场方向。但由于热运 动的存在,不会完全一致。
有极分子的取向极化!
+ E + 外 + + + +
+
两端面出现极化电荷层
电介质被极化的宏观效果
①外电场越强,极化电荷越多; ②电介质不均匀,则不仅在电介质表面会出现极 化电荷,在电介质内部也会出现极化电荷; ③对均匀电介质,在其内部任一小区域内,正负 电荷数量仍然相等,因而仍然表现出电中性。
二、电极化强度和极化电荷
单位体积内分子电偶极矩的矢量和 P
1、电极化强度(矢量)
pi
V
物理意义:描述了电介质极化强弱,反映了电介质 内分子电偶极矩排列的有序或无序程度。
在各向同性的电介质中,P 0 E
称为电介质的电极化率,它取决于电介质的性质。
2、极化电荷和自由电荷 极化电荷
E E0
++++++ r + ------- C
《大学物理学》习题解答(第12章 静电场中的导体和电介质)(1)

(2)两输电线的电势差为 U
xR
E dl
R
Ed x
d R ln 0 R
(3)输电线单位长度的电容 C
U
0 / ln
d R d 0 / ln 4.86 1012 F R R
【12.9】半径为 R1 的导体球被围在内半径为 R2 、外半径为 R3 、相对电容率为 r 的介质球壳内,它们是同 球心的。若导体带电为 Q ,则导体内球表面上的电势为多少? 【12.9 解】先求各区域电场 (1)
Q 4 0 R3
( R3 r )
B 球壳为等势体,其电势为
V
R3
E dr
Q 4 0
R3
r
dr
2
【12.2】一导体球半径为 R1,外罩一半径为 R2 的同心薄导体球壳,外球壳所带总电荷为 Q,而内球的电势为 V0.求此系统的电势和电场分布。 【12.2 解】已知内球电势为 V0 ,外球壳带电 Q 。 (1)先求各区域的电场强度:设内球带电荷 q 。由高斯定理,有
E
U
z
2R
( 1 )一根带电 的输电线在两线之间、距其轴心 x 处 p 点的场强为
x
dx
p
E i 2 0 x
另一根带电 的输电线在 p 点产生的电场强度为
x
E
2 0 ( d x )
i
p 点的总电场强度为
E E E
d R
1 1 ( )i 2 0 x d x
E1 0
(r R1 ) ( R1 r R2 ) 4 r 2 D Q , D 0 r E3
2.静电场中的电介质
自由电荷 束缚电荷
1 E dS
S
0
q
S
0
1
0
P dS
S
( 0 E P) dS q0
S S
电位移矢量定义:
D 0E P
( 0 E P) dS q0
S S
自由电荷
3、极化(束缚)电荷与极化强度的关系: 对于均匀的电介质,极化电荷集中在它的表面。电介质 产生的一切宏观效果都是通过未抵消的束缚电荷来体现。
如图,在平板电容器两极板间的介 质内沿着方向取一长度为dl,横截面为 dS的小圆柱体,在其内部极化可视为 是均匀的。
dl
' dS
' dS
P
点的总场强为:
' 退极化场 是电介质中的总电场强度。 E E E 0 E0 是自由电荷产生的电场。
' E 是极化电荷产生的退极化场
E E0 E'
' '
2.电极化强度矢量
宏观上,电介质极化程度用电极化强度矢量来描述, 其定义式为:
P lim
pi
S S S in
Pn '
P dS dS
'
极化强度力线
在任一曲面内极化电荷的负值等于极化强度的通量。
四、电介质中的高斯定理
根据介质极化和 真空中高斯定律 ' P d S q
S S
S
电位移矢量
0
' ( q q 0 ) S
1 E dS
(2)对各向同性电介质( P e 0 E)
静电场中 的电介质

静电场中的电介质 , ,
1.2 电介质的极化
1.电介质极化的机理
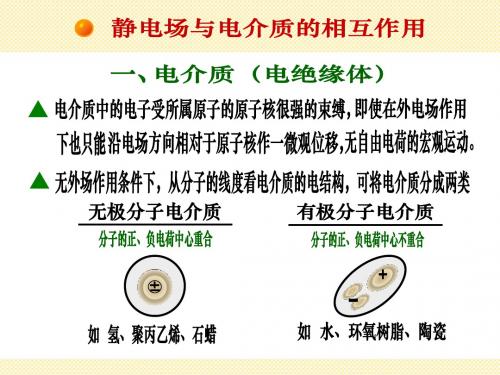
对于无极分子,在外电场的作用下,正、负电荷的中心被电场力拉开,使得正、负电荷中心产 生相对位移(这种极化称为位移极化),形成电偶极子。
在此力偶矩的作用下,有极分子的电偶极矩方向将转向与外电场基本一致的方向,这种极化称 为转向极化,其结果是电介质的两端出现等量异号的电荷.
真空中 r 1,空气中 r 1.005 ,可认为近似等于 1,其他电介质的 r 都大于 1。电介质的相对电容
率 r 和真空中电容率 0 的乘积称为电介质的电容率 ,即 r0
静电场中的电介质 , ,
1.2 电介质的极化
3.电介质的击穿
如果外电场足够大,电介质分子就会摆脱分子的束缚成为自由电子,电介质的绝缘性被破坏而 成为导体,这个过程称为电介质的击穿,这个外电场的场强称为击穿场强。
大学物理
静电场中的电介质 , ,
1.1 电介质的分类
电介质又称绝缘体。我们通常把气体、油类、蜡脂、玻璃、云母、陶瓷、橡胶等这些基本不导 电的物质称为电介质。
对于各向同性的电介质可分为无极分子和有极分子两类。
静电场中的电介质 , ,
1.2 电介质的极化
电介质的极化是指在外电场作用下电介质表面产生极化电荷的现象。 其中,极化电荷又称束缚电荷,是指在外电场中,均匀介质内部各处仍成电中性,但在介质表 面出现的不能离开电介质到其他带电体,也不能在电介质内部自由移动的电荷。
静电场中的电介质 , ,
1.2 电介质的极化
2.电介质对电场的影响
如果不存在电介质(真空),自由电荷激发的场强大小为 E0 ,引入均匀电介质后,当均匀电介质充
满电场不为零的空间,或几种均匀电介质分区充满电场且分界面都是等势面时,电介质的场强大小 E 将
静电场中的电介质(一)(二)

3.一个大平行板电容器水平放置,两极板间的一半空间充有 各向同性均匀电介质,另一半为空气,如图.当两极板带上恒 定的等量异号电荷时,有一个质量为m、带电量为+q的质点, 平衡在极板间的空气区域中.此后,若把电介质抽去,则该质 点 Q (A)保持不动. (B)向上运动. m, q (C)向下运动. (D)是否运动不能确定.
C1 C2
4.三个电容器联接如图.已知电容C1 = C2 = C3 ,而 图 1-3 C1、C2、C3的耐压值分别为100 V、200 V、300 C1 V.则此电容器组的耐压值为 (A) 500 V. (B) 400 V. C2 (C) 300 V. (D) 150 V. (E) 600 V. 图 1-4
电 介 质
图1-5 二.填空题 1.在相对介电常量为εr的各向同性的电介质中,电位移矢量与 D 0 r E 场强之间的关系是___________________ . 2.一平行板电容器,充电后切断电源,然后使两极板间充满 相对介电常量为εr 的各向同性均匀电介质.此时两极板间的电 场强度是原来的1/εr倍;电场能量是原来的1/εr 倍.
解:在圆柱导体内、外分别作半径为r、长为L的同轴圆柱形高 斯面,并应用 的高斯定理. 圆柱内: 2rLD=0 得 D=0 E=0 (a<r) 圆柱外:2rLD = L 得
/2π r r0 D
(r>a)
r0 为径向单位矢量
E1 D / 0 r /2 0 r r r0 π
应用
的高斯定理,取半径为r的球形高斯面. D
2 球内: 4πr D1 4πk 0 rdr 2πkr 2 r
dr
D1 = k / 2 ,
ˆ D1 D1r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中储存的能量为[ ]。
(A) rW0 (B) W0 /r (C) (1r )W0 (D) W 0
可编辑ppt
12
例题2
2、一空气平行板电容器始终与电源相连,这时电容器 中储存的能量为 W0,然后在两极板之间充满相对介电
常数为 r 的各向同性均匀电介质时,则该电容器中储
(D)储能增加,但与金属板相对极板的位置有关。
可编辑ppt
16
例题6
6、一个带电量为 q,半径为 R的薄金属壳里充满了相
对介电常数为 r 的均匀电介质,球壳外为真空,则球
壳的电势U为[ ]。
q (A) 4 0 R
q
(B)
(C) 0
4 r 0 R
(D) q (r R)
40r
பைடு நூலகம்
可编辑ppt
17
例题7
存的能量为[ ]。
(A) rW0(B) W0 /r (C) (1r )W0 (D) W 0
可编辑ppt
13
例题3
3、一空气平行板电容器始终与一端电压一定的电源相
连位的,移各当为向电同D0容 性,器 均然两 匀后极 电在板介两间质极为时板真,之空场间时强充,度满电为相场E对强,介度电电为位常移E数0 为为,D电 r,
实验证明,在各向同性的电介质中,P(r1 )0E,
式中, r是电介质的相对介电常数,是一个无单位的纯数。
E为介质中总的电场强度。
可编辑ppt
4
电场强介质E0中与的极电化场电:荷电q '介的质场中强的E'场两强者E叠是加自的由结电果荷。q 0 的
EE0E'
电位移矢量D: 由于静止的极化电荷和自由电荷产生
矢量
的电场
电介质中的 高斯定理
电容
静电场的 能量
可编辑ppt
3
电介质:电阻率很大、导电能力很差的绝缘体称为电
介质;电介质分为极性分子和无极性分子两类。电介
质放入电场中,介质表面出现极化电荷,反过来影响
电场的分布。 电极化强度矢量 P:电介质内部某点附近的单位体积
的分子电偶极矩的矢量和,即
P( pi) V
D 0 E P 0r E E
式中, r0称为电介质的介电常数。
可编辑ppt
6
电介质中的高斯定理:电介质中通过任一闭合曲面的
电位移通量等于该曲面所包围的自由电荷的代数和。
sDds(s面内 q) 0
当自由电荷的分布和电介质的形状都具有一定的对
称再性由D 时,可利D 求用出电E 电介介质质中中的的高电斯场定强理度求,出它电的位优移点矢是量不 ,
的能量储存在整个电场空间,是电场的能量。单位体积
内的能量(能量体密度)为
we
1DE1E2
22
整个电场空间的总能量为
We
VwedV
1DEdV V2
积分区域遍及整个电场所在的空间。
可编辑ppt
11
例题1
1、一空气平行板电容器,充电后把电源断开,这时电 容器中储存的能量为 W0,然后在两极板之间充满相对
然匀后电在介两质极 时板 ,之 场间 强充度满为相E 对,介电电位常移数为为D,r 的则各[ 向同]。性均
(A) E E 0/r,D D 0 (B) E E 0,D rD 0
(C) E E 0 /r ,D D 0 /r(D) EE 0,D D 0
可编辑ppt
15
例题5
每个电容器两端电压相等,并等于等效电容器的两端的 电压。
C 等 效 C 1C 2 C n
可编辑ppt
9
静电场的能量:在电荷移动过程中,外力必须做正功。外 力做的功转化为电能储存在电场中。
孤立导体或电容器储存的电场能量为
q2 W
1CU2 1qU
2C 2
2
可编辑ppt
10
带电电容器周围存在静电场。实际上,带电电容器
第四章 静电场中的电介质 教学基本要求 基本概念 例题分析
可编辑ppt
1
第四章 静电场中的电介质 一、教学基本要求:
1、了解电介质极化及其微观解释。了解各向同性电介 质中的 D与E的联系和区别。
2、了解电容器及电容,了解电场能量密度的概念,了 解电场的物质性。
可编辑ppt
2
二、基本概念
电介质
极化强度 电介质中 电位移矢量
必求 。 q '
可编辑ppt
7
电容: 电容是表征导体或导体组储存电荷能力的物理量。
电容器的电容:C q
式中,q为电容器任U意一AB 个极板所带的电量的绝对值;
U AB 为两导体板间的电势差;
电容只与导体本身的形状、大小、相对位置及周围介
质有关,与带电多少及是否带电无关。
孤立导体的电容: C q U
5、将一空气平行板电容器接到电源上充电到一定电压 下,断开电源,再将一块极板面积相同的金属板平行的 插入两极板之间,则由于金属板的插入及其位置的不同, 对电容器储能的影响为[ ]。
(A)储能减少,但与金属板相对极板的位置无关;
(B)储能减少,但与金属板相对极板的位置有关;
(C)储能增加,但与金属板相对极板的位置无关;
7、真空中有一均匀带电导体球,半径为R,所带的电 量为Q,则导体球产生的静电场的能量为[ ]。
(A) Q 2 16 0 R
(B) Q 2 (C) Q 2 (D) Q 2
8 0 R
4 0 R
2 0 R
可编辑ppt
18
例题8
8、如图所示,两个同样的平行板电容器A和B串联后接在
电源上,再把电容器B充满相对介电常数为
则[ ]。
(A) E E 0/r,D D 0 (B) E E 0,D rD 0
(C) E E 0 /r ,D D 0 /r (D) EE 0,D D 0
可编辑ppt
14
例题4
4器、两一极空板气间平为行真板空电时容,器电,场充强电度后为把E电0 ,源电断位开移,为当D电0容,
(可认为电容器的另一极板处于无限远时所得的电容)
式中,q为孤立导体相对于无限远处的电势;U孤立导体
所带的电量;
可编辑ppt
8
电容器串联可提高耐压能力,且每个电容器的两极
板上都带有相同的等量异号电荷,并等于等效电容器两 极板上的电荷。
1 11 1
C等效C1 C2
Cn
电容器并联在满足耐压的情况下,增大电容量,且
的都是静电场。因而静电场的基本定理仍然成立,即
sE ds 10(s面()内 q0q')
LEdl 0
可编辑ppt
5
由于极化电荷q ' 不易求得,应用高斯定理求介质中 的电场E 时遇到困难,为避免在计算中出现与极化电荷
有关的项,引入电位移矢量,表示为
D0EP
对于各向同性的均匀电介质,有
