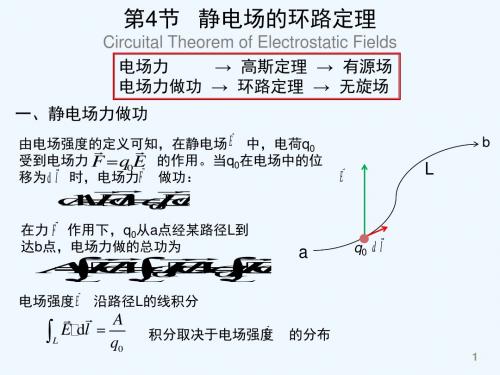
静电场的环路定理
静电场的环路定理
例3、求均匀带电球面电场中电势的分布，已知 ，q 、求均匀带电球面电场中电势的分布，已知R 微元法) 微元法 解: 方法一 叠加法 (微元法
dq = σdS = σ 2πR2 sinθdθ π 任一圆环 dS = 2 RsinθRdθ
dq 1 σ 2πR sinθdθ du = = 4πε0l 4πε0 l
B A
1 1 dr = ( − ) 2 4πε0r 4πε0 RA RB RA
q
q
2.如图已知 、-q、R 如图已知+q 如图已知 、 移至c ①求单位正电荷沿odc 移至 ，电场力所作的功 求单位正电荷沿
d q −q A = uo − uc = 0−( ) + oc 4πε0 3R 4πε0R a b c q 0 +q −q = 6 0R πε R R R
方法二
定义法
∞ P
q 4 0r2 πε
由高斯定理求出场强分布 E =
r>R r<R
r r 由定义 u = ∫ E • dl
r<R R r r ∞r r u = ∫ E • dl + ∫ E • dl
r R
0
r>R
R
dθ
O∞θຫໍສະໝຸດ lP= 0+ ∫
∞
q
4 0r πε R q = 4 0R πε
dr 2
u= ∫
r r uP = ∫ E • dl
P
∞
♠由点电荷电势公式，利用电势叠加原理计算 由点电荷电势公式，
求电偶极子电场中任一点P的电势 例1 、求电偶极子电场中任一点 的电势
Y
由叠加原理
q(r2 − r1) uP = u1 + u2 = − = 4πε0r1 4πε0r2 4πε0r1r2 q q
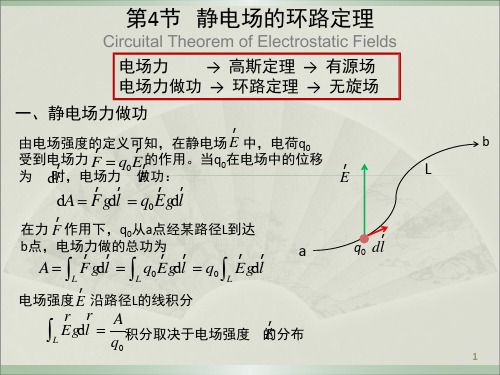
静电场的环路定理
q
j
V V V 1 2 k q q q 1 2 n 4 r r 4 r 0 1 4 0 2 0 n
q i
电势叠加原理
V V P i r 0 i i i 4
任意带电体场中的电势
VP q
4 0r
dq
a b
即：a、b两点的电势差 = A/q0
将单位正电荷 从ab电场力作的功 与路径无关
6
例: 已知真空中两金属圆筒电极间电压为U ，半径分别为 R1、 R2 。 求：负极上静止电子到正极时的速度？ 解：由电势差的定义可得
A q ( V V )
( e)( U )
R
R
2
1
F
c
dl
q0
dr
b
r +dr
r
a
rb
+
积分
1 1 q q q q 0 0 A d r 2 a4 r 4 r 0 0 a r b
b
ra
q
——点电荷的电场力作功 只与被移动电荷距离场源电荷的距离相关 与路径无关
2
2.在点电荷系的电场中(或连续带电体的电场)
结论
b b b A q E d l q E d l q E d l 0 1 0 2 0 n a a a
电场强度的线积分与路径无关
电场力是保守力，静电场是保守力场。
3
二、环路定理
在任意电场中, 将q0从a
b L2 经L1
经L2
b电场力作功：
A q E d l 0 L
04静电场的环路定理 电势
1
•II区：球壳外电势
rR
U2
r
1 E2 dl r E 2 dr r
q q dr 2 4 0 r 4 0 r
Fan
I区：球面内
r R , E1 0
1
U1
q 4 0 R
q q II区：球面外 r R , E 2 4 0 r 2 U 2 4 0 r
U 4
i i
r
（2）连续带电体：将带电体分割成无限多个电荷元， 将每个电荷元看成点电荷，根据点电荷电势公式求电 荷元的电势，迭加归结于积分。
U dU
dq 4 0 r
注意电荷元的选取！
Fan
特别注意：
点势法的使用，必须是以无穷远处为电势零点为前提 条件。
up
q 40 rp
uab
b
a
E dl
Aab Wa Wb q0 q0 q0
b
a
E dl
移动单位正电荷自 ab 过程中电场力作的功。
移动单位正电荷 自该点 “势 能零点” 过程 中电场力作的 功。
b Wa Aab • 电势定义 ua E dl a q0 q0
意义：把单位正电荷从a点沿任意路径移到b点时电 场力所作的功。 电势差和电势的单位相同，在国际单位制中，电势 的单位为：焦耳/库仑（记作J/C），也称为伏特（V） ，即1V＝1J/C。
Fan
注意几点：
1.电势是标量，只有正负之分。
2. 电势和电势能一样都是相对的量，为了让它有确 定的值，必须选择一个零点作为参考点。但电势差 的值具有绝对的意义，与零点的选择无关。 3. 电势零点的选择： •对有限带电体一般选无穷远为电势零点。 在实际问题中，也常常选地球的电势为零电势。 •对无限带电体不宜选无穷远为电势零点。此时只有电 势的相对值（即电势差）有意义。 4.电势能与电势的区别：WP 可正可负，取决于 q 和 q0 ； U只取决于场源电荷 q 。
静电场的环路定理表达式
静电场的环路定理表达式
静电场的环路定理公式：D=pL/S。
在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率。
这个结论称为安培环路定理。
静电场，指的是观察者与电荷量不随时间生变化的电荷相对静止时所观察到的电场。
静电场性质
根据静电场的高斯定理
静电场的电场线起于正电荷或无穷远，终止于负电荷或无穷远，故静电场是有源场。
从安培环路定理来说它是一个无旋场。
根据环量定理，静电场中环量恒等于零，表明静电场中沿任意闭合路径移动电荷，电场力所做的功都为零，因此静电场是保守场。
根据库仑定律，两个点电荷之间的作用力跟它们的电荷量的乘积成正比，和它们距离的平方成反比，作用力的方向在它们的连线上，即F=(kq1q2)/r2；，其中q1、q2为两电荷的电荷量(不计正负性)、k为静电力常量，约为9.0e+09(N·m2)/(C2；)，r为两电荷中心点连线的距离。
注意，点电荷是不考虑其尺寸、形状和电荷分布情况的带电体。
是实际带电体的理想化模型。
当带电体的距离比它们的大小大得多时，带电体的形状和大小可以忽略不计的点电荷。
第10章静电学-3-静电场环路定理
+q
11
(2)电荷分布如图所示, 将点电荷qo从a 经半圆b移到c的 过程中, 电场力对qo的功？
解 Aac qo (Ua Uc )
b
Ua
q
4o R
q
4o R
0
-q
a
+q R
o
c
Uc
q
4 o (3 R)
q
4o R
R
R
q
6o R
Aac
qqo
6o R
12
例10-14 一均匀带电直线段，长为L，电量为q ;取无穷远为电 势零点，求直线延长线上离一端距离为d 的P点的电势。
9
③对于电荷连续分布的带电体，可将其分割为无数多电荷元
dq，每个电荷元dq当作点电荷，其电势为
dU dq 4πε0r
根据电势叠加原理
U
V
dq
4 0r
dl dq dS
dV
积分遍及整个带电体，V是带电体的体积。
电势叠加原理也可以计算多个带电体所产生电场的总电 势，总电势应等于各带电体所产生电场的电势的代数和。
(3)电势差：
b
Uab Ua Ub E dl
a
静电场中a、b两点的电势差等于将单位正电荷由a沿任意路 径移至b过程中电场力做的功。
电势差是绝对量，与电势零点的选择无关。
6
由Wa
q
零势点 E
a
dl ,
得 Wa qUa
由Aab
q
b
E dl
a
Wa Wb ,
得 Aab q(Ua Ub )
(3)等于场强从该点沿任意路径到零势点的线积分。
说明：
(1)电势是相对量，要确定场中各点的电势必须选定电势零点。
静电场的环路定理
已知q的电场分布 E
根据定义, P点的电势为
4
q
0r
2
er
VP
P
E dl
r
q
40r
2Pdr4q04r2qe0rrP dl
q > 0时, VP为正, r V, r处V= 0 min q < 0时, VP为负, r V, r处V = 0 max
2.电场强度与电势梯度的关系
根据电势差的定义, 把单位正电荷从P1移到P2 电场力所作的功为：
dA E dn V (V dV )
r E
dn
n
P1
P2
V V dV
E dn dV
E
dV dn
grad V
E
ቤተ መጻሕፍቲ ባይዱ
dV dn
n
r E grad V
r 即:电场中某点的场强 E 等于该点电势梯度的负值
无意义
VP
P
E
dr
rP
2 0r
dr
2 0
ln
rP
r
P
P'
令某处 r = r0（有限值） V=0，则
VP
P0
P
E
dl
P
P
E dl
P0
P
E dl
r0 P0
P
P
2
0r
dr
2 0
ln
r0 r
可见：当电荷分布到无穷远时，
22
归纳 电场强度与电势的关系
积分关系：
静电场环路定理
方法二 定义法 先由高斯定理求出场强分布
q
再由定义 u E dl
rR
P
E
4 0 r 2
rR
0
rR
rR
u E dl E dl
R r R
R
O
r＜ R
P
r＞ R
0
q
2
4 0 r q 4 0 R
R
dr
u
2 2
方法二 定义法 已知轴线上的场强分布函数
E qx
2
4 0
R x
u Edx
4 0 ( x R ) qxdx
2
3
2
q
xp
xp
4 0 ( x R )
2 2
3
2
4 0 r
例4、求均匀带电球面电场中电势的分布，已知R，q 解: 方法一 叠加法 (微元法) 球面上任取一圆环
q
r1 r2 r
2
r2
l cos u 2 4 0 r
其中
q
O
r r 1
q
X
r x y
2 2
2
l
u 1 4 0
2
cos
x x y
2 2
px (x y )
3 2 2
课堂练习： 已知正方形顶点有四个等量的电点荷 q1 q 4.0 10 9 C r=5cm
静电场环路定理得
对任意大小面积S都成立。环路定理的微分形式。
( E ) dS 0
s
E 0; 或者rotE 0
旋度处处为零的矢量场，称为无旋场。静电场是无旋场。 高斯定理的微分形式。
静电场环路定理
i
l
结论：静电场力做功，与路径无关.
10-4 静电场的环路定理
静电场的环路定理
q0 E dl q 0
q 0 ( E dl
ABC
ABC
E dl 0
l
CDA
E dl ) 0
A
ADC
E dl
B
D
C
E
结论：沿闭合路径一 周，电场力作功为零.
q1
r1
n
n
U i
i 1
i 1
Ei dl
E3
q2
r2
E2
q3
r3
A
E1
10-4 静电场的环路定理
电荷连续分布时 dq dV
dq dU 4πε0 r
1 dq UA 4πε0 r
dq
r
A
10-4 静电场的环路定理
计算电势的方法
q
令 U 0 qdr U E dl r 2
r
4πε0 r
er
r
q U 4 πε0 r
10-4 静电场的环路定理
四
电势的计算
点电荷系 E Ei
i
qi UA i 1 4 π ε0 ri
n
UA
A
E dl
A
10-4 静电场的环路定理
一
电场的环量
E dl E cos dl
l l
环量：场强沿闭合路径的线积分称为电场的环量
dl
l
F dl q0 E cos dl
静电场的环路定理
➢ 本节的研究目的
研究ห้องสมุดไป่ตู้电场的旋度特性
➢ 本节的研究内容
一、静电场环路定理的微分形式 二、静电场环路定理的积分形式
一、静电场环路定理的微分形式
E ()
0
E 0
静电场是无旋场； 静电场的电力线不可能是闭合曲线；
二、静电场环路定理的积分形式
根据斯托克斯定理
L E dL S E dS L E dL 0
分析：对闭合曲线应用环路定理
a
E dL E dL E dL 0
acbda
acb
bda
c d
E dL E dL E dL
acb
bda
adb
b
说明：两点之间的电位差与积分路径无关
二、静电场环路定理的积分形式
根据斯托克斯定理
L E dL S E dS L E dL 0
静电场的环量为零； 静电场是保守力场，位场； 静电场中电场力作功与路径无关；
本节要点
➢ 本节的研究目的 研究静电场的旋度特性；
E 0
L E dL 0
静电场的环路定理
静电场的环路定理的数学表示式为
静电场的环路定理的数学表示式为
静电场的环路定理是物理学中一个重要的定理，它描述了电场的流动规律。
它
的数学表示式为：
∮E·dl=0
其中，E表示电场，dl表示电场的矢量，∮表示积分。
静电场的环路定理指出，在一个闭合的环路上，电场的矢量积分为零。
这意味着，在一个闭合的环路上，电场的矢量总和为零，也就是说，电场的流动是不变的，不会有任何变化。
静电场的环路定理可以用来解释电场的流动规律，也可以用来计算电场的大小。
它可以用来解决电场的问题，也可以用来计算电场的分布情况。
静电场的环路定理是物理学中一个重要的定理，它描述了电场的流动规律，并
且可以用来解决电场的问题。
它的数学表示式为∮E·dl=0，其中，E表示电场，
dl表示电场的矢量，∮表示积分。
它指出，在一个闭合的环路上，电场的矢量积
分为零，也就是说，电场的流动是不变的，不会有任何变化。
它可以用来解释电场的流动规律，也可以用来计算电场的大小，从而解决电场的问题。
静电场的环路定理数学表达式
静电场的环路定理数学表达式静电场是一个有趣的物理现象，它作用于每一个电子粒子。
静电场的研究可以追溯到古代希腊哲学家Aristotle，他认为宇宙中的物体有内在的“力量”，他将其称为“力学”。
随后雅克•笛卡尔和伽利略更进一步地探讨了这种现象，并将其称为“电力”。
然而，直到二十世纪初，电磁学家Maxwell提出了静电场的最终形式，即描述电磁场的四个基本方程，用来表示静电场的上下文，电流和电压的关系，以及电磁波在介质中的行为。
最重要的是，Maxwell提出了一项重要的理论，即电磁波可通过任意曲线而不会破坏传播，这被称为Maxwell环。
环路定理（又名Maxwell环路定理或Maxwell-Faraday方程）是一种电磁学的数学运算，它旨在确定电磁场的变化要素和电流的交互关系。
它表明：对于任意给定的点，如果其周围存在一个环形变化的电流，则电场的变化率将等于电流的变化率。
这就是说，随着电流的增加，电场也会随之增加，反之亦然。
数学上，Maxwell环路定理可以表述为：∮ E·dl = −dφ/dt这里，E表示无负载电场，dl 表示从圆环中任意一点到另一点的理想导线段，φ 表示以安培为单位的电流场。
Maxwell环路定理的形式表明，如果电流在某个特定的时间尺度内发生变化，则电磁场也会发生变化。
maxwe11环定理也表明，如果存在一个环形电路，则它会产生一个电磁场，这就是伽利略发现的现象。
有时这种电磁场也会由于算术变换而被称为电动势场。
Maxwell环路定理对研究静电场、电动势场以及电气工程具有重要意义。
它是用来解释很多电磁现象的基础，比如能量传输、电磁辐射、接地效应、电场色散等。
通过Maxwell环路定理，可以系统地推导电磁学的数学关系和定律。
Maxwell环路定理对静电场的深入理解也至关重要，其中包括球形、面形、应力线电路等多种静电场模型，它们研究无刷电机、电动车和飞机等设备。
环路定理
解：
a
r P
x
U=
q 4 0 x2 +a2 πε
x
dU qx E = Ex = − = 2 2 32 dx 4 0(x +a ) πε
U(x, y, z) =C
• 常用一组等势面描述静电场，并规定相邻两等势面之间的 常用一组等势面描述静电场， 电势差相等。 电势差相等。
点电荷的电场线与等势面
+
电偶极子的电场线与等势面
+ +
+ +
+
+
+
+场线的关系: 等势面与电场线的关系: （a） 等势面与电场线处处正交； 等势面与电场线处处正交； 电场线指向电势降低的方向； （b） 电场线指向电势降低的方向； （c） 等势面和电场线密集处场强量值大，稀疏处场强量值小。 等势面和电场线密集处场强量值大，稀疏处场强量值小。
q
r
a
r+dr r dl θ r q0 E
结论：在点电荷电场中， 结论：在点电荷电场中，电场力所作的功只与试验电荷始末 位置有关，而与试验电荷运动路径无关。 位置有关，而与试验电荷运动路径无关。
（2）在任意电荷系的电场中： 在任意电荷系的电场中：
r v E = ∑Ei
r r v r v r A= q0 ∫ E⋅ dl = q0 ∫ ∑E ⋅ dl = ∑ 0 ∫ E ⋅ dl = ∑A q i i i
例2、 均匀带电圆板，半径为 R ，电荷面密度为 σ 。求轴线上 均匀带电圆板， 电势。 任一点 P 的电势。 解： dU =
dq 4 0 x +r πε
2 2
dr r
R P
dq =σ2π rdr
9-5 静电场的环路定理解析
E dl
q0U AB
q0 VA
VB
A
五、点电荷电场的电势
V E dl Edr
r
r
q
4 0r
2
r
dr
V q
4 0r
正电荷的电势为正，离电荷越远，电势越低；
负电荷的电势为负，离电荷越远，电势越高。
六、电势叠加原理
E dl
AB
VB
当电荷分布在有限空间时，无限远处的电势能和 电势为零
v v
VA
E dl
A
•电场中某点的电势在数值上等于放在该点的单 位正电荷的电势能
•电场中某点的电势在数值上等于把单位正电荷 从该点移到势能为零的点时，电场力所作的功。
2、说明：
•电势是标量，有正有负； •电势的单位：伏特 1V=1J.C-1； •电势具有相对意义，它决定于电势零点的选择。 在理论计算中，通常选择无穷远处的电势为零；
复习
9-3、4 电场线 静电场的高斯定理
• 电场线 • 电场强度通量 • 高斯定律 • 高斯定律应用举例
9-5 静电场的环路定理
一、静电场力所作的功
1、点电荷电场
点电荷Q固定于原点O，试验 电荷q0在Q的电场中由A点沿 任意路径ACB到达B点，取
微为元ddlW，电 场F力 dl对q0q的0 E元 d功l
ADC
ABC
电场力作 功
与路径无 关
W＝q0 E dl＝0
E
dl＝0
定义：电场强度沿任意闭合路径的线积分叫电 场强度的环流。
静电场的环路定理：在静电场中，电场强度的 环流为零。
三、电势能
第10章 静电学 - 3 - 静电场环路定理
由此可见, 在点电荷q的电场中, 电场力的功只与路径的起 点和终点位置有关, 而与路径形状无关。 此结论可通过场强叠加原理推广到任意点电荷系(包括带电 体)的电场。
2
即：电场力做功只与路径的起点和终点位置有关, 而与所经
过的路径无关——电场力是保守力。
A F dl q0 E dl 0 E dl 0
R2 ln 1 R1
dV R2 E0 ln E0 0 令 dR1 R1
A
R2 e R1
B
R1
Vmax
R2 E0 =33kV e
R2
22
例10-19一半径为R的均匀带电球面，带电量为q；球面外有一 均匀带电细线，电荷线密度为 , 长为l, 细线近端离球心距离 为ro, 求细线受的力和细线在球面电场中的电势能。
A
A e(U A U B ) eV
B
1 eV m 2 , =1.03107(m/s) 2
21
(4)若击穿场强Eo=200kV/cm, R1可调整, 能承受的最大电压是 多少?
E
V R2 r ln R1
显然r=R1处的场强最强，最先击穿，令E=E0
R2 得： V E0 R1 ln R1
§10. 4 1.电场的环量
静电场环路定理 l
dl
----场强沿闭合路径的线积分。即
E dl E cos dl
l l
E
设想将试验电荷q0沿闭合路径移动一周，则电场力作功
A l F dl l q0 E dl q0 l E cos dl
n
n
4 o ri
qi
式中: Ui代表第i个点电荷qi单独存在时在a点产生的电势。
静电场的环路定理
无限扩展的源电荷(如无限长带电圆柱面)只 能选在有限区域内的任一点为电势零点。
2 电势差UAB=VA-VB
UABVA VB AB E dl
静电场中A、B两点电势差UAB，在数值上等于把
单位正电荷从A点移到B点时，静电场力所作的功。 电势差是绝对的，与电势零点的选择无关；
们的代数和也必然与路径无关。
3 结论：
一试验电荷q0在静电场中从一点沿任意路径
运动到另一点时，静电场力对它所作的功，仅与
试验电荷q0及路径的起点和终点的位置有关，而
与该路径的形状无关。
说明：静电场力是保守力，静电场是保守场。
二 静电场的环路定理
q0沿闭合路径l移动一周，电场力作功为：
W
l
q E dl 0
8-6 静电场的环路定理 电势能
一 静电场力所作的功
B
1 点电荷电场中移动试验电荷q0
正点电荷q固定于原点o，
试验电荷q0在q的电场中，由
A点沿任意路径ACB到达B点。
点电荷q的电场强度为：
E
1
4
0
q r2
er
q
o
C
E
q0
r
A
q0移过元位移dl 时，电场力作的元功为：
dW q0E dl
电势大小是相对的，与电势零点的选择有关。
一般情况下，电势是源电荷和空间位置的函数，
当电势分布已知时，可以方便地求出电荷q在电 场中某点的电势能和在电场中移动电荷q时静电
场力作的功。
EpA qVA WAB q0VA q0VB q0UBA
静电场的环路定理
b
a ( L1 )
v v b q0 E ⋅ dl − ∫
v v q0 E ⋅ dl
环路定理
=0
∫
L
v v E ⋅ dl = 0
该定理还可表达为：电场强度的环流等于零。 该定理还可表达为：电场强度的环流等于零。 根据保守力的定义，任何力场， 根据保守力的定义，任何力场，只要其场强的环流 为零，该力场就叫保守力场 势场。 保守力场或 为零，该力场就叫保守力场或势场。可以引入相应 的势能，即电势能。 的势能，即电势能。
q 4πε 0 x
•从电荷分布求场强，再由场强分布求电势 从电荷分布求场强， 从电荷分布求场强
U P = ∫ E • d r （场强积分法） 场强积分法）
P ∞
例4 求均匀带电球面的电场中电势的分布 解 由高斯定理可以求的球面内外的场强分布为
+ P1 + + + + +
2
r <R r ≥R
对球外一点P 对球外一点
二 电势
某点电势电W 之比只取决于电场， 某点电势电 a与q0之比只取决于电场，定义电该 点的电势 单位：伏特（ ） 电势. 点的电势. 单位：伏特（V） 电势电
W a = q0 ∫
"0"
a
v E ⋅ dl
电势
WA VA = q0
=∫
"0"
A
v E⋅ E⋅ dl
由上式可以看出, 由上式可以看出,静电场中某点的电势在数值上 等于单位正电荷放在该点处时的电势能, 等于单位正电荷放在该点处时的电势能,也等于单位 正电荷从该点经任意路径到电势零点处(无穷远处) 正电荷从该点经任意路径到电势零点处(无穷远处) 时电场力所做的功。 时电场力所做的功。
3.3 静电场的环路定理 大学物理
R
+
o + + +
4 0 r （3）确定电势分布；
2
E
er
(r R)
主讲：张国才
U P E dl E dr + r+ r r + + 1 q q r p + + 2 dr R R 4 + + 4 o R 0 r o + + (2)当r>R时 + + + + U P E dl E dr + + "P" r
主讲：张国才
3.3 静电场的环路定理
基础物理学
4
试验电荷q0在静电场中沿任意闭合路径 L运动一周时，电场力对q0做的功W=？
L
W q0 E dl 0
E dl 0
L
主讲：张国才
3.3 静电场的环路定理 静电场的 Nhomakorabea路定理基础物理学
5
在静电场中，场强沿任意闭合路径的线积 分（称为场强的环流）恒为零。
2 2
0
主讲：张国才
q 4 0 R x
2 2
基础物理学 3.3 静电场的环路定理 二、从电荷分布求场强，从场强分布求电势。 例2 计算均匀带电球面的电场中的电势分布。球面半 径为R，总带电量为q。
13
解：
q
+
+ + + +
+ +
+
（1）取无穷远处为电势零点； + （2）由高斯定律可知电场分布为； + E 0 (r R) + + 1 q
电磁学_静电场_1.4 环路定理
P、Q两点之间的电势差定义为
从P点到Q点移动单位正电荷时电场力所作的功 单位正电荷的电势能差
空间某点的电势值
为了确定某点的值，还需要选择零点 一般选择无穷远为势能零点,P点电势值为 AP U ( p) U P E dl P q0 两点之间电势差可表为两点电势值之差
点电荷的势能零点是否可以选在电荷上？ 无限大平面板ห้องสมุดไป่ตู้势能零点能否选在无穷远？
例题10一示波器中阳极A和阴极K之间的电压是 3000 V，试求阴极发射的电子到达阳极时的速度， 设电子从阴极出发时初速为零。
[解]电子带负电，它沿电势升高的方向加速运动，即从阴极 K出发到达阳极 A. 静电场力是保守力，按能量守恒
连续带电体有
1
U P E d l dU
P
i
dq 1 dq 1 dq dU ( 2 4 0 P r 4 0 r P 4 0 rP
讨论
电势与场强一样是一个描述场本身性质的物理量， 与试探电荷无关，是标量。电势叠加是标量叠加。 电势UP：P与无穷处电势差 电势零点 选取
可以任意选取 选择零点原则：场弱、变化不太剧烈 选无穷远为零点？选地为零点即地和无穷远等电 势吗？
问题
地与无穷远的电势差
实际地球周围大气中有一个方向向下的静电场 是地球所带的负电荷和大气中的等离子体产生 的 若以无穷远为势能零点，则地球的电势为
U地 5.4 10 V
8
思考：
电势能、电势差、电势
电场力 的功 定义
Q
静电场与 q0有能量交换
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
静电场的环路定理
物理学
第五版
一、静电场力所做的功
0d d A q E l
=⋅l r
r
εqq d ˆπ42
00
⋅=0
2
0d d 4πqq A r εr
= 点电荷的电场
q
q A
r A
B
B
r E
r
r
ˆl d θ
r
d r θl l r
d cos d d ˆ==⋅
物理学
第五版
20
d 4πB
A
r r qq r A εr
=
⎰
)11(π400B
A r r εqq -=结论: A 仅与q 0的始末位置有关，
与路径无关
2
0d d 4πqq A r εr
=q
q A
r A
B
B
r E
r
r
ˆl d θ
r
d
物理学
第五版
任意带电体的电场
∑=i
i
E E 0d l
A q E l =⋅⎰⎰∑⋅=l
i i
l
E q
d 0结论：静电场力做功，与路径无关。
静电场力是保守力。
（点电荷的组合）
++=+⋅+⋅=
⎰
⎰212010A A l d E q l d E q b
a
b
a
物理学
第五版
二、静电场的环路定理
⎰
⎰⋅=⋅ADC
ABC
l E q l E q
d d 0
00
)d d (0=⋅+
⋅⎰⎰CDA
ABC
l E l E q
d =⋅⎰l
l E
静电场是保守场
结论：沿闭合路径一周，电
场力作功为零.
E
A
B
C
D
物理学
第五版
静电场的环流定理反映了静电场的一个重要性质。
它说明静电场是保守场（无旋场），可以引入势的概念，所以也叫势场。
根据斯托克斯公式
s d E l d E l
s
⋅⨯∇=⋅⎰
⎰
)(0
=⨯∇E
静电场的旋度为零，静电场是无旋场
物理学
第五版
例：用环流定理证明“静电场电力线不会闭合”。
证：用反证法证明：先假设电力线形成闭合线，则以此闭合线为路径应用环流定理
E
l
⎰⎰⎰>=
=
⋅l
Edl Edl l d E 0
cos 0
与 ⎰=⋅l
l d E 0
相矛盾
说明：假设不正确，静电场的电力线不会闭合
物理学
第五版
例：证明非无限大平行板电容器电力线不可能只分布内部。
带电平行板电容器的电场线
+ + + + + + + + + + + + +
- - - - - - - - - - - - -
物理学
第五版
+ + + + + + + + + + + + +
- - - - - - - - - - - - - 证：用反证法，假设外部 0=E 如图作一闭合回路 ⎰
=⋅l
l d E
⎰⎰⎰⎰⋅+⋅+⋅+⋅DA
CD AB BC l d E l d E l d E l d E EL =与 ⎰=⋅l l d E 0
相矛盾，
A B C
D
说明：假设不正确。