2019中考全等三角形经典培优题(教师版)

合集下载

全等三角形培优经典题

全等三角形培优习题1、已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF ⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）直接写出线段EG 与CG 的数量关系；（2）将图1中△BEF 绕B 点逆时针旋转45o ，如图2所示，取DF 中点G ，连接EG ，CG ．你在（1）中得到的结论是否发生变化？写出你的猜想并加以证明．（3）将图1中△BEF 绕B 点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立？2、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．ADFC GE B图1ADF C GE B 图2 ADFC GE B图3FB D图1BDE图2B 图3D7.已知如图，E.F 在BD 上，且AB ＝CD ，BF ＝DE ，AE ＝CF,求证：AC 与BD 互相平分.8.如图, 已知：AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF ．猜想线段AC 与EF 的关系，并证明你的结论.9如图ABD ∆和ACE ∆FG E DC B A A B EO F DOE DCB A10.如图∠ABC ＝90°AB ＝BC ，D 为AC 上一点分别过A.C 作BD 的垂线，垂足分别为E.F,求证：EF ＝CF －AE.11.如图5，已知AB ∥CD ，AD ∥BC ， E.F 是BD 上两点，且BF ＝DE ，则图中共有对全等三角形.12.如图7，AB ∥CD ，AD ∥BC ，OE=OF, 图中全等三角形共有______对. 1. 填空题常见题型13.两三角形有以下元素对应相等，不能判定全等的是（） A. 两角和一边 B. 两边及夹角 C. 三个角 D. 三条边14.如果两个三角形两边对应相等，且其中一边所对的角也相等，那么这两个三角形（） A. 一定全等 B. 一定不全等 C. 不一定全等 D. 面积相等15.如果两个三角形中两条边和其中一边上的高对应相等，那么这两个三角形的第三条边所对的角的关系是（）A. 相等B. 不相等C. 互余或相等D. 互补或相等 2. 常见题的解题方法与分析16. 下列各图中，一定全等的是（） A. 各有一个角是︒45的两个等腰三角形 B. 两个等边三角形 C. 各有一个角是︒45，腰长都是3cm 的两个等腰三角形 D. 腰和顶角对应相等的两个等腰三角形 17．已知如图，CE ⊥AB 于点E ，BD ⊥AC 于点D ，BD 、CE 交于点O ，且AO 平分∠BAC ，（1）图中有多少对全等的三角形？请你一一列举出来（不要求说明理由）（2）求证BE=CD （3）要得到BE=CD ，你还有其他的思路吗？18.则∆图5A. 6cmB. 7cmC. 8cmD. 9 cm19如图，已知∠1=∠2，∠3=∠4，AB 与CD 相等吗？请你说明理由.20.已知：如图，△ABC 中，∠ABC =45°，CD ⊥AB 于D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，H 是BC 边的中点，连结DH 与BE 相交于点G 。

《全等三角形》培优题型全集

《全等三角形》培优题型全集题型一：倍长中线（线段）造全等1.已知：如图,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证：AC=BFC2.如图,△ABC中,AB=5,AC=3,则中线AD的取值规模是______.D CBA3.在△ABC中,AC=5,中线AD=7,则AB边的取值规模是( )A.1<AB<29B.4<AB<24C.5<AB<19D.9<AB<194.已知：AD.AE分离是△ABC和△ABD的中线,且BA=BD,求证：AE=21ACC E5.已知：如图,在ABC∆中,ACAB≠,D.E在BC上,且DE=EC,过D作BADF//交AE于点F,DF=AC.求证：AE等分BAC∠ABFD E C题型二：截长补短1.已知,四边形ABCD中,AB∥CD,∠1＝∠2,∠3＝∠4. 求证：BC＝AB＋CD.2.已知：如图,在△ABC中,∠C＝2∠B,∠1＝∠2,求证：AB=AC+CD.3.如图,在△ABC中,∠BAC=60°, AD是∠BAC的等分线,且AC=AB+BD,求∠ABC 的度数D CBA4.已知ABC∆中,60A∠=,BD.CE分离等分ABC∠和.ACB∠,BD.CE交于点O,试断定BE.CD.BC的数目关系,并加以证实．DOECBA题型三：角等分线上的点向角双方引垂线段1.如图,在四边形ABCD中,BC＞BA,AD＝CD,求证：∠BAD+∠C=180°2.如图,四边形ABCD中,AC等分∠BAD,CE⊥AB于D CBA12姓名E,AD+AB=2AE,则∠B 与∠ADC 互补,为什么？3.如图,△ABD 和△ACD,BD=CD,∠ABD=∠ACD,求证AD 等分∠BAC.4.已知,AB ＞AD,∠1＝∠2,CD ＝BC. 求证：∠ADC ＋∠B ＝180°.图九21CBAD5.如图,在△ABC 中∠A BC,∠A CB 的外角等分线订交于点P,求证：AP 是∠BAC 的角等分线图十一4321PABC6.如图,∠B=∠C=90°,AM 等分∠DAB,DM 等分∠ADC. 求证:点M 为BC 的中点题型四：衔接法（结构全等三角形）1.已知：如图,AB ＝AD,BC ＝DC,E.F 分离是DC.BC 的中点,求证： AE ＝AF.2.如图,直线AD 与BC 订交于点O,且AC=BD,AD=BC ．求证：CO=DO ．AOD CB3.已知：如图,AB=AE,BC=ED,点F 是CD 的中点,AF ⊥CD ．求证：∠B=∠E ．DAFEABCDAF DC BE4.在等边ABC ∆内取一点D ,使DA DB =,在ABC ∆外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.题型五：全等+角等分线性质 1.如图,AD 等分∠BAC,DE ⊥AB 于E,DF ⊥AC 于F,且DB=DC,求证：EB=FC2.已知：如图所示,BD 为∠ABC 的等分线,AB=BC,点P 在BD 上,PM ⊥AD 于M,•PN ⊥CD 于N,求证：PM= PNP D ACBM N题型六：全等+等腰三角形的性质1.如图,在△ABE 中,AB ＝AE,AD ＝AC,∠BAD ＝∠EAC, BC.DE 交于点O.求证：(1) △ABC ≌△AED; (2) OB ＝OE .OCEBDA2..已知：如图,B.E.F.C 四点在统一条直线上,AB ＝DC, BE ＝CF,∠B ＝∠C ．求证：OA ＝OD ．题型七：两次全等1.如图,AB=AC,DB=DC,F 是AD 的延伸线上的一点.求证：BF=CFFDCBA2.如图,D.E.F.B 在一条直线上AB=CD, ∠B=∠D,BF=DE. 求证：（1）AE=CF;（2）AE ∥CF （3）∠AFE=∠CEF3.如图：A.E.F.B 四点在一条直线上,AC ⊥CE,BD ⊥DF,AE=BF,AC=BD.求证：△ACF ≌△BDEACEF4.如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6．654321E D CBA5.已知如图,E.F 在BD 上,且AB ＝CD,BF ＝DE,AE ＝CF,求证：AC 与BD 互相等分ADFECBDECBA6.如图,在四边形ABCD 中,AD ∥BC,∠ABC=90°DE ⊥AC 于点F,交BC 于点G,交AB 的延伸线于点E,且AE=AC.求证：BG=FG题型八：直角三角形全等（余角性质）1.如图,在等腰Rt △ABC 中,∠C ＝90°,D 是斜边上AB 上任一点,AE ⊥CD 于E ,BF ⊥CD 交CD 的延伸线于F ,CH ⊥AB 于H 点,交AE 于G ．求证：BD ＝CG ．2.如图,将等腰Rt △ABC 的直角极点置于直线l 上,且过A,B 两点分离作直线l 的垂线,垂足分离为D,E,请你在图中找出一对全等三角形,并写出证实它们全等的进程．3.如图,∠ABC ＝90°,AB ＝BC,D 为AC 上一点,分离过A.C 作BD 的垂线,垂足分离为E.F,求证：EF ＝CF －AE题型九：延伸角等分线的垂线段1.如图,在△ABC 中,AD 等分∠BAC,CE ⊥AD 于E ．求证：∠ACE=∠B+∠ECD ．AF DCBE2.如图,△ABC 中,∠BAC=90度,AB=AC,BD 是∠ABC 的等分线,BD 的延伸线垂直于过C 点的直线于E,直线CE 交BA 的延伸线于F ．求证：BD=2CE ．FE DCB A3.已知,如图34,△ABC 中,∠ABC=90º,AB=BC,AE 是∠A 的等分线,CD ⊥AE 于D ．求证：CD=21AE ．CEBAD题型十：面积法AB CFDEAFCBDEGABEO FDC1.如图,在△ABC 中,∠BAC 的角等分线AD 等分底边BC, 求证AB=AC.2.如图,在△ABC 中,∠A=90°,D 是AC 上的一点,BD=DC,P 是BC 上的任一点,PE ⊥BD,PF ⊥AC,E.F 为垂足．求证：PE+PF=AB ．3.己知,△ABC 中,AB=AC,CD ⊥AB,垂足为D,P 是线段BC 上任一点,PE ⊥AB,PF ⊥AC 垂足分离为E.F,求证： PE+PF=CD.4.己知,△ABC 中,AB=AC,CD ⊥AB,垂足为D,P 是射线BC 上任一点,PE ⊥AB,PF ⊥AC 垂足分离为E.F,求证： PE – P F=CD.题型十一：扭转型1.如图,正方形ABCD 的边长为1,G 为CD 边上一动点（点G 与C.D 不重合）, 以CG 为一边向正方形ABCD 外作正方形GCEF,衔接DE 交BG 的延伸线于H.求证：①△BCG ≌△DCE,② BH ⊥DE2.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E 在统一条直线上,贯穿连接DC ．（1）请找出图2中的全等三角形,并赐与证实（解释：结论中不得含有未标识的字母）;（2）证实：DC ⊥BE ．3.（1）如图7,点O 是线段AD 的中点,分离以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD,贯穿连接AC 和BD,订交于点E,贯穿连接BC ．求∠AEB 的大小;（2）如图8,ΔOAB 固定不动,保持ΔOCD 外形和大小不变,将ΔOCD 绕着点O 扭转（ΔOAB 和ΔOCD 不重叠）,求∠AEB .4.如图,AE ⊥AB,AD ⊥AC,AB=AE,∠B=∠E, 求证：（1）BD=CE;（2）BD ⊥CE ．5.如图所示,已知AE ⊥AB,AF ⊥AC,AE=AB,AF=AC.BAODCE 图CBO D图7AE图1图2DABFEDCAB GHFEDC ABGPF EDCA BGP求证：（1）EC=BF;（2）EC⊥BF6. 正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.7.D为等腰Rt ABC∆斜边AB的中点,DM⊥DN,DM,DN分离交BC,CA于点E,F.①当MDN∠绕点D迁移转变时,求证DE=DF.②若AB=2,求四边形DECF的面积. 8.五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°, 求证：AD等分∠CDECEDBA9.如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°, 求五边形ABCDE的面积10.已知Rt ABC△中,90AC BC C D==︒，∠，为AB边的中点,90EDF∠=°，EDF∠绕D点扭转,它的双方分离交AC.CB（或它们的延伸线）于E.F．（1）当EDF∠绕D点扭转到DE AC⊥于E时（如图1）,求证：12DEF CEF ABCS S S+=△△△．（2）当EDF∠绕D点扭转到DE AC和不垂直时（如图2）,求DEFS△.CEFS△.ABCS△之间的数目关系？（3）当EDF∠绕D点扭转到DE AC和不垂直时（如图3）,求DEFS△.CEFS△.ABCS△之间的数目关系？AEB MCF11.在△ABC 中,∠ACB =90°,AC=BC,直线MN 经由点C,且AD ⊥MN 于D,BE ⊥MN 于E. （1）.当直线MN 绕点C 扭转到图1的地位时,求证：①△ADC ≌△CEB;②DE=AD ＋BE; （2）.当直线MN 绕点C 扭转到图2的地位时,求证：DE=AD-BE;（3）.当直线MN 绕点C 扭转到图3的地位时,试问DE.AD.BE 具有如何的等量关系？ACBED NM 图3ACDEMN图2CBAED图1NMAECF BD图1图3ADFECBADBCE图2F。

八年级数学全等三角形(培优篇)(Word版含解析)

八年级数学全等三角形（培优篇）（Word版含解析）一、八年级数学轴对称三角形填空题（难）1.如图，在菱形ABCD中，ZABC=120° , AB=10cm，点P是这个菱形内部或边上的一点.若以P,B f C为顶点的三角形是等腰三角形，则P, A（P, A两点不重合）两点间的最短距离为____________ c m .【答案】1OJJ-1O【解析】解：连接3D,在菱形A3CD中，T Z ABC=120° , AB=BC=AD=CD=10 , :. Z A=Z C=60° ,二△ ABD , △ BCD都是等边三角形，分三种情况讨论：①若以边8C为底，则3C垂直平分线上（在菱形的边及其内部）的点满足题意，此时就转化为了"直线外一点与直线上所有点连线的线段中垂线段最短"，即当点P与点D重合时，必最小，最小值^4=10 ；②若以边P3为底，ZPCB为顶角时，以点C为圆心，BC长为半径作圆，与AC相交于一点，则弧3D （除点8外）上的所有点都满足APBC是等腰三角形，当点P在AC上时，AP 最小，最小值为lOjJ-10 ；③若以边PC为底，ZPBC为顶角，以点3为圆心，BC为半径作圆，则弧AC上的点&与点D均满足APBC为等腰三角形，当点P与点A重合时，必最小，显然不满足题意，故此种情况不存在；综上所述，必的最小值为10>/3-10 （cm）.故答案为：10x/I—10 .点睹：本题考查菱形的性质、等边三角形的性质，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型.2.在等腰△遊中，肋丄肚交直线％于点以若妙丄万G则△磁的顶角的度数为【答案】30。

或150。

或90°【解析】试题分析：分两种情况：①3C为腰，②BC为底，根据直角三角形30。

角所对的直角边等于斜边的一半判断岀ZACD=3O°,然后分AD在^ABC内部和外部两种情况求解即可.解：①BC为腰，VAD丄 BC 于点D t AD= - BC f2:.ZACD二30。

全等三角形专题培优(带答案)(精选.)

全等三角形专题培优考试总分： 110 分考试时间： 120 分钟卷I（选择题）一、选择题（共 10 小题，每小题 2 分，共 20 分）1.如图为个边长相等的正方形的组合图形，则A. B.C. D.2.下列定理中逆定理不存在的是（）A.角平分线上的点到这个角的两边距离相等B.在一个三角形中，如果两边相等，那么它们所对的角也相等C.同位角相等，两直线平行D.全等三角形的对应角相等3.已知：如图，，，，则不正确的结论是（）A.与互为余角B.C.D.4.如图，是的中位线，延长至使，连接，则的值为（）A. B. C. D.5.如图，在平面直角坐标系中，在轴、轴的正半轴上分别截取、，使；再分别以点、为圆心，以大于长为半径作弧，两弧交于点．若点的坐标为，则与的关系为（）A. B.C. D.6.如图，是等边三角形，，于点，于点，，则下列结论：①点在的角平分线上；②；③；④．正确的有（）A.个B.个C.个D.个7.如图，直线、、″表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有（）A.一处B.二处C.三处D.四处8.如图，是的角平分线，则等于（）A. B.C. D.9.已知是的中线，且比的周长大，则与的差为（）A. B.C. D.10.若一个三角形的两条边与高重合，那么它的三个内角中（）A.都是锐角B.有一个是直角C.有一个是钝角D.不能确定卷II（非选择题）二、填空题（共 10 小题，每小题 2 分，共 20 分）11.问题情境：在中，，，点为边上一点（不与点，重合），交直线于点，连接，将线段绕点顺时针方向旋转得到线段（旋转角为），连接．特例分析：如图．若，则图中与全等的一个三角形是________，的度数为________．类比探究：请从下列，两题中任选一题作答，我选择________题．：如图，当时，求的度数；：如图，当时，①猜想的度数与的关系，用含的式子表示猜想的结果，并证明猜想；②在图中将“点为边上的一点”改为“点在线段的延长线上”，其余条件不变，请直接写出的度数（用含的式子表示，不必证明）12.如图，正方形纸片的边长为，点、分别在边、上，将、分别沿、折叠，点、恰好都落在点处，已知，则的长为________．13.在中，为的平分线，于，于，面积是，，，则的长为________．14.在中，，的垂直平分线与所在的直线相交所得到锐角为，则等于________．15.如图，平分，于，于，，则图中有________对全等三角形．16.如图，在中，，点从点出发沿射线方向，在射线上运动．在点运动的过程中，连结，并以为边在射线上方，作等边，连结．当________时，；请添加一个条件：________，使得为等边三角形；①如图，当为等边三角形时，求证：；②如图，当点运动到线段之外时，其它条件不变，①中结论还成立吗？请说明理由．17.如图，从圆外一点引圆的两条切线，，切点分别为，．如果，，那么弦的长是________．18.如图，在中，，，是的平分线，平分交于，则________．19.阅读下面材料：小聪遇到这样一个有关角平分线的问题：如图，在中，，平分，，求的长．小聪思考：因为平分，所以可在边上取点，使，连接．这样很容易得到，经过推理能使问题得到解决（如图）．请回答：是________三角形．的长为________．参考小聪思考问题的方法，解决问题：如图，已知中，，，平分，，．求的长．20.如图，在和中，，，若要用“斜边直角边．．”直接证明，则还需补充条件：________．三、解答题（共 7 小题，每小题 10 分，共 70 分）21.如图，已知为等边三角形，为延长线上的一点，平分，，求证：为等边三角形．22.尺规作图（不要求写作法，保留作图痕迹）如图，作①的平分线；②边上的中线；22.一块三角形形状的玻璃破裂成如图所示的三块，请你用尺规作图作一个三角形，使所得的三角形和原来的三角形全等．（不要求写作法，保留作图痕迹．不能在原图上作三角形）22.如图：在正方形网格中有一个，按要求进行下列画图（只能借助于网格）：①画出中边上的高（需写出结论）．②画出先将向右平移格，再向上平移格后的．23.平行四边形中，，点为边上一点，连结，点在边所在直线上，过点作交于点．如图，若为边中点，交延长线于点，，，，求；如图，若点在边上，为中点，且平分，求证：；如图，若点在延长线上，为中点，且，问中结论还成立吗？若不成立，那么线段、、满足怎样的数量关系，请直接写出结论．24.如图，直线与轴、轴分别交于、两点，直线与直线关于轴对称，已知直线的解析式为，求直线的解析式；过点在的外部作一条直线，过点作于，过点作于，请画出图形并求证：；沿轴向下平移，边交轴于点，过点的直线与边的延长线相交于点，与轴相交于点，且，在平移的过程中，①为定值；②为定值．在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值．25.如图：，，过点，于，于，．求证：．26.如图，点，在上，，，，与交于点．求证：；试判断的形状，并说明理由．27.如图，已知点是平分线上一点，，，垂足为、吗？为什么？是的垂直平分线吗？为什么？答案1.B2.D3.D4.A5.B6.D7.D8.A9.B10.B11.[ “”, “” ][ “” ]12.[ “” ]13.[ “” ]14.[ “或” ]15.[ “” ]16.[ “；” ][ "添加一个条件，可得为等边三角形；故答案为：；①∵与是等边三角形，∴，，，∴，即，在与中，，∴，∴；②成立，理由如下；∵与是等边三角形，∴，，，∴，即，在与中，，∴，∴．" ]17.[ “” ]18.[ “” ]19.[ "解：是等腰三角形，在与中，，∴，∴，，∵，∴，∴，∴是等腰三角形；" ][ "的长为，∵中，，，∴，∵平分，∴，在边上取点，使，连接，则，∴，∴，∴，在边上取点，使，连接，则，∴，，∵，∴，∴，∵，∴．" ]\"go题库\"20.[ “” ]21.证明：∵为等边三角形，∴，，即，∵平分，∴，在和中，，∴，∴，，又，∴，∴为等边三角形．22.解：如图所示：；如图所示：即为所求；；①如图所示：即为所求；②如图所示：即为所求；．．23.解：如图，在平行四边形中，，∴，∵在中，为的中点，，∴，又∵，∴，故可设，，则中，，解得，∴，又∵，，∴为的中点，∴；如图，延长交的延长线于点，则，∵，∴，又∵平分，∴，∴是等腰直角三角形，∴，又∵，∴，∴，，又∵为的中点，∴，∴，∴，∵，∴；若点在延长线上，为中点，且，则中的结论不成立，正确结论为：．证明：如图，延长交的延长线于点，则，∵，∴，∴，又∵，∴，∴，，又∵为的中点，∴，∴，∴，∵，∴．24.解：∵直线与轴、轴分别交于、两点，∴，，∵直线与直线关于轴对称，∴∴直线的解析式为：；如图．．∵直线与直线关于轴对称，∴，∵与为象限平分线的平行线，∴与为等腰直角三角形，∴，∵，∴∴∴，，∴；①对，过点作轴于，直线与直线关于轴对称∵，，又∵，∴，则，∴∴∴∴∴．25.证明：连接，∵，∴，∵，∴，∴，∵，，∴，在和中，∴．26.证明：∵，∴，即．又∵，，∴，∴．解：为等腰三角形理由如下：∵，∴，∴，∴为等腰三角形．27.解：．理由：∵是的平分线，且，，∴，∴；是的垂直平分线．理由：∵，在和中，，∴，∴，由，，可知点、都是线段的垂直平分线上的点，从而是线段的垂直平分线．最新文件仅供参考已改成word文本。

全等三角形证明培优题

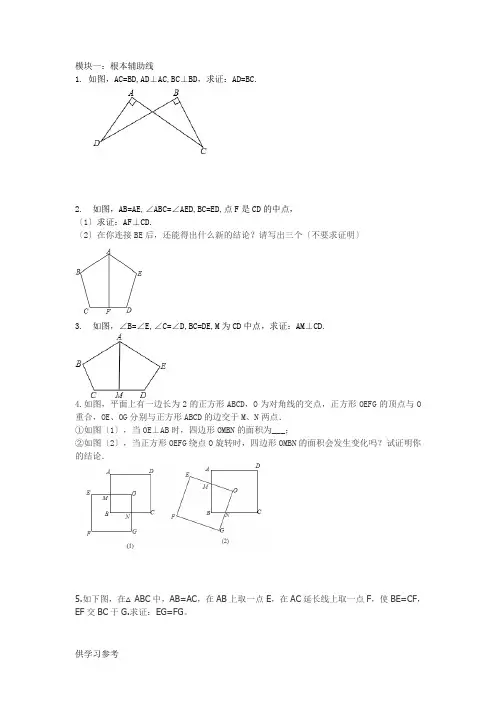
模块一：根本辅助线1.如图，AC=BD,AD⊥AC,BC⊥BD，求证：AD=BC.2.如图，AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点，〔1〕求证：AF⊥CD.〔2〕在你连接BE后，还能得出什么新的结论？请写出三个〔不要求证明〕3.如图，∠B=∠E,∠C=∠D,BC=DE,M为CD中点，求证：AM⊥CD.4.如图，平面上有一边长为2的正方形ABCD，O为对角线的交点，正方形OEFG的顶点与O 重合，OE、OG分别与正方形ABCD的边交于M、N两点．①如图〔1〕，当OE⊥AB时，四边形OMBN的面积为___；②如图〔2〕，当正方形OEFG绕点O旋转时，四边形OMBN的面积会发生变化吗？试证明你的结论．5.如下图，在△ABC中，AB=AC，在AB上取一点E，在AC延长线上取一点F，使BE=CF，EF交BC于G.求证：EG=FG。

6.如图，在△ABC中，AB=AC，E在线段AC上，D在AB的延长线，连DE交BC于F，过点E 作EG⊥BC于G．〔1〕假设∠A=50°，∠D=30°，求∠GEF的度数；〔2〕假设BD=CE，求证：FG=BF+CG．模块二：母子型1：如图，点C为线段AB上一点，△ACM, △CBN都是等边三角形，AN交MC于点E，BM 交CN于点F.(1)求证：AN=BM;(2)求证：△CEF为等边三角形2.如图，，等腰Rt△OAB中，∠AOB=90°，等腰Rt△EOF中，∠EOF=90°，连结AE、BF。

求证：〔1〕AE=BF；〔2〕AE⊥BF。

3.如图1，假设四边形ABCD、四边形GFED都是正方形，显然图中有AG=CE，AG⊥CE；〔1〕当正方形GFED绕D旋转到如图2的位置时，AG=CE是否成立？假设成立，请给出证明；假设不成立，请说明理由；〔2〕当正方形GFED绕D旋转到如图3的位置时，延长CE交AG于H，交AD于M．①求证：AG⊥CH；②当AD=4，DG=2时，求CH的长．4.如图，△ABD、△AEC都是等边三角形，AF⊥CD于点F，AH⊥BE于点H,问：〔1〕BE与CD 有何数量关系？为什么？〔2〕AF、AH有何数量关系？为什么？5.：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．〔1〕求证：①BE=CD；②△AMN是等腰三角形；〔2〕在图①的根底上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出〔1〕中的两个结论是否仍然成立；〔3〕在〔2〕的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6.〔2021•丰台区一模〕如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．〔1〕如果AB=AC，∠BAC=90°，①当点D在线段BC上时〔与点B不重合〕，如图2，线段CF、BD所在直线的位置关系为______，线段CF、BD的数量关系为______；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；〔2〕如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC〔点C、F不重合〕，并说明理由．模块三倍长中线（1）倍长中线〔2〕倍长类中线1.：如图，△ABC中，AD平分∠BAC，且BD=CD，求证：AB=AC．2.，如图△ABC 中，AC>AB,AM 是BC 边上的中线，求证：21〔AC-AB 〕＜AM ＜21(AB+AC)．3. 如下图，△ABC 中，AD 平分∠BAC,E,F 分别在BD,AD 上，DE=CD,EF=AC,求证:EF//AB.4.如图，AD 是△ABC 的中线，E 、F 分别在AB 、AC 上，且DE ⊥DF 求证：BE+CF ＞EF ．4. 如图，在△ABC 中，AB=AC ，CE 是AB 边上的中线，延长AB 到D ，使BD=AB ，连接CD ．求证：CE=21CD.5. 证明：直角三角形斜边上的中线等于斜边上的一半。

全等三角形专题培优(带答案)

全等三角形专题培优考试总分： 110 分考试时间： 120 分钟卷I（选择题）一、选择题（共 10 小题，每小题 2 分，共 20 分）1.如图为个边长相等的正方形的组合图形，则A. B.C. D.2.下列定理中逆定理不存在的是（）A.角平分线上的点到这个角的两边距离相等B.在一个三角形中，如果两边相等，那么它们所对的角也相等C.同位角相等，两直线平行D.全等三角形的对应角相等3.已知：如图，，，，则不正确的结论是（）A.与互为余角B.C.D.4.如图，是的中位线，延长至使，连接，则的值为（）A. B. C. D.5.如图，在平面直角坐标系中，在轴、轴的正半轴上分别截取、，使；再分别以点、为圆心，以大于长为半径作弧，两弧交于点．若点的坐标为，则与的关系为（）A. B.C. D.6.如图，是等边三角形，，于点，于点，，则下列结论：①点在的角平分线上；②；③；④．正确的有（）A.个B.个C.个D.个7.如图，直线、、″表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有（）A.一处B.二处C.三处D.四处8.如图，是的角平分线，则等于（）A. B.C. D.9.已知是的中线，且比的周长大，则与的差为（）A. B.C. D.10.若一个三角形的两条边与高重合，那么它的三个内角中（）A.都是锐角B.有一个是直角C.有一个是钝角D.不能确定卷II（非选择题）二、填空题（共 10 小题，每小题 2 分，共 20 分）11.问题情境：在中，，，点为边上一点（不与点，重合），交直线于点，连接，将线段绕点顺时针方向旋转得第1页，共7页第2页，共7页………外………○……………………○……………………○※※请※※不※※答※※题※………内………○……………………○……………………○到线段（旋转角为），连接．特例分析：如图．若，则图中与全等的一个三角形是________，的度数为________．类比探究：请从下列，两题中任选一题作答，我选择________题．：如图，当时，求的度数；：如图，当时，①猜想的度数与的关系，用含的式子表示猜想的结果，并证明猜想；②在图中将“点为边上的一点”改为“点在线段的延长线上”，其余条件不变，请直接写出的度数（用含的式子表示，不必证明）12.如图，正方形纸片的边长为，点、分别在边、上，将、分别沿、折叠，点、恰好都落在点处，已知，则的长为________．13.在中，为的平分线，于，于，面积是，，，则的长为________．14.在中，，的垂直平分线与所在的直线相交所得到锐角为，则等于________．15.如图，平分，于，于，，则图中有________对全等三角形．16.如图，在中，，点从点出发沿射线方向，在射线上运动．在点运动的过程中，连结，并以为边在射线上方，作等边，连结．当________时，；请添加一个条件：________，使得为等边三角形； ①如图，当为等边三角形时，求证：；②如图，当点运动到线段之外时，其它条件不变，①中结论还成立吗？请说明理由．17.如图，从圆外一点引圆的两条切线，，切点分别为，．如果，，那么弦的长是________．18.如图，在中，，，是的平分线，平分交于，则________．19.阅读下面材料：小聪遇到这样一个有关角平分线的问题：如图，在中，，平分，，求的长．小聪思考：因为平分，所以可在边上取点，使，连接．这样很容易得到，经过推理能使问题得到解决（如图）．请回答：是________三角形．的长为________．参考小聪思考问题的方法，解决问题：如图，已知中，，，平分，，．求的长．20.如图，在和中，，，若要用“斜边直角边．．”直接证明，则还需补充条件：________．三、解答题（共 7 小题，每小题 10 分，共 70 分）21.如图，已知为等边三角形，为延长线上的一点，平分，，求证：为等边三角形．22.尺规作图（不要求写作法，保留作图痕迹）如图，作①的平分线；②边上的中线；22.一块三角形形状的玻璃破裂成如图所示的三块，请你用尺规作图作一个三角形，使所得的三角形和原来的三角形全等．（不要求写作法，保留作图痕迹．不能在原图上作三角形）22.如图：在正方形网格中有一个，按要求进行下列画图（只能借助于网格）：①画出中边上的高（需写出结论）．②画出先将向右平移格，再向上平移格后的．23.平行四边形中，，点为边上一点，连结，点在边所在直线上，过点作交于点．如图，若为边中点，交延长线于点，，，，求；如图，若点在边上，为中点，且平分，求证：；如图，若点在延长线上，为中点，且，问中结论还成立吗？若不成立，那么线段、、满足怎样的数量关系，请直接写出结论．24.如图，直线与轴、轴分别交于、两点，直线与直线关于轴对称，已知直线的解析式为，求直线的解析式；过点在的外部作一条直线，过点作于，过点作于，请画出图形并求证：；沿轴向下平移，边交轴于点，过点的直线与边的延长线相交于点，与轴相交于点，且，在平移的过程中，①为定值；②为定值．在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值．25.如图：，，过点，于，于，．求证：．第3页，共7页第4页，共7页26.如图，点，在上，，，，与交于点．求证：；试判断的形状，并说明理由．27.如图，已知点是平分线上一点，，，垂足为、吗？为什么？是的垂直平分线吗？为什么？答案 1.B 2.D 3.D 4.A 5.B 6.D 7.D 8.A 9.B 10.B11.[ “”, “” ][ “” ] 12.[ “” ] 13.[ “” ] 14.[ “或” ]15.[ “” ] 16.[ “；” ][ "添加一个条件，可得为等边三角形；故答案为：；①∵与是等边三角形， ∴，，， ∴，即，在与中，， ∴， ∴；②成立，理由如下； ∵与是等边三角形， ∴，，， ∴，即，在与中，， ∴， ∴．" ] 17.[ “” ] 18.[ “” ]19.[ "解：是等腰三角形，在与中，， ∴， ∴，， ∵， ∴， ∴，∴是等腰三角形；" ][ "的长为， ∵中，，， ∴， ∵平分， ∴，在边上取点，使，连接，则，∴， ∴， ∴，在边上取点，使，连接，则， ∴，， ∵， ∴， ∴， ∵，∴．" ]\"go题库\"20.[ “” ]21.证明：∵为等边三角形，∴，，即，∵平分，∴，在和中，，∴，∴，，又，∴，∴为等边三角形．22.解：如图所示：；如图所示：即为所求；；①如图所示：即为所求；②如图所示：即为所求；．．23.解：如图，在平行四边形中，，∴，∵在中，为的中点，，∴，又∵，∴，故可设，，则中，，解得，∴，又∵，，∴为的中点，∴；如图，延长交的延长线于点，则，∵，∴，又∵平分，∴，∴是等腰直角三角形，∴，又∵，∴，∴，，又∵为的中点，∴，∴，∴，∵，∴；第5页，共7页第6页，共7页…○…………装订…………○…※※请※※不※※内※※答※※题※※…○…………装订…………○…若点在延长线上，为中点，且，则中的结论不成立，正确结论为：．证明：如图，延长交的延长线于点，则，∵， ∴， ∴，又∵， ∴， ∴，，又∵为的中点， ∴， ∴， ∴， ∵， ∴．24.解：∵直线与轴、轴分别交于、两点， ∴，，∵直线与直线关于轴对称， ∴∴直线的解析式为：；如图．．∵直线与直线关于轴对称， ∴，∵与为象限平分线的平行线， ∴与为等腰直角三角形， ∴， ∵， ∴ ∴ ∴，，∴；①对，过点作轴于，直线与直线关于轴对称∵，，又∵， ∴，则， ∴ ∴ ∴ ∴ ∴．25.证明：连接， ∵， ∴， ∵， ∴， ∴， ∵，， ∴，在和中，∴．26.证明：∵，∴，即．又∵，，∴，∴．解：为等腰三角形理由如下：∵，∴，∴，∴为等腰三角形．27.解：．理由：∵是的平分线，且，，∴，∴；是的垂直平分线．理由：∵，在和中，，∴，∴，由，，可知点、都是线段的垂直平分线上的点，从而是线段的垂直平分线．第7页，共7页。

【全等三角形】培优题型全集

《全等三角形》培优题型全集题型一：倍长中线（线段）造全等1、已知：如图，AD 是△ABC 的中线，BE 交AC 于E ，交AD 于F ，且 AE=EF ，求证：AC=BFC2、如图，△ABC 中，AB=5，AC=3，则中线AD 的取值范围是______.DCBA3、在△ABC 中,AC=5,中线AD=7，则AB 边的取值范围是( ) A 、1<AB<29 B 、4<AB<24C 、5<AB<19D 、9<AB<194、已知：AD 、AE 分别是△ABC 和△ABD 的中线，且BA=BD ，求证：AE=21AC CE5、已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠ABFDEC题型二：截长补短1、已知，四边形ABCD 中，AB ∥CD ，∠1＝∠2，∠3＝∠4。

求证：BC ＝AB ＋CD 。

2、已知：如图，在△ABC 中，∠C ＝2∠B ，∠1＝∠2，求证：AB=AC+CD.3、如图，在△ABC 中，∠BAC=60°， AD 是∠BAC 的平分线，且AC=AB+BD ，求∠ABC 的度数DCBA4、已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．DOECB ADCB A 12题型三：角平分线上的点向角两边引垂线段1、如图，在四边形ABCD中，BC＞BA,AD＝CD，求证：∠BAD+∠C=180°C2、如图，四边形ABCD中，AC平分∠BAD，CE⊥AB于E，AD+AB=2AE，则∠B与∠ADC互补，为什么？3、如图，△ABD和△ACD，BD=CD，∠ABD=∠ACD,求证AD平分∠BAC.4、已知，AB＞AD，∠1＝∠2，CD＝BC。

全等三角形培优题

数学练习七一、选择题：1、下列说法中正确的是（）A 、两个直角三角形全等B 、两个等腰三角形全等C 、两个等边三角形全等D 、两条直角边对应相等的直角三角形全等 2、三角形内到三个顶点的距离相等的点是（）A 、三角形的三条角平分线的交点B 、三角形的三条高的交点C 、三角形的三条中线的交点D 、三角形的三边的垂直平分线的交点 3、下列说法中，错误的有（） ①面积相等的两个三角形是全等三角形②三个角分别相等的两个三角形是全等三角形 ③全等三角形的周长相等④有两边及其中一边的对角分别对应相等的两个△全等． A ．1个B ．2个C ．3个 D. 4个4、如右上图，在△ABC 中，AB=BC=CA ，且AD=BE=CF ，但D ，E ，F 不是AB ，BC ，CA 的中点、又AE ，BF ，CD 分别交于M ，N ，P ，如果把找出的三个全等三角形叫做一组全等三角形，那么从图中能找出全等三角形（） A ．2组B ．3组C ．4组 D.5组5、如图，△ABC ≌△CDA ，并且AB=CD ，那么下列结论错误的是（）（A ）∠DAC=∠BCA （B ）（C ）∠D=∠B （D ）AC=BC6、全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC 和△A1B1C1是全等（合同）三角形，点A 与点A1对应，点B 与点B1对应，点C 与点C1对应，当沿周界A→B→C→A，及A1→B1→C1→A1环绕时，若运动方向相同，则称它们是真正合同三角形如图，若运动方向相反，则称它们是镜面合同三角形如图，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合，两个镜面合同三角形要重合，则必须将其中一个翻转180° 如图，下列各组合同三角形中，是镜面合同三角形的是（）A B C D7、如图，△ABC中，∠B=∠C，BD=CF，BE=CD，∠EDF=a，则下列结论正确的是A．2a+∠A=180°B．a+∠A=90°（）C．2a+∠A=90°D．a+∠A=180°8、若AB=AC，BG=BH，AK=KG，则∠BAC=______．二、填空题9、如图，已知AE＝CE，BD⊥AC．若AD=5cm，BC=3cm，则CD+AB=_________ 10、如图，DO是边AC的垂直平分线，交AB于点D，若AB=7cm，BC=5cm，则△BDC的周长是11、如图3，已知AB∥CD，AD∥BC，E.F是BD上两点，且BF＝DE，则图中共有对全等三角形.12、如图4，四边形ABCD的对角线相交于O点，且有AB∥DC，AD∥BC，则图中有______对全等三角形.13、如图5，⊿ABC≌⊿ADE，若∠B=40°，∠EAB=80°，∠C=45°，则∠EAC = ，∠D= ，∠DAC= 。

全等三角形培优专题训练

全等三角形培优专题训练第一篇：全等三角形培优专题训练做最适合你的数学培训八年级数学培优专题训练（二）探索三角形全等的条件1、一张长方形纸片沿对角线剪开，得到两张三角形纸片，再将这两张纸片摆成如下图形式，使点B、F、C、DCA在同一条直线上.EAEP MN⑴求证：AB⊥ED；⑵若PB＝BC，请找出图中与此条件有关的一对全等三角形，并给予证明2、如图，在△ABC中，AC＝BC，∠ACB＝90°，AD平分∠BAC，BE⊥AD交AC的延长线于F，E为垂足，则结论：①AD＝BF；②CF ＝CD；③AC＋CD＝AB；④BE＝CF；⑤BF＝2BE.其中正确的是（）3、如图，点C在线段AB上，DA ⊥AB，EB⊥AB，FC⊥AB，且DA＝BC，EB＝AC，FC＝AB，∠AFB＝51°，求∠DFC的度数.DFFBDBFCDBEDCAEACBF__________________________________________________________ ______________________________________________________周老师·数学培优做最适合你的数学培训4、如图，四边形ABCD中，AB∥CD，AD∥BC，O为对角线AC 的中点，过点O作一条直线分别与AB、CD交于点M、N，点E、F 在直线M、N上，且OE＝OF.⑴图中共有几对全等三角形，请把它们都写下来；⑵求证：∠MAE＝∠NCFAEBMONCDF5、在△ABC中，高所在直线AD和BE交于H点，且BH＝AC，则∠ABC＝_____________.6、下列三个判断：⑴有两边及其中一边上的高对应相等的两个三角形全等；⑵有两边及第三边上的高对应相等的两个三角形全等；⑶一边及其它两边上的高对应相等的两个三角形全等.上述判断是否正确？若正确，说明理由；若不正确，请举出反例._________________________________________________________________ _______________________________________________周老师·数学培优做最适合你的数学培训八年级数学培优专题训练（三）全等三角形的应用全等三角形常用来转移线段和角，用它来证明：①线段和角的等量关系②线段和角的和差倍分关系③直线与直线的平行或垂直等位置关系1、如图，已知BD、CE分别是△ABC的边AC和AB上的高，点P在BD的延长线上，BP＝AC，点Q在CE上，CQ＝AB.试判断AP 与AQ的关系，并证明.2、如图，AD是△ABC的高，E为AC上一点，BE交AD于点F，且BF＝AC，FD＝CD，求证：BE⊥AC FAADQPEBCE3、（2012〃阜新中考）如图,在△ABC中,AB＝AC,AD＝AE,∠BAC＝∠D AC＝90°.⑴当点D在AC上时,如图①,线段BD,CE有怎样的数量和位置关系?证明你猜想的结论.⑵将图①中的△ADE绕点A顺时针旋转α角(0°＜α＜90°)，如图②，线段BD、CE 有怎样的数量关系和位置关系？问明理由.BEABDCDC①AEDBC②__________________________________________ ____________________________________________________________________ __周老师·数学培优做最适合你的数学培训4、在△ABC中，AB＝AC，点D是直线 BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE.⑴如图①，当点D在线段BC上时，若∠BAC＝90°，则∠BCE＝_______度.⑵设∠BAC＝α，∠BCE＝βa、如图②，当点D在线段BC上移动时，α，β之间有怎样的数量关系？请说明理由.b、当点D在直线BC上移动时，α，β之间有怎样的数量关系？请直接写出你的结论.BDAEBDC①AEC②______________________________________________ __________________________________________________________________ 周老师·数学培优做最适合你的数学培训八年级数学培优专题训练（四）辅助线作法之连接法在几何证明中，常通过添加辅助线来构造全等三角形.常见的添加辅助线方法有：连接法、截长补短法、倍长中线法、翻折法、旋转法以及利用特殊条件构造全等三角形等等.1、如图，△ABC的两条高BD，CE相交于点P，且PD＝PE.证明∶AC＝AB2、已知AB＝DE，BC＝EF，∠B＝∠E，AF＝CD 求证：AC∥DF3、如图，AB交CD于点O，AD、CB的延长线相交于点E，且OA＝OC，EA＝EC.∠A＝∠C吗？点O在∠AEC的平分线上吗？EBCDOABCDAFEAEBDPC_____________________________________ ____________________________________________________________________ _______周老师·数学培优做最适合你的数学培训八年级数学培优专题训练（五）辅助线作法之倍长中线法在题目条件中含有中线的问题，我们常用的辅助线就是将中线延长一倍，其目的是为了得一对全等三角形，将分散的条件集中到一个三角形中去.1、△ABC中，AB＝5，AC＝3，求中线AD的取值范围.2、如图，在△ABC中，AD是∠BAC的平分线，又是BC上的中线求证：AB＝AC3、（2014〃襄阳初三模拟）在△ABC中，D是边BC上的一点，且CD＝AB，∠BAD＝∠BDA，AE是△ABD的中线.求证∶AC＝2AE BEDCABDCAABDC____________________________________________ ____________________________________________________________________做最适合你的数学培训AFE4、（竞赛014）△ABC中，D为BC的中点，DE⊥DF交AB，AC于点E，F.求证：BE＋CF＞EF6、（竞赛015）例：已知AD是△ABC的中线，BE交AC于点E，交AD于点F，且AE＝EF.求证:AC＝BFBDCAEFDBC___________________________________________________ _____________________________________________________________ 周老师·数学培优做最适合你的数学培训八年级数学培优专题训练（六）辅助线作法之截长补短法截长法：在第三条线段上截下一段使其等于两条线段中的一条，再证明剩余部分与另一条相等.补短法：把两条线段中的一条补到另一条线段上去，证明所得新线段与第三条线段相等.1、已知A C∥BD，EA，EB分别平分∠CAB和∠DBA，点E在CD上.求证：AB＝AC＋BD2、在四边形ABCD中，AC平分∠BAD，CE⊥AB于点E，且AE ＝½（AB＋AD）.求证∶∠B＋∠D＝180°3、如图，已知△ABC中，∠A＝90°，AB＝AC，D为AC的中点，AE⊥BD于E，延长AE交BC于F.求证：∠ADB＝∠CDF________________________________________________________________ ________________________________________________BFCAECDABADEBCED周老师·数学培优做最适合你的数学培训4、如图，∠C＝90°，AC＝BC，AD是∠BAC的角平分线.求证∶AC＋CD＝AB12、如图，已知AB＝CD＝AE＝BC＋DE＝2，∠ABC＝∠AED＝90°，求五边形ABCDE的面积.CBABDCDAE____________________________________________________ ____________________________________________________________做最适合你的数学培训八年级数学培优专题训练（七）辅助线作法之利用特殊条件构造全等三角形2、（2012〃“华罗庚杯”）如图，在△ABC中，AC＝½AB，AD平分∠BAC，且AD＝BD 求证：CD⊥ACACBD__________________________________________________________ ______________________________________________________周老师·数学培优做最适合你的数学培训八年级数学培优专题训练（八）全等三角形在动态几何中的运用1、(竞赛〃014〃3)如图，△ABC的边BC在直线l上，AC⊥BC，且AC＝BC.△EFP的边FP也在直线l上，边EF与边AC重合，且EF＝FP.⑴在图①中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系;⑵将△EFP沿直线l向左平移到图②的位置时,EP 交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;⑶将△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为⑵中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.A(E)EAEAQllBC(F)PFPBClBFCP Q__________________________________________________________________ ______________________________________________周老师·数学培优做最适合你的数学培训八年级数学培优专题训练（九）探究角平分线一、知识清单角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线.三角形的角平分线定义：三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线（也叫三角形的内角平分线）.由定义可知，三角形的角平分线是一条线段.角平分线性质:1、角平分线上的点，到这个角的两边的距离相等.2、角平分线分得的两个角相等，都等于该角的一半.3、三角形的三条角平分线交于一点，且到各边的距离相等，这个点称为内心.二、方法点拨证明角平分线有两种方法:一是运用定义证明两个角相等;二是运用角平分线的判定方法.三、规律清单①遇到角平分线,可从角平分线上的某一点向角的两边作垂线段(图1).②遇到角平分线,常可利用翻折法或截长补短法解题(图2).③有两条角平分线(内角或外角)交于一点,则连接该点与三角形第三个顶点的线段会平分一个内角或外角(图3).④有垂直于角平分线的线段,则延长这条线段以利用三线合一解题(图4).⑤遇到角内的一点到角的两边有垂线段时,就连接这点与角的顶点,看能否平分已知角(图5).⑥遇到有多条角平分线时,可尝试用整体的思想解题(图6).⑦有翻折条件时,除注意全等的结论,还应关注折线就是角平分线、是对称轴（如图7）.⑧角平分线、平行线、等腰三角形三个条件中出现任意两个,常可直接得到另一个(如图8）.AAACBDAFAEGDBDBC图2B图1CD图3DCBC_____________________________________________________________ ___________________________________________________周老师·数学培优做最适合你的数学培训AACFEBDC图4BFEDECF图5ADBA1D2B3A1APFC'D'DAD2CB图6EF∠1＋∠2＋∠3＝90°∠1＋∠2＝90°－½∠BCBEC图7B图8CD四、真题训练1、(2011〃鄂州〃竞赛〃018 〃重庆中考）如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP相交于点P，若∠BPC＝40°，则∠CAP＝_____________.BCDAP2、(竞赛〃019)如图，∠B＝∠C ＝90°，M是BC的中点，DM平分∠ADC.求证:AM平分∠DAB DCMAB_______________________________________________________ _________________________________________________________ 周老师·数学培优做最适合你的数学培训3、(竞赛〃019)如图,在△ABC中,∠BAC＝90°,AB＝AC,BE平分∠ABC,CE⊥BE.AED1求证:CE＝ BD 2BCA4、如图，在△ABC中，AD平分∠BAC，BD＝CD 求证：∠B＝∠C5、如图，在Rt△ABC中，∠C＝90°，AC＝BC，AD是∠BAC的平分线，交BC于D，DE⊥AB于E，若AB＝10cm，则△DBE的周长是多少？ABDCAECDB6、（2011，恩施中考）AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为多少？BEFGDC_______________________________________________________ _________________________________________________________ 周老师·数学培优做最适合你的数学培训7、如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F.求证：BE＝CF8、在△ABC中，AD是∠BAC的平分线，E、F分别为AB、AC上的点，且∠EDF＋∠BAF＝180°⑴求证：DE＝DF ⑵如果把最后一个条件改为AE＞AF，且∠AED ＋∠AFD＝180°，那么结论还成立吗？9、如图，已知AB＝AC，BE⊥AC于E，CF⊥AB于F，BE与CF 交于点D 求证：点D在∠BAC的平分线上.10、如图，在四边形ABCD 中，对角线AC平分∠BAD，AB＞AD，下列结论正确的是()A.AB－AD ＞CB－CD B.AB－AD＝CB－CD C.AB－AD＜CB－CD D.AB－CD与CB－CD的大小关系不确定BCAAEBGCFDAFEBDCBFDAECD______________________________ ____________________________________________________________________ ______________周老师·数学培优做最适合你的数学培训11、（竞赛014）如图，已知△ABC中，∠B＝60°，∠BAC，∠BCA的平分线AD，CE相交于点O.求证：DC＋AE＝AC12、(竞赛〃019)如图，已知△ABC，P为内角平分线AD、BE、CF的交点，过点P作PG⊥BC于G点。

全等三角形经典题型汇集(培优专练)

；
（2）如图 2，当点 E，F 分别在 CB，DC 的延长线上，CF＝2 时，求△CEF 的周长；
拓展提升：
如图 3，在 Rt△ABC 中，∠ACB＝90°，CA＝CB，过点 B 作 BD⊥BC，连接 AD，在 BC 的延长线上取一点 E，使∠EDA＝30°，连接 AE，当 BD＝2，∠EAD＝45°时，请直接写出线段 CE 的长度．
7．阅读下面材料：
小炎遇到这样一个问题：如图 1，点 E、F 分别在正方形 ABCD 的边 BC，CD 上，∠EAF=45°，连结 EF，则 EF=BE+DF，试说明理由．
小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段 AB，AD 是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE 绕着点 A 逆时针旋转 90°得到△ADG，再利用全等的知识解决了这个问题（如图 2）．
2.阅读下面材料：
数学课上，老师给出了如下问题：如图，AD 为△ABC 中线，点 E 在 AC 上，BE 交 AD 于点 F，AE＝EF．求证：AC＝BF．经过讨论，同学们得到以下两种思路：
思路一如图①，添加辅助线后依据 SAS 可证得△ADC≌△GDB，再利用 AE ＝EF 可以进一步证得∠G＝∠FAE＝∠AFE＝∠BFG，从而证明结论．
3.如图，分别以 ABC 的边向外作正方形 ABFG 和 ACDE，连接 EG，若 O 为 EG 的中点，
求证：（1） AO 1 BC ；（2） AO BC ． 2
4．如图所示，已知 ⶠࢼ 中，平分 ⶠ ࢼ，、分别在 ⶠ 、上．
ࢼ，
ࢼ．求证： ∥ ⶠ．
5．如图所示， ⶠ ࢼ

全等三角形培优竞赛题精选

全等三角形证明1、已知：∠1=∠2，CD=DE ，EF知：AB知：如图所示，AB ＝AD ，BC ＝DC ，E 、F 分别是DC 、BC 的中点，求证： AE ＝AF 。

10．如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6． 11．如图：BE ⊥AC ，CF ⊥AB ，BM=AC ，CN=AB 。

求证：（1）AM=AN ；（2）AM ⊥AN 。

12.如图所示，△ABC ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，求∠DEF 的度数。

13．如图，AD 是△ABC 的角平分线，DE ⊥AB,DF ⊥AC,垂足分别是E,F ，连接EF,交AD 于G,AD 与EF 垂直吗？证明你的结论。

FAEDC BP DACBDCBAFEBA CDF2 1 EA14.如图所示，在△ABC 中，AD 为∠BAC 的角平分线，DE ⊥AB 于E,DF ⊥AC 于F, △ABC 的面积是28cm 2,AB=20cm,AC=8cm,求DE 的长。

15．如图，在R t △ABC 中，∠ACB=450，∠BAC=900，AB=AC ，点D 是AB 的中点，AF ⊥CD 于H 交BC 于F ，BE ∥AC 交AF 的延长线于E ，求证：BC 垂直且平分DE.16、已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF ⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）直接写出线段EG 与CG 的数量关系；（2）将图1中△BEF 绕B 点逆时针旋转45º，如图2所示，取DF 中点G ，连接EG ，CG ．你在（1）中得到的结论是否发生变化？写出你的猜想并加以证明．（3）将图1中△BEF 绕B 点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立？17、已知Rt ABC △中，90AC BC C D ==︒，∠，AB 边的中点，90EDF ∠=， EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12CEF ABC S S S +=△△△．当EDF ∠绕D 点旋转到DE AC 和不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABC S △又有怎样的数量关系？请写出你的猜想，不需证明．18、在中，将绕点顺时针旋转角得交于点，分别交于两点．（1）如图1，观察并猜想，在旋转过程中，线段与有怎样的数量关系？并证明你的结论；B DCF AE GAEFBDCA DE G图1F A DE G图2 FAE 图3 D AE CFBD图1图3AD FECBA DBCE 图2F（2）如图2，当时，试判断四边形的形状，并说明理由；（3）在（2）的情况下，求的长．19、如图9，若△ABC 和△ADE 为等边三角形，M ，N 分别EB ，CD 的中点，易证：CD=BE ，△AMN 是等边三角形．（1）当把△ADE 绕A 点旋转到图10的位置时，CD=BE 是否仍然成立？若成立请证明，若不成立请说明理由；（4分）（2）当△ADE 绕A 点旋转到图11的位置时，△AMN 是否还是等边三角形？若是，请给出证明，并求出当AB =2AD 时，△ADE 与△ABC 及△AMN 的面积之比；若不是，请说明理由．（6分）20、如图，直角梯形ABCD 中，BC AD ∥，90BCD ∠=°，且2tan 2CD AD ABC =∠=，，过点D 作AB DE ∥，交BCD ∠的平分线于点E ，连接BE ．（1）求证：BC CD =；（2）将BCE △绕点C ，顺时针旋转90°得到DCG △，连接EG.．求证：CD 垂直平分EG . （3）延长BE 交CD 于点P ．求证：P 是CD 的中点．21、如图，四边形ABCD 是正方形，△ABE 是等边三角形，M 为对角线BD （不含B 点）上任意一点，将BM 绕点B 逆时针旋转60°得到BN ，连接EN 、AM 、CM. ⑴ 求证：△AMB≌△ENB；⑵ ①当M 点在何处时，AM ＋CM 的值最小；②当M 点在何处时，AM ＋BM ＋CM22、如图，△ABC 中，D 是BC 的中点，过D 点的直线行线BG 于G 点，DE ⊥DF ，交AB 于点E ，连结EG 、EF.求证：EG=EF;请你判断BE+CF 与EF 23、如图，等腰直角三角形ABC 中，∠ACB ＝90°，AD 为腰CB 上的中线，CE ⊥AD 交AB 于E ．求证∠CDA ＝∠EDB ．24、在Rt △ABC 中，∠A ＝90°，CE 是角平分线，和高AD 相交于F ，作FG ∥BC 交AB 于G ，求证：AE ＝BG ．AD BECFD BECFADGECB图9 图10 图11E A DB C C25、如图，已知∠BAC=90º,AD ⊥BC, ∠1=∠2,EF ⊥BC, FM ⊥AC,说明FM=FD 的理由26、用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A 重合，两边分别与AB 、AC 重合.将三角尺绕点A 按逆时针方向旋转.（1）当三角尺的两边分别与菱形的两边BC 、CD 相交于点E 、F 时（如图所示），通过观察或测量BE 、CF 的长度，你能得出什么结论？并证明你的结论；（2）当三角尺的两边分别与菱形的两边BC 、CD 的延长线相交于点E 、F 时（如图所示），你在（1）中得到的结论还成立吗？说明理由。

全等三角形证明题培优(38题)(方法)

全等三角形证明题（经典38题）（方法）1.(方法：巧做辅助线）如图，在△ABC中，∠B=2∠C,AD⊥BC于D,求证：CD=BD+AB.2.(方法：巧做辅助线）如图所示，在△ABC中，AB=AC，在AB上取一点E，在AC延长线上取一点F，使BE=CF，EF交BC于G.求证：EG=FG。

3.(方法：巧做辅助线）如图，已知AC=BD,AD⊥AC,BC⊥BD，求证：AD=BC.4.图，∠B=∠E,∠C=∠D,BC=DE,M为CD中点，求证：AM⊥CD.5.(方法：巧做辅助线）如图，已知，等腰Rt△OAB中，∠AOB=90°，等腰Rt△EOF中，∠EOF=90°，连结AE、BF。

求证：（1）AE=BF；（2）AE⊥BF。

6.(方法：巧做辅助线）如图，在△ABC中，AB=AC，E在线段AC上，D在AB的延长线，连D E交BC于F，过点E作EG⊥BC于G．（1）若∠A=50°，∠D=30°，求∠GEF的度数；（2）若BD=CE，求证：FG=BF+CG．7.(方法：火眼金睛找条件）如图所示，∠BAC=∠DAE=90°，M是BE的中点，AB=AC，AD=AE，求证：（1）CD=2AM,（2）AM⊥CD．8.(方法：火眼金睛找条件）已知：如图，点C为线段AB上一点，△ACM, △CBN都是等边三角形，AN交MC于点E，BM交CN于点F.(1)求证：AN=BM;(2)求证：△CEF为等边三角形9.(方法：火眼金睛找条件）如图，在△ABC中，AD平分∠BAC，E为BC的中点，过点E 作EF∥AD交AB于点G，交CA的延长线于点F．求证：BG=CF．FDE CBA(2)10.(方法：巧做辅助线）如图，AB=AE,∠ABC=∠AED,BC=ED,点F 是CD 的中点，求证：AF ⊥CD.11.(方法：巧做辅助线）如图，在正方形ABCD 中，M 、N 分别是BC 、CD 上的点，∠MAN=45°．求证：MB+ND=MN ．12.(方法：巧做辅助线）已知：如图，ABCD 是正方形，∠FAD=∠FAE ．求证：BE+DF=AE ．13.(方法：火眼金睛找条件）如图E 为正方形ABCD 边BC 的中点，F 为DC 的中点，BF 与AE 有何关系？请解释你的结论。

全等三角形经典培优题型(含标准答案)

三角形培优练习题1已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE6如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

已知：AB=CD ，∠A=∠D ，求证：∠B=∠C78.P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-ABCDBA BC DEF 2 1ADBCA B CD ABACDF2 1 E9已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC10．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．11如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B12如图：AE 、BC 交于点M ，F点在AM 上，BE∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

13已知：如图，AB =AC ，BD ⊥AC ，CE ⊥AB ，垂足分别为D 、E ，BD 、CE 相交于点F 。

求证：BE =CD ．14在△ABC 中，︒=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时，求证： ①ADC ∆≌CEB ∆；②BE AD DE +=；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.15如图所示，已知AE ⊥AB ，AF ⊥AC ，AE=AB ，AF=AC 。

全等三角形经典培优题型(含答案)

全等三角形经典培优题型(含答案)1.已知三角形ABC中，AB=4，AC=2，D是BC的中点，AD是整数，求AD的长度。

解：由题意可得AD=AB-DB，又BD=DC=AC/2=1，故AB=AD+DB=AD+1，代入AB=4得AD=3.2.已知四边形BCDE中，BC=DE，∠B=∠E，∠C=∠D，F是CD的中点，证明∠1=∠2.解：由于BC=DE，且∠B=∠E，所以△BCE≌△EDC，从而∠1=∠BCE=∠EDC=∠2.3.已知四边形ABCD中，∠1=∠2，CD=DE，EF//AB，证明EF=AC。

解：由于EF//AB，所以△EFC∼△ABC，从而EF/AC=FC/BC，而CD=DE，所以FC=CD，代入得EF/AC=CD/BC，又由于∠1=∠2，所以△BCD∼△ECD，从而CD/BC=ED/AC，代入得EF/AC=ED/AC，即EF=AC。

4.已知三角形ABC中，AD平分∠BAC，AC=AB+BD，证明∠B=2∠C。

解：由于AD平分∠BAC，所以∠BAD=∠CAD，从而∠B=∠BAD+∠ABD=∠CAD+∠ACD，又由于AC=AB+BD，所以BD=AC-AB，代入得∠B=∠CAD+∠ACD=∠CAD+∠ABC，又由于∠CAD=∠CAB，所以∠B=∠CAB+∠ABC=2∠C。

5.已知三角形ABC中，AC平分∠BAD，CE⊥AB，∠B+∠D=180°，证明AE=AD+BE。

解：由于AC平分∠BAD，所以∠CAD=∠CAB，从而△ABE∼△DCE，所以AE/AD=BE/CD，又由于∠B+∠D=180°，所以CD=AB，代入得AE/AD=BE/AB，即AE=AD·(BE/AB)，又由于CE⊥AB，所以△CEB为直角三角形，从而BE/AB=CE/AC，代入得AE=AD·(CE/AC)，又由于AC平分∠BAD，所以△ACD∼△ABC，从而CE/AC=CD/AB，代入得AE=AD·(CD/AB)，又由于CD=AB-BD，所以AE=AD·((AB-BD)/AB)，即AE=AD+BE·(AB/AD-1)，又由于AB>AD，所以AB/AD-1<AB/AD，从而AE<AD+BE·(AB/AD)，即AE<AD+BE。

2019年江苏苏教版中考相似三角形专题培优汇编真题（含答案）

2019年江苏苏教版中考相似三角形专题培优汇编真题（含答案）2019年江苏中考相似三角形培优汇编1.（2019扬州）如图，在△ABC 中，AB=5，AC=4，若进行一下操作，在边BC 上从左到右一次取点D 1、D 2、D 3、D 4…；过点D1作AB 、AC 的平行线分别交于AC 、AB 与点E 1、F 1；过点D 2作AB 、AC 的平行线分别交于AC 、AB 于点E 2、F 2；过点D 3作AB 、AC 的平行线分别交于AC 、AB 于点E 3、F 3…，则4（D 1E 1+D 2E 2+…+D 2019E 2019）+5（D 1F 1+D 2F 2+…+D 2019F 2019）= ．解：∵D 1E 1∥AB D 1F 1∥AC ∴CB CD AB E D 111=BCBD AC F D 11=∵AB=5 AC=4 ∴CB CD E D 1115= BC BD F D 114= ∴14511111==+=+BCBCBC BD CB C D F D E D ∴4D 1E+5D 1F=20有2019组，即2019×20=403802.（2019扬州）如图，平面内的两条直线l 1、l 2,点A 、B 在直线l 2上，过点A 、B 两点分别作直线l 1的垂线，垂足分别为A 1、B1，我们把线段A 1B 1叫做线段AB 在直线l 2上的正投影，其长度可记作T （AB ，CD ）或T （AB ，l 2）,特别地，线段AC 在直线l 2上的正投影就是线段A 1C 请依据上述定义解决如下问题（1）如图1，在锐角△ABC 中，AB=5，T （AC ，AB ）=3，则T （BC ，AB ）= ；（2）如图2，在Rt △ABC 中，∠ACB=90°，T （AC ，AB ）=4，T （BC ，AB ）=9，求△ABC 的面积；（3）如图3，在钝角△ABC 中，∠A=60°，点D 在AB 边上，∠ACD=90°，T （AB ，AC ）=2，T （BC ，AB ）=6，求T （BC ，CD ）.解：(1)过C 作CE ⊥AB ，垂足为E∴由T （AC ，AB ）=3投影可知AE=3∴BE=2即T （BC ，AB ）=2 (2)过点C 作CF ⊥AB 于F∵∠ACB=90°CF ⊥AB ∴△ACF ∽△CBF ∴CF 2=AF ·BF ∵T （AC ，AB ）=4，T （BC ，AB ）=9∴AF=4 BF=9即CF=6 △ABC =2，T =6∴AC=2 BM=63.（2019泰州）如图，⊙O 的半径为5，点P 在⊙O 上，点A 在⊙O 内，且AP ＝3,过点A 作AP 的垂线交于⊙O 点B 、C.设PB=x,PC=y,则y 与x 的函数表达式为．解：如图，连接PO 并延长交⊙O 于点N ，连接BN ，∵PN 是直径，∴∠PBN=90°. ∵AP ⊥BC,C∴∠PAC =90°，∴∠PBN=∠PAC ，又∵∠PNB=∠PCA ，∴△PBN ∽△PAC ，∴PA PB =PCPN , ∴3x =y10 ∴y=x 30.故答案为：y=x30. 4.（2019无锡）如图，在△ABC 中，AB ＝AC ＝5，BC＝D 为边AB 上一动点（B 点除外），以CD 为一边作正方形CDEF ，连接BE ，则△BDE 面积的最大值为．5.（2019宿迁）．如图①，在钝角△ABC中，∠ABC＝30°，AC＝4，点D为边AB中点，点E为边BC中点，将△BDE绕点B逆时针方向旋转α度（0≤α≤180）．（1）如图②，当0＜α＜180时，连接AD、CE．求证：△BDA∽△BEC；（2）如图③，直线CE、AD交于点G．在旋转过程中，∠AGC的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；解：（1）如图②中，由图①，∵点D为边AB中点，点E为边BC中点，∴DE∥AC，∴＝，∴＝，∵∠DBE＝∠ABC，∴∠DBA＝∠EBC，∴△DBA∽△EBC．（2）∠AGC的大小不发生变化，∠AGC＝30°．理由：如图③中，设AB交CG于点O．∵△DBA∽△EBC，∴∠DAB＝∠ECB，∵∠DAB +∠AOG +∠G ＝180°，∠ECB +∠COB +∠ABC ＝180°，∠AOG ＝∠COB ，∴∠G ＝∠ABC ＝30°．6.（2019连云港）如图，在平面直角坐标系xOy 中，抛物线L 1：2y x bx c =++过点C (0，﹣3)，与抛物线L 2：213222y x x =--+的一个交点为A ，且点A 的横坐标为2，点P 、Q 分别是抛物线L 1、抛物线L 2上的动点．（1）求抛物线L 1对应的函数表达式；（2）设点R 为抛物线L 1上另一个动点，且CA 平分∠PCR ，若OQ ∥PR ，求出点Q 坐标．详解：（1）将2x =代入213222y x x =--+，得3y =-，故点A 的坐标为()23-，. 将()()2303A C --，，，代入2y x bx c =++，得2322300b c c-=++?-=++?，解得23b c =-??=-?.所以抛物线1L 对应的函数表达式为223y x x =--.（2）当点P 在y 轴左侧时，抛物线1L 不存在动点R 使得CA 平分PCR ∠.的当点P 在y 轴右侧时，不妨设点P 在CA 的上方，点R 在CA 的下方，过点P 、R 分别作y 轴的垂线，垂足分别为S T 、，过点P 作PH TR ⊥，垂足为H ，则有90PSC RTC ∠=∠=?. 由CA 平分PCR ∠，得PCA RCA ∠=∠，则PCS RCT ∠=∠，故PSC RTC ??∽，所以PS TR CS TC=. 设点P 坐标为()211123x x x --，，点R 坐标为()222223x x x --，，所以有()()12221122233323x x x x x x =--------，整理得124x x +=.在Rt PRH 中，.过点Q 作QK x ⊥轴，垂足为K .设点Q 坐标为213222m m m ??--+，. 若OQ PR ∥，则需QOK PRH ∠=∠.所以2132222m m m =--+.解得m =.所以点Q 坐标为7-?或7-?.7.（2019连云港）问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上，（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN翻折，点P落在点P'处．若正方形ABCD的边长为4 ，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD 中，点M 、N 分别为边AB 、CD 上的点，将正方形ABCD 沿着MN 翻折，使得BC 的对应边B'C '恰好经过点A ，C'N 交AD 于点F ．分别过点A 、F 作AG ⊥MN ，FH ⊥MN ，垂足分别为G 、H ．若AG ＝52，请直接写出FH 的长．解：问题情境：因为四边形ABCD 是正方形，所以90ABE BCD AB BC CD DC AB ∠=∠=?==，，∥. 过点B 作BF MN ∥分别交AE CD 、于点G F 、. 所以四边形MBFN 为平行四边形.所以NF MB =.所以90BF AE BGE ∠=?⊥，，所以90CBF AEB ∠+∠=?，又因为90BAE AEB ∠+∠=?，所以CBF BAE ∠=∠.ABE BCF △△≌，所以BE CF =.因为DN NF CF BE EC ++=+，所以DN NF EC +=，所以DN MB EC +=.问题探究：（1）连接AQ ，过点Q 作HI AB ∥，分别交AD BC 、于点H I 、.易得四边形ABIH 为矩形. 所以HI AD HI BC ⊥⊥，且HI AB AD ==.因为BI 是正方形ABCD 的对角线，所以45BDA ∠=?. 所以DHQ 是等腰直角三角形，HD HQ =.所以AH QI =.因为MN 是AE 的垂直平分线，所以AQ QE =.所以Rt Rt AHQ QIE △≌△.所以AQH QEI ∠=∠.所以90AQH EQI ?∠+∠=.所以90AQE ∠=?.所以AQE 是等腰直角三角形，45EAQ AEQ ∠=∠=?，即45AEF ∠=?.（2）如图所示，连接AC 交BD 于点O ，由题意易得APN 的直角顶点P 在OB 上运动. 设点P 与点B 重合，则点P '与点D 重合；设P 与点O 重合，则点P 的落点为O '.易知45ADO '∠=?.当点P 在线段BO 上运动时，过点P 作CD 的垂线，垂足为G ，过点P '作P H CD '⊥，垂足为点H .易证：Rt PGN Rt NHP '△△≌，所以PG NH G H P N '==，，因为BD 是正方形ABCD 的对角线，所以45PDG ∠=?，易得PG GD =，所以GN DH =. 所以DH H P '=.所以45P DH '∠=?，故45P DA '∠=?. 所以点P '在线段DO '上运动.过点S 作SK DO '⊥，垂足为K ，因为点S 为AD 的中点，所以2DS =，则P S '.问题拓展：解：延长AG 交BC 于E ，交DC 的延长线于Q ，延长FH 交CD 于P ，如图4：则EG＝AG＝52，PH＝FH，∴AE＝5，在Rt△ABE中，BE3，∴CE＝BC﹣BE＝1，∵∠B＝∠ECQ＝90°，∠AEB＝∠QEC，∴△ABE∽△QCE，∴1520 QE AE,AQ AE QE333===+=∵AG⊥MN，∴∠AGM＝90°＝∠B，∵∠MAG＝∠EAB，∴△AGM∽△ABE，∴AM AGAE AB=，即5254AM=，解得：25 AM8=，由折叠的性质得：AB'＝EB＝3，∠B'＝∠B＝90°，∠C'＝∠BCD＝90°，∴B'M7,AC1 8'==，∵∠BAD＝90°，∴∠B'AM＝∠C'FA，∴△AFC'∽△MAB'，∴''1,25788 AF AC AFAM MB==，解得：25253 AF,DF4777 ==-=∵AG⊥MN，FH⊥MN，∴AG∥FH，∴AQ∥FP，∴△DFP∽△DAQ，∴FP DFAQ DA=，即372043FP=，解得：FP＝57，∴FH＝15 FP214=．8.（2019南通）如图，矩形ABCD中，AB=2,AD=4,E,FF分别在AD,BC上，点A与点C关于EF所在的直线对称，P 是边DC上的一动点，（1）连接AF，CE，求证四边形AFCE是菱形；（2）当PEF ?的周长最小时，求CPDP的值；（3）连接BP 交EF 于点M ，当?=∠45EMP 时，求CP 的长。