苏科版年七下期末复习专题一几何证明综合题
苏科版数学七年级下册期末复习第12章《证明》知识点归纳与巩固训练(有答案)

七下第12章《证明》知识点归纳与巩固训练知识要点:1、叫命题,叫真命题,叫假命题2、证明与图形有关的命题的一般步骤有:(1)(2)(3)3、三角形的内角和为,直角三角形的两个锐角,三角形的外角等于;4、叫互逆命题;巩固训练一、选择题1.在下列命题中,为真命题的是()A. 相等的角是对顶角B. 平行于同一条直线的两条直线互相平行C. 同旁内角互补D. 垂直于同一条直线的两条直线互相垂直2.下列命题:①同旁内角互补;②若|a|=|b|,则a=b;③同角的余角相等;④三角形的一个外角等于两个内角的和.其中是真命题的个数是()A. 4个B. 3个C. 2个D. 1个3.要证明命题“若a>b,则a2>b2”是假命题,下列a,b的值不能作为反例的是()A. a=3,b=−2B. a=0,b=−1C. a=−2,b=−3D. a=1,b=−34.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为()A. 120°B. 80°C. 60°D. 40°5.如图,在△ABC中,AB=AC,BC=BD=AD,则∠A的度数为()A. 30°B. 36°C. 40°D. 45°6.如图,l//m,∠1=120°,∠A=55°,则∠ACB的大小是()A. 55°B. 65°C. 75°D. 110°7.△ABC中,∠B=∠A+10°,∠C=∠B+10°,则∠A的度数为()A. 30°B. 40°C. 50°D. 60°8.如图,AD、AE分别是△ABC的高和角平分线,且∠B=76°,∠C=36°,则∠DAE等于()A. 20°B. 18°C. 45°D. 30°二、填空题9.命题“等边三角形的三个内角相等”的逆命题是__________________.10.命题“内角和与外角和相差360°的多边形是六边形”的条件是________,结论是________.11.如图,ΔABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=50∘,则∠BOC=_____∘12.在△ABC中,∠B=∠A+30°,∠C=∠B+30°,则∠C=________.13.如图所示,已知∠B=60°,∠C=20°,∠1=120°,则∠A=________.14.如图,AB//CD,∠1=42°,∠3=77°,则∠2的度数为.15.如图,D、E、F分别是△ABC三边延长线上的点,则∠D+∠E+∠F+∠1+∠2+∠3=______ 度.三、解答题16.写出命题“如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等”的逆命题,并判断原命题和逆命题的真假.若是假命题,请举出反例.17.如图,在△ABC中,BD平分∠ABC,交AC于点D,过D作DE//BC交AB于点E.已知∠A=45°,∠C=105°,求∠EDB的度数.18.如图所示,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60∘,∠BCE=45∘,求∠ADB的大小。
苏科版数学七年级下册几何证明综合题.docx

几何证明综合题1、探究与发现:如图所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:(1)如图1,观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系是_______ 。
(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=________°;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°则∠DCE=_______°;③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,则∠A=_______°.2、某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF的直角边DE 与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).(1)在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐_______;连接FC,∠FCE 的度数逐渐_______.(填“不变”、“变大”或“变小”)(2)△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;(3)能否将△DEF移动至某位置,使F、C的连线与AB平行?请求出∠CFE的度数.3、ΔABC中,∠C=80°,点D、E分别是ΔABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α。
苏科版七年级下册数学 12.2 证明(1).docx

初中数学试卷 马鸣风萧萧12.2 证明(1)探究活动一 先猜一猜图中的两条线段AB 与CD 哪一条长一些?探究活动二图(1)中有曲线吗?请把图(2)中编号相同的点用线段连接起来.悟归纳 从以上两个探究活动中,你有什么感悟啊?实验、观察、操作是人们认识事物的重要手段,但仅凭实验、观察、操作是不够的,所以正确地认识事物,不能单凭直觉,还要加以证实!例题讲解例1 有两条如图所示小路,这两条小路哪个长?这两条小路的面积怎样?例2.你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大一些?请你猜一猜,并用学过的知识和数学方法验证你的猜想.例3、一位老农有一块地,形状是平行四边形,地里有一口水井,他将水井与地的4角分别相连,把地分成4块,然后对他的儿子说:“地分给你们了,每人各取相对的两块;水井不分,两家共用.”精明的弟弟D C BA1234567887654321(图1) (图2)要求先选,在看到土地后果断地选择了①、③两地,同学们,老实的哥哥吃亏了吗?基本事实(1)同位角相等,两直线平行; (2)两直线平行,同位角相等;例题讲解从基本事实出发,证明“垂直于同一条直线的两条直线平行”例1 如图,直线EF 分别交直线AB 、CD 于点M 、N ,AB ∥CD ,MG 平分∠EMB ,NH 平分∠END .求证:MG ∥NH .随堂练习1.已知:如图,AD ∥BC ,∠BAD =∠DCB .求证:∠1=∠3.2.已知:A 、O 、B 在一直线上,OM 平分∠AOC ,ON 平分∠BOC . 求证:OM ⊥ON .AB CD EF M N H水井① ② ③④G。
七年级数学苏科版(下册)第12章证明综合测试题(二).docx

第12章证明综合测试题(二)一・选择题(&小题4分•共32分)1 •下列语句中•不是命题的是B. 钓鱼岛是中国固仃领上C. 无限不循环小数圧无理数 11获诺贝尔文学奖的是更育吗2. 匕知命flh 如果7•那么|<i |・|6 I •该匍■的逆命題圧()A. 如果 0=6■那么 |« |«|6 |丨T 丿‘丨・c.如果“1*厶.那么|<> |鼻|厶| D 如豪|<1|鼻|6|•那么u0b 3. 下面四个金越中.假命越塑()\川曝s3・那么|“卜3B. 如泵龙7・那么C. 如最(u-l)(x2)=0•那么 <>-1=0 或处2=0 I )•如架(4 IP •(从 2 )7) •那么 g| 或 6—24.把命題“同角的补角棚尊-用-如豪…….* 么……”的形式可出来.卜列叮法正确的是( ) A. 如泉几个如腿同一个角的补和•那么这几 个角都相尊B. 如泉一个的晁这个角的补角•那么这两个C. 如果两个角晁同角.那么同角的补角都 I ).如果两个角的和为90S 那么这两个角可 徒相等5•下列命题:①两r [线甲行•内错角相等: ②如果 m 那么皿>0:③等边=角形E 说角 三角形.A. 1个D. 0个6. 已知ZBC 的三个内角乙/<•乙伏乙C 満 足艾系乙8♦乙04厶4.则下列说法正确的是( )A. ZUBC 中・定有一个内角停于36。
B.定布一个内角F45°C. ^ABC 中•定有•个内角專于60°D. MBC -定是直角三角形7. 如图1所示•下列说法•定不正确的展 ) A. LAED>厶BDC B. 乙 DBC ♦乙乙 BDC C ・ LABIAL 乙 3=5”B.因为乙457。
=乙3•所以<i 〃6・故乙1=乙2= 6CTG 因为乙2二乙5・乙13.乙23 •所以乙5= Z 18 •所以a 〃氛所以厶4厶457*D. 因为2.1=60%厶2=W3^57。
苏科版七下期末复习专题一几何证明综合题

七年级下几何证明综合题1、探究与发现:如图所示的图形,像我们常见的学习用品一一圆规.我们不妨把这样图形叫做“规形图” 那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以 问题: 图1,观察 “规形图” 探究/BDC / A 、/ B 、/间的关系是以下三个问题:① 如图2,把一块三角尺XYZ 放置在△ ABC 上,使三角尺的两条直角边XY 、XZ 恰好经过点B 、C, 若/ A = 50° ,贝U / ABX + Z ACX = _________ ° ;② 如图 3, DC 平分 Z ADB , EC 平分 Z AEB ,若 Z DAE = 50° , Z DBE = 130° 贝U Z DCE= _____ ° ; ③ 如图 4, Z ABD, Z ACD 的 10 等分线相交于点 G1、G2 …、G9,若 Z BDC = 140 ° , Z BG1C = 77°2、 某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,Z B = 90° ,Z A=30° ;图②中,Z D = 90° , Z F = 45° .图③是该同学所做的一个实验:他将△ DEF 的直角边DE 与厶ABC的斜边AC 重合在一起,并将△ DEF 沿AC 方向移动.在移动过程中,D 、E 两点始终在AC 边 上(移动开始时点D 与点A 重合).(1) 在厶DEF 沿AC 方向移动的过程中,该同学发现:F 、C 两点间的距离逐渐 _______________ ;连接FC , Z FCE的度数逐渐 ________.(填“不变”、“变大”或“变小”)(2) △ DEF 在移动的过程中,Z FCE 与Z CFE 度数之和是否为定值,请加以说明; (3) 能否将△ DEF 移动至某位置,使F 、C 的连线与AB 平行?请求出Z CFE 的度数.3、 △ ABC 中,Z C=80°,点D E 分别是△ ABC 边AC BC 上的点,点P 是一动点•令Z PDA=Z 1, Z PEB=Z 2, Z DPE=Z 。
苏科版七年级下册数学第12章 证明 含答案(综合题)

苏科版七年级下册数学第12章证明含答案一、单选题(共15题,共计45分)1、如图,△ABC为等边三角形,点D,E分别在AC,BC上,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若PF=3,则BP=( )A.6B.5C.4D.32、在下列的计算中,正确的是( )A.2x+3y=5xyB.(a+2)(a-2)=a 2+4C.a 2•ab=a 3bD.(x-3) 2=x 2+6x+93、如图,矩形ABCD的对角线AC⊥OF,边CD在OE上,∠BAC=70°,则∠EOF等于()A.10°B.20°C.30°D.70°4、若x2+kx+81是一个完全平方式,则k的值为( )A.18B.-18C.±9D.±185、如图,已知∠1+∠2=180°,∠3=55°.那么∠4的度数是()A.45°B.125°C.35°D.55°6、如图,点 E 在 AD 的延长线上,下列条件中不能判断 AB∥CD 的是()A.∠1=∠ 2B.∠3=∠4C.∠A=∠CDED.∠C+∠ABC=180°7、下列说法正确的是()A.同一平面内没有公共点的两条直线平行B.两条不相交的直线一定是平行线C.同一平面内没有公共点的两条线段平行D.同一平面内没有公共点的两条射线平行8、下列命题是真命题的是()A.任何数的0次幂都等于1B.顺次连接菱形四边中点的线段组成的四边形是正方形C.图形的旋转和平移会改变图形的形状和大小D.角平分线上的点到角两边的距离相等9、下列关系式中,正确的是()A.(a﹣b)2=a 2﹣b 2B.(a+b)(a﹣b)=a 2+b 2C.(a+b)2=a 2+b 2D.(a+b)2=a 2+2ab+b 210、下列说法中,正确的有()①有一个角为60°的等腰三角形是等边三角形;②三边分别是1,,3的三角形是直角三角形;③一边上的中线等于这条边的一半的三角形是直角三角形;④三个角之比为3:4:5的三角形是直角三角形;A.1个B.2个C.3个D.4个11、若x2+ax+9=(x+3)2,则a的值为()A.3B.±3C.6D.±612、下列命题中的假命题是()A.同旁内角互补B.三角形的一个外角等于与它不相邻的两个内角之和 C.三角形的中线,平分这个三角形的面积 D.全等三角形对应角相等13、下列运算正确的是()A.m 2•m 3=m 6B.(m 4)2=m 6C.m 3+m 3=2m 3D.(m﹣n)2=m 2﹣n 214、若等腰三角形的一个内角为50°,则另两个角的度数为()A.65°、65°B.65°、65°或50°、80°C.50°、80° D.50°、50°15、如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F等于( )A.360°B.720°C.540°D.240°二、填空题(共10题,共计30分)16、在△ABC中,∠ABC=100°,∠ACB=20°,CE平分∠ACB交AB于E,D在AC 上,且∠CBD=20°,则∠CED的度数是________.17、如图,已知中,,于D,于E,BD、CE交于点F,、的平分线交于点O,则的度数为________.18、若是完全平方式,则k的值为________。
七年级下册数学期末考试几何大题证明必考题精选
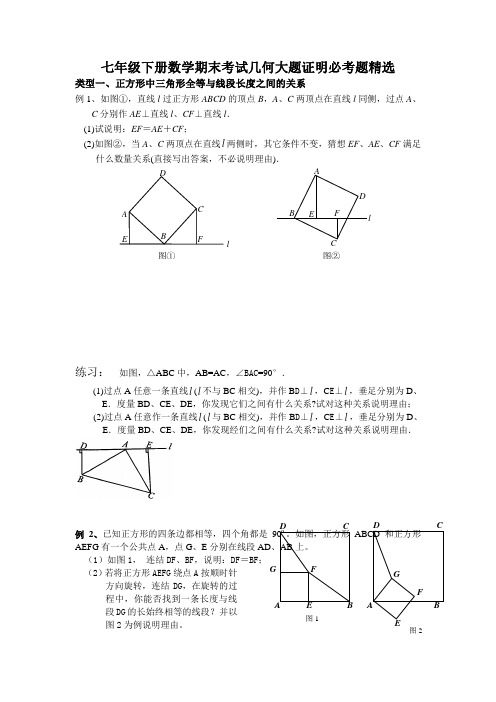
图①DA EC B Fl图②ABEF C lD 七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
(1)如图1, 连结DF 、BF ,说明:DF =BF ;(2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
A EB 图1D CG FA BD C GFE 图2练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上画出示意图,并请求出这个大正方形的面积.附加:如图,△ABC 与△ADE 都是等边三角形,连结BD 、CE 交点记为点F . (1)BD 与CE 相等吗?请说明理由.(2)你能求出BD 与CE 的夹角∠BFC 的度数吗?(3)若将已知条件改为:四边形ABCD 与四边形AEFG 都是正方形,连结BE 、DG 交点记为点M (如图).请直接写出线段BE 和DG 之间的关系?例3、正方形四边条边都相等,四个角都是90.如图,已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,点E 是直线MN 上一点,以AE 为边在直线MN 的上方作正方形AEFG .(1)如图1,当点E 在线段BC 上(不与点B 、C 重合)时: ①判断△ADG 与△ABE 是否全等,并说明理由;②过点F 作FH ⊥MN ,垂足为点H ,观察并猜测线段BE 与线段CH 的数量关系,并说明理由;(2)如图2,当点E 在射线CN 上(不与点C 重合)时: ①判断△ADG 与△ABE 是否全等,不需说明理由;A BC FDE GP32M F G A B C DE F EAB C D②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度α,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C图 2H FG D A NM B C E 图 1H F G D A MN B C E外.(1)请探究:图(2)--(5)中,h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论. (4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o ,R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为:;图(4)与图(6)中的等式有何关系?练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中,点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又 F A B C D EP M (4) A B C DE P M (3) A B C D EP M (2) A B C D EM (P )(1) A B C D E P M (5) FAB C DEP M (6) R SC B APDEFC B HGADE 因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中,h1、h2、h3、h之间的关系;(直接写出结论)⑵⑶⑷⑸(2)说明图(2)所得结论为什么是正确的; (3)说明图(5)所得结论为什么是正确的.例2、已知△ABC 是等边三角形,将一块含30角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存在,请指出这条线段,并证明;如果不存在,请说明理由.(B)ACDE F图1F ABC DEP M (4)ABCDEPM(3)ABCDE P M (2)ABCDEM (P ) (1)ABCDEP M(5)练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转. (1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是。
苏科版七年级下册数学第12章 证明含答案(备考题)

苏科版七年级下册数学第12章证明含答案一、单选题(共15题,共计45分)1、如图,在□ABCD中,CE⊥AB,E为垂足.如果∠A=125°,则∠BCE的度数为()A.55°B.35°C.25°D.30°2、满足下列条件的△ABC是直角三角形的是()A.∠A:∠B:∠C=3:4:5B.a:b:c=1:2:3C.∠A=∠B=2∠C D.a=1,b=2,c=3、适合条件∠A=∠B=∠C的三角形一定是()A.锐角三角形B.钝角三角形C.直角三角形D.任意三角形4、如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是()A.①③B.②④C.①③④D.①②③④5、一副三角板按如图所示叠放在一起,则图中∠α的度数是()A.60°B.75°C.90°D.105°6、下列运算正确的是()A.a+a 2=a 3B.(a 2)3=a 6C.(x﹣y)2=x 2﹣y 2D.a 2a 3=a 67、下列说法中,正确的是()A.“若a<b,则a﹣b>0”是真命题B.“等角的邻补角相等”是假命题 C.“若两个单项式的次数相同,则它们是同类项”是假命题 D.“两条相交线只有一个交点”是假命题8、下列计算可以用平方差公式的是()A.(m+n)(-m+n)B.(-m+n)(m-n)C.(m+n)(-m-n) D.(m-n)(m-n)9、下列哪一个是假命题()A.五边形外角和为360°B.切线垂直于经过切点的半径C.(3,﹣2)关于y轴的对称点为(﹣3,2)D.抛物线y=x 2﹣4x+2017对称轴为直线x=210、下列定理中,没有逆定理的是()A.同旁内角互补,两直线平行B.直角三角形的两锐角互余C.互为相反数的两个数的绝对值相等D.同位角相等,两直线平行11、下列多项式乘法计算题中,不能用平方差公式计算的是( )A.(2x-3y)(2x+3y)B.(2x-3y)(-2x-3y)C.(2x-3y)(-2x+3y)D.(2x+3y)(-2x+3y)12、如图所示的图形中x的值是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下几何证明综合题1、探究与发现:如图所示的图形,像我们常见的学习用品——圆规.我们不妨把这
样图形叫做
“规形
图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)如图1,观察“规形图”,试探究∠B D C与∠A、∠B、∠C之间的关系是_______。
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺X Y Z放置在△A B C上,使三角尺的两条直角边X Y、X Z恰好
经过点B、C,
若∠A=50°,则∠A B X+∠A C X=________°;
②如图3,D C平分∠A D B,E C平分∠A E B,若∠D A E=50°,∠D B E=130°则∠D C E=
_______°;
③如图4,∠A B D,∠A C D的10等分线相交于点G1、G2…、G9,若∠B D C=140°,
∠B G1C=77°,
则∠A=_______°.
2、某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,
∠B=90°,
∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△D E F的直角边D E与△A B C的斜边A C重合在一起,并将△D E F沿A C方向移动.在移动过程中,D、E两点始终在A C边上(移动开始时点D与点A重合).
(1)在△D E F沿A C方向移动的过程中,该同学发现:F、C两点间的距离逐渐_______;
连接F C,∠F C E的度数逐渐_______.(填“不变”、“变大”或“变小”)
(2)△D E F在移动的过程中,∠F C E与∠C F E度数之和是否为定值,请加以说明;
(3)能否将△D E F移动至某位置,使F、C的连线与A B平行?请求出∠C F E的度数.3、ΔA B C中,∠C=80°,点D、E分别是ΔA B C边A C、B C上的点,点P是一动点.
令∠P D A=∠1,
∠P E B=∠2,∠D P E=∠α。
(1)若点P在线段A B上,如图1所示,且∠α=50°,则∠1+∠2=°;(2)若点P在边A B上运动,如图2所示,则∠α、∠1、∠2之间的关系为:;
(3)若点P运动到边A B的延长线上,如图3所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
(4)若点P运动到ΔA B C形外,如图4所示,则∠α、∠1、∠2之间的关系
为:.
4、利用“转化”的思想,将未知的转化为已知的:
(1)课本42页第20题:如图①,B O、C O分别为∠A B C和∠A C B的平分线,我们易得
∠B O C=90°+1
2∠A(不必证明,本题可直接运用);在图②中,当B O'、C O'分别为
∠A B C和∠A C B的外角平分线时,求∠B O'C与∠A的数量关系.我们可以利用“转化”的思想,将未知的∠B O'C转化为已知的∠B O C:如图②,作B O、C O平分∠
A B C和∠A C B.
Ⅰ.在图②中存在如图③的基本图形:点A、B、D在同一直线上,且B O、B O'分别平分∠A B C和
∠D B C,试证明:B O⊥B O';
Ⅱ.试直接利用上述基本图形的结论,猜想并证明图②中∠B O'C与∠A的数量关系;Ⅲ.如图④,B P、C P分别为内角∠A B C和外角∠A C F的平分线,试运用上述转化的思想猜想并证明
∠B P C与∠A的数量关系.
(2)如图,∠A O B=90°,点C、D分别在射线O A、O B上,C E是∠A C D的平分线,
C E的反向延长线与∠C
D O的平分线交于点F.
Ⅰ.当∠O C D=50°(图1),试求∠F.
Ⅱ.当C、D在射线O A、O B上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由:若不变化,求出∠F.
(3)好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,∠BAC=50°,点I是两角∠A B C、∠A C B 的平分线的交点.
Ⅰ.填空:∠BIC=°.
Ⅱ.若点D是两条外角平分线的交点,填空:∠BDC
=°.
Ⅲ.若点E是内角∠ABC、外角∠ACG的平分线的交点,
试探索:∠BEC与∠BAC的数量关系,并说明理由.(请在下面空白处写出推理过程)
(4)在问题(3)的条件下,当∠ACB=度时,CE∥AB.
5、(1)如图①,把△A B C纸片沿D E折叠,使点A落在四边形B C E D的内部点A'的位
置,
试说明:2∠A=∠1+∠2;
(2)如图②,若把△A B C纸片沿D E折叠,使点A落在四边形B C E D的外部点A'的位
置,此时∠A与∠1、∠2之间的等量关系是______________________________(无
需说明理由);
(3)如图③,若把四边形A B C D沿E F折叠,使点A、D落在四边形B C F E的内部点A'、
D'的位置,请你探索此时∠A、∠D、∠l与∠2之间的数量关系,写出你发现的结论并说明理由.
6.如图,已知等边△A B C和点P,设点P到△A B C三边A B、A C、B C(或其延长线)的距离分别为h1、h2、h3,△A B C的高为h.
.在图(1)中,点P是边B C的中点,此时h3=0,可得结论:h
h
+
+
h
h=
1
2
3在图(2)--(5)中,点P分别在线段M C上、M C延长线上、△A B C内、△A B C 外.
(1)请探究:图(2)--(5)中,h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
(4)(附加题2分)在图(6)中,若四边形R B C S是等腰梯形,∠B=∠C=60o,R S=n,B C=m,
点P在梯形内,且点P到四边B R、R S、S C、C B的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为:;图(4)与图(6)中的等式有何关系?
图3
图2
图1
7、P C B F 和∠B C E 的角中∠B P C 和
∠A 加以证明. 8、如图,在△A B C 中,∠分线交于点
A 1,得∠A 1;∠
A 1
B
C 与∠A 1C
D 的平分线相交于
点A 2,得∠A 2; ……;∠A 2008B C 与∠A 2008C D 的平分线相交于点A 2009,得∠A 2009 .则∠A 2009= .。
