指数函数和复合函数

合集下载

大一高等函数知识点总结

大一高等函数知识点总结高等函数是大一学生在数学课程中学习的一门重要内容。

掌握高等函数的知识对于理解和应用数学定理、解决实际问题等都具有重要意义。

下面将对大一高等函数的一些重要知识点进行总结，供大家参考。

一、函数的定义与性质1. 函数的定义：函数是一种关系，它把一个集合的每一个元素都对应到另一个集合的唯一元素上。

2. 函数的性质：a. 定义域和值域：函数的定义域是指函数可以取值的所有实数的集合，值域是指函数实际取到的所有值所组成的集合。

b. 单调性：函数在定义域上递增或递减的性质。

c. 奇偶性：奇函数是具有f(-x)=-f(x)的性质，而偶函数是具有f(-x)=f(x)的性质。

d. 周期性：函数在一个周期内具有相同的函数值。

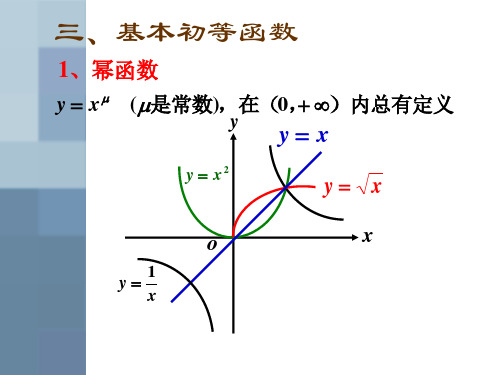
二、常见函数类型1. 幂函数：幂函数是指形如y=x^n的函数，其中n为正整数。

它们的图像表现出不同的形状，如y=x^2对应抛物线，y=x^3对应双曲线等。

2. 指数函数：指数函数是指形如y=a^x的函数，其中a为任意正实数且不等于1。

它们的图像呈现出递增或递减的曲线。

3. 对数函数：对数函数是指形如y=log_a(x)的函数，其中a为正实数且不等于1。

它们是指数函数的反函数，图像呈现出递增或递减的曲线。

4. 三角函数：包括正弦函数、余弦函数、正切函数等，它们的图像具有周期性和振荡性。

5. 反三角函数：包括反正弦函数、反余弦函数、反正切函数等，它们是三角函数的反函数。

三、函数的运算与组合1. 四则运算：函数可以进行加、减、乘、除等运算。

两个函数相加减得到的结果仍为函数，而两个函数相乘除得到的结果不一定是函数。

2. 复合函数：将一个函数的输出作为另一个函数的输入，形成复合函数。

复合函数的定义域和值域由两个函数共同决定。

3. 反函数：如果一个函数的定义域和值域与另一个函数的相反，且它们的输出和输入可以相互对应，那么这两个函数互为反函数。

四、高等函数的应用1. 极值与最值：通过求解函数的极值点，即导函数为零的点，可以求得函数的最大值和最小值。

1.3复合函数和初等函数

u ( x) 称为内层。
（4）分解方法：由外到内，逐层分解，直至每一层均为简单函数为止。
2. 初等函数 – 由基本初等函数经过有限次的四则运算或复合运算构成的，并可用一个式子表示的函数，称为初等函数. – 本课程讨论的函数绝大多数都是初等函数. 3. 分段函数 – 分段函数是其定义域内的一个函数. – 分段函数一般不是初等函数，但如果分段函数可以用一个解析式表示，那么它就是一个初等函数．
例如： y arcsinx 可看作由 y arcsinu 和
2
u x
2
复合而成。
2 为内层。 u x y arcsin u 为外层，其中，
3、不是任何函数都可以复合成一个函数。
2 y f ( u ) arcsin u , u 2 x 如不能复合。
复合后的函数要有意义
2
2 y sin( x 1) Ｃ．
2
Ｂ． y sin ( x 1)
2 2
Ｄ． y sin x 1
2 2
（ B ）4.下列函数不是初等函数的为
x 1 Ａ． y x 1
2
x 1 x 1 Ｂ． y x 1 x 1
1 x x 1 Ｃ． y x 1 x 1
2
2
5、复合可以多次进行，也就是说，中间变量可以有多个。
例
设 y u , u ln v, v cos x 2 , 则这三个函数的复合为
2
y ln v ln (cos x 2)
2
2
例
函数 y
lg(sin x ) 可看成函数
2
2
y u , u lg v , v sinw , w x

大一高数之函数

……
……
t 年后人口为p＝9.6259×(1+12‰) t
即
p 9.6259 1.012t
到2005年底,即27年后, 我国人口为 p 9.6259 1.012 .
27
两边取常用对数, lg p lg 9.6259 27 lg1.012 4.9835 27 0.0051 5.1212, 查反对数表, p 13.22(亿).
即根据1978年的数据,可推算出2005年底我国人口为13.22亿.
人口模型 : 设某地某年人口为p0，人口自然增长率为r，那么t 年后的人口p为 p p0 (1 r ) .
t
马尔萨斯（malthus，英，1776 — 1834）根据上述模型提出了他的人口理论，这一模型只适用于生物种群的生存环境较为优雅宽松的情况.当生物种群数量增长到一定值时，恶化的生态环境将抑制种群数量的增长，进而出现负增长，此时马尔萨斯人口模型就不适用了.
A1 A(1 r )t ；
r 若每期结算m次，则每次利率为， m t期内共结算mt次，t期后的本利和为
r mt Am A(1 ) . m 如果，即按照每个瞬间“即存即算” 来计算本利和，则归结为求极限
r mt lim A(1 ) m m
这个求极限问题将在第二章的应用中介绍.
y cos x
正切函数
y tan x
π π 定义域 : ( kπ , kπ ), k Z; 值域( , ), 2 2 π π 以π 为周期, 在每个开区间( kπ , kπ )上 2 2 递增.
余切函数
y cot x
定义域 : kπ ,( k 1)π ), k Z；值域( , ), （以π 为周期, 在每个开区间( π ,( k 1)π ) k 上递减.

3.3复合函数,商的导数,指数,对数的导数

u( x x ) u( x ) v ( x x ) v ( x ) v ( x ) u( x ) y x x x v ( x x )v ( x )
因为v ( x )在点x处可导，所以它在点 x处连续，于是当 x 0时， v ( x x ) v ( x ),
2x
例10.求y a 的导数.
5x
解：y a 5 x ln a(5 x ) 5a 5 x ln a.
3.4复合函数的导数
提问：
1、常用的函数的导数：
(C ) 0
/
( x n ) / nx n1 ( n N * )
公式一
公式二
/ （sin x） cos x
/ （cos x） sin x
公式三
公式四
（1）和或差的导数 [u v ]
/
2、导数的运算法则：
/
u v ；
则复合函数 y f ( (( x )) 在点x处也有导数，且
y x yu ux
或写作 f x ( ( x )) f (u) ( x ).
这就是复合函数的求导法则，即复合函数对自变量的导数，等于已知函数对中间变量的导数，乘中间变量对自变量的导数。
例4.求y (2 x 1) 的导数。
例3.求y ( 3 x 2) 的导数。 2 2 解：y ( 3 x 2) 9 x 12 x 4 2 y (9 x 12 x 4) 18 x 12
2
函数y ( 3 x 2) 2 可以看成由 y u 2 , u 3 x 2复合而成
设y u , u 1 3 x , 则
4 y x y u u x ( u ) u (1 3) x

高三数学复合函数的导数、对数与指数函数的导数人教版知识精讲

高三数学复合函数的导数、对数与指数函数的导数人教版【本讲教育信息】一. 教学内容：复合函数的导数、对数与指数函数的导数二. 本周教学重、难点： 1. 复合函数的求导法则设)(x u ϕ=在点x 处有导数)(x u x ϕ'='，)(u f y =在点x 的对应点u 处有导数)(u f y u '='，则))((x f ϕ在点x 处也有导数，且x u x u y y '⋅'='或)()())((x u f x f x ϕϕ''='2. 对数函数的导数（1）x x 1)(ln =' （2）e xx a a log 1)(log =' 3. 指数函数的导数（1）xxe e =')( （2）a a a xxln )(='【典型例题】[例1] 求下列函数的导数（1）32)2(x x y += （2）245x e y +=（3）32c bx ax y ++=（4）312)(sin x y =（5）)1ln(2x x y ++= （6）x x y 33log =（7）xxy 2sin 5cos =解：（1）22222)2)(1(6)22()2(33x x x x x x u u y ++=++='⋅=' （2）x e u e y x u 8245⋅='⋅='+（3）)2()(313132232b axc bx ax u u y +++='='--（4）3222232232)(sin 3cos 22cos )(sin 31)2(cos 31x x x x x x x v u v u y y x v u =⋅=⋅⋅='⋅'⋅'='-- （5）])1(1211[11)1(1122222'+++++='++++='x x x x x x x x y 22211)11(11x x x x x +=++++= （6）)(log log 1log 33323332ex x e xx x x y =⋅+='（7）2)2(sin )2(sin 5cos 2sin )5(cos )2sin 5cos (x x x x x x x y '-'='=' 2)2(sin 2cos 5cos 22sin 5sin 5x xx x x ⋅-⋅-=[例2] 若)5ln()(-+=x x x f ，)1ln()(-=x x g 解不等式)()(x g x f '>'解：511)(-+='x x f 11)(-='x x g ∵ )()(x g x f '>' ∴ 11511->-+x x ∴ 0)1)(5()3(2>---x x x ∴ 5>x 或1<x ∵ 两函数定义域为⎩⎨⎧>->-0105x x ∴ 5>x∴ 解集为（5，∞+）[例3] 设曲线)0(≥=-x e y x 在点M （te t -,）处的切线l 与y x ,轴围成的三角形面积为)(t s ，求切线l 的方程。

复合函数和初等函数

w z3, z ln t, t 1 x 复合而成
2.初等函数
定义1.7 由基本初等函数经过有限次的四则运算或复合运算构成的，并可用一个式子表示的函数，称为初等函数.
本课程讨论的函数绝大多数都是初等函数.
例如， y 1 x2 ， y sin2 x ，y ln x e2x
y ln(1 sin x)，等等。
1.1.4 复合函数、初等函数
基本初等函数
课前复习
1、常数函数 2、幂函数
y C (C是常数)
y xa (a是常数, a 0)
3、指数函数
y a x (a 0, a 1)
4、对数函数
y loga x (a 0,a 1)
5、三角函数
y sin x y tan x
y secx
y cos x
y cot x
y csc x
6、反三角函数
y arcsinx
y arccosx y arctanx
y arccot x
1.复合函数定义 1.6 设 y 是 u 的函数 y f (u) ， u 又是 x 的函
数 u (x) ，如果函数 u (x) 的值域包含在函数
多项式函数：
f (x) an xn an1xn1 a1x a0
(ai为常数，i 0 ，1 ，2 ，...，n)
有理函数：
f
(x)
an xn an1xn1 bm xm bm1xm1
a1x a0 b1x b0
(ai ,b j为常数 , i 0，1，2，，n；j 0，1，2，，n)
课堂练习
（ D ）1．下列函数为复合函数的是
Ａ．
y
(1) 2
x

复合函数举例50个

复合函数举例50个1. f(g(x)) = sin(x^2)2. f(g(x)) = ln(1 - x)3. f(g(x)) = (x^2 + 1)^34. f(g(x)) = cos(2x)5. f(g(x)) = e^x / (1 + e^x)6. f(g(x)) = tan(sin(x))7. f(g(x)) = ln(cos(x))8. f(g(x)) = (2x + 1)^29. f(g(x)) = sqrt(ln(x))10. f(g(x)) = (1 - x^2)^311. f(g(x)) = sin(cos(x))12. f(g(x)) = e^tan(x)14. f(g(x)) = cos(x^3)15. f(g(x)) = 1 / (1 + e^x)16. f(g(x)) = sqrt(cos(x))17. f(g(x)) = (x - 2)^218. f(g(x)) = sin(x^2) / cos(x^2)19. f(g(x)) = ln(1 + e^x)20. f(g(x)) = e^(sin(x))21. f(g(x)) = tan(x^2)22. f(g(x)) = sqrt(e^x - 1)23. f(g(x)) = (x + 1)^324. f(g(x)) = sin(ln(x))25. f(g(x)) = ln(cos(x^2))26. f(g(x)) = e^(cos(x))28. f(g(x)) = sqrt(1 - x^2)29. f(g(x)) = (2x - 1)^430. f(g(x)) = sin(e^x)31. f(g(x)) = ln(1 + e^-x)32. f(g(x)) = cos(ln(x))33. f(g(x)) = e^(tan(x))34. f(g(x)) = sqrt(cos(x^3))35. f(g(x)) = (x + 2)^236. f(g(x)) = sin(2x)37. f(g(x)) = ln(e^x + 1)38. f(g(x)) = cos(sin(x))39. f(g(x)) = e^cos(x)40. f(g(x)) = tan(cos(x))42. f(g(x)) = (2x - 1)^243. f(g(x)) = sin(e^x - 1)44. f(g(x)) = ln(1 - e^x)45. f(g(x)) = cos(3x)46. f(g(x)) = e^(sin(x^2))47. f(g(x)) = tan(ln(x) + 1)48. f(g(x)) = sqrt(x^2 - 1)49. f(g(x)) = (x - 3)^350. f(g(x)) = sin(ln(e^x - 1))复合函数是指将一个函数的输出作为另一个函数的输入，形成一个新的函数。

初中数学知识点指数函数与对数函数的运算与复合函数

初中数学知识点指数函数与对数函数的运算与复合函数初中数学知识点：指数函数与对数函数的运算与复合函数在初中数学中，指数函数和对数函数是非常重要的数学概念。

本文将详细介绍指数函数与对数函数的运算以及复合函数的相关知识。

一、指数函数的定义和性质指数函数是以一个常数为底数的幂函数，其定义如下：f(x) = a^x，其中a为底数，x为指数。

1. 指数函数的性质：（1）指数函数的定义域为实数集R，值域为正实数集(0, +∞)。

（2）当底数a>1时，指数函数是递增函数；当0<a<1时，指数函数是递减函数。

（3）指数函数在原点处的函数值为1，即f(0) = 1。

（4）指数函数的图像在x轴正半轴无渐近线。

二、对数函数的定义和性质对数函数是指数函数的逆运算，其定义如下：f(x) = loga(x)，其中a为底数，x为真数。

1. 对数函数的性质：（1）对数函数的定义域为正实数集(0, +∞)，值域为实数集R。

（2）当底数a>1时，对数函数是递增函数；当0<a<1时，对数函数是递减函数。

（3）对数函数在底数为1时，函数值为0，即log1(x) = 0。

（4）对数函数在x轴正半轴有一条纵轴为x=1的渐近线。

三、指数函数和对数函数的运算1. 指数函数的运算：（1）指数函数的乘法：a^m * a^n = a^(m+n)（2）指数函数的除法：a^m / a^n = a^(m-n)（3）指数函数的幂运算：(a^m)^n = a^(m*n)2. 对数函数的运算：（1）对数函数的乘法：loga(x) + loga(y) = loga(x * y)（2）对数函数的除法：loga(x) - loga(y) = loga(x / y)（3）对数函数的幂运算：loga(x^n) = n * loga(x)四、复合函数的定义和性质复合函数是指将一个函数的输出作为另一个函数的输入，其定义如下：f(x) = g(h(x))，其中h(x)为内函数，g(x)为外函数。

高中数学.复合函数、抽象函数、函数零点

1、复合函数的性质：对于单调性，有“同步增，异步减”．对于奇偶性，若每层函数均有奇偶性，则有“全奇才奇，有偶则偶”．对于周期性，内层函数为周期函数的复合函数仍为周期函数．2、抽象函数往往有它所对应的具体函数模型，常见的抽象函数模型有： ⑴ 正比例函数：()()()f x y f x f y +=+； ⑵ 指数函数：()()()f x y f x f y +=； ⑶ 对数函数：()()()f xy f x f y =+； ⑷ 幂函数：()()()f xy f x f y =．3、函数的零点⑴ 满足()0f a =的a 叫做函数()f x 的零点，即方程()0f x =的实数根，也即函数()y f x =的图象与x 轴的交点的横坐标．⑵ 零点定理：若函数()y f x =在闭区间[],a b 上的图象是连续不断的曲线，并且在区间端点的函数值符号相反，即()()0f a f b ⋅<．则在区间(),a b 内，函数()y f x =至少有一个零点．特别的，如果函数在此区间上单调，则函数()y f x =在此区间上有且只有一个零点．⑶ 零点个数的判断通常借助函数图象，零点问题和交点问题往往需要通过互相转化解决．知识梳理知识结构图复合函数、抽象函数、函数零点1、（2007北京理）对于函数①()()lg 21f x x =-+，②()()22f x x =-，③()()cos 2f x x =+，判断如下三个命题的真假：命题甲：()2f x +是偶函数；命题乙：()f x 在(),2-∞上是减函数，在()2,+∞上是增函数；命题丙：()()2f x f x +-在(),-∞+∞上是增函数．能使命题甲、乙、丙均为真的所有函数的序号是．A ．①③B ．①②C ．③D ．②【解析】 D2、（2011北京理13）已知函数()()32212x x f x x x ⎧⎪=⎨⎪-<⎩，≥，，若关于x 的方程()f x k =有两个不同的实根，则实数k 的取值范围是．【解析】 ()0,1；1、()213log 54y x x =-+的单调递增区间为（）A ．(),1-∞B ．5,2⎛⎫-∞ ⎪⎝⎭C ．5,42⎛⎫⎪⎝⎭D ．()4,+∞ 2、设函数()xf x a -=（0a >且1a ≠），()24f =，则（）A ．()()21f f ->-B ．()()12f f ->-C ．()()12f f >D ．()()22f f ->3、已知()()log 2a f x ax =-是[]0,1上的减函数，则a 的值可能为（） A ．12 B ．32C ．2D ．3 4、已知函数()2x f x x =+，()2log g x x x =+，()2log 2h x x =-的零点分别为a 、b 、c ，则（）A ．a b c <<B ．a c b <<C ．b a c <<D ．c a b <<5、已知函数()()()2f x x a x b =---（a b <），并且α、β是方程()0f x =的两个根（αβ<），则实数a 、b 、α、β的大小关系是（）A ．a b αβ<<<B ．a b αβ<<<C ．a b αβ<<<D ．a b αβ<<<6、已知函数()22f x x x c =-+，()()1f x f x =，()()()1n n f x f f x -=（2n ≥，n *∈N ），若函数()n f x x -不存在零点，则c 的取值范围是（） A ．14c <B ．34c ≥C ．94c >D ．94c ≤ 小题热身真题再现7、下列关于函数()()log 1x a f x a =-（0a >且1a ≠）的命题： ① 无论a 取何值，()f x 均为R 上的增函数； ② 无论a 取何值，()f x 的值域均为R ； ③ 无论a 取何值，()f x 一定有零点； ④ 存在某个a ，使得()f x 恰好有两个零点．其中正确的命题个数为（）A ．0B ．1C ．2D ．38、若单调函数()f x （x ∈R ）满足()()()f x y f x f y +=⋅，则()f x 的值域为（） A ．R B ．()(),00,-∞+∞ C ．()0,+∞ D ．不能确定9、已知函数()2243f x x x -=-+-，设()()()()F x p f f x f x =⋅+，其中p 为负实数．若()F x 在区间(),3-∞-上是减函数，在区间()3,0-上是增函数，则p 的值为（）A ．1-B ．18-C ．116-D ．12-10、已知函数()2f x ax bx c =++（0a ≠），则关于x 的方程()()20m f x nf x p ++=⎡⎤⎣⎦（实数,,,,,0a b c m n p ≠）的解集不可能是（）A ．{}1,2B ．{}1,4C ．{}1,2,3,4D ．{}1,4,16,641 2 3 4 5 6 7 8 9 10 AABAACCCCD考点：复合函数的定义域与值域【例1】 ⑴函数()12xf x ⎛⎫= ⎪⎝⎭的定义域为，值域为．⑵函数211()2x f x -⎛⎫= ⎪⎝⎭的定义域为，值域为．⑶函数21122log log 2y x x ⎛⎫=+- ⎪⎝⎭的定义域为_________，值域为____________．【解析】 ⑴ [)0,+∞，(]0,1；⑵ [11]-，，1,12⎡⎤⎢⎥⎣⎦；⑶ [)1042⎛⎤+∞ ⎥⎝⎦，，，[0)+∞，；4.1复合函数经典精讲【例2】 ⑴已知函数()()2lg 21f x ax x =++的定义域为R ，求实数a 的取值范围．⑵已知函数()()2lg 21f x axx =++的值域为R ，求实数a 的取值范围．【解析】 ⑴ ()1,+∞；⑵[]0,1；【拓1】 ⑴ 已知()32log f x x =+，[]1,9x ∈，求函数()()22y f x f x =+⎡⎤⎣⎦的值域．⑵ 设2,1(),1x x f x x x ⎧⎪=⎨<⎪⎩≥，()g x 是二次函数，若()f g x ⎡⎤⎣⎦的值域是[)0,+∞，求函数()g x 的值域．⑶ 设[]2,8x ∈，函数()()21()log log 2a a f x ax a x =⋅的最大值是1，最小值是18-，求a 的值．【解析】 ⑴ []6,13⑵ [)0,+∞． ⑶ 12a =．考点：复合函数的性质初步【例3】 ⑴函数()212log 56y x x =-+的单调增区间为（）A ．52⎛⎫+∞ ⎪⎝⎭，B ．(3)+∞，C ．52⎛⎫-∞ ⎪⎝⎭， D ．(2)-∞，⑵函数2212x x y -++⎛⎫= ⎪⎝⎭的单调递增区间是（）A ．11,2⎡⎤-⎢⎥⎣⎦B ．(],1-∞-C ．[)2,+∞D ．1,22⎡⎤⎢⎥⎣⎦⑶函数421x x y =-+的值域为_______，单调递减区间为________．【解析】 ⑴ D ；⑵ D ；⑶ 3,4⎡⎫+∞⎪⎢⎣⎭；(),1-∞-．考点：复合函数的性质综合【例4】 ⑴函数()()212log 23f x x ax =-+，若()f x 在(],1-∞内是增函数，则a 的取值范围为________；若()f x 的单调递增区间是(],1-∞，则a 的取值范围为________． ⑵已知函数()()31axf x a -=≠，若()f x 在区间(]0,1上是减函数，则实数a 的取值范围是． ⑶若函数()()2log 2a f x x x =+（0a >且1a ≠）在区间10,2⎛⎫⎪⎝⎭内恒有()0f x >，则()f x 的单调增区间是．【解析】 ⑴ [12)，；{1}．⑵()(],01,3-∞；⑶1,2⎛⎫-∞- ⎪⎝⎭考点：抽象函数的函数值问题【例5】 ⑴若奇函数()f x （x ∈R ）满足()21f =，()()()22f x f x f +=+，则()1f = ； ⑵定义在实数R 上的函数()y f x =具有如下性质： ①对任意x ∈R ，都有()()33f x f x =⎡⎤⎣⎦；②对任意12x x ∈R ，，且12x x ≠，都有()()12f x f x ≠．则()()()101f f f -++=________． ⑶已知函数()f x （x ∈R ）满足()12f =，()()()2f x y f x f y xy +=++，则 ()2f = ，()3f = ，()3f -= ．⑷()f x 是定义在(0)+∞，上的增函数，对正实数x 、y 都有()()()f xy f x f y =+成立．则不等式()2log 0f x <的解集为_ ______．【解析】 ⑴12； ⑵ 0；⑶ 6，12，6； ⑷ ()1,2；【拓2】定义在[]0,1上函数()f x 满足：① ()00f =；② ()()11f x f x +-=； ③ ()132x f f x ⎛⎫= ⎪⎝⎭；④ 对任意12,x x []0,1∈，若12x x <，则()()12f x f x ≤．则()1f = ，12f ⎛⎫= ⎪⎝⎭ ，13f ⎛⎫= ⎪⎝⎭ ，18f ⎛⎫= ⎪⎝⎭．【追问】12013f ⎛⎫= ⎪⎝⎭．【解析】 ()11f =；1122f ⎛⎫= ⎪⎝⎭；1132f ⎛⎫= ⎪⎝⎭；1184f ⎛⎫= ⎪⎝⎭．【追问】112013128f ⎛⎫=⎪⎝⎭． 4.2抽象函数考点：抽象函数的性质【例6】 ⑴若函数()f x （x ∈R ，且0x ≠）对任意的非零实数,x y 满足()()()f xy f x f y =+．求证：()f x 为偶函数．⑵定义在R 上的函数()f x 同时满足下列条件：① 对任意x ，y ∈R ，恒有()()()f x y f x f y +=+； ② 当0x >时，()0f x <，且()12f =-．判断函数()f x 的奇偶性，并求函数()f x 在区间[]2,4-上的最大值和最小值．【解析】 ⑴ 令1,1x y ==-得(1)(1)(1)f f f -=+-，于是(1)0f =；再令1x y ==-得(1)2(1)0f f =-=，于是(1)0f -=．令1y =-得()()(1)()f x f x f f x -=+-=，又()f x 的定义域关于原点对称．故()f x 为偶函数． ⑵ ()f x 在区间[]2,4-上的最大值是(2)4f -=，最小值为(4)8f =-．【备注】本题可以通过函数原型快速得到答案或得到启发．对于⑴()ln f x x =（x ∈R ）是符合函数的函数原型；对于⑵()2f x x =-（x ∈R ）是符合函数的函数原型．【拓3】函数()f x 的定义域为R ，且()f x 的值不恒为0，又对于任意的实数m ，n ，总有()()22n m f m f n mf nf⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭成立． ⑴ 求(0)f 的值；⑵ 求证：()0t f t ⋅≥对任意的t ∈R 成立； ⑶ 求所有满足条件的函数()f x ．【解析】 ⑴ (0)0f =；⑵ 对任意t ∈R ，令2m n t ==，得2(2)4()f t t f t =⋅，于是21()(2)04t f t f t ⋅=≥； ⑶ ()f x x =．考点：零点定理【例7】 ⑴函数()237x f x x =+-在区间[02]，上的零点必在下面的区间（）内．Ａ．102⎡⎤⎢⎥⎣⎦，Ｂ．112⎡⎤⎢⎥⎣⎦，Ｃ．312⎡⎤⎢⎥⎣⎦，Ｄ．322⎡⎤⎢⎥⎣⎦， ⑵设函数()32log x f x a x+=-在区间()1,2内有零点，则实数a 的取值范围是（） A ．()31,log 2-- B ．()30,log 2 C ．()3log 2,1 D ．()31,log 4 【解析】 ⑴ C ；⑵ C ；4.3函数零点考点：函数图象与零点、交点问题【例8】 ⑴方程2log (3)2x x +=的解的情况是（）A ．仅有一根B ．有两个正根C ．有一个正根和一个负根D ．有两个负根⑵已知()2881651x x f x x x x -⎧=⎨-+>⎩，≤，，()ln g x x =，则()f x 与()g x 的图象的交点个数为（）A ．1B ．2C ．3D ．4⑶若函数()x f x a x a =--（0a >且1a ≠）有两个零点，则实数a 的取值范围是． ⑷若不等式2log 0a x x -<对102x ⎛⎫∈ ⎪⎝⎭，恒成立，则实数a 的取值范围是_______．【解析】 ⑴ C ；⑵ C ；⑶ (1,)+∞；⑷ 1116⎡⎫⎪⎢⎣⎭，；考点：复合函数的零点问题【例9】 ⑴已知函数()y f x =和()y g x =在[]2,2-的图象如下所示：-22-22y -11-11Ox-22-22y -11-11Oxf xg x 给出下列四个命题：①方程()0f g x =⎡⎤⎣⎦有且仅有6个根 ②方程()0g f x =⎡⎤⎣⎦有且仅有3个根 ③方程()0f f x =⎡⎤⎣⎦有且仅有5个根 ④方程()0g g x =⎡⎤⎣⎦有且仅有4个根其中正确的命题是．（将所有正确的命题序号填在横线上）． ⑵设1,11()1,1x x f x x ⎧≠⎪-=⎨⎪=⎩，若关于x 的方程()()20f x bf x c ++=⎡⎤⎣⎦有三个不同的实数解123,,x x x ，则222123x x x ++等于．【解析】 ⑴ ①③④；⑵ 5；【拓4】已知()2f x x px q =++，关于x 的方程()()0f f x =有且只有一个实数根，求证：p 与q 同时大于0或者p 与q 同时等于0．【解析】关于x 的方程()()0f f x =有且只有一个实数根，()f x 的图象只有如图两种情形（分别对应0∆>和0∆=的情形）．进而容易证明命题成立．y=x 2y=x 1x 2x 1 yOx O xy一、选择题 1、设()()23132x x f x k =-+⋅+，当0x >时()f x 恒取正值，则k 的取值范围为（） A ．(),1-∞- B ．(),221-∞- C ．()1,221-- D ．()221,221---【解析】 B ；2、设函数3y x =与212x y -⎛⎫= ⎪⎝⎭的图象的交点为00()x y ，，则0x 所在的区间是（）A ．(01)，B ．(12)，C ．(23)，D ．(34)，【解析】 B ；3、关于x 的方程1log (0x aa x a =>且1)a ≠（）A ．仅当1a >时，有唯一解B ．仅当01a <<时，有唯一解C ．有唯一解D ．无解【解析】 C ．4、设函数()f x x x bx c =++，给出下列四个命题：①当0c =时，()y f x =是奇函数；②当00b c =>，时，方程()0f x =只有一个实根； ③函数()y f x =的图象关于点(0)c ，对称； ④方程()0f x =至多有两个实根；其中正确命题的个数为（）A ．1个B ．2个C ．3个D ．4个【解析】 C ；二、填空题 5、设函数22()log log (1)f x x x =+-，则()f x 的定义域是_______；()f x 的最大值是_____．【解析】 (0,1)；2-．6、函数22()log (3)log (1)f x x x =++-的值域是___________，单调递增区间为_______．【解析】 (,2]-∞，(3,1)--．课后习题7、若log (2)a y ax =-在[]01，上是x 的减函数，则a 的取值范围是______．【解析】 (12)a ∈，；三、解答题 8、已知定义域为R 的函数()f x 满足：()()()f x y f x f y +=，且()31f >． ⑴求()0f ；⑵求证：()41f -<．【解析】 ⑴ (0)1f =；⑵ 3(3)(2)(1)(1)1f f f f ==>，故(1)1f >，从而24(4)(2)(1)1f f f ==>．令4,4x y ==-得，(4)(4)(0)1f f f -==，故1(4)1(4)f f -=<．命题得证．【备注】()()()f x y f x f y +=的函数原型是指数函数()x f x a =，由(3)1f >知，1a >． 9、函数()2x f x =和()3g x x =的图象的示意图如图所示．设两函数的图象交于点()11,A x y 、()22,B x y ，且12x x <．x 1x 2BA C 2C 1yO x⑴ 请指出示意图中曲线1C 、2C 分别对应哪一个函数？⑵ 若[]1,1x a a ∈+，[]2,1x b b ∈+，且{},1,2,3,4,5,6,7,8,9,10,11,12a b ∈，指出a 、b 的值，并说明理由；⑶ 结合函数图象示意图，请把()πf 、()πg 、()2013f 、()2013g 四个数从小到大顺序排列．【解析】 ⑴ 1C 对应函数()3g x x =，2C 对应函数()2x f x =；⑵ 如下表，可得1a =，9b =．1 2 3 4 5 6 7 8 9 10 11 12()f x 2 4 8 16 32 64 128 256 512 1024 2048 4096 ()g x1 8 27 641252163435127291000 1331 1728()()()() 10、已知关于x 的二次方程22210x mx m +++=．⑴ 若方程有两根，其中一根在区间()1,0-内，另一根在区间()1,2内，求m 的范围． ⑵ 若方程两根均在区间()0,1内，求m 的范围．【解析】 ⑴5162m -<<-．⑵1122m -<-≤。

高数1_2初等函数

⑶ 反正切函数
定义：正切函数 y = tanx 在
, 2 2
上的反函数，称为反正切
函数.记作 y = arctanx. (反正切函数的主值)
定义域：
x ,
y 值域： , 2 2 y = arctanx是有界函数
例1
分析函数 y ln sin x 的复合结构.
解函数 y ln sin x 是由 y ln u , u sin v , v x 复合而成.
例2
设 f ( x) x 2 , g ( x) 2x , 求 f [ g ( x)] , g[ f ( x)].
解 f ( x) x2 f [ g ( x)] [ g ( x)]2 (2 x ) 2 4 x

x 1 x
f { f [ f ( x)]}
1 1 f [ f ( x)]
1 x x 1 1 x
例4 解
设 f(x) 的定义域是（0，1），求f(lgx)的定义域. 令u = x，则0< u <1
当u = lgx时，0< lgx <1，所以1< x <10
即
函数的定义域为x ∈(1，10)
例如函数 y sin 2 x 由 y u 2 , u sin x复合而成;
函数 y 1 x 2 是由y u , u 1 x 2复合而成的.
说明： ⑴ 并不是任何两个函数都可以构成一个复合函数；例如 y arcsin u, u 2 x 2就不能复合成一个函数. 因为u=2+x2的值域u>2，全部落在y=arcsinu的定义域之外. ⑵ 复合函数的中间变量可以不只一个 (两个以上函数也可构成复合函数) 例： y 2u ，u cos v，v x 复合得到 y 2cos x ； ⑶ 分解复合函数时，每一步必须都是基本初等函数或基本初等函数的四则运算.

1-2初等函数

19
1 x 0 x 1 0 x1 2 x 例2 若 f ( x ) 1 x1 x1 ( x ) 1 ln x 1 x 2 , x 1 1 x 2 ,
求 f [ (x)]。
解:
1 ( x ) f [ ( x )] 1 ln ( x )
y sin x
5
余弦函数 y cos x 定义域:(-,∞+∞)，值域:[-1,1]
y cos x
6
正切函数 y tan x 定义域: x n

2
，值域:(-∞,+∞)
y tan x
7
余切函数 y cot x 定义域: x
n ，值域:(-∞,+∞)
y cot x
y arccos x
12
反正切函数 y arctan x
y arctan x
13
反余切函数 y arccot x
y arccot x
幂函数,指数函数,对数函数,三角函数和反三角函数统称为基本初等函数.
14
复合函数初等函数
1.复合函数
代入法
设 y u, u 1 x 2 ,
25
反双曲正切 y arthx
y arthx
1 1 x ln . 2 1 x
D : ( 1,1)
奇函数,
y ar tanh x
在 (1,1) 内单调增加.
26
小结
函数的分类:
代数函数有理函数
有理整函数(多项式函数)
有理分函数(分式函数)
函数
初等函数
无理函数超越函数
例如 y arcsinu, u 2 x 2 ;

探究指数函数型复合函数

探究指数函数型复合函数作者：李秀兰
来源：《新高考·高二数学》2018年第07期
指数函数与其他代数函数复合后形成复合函数，如y=a f（x）和y=f（ax）（a>0且
a≠1），通过对这些复合函数性质的研究，弄清楚指数函数与其他代数函数之间的联系，明确复合函数的性质与指数函数性质的区别与联系，下面我们不妨对指数型复合函数的图象与性质的应用进行举例说明.
一、与指数有关的复合函数图象
把指数函数y=ax（a>0且a≠1）的图象进行平移、对称，得到复合函数y=f（a x）（a>0
且a≠1）.
例1 把函数y=f（x）的图象向左、向下分別平移2个单位长度，得到函数y=2 x的图象，求f（x）.
分析本题可运用逆向思维，再利用函数图象的平移规律可得.
二、复合函数的性质
1.定义域、值域
点评对于上述两个函数，要先确定出复合过程，同时先求出f（x）的值域，再确定出整
个函数的值域.
2.单调性
点评对于复合函数的单调性，首先要注意该函数的定义域，其次才考虑在其定义域内的
单调性问题.
分析平方展开后重新配方，则可以得到所求函数的形式，然后根据二次函数的知识来确
定最值.
点评这是复合函数求最值问题，为了求得最值，通过换元转化为二次函数，再由二次函
数在区间上的单调性确定最值.
因此，研究指数函数复合函数问题，需要找出函数的复合过程，然后再确定其相关的性质.。

初等函数_反函数_复合函数

定义
在定义域的不同区间内用不同的对应法则表示的函数叫分段函数。
例
已知函数y
f
(x)

2
x,
0 x 1，
1 x, x 1
并求出f (0), f (0.5), f (1), f (3)的值
解
f (0) 0，f (0.5) 2 0.5, f (1) 2，f (3) 4
f 的反函数.
只有在一一对应的前提下才能有反函数.
y f (x)与 x f -1( y) 互为反函数
y
反函数的图形
y f (x)
y x
函数 y = f (x) 与其反函数 y = f 1(x) 的图形关于
y f 1(x)
第Ⅰ、Ⅲ 象限的角平分线 y = x 对称
O
x
反函数的图形
(1) y sin 1 x2
(2) y ln cos 2x
解 (1) y sin u, u t , t 1 x2
(2) y ln u, u cost, t 2x
以上过程称为分解过程
复合函数分解到什么时候为止？
分解到基本初等函数或基本初等函数的四则运算为止 .
四、分段函数
(1)分段函数是一个函数注意： (2)分段函数的定义域是各个表达式定义域的并集
(3)求值时应把自变量代入相应区间的表达式中计算
变量 u 称为中间变量
类似地，可以定义多于两重复合关系的复合函数
外层函数 y f (u)
u g(x) 内层函数
y
f
u
gx
y f (g(x))
例1 写出y sin u， u 2x2 1的复合函数

(完整版)高数上册知识点

高等数学上册知识点第一章函数与极限（一）函数1、函数定义及性质（有界性、单调性、奇偶性、周期性）；2、反函数、复合函数、函数的运算；3、初等函数：幂函数、指数函数、对数函数、三角函数、反三角函数、双曲函数、反双曲函数； 4、函数的连续性与间断点；函数)(x f 在0x 连续 )()(lim 00x f x f xx =→第一类：左右极限均存在。

间断点可去间断点、跳跃间断点第二类：左右极限、至少有一个不存在。

无穷间断点、振荡间断点5、闭区间上连续函数的性质：有界性与最大值最小值定理、零点定理、介值定理及其推论。

（二）极限 1、定义 1）数列极限εε<->∀N ∈∃>∀⇔=∞→a x N n N a x n n n , , ,0lim2）函数极限εδδε<-<-<∀>∃>∀⇔=→A x f x x x A x f x x )( 0 , ,0 ,0)(lim 00时，当左极限：)(lim )(00x f x f x x -→-= 右极限：)(lim )(00x f x f xx +→+= )()( )(lim 000+-→=⇔=x f x f A x f x x 存在2、极限存在准则 1）夹逼准则： 1）)(0n n z x y n n n ≥≤≤2）a z y n n n n ==→∞→∞lim lim a x n n =∞→lim2）单调有界准则：单调有界数列必有极限。

3、无穷小（大）量1）定义：若0lim =α则称为无穷小量；若∞=αlim 则称为无穷大量。

2）无穷小的阶：高阶无穷小、同阶无穷小、等价无穷小、k 阶无穷小 Th1 )(~ααββαo +=⇔;Th2 αβαβαβββαα''=''''lim lim lim ,~,~存在，则（无穷小代换） 4、求极限的方法 1）单调有界准则； 2）夹逼准则；3）极限运算准则及函数连续性； 4）两个重要极限：a) 1sin lim 0=→xx x b)e x x xx xx =+=++∞→→)11(lim )1(lim 10 5）无穷小代换：（0→x ） a)x x x x x arctan ~arcsin ~tan ~sin ~b) 221~cos 1x x -c) x e x ~1- （a x a x ln ~1-） d) x x ~)1ln(+ （ax x a ln ~)1(log +）e) x x αα~1)1(-+第二章导数与微分（一）导数1、定义：000)()(lim )(0x x x f x f x f x x --='→ 左导数：000)()(lim )(0x x x f x f x f x x --='-→-右导数：000)()(lim )(0x x x f x f x f x x --='+→+ 函数)(x f 在0x 点可导)()(00x f x f +-'='⇔2、几何意义：)(0x f '为曲线)(x f y =在点())(,00x f x 处的切线的斜率。

函数专题：指数型与对数型复合函数的单调性与值域-【题型分类归纳】高一数学上学期同步讲与练(解析版)

函数专题：指数型与对数型复合函数的单调性与值域一、复合函数的概念如果函数()=y f t 的定义域为A ，函数()=t g x 的定义域为D ，值域为C ，则当⊆C A 时，函数()()=y f g x 为()f t 与()g x 在D 上的复合函数，其中()=t g x 叫做内层函数，()=y f t 叫做外层函数二、复合函数的单调性1、复合函数单调性的规律：“同增异减”若内外两层函数的单调性相同，则它们的复合函数为增函数；若内外两层函数的单调性相反，则它们的复合函数为减函数 2、具体判断步骤（1）求出原函数的定义域；（2）将复合函数分解为内层函数和外层函数；（3）分析内层函数和外层函数的单调性；（4）利用复合函数法“同增异减”可得出结论. 三、指数型复合函数值域的求法1、形如()=x y f a （0>a ，且1≠a ）的函数求值域借助换元法：令=x a t ，将求原函数的值域转化为求()f t 的值域，但要注意“新元t ”的范围2、形如()=f x y a （0>a ，且1≠a ）的函数求值域借助换元法：令()=f x μ，先求出()=f x μ的值域，再利用=y a μ的单调性求出()=f x y a 的值域。

四、对数型复合函数值域的求法1、形如(log )=a y f x （0>a ，且1≠a ）的函数求值域借助换元法：令log =a x t ，先求出log =a x t 的值域M ，再利用()=y f t 在M 上的单调性，再求出()=y f t 的值域。

2、形如()log =a y f x （0>a ，且1≠a ）的函数的值域借助换元法：令()=f x μ，先求出()=f x μ的值域，再利用log =a y μ的单调性求出()log =a y f x 的值域。

题型一复合函数的单调性判断【例1】（多选）函数2(65)1()()2x x f x -+-=在下列哪些区间内单调递减（）A ．(3),-∞B ．(3,5)C ．(1,3)D ．(2,3) 【答案】ACD【解析】由题意，函数1()2xy =在R 上单调递减，又由函数265y x x =-+-在(3),-∞上单调递增，在(3,)+∞上单调递减，由复合函数的单调性可知，函数()f x 在(3),-∞上单调递减，结合选项，可得选项ACD 符合题意. 故选：ACD.【变式1-1】求函数21181722xxy ⎛⎫⎛⎫=-⋅+ ⎪ ⎪⎝⎭⎝⎭的单调区间___________.【答案】增区间为[2,)-+∞，减区间为(,2)-∞-【解析】设t ＝12x⎛⎫⎪⎝⎭>0，又22817(4)1y t t t =-+=-+在(0,4]上单调递减，在(4,)+∞上单调递增.令12x⎛⎫ ⎪⎝⎭≤4，得x ≥－2，令12x⎛⎫⎪⎝⎭>4，得x <－2. 而函数t ＝12x⎛⎫⎪⎝⎭在R 上单调递减，所以函数21181722x xy ⎛⎫⎛⎫=-⋅+ ⎪ ⎪⎝⎭⎝⎭的增区间为[2,)-+∞，减区间为(,2)-∞-.故答案为：增区间为[2,)-+∞，减区间为(,2)-∞-【变式1-2】函数()()212log 32f x x x =-+-的单调递减区间为（） A ．3,2⎛⎫-∞ ⎪⎝⎭B ．31,2⎛⎫⎪⎝⎭ C ．3,22⎛⎫ ⎪⎝⎭D ．3,2⎛⎫+∞ ⎪⎝⎭【答案】B【解析】由2320x x -+->得：12x <<，即()f x 定义域为()1,2；令232t x x =-+-，则t 在31,2⎛⎫⎪⎝⎭上单调递增，在3,22⎛⎫ ⎪⎝⎭上单调递减；又12log y t=在()0,∞+上单调递减，()()212log 32f x x x ∴=-+-的单调递减区间为31,2⎛⎫ ⎪⎝⎭.故选：B.【变式1-3】函数()()2ln 4f x x =-的单调增区间是______．【答案】(2,0]-【解析】由240x ->，得22x -<<，所以函数的定义域为(2,2)-，令24t x =-，则ln y t =，因为24t x =-在(2,0]-上递增，在[0,2)上递减，而ln y t =在(0,)+∞上为增函数，所以()f x 在(2,0]-上递增，在[0,2)上递减，故答案为：(2,0]-题型二根据复合函数的单调性求参数【例2】若函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，则a 的取值范围（）A ．4a ≤-B ．2a ≤-C ．2a ≥-D ．4a ≥- 【答案】C【解析】依题意函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，15xy =在R 上递减， 2y x ax =+的开口向上，对称轴为2ax =-，根据复合函数单调性同增异减可知，122a a -≤⇒≥-.故选：C【变式2-1】若函数22113x mx y +-⎛⎫= ⎪⎝⎭在区间[]1,1-上为增函数，则实数m 的取值范围为______.【答案】1m ≤-【解析】由复合函数的同增异减性质可得，221y x mx =+-在[1,1]-上严格单调递减，二次函数开口向上，对称轴为x m =- 所以1m -≥，即1m ≤- 故答案为：1m ≤-【变式2-2】已知f （x ）＝()212log 3x ax a -+在区间[2，＋∞）上为减函数，则实数a 的取值范围是________．【答案】](4,4-【解析】二次函数23=-+y x ax a 的对称轴为2=a x ，由已知，应有22≤a，且满足当x ≥2时y ＝x 2－ax ＋3a >0，即224230⎧≤⎪⎨⎪-+>⎩a a a ，解得44-<≤a ．故答案为：](4,4-【变式2-3】若函数()f x =312⎛⎫⎪⎝⎭，单调递减，则a 的取值范围是（） A ．32⎡⎫+∞⎪⎢⎣⎭，B ．32⎛⎫+∞ ⎪⎝⎭， C ．3724⎡⎤⎢⎥⎣⎦， D ．3724⎛⎫ ⎪⎝⎭，【答案】C【解析】因为()f x =312⎛⎫⎪⎝⎭，单调递减，所以，函数()212log 22y x ax =-+-在312⎛⎫⎪⎝⎭，单调递减，且函数值非负，所以函数222t x ax =-+-在312⎛⎫ ⎪⎝⎭，是单调递增且01t <≤，故2232332121220a a a ⎧≥⎪⎪⎪⎛⎫-+-≤⎨ ⎪⎝⎭⎪⎪-+-≥⎪⎩，解得3724a ≤≤，故选：C【变式2-4】已知()()2log 3(0a f x x ax a =-+>且1)a ≠，对任意12,(,]2a x x ∈-∞且12x x ≠，不等式()()12120f x f x x x -<-恒成立，则a 的取值范围是__________．【答案】(【解析】因为对任意12,(,]2a x x ∈-∞且12x x ≠，不等式()()12120f x f x x x -<-恒成立，所以()f x 在(,]2a-∞上单调递减，因为23y x ax =-+在(,]2a-∞上单调递减，由复合函数的单调性知1a >，又由对数函数的定义域知，当(,]2a x ∈-∞时，230x ax -+>恒成立，可得2()3022a a a -⨯+>，解得a -<<综上可得；1a <<a 的取值范围为(.【变式2-5】已知函数()log a f x x =，记()()()()21g x f x f x f ⎡⎤=⋅+-⎣⎦，若()g x 在区间1,22⎡⎤⎢⎥⎣⎦上是增函数，则实数a 的取值范围是（）A ．10,2⎛⎤⎥⎝⎦ B ．1,12⎡⎤⎢⎥⎣⎦C ．()()0,11,2UD ．[)2,+∞【答案】A【解析】()()()()()21log log log 21a a a g x f x f x f x x ⎡⎤=⋅+-=+⎣-⎦，则()()22lg lg lg 21lg lg lg 2lg lg lg lg lg 1x x g x x a x a a a a ⎛⎫-⎡⎤=+=-- ⎪⎣⎦⎝⎭，令lg t x =，由1,22x ⎡∈⎤⎢⎥⎣⎦，所以[]lg 2,lg 2t ∈-，令()()221lg lg 2lg M t t a t a⎡⎤=--⎣⎦，因为()g x 在区间1,22⎡⎤⎢⎥⎣⎦上是增函数，所以()M t 在[]lg 2,lg 2t ∈-也是增函数，所以lg lg 21lg 2lg lg 2lg 22a a -≤-⇒≤-=，则102a <≤，即10,2a ⎛⎤∈ ⎥⎝⎦故选：A.题型三复合函数的值域求解【例3】函数()2212x xf x -+⎛⎫= ⎪⎝⎭的值域为（）A ．1,2⎛⎤-∞ ⎥⎝⎦ B ．10,2⎛⎤⎥⎝⎦ C ．1,2⎡⎫+∞⎪⎢⎣⎭ D ．[)2,+∞【答案】C【解析】令22t x x =-+，则2(1)11t x =--+≤，因为1()2ty =在R 上单调递减，所以12y ≥，故函数()2212x xf x -+⎛⎫= ⎪⎝⎭的值域为1,2⎡⎫+∞⎪⎢⎣⎭，故选：C【变式3-1】函数113()934x xf x --⎛⎫=++ ⎪⎝⎭在[1,)-+∞上的值域为___________.【答案】375,44⎛⎤⎥⎝⎦【解析】2113113()9334334x x xx f x --⎛⎫⎛⎫⎛⎫⎛⎫=++=+ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭+⎝⎭∵[1,)x ∈-+∞则令(],3130xt ⎛⎫⎪⎭∈= ⎝，2334y t t =++在(]0,3递增∴375,44y ⎛⎤∈ ⎥⎝⎦【变式3-2】已知函数2()421x x f x +=--，[0,2]x ∈则其值域为___________. 【答案】[]5,1--【解析】令2x t =，∵[0,2]x ∈，∴14t ≤≤，∴22()41(2)5f t t t t =--=--，又()y f t =关于2t =对称，2t ∴=即1x =时，函数取得最小值，即min ()5f x =-，4t =即2x =时，函数取得最大值，即max ()1f x =-， ()[5f x ∴∈-,1]-.【变式3-3】已知函数()()()44log 1log 3f x x x =++-，求()f x 的单调区间及最大值．【答案】单调递增区间为()1,1-，单调递减区间为()1,3；()max 1=f x【解析】由1030x x +>⎧⎨->⎩得：13x -<<，()f x ∴的定义域为()1,3-；()()()()()224444log 1log 3log 23log 14f x x x x x x ⎡⎤=++-=-++=--+⎣⎦，令()()214t x x =--+，则()t x 在()1,1-上单调递增，在()1,3上单调递减，又4log y t =在定义域内单调递增，由复合函数单调性可知：()f x 的单调递增区间为()1,1-，单调递减区间为()1,3；由单调性可知：()()4max 1log 41f x f ===.【变式3-4】已知()222()log 2log 4,[2,4]f x x x x =-+∈．（1）设2log ,[2,4]t x x =∈，求t 的最大值与最小值；（2）求()f x 的值域．【答案】（1）2t =最大，1t =最小；（2）[3，4].【解析】（1）因为函数2log t x =在区间[2，4]上是单调递增的，所以当4x =时，2log 42t ==最大，当2x =时，2log 21t ==最小．（2）令2log t x =，则()()()222413f x g t t t t ==-+=-+，由（1）得[]1,2t ∈，因为函数()g t 在[]1,2上是单调增函数，所以当1t =，即2x =时，()min 3f x =；当2t =，即4x =时，()max 4f x =，故()f x 的值域为[]3,4.【变式3-5】已知函数()2421x xf x a =⋅-⋅+，求函数()f x 在[]0,1上的最小值．【答案】()2min3,41,48892,8a a a f x a a a -≤⎧⎪⎪=-<≤⎨⎪-≥⎪⎩【解析】设2x t =，由[0,1]x ∈得[1,2]t ∈，2()()21f x g t t at ==-+，222()212()148a a g t t at t =-+=-+-，当14a ≤，即4a ≤时，min ()(1)3g t g a ==-，当124a <≤，即48a <≤时，2min ()()148a a g t g ==-，当，即8a >时，min ()(2)92g t g a ==-，综上()2min3,41,48892,8a a a f x a a a -≤⎧⎪⎪=-<≤⎨⎪-≥⎪⎩．【变式3-6】已知函数()1423x x f x a +=⋅--，若0a >，求()f x 在区间[]1,2上的最大值()g a ．【答案】()147,0311611,3a a g a a a ⎧-<<⎪⎪=⎨⎪-≥⎪⎩.【解析】令[]22,4x t =∈，即求()223h t at t =--在区间[]2,4上的最大值．当0a >时，二次函数()223h t at t =--的图象开口向上，对称轴为直线1t a=.①当12a ≤时，即当12a ≥时，函数()h t 在区间[]2,4上单调递增，则()()41611g a h a ==-； ②当123a<≤时，即当1132a ≤<时，函数()h t 在区间12,a ⎡⎫⎪⎢⎣⎭上单调递减，在区间1,4a ⎛⎤ ⎥⎝⎦上单调递增，因为()247h a =-，()41611h a =-，()()421240h h a -=-≥，则()()41611g a h a ==-； ③当134a<<时，即当1143a <<时，函数()h t 在区间12,a ⎡⎫⎪⎢⎣⎭上单调递减，在区间1,4a ⎛⎤ ⎥⎝⎦上单调递增，此时，()()42h h <，则()()247g a h a ==-；④当14a ≥时，即当104a <≤时，函数()h t 在区间[]2,4上单调递减，所以，()()247g a h a ==-.综上所述，()147,0311611,3a a g a a a ⎧-<<⎪⎪=⎨⎪-≥⎪⎩.题型四根据复合函数的值域求解【例4】若函数()22312ax x f x -+⎛⎫= ⎪⎝⎭的最大值是2，则=a （）A ．14B ．14-C ．12 D ．12- 【答案】A【解析】由1()2uy =在定义域上递减，要使()f x 有最大值，则223u ax x =-+在定义域上先减后增，当max ()2f x =，则223u ax x =-+的最小值为1-，所以0131a a>⎧⎪⎨-=-⎪⎩，可得14a =.故选：A【变式4-1】已知函数22414ax x y -+⎛⎫= ⎪⎝⎭的值域为10,16⎛⎤ ⎥⎝⎦，若不等式()()log 4log 2x a xa t t ⋅<-在[]1,2x ∈上恒成立，则t 的取值范围是（）A ．2,25⎛⎫ ⎪⎝⎭B ．2,5⎛⎫+∞ ⎪⎝⎭C ．(,2)-∞D ．()0,2【答案】A【解析】由题意，函数22414ax x y -+⎛⎫= ⎪⎝⎭的值域为10,16⎛⎤ ⎥⎝⎦，可得函数y 的最大值为116，当0a =时，函数2414x y -+⎛⎫= ⎪⎝⎭显然不存在最大值；当0a >时，函数22414ax x y -+⎛⎫= ⎪⎝⎭在1,x a ⎛⎫∈-∞ ⎪⎝⎭上单调递增，在1,x a ⎛⎫∈+∞ ⎪⎝⎭上单调递减，当1x a =时，函数y 有最大值，即12411416a a -+⎛⎫=⎪⎝⎭，解得12a =；当0a <时，22414ax x y -+⎛⎫= ⎪⎝⎭在1,x a⎛⎫∈-∞ ⎪⎝⎭上单调递减，在1,x a ⎛⎫∈+∞ ⎪⎝⎭上单调递增，此时函数y 无最大值，所以()()1122log 4log 2x xt t ⋅<-在[]1,2x ∈上恒成立，即402042x xx x t t t t ⎧⋅>⎪->⎨⎪⋅>-⎩在[]1,2x ∈上恒成立，由40x t ⋅>在[]1,2x ∈上恒成立，可得0t >；由20x t ->在[]1,2x ∈上恒成立，即2x t <在[]1,2上恒成立，可得2t <；由42x x t t ⋅>-在[]1,2x ∈上恒成立，即2114122x x x xt >=++在[]1,2上恒成立，令()122xxf x =+，可得函数()f x 在[]1,2上单调递增，所以()()min512f x f ==，即25t >，综上可得225t <<，即实数t 的取值范围是2,25⎛⎫⎪⎝⎭.故选：A.【变式4-2】已知函数()()2log 41x f x ax =++是偶函数，函数()()22222f x x x g x m -=++⋅的最小值为3-，则实数m 的值为（）A ．3B ．52-C ．2-D ．43【答案】B【解析】因为函数()()2log 41x f x ax =++是偶函数，所以()()f x f x -=，即()()22log 41log 41x x ax ax -+-=++，所以()()222log 41log 410x x ax -++-+=，其中()()()()()22222241441441log 41log 41log log log log 424141414x x x x x x x x x x x x x ---+⋅+⋅++-+=====+++⋅，所以220ax x +=，解得1a =-，所以()()2log 41x f x x =+-，所以()()2log 414122222x x x f x x x x +--+===+，故函数()()222222x x x x g x m --=+++的最小值为3-．令22x x t -+=，则2t ≥，故函数()()222222x x x x g x m --=+++的最小值为3-等价于()()222h t t mt t =+-≥的最小值为3-，等价于()2? 22223m h m ⎧-≤⎪⎨⎪=+=-⎩或22? 22324m m m h ⎧->⎪⎪⎨⎛⎫⎪-=--=- ⎪⎪⎝⎭⎩，解得52m =-．故A ，C ，D 错误.故选：B ．【变式4-3】函数()22lg 34a f x ax x ⎛⎫=++ ⎪⎝⎭没有最小值，则a 的取值范围是______．【答案】22,33⎛⎤- ⎥⎝⎦【解析】令()2234a t x ax x =++，则外函数为()lg f t t =，因为lg y t =在定义域上单调递增，要使函数()22lg 34a f x ax x ⎛⎫=++ ⎪⎝⎭没有最小值，即()2234a t x ax x =++的值域能够取到0，且不恒小于等于0，当0a =时()23t x x =，符合题意，当0a <时()2234a t x ax x =++开口向下，只需224034a a ⎛⎫∆=-⨯⨯> ⎪⎝⎭，解得2233-<<a ，即203a -<<；当0a >时()2234a t x ax x =++开口向上，只需224034a a ⎛⎫∆=-⨯⨯≥ ⎪⎝⎭，解得2233a -≤≤，即203a <≤；综上可得2233a -<≤，即22,33a ⎛⎤∈- ⎥⎝⎦.【变式4-4】已知函数()()213log 25f x x mx =-+，若()f x 的值域为R ，求实数m 的取值范围.【答案】(),-∞⋃+∞ 【解析】由()f x 的值域为R ，可得225u x mx =-+能取()0,∞+内的一切值，故函数225u x mx =-+的图象与x 轴有公共点，所以24200m -≥，解得m ≤m ≥故实数m 的取值范围为(),-∞⋃+∞．。

复合函数导数的基本公式14个

复合函数导数的基本公式14个下面是复合函数导数的14个基本公式：1.链式法则链式法则是求解复合函数导数的基本方法。

设函数y=f(u)和u=g(x)，则复合函数y=f(g(x))的导数dy/dx等于dy/du乘以du/dx，即(dy/dx)=(dy/du)(du/dx)。

2.反函数法则如果函数y=f(x)的反函数存在，则反函数y=f^(-1)(x)的导数为1/f'(f^(-1)(x))。

3.乘积法则设函数y=u(x)v(x)，其中u(x)和v(x)是关于x的函数，则函数y的导数dy/dx等于u'(x)v(x)+u(x)v'(x)，即(dy/dx)=(u'(x)v(x))+(u(x)v'(x))。

4.商法则设函数y=u(x)/v(x)，其中u(x)和v(x)是关于x的函数，且v(x)不等于0，则函数y的导数dy/dx等于(u'(x)v(x)-u(x)v'(x))/(v(x))^2，即(dy/dx)=(u'(x)v(x)-u(x)v'(x))/(v(x))^25.幂函数法则设函数y=u(x)^n，其中u(x)是关于x的函数，n是常数，则函数y的导数dy/dx等于n(u(x))^n-1*u'(x)，即(dy/dx)=n(u(x))^n-1*u'(x)。

6.指数函数法则设函数y=a^u(x)，其中a是常数，u(x)是关于x的函数，则函数y的导数dy/dx等于a^u(x)ln(a)*u'(x)，即(dy/dx)=a^u(x)ln(a)*u'(x)。

7.对数函数法则设函数y=log_a(u(x))，其中a是常数，u(x)是关于x的函数，则函数y的导数dy/dx等于1/(u(x)ln(a))*u'(x)，即(dy/dx)=1/(u(x)ln(a))*u'(x)。

8.双曲函数法则设函数y=sinh(u(x))，其中u(x)是关于x的函数，则函数y的导数dy/dx等于u'(x)cosh(u(x))，即(dy/dx)=u'(x)cosh(u(x))。

与指数函数、对数函数有关的复合函数

2021-2022学年高一数学必修一第4章微专题5 与指数函数、对数函数有关的复合函数指数函数、对数函数有关的复合函数，主要是指数函数、对数函数与一次函数、二次函数复合成的新函数，求新函数的单调性、奇偶性、最值、值域等问题，一般采用换元思想，把复杂的复合函数化成简单的初等函数．一、判断复合函数的单调性例1 (1)函数2211()2x x f x --⎛⎫=⎪⎝⎭的单调增区间为________．答案 (－∞，1)解析令t ＝x 2－2x －1，所以函数t ＝x 2－2x －1在(－∞，1)上单调递减，在(1，＋∞)上单调递增．又y ＝⎝⎛⎭⎫12t 是R 上的减函数，故2211()2x x f x --⎛⎫= ⎪⎝⎭在(－∞，1)上单调递增，在(1，＋∞)上单调递减．(2)已知函数f (x )＝log a (a －a x )(a >1)，判断并证明f (x )的单调性．解 f (x )在(－∞，1)上为减函数，证明如下：由f (x )＝log a (a －a x )(a >1)，得a －a x >0，即x <1.所以f (x )的定义域为(－∞，1)．任取1>x 1>x 2，因为a >1，所以12x x a a a >>，所以120x xa a a a <<－－，所以12log l ())g (o x x a a a a a a <－－，即f (x 1)<f (x 2)，故f (x )在(－∞，1)上为减函数．反思感悟形如y ＝log a f (x )的函数单调性判断：首先要求定义域，当a >1时，y ＝log a f (x )的单调性与y ＝f (x )的单调性保持一致，当0<a <1时，y ＝log a f (x )的单调性与y ＝f (x )的单调性相反．二、已知复合函数单调性求参数范围例2 已知函数212log ()y x ax a =-+在区间(－∞，2)上是增函数，求实数a 的取值范围．考点对数函数的单调性题点由对数型复合函数的单调性求参数的取值范围解令g (x )＝x 2－ax ＋a ，g (x )在⎝⎛⎦⎤－∞，a 2上是减函数，∵0<12<1，∴12log ()y g x =是关于g (x )的减函数．而已知复合函数212log ()y x ax a =-+在区间(－∞，2)上是增函数，∴只要g (x )在(－∞，2)上单调递减，且g (x )>0在x ∈(－∞，2)上恒成立，即⎩⎪⎨⎪⎧ 2≤a 2，g (2)＝(2)2－2a ＋a ≥0，∴22≤a ≤2(2＋1)，故所求a 的取值范围是[22，22＋2]．三、求复合函数的值域例3 求下列函数的值域：(1)212x y －＝；(2)212log (32).y x x =+-解 (1)∵1－x 2≤1，∴212x －≤21＝2，∴0<y ≤2，故212x y －＝的值域为(0,2]．(2)设u ＝3＋2x －x 2＝－(x －1)2＋4≤4.∵u >0，∴0<u ≤4.又12log y u =在(0,4]上为减函数，∴2121lo lo g 4g 2,u =-≥∴212log (32)y x x =+-的值域为[－2，＋∞)．四、求复合函数的最值例4 求函数211221log log 52y x x ⎛⎫=-+ ⎪⎝⎭在区间[2,4]上的最大值和最小值．解因为2≤x ≤4，所以112212log 2log log 4,x ≥≥即－1≥12log x ≥－2.设12log t x =，则－2≤t ≤－1.所以y ＝t 2－12t ＋5，其图象的对称轴为直线t ＝14，所以当t ＝－2时，y max ＝10；当t ＝－1时，y min ＝132. 五、与复合函数有关的不等式问题例5 已知x ∈(－∞，－1]时，不等式(m 2－m )·4x －2x <0恒成立，求实数m 的取值范围．解原不等式变形为m 2－m <⎝⎛⎭⎫12x ，因为函数y ＝⎝⎛⎭⎫12x 在(－∞，－1]上是减函数．所以⎝⎛⎭⎫12x ≥⎝⎛⎭⎫12－1＝2，当x ∈(－∞，－1]时，m 2－m <⎝⎛⎭⎫12x 恒成立等价于m 2－m <2，结合f (m )＝m 2－m －2的图象解得－1<m <2.故实数m 的取值范围为(－1,2)．六、判断复合函数的奇偶性例6 函数f (x )＝lg(1＋x 2－x )，判断f (x )的奇偶性．解因为|x |≥x ，所以1＋x 2>x 2＝|x |≥x ，所以1＋x 2－x >0，所以f (x )的定义域为R ，又f (－x )＋f (x )＝lg(1＋x 2＋x )＋lg(1＋x 2－x )＝lg[(1＋x 2＋x )(1＋x 2－x )]＝lg(1＋x 2－x 2)＝lg 1＝0，所以f (－x )＝－f (x )，故f (x )为奇函数．。

指数函数比较大小及复合函数的单调性测试题(含答案)

指数函数比较大小及复合函数的单调性一、单选题(共8道，每道12分)1.已知实数a，b满足，则( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：指数函数单调性的应用2.设，则这三个数的大小关系是( )A.a>b>cB.b>a>cC.c>a>bD.a>c>b答案：C解题思路：试题难度：三颗星知识点：指数函数的图象与性质3.已知，这三个数的大小关系是( )A.b<a<cB.c<a<bC.a<b<cD.c<b<a答案：C解题思路：试题难度：三颗星知识点：指数函数的图象与性质4.设，那么( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：指数函数单调性的应用5.函数的单调递减区间是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：指数型复合函数的性质及应用6.若函数，满足，则的单调递减区间是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：指数型复合函数的性质及应用7.函数，在上的最大值和最小值之和是5，则a＝( )A. B.C.2D.4答案：C解题思路：试题难度：三颗星知识点：指数函数单调性的应用8.函数的单调递增区间与值域相同，则实数a的值是( )A.﹣2B.2C.﹣1D.1答案：B解题思路：试题难度：三颗星知识点：指数型复合函数的性质及应用。

指数和对数的复合函数的单调性、奇偶性、最值问题(主要内容)

青苗辅导1
21
例：求函数y
1 2
2x
4
1 2
x
+5的值域.
-，5
青苗辅导1
22
例：求函数y=22x -2x-1+1的最值，并求出相应的x的值
变题1：已知函数y=9x -2 3x +2，
x 1, 2,求函数的值域。
青苗辅导1
23
变题2：已知函数y=（1）x -（1）x +1的 42
定义域为3, 2,求函数的值域.
求实数c的取值范围；
（3）若方程f(x) c 3x在0,1上有唯一
实数解，求实青数苗辅导c1 的取值范围。 25
例：当x
2, 8时，求函数y
log2
x 2
log2
x 4
的最大值和最小值.
ymin
7 4 , ymax
2.
青苗辅导1
26
26.若 1 27
x
9，则f(x)=log3
x 27
log3 3x ( )
log1
x
6 log1 x 2.
3
3
答案：（1）递增区间为-，-1，递减区间为3，+；
（2）递增区间为
1 27
，+ ，递减区间为青苗辅导1
0，1 27
。14
例：函数y
1 2
2
x
+4
1 2
x
-1，+
+5的递减区间是_______.
青苗辅导1
15
例：已知函数f (x) loga(3 ax)在x 0, 2
（2）讨论f (x)的奇偶性
（3）求证f (x) 0