GT-2A航空重力仪精度评定
航空重力仪器、技术发展现状及趋势
航空重力仪器、技术发展现状和趋势引语测定地球重力场的传统方法是利用重力测量仪器进行绝对重力测量和相对重力测量。
绝对重力测量虽然能够得到很高精度的绝对重力值，但由于仪器体积庞大、设备复杂、对外界环境条件要求高、观测时间长、成本高等因素，其不宜在地面上进行大规模的采用。
近一百多年来，在地面进行重力测量的主要手段是采用相对重力测量，即通过测定未知点与重力已知点之间的重力值之差，从而得到未知点的绝对重力值。
与绝对重力测量相比，相对重力测量具有仪器体积小、设备简单、对外界环境要求低、测量时间短、成本费用低等优点，适于进行地面大规模的测量。
然而在一些条件恶劣、交通不便、无人居住以及陆海交界等区域进行地面重力测量时，不仅效率低下并且很难达到精度要求，甚至有些地区根本无法进行测量。
传统的地面重力测量无法进行测定占地球面积七成之多的海洋重力场，而船载重力测量技术的出现及逐步发展使开展大面积的海洋重力测量成为可能，然而其由于速度慢并且需要载体行驶在一个平均海面上，其仍是一种效率很低的重力测量手段。
令人振奋的是，卫星测高技术的出现和逐渐成熟很好地解决了获取高精度海洋重力场的问题。
一、航空重力测量基本原理航空重力测量按其复杂程度,可依次分为航空标量重力测量、航空矢量重力测量和航空梯度重力测量。
原理上它们均需解决两个基本问题:①运动状态下,在空中如何稳定传感器的指向? ②如何分离引力加速度和惯性加速度? 为此,一个航空重力测量系统必须包括如下三部分,即用于测量比力的加速度计(或重力仪,称之为重力传感器分系统)、使加速度计保持水平的系统(或计算其姿态,称为平台分系统)和测量飞机惯性加速度的定位分系统。
其中,第二分系统用于解决问题①,第一、第三分系统用于解决问题②。
依据所使用的重力传感器和平台分系统的不同,航空标量重力测量系统又可分为平台式、捷联式和旋转不变式。
平台式是将精密加速度计安装到稳定平台上,定向由稳定平台维持,如UCoset & Rombe飞航空重力仪采用的是两轴阻尼平台。
航空重力仪减振系统振动研究
航空重力仪减振系统振动研究屈进红;周锡华;姜作喜;王蓬;高维【摘要】航空重力减振系统是有效减弱机载环境下高频振动的主要途径，从而提高航空重力的测量精度。
因此，设计减振系统的首要问题是设定其合理的刚度、阻尼和质量等重要的特性参数。
笔者通过建立航空重力仪两种减振系统类型运动微分方程，经过理论和实例探讨了减振系统模型，旨在深入了解航空重力减振系统的减振规律，为其特性参数设计提供理论依据。
%The airborne gravity vibration reduction system is an effective way to attenuate high frequency vibration in the airborne envi⁃ronment,thus improving measurement accuracy of aviation gravity.Therefore,the primary problem in the design of the vibration reduction system is to set up such important parameters as reasonable stiffness,damping,and quality.The authors established differential equations of motion for two types of vibration reduction system of airborne gravimeter.With theoretical and investigate instances,the authors dis⁃cussed vibration reduction system model,with the purpose of in-depth understanding of the law of airborne gravity vibration reduction system and providing the necessary theoretical support for its parameter design.【期刊名称】《物探与化探》【年(卷),期】2016(040)004【总页数】7页(P831-837)【关键词】航空重力;高频振动;减振系统;微分方程【作者】屈进红;周锡华;姜作喜;王蓬;高维【作者单位】中国国土资源航空物探遥感中心，北京 100083; 国土资源部航空地球物理与遥感地质重点实验室，北京 100083;中国国土资源航空物探遥感中心，北京 100083; 国土资源部航空地球物理与遥感地质重点实验室，北京 100083;中国国土资源航空物探遥感中心，北京 100083; 国土资源部航空地球物理与遥感地质重点实验室，北京 100083;中国国土资源航空物探遥感中心，北京 100083; 国土资源部航空地球物理与遥感地质重点实验室，北京 100083;中国国土资源航空物探遥感中心，北京 100083【正文语种】中文【中图分类】P631机载环境下，由于飞机发动机等引起的高频扰动加速度往往是所测重力异常信号的成百上千倍，同时高频振动信号也会使导航解算误差增大，这些噪声单靠数字滤波是不能完全消除的[1]。
2-2物探评分标准—重力法
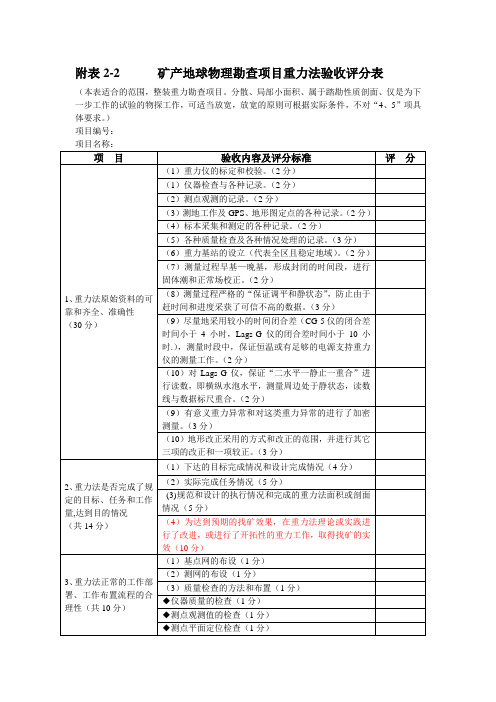
（1）提交的工作总结是否全面系统（10分）
（2）按“物化探规范”报告编写要求，逐条进行编写，如实地反映重力法取得的成果并与反映了地质现象或找矿信息。(2分)
（3）在重力法上，具有了开拓性的认识或在找矿上，对矿体有深入认识，或在其它方面有独到的建解（5）
（4）提出进一步工作建议，并具有前瞻性（5分）
（3）重力法异常的解释(共12分)
◆用重力法异常得到了矿化体或矿体的信息，或其它地质信息（2分）
◆把地质现象有机地与密度参数结合了，得到重力法找矿的信息（3分）
◆结合地质进行了综合研究和分析，是否解决重力法异常所反映的地质意义，或其它的找矿意义。(5分)
◆建立了本区的利用重力法找矿模式和标志（5分）
合计
重力法野外工作质量等级评分标准
优秀：100—90分良好：89—75分
及格：74—60分不及格：＜60分
质量评定等级
审查人签字：
年月日
专家组长签字：
年月日
注：本次验收过程中，若属于正常工作程序要达到的部分，最高达100分（黑的字），具有找矿意义或在找矿理论或实践中有深入认识的可达145分（红色字）。
（7）测量过程早基—晚基，形成封闭的时间段，进行固体潮和正常场校正。（2分）
（8）测量过程严格的“保证调平和静状态”，防止由于赶时间和进度采获了可信不高的数据。（3分）
（9）尽量地采用较小的时间闭合差（CG-5仪的闭合差时间小于4小时，Lags-G仪的闭合差时间小于10小时.），测量时段中，保证恒温或有足够的电源支持重力仪的测量工作。（2分）
（3）测点值及精度计算、仪器格值、一致性标定结果资料整理及精度计算等符合那级精度标准（2分）
多型航空重力仪同机测试及其数据分析
２ ０ １ ３年 ７月
海
洋
测
绘
Ｖｏ １ ＿ ３ ３． ＮＯ． ４ Ｊ ｕ１ ．。 ２ ０１ ３
ＨＹＤＲｏＧＲＡＰＨＩ Ｃ Ｓ ＵＲＶＥＹＩ ＮＧ ＡＮＤ ＣＨＡＲＴ Ｇ
Ｄ Ｏ Ｉ ： １ ０ ． ３ ９ ６ ９ ／ ｊ ． ｉ ｓ ｓ ｎ ． １ ６ ７ １ — ３ Ｏ ４ ４ ． ２ ０ １ ３ ． ０ ４ ． ０ ０ ２
转 向采用平 台式 惯导系统 的重力仪 ， Ｓ ａ ｎ ｄ ｅ ｒ 公 司现 已 拥有 ４套 Ａ Ｉ Ｒ Ｇ ｒ ａ ｖ航空重力仪 ， 我 国国土 资源航 空物
探遥感 中心 于 ２ ０ ０ ７年引进 了 Ｇ Ｔ 一 １ Ａ航 空重力 仪 ， 形
无 法 使 飞 机 垂 直 扰 动 加 速 度 的 测 定 精 度 优 于
不仅全过程测试了俄罗斯gt一1a航空重力仪和美国tagslrs158航空重力仪两型国际上最为经典的商用航空重力仪的运行性能全面掌握了两型重力仪的性能技术指标为引进国外航空重力测量装备选型提供了决策依据而且对国内自主研制的sgawz01捷联式航空重力仪gdp一1重力仪进行了全面检工程化提供了极有价值的试验评估条件
的Ｇ Ｄ Ｐ － １ 重力仪首次成功实现 了航空重力测量功能 ， 平差前测量精度为± ４ ． ５ ２ ｍ Ｇ ａ ｌ 。
关键词 ： 航空重力仪 ； 重复线 ； 测量精度 ； Ｇ Ｔ 一 １ Ａ； Ｔ Ａ Ｇ Ｓ ； Ｓ Ｇ Ａ — ＷＺ ０ １ ； Ｇ Ｄ Ｐ 一 １
中 图分 类号 ： Ｐ ２ ２ ３ ． ６ 文献标志码 ： Ａ 文章编号 ： １ ６ ７ １ — ３ ０ ４ ４ （ ２ ０ １ ３ ） ０ ４ — ０ ０ ０ ６ — ０ ６
航空重力测量内符合精度计算方法
收稿日期: 2010- 03- 23 基金项目: ∀ 863#计划重大项目课题 ( 2006AA 06A 202) 资助
5期
姜作喜等: 航空重力测量内符合精度计算方法
∃ 673∃
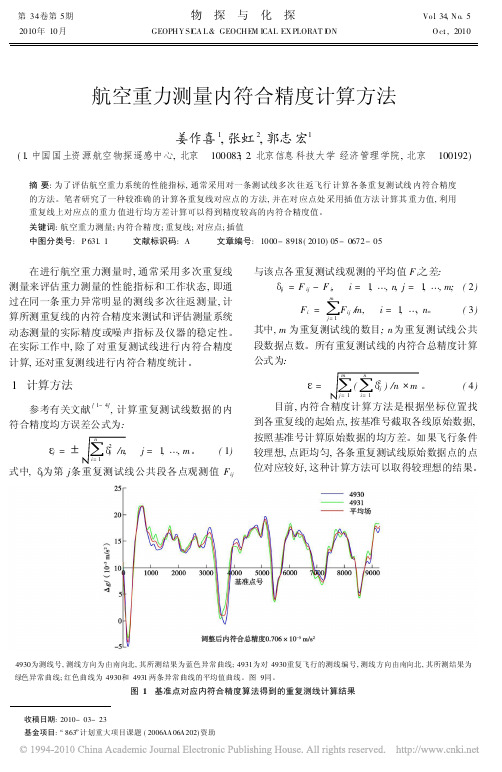
当飞行条件不理想时, 特别是飞行方向上风速较大 时, 飞机可能达不到正常状态下设定的飞行速度, 而 重力仪以固定频率采样, 将造成顺风飞行与逆风飞 行取样点距出现差异。当重复测试线间的平均取样 点距不同时, 基准号实际对应的是测线上不同位置 的点, 并不是真正位置上的对应点位, 这将使内符合 精度计算引入误差。航空重力飞行利用 GPS控制 在同一高度平飞, 高度变化控制在 5 m 之内, 重复 线内符合精度分析时可以不考虑高度的影响。图 1 所示为某测区内一条重复测线基准点对应内符合精 度计算所得到的结果, 由于前后两次飞行方向上风 速的不同, 两条曲线存在偏移。
摘 要: 为了评估航空重力系统的性能指标, 通常采用对一条测试线多次 往返飞行 计算各条重 复测试线 内符合精度 的方法。笔者研究了一种较准确 的计算各重复线对应点的 方法, 并在对 应点处 采用插 值方法 计算其 重力值, 利用 重复线上对应点的重力 值进行均方差计算可以得到精度较高的内符合精度值。
关键词: 航空重力测量; 内符合精 度; 重复线; 对应点; 插值
中图分类号: P 631. 1
文献标识码: A
文章编号: 1000- 8918( 2010) 05- 0672- 05
在进行航空重力测量时, 通常采用多次重复线 测量来评估重力测量的性能指标和工作状态, 即通 过在同一条重力异常明显的测线多次往返测量, 计 算所测重复线的内符合精度来测试和评估测量系统 动态测量的实际精度或噪声指标及仪器的稳定性。 在实际工作中, 除了对重复测试线进行内符合精度 计算, 还对重复测线进行内符合精度统计。
航空重力测量的分辨率和精度分析
举例
本次实验数据来源于大同航空重力测量.该实验区属 中等山区,范围1°40′×2°00′.测区东部地形起 伏较大,最高峰海拔2800m,西北部为丘陵,平均海拔 1000m,全区最大高差2100m,飞行高度上的重力异 常变化为 -50 ~ 80mGal.测区内已有高精度,高分辨 率的地面重力测量,向上延拓获得的参考值的精度优 于2.0mGal.飞行高度3400m的测线共30条,覆盖整个 实验区,相邻测线的间距5′.平均飞行速度360km/h.由 于飞行速度变化不大,此处侧重分析重力异常精度, 分辨率与所用低通滤波器的关系.
84070301班 84070301班 2008040703014 刘皓
本讲重点及摘要
航空重力测量分辨率与飞行高度的关系后， 表明对于300km/h的飞行速度和2.5km的飞行 高度在山区和平地可恢复的最小波长分辨率 分别为9km和14km，在此高度该频段重力异常 的衰减率约为50%.这里探讨了低通滤波器截 止频率对于航空重力测量沿线分辨率和精度 的影响，对于大同航空重力测量，滤波尺为 150.200.250s时.沿线半波长分辨率分别为 7.5，10和12.5km.
总结
航空重力测量可用于获取中高频的地球重力场信息,其实际可 获得的分辨率与飞行高度、飞行速度、低通滤波器的截止频 率等有关,其所能达到的精度除取决于测量环境因素（如大气 湍流等）外,还与所用的低通滤波器进而与其沿线空间分辨率 密切相关.分析表明,对于2.5km的飞行高度和300km/h的飞行 速度,可获得满足大地测量应用要求的分辨率(如9km),若降低 飞行高度和飞行速度,可进一步提高分辨率.实际数据处理时, 采用不同的滤波器截止频率,交叉点重力异常不符值的中误差 （内部精度）是随之而变的,根据这种变化特性以及所需的分 辨率和精度，可确定合适的滤波器截止频率．如对大同航空 重力测量的基本要求是测定5′×5′网格平均重力异常的精度 为5~7mGal,此时选用200s的滤波尺度（截止频率0.005Hz） 是合适的．
相关性分析在GT航空重力仪零漂改正中的应用
相关性分析在GT航空重力仪零漂改正中的应用屈进红;郭素然;周锡华;姜作喜;刘乾坤【摘要】In airborne gravimeter and ground gravimeter measurement unit,there often occur drift phenomena.If this drift is regarded as a linear relationship,the first and last data are used to do drift correction process.Nevertheless,the airborne gravimeter structure is com⁃plex,and the sensor drift is caused by many factors,with the most critical factor being the environment temperature change disturbance. It is impossible for us to avoid airborne gravity dramatic changes in the temperature difference of flight measurement between summer and winter.The authors used the airborne gravimeter static data as an example.First,the data need gravity tide correction and drift cor⁃rection by using a least squaresmethod.Secondly,correlation analysis is used to analyze the static data and instrument thermostatic tem⁃perature to obtain a strong correlation characteristics.Finally,linear regression equation is set up to calculate the static data and,as a re⁃sult,the gravity of the final corrected precision is greatly improved.This correlation analysis method has practical significance for the in⁃depth understanding of sensor drift correction methods and pre⁃study of dynamic measurement data in the drift correction.%航空重力仪测量传感器和地面重力仪测量单元类似，往往存在零点漂移现象，通常把这种漂移视为线性关系，用前、后校数据做零漂改正处理。
DGP S在航空重力测量中的应用
DGP S在航空重力测量中的应用罗锋;李冰;姜作喜;屈进红;王志博【摘要】基于DGPS在GT⁃1A型航空重力系统测量中的应用，针对GPS基站的位置精度和选择展开探讨，并对计算获得的空间重力异常结果进行对比分析。
对比结果表明GPS基站所用位置值不同会引起测线空间重力异常的水平误差，相同测线经过水平调整后基本保持一致。
GPS基站和移动站的距离长短对测线空间重力异常的局部细节幅值有影响，进行水平调整后相同测线间的内符合总精度为0．3 mGal左右。
%Based on the application of DGPS in GT⁃1A airborne gravity measurement system, the authors discussed the selection and precision of GPS stations, and analyzed a variety of calculated free air anomaly results in detail. The final results indicate that the dif⁃ferent values of GPS basic station position induces the horizontal error of free air anomaly on survey lines, and the results on the same survey line can almost reach the same precision after horizontal adjustments. In addition, the distances between GPS basic stations and rover stations have impacts on the locally detailed amplitudes of free air anomaly. After horizontal adjustments, the internal accord accu⁃racy on the same survey line can reach almost 0.3.【期刊名称】《物探与化探》【年(卷),期】2014(000)006【总页数】7页(P1212-1217,1221)【关键词】航空重力;DGPS;基站;移动站【作者】罗锋;李冰;姜作喜;屈进红;王志博【作者单位】中国国土资源航空物探遥感中心，北京 100083;中国国土资源航空物探遥感中心，北京 100083;中国国土资源航空物探遥感中心，北京 100083;中国国土资源航空物探遥感中心，北京 100083;中国国土资源航空物探遥感中心，北京 100083【正文语种】中文【中图分类】P631航空重力测量是以飞机为载体，搭载重力仪、GPS(global positioning system)和测高等设备测定近地空间重力加速度的测量方法。
高精度航空重力测量系统分项指标设计分析
高精度航空重力测量系统分项指标设计分析张虹;屈进红;姜作喜;王萌;李行素【摘要】为研制高精度航空重力仪,开展了高精度航空重力仪分项指标设计与分析,为高精度航空重力测量系统设计提供依据.笔者基于航空重力测量的数学模型,归纳出影响航空重力测量的主要因素;结合航空重力测量的相关理论公式,使用理论模型,推导出各影响因素的误差模型;开展了各项误差的分析研究,并通过设定合理的分项指标精度来有效地控制分项误差,确保航空重力测量精度优于0.6×10-5 m/s2.【期刊名称】《物探与化探》【年(卷),期】2019(043)002【总页数】7页(P408-414)【关键词】高精度航空重力仪;误差模型;各项误差分析;分项指标精度【作者】张虹;屈进红;姜作喜;王萌;李行素【作者单位】北京信息科技大学信息管理学院,北京 100192;自然资源部航空地球物理与遥感地质重点实验室,北京 100083;中国自然资源航空物探遥感中心,北京100083;自然资源部航空地球物理与遥感地质重点实验室,北京 100083;中国自然资源航空物探遥感中心,北京 100083;中国自然资源航空物探遥感中心,北京100083;自然资源部航空地球物理与遥感地质重点实验室,北京 100083;中国自然资源航空物探遥感中心,北京 100083【正文语种】中文【中图分类】P6310 引言早期航空重力测量技术主要是发达国家来研究和应用。
1958年，美国空军进行了第一次航空重力测量试验，直到20世纪90年代以来，随着GPS、INS技术及高灵敏度、高稳定度重力仪器的发展及应用，使航空重力测量的研究与应用取得了突破性进展[1-2]。
21世纪初，相继研制出二轴惯性稳定平台型、三轴惯性稳定平台型和捷联式航空重力仪试验样机，便逐步形成实用化的航空重力仪。
其中三轴惯性稳定平台型航空重力仪的测量精度最高，测量精度达到0.6×10-5 m/s2，开始了大规模的商业应用[3-5]。
航空重力测量在近海区域的精度评估与分析
航空重力测量在近海区域的精度评估与分析翟振和;孙中苗;李迎春;肖云【摘要】利用泊松积分法和点质量法对澳大利亚West Arnhem Land区域的航空重力测量数据进行了精度评估，两种方法得到精度结果基本一致，评估结果表明GT‐1A测量系统2′分辨率数据的测量精度优于3×10－5 m／s2，5′分辨率数据的测量精度优于2×10－5 m／s2。
利用交叉点平差和泊松积分法、点质量法对渤海区域的航空重力测量进行了内部交叉点平差和外部精度评估，结果表明，内部评估精度与外部评估精度存在一定的差异，以外部评估为准则，CHAGS测量系统在渤海区域5′分辨率的航空重力数据精度优于35．×10－5 m／s2。
综合国内外试验情况分析得到，在近海区域，航空重力数据的分辨率和精度受测量仪器的性能而不同，整体上对于5′分辨率数据而言，可以达到或优于3×10－5 m／s2的精度。
%The two methods including Poisson integral and point masses are used to evaluate the accuracy of airborne gravimetry data in Australia West ArnhemLand.Theresults show that the accuracy of Australia airborne gravimetry data are respectively 2 8.1 × 10-5 m/s2 and 2 9.5 × 10-5 m/s2 according to the 2′resolu‐tion ,and the accuracy of 5′resolution is better than 3 × 10-5 m/s2 .The Bohai airborne gravimetry using CHAGS system is evaluated by using the crossover point adjustment and Poisson integral method , the analysis results show that the two estimation modes has different accuracy value .Based on the external l and and sea gravitydata ,the Bohai airborne gravimetry has the accuracy better than 3 5. × 10-5 m/s2 according to the 5′resolution although the data has the 3 × 10-5 m/s2 systematic error .In the coastal area , the accuracy of airbornegravimetry is affected by the performance of surveying system ,and the general accuracy of airborne gravimetry is about or better than 3 × 10-5 m/s2 according to the 5′resolution .【期刊名称】《测绘学报》【年(卷),期】2015(000)001【总页数】5页(P1-5)【关键词】航空重力测量;泊松积分;点质量模型;精度评估【作者】翟振和;孙中苗;李迎春;肖云【作者单位】信息工程大学地理空间信息学院，河南郑州450052; 西安测绘研究所，陕西西安710054;西安测绘研究所，陕西西安710054;西安测绘研究所，陕西西安710054;西安测绘研究所，陕西西安710054【正文语种】中文【中图分类】P22831 引言航空重力测量是获取局部区域重力场信息的有效手段，其测量效率高、精度均匀，分辨率较高，我国于2002年自行成功研发了航空重力测量系统（CHAGS），并相继在大同、哈尔滨等试验中获得了较好的测量结果［1］。
航空重力测量的精度评估
航空重力测量的精度评估
孙中苗;元宝莹;翟振和
【期刊名称】《测绘科学与工程》
【年(卷),期】2013(033)002
【摘要】精度评估是航空重力测量的一项重要内容，可分为内符合精度和外符合
精度两类，即基于交叉点不符值评估单个采样点观测值的内符合精度和基于外部重力参考数据评估格网平均重力异常的外符合精度。
由于许多测区没有或少有外部参考重力数据，因此，为了合理评估格网平均重力异常的（内符合）精度，本文引入了所谓的“重叠格网比较法”。
四个区域的实测航空重力测量数据分析表明，交叉点不符值的加权估计精度、重叠格网比较精度与外符合精度之间具有较好的一致性，实用中可视情况采用这三种方法评估航空重力测量的精度。
【总页数】5页(P6-10)
【作者】孙中苗;元宝莹;翟振和
【作者单位】
【正文语种】中文
【中图分类】P223
【相关文献】
1.航空重力测量在近海区域的精度评估与分析 [J], 翟振和;孙中苗;李迎春;肖云
2.澳大利亚近海区域航空重力测量数据精度评估 [J], 翟振和;孙中苗;江东
3.航空重力测量技术及应用研究 [J], 刘站科
4.航空重力测量中垂直加速度改正的固定区间平滑算法研究 [J], 郑崴;魏辉;陈学锋;闫雷兵
5.航空重力测量中垂直加速度改正的固定区间平滑算法研究 [J], 郑崴;魏辉;陈学锋;闫雷兵
因版权原因，仅展示原文概要，查看原文内容请购买。
国外航空重力测量与数据处理技术最新进展
国外航空重力测量与数据处理技术最新进展张虹; 周能; 邓肖丹; 王萌; 李行素【期刊名称】《《物探与化探》》【年(卷),期】2019(043)005【总页数】8页(P1015-1022)【关键词】航空重力; 测量方法; 数据处理技术【作者】张虹; 周能; 邓肖丹; 王萌; 李行素【作者单位】北京信息科技大学信息管理学院北京100192; 北京越音速科技有限公司北京 100192; 自然资源部航空地球物理与遥感地质重点实验室北京 100083【正文语种】中文【中图分类】P6310 引言航空重力测量技术作为一种新兴的勘查技术，在近10年内得到迅速发展，尤其是西方发达国家[1]。
国外航空重力测量主要使用加拿大SGL公司(sander geophysics limited)的AIRGrav、俄罗斯GT(gravimeter technologies ltd)公司的GT-1A/2A航空重力测量系统，利用中小型的固定翼飞机、直升机等集成了航空重力、航空重(磁)和航空重(磁、放)等多种形式的勘查系统，测量参数也由单一的重力测量发展为重(磁)、重(磁、放)等综合测量，测量效率明显提高。
每年航空重力勘查任务大约30～40万测线公里，主要用于基础地质研究、石油天然气调查、大地水准面测量、区域地球物理勘探、矿产资源勘查和军事基础建设等工作，应用前景广泛，成果十分显著，对地球重力场研究做出了重大的贡献。
国外开展航空重力测量先于我国，大规模高精度航空重力测量始于21世纪初[1-2]。
经过近20年的快速发展，已经形成了成熟的航空重力勘查系统集成技术及基于地球物理测量的通用航空重力测量方法和数据处理技术，推动了航空重力测量技术的进步和事业的发展。
笔者系统总结和研究了国外航空重力勘查系统集成、测量方法和数据处理等3个方面的方法技术，向读者详细介绍了该领域国外发展的最新技术，供借鉴和进一步研究，以此来促进我国航空重力测量技术的快速发展，赶超国外先进水平，为地球系统科学研究提供高精度的基础数据。
航空重力梯度测量飞行姿态影响及误差校正
航空重力梯度测量飞行姿态影响及误差校正王泰涵;肖锋;袁园;周文月【摘要】在石油和金属矿勘探中,相对于重力异常数据,航空重力梯度数据含有更多的高频信号成分,能更好的描述小的异常特征.为了得到地下异常体的真实重力梯度数据,需要全张量梯度测量数据中有效地去除飞机自身梯度值的影响.针对这一影响,提出线性的校正方法.考虑飞行姿态的改变引起的空间坐标系的变化,在校正过程中给出旋转矩阵和张量转换矩阵来实现坐标系的统一.通过模型实验分析了自身梯度值随姿态角变化情况,用实际梯度数据计算证明了该方法能够减小几个E的姿态误差,有效提高数据的精度.【期刊名称】《世界地质》【年(卷),期】2014(033)003【总页数】7页(P680-686)【关键词】航空重力梯度测量;飞行姿态;旋转矩阵;张量转换;自身梯度值【作者】王泰涵;肖锋;袁园;周文月【作者单位】吉林大学地球探测科学与技术学院,长春130026;吉林大学地球探测科学与技术学院,长春130026;吉林大学地球探测科学与技术学院,长春130026;吉林大学地球探测科学与技术学院,长春130026【正文语种】中文【中图分类】P631.1250 引言航空重力测量是利用机载重力仪、定位传感器组合系统进行空中重力测量，能够迅速获取较大范围的重力场信息，其基本原理是从机载重力仪测得比力① 厄(E)为非法定计量单位，1E=10－9S－2加速度中分离各种扰动加速度[1]，解算出采样点的加速度值。
航空重力测量较地面重力测量具有速度快、效率高、不受测区条件限制和地形起伏影响等优点。
与航空重力测量相比，航空全张量重力梯度测量除具有以上的优点外，还可以测量引力位的二阶导数，即重力全部梯度张量(Full Tensor Gravity Gradient)。
重力梯度能够准确地测量出由于地下密度变化引起的重力值的微弱变化，相比测得的重力异常具有更高的分辨率，能提高地质解释的准确性[2]。
近些年来，航空重力梯度测量也逐渐应用于军事、大地测量和地球物理勘探等领域[3--5]。
航空重力测量技术的现状
航空重力测量技术及其运用探析摘要：随着我国国民经济的快速发展,矿产资源需求与保障能力之间的矛盾日益突出,金属矿勘查已成为当前地质工作的重要任务。
找矿深度的不断增加,使得找矿难度也随之加大,这就为地球物理勘查技术提供了发展空间。
本文对高精度航空重力测量技术进行了总结,较为全面地阐述了这些方法技术的研究及应用现状。
这些方法技术是当前矿产勘查有效的地球物理方法技术,或是近年来研发的新方法、新技术,在新一轮的矿产勘查中具有广阔的应用前景。
航空重力测量技术是一种新型的高科技技术，虽然还没有完全的成熟，但是已经被广大的国家所重视和应用，它的主要贡献是针对地球的地貌特征等对地球的各地域及各领域进行重力的测量，在许多发达国家和发展中国家的应用越来越广泛和活跃，继而成为地球的重力研究最热门的技术，对地球的重力领域做出了重大的贡献。
回顾航空重力测量技术的发展历程能够让我们看到航空重力测量技术在这个世界上呈现的与众不同的发展趋势。
关键词：航空重力；测量技术；运用；地球物理；勘探应用引言：航空重力测量技术以其自身的优势在短时期内一跃成为地球重力领域所重视的佼佼者，我们看到了航空重力测量技术在地球的应用，也看到了这个领域的光明的前景，那么航空重力测量技术是怎么来的呢？下文就讲述了航空重力测量技术的概念、航空重力测量技术的不同的方法及原理、航空重力测量技术的广泛应用以及列举了航空重力测量技术在北极和南极地区的应用分析。
一、航空重力测量技术的概念航空重力测量技术是一种用来测量在异常情况下的接近地的天空的重力技术，是一种用飞机做载体，并且将GPS、激光、计算机、重力传感器、无线电、INS等技术集合于一体的重力测量方法。
航空重力测量技术是一种新的技术，是1958年在美国开始的一种技术，后来陆续被一些国家所重视，俄罗斯等不少国家的航空机构开始进行航空重力侧量技术的实验，并且由于技术的不断发展，航空重力测量也有了重大的突破，为国家和整个世界的航空事业做出巨大的贡献。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
GT-2A航空重力仪精度评定宛家宽;罗志才;刘站科【摘要】选择地形平坦的实验区A和地形起伏较大的实验区B,采用GT-2A航空重力测量数据和高精度地面重力测量数据,依据测线网交叉点平差方法评定GT-2A 航空重力仪的内符合精度,通过地面重力与航空重力延拓结果的比对实验评定其外符合精度.结果表明,GT-2A重力扰动测量结果的内符合精度优于1 mGal,外符合精度在实验区A优于2 mGal,在实验区B优于3 mGal.%Our research is based on the airborne gravity data from GT-2A gravimeter and the high-precision ground gravity data collected in two areas,marked as A,which is flat,and B,which is steep.We calculate the internal precision of GT-2A gravimeter by network crossover adjustment,and evaluate its external precision by comparing the continuation results of airborne and ground gravity data.The results show that the inner precision of GT-2A gravimeter is less than 1 mGal,while its external precision is less than 2 mGal in zone A,and 3 mGal in zone B.【期刊名称】《大地测量与地球动力学》【年(卷),期】2017(037)010【总页数】5页(P1096-1100)【关键词】GT-2A航空重力仪;重力扰动;精度评定;重力延拓;交叉点平差【作者】宛家宽;罗志才;刘站科【作者单位】武汉大学测绘学院,武汉市珞喻路129号,430079;武汉大学测绘学院,武汉市珞喻路129号,430079;武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079;武汉大学测绘学院,武汉市珞喻路129号,430079;国家测绘地理信息局第一大地测量队,西安市测绘路4号,710054【正文语种】中文【中图分类】P223相比于卫星重力测量，航空重力测量空间分辨率更高，具备恢复重力场中短波信号的能力；相比于地面重力测量，航空重力测量具有高效率、低成本的优势，不受地面环境影响，在高山和荒漠地区也可以获取空间分布均匀的重力观测资料[1-3]。
GT-2A航空重力仪在GT-1A的基础上将测量动态范围由±500 Gal提高到了±1 000 Gal，能够适用于更复杂的测量环境。
欧阳永忠等[4]的同机测试实验表明，相比于TAGS、WZ01和GDP-1三种型号的航空重力仪，GT-1A具有更好的综合性能技术指标。
Wooldrigde[5]通过对重复测线的数据分析发现，GT-1A获取的2 km分辨率重力测量结果的精度优于1 mGal。
之后他又通过对200 000 km航线上GT-1A重力观测值100 s滤波结果进行统计得出，由交叉点数据计算的测量精度为0.67 mGal，由重复测线数据计算的测量精度为0.70 mGal[6]。
Olson [7]的研究表明，GT-2A与GT-1A的观测精度一致，且均优于AIR-Grav重力仪，在山谷地带进行的GT-1A和GT-2A同机测试实验中，有195个观测数据超出GT-1A 的量程而无法记录，GT-2A却没有出现记录中断的情况。
2015年国家测绘地理信息局第一大地测量队采用引进的国内首台GT-2A航空重力仪在两个实验区实施了航空重力测量，同时在实验区地面布网，进行高精度的重力测量。
本文基于两个实验区的航空重力和地面重力测量结果，评定GT-2A航空重力仪的内符合和外符合精度，为GT-2A航空重力仪在全国开展基础性航空重力测量业务提供技术指标的制定依据。
1.1 航空重力数据归算航空重力数据归算包括将测线上的重力观测值归算到平均高程面上，然后进行测线网平差，并且格网化，具体方法见文献[8]。
本文不同之处在于采用整体网平差法取代文献[8]中的两步平差法进行测线网平差，整体网平差法的具体实施见文献[9]。
主副测线交叉点不符值主要由传感器测量误差等低频误差引起[9]。
本文假设这些误差为观测时间的线性函数，则第i条测线上第j个测点的观测误差可以表示为：式中，vi,j为观测误差，ti,j为由测线i第一个观测历元起算的第j个测点的观测时间， ai、bi为系统误差参数，Δi,j为随机误差。
假设第i条测线上的第j个测点与第k条测线上第p个测点重合形成交叉点，交叉点不符值可以表示为：写成矩阵形式为：式中测线网平差属于秩亏网平差，本文采用L曲线法确定正则化参数α，依据最小二乘准则求解系统误差参数，即式中，I为单位阵。
1.2 重力扰动延拓采用泊松积分法实现重力扰动延拓。
对于球外的调和函数，可以利用泊松积分由球面上的函数值计算球外任意一点的函数值，即式中，Vr和VR分别为球外和球面上的调和函数，R为球半径，r为球心与计算点的距离，l为球上面元dΩ到计算点的距离。
重力扰动是地球外部的调和函数，可以采用泊松积分实现重力扰动向上延拓。
利用泊松积分将地面重力数据向上延拓到航空重力数据归算结果所在格网点上，实现航空重力与地面重力测量结果的比较。
另一种方法是将航空重力测量得到的空中重力扰动向下延拓到地面重力观测点上进行比较。
本文采用泊松积分迭代法先将空中重力扰动延拓到大地水准面，再向上延拓到地面重力数据观测点处。
泊松积分迭代法具体实施可参考文献[10-12]。
将空中重力扰动延拓到大地水准面上时，为了使重力扰动在大地水准面外满足泊松积分条件，需要先移除出大地水准面外的地形质量，计算得到地面重力扰动后，再恢复大地水准面外地形质量的影响。
本文采用SRTM3地形模型和线质量模型[13]计算大地水准面外地形质量对重力扰动的影响：式中为地形对重力扰动的影响，G为引力常数，(xp,yp,zp)为计算点坐标。
利用数字地形模型进行数值计算时，将地形划分为多个棱柱形质量块， xi、yi分别为质量块i的底面中心位置，ΔxiΔyi为质量块i的底面积，hi为地形模型中提取的质量块i的高程，ρ取地壳平均密度2.67 g/cm3。
另外，在利用泊松积分向上延拓时，将积分区域划分为近区和远区，近区贡献可以采用重力观测资料进行数值积分计算，远区贡献则采用重力位模型计算。
泊松积分的远区贡献计算公式为：式中，V为调和函数，Vn(Ω)为计算点Ω处V的第n阶分量，V代表重力扰动时，可以由重力位模型计算Vn(Ω)；N为截断阶数，其选取可参考文献[14]；Qn(ψ0)为泊松截断系数，ψ0为近区半径。
Qn(ψ0)的逼近公式为[15]：式中，H为延拓高度，Pn(cos)为勒让德多项式。
2.1 实验数据说明采用A、B两个测区的航空重力实测数据和对应的地面重力观测数据对GT-2A的精度进行评定。
A区属于荒漠地区，地形起伏平缓；B区为山地，地形起伏较大。
表1为测区内SRTM3数据的统计结果(单位m)。
空中作业范围约为1°×0.5°，东西向测线与南北向测线交叉，飞行速度约为80m/s，数据处理中空中重力扰动结果经过100 s低通滤波，相邻测线间隔约5 km，即空中重力扰动的空间分辨率为4～5 km。
同时采用相对重力仪采集测区内的地面重力数据，在A区布设间隔为5 km的规则重力观测网点；B区受到地形限制，地面重力观测点沿公路布设，分布不均匀。
两个测区在实施地面重力测量时都进行了二等重力联测，结果表明，地面重力观测结果的精度优于0.07 mGal，远高于航空重力测量的精度。
空中和地面重力数据的空间分布见1，图中灰色线为飞机航线，即空中测量结果的分布情况，黑色圆点为地面重力观测点。
2.2 内符合精度采用南北向与东西向测线交叉点处的重力扰动观测结果评定GT-2A的内符合精度。
分别计算测线网平差前与平差后的交叉点不符值，其分布见图2和图3，统计结果见表2(单位mGal)。
从表2可以看出，平差前A区交叉点不符值的标准差为±1.70 mGal，B区交叉点不符值的标准差为±2.29 mGal；平差后A区交叉点不符值的标准差为±1.39 mGal，B区交叉点不符值的标准差为±1.25 mGal。
根据误差传播定律，将交叉点不符值标准差的1/视为观测数据的内符合精度。
平差后，A区空中重力扰动数据的内符合精度为0.98 mGal，B区空中重力扰动数据的内符合精度为0.88 mGal。
从图3可知，平差后B区交叉点不符值更接近于正态分布。
B区交叉点数量为410个，A区交叉点数量为331个，B区交叉点更多，统计结果更接近于真实精度。
而A区由于交叉点较少，统计结果容易受到个别较大不符值的影响，这可能是导致A区交叉点统计精度比B区略低的原因。
总体而言，GT-2A航空重力仪的内符合精度优于1.0 mGal。
2.3 外符合精度采用精度较高的地面重力数据评定GT-2A的外符合精度，主要工作在于将两类数据延拓到相同的位置进行比较。
对于A区，由于地面重力数据分布均匀且超出空中作业范围，可以将地面重力扰动延拓到空中数据归算后所在格网点上进行比较，也可以将空中重力扰动延拓到地面重力观测点上进行比较；对于B区，由于地面重力数据较少且分布不均匀，只能将空中重力扰动延拓到地面重力观测点上进行比较。
在延拓过程中，为了减弱边缘效应的影响，采用EGM08重力场模型填充重力扰动数据，使得原有测区向外扩展30′。
A区地面重力扰动数据向上延拓到空中格网点，与空中重力扰动观测结果的差值见图4。
A区和B区的空中重力扰动数据分别向下延拓到地面，与地面重力扰动观测结果的差值分别见图5和图6。
表3给出了3项比对实验的差值统计结果(单位mGal)。
表3的统计结果表明，无论是采用向上延拓还是向下延拓的方式进行比较，A区差值标准差均为±1.66 mGal；B区采用向下延拓的方式进行比较，差值标准差为±2.83 mGal。
由于地面重力测量结果的精度远远高于航空重力测量，所以在不考虑格网化和延拓等数据处理过程引入的误差时，此处的差值标准差可以直接代表航空重力测量获取的空中重力扰动的外符合精度。
GT-2A航空重力测量结果在A、B测区的内符合精度一致，均优于1 mGal。
用地面重力观测结果评定的外符合精度存在差异，在A区为1.66 mGal，在B区为2.83 mGal。