矩形截面偏心受压构件计算解析
偏心受压构件计算方法

非对称配筋矩形截面偏心受压构件正截面承载力设计与复核1大小偏心的判别当e < h o时,属于小偏心受压。
时,可暂先按大偏心受压计算,若b,再改用小偏心受压计算2、大偏心受压正截面承载力设计1).求A s和A,令b,(HRB33歐,b 0.55; HRB40C级,b 0.52)2Ne i f c bh o b(1 0.5 b)A s REf y(h o a)(混规,f y2).求A sA s A si A s2 A S3(0)若 b 按照大偏心(1)若 b cy 2 i bA ;Ne i f c bh o2 (1 /2)f y(h o a )i f c bh o b NA s 主A s f y适用条件: A s/bh > min,且不小于f t / f y ;A;/ bh > min 0如果 x<2a/,A s N(e h/2 a') f y (h o a/)适用条件:A;/ bh > min,且不小于f t/f y ;A;/bh > min 0 3、小偏心受压正截面承载力设计如果s QA s min bh 再重新求,再计算A s(2)若 h/ h oNe i f c bh(h 。
h )2f y (h o a)然后计算和A sN(h/2 e Q e a a 7)1 f cbh(h/2 a 7) f y (h o a )情况(2)和(3)验算反向破坏。
4、偏心受压正截面承载力复核1).已知N ,求M 或仓。
先根据大偏心受压计算出X : (1)如果 x 2a / ,⑵ 如果2a / x b h 。
,由大偏心受压求e ,再求e 0 ⑶若 b ,可由小偏心受压计算 。
再求e 、e o2).已知e o ,求N 先根据大偏心受压计算出x (1) 如果 X 2a /,(2) 若2a / x b h o ,由大偏心受压求N 。
(3) 若x> b h o ,可由小偏心受压求N 。
完整版矩形截面偏心受压构件正截面的承载力计算
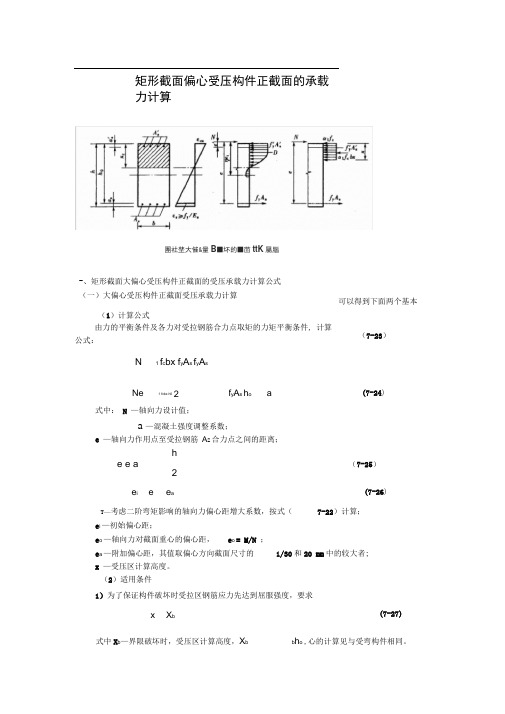
矩形截面偏心受压构件正截面的承载力计算-、矩形截面大偏心受压构件正截面的受压承载力计算公式(一)大偏心受压构件正截面受压承载力计算(1)计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件, 计算公式:N 1 f c bx f y A s f y A s式中:N —轴向力设计值;a —混凝土强度调整系数;e —轴向力作用点至受拉钢筋A S合力点之间的距离;he e a (7-25)2e i e°e aT—考虑二阶弯矩影响的轴向力偏心距增大系数,按式(7-22)计算;e i —初始偏心距;e o —轴向力对截面重心的偏心距,e o = M/N ;e a —附加偏心距,其值取偏心方向截面尺寸的1/30和20 mm中的较大者;x —受压区计算高度。
(2)适用条件1)为了保证构件破坏时受拉区钢筋应力先达到屈服强度,要求x X b式中X b—界限破坏时,受压区计算高度,X b b h o ,心的计算见与受弯构件相同。
Ne 1 fcbx h02 f y A s h o a (7-24)可以得到下面两个基本(7-23)(7-26)(7-27)團社埜大催&量B■坏的■茴ttK屬腦2)为了保证构件破坏时,受压钢筋应力能达到屈服强度,和双筋受弯构件相同,要求满足:x 2a式中a'—纵向受压钢筋合力点至受压区边缘的距离。
(二)小偏心受压构件正截面受压承载力计算(1)计算公式根据力的平衡条件及力矩平衡条件可得式中x —受压区计算高度,当x> h,在计算时,取x= h;os —钢筋As的应力值,可根据截面应变保持平面的假定计算,亦可近似取:(7-28)N i f c bx f y A s s A sxNe 1 f c bx h02f y A s h o a sNe' i f c bx | ass A s h0 a s(7-29)(7-30)(7-小備心5E压计算图解(■M虚拉不思■加儿豎氐F腑IMG儿曼压屈要求满足:x b —界限破坏时受压区计算高度,X bb ho ;X b /h o ;e 、e '‘一分别为轴向力作用点至受拉钢筋A 合力点和受压钢筋 A’合力点之间的距离(2)对于小偏心受压构件当 N f c bh 时,除按上述式(7-30)和式(7-31)或式(7-32)计算外,还应满足下列条件:式中h o —钢筋A s 合力点至离纵向较远一侧边缘的距离,即 h o h a s 。
钢筋混凝土矩形空心截面偏心受压构件正截面承载力计算

以给出其正截面承载力计算公式及其适用情况。
1 基本假 定
直线插入法求得 ; h; 。 ——第 i 层纵向钢筋截面重心至受压较大边 边缘的距离 ;
截面受压区高度。 2 计算公式及适用情况 矩形空心截面按 中性轴位置不 同, 可分为以下
四种 情况 :
在试验研究的基础上, 公桥规》 《 引入下列基本
假定作为钢筋混凝土偏心受压构件正截面承载力计
算 的基 础 :
①构件截面变形符合平截面假设 ; ②在极 限状态下 , 受压混凝土应力达到混凝土
抗压强度设计值 , 并取矩形应力 图计算, 矩形应 力图的高度为 X 受压较大边钢筋的应力取钢筋抗 ; 压强度设计值 ;
— —
・ 9・ 5
公式应满足下列条件 :  ̄2 x a > 。
偏 心 距 增 大 系 数 , 公 式 =1+ 按
若不满足上述 条件 , 则取 x 2 , ∑M = =a 由 0
得构件的正截面承载力计算公式为: Ne ≤ d 。 A ( 0 a ) 。H 一 。
A。 。 。 一叮A () 5
由 M. 0  ̄ d ≤ xh一 +c ; = 得:o e b(o 寺) f N d
L,
( _ ) t h 一 ) A 。h 一 b b h (0 + f 。 a) ( 。
关 键词 矩 形 空心截 面 偏心 受压 承 载力
f ≤ 叮 ≤ fd “ i
近年来 , 随着我 国公路建设 和交通事业 的迅速
一
叮 ——第 i 层纵向钢筋的应力, 按公式计算为 发展, 跨越江河湖海和深山峡谷的大跨 、 高架桥愈来 式中 : 愈多。这种桥的桥墩 由于身高、 截面尺寸大, 多采用 正值表示拉应力 , 负值表示压应力 ; 空心截面, 以节省材料, 降低 自 , 重 增大高墩的柔性 。 8 ——截面非均匀受压时 , 混凝 土的极 限压应 如作为“ 世界第三 、 中国第一” 的润扬大桥 的桥墩 即 为矩形空心截面。由受力分析知 , 矩形空心截面偏 变, 当混凝 土强 度等级 为 C 0及 以下时, 8 = 5 取
第七章 偏心受压构件的强度计算
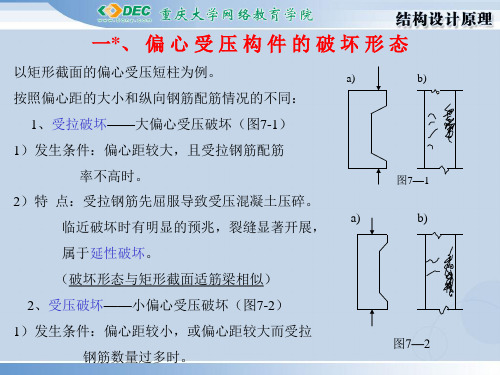
影响,各截面所受的弯矩不再是Ne0,而
变成N(e0+y)见图(7-4)所示,y为构件 任意点的水平侧向挠度。在柱高度中心处,
y
N
侧向挠度最大,截面上的弯矩为N(e0+f)。
一般,把偏心受压构件截面弯矩中心的Ne0称为初始弯矩或一
阶弯矩(不考虑侧向挠度时的弯矩),将Nf或Ny称为附加弯矩或
二阶弯矩。
由于二阶弯矩的影响,将造成偏心受压构件不同的破坏类型。(见教材122 页图7-12) 短柱——材料破坏,即由于截面中材料达到其强度极限而发生的破坏; 长柱(8<lo /h≤30) ——材料破坏 细长柱——失稳破坏。即当偏心压力达到最大值时,侧向挠度f突然剧增, 但材料未达到其强度极限情况下发生的破坏。由于失稳破坏与材料破坏有本 质的区别,设计中一般尽量不采用细长柱。
rb N j e M u Rg Ag (h0 a ' ) (7-12) rs 当按式(7-12)求得的正截面承载力M u比不考虑受压钢筋A/g时更小,则 在计算中不应考虑受压钢筋A/g 。
'
3)当偏心压力作用的偏心距很小,即小偏心受压情况下且全截面受压。 若靠近偏心压力一侧的纵向钢筋A/g配置较多,而远离偏心压力一侧的纵向钢 筋Ag配置较少时,钢筋Ag的应力可能达到受压屈服强度,离偏心压力较远一 侧的混凝土也有可能压坏,这时的截面应力分布如图(7-8)所示。为使钢筋 Ag数量不致过少,防止出现一侧压应力负担较大引起的破坏,《公路桥规》 规定:对于小偏心受压构件,若偏心压力作用于钢筋Ag合力点和A/g合力点之 间时,尚应符合下列条件:
e
e/
e0
e/
x
Ra
z
x 2a '
rb / Rg Ag C rs
钢筋混凝土矩形空心截面偏心受压构件强度计算探讨

2 , a 即假 设 混 凝 土 压应 力 合 力 作 用 点 与 受
压 钢 筋 A 台 力 作 用 点 相 重 合 , 受 压 钢 筋 对
A 台 力 作 用 点 取 矩得 计 算 公 式 如下 :
≤ R A ( o一 ⅡE h )+
∑
.
() 3
2 强 度计 算公 式
=
④ 混 凝 土 的压 应 力 图 形 为 矩 形 , 力 集 度 应 为 。矩 形 应 力 图 的高 度 取 等于按 平 截 面 确 , 定 的 中和轴 高度 乘 以系 数 O 9 即 =0 9 ., .x。 ⑤钢筋视为理想 的弹塑性体 , 即应 变 在 其 屈 服 应变 前 为理 想 弹性 体 , 屈 服 后 为 理 想 塑 在 性 体。
筋 程 凝 土 矩 形 空 心 截 面 偏 心 受 压 构 件 正 截 面 强 度 计 算 公 式 , 用 来 精 确 计 算 恢 共 构 件 的 极 限 承 载 可 力 为 正 确 的 设 计 提 供 理 论 依 据 。
【 关键词 】 空心截面 偏心受压 强计计算 探讨
在 桥 梁 设 计 中 , 节 省 材 料 , 大 桥 墩 的 为 增 柔 度 , 轻 下 部 结 构 的 自重 , 架 桥 墩 越 来 越 减 高 多 的 采 用 矩 形 空 心 截 面 。现 行 规 范 中 只 给 出 了计 入 主 边 所 配 钢 筋 , 余 两个 侧 边 所 配 钢 筋 其 则 忽 略 不 计 的 矩 形 和 T型 截 面 偏 心 受 压 构 件 的正 截 面 强 度 计 算 公 式 。这 种 在 设 计 上 偏 于 安 全 的计 算 , 造 成 材 料 浪 费 或 安 全 度 不 足 , 易 且计 算结 果 不 能 反 映该 类 构 件 的 实 际 结 构 性 能 。经 研 究 分 析 , 文 提 出 了 考 虑 侧 边 配 筋 影 本 响 的钢筋 混 凝 土 矩 形 空 心 截 面 偏 心 受 压 构 件 正截面强度计算公式 。 1 基 本 假 定
基本构件计算矩形截面偏心受压构件承载力的计算

矩形截面偏心受压构件正截面承载力的计算一、基本公式1. 计算图式2. 基本公式由0=∑x N 得:)](11[g g g gsa cb u j A A R bx R N N σγγγ-''+=≤ 由0=∑gA M 得:)](1)2(1[00g g g sa cb u j a h A R x h bx R M e N '-''+-=≤γγγ由0=∑'gA M 得:)](1)2(1[0g g g sg a c b u j a h A a x bx R M e N '-+'--=≤'σγγγ 混凝土受压区高度由下式确定:e A R e A xh e bx R g gg g a '''-=+-σ)2(0(对偏心作用力点取矩) e e '、-分别为偏心压力j N 作用点至钢筋g A 合力作用点和钢筋g A '合力作用点的距离,按下式计算:η=e g a h e -+20;η='e g a h e '+-203.公式的注意事项(1)钢筋g A 的应力g σ取值当jg h x ξξ≤=0时,构件属于大偏心受压构件,这时取g g R =σ(受拉钢筋屈服);当jg h x ξξ>=0时,构件属于小偏心受压构件,这时g σ按下式计算,但不大于g R 值:)19.0(003.0-=ξσg g E ,式中g E 为受拉钢筋的弹性模量。
(2)为保证构件破坏时,大偏心受压构件截面上的受压钢筋能达到抗压设计强度gR ',必须满足g a x '≥2,否则受压钢筋的应力可能达不到g R '。
与双筋截面受弯构件类似,这时可近似取g a x '=2,由截面受力平衡条件(0=∑'g A M )可得:)(0gg g s bu j a h A R M e N '-=≤'γγ 上式计算的正截面承载力u M 比不考虑受压钢筋gA '更小时,计算中不考虑受压钢筋g A '的影响。
矩形截面偏心受压构件的正截面承载力计算

1.当 bh0 x h 时, 钢筋应力由下式计算
s
cu
Es
(
h0
x
1)
由(5-1)可求得NU
0Nd fcdbx fsd As s As
2.当 x 时h,取 求x得 钢h 筋应力
力NU1
近偏心侧破坏
再由(s 5-1)求得截面承载
由公式(5-7)求截面承载力NU2 远偏心侧破坏
构件截面承载力为NU1, NU2中较小者
2)垂直于弯矩作用平面内的截面承载力复核
《公桥规》规定,对于偏心受压构件除应计算弯矩作用 平面内的强度外,尚应按轴心受压构件复核垂直于弯矩作 用平面内的强度。这时,不考虑弯矩作用,而按轴心受压
1、截面设计 大、小偏心偏心受压构件的初步判别
根据经验, 当 e0 0.时3h0,可假定截面为大偏心受压;当 时,可e假0 定0.截3h0面为小偏心受压。
注意:仅适用于矩形截面
1)当e0 0.3时h0
第一种情况:
已知:b h
求: As 、As'
Nd Md
fcd
f sd
(两个方程三个未知数)
解:(1)取 b 即x bh0
fcd b
as'
)]
➢当 2as x 时bh,0
As
fcdbx
f
' sd
As'
0 Nd
f sd
➢当 x ,bh且0
时x, 2as
令 x ,2则a可s 求得
As
0 Nd es
fsd (ho as )
2)当 e0 0时.3h0
已知:b h N d M d
f cd
f sd
f sd
l0
4.3 偏心受压构件承载力计算

4.2轴心受压构件承载力计算一、偏心受压构件破坏特征偏心受压构件在承受轴向力N和弯矩M的共同作用时,等效于承受一个偏心距为的偏心力N的作用,当弯矩M相对较小时,气就很小,构件接近于轴心受压,相反当N相对较小时,气就很大,构件接近于受弯,因此,随着气的改变,偏心受压构件的受力性能和破坏形态介于轴心受压和受弯之间。
按照轴向力的偏心距和配筋情况的不同,偏心受压构件的破坏可分为受拉破坏和受压破坏两种情况。
1.受拉破坏当轴向压力偏心距分较大,且受拉钢筋配置不太多时,构件发生受拉破坏。
在这种情况下,构件受轴向压力N后,离N较远一侧的截面受拉,另一侧截面受压。
当N增加到一定程度,首先在受拉区出现横向裂缝,随着荷载的增加,裂缝不断发展和加宽,裂缝截面处的拉力全部由钢筋承担。
荷载继续加大,受拉钢筋首先达到屈服,并形成一条明显的主裂缝,随后主裂缝明显加宽并向受压一侧延伸,受压区高度迅速减小。
最后,受压区边缘出现纵向裂缝,受压区混凝土被压碎而导致构件破坏(图4.3.1)。
此时,受压钢筋一般也能屈服。
由于受拉破坏通常在轴向压力偏心距分较大发生,故习惯上也称为大偏心受压破坏。
受拉破坏有明显预兆,属于延性破坏。
2.受压破坏当构件的轴向压力的偏心距分较小,或偏心距分虽然较大但配置的受拉钢筋过多时,就发生这种类型的破坏。
加荷后整个截面全部受压或大部份受压,靠近轴向压力M 一侧的混凝土压应力较高,远离轴向压力一侧压应力较小甚至受拉。
随着荷载逐渐增加,靠近轴一侧混凝土出现纵向裂缝,进而混凝土达到极限应变先被压碎,受压钢筋的应力也达到远离一侧的钢筋可能受压,也可能受拉,但因本身截面应力太小,或因配筋过多,都达不到屈服强度(图4.3.2)。
由于受压破坏通常在轴向压力偏心距%较小时发生,故习惯上也称为小偏心受压破坏。
受压破坏无明显预兆,属脆性破坏。
3.受拉破坏与受压破坏的界限综上可知,受拉破坏和受压破坏都属于“材料破坏”。
其相同之处是,截面的最终破坏都是受压区边缘混凝土达到极限压应变而被压碎。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)偏心距大,但受拉钢筋配置较多。由于受拉钢筋配置较多, 钢筋应力小,破坏时达不到屈服强度,破坏是由于受压区混 凝土压碎而引起,类似超筋梁。
特征:破坏是由于混凝土被压碎而引起的,破坏时靠近纵向力 一侧钢筋达到屈服强度,另一侧钢筋可能受拉也可能受压, 但都未屈服。
产生受压破坏的条件有两种情况:
⑴当相对偏心距e0/h0较小
⑵或虽然相对偏心距e0/h0较大,但受拉侧纵向钢筋配置较多时
N
N
As 太
多
ssAs
f'yA's
ssAs
f'yA's
小偏心受压破坏又有三种情况
(1)偏心距小,构件全截面受压,靠近纵向力一侧压应力 大,最后该区混凝土被压碎,同时压筋达到屈服强度,另一 侧钢筋受压,但未屈服。
e的i能,力其是承不受同纵的向,力即N值由
于长细比加大降低了构 件的承载力
N0
Nus Num
Nusei Numei
Nul Nul ei
Num fm Nul fl
M0
M
当构件两端的弯矩不同时,由于纵向弯曲引起的二 阶弯矩对构件的影响程度也将不同。
• 构件两端作用相等的弯矩情况
构件中任意点弯矩M= Nei+ Ny,
对于长柱, l0/h=8~30,二阶 效应引起附加弯矩在计算中不 能忽略, M与N 不是直线关系, 承载力比相同截面的短柱 要小, 但破坏仍为材料破坏。
x
N
ei
对于长细柱,构件将发生失 稳破坏。
第七章 偏心受力构件的截面承载力计算
N
长细比加大降低了构 件的承载力
这三个柱虽然具有相同 的外荷载初始偏心距值
N M1 = -N e1 M1
Mmax= M0+ Nf
结论:
•构件两端作用相等弯矩时,一阶、 二阶弯矩最大处重 合,一阶弯矩增加最大,即,临界截面弯矩最大。
•两端弯矩不等但符号相同时,一阶弯矩仍增加较多。 •两端弯矩不等符号相反时,一阶弯矩增加很小或不增加。
“界限破坏”
破坏特征:破坏时纵向钢筋达到屈服强度,同时压区混凝 土达到极限压应变,混凝土被压碎。同受弯构件的适筋梁 和超筋梁间的界限破坏一样。此时相对受压区高度称为界 限相对受压区高度b。
受压区边缘混凝土极极限应变值。各国取值相差不大, 美国ACI一318—8取0.003;“CEB—FIP一70”和 “DINl045-72‘’取0.0035;我国《规范》根据试验研究取 0.0033.
eiN
y
f
N ei
M0=N ei
Mmax= M0+ Nf
M0
Nf
M0 =N ei
•两端弯矩不相等,但符号相同
• 构件的最大挠度位于离端部某位置。
• 最大弯矩Mmax= M0+ Nf
e0 N
M2=N e0
M2 Nf
N
M0
Mmax= M0+ Nf M2
Nf M0
N
N
e1
M1 =N e1
M1
M1
二阶弯矩对杆件的影响降低, M1, M2 相差越大,杆件 临界截面的弯矩越小,即,二阶弯矩的影响越小。
ei
N
y
N ei
y f ?sin px
le f
le
N ( ei+ f )
偏心受压构件在荷载作用下, 由于侧向挠曲变形,引起附加 弯矩Nf,也称二阶效应,即跨 中截面的弯矩为M =N ( ei + f )。
对于短柱,l0/h8, Nf较小, 可忽略不计,M与N为直线关 系,构件是由于材料强度不足 而破坏,属于材料破坏。
由于施工误差及材料的不均
匀性等,将使构件的偏心距产
生偏差,因此设计时应考虑一
个附加偏心距ea,规范规定:附 加偏心距取偏心方向截面尺寸
的1/30 和20mm中的较大值。
考虑附加偏心距后的偏心距: ei — —初始偏心距
ei e0 ea
6.4.3偏心距增大系数
一、二阶弯矩
1 .纵向弯曲引起的二阶弯矩
• 由于M0小于M2,所以临界截面Mmax比两端弯矩相等时小。
• 最大弯矩Mmax= M0+ Nf
e0 N
M2=N e0
M2 Nf
Mmax= M0+ Nf M2
N
M0
Nf M0
N
N
e1
M1 =N e1
M1
M1
•两个端弯矩不相等而符号相反
• 一阶弯矩端部最大M2,二阶弯矩Nf在距端部某 位置最大。Mmax= M0+ Nf有两种可能的分布。
6.4矩形截面偏心受压构件计算
6.4.1 偏心受压构件的破坏形态
N M=N e0
As
As = As
e0 N As
N
As
As
As
M=N e0
As
As
N M=N e0
As
试验表明,钢筋混凝土偏心受压构件的破坏,有两种 情况:
1.受拉破坏情况 tensile failure(大偏心受压破坏) 2. 受压破坏情况 compressive failure(小偏心受压破坏) 一.受拉破坏情况 tensile failure(大偏心受压破坏)
◆ 形成这种破坏的条件是:偏心距e0较大,且受拉侧纵 向钢筋配筋率合适,是延性破坏。
破坏特征:截面受拉侧混凝土较早出现裂
N
缝,As的应力随荷载增加发展较快,首先 达到屈服。最后受压侧钢筋A‘s 受压屈服, 压区混凝土压碎而达到破坏。有明显预兆,
变形力较大,与适筋梁相似。
fyAs
f'yA's
二、受压破坏compressive failur(小偏心受压破坏)
e0 N
M2=N e0 M2 Nf
N
M0
M2
M2
N e1
N M1 = -N e1 M1
Mmax= M0+ Nf
情形1最大弯矩M2,二阶弯矩不引起最大弯矩 的增加
情形2最大弯矩Mmax ,距离端部某距离,Nf只能使Mmax比 M2稍大。
e0 N
M2=N e0 M2 Nf
N
M0
情形1 情形2
M2
M2
N e1
Nei ---一阶弯矩, Ny----二阶弯矩
eiN
M0=N ei
最大弯矩Mmax= M0+ Nf
Mmax= M0+ Nf
y
f
M0
Nf
N ei
M0 =N ei
• 承受N和Mmax作用的截面是构件最危险截面---临界截面
• Nf ----构件由纵向弯曲引起的最大二阶弯矩
• 最大弯矩Mmax= M0+ Nf
当 当因此,hh受xx00 压 构bb时 时件, ,的界为 为限大 小相偏 偏对心 心受受 受压压 压区破 破高坏 坏度同受弯构件一样。
N
M
As'
As'
As' 不屈服
受拉破坏
xcb
y
a
' s
界限破坏
受压破坏
h0
' y
cu
6.4.2附加偏心距
构件受压力和弯矩作用,其偏心距为:e0
M N
e0为相对偏心距。
