1.解题技巧专题:平面直角坐标系中的图形面积
平面直角坐标系中的面积计算专题

平面直角坐标系中的面积计算知识点一:已知点的坐标求图形面积类型一:平面直角坐标系中三角形的面积①三角形有一边在坐标轴上例1:平面直角坐标系中,A(4,-4), B(1,0),C(6,0). 求△ABC 的面积. x yO A (4,-4)B (1,0)C (6,0)例2:平面直角坐标系中,A(0,3), B(0,-3),C(2,1). 求△ABC 的面积. x y123–1–2123–1–2–3OCB A②三角形有一边平行于坐标轴例3:平面直角坐标系中,A(-2,3), B(-2,-3),C(2,1). 求△ABC 的面积.xy –1–2–3123–1–2–3123OA (-2,3)B (-2,-3)C (2,1)③三角形没有一边平行于坐标轴变式1.保持A 、C 不动,改变点B 的位置:B (0,-3), 求△ABC 的面积. x y –1–2–3–4123–1–2–31234OA (-2,3)C (2,1)B x y –1–2–3–4123–1–2–31234O A (-2,3)C (2,1)B x y –1–2–3–4123–1–2–31234O A (-2,3)C (2,1)B练习:如图中,A 、B 两点的坐标分别为(2,3)、(4,1),求△ABO 的面积.类型二:平面直角坐标系中不规则多边形的面积例4:平面直角坐标系中,A(-3,-2),B(3,-2),C(1,3),D(-2,1),求四边形ABCD 的面积. xyO A (-3,-2)B (3,-2)C (1,3)D (-2,1)练习:如图,已知四边形ABCD 四个顶点的坐标分别是A (-5,2),B (1,5),C (5,-2),D (-4,-5).求四边形ABCD 的面积.知识点二:已知图形面积求点的坐标例5:(1)▲ABC 的两个顶点分别为A (2,3),B (-2,0),且▲ABC 的面积为9,若点C 在x 轴上,求点C 的坐标.(2)已知A (1,0),B (0,3),点P 在x 轴上,且▲PAB 的面积为6,求点P 的坐标.(3)已知O (0,0),B (3,2),点A 在坐标轴上,且6=∆OAB S ,求A 点的坐标.练习1.如图A (﹣4,0),B (6,0),C (2,4),D (﹣3,2).(1)求四边形ABCD 的面积;(2)在y 轴上找一点P ,使△APB 的面积等于四边形的一半.求P 点坐标.练习2.如图,已知A (﹣2,0),B (4,0),C (2,4),D (0,2)(1)求三角形ABC 的面积;(2)设P 为坐标轴上一点,若S △APC =S △ABC ,求P 点的坐标.练习3.如图,已知三点A (0,1),B (2,0),C (4,3)(1)求三角形ABC 的面积;(2)设点P 在坐标轴上,且三角形ABP 与三角形ABC 的面积相等,求点P 的坐标.。
专题在平面直角坐标系中求图形的面积(四大题型)(原卷版)
1.上面题主要考查坐标与图形性质,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答.
2.由于点的位置不明确,因此在解题时要注意分情况讨论.
【变式41】已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )
A.(0,﹣4)B.(0,﹣8)C.(﹣4,0)D.(6,0)
(2)直接写出A1,B1,C1三点的坐标;
(3)求△ABC的面积.
【例题3】(2022春•长安区校级月考)如图所示,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为( )
A.9B.10C.11D.12
解题技巧提炼
1、当四边形的其中有一边在坐标轴上(或与坐标轴平行)时,可以用分割法;
【变式45】(2022秋•渭滨区期末)如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是;
(2)若点D与点C关于y轴对称,则点D的坐标为;
(3)已知P为x轴上一点,若△ABP的面积为1,求点P的坐标.
【变式46】(2022•天津模拟)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
【变式24】(2022春•雷州市期末)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC.
【变式25】在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在如图所示的网格平面内画出平面直角坐标系;
中考数学专题:平面直角坐标系

中考数学专题:平面直角坐标系教学目标:1.学会在平面直角坐标系中求点的坐标,图形的面积,字母的取值范围。
2.解决平面直角坐标系中的综合问题1. 复习定义:为了用一对实数表示平面内的点,在平面内画两条互相垂直的数轴,组成平面直角坐标系。
水平的数轴叫做x 轴或横轴,铅直的数轴叫做y 轴或纵轴。
⎡⎤⎣⎦数轴平面直角坐标系 ,x x y x y ⎧⎪⎪⎧⎡⎤⎣⎦⎪⎪⎪→→⎨⎨⎪⎪→→⎡⎤⎣⎦⎩⎪⎪⎪⎩b 第一象限第二象限轴位置轴垂直于y 轴且原点重合第三象限第四象限轴平面轴把平面分成六个部分x 轴y 轴⎡⎤⎣⎦点数轴→点平面直角坐标系→点→点的坐标 ⎧⎪→⎨⎪⎩b 已知点确定坐标+-已知坐标确定点点的坐标→点到点的距离[]∍直线()()()[]|a-h||b-m|x y x h y m ⎧⎧⎪⎪⎨⎪⎪⎩⎪=⎧⎪⎪⎪⎨=⎨⎪⎩⎪⎪⎪⎪⎪⎩轴:P(a,b)到x 轴的距离为|b|坐标轴轴:P(a,b)到y 轴的距离为|a|点p a,b 到的距离为[与坐标轴平行的直线]点p a,b 到的距离为[任意直线]点p a,b 到直线Ax+By+C=0的距离为|Aa+Bb+C|[点]d =任意两点⊃1122121211221221(,0)(,0)||||(0,)(0,)||||P a P a PP a a P b P b PP b b ⎧→=-⎧⎪⎨→=-⎩⎨⎪⎩与在坐标轴上的两点与点到原点的距离:P(a,b)到原点的距离 点的坐标⊃[一点]特殊位置上的点的坐标⊃(,)0[](,)0[][](,)P a b x b P a b a P a b y =⎧⎨=⎩⎧⎪⎪⎨⎪⎪⎩⎧⎨⎩€€€€€€€€在轴上坐标轴在y 轴上P(a,b)在第一象限a>0,b>0P(a,b)在第二象限a<0,b>0[象限]P(a,b)在第三象限a<0,b<0P(a,b)在第四象限a>0,b<0象限角平分线一三象限角平分线上点P(a,b)a=b 二四象限角平分线上点P(a,b)a=-b 与坐标轴平行的直线在与轴平行的直(,)x h a h P a b k b k⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪==⎧⎪⎨⎪==⎩⎩€€线在与x 轴平行的直线y 点的坐标 →[]对称点的坐标直线(,)[](,)x P a b x P a b ⎧⎪⎪⎨⎪⎪⎩轴:关于轴对称点的坐标为(a,-b)坐标轴y 轴:关于y 轴对称点的坐标为(-a,b) ''[](,)(2,)(,)(,2)P a b x h P h a b P a b y m P a m b =⎧⎪-⎪⎨=⎪⎪-⎩与坐标轴平行的直线关于对称的点的坐标为关于对称的点的坐标为 (,)(,)b a b a ⎧⎪⎪⎨⎪⎪-⎩''P(a,b)关于y=x 对称的点坐标为P [角平分线]P(a,b)关于y=-x 对称的点坐标为P[点]'(,)(,)(2,2)P a b x y P x a y b --关于点对称的点坐标为'00(,)P a b ⊃--关于(,)对称的点的坐标为 点的坐标→平移后的点的坐标()()()()()()()()'''',,,,,,,,p a b mp a b m p a b mp a b m p a b mp a m b p a b mp a m b ⎧⎧+⎡⎤⎪⎣⎦⎪⎨-⎪⎡⎤⎪⎣⎦⎪⎩⎨⎧-⎡⎤⎪⎪⎣⎦⎨⎪+⎡⎤⎪⎪⎣⎦⎩⎩u u u u u u r u u u u u u r u u u u u u r u u u u u u r 向上平移点向上上下平移后点的坐标向下平移点向下向左平移点向左左右平移后点的坐标向右平移点向右[对应]平面直角坐标系的点与有序实数对一一对应[点] 平面直角坐标系←⎧⎨⎩定义画法→确定平面内点的位置(点表示出无理数)二.综合题(一)求点的坐标∨点的位置A 、(1)位置,距离直接求点的坐标点的坐标⎧←⎧→→⎪⎨←⎪⎩→⎨←⎧⎪→→⎨⎪←⎩⎩符号点在直角坐标系的位置横坐标实数绝对值点到坐标轴(y 轴)的距离符号点在直角坐标系的位置纵坐标实数绝对值点到坐标轴(x 轴)的距离 例1.已知点p 在第二象限,且到x 轴的距离是2,到y 轴的距离是3,则点p 的坐标为_______小结:首先确定点p 所在位置(象限)来确定横纵坐标的符号,再确定点到坐标轴距离确定横纵坐标的绝对值→p 点的坐标用所学知识点:1.坐标所在象限位置2.点到直线的距离练习:1.一个点在x 轴上,距离原点2个单位长度,这个点是_____2.点N 在y 轴左侧,且到x 轴,y 轴的距离依次是4,3.则点N 的坐标为_______,ON=_______3.已知点A 在x 轴的下方及y 轴的的右侧,且点A 到x 轴的距离为23,到y 轴的距离为4,则点A 的坐标为_________例2. 已知直线AB 平行于x 轴,且A 点坐标为(-3) 则B 点坐标为_______,条件是_______小结:利用与坐标轴平行直线点的特征直线的判定练习:①已知A(a,3),B(5,b),且AB//x 轴,则a= ,b= .A 点的坐标为 ,B 点的坐标为 。
人教版八年级数学下册期末复习专题在直角坐标系中求几何图形的面积(含答案)

人教版八年级数学下册期末复习专题训练——在直角坐标系中求几何图形的面积1.如图,四边形是矩形,点,在坐标轴上,是由绕点顺时针旋转得到的,点在轴上,直线交轴于点,交于点,线段=2,=4(1)求直线的解析式.(2)求的面积.2.直线a:y=x+2和直线b:y=﹣x+4相交于点A,分别与x轴相交于点B和点C,与y轴相交于点D和点E.(1)在同一坐标系中画出函数图象;(2)求△ABC的面积;(3)求四边形ADOC的面积;(4)观察图象直接写出不等式x+2≤﹣x+4的解集和不等式﹣x+4≤0的解集.3.如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b 与y=﹣2x+4是“平行一次函数”(1)若函数y=kx+b的图象过点(3,1),求b的值;(2)若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的,求y=kx+b的解析式.4.如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,求该直线l的解析式5.如图1,直线3=xy分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D -3+3为直线AB上一动点,连接CD交y轴于点E(1) 点B的坐标为__________,不等式+-x的解集为___________3>33(2) 若S△COE=S△ADE,求点D的坐标(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.6.在直角坐标系中,一条直线经过A(﹣1,5),P(﹣2,a),B(3,﹣3)三点.(1)求a的值;(2)设这条直线与y轴相交于点D,求△OPD的面积.7.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,求线段BC扫过的面积8.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.(1)求A、B两点的坐标;(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;9. 如图,已知直线343+=x y 与坐标轴交于B,C 两点,点A 是x 轴正半轴上一点,并且15=∆ABC S .点F 是线段AB 上一动点(不与端点重合),过点F 作FE ∥x 轴,交BC 于E.(1) 求AB 所在直线的解析式;(2) 若FD ⊥x 轴于D,且点D 的坐标为)0,(m ,请用含m 的代数式,表示DF 与EF 的长;(3) 在x 轴上是否存在一点P,使得△PEF 为等腰直角三角形,若存在,请直接写出点P 的坐标,若不存在,请说明理由.10.如图,在平面直角坐标系xOy 中,直线y=﹣2x +a 与y 轴交于点C (0,6),与x 轴交于点B .(1)求这条直线的解析式;(2)直线AD 与(1)中所求的直线相交于点D (﹣1,n ),点A 的坐标为(﹣3,0).①求n 的值及直线AD 的解析式; ②求△ABD 的面积;③点M 是直线y=﹣2x+a 上的一点(不与点B 重合),且点M 的横坐标为m ,求△ABM 的面积S 与m 之间的关系式.11.已知一次函数的图象经过(1,1)和(﹣1,﹣5).(1)求这个一次函数的表达式;(2)求这个一次函数的图象与x 轴、y 轴的交点坐标,并求出该图象与两坐标轴围成的三角形的面积.12.如图,边长为5的正方形OABC的顶点0在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是0A边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.(1)求证:CE=EP;(2)若点E的坐标为(3,O),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标:若不存在,说明理由.13.已知一次函数的图象经过(1,1)和(﹣1,﹣5).(1)求这个一次函数的表达式;(2)求这个一次函数的图象与x轴、y轴的交点坐标,并求出该图象与两坐标轴围成的三角形的面积.14.直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).(1)求直线AB的解析式;(2)若直线AB上一点C在第一象限且点C的坐标为(2,2),求△BOC的面积.15.在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.(1)如图,直线y=-2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.①求点B的坐标及k的值;②直线y=-2x+1、直线y=kx+4与y轴所围成的△ABC的面积等于____________;(2)直线y=kx+4(k≠0)与x轴交于点E(x0,0),若-2<x0<-1,求k的取值范围.16.如图,己知直线l:y=x+1(k≠0)的图象与x轴、y轴交于A、B两点.(1)直接写出A、B两点的坐标;(2)若P是x轴上的一个动点,求出当△PAB是等腰三角形时P的坐标;(3)在y轴上有点C(0,3),点D在直线l上.若△ACD面积等于4.请直接写出D的坐标.17.如图①所示,正方形ABCD的边长为6 cm,动点P从点A出发,在正方形的边上沿A→B →C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:(1)点P在AB上运动的时间为________s,在CD上运动的速度为________cm/s,三角形APD的面积S的最大值为________cm2;(2)求出点P在CD上运动时S与t之间的函数解析式;(3)当t为何值时,三角形APD的面积为10 cm2?18.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.(1)求A、B两点的坐标;(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF ⊥y轴于点F,连接EF,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;答案:1. (1)OC=4,BC=2,B(-2,4),.设解析式为,.(2),.直线,.当,,,.2.(1)依照题意画出图形,如图所示.(2)令y=x+2中y=0,则x+2=0,解得:x=﹣2,∴点B(﹣2,0);令y=﹣x+4中y=0,则﹣x+4=0,解得:x=4,∴点C(4,0);联立两直线解析式得:,解得:,∴点A (1,3).S △ABC =BC•y A =×[4﹣(﹣2)]×3=9.(3)令y=x +2中x=0,则y=2,∴点D (0,2).S 四边形ADOC =S △ABC ﹣S △DBO =9﹣×2×2=7.(4)观察函数图形,发现:当x <1时,直线a 在直线b 的下方,∴不等式x +2≤﹣x +4的解集为x ≤1;当x >4时,直线b 在x 轴的下方,∴不等式﹣x +4≤0的解集为x ≥4.3.(1)∵一次函数y=kx +b 与y=﹣2x +4是“平行一次函数”,∴k=﹣2,即y=﹣2x +b . ∵函数y=kx +b 的图象过点(3,1),∴1=﹣2×3+b ,∴b=7.(2)在y=﹣2x +4中,令x=0,得y=4,令y=0,得x=2,∴A (2,0),B (0,4),∴S △AOB =OA•OB=4.由(1)知k=﹣2,则直线y=﹣2x +b 与两坐标轴交点的坐标为(,0),(0,b ),于是有|b |•||=4×=1,∴b=±2,即y=kx +b 的解析式为y=﹣2x +2或y=﹣2x ﹣2.4.设直线l 和10个正方形的最上面交点为A ,过A 作AB ⊥OB 于B ,过A 作AC ⊥OC 于C , ∵正方形的边长为1,∴OB=3,∵经过原点的一条直线l将这10个正方形分成面积相等的两部分,∴两边分别是5,∴三角形ABO 面积是7,∴OB•AB=7,∴AB=,∴OC=AB=,由此可知直线l 经过(,3),设直线方程为y=kx (k ≠0),则3=k ,解得k=∴直线l 解析式为y=x .故答案为:y=x .5.(1) (3,0)、x <3(2) ∵S △COE =S △ADE ∴S △AOB =S △CBD 即33321621⨯⨯=⨯⨯D y ,y D =233 当y =233时,23233333==+-x x ,∴D (23323,) (3) 连接CF ∵∠CDF =60°∴△CDF 为等边三角形连接AC ∵AB =AC =BC =6∴△ABC 为等边三角形∴△CAF ≌△CBD (SAS )∴∠CAF =∠ACB =60°∴AF ∥x 轴设D (m ,333+-m )过点D 作DH ⊥x 轴于H ∴BH =3-m ,DB =6-2m =AF∴F (2m -6,33)由平移可知:G (m -9,m 3-)令⎪⎩⎪⎨⎧-=-=m y m x 39∴点G 在直线393--=x y 上6. (1)设直线的解析式为y=kx +b ,把A (﹣1,5),B (3,﹣3)代入,可得:{533=+--=+b k b k ,解得:,所以直线解析式为:y=﹣2x +3,把P (﹣2,a )代入y=﹣2x +3中,得:a=7; (2)由(1)得点P 的坐标为(﹣2,7),令x=0,则y=3,所以直线与y 轴的交点坐标为(0,3),所以△OPD 的面积=.7.∵点A 、B 的坐标分别为(2,0)、(8,0),∴AB=6,∵∠CAB=90°,BC=10, ∴CA==8,∴C 点纵坐标为:8,∵将△ABC 沿x 轴向右平移,当点C 落在直线y=x ﹣5上时,∴y=8时,8=x ﹣5,解得:x=13,即A 点向右平移13﹣2=11个单位, ∴线段BC 扫过的面积为:11×8=88.故选:B .8.(1)令x=0,则y=8,∴B (0,8),令y=0,则﹣2x +8=0,∴x=4,∴A (4,0), (2)∵点P (m ,n )为线段AB 上的一个动点,∴﹣2m +8=n ,∵A (4,0),∴OA=4,∴0<m <4∴S △PAO =OA ×PE=×4×n=2(﹣2m +8)=﹣4m +16,(0<m <4) )3,0(30343)1(,9B y x x y 即时,中,当在==+= ∴OB=3同理OC=4 ∵15)(21=⋅+OB OA OC ,153)4(21=⨯+⨯OA ∴OA=6 即点A 的坐标为(6,0) 设AB 所在直线的解析式为y=kx+b⎩⎨⎧⎩⎨⎧=+=-==213063k b b k b 解得则∴AB 所在直线的解析式为 (2)在中,当,即DF= 在中,当m x m y 32,321-=+-=时 mm m EF 35)32(=--= (3)10.(1)∵直线y=﹣2x +a 与y 轴交于点C (0,6),∴a=6,∴该直线解析式为y=﹣2x +6 (2)①∵点D (﹣1,n )在直线BC 上,∴n=﹣2×(﹣1)+6=8,∴点D (﹣1,8)设直线AD 的解析式为y=kx +b ,将点A (﹣3,0)、D (﹣1,8)代入y=kx +b 中,得:,解得:,∴直线AD 的解析式为y=4x +12.②令y=﹣2x +6中y=0,则﹣2x +6=0,解得:x=3,∴点B (3,0).∵A (﹣3,0)、D (﹣1,8),∴AB=6.S △ABD =AB•y D =×6×8=24.③∵点M 在直线y=-2x+6上,∴M (m ,-2m+6),时,即S=6m-18.11. (1)设函数解析式为y=kx +b , 由题意将两点代入得:{15=+-=+-b k b k ,解得:{32=-=k b .∴一次函数的解析式为:y=3x ﹣2;(2)令y=0,得x=32,令x=0,得y=﹣2, 3232221=⨯⨯=∴s 12.(1)在OC 上截取OK =OE .连接EK .∵OC =OA ,∠1=90°,∠OEK =∠OKE =45°,∵AP 为矩形外角平分线,∴∠BAP =45°∴∠EKC =∠PAE =135°.∴CK =EA .∵EC ⊥EP ,∴∠3=∠4.∴△EKC ≌△PAE . ∴EC =EP (2)y 轴上存在点M ,使得四边形BMEP 是平行四边形.如图,过点B 作BM ∥PE 交y 轴于点M ,∴∠5=∠CEP =90°,∴∠6=∠ 4.在△BCM 和△COE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠,,,46C O E B C M OC BC ∴△BCM ≌△COE ,∴BM =CE 而CE =EP ,∴BM =EP .由于BM ∥EP ,∴四边形BMEP是平行四边形由△BCM ≌△COE 可得CM =OE =3,∴OM =CO -CM =2.故点M 的坐标为(0,2).13.(1)设函数解析式为y=kx +b ,由题意将两点代入得:,解得:.∴一次函数的解析式为:y=3x ﹣2;(2)令y=0,得x=,令x=0,得y=﹣2,∴S=×2×=.14.(1)设直线AB 的解析式为y =kx +b(k ≠0).将A(1,0),B(0,-2)代入解析式,得⎩⎪⎨⎪⎧k +b =0,b =-2.解得⎩⎪⎨⎪⎧k =2,b =-2.∴直线AB 的解析式为y =2x -2.(2)S △BOC =12×2×2=2.15.(1)32 当x =-1时,y =-2×(-1)+1=3,∴B(-1,3).将B(-1,3)代入y =kx +4,得k =1.(2)y =kx +4与x 轴的交点为(-4k ,0),∵-2<x 0<-1,∴-2<-4k<-1,(1)解得2<k<4.16.(1)当y=0时,x+1=0,解得x=﹣2,则A(﹣2,0),当x=0时,y=x+1=1,则B(0,1);(2)AB==,当AP=AB时,P点坐标为(﹣,0)或(,0);当BP=BA时,P点坐标为(2,0);当PA=PB时,作AB的垂直平分线交x轴于P,连结PB,如图1,则PA=PB,设P(t,0),则OA=t+2,OB=t+2,在Rt△OBP中,12+t2=(t+2)2,解得t=﹣,此时P点坐标为(﹣,0);(3)如图2,设D(x,x+1),当x>0时,∵S△ABC+S△BCD=S△ACD,∴•2•2+•2•x=4,解得x=2,此时D点坐标为(2,2);当x<0时,∵S△BCD﹣S△ABC=S△ACD,∴•2•(﹣x)﹣•2•2=4,解得x=﹣6,此时D点坐标为(﹣6,﹣2),综上所述,D点坐标为(2,2)或(﹣6,﹣2).故答案为(﹣2,0),(0,1);(2,2)或(﹣6,﹣2).17.略18.(1)令x=0,则y=8,∴B(0,8),令y=0,则﹣2x+8=0,∴x=4,∴A(4,0),(2)∵点P(m,n)为线段AB上的一个动点,∴﹣2m+8=n,∵A(4,0),∴OA=4,∴0<m<4∴S△PAO=OA×PE=×4×n=2(﹣2m+8)=﹣4m+16,(0<m<4)。
《平面直角坐标系中的面积问题》教学设计

A
A
(1) 能否通过小房子的各点坐标求出小房子的面积引入课题 回顾旧知
1.若P (-2,4)则点P 到x 轴的距离为 点P 到y 轴的距离为
2.若A (2,0) B (5,0) 则AB=
若A (0,3),B (0,-5) 则AB=
若A (2,3),B (2,6) 则AB=
若A (4,1),B (-3,1) 则AB=
3.已知:A (1,4),B (-4,0),C (2,0)则三角形ABC 的面积
(二)探索方法
若A (4,0),B (3,3),C (0,2)求四边形OABC 的面积
复习在平面直角坐标系内①两点在
轴上;②两点不在轴上却与坐标轴平行;
两点间的距离。
为解
决简单三角形面积
做铺垫。
通过小组合作交流,不仅可以突破难点,学习更多解题方
法。
同时,利用面积和差求得.渗透转化
思想解;通过不同方法的选择,培养学生设计解决问题方案
时要考虑可行性的习惯;通过一题多解发展学生的创新思维.
(三)巩固练习
已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),求△ABO的面积.学生体验解题方法和技巧,感受解题的快乐。
通过自我展示,提高学生的语言表达能力,锻炼他们的胆识。
(四)归纳方法
1、知识方面
在平面直角坐标系中,求面积的方法有:2、数学思想方面1、通过自己的归纳总结,逐步提高学生提炼方法和技巧的
意识。
2、通过学生的表述,。
期末专项训练 专题一 探索平面直角坐标系中点的坐标特征

8.已知点 M(3,-2)与点 M′(x,y)在同一条平行于 x 轴的直线上,且 M′
到 y 轴的距离等于 4,则点 M′的坐标是 (4,-2)或(-4,-2)
.
9.已知点 P 的坐标为(a-3,a2-4). (1)若点 P 在 y 轴上,试确定点 P 的坐标; (2)若点 P 在 x 轴上,试确定点 P 的坐标. 解:(1)若点 P 在 y 轴上,则 a-3=0,解得 a=3,所以 a2-4=5,所以点 P 的坐标为(0,5); (2)若点 P 在 x 轴上,则 a2-4=0,解得 a=2 或-2,所以 a-3=-1 或-5,所以点 P 的坐标为(-1,0)或(-5,0).
(2)设△APB 的 AB 边上高为 h,则由 S△APB=12×S 四边形 ABCD 得12×10×h=12 ×24,解得 h=2.4,又∵P 点在 y 轴上,∴P(0,2.4)或(0,-2.4).
考点四:坐标与平移 15.将点 P(-3,y)先向下平移 3 个单位长度,再向左平移 2 个单位长度后得 到点 Q(x,-1),则 xy= -10 . 16.如图,把左图中的圆 A 经过平移得到右图中的圆 O.如果左图中圆 A 上一 点 P 的坐标为(m,n),那么平移后在右图中的对应点 P′的坐标为( D )
期末专项训练
专题一 探索平面直角坐标系 中点的坐标特征
考点一:坐标系内点的坐标特征
1.在平面直角坐标系中,点 P(2,-4)所在象限为( D )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.坐标平面内,在第二象限内有一点 P,且 P 点到 x 轴的距离是 4,到 y 轴
的距离是 5,则 P 点的坐标为( A )
5.若点 M(x,y)满足(x+y)2=x2+y2-2,则点 M 所在象限是( B )
平面直角坐标系中的面积问题

∴OA=4, yB =3
∴ S△AOB
1 OA OB 2
=1 43 2
6 【典型例题】 类型 1 有一边在坐标轴上
∴ S△AOB
1 OA 2
yB
=1 43 2
6
例 1 如图 1,△ABC 的三个顶点的坐标分别是 A(4,0),B(-2,0),C(2,4),求△ ABC 的面积.
山东大学附属中学初二数学组 张永坤整理
【点拨】(1)“补”的思想;(2)三角形的面积公式:
“底乘高除以 2”.
图5
山东大学附属中学初二数学组 张永坤整理
例 6 如图 6,已知△ABC 中,A(4,1),B(4,5),C(-1,2),求△ABC 的 面积.
图6 【分析】采用“补”的思想,将△ABC 补成一个正方形或者梯形. 【方法】
例 7 如图 7,以 OA 为边的△OAB 的面积为 2,试找出符合条件得且顶点是第一象 限格点的点 C,你能找出几个这样的点?
【分析】要求三角形的面积,需要分别求出底边及其高.由图 1 可知,△ABC 的边 AB 在 x 轴上,容易求得 AB 的长,而 AB 边上的高,恰好是 C 点到 x 轴的距离,也就是 C 点的纵坐标的绝对值.
解:∵A(4,0),B(-2,0),
∴AB=4-(-2)=6.
∵C 点坐标为(2,4),
∴C 点到 x 轴的距离为 4,
【分析】明确底和高,以及利用平行线之间的距 离处处相等进行面积转化.【同底等高模型】
【方法】
图7
山东大学附属中学初二数学组 张永坤整理
例 8 如图所示,已知:A(0,1),B(2,0),C(4,3). (1)在坐标系中描出各点,画出△ABC. (2)求△ABC 的面积; (3)设点 P 在坐标轴上,且△ABP 与△ABC 的面积相等,求点 P 的坐标. 【分析】(1)确定出点 A、B、C 的位置,连接 AC、 CB、AB 即可; (2)过点 C 向 x、y 轴作垂线,垂足为 D、E, S△ABC = S 四边形 DOEC -S△ACE -S△BCD -S△AOB; (3)当点 P 在 x 轴上时,由 S△ABP =4,求得:BP=8, 故此点 P 的坐标为(10,0)或(﹣6,0);当点 P 在 y 轴 上时,S△ABP =4,解得:AP=4.所以点 P 的坐标为(0,5) 或(0,﹣3). 【解答】 解:(1)如图所示:△ABC 即为所求.
八年级数学上册第3章小专题_平面直角坐标系中计算图形的面积(北师大版)
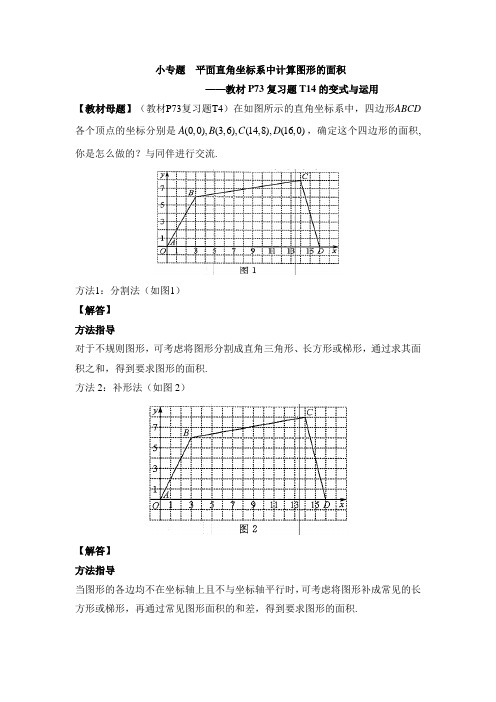
小专题平面直角坐标系中计算图形的面积——教材P73复习题T14的变式与运用【教材母题】(教材P73复习题T4)在如图所示的直角坐标系中,四边形ABCDA B C D,确定这个四边形的面积,各个顶点的坐标分别是(0,0),(3,6),(14,8),(16,0)你是怎么做的?与同伴进行交流.方法1:分割法(如图1)【解答】方法指导对于不规则图形,可考虑将图形分割成直角三角形、长方形或梯形,通过求其面积之和,得到要求图形的面积.方法2:补形法(如图2)【解答】方法指导当图形的各边均不在坐标轴上且不与坐标轴平行时,可考虑将图形补成常见的长方形或梯形,再通过常见图形面积的和差,得到要求图形的面积.【母题变式】如图在平面直角坐标系内,已知点80A (,),点B 的横坐标是2,AOB V 的面积为12.(1)求点B 的坐标;(2)如果P 是直角坐标平面内的点,那么点P 的纵坐标为多少时,2AOP AOB S S =V V ?【解答】方法指导已知坐标系中图形的面积,求点的坐标时,可将点的横(纵)坐标转化为到坐标轴的距离,利用面积求得线段长,从而转化为点的坐标.变式训练1.如图,已知(2,0),(4,0),(4,4)A B C --,则ABC V 的面积为__________.2.已知点00O (,),点32A -(,),点B 在y 轴的正半轴上.若AOB V 的面积为12,则点B 的坐标为___________.3.如图,已知点(3,1),(1,3),(3,4)A B C --,则ABC V 的面积为_________.4.(三门峡期中)如图,四边形ABCD 各顶点的坐标分别是(0,0),(8,0)A B ,(6,4)C ,(3,6)D ,求出四边形ABCD 的面积.参考答案【教材母题】方法1:按如图所示方法将四边形分割成四部分.其中,三个三角形的两条直角边都平行于坐标轴,一个长方形的两条边也平行于坐标轴.从而四边形的面积111361121168294222S =⨯⨯+⨯⨯+⨯+⨯⨯=.方法2:按如图所示方法将四边形补成一个梯形,则原四边形的面积可通过梯形的面积减去两个三角形的面积得到,即111(1416)88314294222S =⨯+⨯-⨯⨯-⨯⨯=. 【母题变式】(1)设点B 的纵坐标为y .因为80A (,),所以8OA =. 则1||122AOB S OA y =⋅=V ,解得3y =±.所以点B 的坐标为(23)(2,3)-,或. (2)设点P 的纵坐标为h .因为221224AOP AOB S S ==⨯=V V ,所以1||242OA h ⋅=,解得6h =±.所以点P 的纵坐标为6或6-.变式训练1.122.(0,8)3.184.解:过点D 作DE x ⊥轴,交x 轴于点E ,过点C 作CF x ⊥轴,交x 轴于点F. 因为(8,0),(6,4),(3,6)B C D 所以12AED BCF ABCD DEFC S S S S AE DE =++=⋅+V V 四边形梯形 11111()36(64)3242822222DE CF EF BF CF +⋅+⋅=⨯⨯+⨯+⨯+⨯⨯=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解题技巧专题:平面直角坐标系中的图形面积
——代几结合,突破面积及点的存在性问题
◆类型一直接利用面积公式求图形的面积
1.如图,在平面直角坐标系中,△ABC的面积是()
A.2 B.4 C.8 D.6
第1题图第2题图
2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(-4,3),则△ABC 的面积为________.
◆类型二利用分割法求图形的面积
3.如图,在平面直角坐标系中,A(4,0),B(3,2),C(-2,3),D(-3,0).求四边形ABCD的面积.
◆类型三利用补形法求图形的面积
4.如图,已知△ABC,点A(-2,1),B(1,-3),C(3,4),求△ABC的面积.
◆类型四探究平面直角坐标系中与面积相关的点的存在性
5.如图,在平面直角坐标系中,点A (4,0),B (3,4),C (0,2).
(1)求S 四边形ABCO ;
(2)连接AC ,求S △ABC ;
(3)在x 轴上是否存在一点P ,使S △P AB =10?若存在,请求点P 的坐标.
6.如图,在平面直角坐标系中,已知A (0,a ),B (b ,0),C (b ,c )三点,其中a 、b 、c 满足关系式|a -2|+(b -3)2=0和(c -4)2≤0.
(1)求a 、b 、c 的值;
(2)如果在第二象限内有一点P ⎝
⎛⎭⎫m ,12,请用含m 的式子表示四边形ABOP 的面积; (3)在(2)的条件下,是否存在点P ,使得四边形ABOP 的面积与△ABC 的面积相等?若存在,求出点P 的坐标;若不存在,请说明理由.
参考答案与解析
1.B 2.7.5
3.解:分别过C 作CE ⊥x 轴于E ,过B 作BF ⊥x 轴于F .由题意,得DE =1,CE =3,BF =2,AF =1,EF =5.S 四边形ABCD =S △CDE +S 梯形CEFB +S △ABF =12×1×3+12×(3+2)×5+12×1×2=15.
4.解:过点A 作x 轴的垂线,过点B 作y 轴的垂线,过点C 分别作x 轴、y 轴的垂线,交于点D ,E ,F 三点,如图所示.由题意,得CD =EF =5,DE =CF =7,AD =3,CD =5,AE =4,BE =3,BF =2.
方法一:S △ABC =S 长方形CDEF -S △ACD -S △ABE -S △BCF =CD ·DE -12AD ·CD -12AE ·BE -12
BF ·CF =5×7-12×3×5-12×4×3-12×2×7=292
. 方法二:S △ABC =S 梯形BCDE -S △ACD -S △ABE =12(BE +CD )·DE -12AD ·CD -12AE ·BE =12
×(3+5)×7-12×3×5-12×4×3=292
. 方法三:S △ABC =S 梯形CAEF -S △ABE -S △BCF =12(AE +CF )·EF -12AE ·BE -12BF ·CF =12×(4+7)×5-12×4×3-12×2×7=292
. 方法点拨:本题运用了补形法,对于平面直角坐标系中的三角形,可以通过作垂线,运用补形法将三角形补形,将它转化为便于计算面积的图形,通过这些图形面积的和差关系来求原三角形的面积.
5.解:(1)过点B 作BD ⊥OA 于点D .由题意,得OC =2,OD =3,AD =1,BD =4.S 四边形ABCO =S 梯形BCOD +S △ABD =12×(2+4)×3+12
×1×4=11; (2)S △ABC =S 四边形ABCO -S △AOC =11-12
×2×4=7; (3)存在.设点P 的坐标为(x ,0),则AP =|4-x |,由题意,得12
×4×|4-x |=10,∴|4-x |=5,∴x =9或x =-1,∴点P 的坐标为(9,0)或(-1,0).
6.解:(1)∵|a -2|+(b -3)2=0,(c -4)2≤0,∴a =2,b =3,c =4;
(2)∵P ⎝
⎛⎭⎫m ,12在第二象限,∴m <0.S 四边形ABOP =S △ABO +S △AOP =12OA ·OB +12OA ·|m |=12
×2×3+12×2×(-m )=3-m ;
(3)存在.由B (3,0),C (3,4),A (0,2),得S △ABC =12
×3×4=6.由(2)可知S 四边形ABOP =3-m ,∴3-m =6,∴m =-3,∴点P 的坐标为⎝
⎛⎭⎫-3,12.。
