抛物线中的三角形问题
抛物线内的三角形问题-

抛物线内的三角形问题近年来中考数学试题中,经常出现以函数、几何知识为背景的探究性问题,特别是有关抛物线内的三角形问题,此类问题综合性强,往往涉及一次函数、二次函数、一元二次方程、三角形、相似三角形等多方面的知识,既考查学生基本运算的能力,又考查学生对函数、方程、数形结合、分类和待定系数法等思想方法的掌握情况,具有很好的选拔功能.本文举例分析如下:例1 (2005·孝感市)如图1,开口向下的抛物线C:y=a(x-2)(x+3),与x•轴交于A、B两点,y有最大值258.(1)求实数a的值;(2)在抛物线C上是否存在点P,使△APB为直角三角形?若存在,求出P点坐标;•若不存在,说明理由.分析本题是一道中考压轴题,综合性较强.第(1)•问由抛物线顶点坐标直接求得a的值.第(2)问由△APB为直角三角形及相似知识可得△APB内的线段关系,再由方程思想求解.解(1)∵当x=-12时取最大值,∴258=a(-52)·(52).∴a=-12.(2)由图1可知:A、B处不可能为直角,只可能∠APB=90°,且点P不能在x轴及x轴下方.设存在满足条件的点P(x0,y0),(y0>0).作PM⊥AB于M,而A(-3,0),B(2,0),则AM=3+x0,BM=2-x0,PM=y0,由∠APB=90°,PM⊥AB,∴PM 2=AM ·BM .则有y 02=(3+x 0)(2-x 0),即y 02=-x 02-x 0+6. ①∵P (x 0,y 0)在抛物线上,∴y 0=-12x 02-12x 0+3, 即2y 0=-x 02-x 0+6. ②由①、②得y 02=2y 0.∵y 0>0,∴y 0=2,代入②得:x 0=-2或x 0=1.故存在这样的点P 满足题意,P 点坐标为P (-2,2)或P (1,2).注 有关抛物线内直角三角形的问题往往要考虑运用勾股定理或直角三角形相似等知识,并由此得到与所求点的坐标相关的方程.例2 (2005·耒阳市)如图2,二次函数y=13x 2-73x+a 经过点A (3,0)与y 轴交于点B .(1)求二次函数的解析式;(2)在x 轴的负半轴上是否存在一点C ,使△ABC 成为以AB 为腰的等腰三角形,若存在,请求出C 点的坐标,若不存在,请说明理由.分析 以AB 为腰的等腰三角形△ABC 要分两种情况:一是以∠BAC 为底角,另是以∠BAC 为顶角.解 (1)由二次函数y 过(3,0)得a=4.∴y=13x 2-73x+4. (2)∵B (0,4)、A (3,0).∴OB=4,OA=3.当∠BAC 为△ABC 的底角时,则OA=OC ,此时C 的坐标为(-3,0).当∠BAC 为△ABC 的顶角时,则AB=AC .∵2234 ,∴OC=5-3=2,∴C 的坐标为(-2,0).故C点的坐标为(-3,0)或(-2,0).注抛物线内等腰三角形问题通常要分情况讨论,•通过讨论弄清等腰三角形的底和腰,再由两腰相等来解答.例3 (2005·成都市)已知抛物线y=ax2+bx+c(a≠0)与x轴交于不同的两点A(x1,0)和B(x2,0),与y轴的正半轴交于点C,如果x1,x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为152.(1)求此抛物线的解析式;(2)求直线AC和BC的方程;(3)如果P是线段AC上的一个动点(不与点A、C重合),过点P作直线y=m(m 为常数),与直线BC交于点Q,则在x轴上是否存在点R,使得以PQ为一腰的△PQR 为等腰直角三角形?若存在,求出点R的坐标,若不存在,请说明理由.分析第(1)问由面积先求C点坐标,再由待定系数法求得抛物线解析式.第(3)•问要分P、Q分别为直角顶点两种情况讨论,再由两直角边相等来处理.解(1)由题意知A(-2,0)、B(3,0),抛物线与y轴的正半轴交于点C.∴C(0,c)且c>0.∵S△ABC=12·│AB│·│c│=152,而│AB│=5,∴│c│=3,∴C(0,3).再由待定系数法求得抛物线解析式为:y=-12x2+12x+3.(2)由(1)可知:A(-2,0),B(3,0),C(0,3).∴直线AC的方程为y=32x+3,直线BC的方程为y=-x+3.(3)假设存在满足条件的点R,并设直线y=m与y轴的交点为E(0,m).由(1)知│AB│=5,│OC│=3.∵点P不与A、C重合,∴点E(0,m)不与点Q、C重合.∴0<m<3.由于PQ为等腰直角三角形PQR的一腰,过点P作PR1⊥x轴于点R1(如图3),则∠R1PQ=90°.∵│PQ│=│PR1│=│OE│=m,PQ∥AB,∴△CPQ∽△CAB,∴||||||||PQ ECAB QC=,即353m m-=.∴m=158.∴P(x p,158),Q(x Q,158).∵点P在直线AC上,∴32x p+3=158,∴x p=-34,∴P(-34-,158).∴R1(-34,0).过Q作QR2⊥x轴于R,则∠R2QP=90°。
抛物线阿基米德三角形二级结论推广

抛物线阿基米德三角形问题是一个数学领域的经典问题,在本文中,我们将结合相关数学理论和实际运用进行深入探讨、分析及推广。
一、抛物线阿基米德三角形概念及原理抛物线阿基米德三角形是通过将一个抛物线分成若干小等分,然后将每个小等分的顶点与该小等分所在的位置上的斜率相连,将所有这些相连的线段所形成的图形,称为抛物线的阿基米德三角形。
该问题的提出是为了研究曲线上的直线与曲线的交点及其有关性质。
二、抛物线阿基米德三角形的基本性质及特点1. 抛物线的阿基米德三角形具有三条相交于一个点的特点,该点即为抛物线的焦点。
2. 抛物线的阿基米德三角形形状具有一定的规律性,不同抛物线的阿基米德三角形形状可能有所不同,但都具备三条相交于一个点的共同特点。
3. 抛物线的阿基米德三角形结构清晰简洁,可以通过数学方法进行精确的构造。
三、抛物线阿基米德三角形的实际应用1. 数学教育领域:抛物线阿基米德三角形可以作为数学教学中的经典案例,通过该案例的讲解和分析,可以帮助学生更深入地理解曲线与直线的交点问题,增强他们的数学思维和分析能力。
2. 工程设计领域:在工程设计中,抛物线阿基米德三角形的相关理论可以应用于某些特定的曲线结构问题的求解和设计,为工程设计师提供一种新的思路和方法。
3. 计算机图形学领域:在计算机图形学中,抛物线阿基米德三角形的相关理论可以帮助程序设计师更好地理解和处理曲线与直线的交点问题,提高程序设计的精确度和效率。
四、抛物线阿基米德三角形问题的二级结论推广1. 根据抛物线阿基米德三角形的相关理论,可以进行进一步的推广和拓展,将抛物线阿基米德三角形的概念和原理应用于更加复杂和多样化的曲线和图形结构中,发现新的数学规律和特点。
2. 抛物线阿基米德三角形问题的二级结论推广可以帮助人们更深入地理解曲线与直线的交点问题,并在实际问题的解决中更加灵活地运用相关数学理论和方法。
五、结语通过对抛物线阿基米德三角形问题的深入探讨、分析及推广,我们可以更好地理解曲线与直线的交点问题,并将相关数学理论和方法应用于实际问题的解决中,为促进数学理论和实际应用的结合做出更大的贡献。
第五讲+抛物线中三角形的面积问题
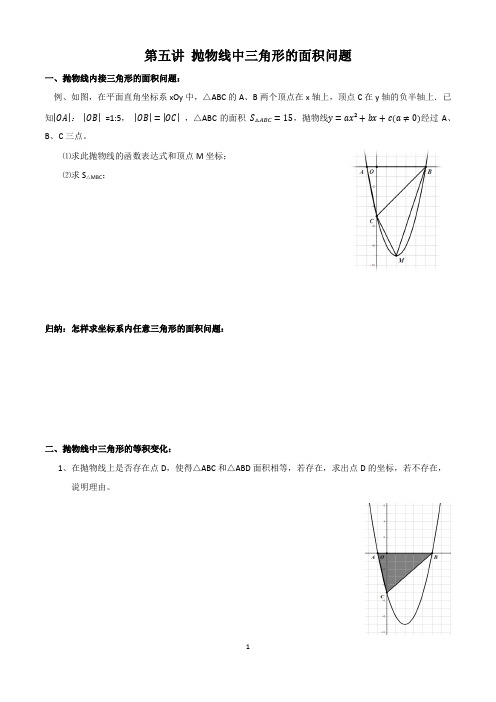
第五讲抛物线中三角形的面积问题一、抛物线内接三角形的面积问题:例、如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax²+bx+c(a≠0)经过A、B、C三点。
⑴求此抛物线的函数表达式和顶点M坐标;⑵求S△MBC;归纳:怎样求坐标系内任意三角形的面积问题:二、抛物线中三角形的等积变化:1、在抛物线上是否存在点D,使得△ABC和△ABD面积相等,若存在,求出点D的坐标,若不存在,说明理由。
2、在抛物线上是否存在点E,使得△ABC和△BCE面积相等,若存在,求出点E的坐标,若不存在,说明理由。
S△ABC。
若存在,求出点M的坐标;若不存在,请说明理由3、在抛物线上是否存在点M,使S△MBC= 134、(2011成都)在抛物线上是否存在异于B、C的点M,使△MBC中BC边上的高为7√?若存在,求出点M的坐标;若不存在,说明理由.5、点P(2,-3)是抛物线对称轴上的一点,在线段OC上有一动点M,以每秒2个单位的速度从O向C 运动,(不与点O,C重合),过点M作MH∥BC,交X轴于点H,设点M的运动时间为t秒,试把△PMH 的面积S表示成t的函数,当t为何值时,S有最大值,并求出最大值;6、在抛物线的对称轴上有一点P的纵坐标为5,在直线上BC求一点M使得S△PBM∶S△ABC=1:5.7、在直线BC下方抛物线上是否存在一个点F,使得△BCF的面积最大,若存在,求出点F的坐标,并求出最大面积,若不存在,说明理由。
练习:1、如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.(1)求A、B两点坐标;(2)求抛物线的解析式;(3)点M是线段AB上的一个动点(不与A、B两点重合),过点M作MN∥BC,交AC于点N,连接CM,在M点运动时,△CMN的面积是否存在最大值?若存在,求出△CMN面积最大时点M的坐标;若不存在,请说明理由.2、(2010玉溪)如图,在平面直角坐标系中,点A的坐标为(1,△AOB(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(4)在(2)中x轴下方的抛物线上是否存在一点P,过点P作x轴的垂线,交直线AB于点D,线段OD 把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.yAB。
抛物线中的等腰三角形问题

抛物线中的等腰三角形问题
在数学中,抛物线广泛被研究和探讨。
而抛物线中的等腰
三角形问题是其中一个经典的问题。
抛物线是一个二次方程的图像,具有对称性质。
而等腰三
角形是指三边长度相等的三角形。
那么,抛物线中是否存在等腰三角形呢?
答案是肯定的。
事实上,抛物线上的任何一点都可以构成
一个等腰三角形。
这是因为抛物线的性质决定了在对称位置上的两个点关于焦点的距离相等,从而满足等腰三角形的定义。
具体来说,我们可以选择抛物线上的一个点P,并且连接P 点与抛物线的焦点F。
然后,从P点向下垂直引一条垂线,与
抛物线的切线交于点Q。
这样,三角形PFQ就是一个等腰三
角形,因为PF和QF的长度相等。
值得注意的是,抛物线上的每个点都可以成为等腰三角形
的顶点,因此存在无数个等腰三角形。
抛物线中的等腰三角形问题不仅有理论上的意义,而且在
实际应用中也有一定的应用。
例如,在物体抛出运动中,抛物线的形状对于确定物体的落点和轨迹起到重要作用。
对于特定起始条件,等腰三角形在抛物线上能够提供更多的信息。
总结而言,抛物线中存在无数个等腰三角形,这是由抛物
线的对称性质所决定的。
这个问题不仅仅是数学理论上的问题,也有着实际应用中的意义。
通过研究抛物线中的等腰三角形,我们可以更深入地了解抛物线的性质和特点。
抛物线中的直角三角形(安松)

解:存在点M,使得∠ADM=90°. 理由如下: 由抛物线y=X2+2x-3,得C(0,-3), ∵CD∥x轴, ∴D的纵坐标为-3, 把y=-3代入y=X2+2x-3,得
X2+2x-3=-3, 解得:x1=-2,x2=0, ∴D的坐标为(-2,-3),
设直线AD的解析式为y1=k1x+b1,则:
k1 b1 0 2k1 b1 3
解得:
b1k1
1 -1
∴直线AD的解析式为y1=x-1.
如图,过点D作直线DM⊥直线 DA交抛物线于点M,
设直线MD的解析式为
y2=-x+b2,
把D(-2,-3)代入y2=-x+b2,得
b2=-5,
∴直线MD的解析式为y1=-x-5.
1
10 39
10
F( 1 , 39) 10 10
综上所述,.....
B
C
范例学习
例题1:如图,抛物线y =x2-2x-3与x轴交 于A(-1,0)、B(3,0),与y轴交于C(0,-3),且对称 轴为x=1.设点P为抛物线的对称轴x=1上的一动 点,求使∠PCB=90°的点P的坐标.
分析:设P(3,m),先 用两点间的距离公式表示 出PC2,PB2及BC2,程 有实数根,则存在;否则不 存在.
当PF⊥PB时,
∵点P(1,4.5)、B(4,0),
∴设直线PB的解析式为 y=-1,5x+6,
∴设直线PF的解析式为
y = 2 x + b, 3
把P(1,4.5)代入y=2/3x+b,得
b = 23,
∴根据题意6得:y
y = -x = 2x
例谈抛物线中三角形面积最值问题的解法

知识导航三角形面积的最值问题一般比较简单,但抛物线中的三角形面积最值问题却较为复杂,这类三角形的面积常与动点的坐标有关,因而此类问题的难度一般较大.解题时需灵活运用平面几何知识、函数的图象和性质、基本不等式、三角形的性质和面积公式、抛物线的定义和性质等知识.那么,如何解答此类问题呢?一般可运用构造法和分割法来求解.下面我们结合实例来进行探讨.一、构造法构造法是指通过添加辅助线,构造出三角形的底或高,以能直接利用三角形的面积公式求得问题的答案.通常,可过三角形的一个顶点作x 轴或y 轴的垂线,使其与三角形的一条边相交,从而确定三角形的底或高,这样就可以根据三角形的面积公式进行计算了.例1.如图1所示,在平面直角坐标系中,点B 的坐标为(-3,-4),线段OB 绕原点逆时针旋转后与x 轴的正半轴重合,点B 的对应点为A ,如果点P 是抛物线上的一个动点且在x 轴的上方,当点P 运动到什么位置时,△PAB 的面积最大?解析:由于点P 是抛物线上的一个动点,所以我们无法确定△PAB 的形状,也就无法确定三角形的高和底,不能直接利用三角形的面积公式来求解,需要构造出三角形的高和底.可过点P 作PE 垂直x 轴交AB 于点E ,则S △ABP =S △APE +S △BPE ,此时△APE 的底为PE ,高为A 到PE 的距离;△BPE 的底为PE ,高为B 到PE 的距离,而A 、B 到PE 的距离之和为A 、B 的横坐标之差.当|PE |最大时,△PAB 的面积最大.借助两点间的距离公式和二次函数的性质便可顺利求得△PAB 面积的最值.解:过P 点作PE ⊥x 轴交AB 于点E ,如图1所示,设点P 坐标为(m ,-16m 2+56m ),可得到点E 的坐标为(m ,-12m -52).所以S △ABP =S △APE +S △BPE =12|PE |×8=4|PE |=4×(-16m 2+56m -12m +52)=-23m 2+43m +10,当m =-b 2a=1,S △ABP 取最大值,即S △ABP =(43)2-4×(-23)×104×(-23)=323.所以,当P 点坐标为(1,23)时,S △ABP 取最大值,且最大面积是323.一般地,当三角形底边的长为定值时,三角形的高与面积成正比,高越大其面积越大,只要求得高的最大值,便可求得面积的最大值.二、分割法当求三角形的面积遇到困难时,我们可以运用分割法,将三角形分割为两个或者两个以上的简单几何图形,借助简单几何图形的面积公式求得三角形的面积.当求抛物线中三角形面积的最值时,我们也可以将三角形分割为几个小三角形、平行四边形、梯形等,然后分别利用三角形、平行四边形、梯形面积公式求出各图形的面积,最后综合所得的结果即可求得三角形面积的表达式,借助函数的性质、基本不等式来求得最值.例2.如图2,已知抛物线y =-x 2+bx +c 与直线相交于A (-1,0),C (2,3)两点,与y 轴交于点N ,其顶点为D ,若点P 是该抛物线上位于直线AC 上方的一个动点,试求△APC 面积的最大值.解:,如图2,过点P 作PQ 垂直x 轴于点H ,交AC 于点Q ,过点C 作CG 垂直x 轴于点G .设Q (x ,x +1),则P (x ,-x 2+2x +3),则S △APC =S △APE +S 直角梯形PHGC -S △AGC=12(x +1)(-x 2+2x +3)+12(-x 2+2x +3)(2-x )-12×3×3=-32(x -12)2+278所以△APC 面积的最大值为278.由于点P 是该抛物线上位于直线AC 上方的一个动点,所以我们无法确定△APC 的形状,可以采用分割法来求解.将△APC 分割成两个小三角形△APE 、△AGC 和一个直角梯形形PHGC ,从而把三角形分割成几个规则的简单几何图形,运用三角形的面积公式和梯形的面积公式便可快速求得△APC 面积的表达式,将其视为关于x 的二次函数,借助二次函数的性质就能求得△APC 面积的最大值.总之,同学们在解答抛物线中三角形面积最值问题时,可根据三角形的特点和已知条件合理添加辅助线,构造出三角形的底或高,也可以将三角形分割为几个简单的几何图形,借助简单几何图形的面积公式来求解.在求得三角形面积的表达式后,可借助函数的性质或基本不等式来求得最值.(作者单位:江苏省盐城中学)陈巧巧图1图238。
抛物线与直角三角形结合的解题方法(二)
抛物线与直角三角形结合的解题方法(二)
抛物线与直角三角形结合的解题方法
1. 介绍
在解题过程中,经常会遇到抛物线与直角三角形的结合问题。
本
文将介绍一些常见的解题方法,帮助读者更好地理解和应用相关概念。
2. 方法一:求解焦点位置
•首先,根据已知条件,确定抛物线的形式方程。
,0),其中p是抛物线•确定抛物线的焦点坐标,用公式F=(p
2
的焦距。
•把焦点坐标带入方程,可以得到p的值。
•求得焦点坐标后,可以进一步应用直角三角形的相关知识,解题过程会更加简洁明了。
3. 方法二:利用直角三角形的性质
•首先,根据已知条件,确定直角三角形的两个已知边长和一个已知角度。
•利用三角函数的定义,求解出与已知角度相对应的弧度值。
•然后,利用三角函数的性质,得出抛物线的焦点坐标。
•最后,将焦点坐标带入方程,得到抛物线的具体形式。
4. 方法三:应用直角三角形的特殊性质
•首先,根据已知条件,判断是否可以构成一个直角三角形。
•如果可以构成直角三角形,利用勾股定理求解出第三条边长。
•然后,利用已知条件和已求得的边长,应用三角函数的基本关系,求解出其余相关角度和边长。
•最后,利用焦点的定义和直角三角形的特殊性质,得到抛物线的焦点坐标。
5. 小结
抛物线与直角三角形的结合是解题过程中常见的情况之一。
通过
应用已知条件和相关概念,可以有效地求解出抛物线的焦点坐标和具
体形式。
希望本文介绍的方法能够帮助读者更好地应用数学知识解决
实际问题。
抛物线与坐标轴交点构成的三角形问题
抛物线与坐标轴交点构成的三角形问题 -- 思考与探索面积篇例 1:已知抛物线 y=-x 2+2x+3与 x 轴交于 A,B 两点,其中 A 点位于 B 点的左侧,与 y 轴交于 C 点,顶点为 P , 半轴交于点 C ,M 为抛物线的顶点,那么△ ACM 与△ ACB 的面积比不变,请你求出这个比值。
2例 2、如图,一元二次方程 x 2 2x 3 0的二根 x 1,x 2( x 1 x 2 )是抛物线 y ax bx c 与 x 轴 的两个交点 B,C 的横坐标,且此抛物线过 A (3,6)点.(1)求此二次函数的解析式.(2)设此抛物线的顶点为 p ,对称轴与线段 AC 相交于点 Q ,求点 P 和点 Q 的坐标.(3)在 X 轴上有一动点 M ,当 MQ+MA 取得最小值时,求点 M 的坐标(4)设 AC 与Y 轴交与 D 点, E 点坐标为(0,1),在 X 轴上找一点 F ,抛物线对称轴上找一点 G ,使四 边形 AFGE 的周长最短,并求出当四边形周长最短时的点 F 、G 点坐标,并求出四边形 AFGE 的周长。
S △COP S△PABy轴负 S △ AOC = _______ S △ BOC 例:在平面直角坐标系中,有两点 小敏发现所有过 A ,B 两点的抛物线如果与形状篇1、已知抛物线y =ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y 轴负半轴交于点C。
若OA=4,OB=1,∠ACB=90°,求抛物线解析式。
A(-1,0)和B( 3,0),顶点为C,若∠ ACB=90度.问2:在抛物线的解析式中,b2 4ac3. 若题设中的A、B 两点的坐标未知,而已知∠ACB有关,那么如果△ ACB是等边三角形,则△是多少?最后, ①思因果; ②思规律; ③思多解; ④思变通;⑤思归类;⑥思错误.ACB=90度,你能求出b2 4ac 吗?4. 从上面的探索中我们看到解析式中的△与∠问1: C 点的坐标是多少?。
抛物线中的三角形问题
抛物线中的三角形问题在数学中,抛物线是一种二次曲线,其形状类似于开口朝上的弧线。
抛物线与三角形之间有着紧密的联系,本文将探讨抛物线中的三角形问题。
一、抛物线的定义与性质抛物线是指平面上满足平方差关系的点的集合。
一般来说,抛物线可以由二次方程的图像表示,常见的抛物线方程形式包括标准型、顶点型等。
根据方程的不同形式,可以得到抛物线的不同性质,如焦点、顶点、对称轴等。
二、抛物线中的三角形问题抛物线与三角形之间存在着丰富的几何关系,其中一些经典问题如下:问题一:抛物线上的三点确定一个三角形,该三角形的面积如何计算?解析:设抛物线的方程为y = ax^2 + bx + c,并选取抛物线上三个点A(x1, y1)、B(x2, y2)、C(x3, y3)。
根据三点确定一个三角形,可以利用三角形的高度与底边长度来计算面积。
首先,我们可以通过求解方程组得到顶点的坐标(xv, yv) = (-b/2a, f(-b/2a)),其中f(x)是抛物线的函数。
然后,利用向量的几何性质,求出三角形的高度h,再计算底边长度d,最后利用面积公式S = 0.5 * d * h计算出面积。
问题二:给定一个抛物线和一个点P,如何确定在抛物线上选择两个点形成的三角形,使其面积最大?解析:设抛物线的方程为y = ax^2 + bx + c,设点P的坐标为(xp, yp)。
对于以点P为顶点的抛物线上的任意一条直线,其倾斜角为θ,直线的方程可以表示为y = tanθ * x + C,其中C是常数。
当直线与抛物线相交时,可将两个方程联立求解,得到交点的坐标(x1, y1)和(x2,y2)。
然后,利用这两个交点与点P形成的三角形面积公式S = 0.5 *|x1y2 - x2y1 - x1yp + xpy1 + x2yp - xpy2|,求解出最大的面积。
问题三:已知一个抛物线,如何确定两个定点,使其与抛物线上的另一个点形成的三角形周长最小?解析:设抛物线的方程为y = ax^2 + bx + c。
抛物线内接直角三角形的一个性质及应用
抛物线内接直角三角形的一个性质及应用抛物线内接直角三角形是几何学中一个重要的定理,它告诉我们:如果一个直角三角形的一个顶点在抛物线上,那么其它两个顶点的坐标也会在这个抛物线上。
本文将简要介绍抛物线内接直角三角形的定义、性质及其应用。
首先,抛物线内接直角三角形定义为:一个直角三角形,其中一个顶点在抛物线上,另外两个顶点也在抛物线上,且抛物线的准线和直角三角形的两条腰都相交。
因此,抛物线内接直角三角形的性质有以下三点:
1)直角三角形的一个顶点在抛物线上,另外两个顶点也在同一
条抛物线上;
2)抛物线的准线与直角三角形的腰相交;
3)抛物线内接直角三角形的面积小于等于抛物线面积的一半。
此外,抛物线内接直角三角形还有一些其它特性:抛物线内接直角三角形的高度等于抛物线的端点之间的距离;两点定理说明了任何一点到抛物线上的点的距离等于直角三角形的斜边的长度。
抛物线内接直角三角形有许多实际应用,其中最为重要的是在机械设计中,抛物线被用来设计螺旋形线路,使得机械运动更加均匀,减少了摩擦力,减少了损耗。
在建筑过程中,抛物线也被用来设计电梯的曲线,使其运行曲线十分柔和,降低了电梯的震动,减少了乘客的不适感受。
另外,抛物线内接直角三角形也被用于医学领域中的X 射线成像技术,使得X射线的扫描更加准确,精确诊断病症。
综上所述,抛物线内接直角三角形是几何学中一个重要的定理,它描述了三角形和抛物线之间的关系,它的定义、性质和应用在许多不同的领域中有广泛的应用,它能够减少摩擦力、降低震动,使X射线扫描更准确,为人类带来科学和技术上的进步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛物线中的三角形问题
一、教学目标:
1、知识、能力目标:
通过复习,使学生了解将抛物线与三角形有机地结合在一起的综合题。
2、情感目标:
感受数形结合的优美与和谐。
二、教学过程:
近年来在各地中考数学试题中出现了一类新的热点题型,将抛物线与三角形有机地结合在一起。
这类题目综合性强,难度较大,本节来归纳这类试题的基本类型与求解。
一、根据已知条件判定或证明抛物线中三角形的形状
例1、已知二次函数y=(a+c)x 2
+2bx-(c-a),其中a,b,c,是△ABC 的三边,且a b ≥,a c ≥, a+c=2b,若这个二次函数的图象过原点,试证△ABC 是等边三角形。
证明 抛物线y=(a+b)x 2
+2bx-(c-a)过原点,将原点坐标(0,0)代入解得:a=c. 又a+c=2b , ∴a=b=c , 故△ABC 是等边三角形。
二、已知抛物线中三角形的形状,求解(证)有关二次函数问题
例2、已知抛物线y=x 2
+kx+1与x 轴的两 个交点A,B 都在原点右侧,顶点是C ,△ABC 是等腰直角三角形。
求证:(1)
;(2)求k 的值。
分析:本题要沟通函数与方程的关系,方程的根即为抛物线与x 轴交点的横坐标。
运用这一解题思想比较简捷。
解 (1)设A ,B 两点的坐标分别是(1x ,0),(2x 0),则 :
121
12x x k x x +=-=
∴AB=
21X X -=
=
(2) 抛物线y=2
x +kx+1的顶点C 的坐标是(-2
k ,2
44k -)。
△ABC 是等腰直角三角形的性质得:
244k -=12
k=±.
A,B 两点在原点的右侧, ∴k=-(12x x +)<0,从而 k=-
三、已知抛物线中三角形的面积。
求抛物线上点的坐标
例3、已知二次函数y=x 2
-(m-2)x+m 的图象经过(-1,15),设此二次函数的图象与x 轴的交点是A,B,图象上的点C 使△ABC 的面积等于1,求点C 的坐标。
分析:根据题设条件易求得A 、B 两点的坐标,然后由面积公式确定C 点的坐标。
解:∵函数2(2)y x m x m =--+的图像过(-1,15), ∴15=2
(1)(2)(1)m m ----+, ∴m=8。
∴二次函数的解析式为2
68x y x -+=令y=0,则2
68x x -+=0。
解得122,4x x ==。
从而求得A(2,0),B(4,0)。
设图象上一点C(x,y),则S △ABC=1
12AB y ⋅⋅=,
∵2x x B A AB -==, ∴1y =,1y =±。
①当y=1时,268x x -+=1,得3x =±y=-1时,2
68x x -+=-1,得312x x ==
故所求C 点的坐标是(3或(3或(3,-1)。
四、已知抛物线中三角形的面积,求函数解析式
例4、已知抛物线2
y x bx c =++的对称轴在y 轴右侧,且抛物线与y 轴交于Q (0,-3),与x 轴交于点A ,B ,顶点是P ,△PAB 的面积是8,求函数的解析式。
解:∵抛物线与y 轴交于Q (0,-3)
∴c=-3,∴2
3y x bx =+-。
设抛物线与x 轴交点坐标是(,0),(,0)12A x B x ,则,31212x b x x x +=-=-。
∴21AB x x =-
∵函数2
3y x bx =+-的顶点P 的坐标是2
12(,)2
4
b
b +--
,∴△PAB 底边AB 上高是
214
b +。
12(12)84
b +=,即2b =±, ∵抛物线在y 轴右侧,∴b=-2, ∴所求函数解析式是2
23y x x =--。
五、探索抛物线中三角形的面积
例5、已知抛物线过M (0,-3),N (2,-3),P (4,5)三点。
在第二象限内抛物线上有一点A 到两坐标轴的距离相等,且抛物线与x 轴交于B 、C 两点,求△ABC 的面积。
解:由题意知:
16a+4b+c=5, a=1, 4a+2b+c=-3,⇒ b=-2, c=-3, c=-3。
∴函数的解析式为2
23y x x =--。
设(-m ,m),则2
23m m m =+-,即2
30m m +-=,得11
2
12
2
m m
-=
-=
∵点在第二象限,∴舍去122m -=
, ∴11(
22
A -,令y=0得: 2
230x x --=⇒3,112x x ==-,∴抛物线与x 轴的交点是(3,0),(-1,0)。
∴BC=4,S △ABC =
114122
-⨯⨯
=。
