第4章_时间频率测量3
信号与系统第4章 周期信号的频域分析(3学时)

T0 /2
0
x(t )sin(n 0t )dt
四、信号对称性与傅里叶系数的关系
3、半波重迭信号
~ x (t ) ~ x (t T0 / 2)
~ x (t )
A t
T0
T0 / 2 0
T0 / 2
T0
特点: 只含有正弦与余弦的偶次谐波分量,而无奇次谐波分量。
四、信号对称性与傅里叶系数的关系
~ x (t )
2 1 -4 -3 -2 -1 1 2 3 4
~ x (t ) ~ x1 (t ) ~ x2 (t )
nπ nπt t~ x (t ) 1.5 Sa ( ) cos( ) 2 2 n 1
~ x1 (t )
2
x 1(t ) 2
1 2 3 4
-4 -3 -2 -1
三、周期信号的功率谱
一、周期信号频谱的概念
连续时间周期信号可以表示为虚指数信号之和,其 中Cn 为傅里叶系数 。
~ x (t )
n =
Cn e
jn0t
1 Cn T0
T0 t 0
t0
~ x (t )e jn 0t dt
问题1:不同信号的傅里叶级数形式是否相同? 相同 问题2:不同信号的傅里叶级数不同表现在哪里? 系数
例3 课本P129
例4 已知连续周期信号的频谱如图,试写出信号的 Fourier级数表示式。 Cn
3 2 1 1 3 4 3 2
9
6
0
3
6
9
n
解: 由图可知 C0 4
C 1 3
C2 1
C 3 2
~ x (t )
第4章 第3讲 匀速圆周运动

例2:如图4-3-2所示,用细 绳一端系着的质量为M=0.6kg的物 体A静止在水平转盘上,细绳另一 端通过转盘中心的光滑小孔O吊着 质量为m=0.3kg的小球B,A的重心 到O点的距离为0.2m.若A与转盘间 的最大静摩擦力为f=2N,为使小球 B保持静止,求转盘绕中心O旋转的 角速度ω的取值范围.(取g=10m/s2, 保留两位有效数字)
例1:如图4-3-1所示的传动装置中,B、 C两轮固定在一起绕同一轴转动,A、B两轮用 皮带传动,三轮半径关系是rA=rC=2rB.若皮带 不打滑,求A、B、C轮边缘的a、b、c三点的角 速度之比、线速度之比和向心加速度之比.
解析:A、B两轮通过皮带传动,皮带不打滑, 则A、B两轮边缘的线速度大小相等,即:va=vb或 va∶vb=1∶1 由v=ωr得:ωa∶ωb=rB∶rA=1∶2 B、C两轮固定在一起绕同一轴转动,则B、C 两轮的角速度相同,即ωb=ωc或ωb∶ωc=1∶1
由v=ωr得:vb∶vc=rB∶rC=1∶2
所以:ωa∶ωb∶ωc=1∶2∶2 va∶vb∶vc=1∶1∶2 因为a=vω,所以aa∶ab∶ac=1∶2∶4
点评:传动装置特点:凡是直接用皮带传动(包括 皮带传动、齿轮传动) 的两个轮子,两轮边缘上各点的 线速度大小相等;凡是同一个轮轴上(各个轮都绕同一 根轴同步转动)的各点角速度相等(轴上的点除外). v2 警示:an= = 2 r=v· 这几个公式是用瞬时量线 r 速度v和角速度 表示的,因而既适用于匀速圆周运动,
(1)物理意义:描述质点沿圆周运动的 慢 . 快
(2)方向:质点在圆弧某点的线速度方向沿 圆弧该点的 切线 方向.
(3)大小:v=s/t(s是t时间内通过的弧长).
2.角速度 (1)物理意义:描述质点绕圆心转动的 慢 . 快
电子测量题库
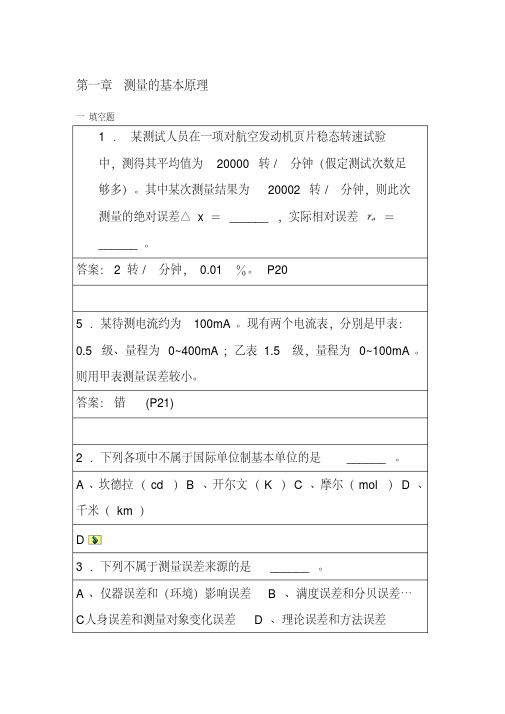
对 8: 在进行阿伦方差的测量时, 组与组之间以及组内两次测量之间必须 都是连续的。( )
答案:
错
三、选择题:
1、在通用计数器测量低频信号的频率时,采用倒数计数器是为了(
)
A. 测量低频周期 B. 克服转换误差 C.测量低频失真 D. 减小测频时的量化误差影响
答案:
D 3、测频量化误差曲线和测周量化误差曲线交点处的频率,称为(
错
9 .在测量不确定度的评定前,要对测量数据进行异常数据判别,一旦 发现有异常数据应先剔除之。
对 三、选择题:
2 .在使用连续刻度的仪表进行测量时,一般应使被测量的数值尽可能在 仪表满刻度值的 ____ 以上。
d 3 .贝塞尔公式利用有限次测量数据对测量值的总体方差进行估计,试 指出下面各式哪个是贝塞尔公式的正确表示 ____ 。
电子计
答案:
多周期
5: 采用电子计数器测频时,当被计数频率一定时, ____可以减小±1
误差对测频误差的影响;当闸门时间一定时, ____,则由±1 误差产
生的测频误差越大。 答案:
增大闸门时间、被计数频率越低
6: 在进行频率比测量时 , 应将 ____的信号加在 B 通道,取出 ____( 周期 倍乘为 1) 作为计数的闸门信号,将 ____ 的信号加在 A 通道,作为被
a 8 .被测电压真值为 100v ,用电压表测试时,指示值为 80v ,则示值相 对误差为( )。 (a) +25% (b) -25% (c) +20% (d) -20%
d
10. 通常在相同的条件下,多次测量同一量时,误差的绝对值和符号保持
恒定或在条件改变时,按某种规律而变化的误差称为
________ 。
《电子测量技术》教案

只要有测量,必须有测量结果,有测量结果必然产生误差。误差影响测量精度。
对误差的特点,性质及分类要有全面系统的了解,最后找出合理的、科学的办法加以消除。
思考题、讨论题、作业:
参考资料(含参考书、文献等):
1.《电子测量技术》夏哲雷主编,机械工业出版社
2.《电子测量技术基础》杨吉祥编著,东南大学出版社
电子测量技术课程教案
授课题目(教学章节或主题):
第3章电压测量
3.1概述
3.2电压的模拟测量
3.3电压的数字化测量
授课类型
理论课
授课时间
第1周周3第6-7节
重点:
测量误差的估计和处理,测量不确定度的评定在科学研究和生产中的重要作用。
难点:
根据误差的性质,将测量误差分为随机误差、系统误差、粗大误差三类,这三类误差的概念和来源;
与测量结果有关的三个术语:准确度、精密度、精确度,及它们与系统误差、随机误差和总误差的关系。
教学手段与方法:
教学方式:讲授
教学资源:多媒体
教学手段与方法:
教学方式:讲授
教学资源:多媒体
思考题、讨论题、作业:
3-4
参考资料(含参考书、文献等):
1.《电子测量技术》夏哲雷主编,机械工业出版社
2.《电子测量技术基础》杨吉祥编著,东南大学出版社
电子测量技术课程教案
授课题目(教学章节或主题):
第4章时间频率测量及调制域分析
4.1时间频率测量
4.2电子计数器
电子测量技术课程教学大纲

《电子测量技术》课程教学大纲学时: 48 学分:2.5理论学时: 28 实验学时:20面向专业:电信工程/电信科技课程代码:先开课程:模拟电子技术、数字电子技术、概率论、信号与系统、微机原理课程性质:必修执笔人:车晓言代爱妮审定人:陈龙猛曹洪波第一部分:理论教学部分一、说明1、课程的性质、地位和任务电子测量技术是电子信息、自动控制、测量仪器等专业的通用技术基础课程。
包括电子测量的基本原理、测量误差分析和实际应用,主要电子仪器的工作原理,性能指标,电参数的测试方法,该领域的最新发展等。
电子测量技术综合应用了电子、计算机、通信、控制等技术。
通过本课程的学习,培养学生具有电子测量技术和仪器方面的基础知识和应用能力;通过本课程的学习,可开拓学生思路,培养综合应用知识能力和实践能力;培养学生严肃认真,求实求真的科学作风,为后续课程的学习和从事研发工作打下基础。
2、课程教学和教改基本要求(1)模块化、多层次教学方法(2)理论联系实际(3)互动式、开放式教学方法(4)课程组的教学方法研讨(5)考试方式的改革通过本课程的学习,培养学生具有电子测量技术和仪器方面的基础知识和应用能力;通过本课程的学习,可开拓学生思路,培养综合应用知识能力和实践能力。
二、教学内容与课时分配第1章.测量的基本原理(4学时)(1)测量的基本概念、基本要素,测量误差的基本概念和计算方法。
(2)计量的基本概念,单位和单位制,基准和标准,量值的传递准则。
(3)测量的基本原理,信息获取原理和量值比较原理。
(4)电子测量的实现原理:变换、比较、处理、显示技术。
重点:掌握测量与计量的基本概念,测量误差的概念与来源,测量的量值比较原理。
了解信息的获取原理,测量的基本实现技术。
难点:测量的量值比较原理第2章.测量方法与测量系统(2学时)(1)电子测量的意义、特点、内容。
(2)电子测量的基本对象——信号和系统的概念、分类。
(3)电子测量方法分类。
(4)测量系统的基本特性——静态特性和动态特性。
《信号与系统》第四章

图 两个矢量正交
矢量的分解
c2V2
V
V2
2
o
1
V1
c1V1
图 平面矢量的分解
c3V3
V3
V
o V1
V2
c2V2
c1V1
V c1V1 c2V2 c3V3
图 三维空间矢量的分解
推广到n维空间
1 正交函数的定义
在区间 (t1,t内2 ),函数集 {0 (t),1(t中),的,各N个(t)函} 数间,若满足下列 正交条件:
➢在波形任一周期内,其第二个半波波形与第一个半波波形相同;
x(t) x(t T0 / 2)
➢这时x(t)是一个周期减半为
的周期非正弦波,其基波频率
为
,即其只含有偶次谐T0波2;
20
4.4波形对称性与傅里叶系数
4 奇半波对称
➢在波形任一周期内,其第二个半周波形恰为第一个半周波形的
负值; x(t) x(t T0 / 2)
交函数集 {0 (t),1(t), ,N (t)} 是完备的,即再也找不到一个函数 (t)
能满足
t2
(t)
* m
(t
)dt
0
t1
m 0,1, , N
则在区间 (t1,t2 ) 内,任意函数x(t)可以精确地用N+1个正交函数地加权和
表示:
N
x(t) c00 (t) c11(t) cN N (t) cnn (t)
T0
3 傅里叶级数系数的确定
➢正弦—余弦形式傅里叶级数的系数
2Bk
2 T0
x(t) cos k0tdt
T0
2Dk
2 T0
x(t) sin k0tdt
程佩青_数字信号处理_经典版(第四版)_第4章_4.3按频率抽选(DIF)的基-2算法
x(7) -1
WN3
X(7)
x(0)
2点
X(0)
x(1)
DFT
X(4)
x(2)
WN0
-1
2点
X(2)
x(3)
WN2 DFT
-1
X(6)
x(4) -1
WN0
x(5) -1
WN1
2点
X(1)
DFT
X(5)
x(6) -1 x(7) -1
WN2 WN3
WN0
-1
2点
X(3)
WN2 DFT
-1
X(7)
x(0) x(1) x(2) x(3) x(4) -1 x(5) -1 x(6) -1 x(7) -1
例:已知x(n)={1,2,3,4}利用频域抽样流图,计算
X (k) DFT{x(k)}; DFT{X (k)}
1 x[0] 2 x[1] 3 x[2] 4 x[3]
4
6
1 W40 1
1
2
W41 j
1
2j 1
X[0] 10 X[2] 2 X[1] 2+2j X[3] 22j
DFT{x[k]}= {10, 2+2j, 2, 22j}
x(n)
x(n
N
/
2)
WNn
W nr N /2
注意括号
(4.3.3)
n0
k = 2r+1
频率抽取FFT
W n(2r1) N
WNnWN2nr
WNnWNnr2
存储单元
输入序列x(n) : N个存储单元
系数WNr:N / 2个存储单元
频率抽取FFT
N / 21
X (2r) [x(k) x(n N / 2)]WNnr/2 n0
第四章系统的频率特性分析
第四章 频率特性分析4.1 什么是频率特性?解 对于线性定常系统,若输入为谐波函数,则其稳态输出一定是同频率的谐波函数,将输出的幅值与输入的幅值之比定义为系统的幅频特性;将输出的相位于输入的相位之差定义为系统的相频特性。
将系统的幅频特性和相频特性统称为系统的频率特性。
4.2 什么叫机械系统的动柔度,动刚度和静刚度?解 若机械系统的输入为力,输出为位移(变形),则机械系统的频率特性就是机械系统的动柔度;机械系统的频率特性的倒数就是机械系统的动刚度;当0=w 时,系统频率特性的倒数为系统的静刚度。
4.3已知机械系统在输入力作用下变形的传递函数为 12+s (mm/kg),求系统的动刚度,动柔度和静刚度。
解 根据动刚度和动柔度的定义有 动柔度()()()12+====jw jw s s G jw G jw λ mm/kg 动刚度 )(jw K =)(1jw G =21+jw kg/mm 静刚度 ()()5.0021010==+====K w jw w jw G w jw kg/mm4.4若系统输入为不同频率w 的正弦函数Asinwt,其稳态输出相应为Bsin(wt+ϕ).求该系统的频率特性。
解:由频率特性的定义有 G (jw )=AB e jw。
4.5已知系统的单位阶跃响应为)(。
t x =1-1.8te 4-+0.8te9-,试求系统的幅辐频特性与相频特性。
解:先求系统的传递函数,由已知条件有)(。
t x =1-1.8te 4-+0.8te9-(t 0≥))(S X i =s 1)(。
S X =s 1-1.841+s +0.891+s )(S G =)()(。
S X S X =()()9436++s s )(jw G =jw s s G =)(=()()jw jw ++9436)(w A =)(jw G =22811636ww +•+)(w ϕ=0-arctan 4w -arctan 9w =-arctan 4w -arctan 9w4.6 由质量、弹簧、阻尼器组成的机械系统如图所示。
第4章-时间与频率测量-习题-答案
电子测量技术第四章(一)填空1、电子计数器的测周原理与测频相反,即由被测信号控制主门开通,而用晶振脉冲进行计数。
2、电子计数器测频的基本原理刚好与测周相反,即由___ _晶振 _____控制主门开门,而用被测信号进行计数。
3、测量频率时,通用计数器采用的闸门时间越____大____,测量准确度越高。
4、测量周期时,通用计数器采用的闸门时间越____大____,测量准确度越高。
5、通用计数器测量周期时,被测信号周期越大,量化误差对测周精确度的影响越小。
6、通用计数器测量频率时,被测信号周期越小,量化误差对测周精确度的影响越小。
7、在用通用计数器测量低频信号的频率时,为了减小测量误差,应采用测周法。
8、电子计数器测周时,选用的时标越小,则显示的位数越多,量化误差的影响就越大。
9、电子计数器的测量误差来源主要有触发误差、闸门时间误差和标准频率误差三种。
10、电子计数器的误差来源有___量化误差___、__标准频率误差__和___触发误差___;其中量化误差是主要来源,其绝对值恒为定值。
11、用电子计数器测量频率比时,周期小的信号应加到输入通道 A 。
用电子计数器测量频率,如闸门时间不变,频率越高,则测量误差越小;测量周期时,如时标(计数脉冲周期)不变,被测信号频率越高,则测量误差越大。
7、计数器测周的基本原理刚好与测频相反,即由_被测周期控制主门开门,而用_标准频率_进行计数。
(二)选择题1、通用计数器测量周期时由石英振荡器引起的主要是( C )误差。
A.随机B.量化C.变值系统D.引用2、下列选项中通用计数器不能测量的量是( D )A.频率B.相位C.周期D.电压3、在通用计数器测量低频信号的频率时,采用倒数计数器是为了( D )A.测量低频周期B.克服转换误差C.测量低频失真D.减小测频时的量化误差影响4、在电子计数法测量频率时,测量误差通常有两部分组成,分别是( A )误差和( C )误差。
A、量化B、触发C、标准频率5、通用计数器在测量频率时,当闸门时间选定后,被测信号频率越低,则( C )误差越大。
机械工程控制基础(第4章_系统的频率特性分析)
对频率 的函数曲线,此即幅频特性曲线;作出相位 ) (
的函数曲线,此即相频特性曲线。
对频率
由上可知,一个系统可以用微分方程或传递函数来描述,也可以
用频率特性来描述。它们之间的相互关系如图4.1.2所示。将微分方程
的微分算子 中的s再换成 j,传递函数就变成了频率特性;反之亦然。
d 换成s后,由此方程就可获得传递函数;而将传递函数 dt
式中,
u ( ) 是频率特性的实部,称为实频特性 v( ) 是频率特性的虚部,称为虚频特性
武科大城市学院
机电学部
4.1.3 频率特性的求法
1. 根据系统的频率响应来求取
因为
K G s Ts 1 X i X i s 2 s 2
X i xo t L G s 2 s 2
G j 端点的轨迹即为频率特性的极坐标图, 或称为Nyquist 图, 如
实轴开始, 逆时针方向旋转为正, 顺时针方向旋转为负。当从0→∞时,
武科大城市学院
机电学部
图4.2.1所示。它不仅表示幅频特性和相频特性, 而且也表示实频特性和
虚频特性。图中的箭头方向为从小到大的方向。
正如4.1节所述, 系统的幅频特性和相频特
武科大城市学院
机电学部
2. 频率特性
线性系统在谐波输入作用下,其稳态输出与输入的幅值比是输入
信号的频率 的函数,称为系统的幅频特性,记为A( ) 它描述了在稳态情况下,当系统输入不同频率的谐波信号时,其幅值 的衰减或增大特性。显然
X o ( ) A( ) Xi
) 稳态输出信号与输入信号的相位差 ( (或称相移)也是 的函
1
所以
1 T 2 2 X K A o Xi 1 T 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N
Ts Tx ;
测周时
N
Tx T0 。
例:若Ts=1s,T0=1us,则fm=1kHz,在该频率上,测频与测周的量化误差相等。
第6页
T1
电子测量
4)触发误差
◆周期测量时触发误差的影响 ●尖峰脉冲 周期测量时,尖峰脉冲的干扰对测量结果的影响非常 严重。如图,
第7页
2)多周期同步法 ◆多周期同步测频
测频时量化误差是由于闸门与被测信号的非同步引起的。为 减小量化误差,必须使闸门时间等于被测信号整周期数。 ●设计原理
采用预置闸门,用fx 对预置闸门同步,在实际 的同步闸门时间内同时对 fx计数得被测信号整周期 计数得Nx 。为确定同步 闸门时间,用另一计数器 对标准频率f0计数得N0。
x
N fc Tc Tx Nf
式中,N为测周时的计数值。
Ts 10n Tc 1 n f /N c Nf 10 Tx NTc N
Ts=10nTc
第23页
电子测量原理
1)倒数计数器
式
Ts 10n Tc 1 n Nf 10 Tx NTc N
c
表明,N f
1 N
实现:首先对被测信号测周,得计数值N,再在10nTc闸门时 f 1 间内对 NT (晶振的N分频)计数,即得计数值Nf。 N ◆原理图
电子测量原理
4.5 电子计数器的测量误差
4.5.1 测量误差的来源
1)量化误差;2)触发误差;3)标准频率误差
4.5.2 频率测量的误差分析
1)误差表达式;2)量化误差的影响; 3)实例分析
4.5.3 周期测量的误差分析
1)误差表达式;2)量化误差的影响; 3)中界频率; 4)触发误差
第1页
电子测量原理
本章小结
3.电子计数器的主要技术指标有:测试功能、测 量范围、输入特性、测量准确度、石英晶体振荡 器的频率稳定度、闸门时间和时标以及输出等。
电子计数器的基本工作原理是比较测量法,将待 测的时间和频率与标准的时间间隔和标准频率进 行比较,得到整量化数字N。
第19页
电子测量原理
本章小结
4.电子计数器由于闸门信号和计数信号的不同, 而具有:测频、测周、测时间间隔、测频率比、 自校等多种测量测量功能。 5.电子计数器测量频率的误差主要有:量化误 差和闸门时间误差; 电子计数器测量周期的误差主要有:量化误差、时 标误差和触发误差。
实际中,对正弦输入信号,常选择过零点为触发点(具有最 陡峭的斜率),则触发点电压VB满足:VB Vm 于是,有:
T
若考虑在一个周期开始和结束时可能都存在触发误差,分别 用 T1、T2 表示,并按随机误差的均方根合成,得到:
Tx Vn Tn T T2 2 Vm
2 1 2
Vn T V x n tan 2 Vm
4.6.1 多周期同步测量技术
1)倒数计数器;
2)多周期同步法
4.6.2 模拟内插法
1)内插法原理; 2)时间扩展电路
4.6.3 游标法 4.6.4 平均法
第22页
电子测量原理
4.6.1 多周期同步测量技术
1)倒数计数器
◆如前述,对低频信号,为减小量化误差,宜采用测周方案。 但测周时不能直接得到频率值的显示结果,为得到频率 值显示,硬件上采用了一种特殊设计——即倒数计数器。 ◆原理:首先按测周模式,设计数值为N,再设法将1/N予以 显示。 f 思路:设测周的时标来自 晶振(Tc),测频的闸门 为Ts=10nTc,则测频时 计数值
第26页
电子测量原理
4.6.2 模拟内插法
一般时间间隔测量的局限性:
为减小量化误差,需减小时标以增大计数值,但时标 的减小受时基电路和计数器最高工作频率限制,而计数 器也有最大计数容量的限制(最大计数值)。 内插法对已存在的量化误差,测量出量化单位以下的 尾数(零头时间)。如下图所示,
电子测量
4.5.3 周期测量的误差分析
2)量化误差的影响 T ◆由测周的误差表达式: Tx
1 Tc f c k T T Tc fc Txxff0c xff 0c Tx
1 k
其中,第一项即为量化误差。它表示Tx愈大(被测信号 的频率愈低),则量化误差愈小,其意义为Tx愈大则计 入的时标周期数N愈大。另外,晶振的分频系数k愈小, 则时标周期愈小,在相同的Tx内计数值愈大。 此外,第二项为标准频率误差,通常也要求小于测量误 差的一个数量级,这时就可作为微小误差不予考虑。
◆为减小量化误差,应增加计数值N,但也需注意不可使其
溢出。 例如:一个6位的计数器,最大显示为999999,当用T0=1us的时标测
第5页
量Tx=10s(fx=0.1Hz)时,应显示“10000000”us或“10.000000”s,显然溢 出。
电子测量
4.5.3 周期测量的误差分析
3)中界频率 ◆测频时,被测频率fx愈低,则量化误差愈大;
由 T0 kTc (Tc为晶振周期,k为倍频或分频比),
Tc f c Tc fc
Tx f c 而计数值N为: N Tx T x Txf0 T0 kTc k
1 1 Tc f c T k k 所以, T Tx T Tc f fc Txxff0c xf0 c Tx 第4页
●结论:测周时为减小触发误差,应提高信噪比。
第12页
电子测量
4.5.3 周期测量的误差分析
4)触发误差
◆频率测量时触发误差的影响
●尖峰脉冲的干扰 尖峰脉冲只引起触发点的改变,对测频影响不大。 ●高频叠加干扰 产生错误计数。
●措施 增大触发窗或减小信号幅度;输入滤波。
第13页
电子测量原理
4.5.3 周期测量的误差分析
N k N Tx f c
电子测量
4.5.3 周期测量的误差分析
1)误差表达式 ◆由测周的基本表达式: Tx N T0
Tx T0 N 根据误差合成公式,可得: Tx N T0 T N 1
式中, 有: T
T0
0
N
N
和
0
T0
分别为量化误差和时标周期误差。
第20页
电子测量原理
本章小结
减小误差的方法是:增加计数值、提高信噪比和选 用高精度的标准频率。 使测频和测周误差相等的频率称为中界频率。 6.利用游标法测量时间间隔可以消除量化误差并 提高测量精度。
7.E312B型通用电子计数器的使用。
第21页
电子测量原理
4.6 高分辨时间和频率测量技术
测周时,被测频率fx愈高,则量化误差愈大。 可见,在测频与测周之间,存在一个中界频率fm,使得测 频、测周误差相等。 当fx>fm时,应采用测频;当fx<fm时,应采用测周方案。
◆中界频率fm的确定
量化误差取决于计数值N,测频时 Ts Tm 令两式相等,并用Tm表示Tx: 于是,有:Tm TsT0 或
中界频率fm
Tm TsT0
fm
1 TsT0
第2页
N k N Tx f c
电子测量原理
4.5.3 周期测量的误差分析
1)误差表达式 ◆由测周的基本表达式: Tx N T0
Tx T0 N 根据误差合成公式,可得: Tx N T0 T N 1
式中, 有: T
电子计数器测量周期的误差主要有:量化误差、 时标误差和触发误差。第16页
电子测量原理
3、深入分析误差产生的原因及研究解决方法是本章的 另一个重点。在理论分析的基础上,我们讨论了减小 误差的方法,比如采用高精度频率源来减小标准频率 误差;采用多周期测量方法减小触发误差;采用内插 法和游标法减小量化误差等。 4、频率准确度和频率稳定度是标准频率源的两项主要 指标。对标准频率源的测量属于频率精密测量的内容 ,这种测量是通过两个不同精度等级的频率源之间进 行比对来实现的。由于一个频率源的准确度是由它的 频率稳定度来保证的,因此,检定一个频率源的主要 内容是测量它的频率稳定度。 调制域测量是电子测量发展的一个新方向,对它的了 解能够扩展对本领域了解的范围,并把握最新的动态 。
4.5.2 频率测量的误差分析
频率测量的误差表达式:
1 f x f c T f f fx c s x
N 1 1 N N Ts f x
中界频率fm的确定
测周的误差表达式
1 1 Tc f c T k k T Tx T Tc fc Txxff0c xff 0c Tx
电子测量
3)周期的测量
原理框图:
第8页
电子测量
尖峰脉冲的干扰
高频叠加干扰 第9页
T1
电子测量
4)触发误差
◆周期测量时触发误差的影响 ●尖峰脉冲 周期测量时,尖峰脉冲的干扰对测量结果的影响非常 严重。如图,测量误差为:T Tx ' Tx ●分析 设输入为正弦波: vx Vm sin xt ,干扰幅度为Vn。 对触发点A1作切线ab,其斜率为
4)触发误差 ◆频率测量时触发误差的影响
●尖峰脉冲的干扰 如图,尖峰脉冲只 引起触发点的改变, 对测频影响不大。 ●高频叠加干扰 如图,产生错误计数。 ●措施 增大触发窗或减小信号幅度; 输入滤波。
第14页
电子测量原理
本章小结
1、时间与频率是最基本的一个参量。时间与频 率基准的精确度是所有计量基准中最高的一种。 本章首先给出时间和频率的基本概念以及时间和 频率标准的建立。
c
图中计数器1 和计数器2分别工 作在测周和测频模 式。预定标器(由
触发器
Tx
主门 I
计数器I
