第二章 电力网各元件的等值电路和参数计算
合集下载
工学电力网络元件的等值电路和参数计算
Y 2
V2
I&1
Z 2
V1
Z 2
I2
Y
V2
Π型电路
Z B Zcshl
Y
2( A1) B
2(chl 1) Z c shl
T 型电路
Y shl
Zc
Z Zcshl chl
推导： V&1 V&2 I&2 V&2Y / 2 Z
1 ZY / 2V&2 ZI&2
V&1 A&V&2 B&I&2
V I
V2chx V2 shx
ZC
I2 ZC shx I2chx
传播常数
g0 jC0 r0 jL0 z0 y0 j
波阻抗（特性阻抗）ZC
r0 jL0 g0 jC0
z0 y0
RC
jXC
ZC e jc
当 x 时l ，线路首端与末端的电压和电流关系为
V I
V2chx V2 shx
( x0b0
r02
b0 x0
)l
2
kb
1 1 12
x0b0l 2
总结
一、输电线路的方程式
V I
V2chx V2 shx
ZC
I2 ZC shx I2chx
双曲线函数
chrx 1 (ex ex ) 2
V1 I1
V2chl I2 ZC shl
V2 ZC
shl
I2chl
shrx 1 (ex ex ) 2
ddxI&V&(g0
jC ) 0
d 2V& (g dx2 0
jC )(R 00
j L0)V&
第02章系统元件的等值电路和参数计算
%
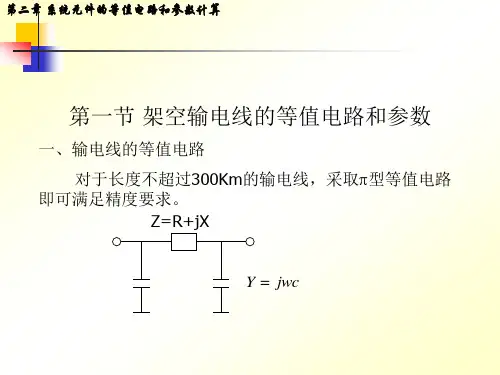
Vs(23)
%
Vs 2
%
Vs (1 2 )
%
Vs ( 2 3) 2
%
Vs(31)
%
Vs3 %
V % s(31)
V % s(23) 2
V % s(12)
Xi
VSi
%
V2 N
100 SN
103
第二章 系统元件的等值电路和参数计算
第三节 标幺制
一、概念 有名制：用实际有名单位表示物理量的单位制系统。 标幺制：用相对值表示物理量的单位制系统。
第二章 系统元件的等值电路和参数计算
电力系统中，220KV以上的输电线长采取分裂导线。具体 说来，220KV线路不分或双分，330KV线路双分裂，500KV 线路三分裂或四分裂，如图示：
d
d: 分裂间距
d
d
双分、三分和四分裂导线的自几何均距分别定义为：
Dsb DS d ,
Dsb 3 DS d 2 ,
L
i
，
M
AB
AB
iB
对于非铁磁材料制成的圆柱形导线，
单导线自感： L 0 (ln 2l 1)H / m 2 Ds
平行导线间互感： M 0 (ln 2l 1)H / m 2 D
第二章 系统元件的等值电路和参数计算
其中，
DS－导线的自几何均距
单股线：DS
1
re 4
铝绞线： Ds (0.724 0.771)r 钢心铝绞线： Ds (0.77 0.9)r
标幺值＝实际有名值 基准值
标幺值无单位，基值不同时，物理量的标幺值也相应变
化。
I*
I IB
,V*
V VB
, S*
第二章 电力网各元件的等值电路
RT 2
2 D P s 2U N = 碬 103 2 SN
RT 1
2 D P s 2U N = 碬 103 2 SN
•对于100/50/100或100/100/50
/ 50 / 100 例：容量比不相等时，如 100 1 2 3
D Ps (1- 2) IN 2 SN 2 ⅱ =D Ps (1- 2) ( ) =D Ps (1- 2) ( ) = 4D Ps? (1- 2) IN / 2 S2 N
ì VS (1- 2) % = VS1 % +VS 2 % ï ï í VS (2- 3) % = VS 2 % +VS 3 % ï ï î VS (3- 1) % = VS 3 % +VS1 %
ì VS 1 %VN2 ï X1 = 碬 103 ï 100 S N ï ï VS 2 %VN2 ï 碬 103 í X2 = 100 S N ï ï ï VS 3 %VN2 碬 103 ï X3 = 100 S N ï î
一些常用概念
1. 实际变比 k k=UI/UII UI、UII :分别为与变压器高、低压绕组实际匝 数相对应的电压。 2. 标准变比
有名制：归算参数时所取的变比 标幺制：归算参数时所取各基准电压之比
3. 非标准变比 k* k*= UIIN UI /UII UIN
2.3电力网络的数学模型
• 问题的提出
IN 2 SN 2 D Ps (2- 3) = D Psⅱ ( ) = D P ( ) = 4D Ps? (2 - 3) s (2 - 3) (2 - 3) IN / 2 S2 N
D Ps (3- 1)
IN 2 ⅱ =D Ps (3- 1) ( ) = D Ps (3- 1) IN
电力系统分析第二章
2-2 架空输电线的等值电路
电力线路的数学模型是以电阻、电抗、电纳和电导来表 示线路的等值电路。 分两种情况讨论： 1） 一般线路的等值电路 一般线路：中等及中等以下长度线路，对架空线 为300km；对电缆为100km。 2）长线路的等值电路 长线路：长度超过300km的架空线和超过100km的电 缆。
I
2
T
YI I
y 20
k k k (k 1) k (k 1)YT ZT ZT ZT
2
(1 k)YT
k (k 1)YT
1)
电力网络中应用等值变压器模型的计算步骤：
有名制、线路参数都未经归算，变压器参数则归在低 压侧。
有名制、线路参数和变压器参数都已按选定的变比归 算到高压侧。 标幺制、线路和变压器参数都已按选定的基准电压折 算为标幺值。
三、三相电力线路结构参数和数学模型
输电线路各主要参数（电阻、电抗、电纳、电导 等）的计算方法及等效电路的意义
*.电力网络数学模型
1、标幺值
1）标幺值＝有名值（实际值）/基准值； 2）在标幺制下，线量（如线电流、线电压等） 与相量（如相电流、相电压等）相等，三相与单 相的计算公式相同
3）对于不同系统采用标幺值计算时，首先要 折算到同一基准下。
S B 3U B I B U B 3I B ZB Z B 1 / YB
Z B U / SB
2 B
YB S B / U
2 B
I B S B / 3U B
功率的基准值=100MVA
电压的基准值=参数和变量归算的额 定电压
三. 不同基准值的标幺值间的换算
V X (有名值) =X (N)* SN
电力网各元件的等值电路和参数计算
第二章电力网各元件的等值电路 和参数计算
电力线路和变压器的等值电路及其参数计算。
标么制的应用
介绍电力系统分析中的 输电线路和变压器的模型及其参数计算 电力系统的分析计算中，常用单相等值电路来描述系统元件的特性。
电力系统的元件是按abc三相对称设计的
电力系统的运行状态基本上是三相对称的（如正常运行状态）或者 是可以化为三相对称的（如用对称分量法），因此，只要研究一相 的情况就可以了。 电力系统中元件的三相接线方式，有星形和三角形， 电力系统中元件的三相等值电路也有星形电路和三角形电路。 为了便于应用一相等值电路进行分析计算，要把三角形等值电路化 为星形等值电路。 等值电路中的参数是计及了其余两相影响（如相间互感等）的一相 等值参数
图 2-4带电的平行长导线
介质的介电系数ε 为常数时，空间任意点P 的电位可以利用叠加原理求得。 因此，当线电荷＋q 和－q 同时存在时，它们共同对 P 点的电位的贡献为
选两线电荷等距离处（图中虚线）作为电位参考点，则有
分析导线 A的表面电位，此时 d1＝r 和 d2＝ D－r，计及 D>> r ，可得
在近似计算中，可以认为每相各个线段单位长度 导线上的电荷都相等，而导线对地电位却不相等。 取a相电位为各段电位的平均值，并计及 qa+qb+qc=0，得
vaI vaII
2－1 架空输电线路的参数
输电线路的参数包括： 电阻r0：反映线路通过电流时产生 的有功功率损失； 电憾L0：反映载流导线产生的磁场 效应； 电导g0：反映线路带电时绝缘介质 中产生泄漏电流及导线附近空气游 离而产生的有功功率损失； 电容C0：反映带电导线周围电场效 应的。
图 2-1单位（每公里）长线路的一 相等值电路
电力线路和变压器的等值电路及其参数计算。
标么制的应用
介绍电力系统分析中的 输电线路和变压器的模型及其参数计算 电力系统的分析计算中，常用单相等值电路来描述系统元件的特性。
电力系统的元件是按abc三相对称设计的
电力系统的运行状态基本上是三相对称的（如正常运行状态）或者 是可以化为三相对称的（如用对称分量法），因此，只要研究一相 的情况就可以了。 电力系统中元件的三相接线方式，有星形和三角形， 电力系统中元件的三相等值电路也有星形电路和三角形电路。 为了便于应用一相等值电路进行分析计算，要把三角形等值电路化 为星形等值电路。 等值电路中的参数是计及了其余两相影响（如相间互感等）的一相 等值参数
图 2-4带电的平行长导线
介质的介电系数ε 为常数时，空间任意点P 的电位可以利用叠加原理求得。 因此，当线电荷＋q 和－q 同时存在时，它们共同对 P 点的电位的贡献为
选两线电荷等距离处（图中虚线）作为电位参考点，则有
分析导线 A的表面电位，此时 d1＝r 和 d2＝ D－r，计及 D>> r ，可得
在近似计算中，可以认为每相各个线段单位长度 导线上的电荷都相等，而导线对地电位却不相等。 取a相电位为各段电位的平均值，并计及 qa+qb+qc=0，得
vaI vaII
2－1 架空输电线路的参数
输电线路的参数包括： 电阻r0：反映线路通过电流时产生 的有功功率损失； 电憾L0：反映载流导线产生的磁场 效应； 电导g0：反映线路带电时绝缘介质 中产生泄漏电流及导线附近空气游 离而产生的有功功率损失； 电容C0：反映带电导线周围电场效 应的。
图 2-1单位（每公里）长线路的一 相等值电路
电力系统分析--第二章 电力系统各元件的等值电路和参数计算
41
电力系统分析
[例2-6]三相三绕组降压变压器的型号为SFPSL120000/220，额定容量为120MVA/120MVA/60MVA， 额定电压为：220kV/121kV/11kV,求变压器归算到 220kV侧的参数,并作出等值电路。
PK (1 2 ) 601kW, PK (13) 182 .5kW , PK ( 23) 132 .5kW,U K (1 2 ) % 14 .85 U K (13) % 28 .25, U K ( 23) % 7.96, P0 135 k W, I 0 % 0.663
18
电力系统分析
2）具有分裂导线的输电线路的等值电感和电抗
19
电力系统分析
0 Deq La ln 2 Dsb
Deq x 2f N L 0.1445 lg Dsb km
Dsb为分裂导线的自几何均距，随分裂根数不同而变化。
2分裂导线： Dsb Ds d
3分裂导线： Dsb Ds d
11
电力系统分析
棒式绝缘子
12
电力系统分析
2.2.2电缆线路 导体 绝缘层 保护层
13
电力系统分析
架空输电线路参数有四个(图2-11） （1）电阻r0：反映线路通过电流时产生的有功功率 损耗效应。 （2）电感L0：反映载流导体的磁场效应。
图2-11
单位长线路的一相等值电路
14
电力系统分析
2. 电抗
根据变压器排列不同，对所提供的短路电压做些处理： 1 U k 1 % (U k (1 2 ) % U k (13) % U k ( 2 3) %) 2 1 U k 2 % (U k (1 2 ) % U k ( 23) % U k (13) %) 2 1 U k 3 % (U k (13) % U k ( 2 3) % U k (1 2 ) %) 2 然后按双绕组变压器相似的公式计算各绕组电阻 2 2 2 U k1 %U N U k 2 %U N U k 3 %U N X T1 , XT 2 , XT3 100 S N 100 S N 100 S N 一般来说，所提供的短路电压百分比都是经过归算的
第二章 电网元件的等值电路和参数计算
第二章电网元件的等值电路和参数计算2-1 架空输电线路的参数2.1.0 概述•电阻：反映线路有功功率损失；•电感：反映载流导线产生磁场效应；•电导：反映泄漏电流及空气游离产生的有功损失；•电容：反映带电导线周围电场效应。
2.1.3 架空输电线路的电导在一般的电力系统计算中可忽略电晕损耗，即认为。
这是由于在设计时，通常按照避免电晕损耗的条件来选择导线的半径。
0g ≈2-2 架空输电线的等值电路2.2.0 概述电力线路按长度可分为：–短线路——L<100km的架空线或不长的电缆；–中长线路——L<100~300km的架空线或L<100km的电缆；–长线路——L>300km的架空线或L>100km的电缆；2.2.2 中长架空线路的等值电路电压在110~330kV的中长线路，电纳的影响不能忽略，等值电路一般有两种表示方法：П型和T型。
Note:П型和T型相互间不等值，不能用Δ—Y 变换。
2-3 变压器的等值电路和参数2.3.1 双绕组变压器等值电路将励磁支路移至电源测：由短路试验得到：由空载试验得到：%S S P V ∆短路损耗：短路电压：00%P I ∆空载损耗：空载电流：T T R X ⇒⇒T TG B ⇒⇒2.3.2 双绕组变压器的短路试验短路实验：将变压器的一绕组短路，另一绕组加电压，使短路绕组中的电流达到额定值，测绕组上的有功损耗ΔP S及短路电压ΔV S%。
2.3.2 双绕组变压器的空载试验空载实验：将变压器一绕组开路，另一绕组加上额定电压，测绕组中的空载损耗ΔP0和空载电流ΔI0%。
2.3.3三绕组变压器等值电路将励磁支路移至电源测：由短路试验得到：由空载试验得到：(12)(23)(13)(12)(23)(13)%%%S S S S S S P P P V V V −−−−−−∆∆∆短路损耗：、、短路电压：、、00%P I ∆空载损耗：空载电流：%Si Si P V ⇒∆⇒Ti Ti R X ⇒⇒13i =∼TTG B ⇒⇒2.3.3 三绕组变压器短路试验短路实验：将三绕组变压器任一绕组(如j)短路,在另一绕组) ，使短路绕组j中电流达其额定电(如i)加电压(Ui流(I)，测i,j绕组间的短路损耗(∆P S(i-j))和短路jN电压降(ΔV S(i-j)%)。
【电力系统分析】第02章(1-2节) 电力系统各元件的等值电路和参数计算
29
本节学习要求
熟记计算公式和公式中各参数的含义、单 位。
学会查表计算线路等值参数电阻、电抗、 电导和电纳。
30
2-2 架空输电线路的等值电路
一、输电线路的方程式
长线的长度范围定义 架空线路：>300km 电缆线路：>100km
31
2-2 架空输电线路的等值电路
长线等值电路
z0 r0 jL0 r0 jx0 y0 g0 jC0 g0 jb0
影响因素：m1:材料表面光滑程度
m2:天气状况系数 空气的相对密度
2.89 103
p
材料半径
273 t
分裂情况
25
对于水平排列的线路，两根边线的电晕临界电压 比上式算得的值搞6%；而中间相导线的则低4%。
Vcr
49.3m1m2 r
lg
D r
kV
增大导线半径是减小电晕损耗的有效方法 220kV以下线路按照免电晕损耗选择导线半径 220kV以上采用分裂导线。
1
I 1
2
V 2
shl
Z c
2c
I Z chl 2c
36
ห้องสมุดไป่ตู้
将上述方程同二端口网络的通用方程相比 可得：
V1
AV
2
B
I2
I1 C V 2 D I2
A
D
ch
l,
B
Zc
sh
l和C
=
sh
Zc
l
输电线就是对称的无源二端口网络，并可用
对称的等值电路来表示。
37
线路的传播常数和波阻抗
对于高压架空线输电线
lg Deq r
(S/km)
• 分裂导线
本节学习要求
熟记计算公式和公式中各参数的含义、单 位。
学会查表计算线路等值参数电阻、电抗、 电导和电纳。
30
2-2 架空输电线路的等值电路
一、输电线路的方程式
长线的长度范围定义 架空线路：>300km 电缆线路：>100km
31
2-2 架空输电线路的等值电路
长线等值电路
z0 r0 jL0 r0 jx0 y0 g0 jC0 g0 jb0
影响因素：m1:材料表面光滑程度
m2:天气状况系数 空气的相对密度
2.89 103
p
材料半径
273 t
分裂情况
25
对于水平排列的线路，两根边线的电晕临界电压 比上式算得的值搞6%；而中间相导线的则低4%。
Vcr
49.3m1m2 r
lg
D r
kV
增大导线半径是减小电晕损耗的有效方法 220kV以下线路按照免电晕损耗选择导线半径 220kV以上采用分裂导线。
1
I 1
2
V 2
shl
Z c
2c
I Z chl 2c
36
ห้องสมุดไป่ตู้
将上述方程同二端口网络的通用方程相比 可得：
V1
AV
2
B
I2
I1 C V 2 D I2
A
D
ch
l,
B
Zc
sh
l和C
=
sh
Zc
l
输电线就是对称的无源二端口网络，并可用
对称的等值电路来表示。
37
线路的传播常数和波阻抗
对于高压架空线输电线
lg Deq r
(S/km)
• 分裂导线
第二章 电力网的等值电路及其计算
架空线路
• 导线：传输电流，传送电能。 • 避雷线：将雷电流引入大地，保护线路免遭雷击。 • 杆塔：支撑导线和避雷线，使导线与导线，导线与大地
间保持一定的安全距离。 • 绝缘子：绝缘子固定在杆塔上，保证导线和杆塔间的绝缘。 • 金具：用于连接导线，导线固定在绝缘子上。
电缆线路
• 导体：传输电流，传送电能。 • 绝缘层：使导线与导线，导线与包护层互相绝缘。 •包护层：保护绝缘层，防止绝缘油外溢和水分侵入。
2.中等长度的等值电路
• 长度在100~300km之间的架空线和不超过100km的电缆线， 称为中等长度线路。电纳不可忽略，
用Π型或T型等值电路
I1
Z
I2
Z I1 2
Z 2 I2
Y
U1
2
Y
U2
2
U1
Y
U2
Z = R + jX = ( r1 + jx 1 ) l Y = G + jB = ( g 1 + jb 1 ) l
(F/km)
b1=
7 . 58 × 10-6
lg D m
r
( S/km )
r为导线半径，对于分裂导线，用req代替
例2-1架空线参数计算-1
• 330KV线路的导线结构有以下两个方案：①使用LGJ— 630/45型导线，直径33.6mm；②使用2×LGJK—300型 分裂导线，直径27.44mm，分裂间距为400mm。两个方
三、电力线路的等值电路
线路通电流：
• 发热，消耗有功功率→R • 交流电流→交变磁场→感应电势(自感、互感)→X • 电流效应→串联
线路加电压：
• 绝缘漏电(较小)，一定电压下发光、放电(电晕)→G • 电场→导线/导线、导线/大地电容→B • 电压效应→并联
• 导线：传输电流，传送电能。 • 避雷线：将雷电流引入大地，保护线路免遭雷击。 • 杆塔：支撑导线和避雷线，使导线与导线，导线与大地
间保持一定的安全距离。 • 绝缘子：绝缘子固定在杆塔上，保证导线和杆塔间的绝缘。 • 金具：用于连接导线，导线固定在绝缘子上。
电缆线路
• 导体：传输电流，传送电能。 • 绝缘层：使导线与导线，导线与包护层互相绝缘。 •包护层：保护绝缘层，防止绝缘油外溢和水分侵入。
2.中等长度的等值电路
• 长度在100~300km之间的架空线和不超过100km的电缆线， 称为中等长度线路。电纳不可忽略，
用Π型或T型等值电路
I1
Z
I2
Z I1 2
Z 2 I2
Y
U1
2
Y
U2
2
U1
Y
U2
Z = R + jX = ( r1 + jx 1 ) l Y = G + jB = ( g 1 + jb 1 ) l
(F/km)
b1=
7 . 58 × 10-6
lg D m
r
( S/km )
r为导线半径，对于分裂导线，用req代替
例2-1架空线参数计算-1
• 330KV线路的导线结构有以下两个方案：①使用LGJ— 630/45型导线，直径33.6mm；②使用2×LGJK—300型 分裂导线，直径27.44mm，分裂间距为400mm。两个方
三、电力线路的等值电路
线路通电流：
• 发热，消耗有功功率→R • 交流电流→交变磁场→感应电势(自感、互感)→X • 电流效应→串联
线路加电压：
• 绝缘漏电(较小)，一定电压下发光、放电(电晕)→G • 电场→导线/导线、导线/大地电容→B • 电压效应→并联
第二章 电力系统各元件的等值电路和参数计算
' ' S (1 − 2 )
( (
SN 2 ) S2N SN min{ S 2 N , S 3 N SN 2 ) S 3N
'
S (2−3)
S ( 3 −1)
(
)2 }
（3）仅提供最大短路损耗的情况
R( S N )
2 ∆PS .maxVN = ×103 2 2S N
2 ∆PSiVN Ri = × 10 3 (i = 1,2,3) 2 SN
2.2.3 三绕组变压器的参数计算
（2）三绕组容量不同（100／100／50、100／50／100） 三绕组容量不同（100／100／50、100／50／100）
∆ PS (1 − 2 ) = ∆ P ∆ PS ( 2 − 3 ) = ∆ P ∆ PS ( 3 − 1 ) = ∆ P
2.2.3 输电线路的参数计算
1.电阻 电阻 有色金属导线单位长度的直流电阻： 有色金属导线单位长度的直流电阻： r = ρ / s 考虑如下三个因素： 考虑如下三个因素： （1）交流集肤效应和邻近效应。 ）交流集肤效应和邻近效应。 （2）绞线的实际长度比导线长度长 ～3 ％。 ）绞线的实际长度比导线长度长2～ （3）导线的实际截面比标称截面略小。 ）导线的实际截面比标称截面略小。 2 因此交流电阻率比直流电阻率略为增大： 因此交流电阻率比直流电阻率略为增大：铜：18.8 Ω ⋅ mm / km 铝：31.5 Ω ⋅ mm 2 / km 精确计算时进行温度修正： 精确计算时进行温度修正： rt = r20 [1 + α (t − 20)]
架空线路的换位问题
A B C C A B B C A A B C
目的在于减少三相参数不平衡 整换位循环： 整换位循环：指一定长度内有两次换位而三相导线 都分别处于三个不同位置，完成一次完整的循环。 都分别处于三个不同位置，完成一次完整的循环。 滚式换位 换位方式 换位杆塔换位
( (
SN 2 ) S2N SN min{ S 2 N , S 3 N SN 2 ) S 3N
'
S (2−3)
S ( 3 −1)
(
)2 }
（3）仅提供最大短路损耗的情况
R( S N )
2 ∆PS .maxVN = ×103 2 2S N
2 ∆PSiVN Ri = × 10 3 (i = 1,2,3) 2 SN
2.2.3 三绕组变压器的参数计算
（2）三绕组容量不同（100／100／50、100／50／100） 三绕组容量不同（100／100／50、100／50／100）
∆ PS (1 − 2 ) = ∆ P ∆ PS ( 2 − 3 ) = ∆ P ∆ PS ( 3 − 1 ) = ∆ P
2.2.3 输电线路的参数计算
1.电阻 电阻 有色金属导线单位长度的直流电阻： 有色金属导线单位长度的直流电阻： r = ρ / s 考虑如下三个因素： 考虑如下三个因素： （1）交流集肤效应和邻近效应。 ）交流集肤效应和邻近效应。 （2）绞线的实际长度比导线长度长 ～3 ％。 ）绞线的实际长度比导线长度长2～ （3）导线的实际截面比标称截面略小。 ）导线的实际截面比标称截面略小。 2 因此交流电阻率比直流电阻率略为增大： 因此交流电阻率比直流电阻率略为增大：铜：18.8 Ω ⋅ mm / km 铝：31.5 Ω ⋅ mm 2 / km 精确计算时进行温度修正： 精确计算时进行温度修正： rt = r20 [1 + α (t − 20)]
架空线路的换位问题
A B C C A B B C A A B C
目的在于减少三相参数不平衡 整换位循环： 整换位循环：指一定长度内有两次换位而三相导线 都分别处于三个不同位置，完成一次完整的循环。 都分别处于三个不同位置，完成一次完整的循环。 滚式换位 换位方式 换位杆塔换位
电力网各元件的等值电路和参数计算
m2：考虑气象状况的系数
干燥和晴朗的天气
m2＝ 1
有雨雪雾等的恶劣天气 m2＝0.8～1
r：导线的计算半径；
D：相间距离；
δ：空气的相对密度
2020/8/30
电力系统分析 第二章 电力网各元件的等值电路和参数计算
24
当实际运行电压过高或气象条件变坏时，运行电压将超 过临界电压而产生电晕——计算等值电导
do1 do2
vp
q
2
ln
d2 d1
导线A的表面：d1＝r和d2＝D-r，D>>r，导线A的电位：
vA＝
q
2
ln
Dr r
q
2
ln
D r
2020/8/30
电力系统分析 第二章 电力网各元件的等值电路和参数计算
29
2. 三相输电线路的等值电容
计算空间任意点的电位时均须考 虑三相架空导线和大地对电场的 影响。
❖ LGJ－120：钢芯铝绞线
2020/8/30
电力系统分析 第二章 电力网各元件的等值电路和参数计算
6
避雷线
又称架空地线，架设在杆塔顶部，一根或二根，用于 防雷，110-220千伏线路一般沿全线架设。 架空送电线着雷时，可能打在导线上，也可能打在杆 塔上。
避雷线可以遮住导线，使雷尽量落在避雷线本身上， 并通过杆塔上的金属部分和埋设在地下的接地装置， 使雷电流流入大地。
H /m
轴间距离
2020/8/30
电力系统分析 第二章 电力网各元件的等值电路和参数计算
14
2. 三相输电线路
a
1）三角形对称布置时：
a相磁链：
a Lia M (ib ic )
c
第二章电力网各元件的参数和等值电路精品文档
如下表，空载电流I0为1.243%，空载损耗P0为132kW。 试求归算到220kV侧的变压器参数。
变压器短路试验数据表(未经归算)
短路电压百分数Us% 短路损耗Ps（kW）
高—中 12.20 343.0
高—低 6.00
251.5
中—低 8.93
285.0
第2章 电力网各元件参数和数学模型
14 发电机组的运行特性和数学模型
φ ——功率因数角，u i ；
S、P、Q——分别为视在功率、有功功率、无功功率。
2.1 发电机组的运行特性和数学模型
一、发电机稳态运行时的相量图和功角特性
1. 隐极式发电机的相量图和功角特性
S ~ ( U d j q ) U I d j q I U d I d U q I q j U q I d U d I q P jQ
Uq EqIdxd EQIdxq Ud Iqxq
jQ E ( U d jq U ) jq x I d jq I
即， EQUjxqI 可以运用作图法求得交轴正方向，从而 E q 确定的正方向。
2.1 发电机组的运行特性和数学模型
P EqUd UdUq UdUq
1 双绕组变压器
电阻
RT
PkU
2 N
1000SN2
RT——变压器高低压绕组的总电阻（Ω ）； Pk——变压器的短路损耗（kW）； SN——变压器的额定容量（MVA）； UN——变压器的额定电压（kV）。
2.2 变压器的参数和数学模型（续1）
1 双绕组变压器
电抗
XT
UN Uk%Uk% UN 2 3IN 100 10SN 0
2.2 变压器的参数和数学模型（续3）
变压器短路试验数据表(未经归算)
短路电压百分数Us% 短路损耗Ps（kW）
高—中 12.20 343.0
高—低 6.00
251.5
中—低 8.93
285.0
第2章 电力网各元件参数和数学模型
14 发电机组的运行特性和数学模型
φ ——功率因数角，u i ；
S、P、Q——分别为视在功率、有功功率、无功功率。
2.1 发电机组的运行特性和数学模型
一、发电机稳态运行时的相量图和功角特性
1. 隐极式发电机的相量图和功角特性
S ~ ( U d j q ) U I d j q I U d I d U q I q j U q I d U d I q P jQ
Uq EqIdxd EQIdxq Ud Iqxq
jQ E ( U d jq U ) jq x I d jq I
即， EQUjxqI 可以运用作图法求得交轴正方向，从而 E q 确定的正方向。
2.1 发电机组的运行特性和数学模型
P EqUd UdUq UdUq
1 双绕组变压器
电阻
RT
PkU
2 N
1000SN2
RT——变压器高低压绕组的总电阻（Ω ）； Pk——变压器的短路损耗（kW）； SN——变压器的额定容量（MVA）； UN——变压器的额定电压（kV）。
2.2 变压器的参数和数学模型（续1）
1 双绕组变压器
电抗
XT
UN Uk%Uk% UN 2 3IN 100 10SN 0
2.2 变压器的参数和数学模型（续3）
电力网各元件的等值电路和参数计算
qa = C= va 2πε 0.0241 ≈ Deq Deq H12 H 23 H 31 lg − ln 3 ln r r H1 H 2 H 3
31
分裂导线的电容
qa C= = va
2πε 0.0241 ≈ Deq Deq H12 H 23 H 31 lg ln − ln 3 req req H1 H 2 H 3
32
三相输电线路的电纳
额定频率下，线路单位长度的一相等值电纳
b = 2π f N C = 7 . 58 × 10 D eq lg r
−6
S / km
与线路结构有关的参数在对数符号内
各种电压等级线路的电纳值变化不大 单根：2.8 ×10-6 S/km 二分裂：3.4×10-6 S/km 三分裂：3.8×10-6 S/km 四分裂：4.1×10-6 S/km
29
2-1、架空输电线路的参数-电容
电容：反映导线带电时在其周围介质中建立的电场效应。
基本公式： （周围介质的介电系数为常数）
C＝q/v
q :导体所带电荷；v：导体的电位 两带电荷平行长导线周围的电场
+q r:导线半径；D:轴间距离； A 单位长度电荷：＋q,-q； D>>r, 忽略导线间静电感应影响 r d O1 d1
高压架空线路
1898 年美国33kV 120km输电线路,针式绝缘子 1906年美国发明悬式绝缘子(11~500kV)，1908和 1923 年分别建成110kV和220kV输变电工程 1959年前苏联500 kV输变电工程 1965年加拿大760 kV输变电工程 1985年前苏联1150kV输变电工程 1910~1914美国和前苏联科学家发现电晕临界电压与 导线直径成比例,促使了铝线，钢芯铝绞线，扩经或 分裂导线的使用
31
分裂导线的电容
qa C= = va
2πε 0.0241 ≈ Deq Deq H12 H 23 H 31 lg ln − ln 3 req req H1 H 2 H 3
32
三相输电线路的电纳
额定频率下，线路单位长度的一相等值电纳
b = 2π f N C = 7 . 58 × 10 D eq lg r
−6
S / km
与线路结构有关的参数在对数符号内
各种电压等级线路的电纳值变化不大 单根：2.8 ×10-6 S/km 二分裂：3.4×10-6 S/km 三分裂：3.8×10-6 S/km 四分裂：4.1×10-6 S/km
29
2-1、架空输电线路的参数-电容
电容：反映导线带电时在其周围介质中建立的电场效应。
基本公式： （周围介质的介电系数为常数）
C＝q/v
q :导体所带电荷；v：导体的电位 两带电荷平行长导线周围的电场
+q r:导线半径；D:轴间距离； A 单位长度电荷：＋q,-q； D>>r, 忽略导线间静电感应影响 r d O1 d1
高压架空线路
1898 年美国33kV 120km输电线路,针式绝缘子 1906年美国发明悬式绝缘子(11~500kV)，1908和 1923 年分别建成110kV和220kV输变电工程 1959年前苏联500 kV输变电工程 1965年加拿大760 kV输变电工程 1985年前苏联1150kV输变电工程 1910~1914美国和前苏联科学家发现电晕临界电压与 导线直径成比例,促使了铝线，钢芯铝绞线，扩经或 分裂导线的使用
0305第二章电力系统各元件的等值电路和参数计算资料
N
xd
)
O'
O
Q
I N
b、运行极限图
2.1 发电机组的运行特性和数学模型
决定隐极式发电机组运行极限的因素： 定子绕组温升约束。取决于发电机的视在 功率。以O点为圆心，以OB为半径的圆弧S。 励磁绕组温升约束。取决于发电机的空载 电势。以O’点为圆心，以O’B为半径的圆弧F。 原动机功率约束。即发电机的额定功率。 直线BC。 其他约束。当发电机以超前功率因数运行 的场合。综合为圆弧T。
×
a b 单相线路 n＝1 首先求外部磁链
r
D dx
x
i
磁动势 F ni 1* i
磁
场
强
度H
x
Fl
1 i
2x ( Am)
磁
通
密
度B
x
xH
x
r0H
x
0 4 107 (H m)
空 气r 1
（1）求外部磁链
2.2 输电线路的等值电路和参数计算
（2）杆塔 木塔：较少采用 铁塔：主要用于220kV及以上系统 钢筋混凝土杆：应用广泛
2.2 输电线路的等值电路和参数计算
（3）绝缘子 针式：10kV及
以下线路
图2-8 针式绝缘子
针式绝缘子
2.2 输电线路的等值电路和参数计算
悬式绝缘子 主要用于35kV及 以上系统，根据电 压等级的高低组成 数目不同的绝缘子 链。
EqU d U dU q xd
UdUq xq
EqU
sin
第2章电力网络各元件的参数和等值电路
§2-1 电力线路的参数和等值电路
4.单位长度电纳b1：
由于架空导线之间及导线与地之间是以空气为绝缘介质，
因而导线之间或导线与地之间存在电容，其中线路电纳主要 a 是导线间电容引起。 b
由电磁场理论(公式推导略)：
c
7.58 b1 10 6 s / kM Dm lg r 分析：
① 同样，由于Dm、r在lg之后，b1变化不大， 一般b1=2.85×10-6西/公里，近似计算时可取此值。
§2-1 电力线路的参数和等值电路
上式也可以写成：
Dm x1 0.1445 lg / km r
2
其中，r 0.779r 导线几何均距
分析： ① 式(1)、(2)是对单股导线推出，可直接应用于求钢芯铝绞线 电抗值，但，(2)式应修正： 铜、铝多股线，取：r′=（0.724~0.771）r 钢芯铝绞线，取：r′=（0.81~0.95）r
2015年11月27日11时52分 17
§2-1 电力线路的参数和等值电路
⑤ 对于钢导线：
钢导线与铝、铜导线的主要差别在于钢导线导磁性材料。
由于属于导磁性材料，r1、x1与其通过电流大小有关。 r1=f（i），x1=f（i） 一般实测； 3.单位长度电导g1：
电晕 (1) 引起 －与导线电压、尺寸有关，其中主要是电晕 泄漏
电晕：强电场作用下导线周围空气的电离现象。 10
2015年11月27日11时52分 18
§2-1 电力线路的参数和等值电路
导线周围空气电离的原因：是由于导线表面的电场强度超过了
某一临界值，以致空气中原有的离子具备了足够的动能，使其 他不带电分子离子化，导致空气部分导电。 计算困难，工程认为，无电晕时g1=0。线路设计时，一般
电力系统分析第2章 电力网各元件的参数和等值电路
三绕组变压器
手册中查到的是两两绕组的短路电压 ，先求出每个绕 组的短路电压(short-circuit voltage)百分数，再计算 每个绕组的电抗，即:
U S1 % 1 2(U S (12) % U S (31) % U S (23) %) U S 2 % 1 2(U S (12) % U S (23) % U S (13) %) U S 3 % 1 2(U S (23) % U S (31) % U S (12) %)
2.3.2
三绕组变压器
三绕组变压器按其三个绕组排列方式的不同有两种结构： 升压结构和降压结构，如图2.10所示。
由于绕组的排列方式不同，绕组间的漏抗不同，因而短
路电压也不同。
图2.10 三绕组变压器的排列方式
电力系统分析
2.3.2
三绕组变压器
导纳 三绕组变压器导纳的计算方法与双绕组变压器相同。
电力系统分析
长线路：
长线路的等值电路
指长度超过300km的架空线路和长度超过100km的 电缆线路。
图2.5 长线路的等值电路
电力系统分析
2.3 变压器的等值电路及参数
2.3.1 双绕组变压器(double-column transformer)
2.3.2
三绕组变压器(three-column transformer)
电力系统分析
2.1.4 电纳(susceptance)
三相电路经整循环换位后，每相导线单位长 度电纳的计算式如下。 1.单相导线线路电纳
b0 7.58 10 6 S / km Deq lg r
2.分裂导线线路电纳
b0 7.58 10 6 S / km Deq lg req
第二章 电力系统的元件参数及等值电路
0.0241 10 6 ( F / km) D lg m r
（2-7）
那么，单导线每相单位长度的电纳为
b1 2f
当f=50Hz时
C1 2f
0.0241 lg
D
r
10 6
m
b1
7.58 lg D r
m
10 6 ( S / km)
（2-8）
显然，Dm、r对b1影响不大，b1在2.85 ×10-6S/km左右。 2）分裂导线每相单位长度的电纳。
（1）电阻。每相导线单位长度的电阻为 其中，S—导线的标称截面积(mm2)；
r
1
S ( / km)
（2-1）
ρ—导线的电阻率（ mm 2 / km ） 铝的电阻率：31.5 mm 2 / km 铜的电阻率：18.8 mm 2 / km 铝、铜的电阻率略大于直流电阻率，有三个原因： （1）交流电流的集肤效应； （2）绞线每股长度略大于导线长度； （3）导线的实际截面比标称截面略小。
r
r
3）同杆架双回路每回线单位长度的电抗。 由于在导线中流过三相对称电流时两回路之间的互感影响 并不大（可以略去不计），故每回线每相导线单位长度电抗的 计算公式与式（2-3）~（2-5）相同。 （3）电纳 1）单导线每相单位长度的电纳C1：
C1
式中，r—导线半径（cm或mm）； Dm —三相导线的几何平均距离（cm或mm)。
• • • • •
对于分裂导线线路的电抗，应按如下考虑：分裂导线 的采用，改变了导线周围的磁场分布，等效地增大了 导线半径，从而减小了每相导线的电抗。 若将每相导线分裂成 n根，则决定每相导线电抗的将 不是每根导线的半径 r，而是等效半径req。如图所示：
第2章电力网元件的等值电路和参数计算
D：相间距离，单位cm。
提高Ucr办法为增大导线半径。
若三相线路每公里的电晕损耗为 Pg ，则每相等值电导：
g Pg (S/km)
U
2 L
式中：Pg 单位为（ MW/km ）；UL为线电压，单位（kV）。
电晕危害：增加有功功率损耗，干扰无线电通信。
措施：220kV以下线路，加大导线半径； 220kV及以上线路，常采用分裂导线增大导线等效半径。
d: 分裂间距
双分、三分和四分裂导线的自几何均距分别定义为：
Dsb DS d ,
Dsb 3 DS d 2 ,
Dsb 4 DS d 3
分裂导线的等值 电感按下式计算：
L 0 ln Deq 2 Dsb
4）输电线路的等值电抗
额定频率下线路每相的等值电抗为:
x 2 fN L
计及 fN 50Hz
●讨论：
1）由于Dsb>>Ds,分裂导线等值电抗较小，所以超高压输 电线常采取分裂导线；
2) 导线间距、导线截面的尺寸会影响Deq，Ds，Dsb等的
数值，从而影响输电线的等值电抗大小，但由于它们 均位于电抗表达式的对数符号内，故影响不显著。
3.电导（g）
电导是反映泄露电流和空气游离引起的有功功率损耗。 一般线路绝缘良好，泄露电流很小，可以忽略。主要只考 虑电晕引起的功率损耗。
其中，Deq 为各相分裂导线重心间的几何均距，
req 为一相导线组的等值半径。
对于二分裂导线， req rd 。
三分裂导线， req 3 r。d 2
四分裂导线， req 1.094 rd3。
d为分裂间距。
分裂导线的等值半径 req 特大于r，故其电容大于单导线。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.2 架空输电线的等值电路
集中参数元件：假定元器件伴随的电磁过程 都分别集中在各元件内部进行，这种元件就称为 集总参数元件，简称为集总元件。 当实际电路的尺寸远小于电路工作时电磁波 的波长时，即可用集总参数电路模型来近似地描 述实际电路。
长线路的等值电路 1）长距离输电线路的稳态方程 设长为l的输电线路其参数沿线均匀分布，单位长度阻抗和 导纳分别为 z1 r1 jx1 y1 g1 jb1 在距离线路末端x处取一微段dx。作出等值电路
o
o
mm2 / km mm2 / km
集肤效应又叫趋肤效应,当交变电流通过导体时, 电流将集中在导体表面流过,这种现象叫集肤效 应。是电流或电压以频率较高的电子在导体中传 导时,会聚集于总导体表层,而非平均分布于整个 导体的截面积中。 邻近效应——当高频电流在两导体中彼此反向流 动或在一个往复导体中流动时，电流会集中于导 体邻近侧流动的一种特殊的物理现象。 导体内电流密度因受邻近导体中电流的影响而分 布不均匀的现象。
2.1 架空输电线路的参数 2.1.1 输电线路 1.架空线 导线 避雷线 杆塔 绝缘子 金具
架空线路
金具
（1）导线和避雷线：电性能，机械强度，抗腐蚀能力； 主要材料：铝，铜，钢；例：LJ TJ LGJ
（2）杆塔 木塔：较少采用 铁塔：主要用于220kV及以上系统 钢筋混凝土杆：应用广泛
2.电感 三相导线排列对称(正三角形)，则三相电感相等。 三相导线排列不对称，则进行整体循环换位后三 相电感相等。
1)单导线每相单位长度电感和电抗：
0 Deq La ln 2 Ds
x 2f N L 0.1445lg Deq Ds
1 4
km
式中：Deq为三相导线间的互几何均距，D 3 D D D eq 12 23 31
1 x 1 x x x (e e )U 2 (e e ) Z C I 2 U 2 chx Z C I 2 shx 2 2 （2-24）
1 (U Z I )ex 1 (U Z I )e x I 2 C 2 2 C 2 2 2
U C1ex C2e x
C1 I ZC
.
e
x
C2 ZC
e
x
C C2 I2 1 ZC
从而有
1 C1 (U 2 Z C I2 ) 2
1 C2 (U 2 Z C I2 ) 2
将此式代入式（2-22）、（2-23）中，便得
U
.
1 1 (U 2 Z C I 2 )ex (U 2 Z C I 2 )e x 2 2
1 shl C I1 Z C
2 chl I D 2
（2-27）
2）长输电线路的集中参数等值电路
. .
. .
I1
.
Z
Y 2
'
I2
Y 2
.
I1
.
I2
Y
'
U1
U2
U1
Z 2
Z 2
.
U2
长线路的等值电路 (a) П型等值电路；(b) Τ型等值电路
第二章 电力系统各元件的等值电路和参数计算
第一节 架空输电线路的参数 第二节 架空输电线路的等值电路
第三节
第四节
变压器的等值电路和参数
标幺值
2.1 架空输电线路的参数
电力系统分析和计算的一般过程 首先将待求物理系统进行分析简化，抽 象出等效电路(物理模型)； 然后确定其数学模型，也就是说把待求 物理问题变成数学问题； 最后用各种数学方法进行求解，并对结 果进行分析。
z y
1
1
传播常数
z1
Z Z C shl
shl shl z1l Z KzZ l l 2(chl 1) 2(chl 1) y1 l 2(chl 1)Y KY Y Y shl l shl l Z shl z1 shl
Ds为导线的自几何均距 Ds re
r为导线的计算半径 实际多股绞线的自几何均距： 非铁磁材料的单股线：Ds=0.779r 非铁磁材料的多股线：Ds=（0.724～0.771)r 钢芯铝线： Ds=（0.77～0.9)r 在工程计算中，可以取架空线路的电抗为 0.40 / km
2）具有分裂导线的输电线路的等值电感和电抗
Z
Y 1 A 2
Z B
即 化简
Z
2( A 1) 2(chl 1) B Z C shl 令全线路总阻抗和总导纳分别为
Y 1 A 2
Z Z C shl
Y
z (r1 jx1 )l z1l
特性阻抗（定义） Z C
ZC
Y y1l
(l ) 2 z1 y1 2 ZY KZ 1 1 l 1 6 2 6 6 (l ) z1 y1 2 ZY KY 1 1 l 1 12 12 12
（2-35）
将z1=r1+jx1，y1= g1+jb1，以及G=g1l=0代入式（2-35）中， 展开后可得 Z 、Y 的近似计算公式
只研究П型等值电路，求 Z 、 Y
U Z ( I U Y ) U ( Z Y 1)U Z I 由等值电路(a) U1 2 2 2 1 2 2 2 2
依二端口网络方程 可得
U1 AU 2 BI 2
Z B
C
7.58 0.0241 b 106 S F / km 2f N C Deq Deq lg lg req req
Deq各相分裂导线重心间的几何均距。 req 一相导线组的等值半径。 对二分裂导线： req rd
req 3 rd 2 对三分裂导线：
对四分裂导线： req 1.09 4 rd 3
g1
Pg U2
103
( S / km)
Pg 电晕损耗有功功率 U 线电压
4 .等值电容和电纳 0.0241 6 (1)单导线：电容 C D 10 （F/km）
lg
eq
r
电纳
7.58 6 b 2f N C 10 （S km ） Deq lg r
（2）分裂导线
图2-1
单位长线路的一相等值电路
（3）电导g0 ：线路带电时绝缘介质中产生的 泄漏电流及导体附近空气游离而产生有功功率 损耗。 （4）电容C0 ：带电导体周围的电场效应。 输电线路的以上四个参数沿线路均匀分布。
图2-11
单位长线路的一相等值电路
1.电阻 有色金属导线单位长度的直流电阻： r /s 考虑如下三个因素： （1）交流集肤效应和邻近效应。 （2）绞线的实际长度比导线长度长2～3 ％。 （3）导线的实际截面比标称截面略小。 因此交流电阻率比直流电阻率略为增大：铜：18.8 铝：31.5 精确计算时进行温度修正： rt r20 [1 (t 20)] 为温度系数： 铜： 0.003821 c / 铝: 0.00361 c /
1 x x 1 ( x x) I (e e )U 2 e e 2 2Z C 2 U2 shx I 2 chx ZC
（2-25）
式（2-24）、（2-25）又可写成矩阵形式 AD-BC=1 chx Z shx 二端口的外部特性可用3个参数确定，则该无源 C U 2 U 二端口可表示为3个阻抗（导纳）的组合 （2-26） shx chx I I ZC A=D ，符合对称二端口网络特点，输电线路可看成是对称无 2 源二端口。可用对称的T型或π型等值电路表示。 当x= l时，可得首端电压和电流的表达式 chl Z CB l sh U A U
0 Deq La ln 2 Dsb
x 2f N L 0.1445lg
Deq Dsb
km
Dsb为分裂导线的自几何均距，随分裂根数不同而变化。
2分裂导线：Dsb Ds d
3分裂导线：Dsb Ds d
3 4
2 3
4分裂导线：Dsb 1.09 Ds d
通常，d>>Ds，因此，分裂导线自几何均距Dsb比单导 线自几何均距Ds大，分裂导线的等值电感小。
110kv
架 空 线 路
（3）绝缘子 针式：10kV及以下线路
针式绝缘子
悬式绝缘子 主要用于35kV及以上系统，根据电压 等级的高低组成数目不同的绝缘子链。
棒式绝缘子 起到绝缘和横担的作用，应用于10～35kV农网。
2.电缆线路 导体 绝缘层 保护层
架空输电线路参数有四个 （1）电阻r0：反映线路通过电流时产生的有功 功率 损耗效应。 （2）电感L0：反映载流导体的磁场效应。
(2 16)
(2 17)
将式（2-16）对x微分，可得 d 2U (r1 jx1 )( g1 jb1 )U z1 y1U （2-20） dx 2 解此二阶常系数齐次微分方程，其通解为
U C1ex C2e x
将其微分后代入式（2-16），可得 C1 x C2 x I ZC e ZC e 式中 (r1 jx1 )( g1 jb1 )
长线路的均匀分布参数电路
dx微段串联阻抗中的电压降落为 dU I (r1 jx1 )dx
dx微段并联导纳中的支路电流为 dI (U dU )( g1 jb1 )dx
将以上两式分别变形为
略去二阶 微小量
dU I (r1 jx1 ) dx dI U ( g1 jb1 ) dx