第十讲主梁内力横隔梁内力计算演示文稿
桥梁工程主梁内力计算详细过程
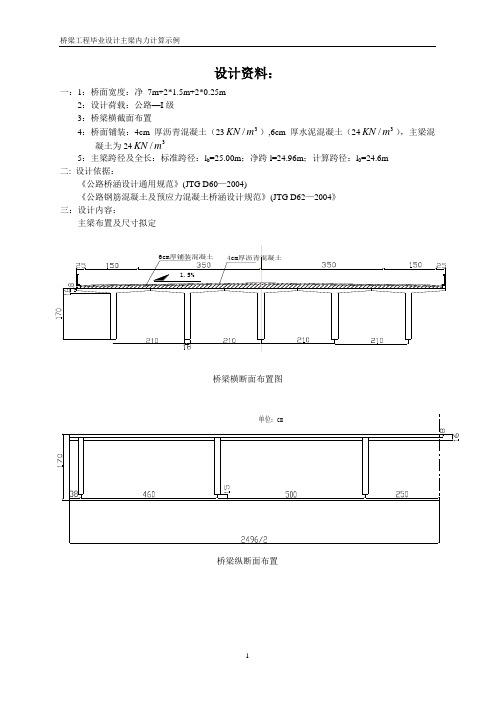
设计资料:一:1:桥面宽度:净 7m+2*1.5m+2*0.25m2:设计荷载:公路—I 级 3:桥梁横截面布置4:桥面铺装:4cm 厚沥青混凝土(233/m KN ),6cm 厚水泥混凝土(243/m KN ),主梁混凝土为243/m KN5:主梁跨径及全长:标准跨径:l b =25.00m ;净跨l=24.96m ;计算跨径:l 0=24.6m 二: 设计依据:《公路桥涵设计通用规范》(JTG D60—2004)《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004》 三:设计内容:主梁布置及尺寸拟定桥梁横断面布置图桥梁纵断面布置主梁内力计算一、恒载内力计算:1: 桥面铺装和人行道重力;人行道和栏杆的重力作用取用 5m KN /;桥面铺装为:m KN /939.252*52372)138.006.0(=+⨯⨯+;为简化计算,将人行道、栏杆和桥面铺装的重力平均分配给各主梁,得: g 2=25.939/5=5.188m KN /;2:横隔梁重力;根据结构尺寸,一块预制横隔梁的体积为:3247.096.018.02)39.147.1(m =⨯⨯+;中主梁有12块横隔梁预制块,而边主梁有6块横隔梁预制块,可将其产生的重力沿主梁纵向均匀分摊,则:中主梁横隔梁产生的重力为:g 1=12*0.247/24.96*24=2.85m KN /; 边主梁横隔梁产生的重力为:g 1’=6*0.247/24.96*24=1.425m KN /; 3:主梁重力;g 01=A*24.96*24=0.5356*1*24=12.854m KN /; 4:一期恒载作用下总重力为:中主梁:g 恒中=2.85+12.854=15.704m KN /; 边主梁:g 恒边=1.425+12.854=14.279m KN /;二、活载内力计算:1:主梁横向分布系数计算:(1) 支点处采用杠杆法,由对称可知只需计算1,2,3号梁。
横梁内力计算课件

有限元法具有较高的计算精度和灵活性,能够考虑各种复杂因素,但计算相对复杂,需要 借助计算机辅助分析软件进行实现。
04
横梁内力计算实例
简单横梁的内力计算
简单横梁的受力分析
简单横梁在受到荷载作用时,会产生弯矩和剪力,通过对这些力 的分析可以了解横梁的内力分布情况。
弯矩计算
弯矩是横梁所承受的弯曲力矩,通过计算可以得到横梁的最大弯矩 值,以此判断横梁的强度和稳定性。
优化程序代码
通过优化程序代码,减少 计算过程中的冗余操作和 重复计算,提高计算效率 。
并行计算
利用多核CPU或分布式计 算资源进行并行计算,以 加速内力计算过程。
运用新技术进行内力计算
人工智能与机器学习
利用人工智能与机器学习技术对大量数据进行训练和学习,实现内力预测和优 化。
云计算与大数据
运用云计算与大数据技术处理和分析大规模数据,为横梁内力计算提供更全面 和深入的支持。
静力平衡法
静力平衡法的基本原理
静力平衡法是一种通过平衡条件求解内力的方法,其基本 原理是假定横梁在外力作用下处于平衡状态,通过已知的 外力可求得横梁的内力。
静力平衡法的适用范围
静力平衡法适用于小变形、线性弹性以及材料性质为常数 的简单问题。
静力平衡法的优缺点
静力平衡法具有计算简单、直观等优点,但无法考虑复杂 结构和材料非线性等复杂因素,计算精度相对较低。
利用经验公式进行内力计算
对于一些常见的复杂横梁类型,可以利用经验公式进行内力计算,这些公式基于大量的工程实践和理论 推导而来,可以快速得到内力值。
工程实例解析
工程实例的选择
选择具有代表性的工程实例,如桥梁 、房屋结构等,通过对这些实例的分 析和计算,可以更好地理解和掌握横 梁内力计算的方法和技巧。
(完整版)梁的内力计算

(2) 荷载简化一一将荷载简化为集中力、线分布力或力偶等;
(3) 支座简化——主要简化为以下三种典型支座:
(a)活动铰支座(或辊轴支座),其构造图及支座简图如图4—3(a)所示。这
种支座只限制梁在沿垂直于支承平面方向的位移, 其支座反力过铰心且垂直于支
(1)求支座反力
正,如图4-7(c)o
由
Y0
Q2
qa
0
得
Q2qa
由
M20
m2
a小
qa 0
2
得
m2
2
qa
2
(4)求3-3截面(D截面左侧边一点)内力
取右端为脱离体,3-3截面无限靠近D点,线分布力q的分布长度趋于0,则3-3
截面上Q=0,M=0o
2.2截面法直接由外力求截面内力的法则
上例说明了运用截面法求任一截面内力的方法。因脱离体的平衡条件丫0的 含义为:脱离体上所有外力和内力在丫轴方向投影的代数和为零。其中只有剪力Q为未知量,移到方程式右边即得直接由外力求任一截面剪力的法则:
对称平面内,称为弯矩
则得
由Mc0,有YaxM0
则得MYaX
注意此处是对截面形心C取矩,因剪力Q通过截面形心C点,故在力矩方程中为 零。同样可取右脱离体,由平衡方程求出梁截面m-n上的内力Q和M,其结果与 左脱离体求得的Q M大小相等,方向(或转向)相反,互为作用力与反作用力 关系。
为使梁同一截面内力符号一致,必须联系到变形状态规定它们的正负号。 若从梁m-n处取一微段梁dx,由于剪力Q作用会使微段发生下错动的剪切变形。 我们规 定:使微段梁发生左端向上而右端向下相对错动的剪力Q为正(如图4—6(a)),反之为负(如图4—6(b));使微段梁弯曲为向下凸时的弯矩M为正,反之为负
主梁内力计算

主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。
根据上述梁跨结构纵、横截面的布置,计算活载作用下的梁桥荷载横向分布系数,求出各主梁控制截面(取跨中、四分点、变化点截面及支点截面)的恒载和最大活载内力,然后再进行主梁内力组合。
一、恒载内力计算1、恒载集度⑴预制梁自重(第一期恒载)①.跨中截面段主梁自重(四分点截面至跨中截面,长7.25m )(1)0.861625.07.25156.165g KN =⨯⨯=②.马蹄抬高与腹板变宽段梁的自重近似计算(长3.7m ) 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③.支点段梁的自重(长3.55m )(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④.横隔梁的自重 中横隔梁体积为:()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为:()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤.主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= (2)第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁(现浇部分)体积:30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁(现浇部分)体积:30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装:0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁,则()717.25/5 3.45/g KN m ==④防撞栏:两侧防撞栏均分给五片主梁,则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用:下面进行永久作用效用计算(参照图1-4),设c 为计算截面至左侧支座的距离,并令/a c l =。
横梁内力计算

1号梁的横向影响线竖标值:11 0.60,15 0.20 2号梁的横向影响线竖标值:21 0.40,25 0 3号梁的横向影响线竖标值:31 0.20,35 0.20
(1)绘制弯矩影响线 M23 :
P=1
作用在1号梁轴上:
M ( 2 3 )1
11
1.5d
21
0.5d
1 1.5d
0.64
✓荷载 P=1 位于截面 r 的右侧
左
Mr R1b1 R2b2 Ribi
左
Vr R1 R2 Ri
R1
R2 M 23R3
R4
R5
b2 b1
图 横隔梁计算图示
b2 :支承反力Ri到计算截面的距离
可以直接利用已经求得的 Ri 的横向影响线绘制横梁的内力影响线。
通常横隔梁的弯矩在靠近桥中线的截面处较大,剪力在靠近桥两侧 边缘处的截面较大。
P=1 作用在计算截面左侧时:V1右 R1,即1Vi右 1i 1
180
180
130
180
图 中横隔梁的内力影响线
求解:3. 计算截面内力
M23 (1 ) P0q
1.254 1144.46 (0.92 0.29) 219.19kN m
V1右 (1 ) P0q
1.254 1144.46 (0.575 0.35 0.188 0.038) 194.74kN
M 31
11 2d
21 d
1 2d
M 32
12
2d
22
d
1 d
M 35
15
2d
25
d
M 36
16
2d
26 d
一、 横隔梁的内力影响线
3-4截面的正弯矩:
横梁内力计算-21页PPT资料

1 n
a1a3 2 ai2
R 2 R 3
+
1 1
+
2 1
+
3 1
1 6 2 6 3 6
26
1 n
a1a2 2 ai2
36
1 n
a1a3 2 ai2
图 主梁支承反力(主梁内力)的横向影响线 M 3 1
1 1 .25d 2d
3 M 1 11 2d21 d 1 2d M
车辆荷载(特种车):
1
P0q 2 Pi yi 车道荷载:
P0q 21(Pk1qk) 人群荷载:
P0r p0r r(影响线上)满布
la
la
P1
P2 P2
2
22
y1
1
y2
y3
Pk
qk
P3 P3 22
中横隔梁影响线
1
中横隔梁影响线
r 汽车荷载范围的影 面响 积线 。
图 作用在中横隔梁上的计算荷载
位于5、6号梁
M 36R 1b 61R 2b 62
3 M 1 11 2d21 d 1 2d
3 M 2 122d22d 1 d
3M 5152d25d 3M 6162d26d
一、 横隔梁的内力影响线
3-4截面的正弯矩:
P=1
和剪力。
75
700
75
(M23和V1右)
Pk qk
1
2
3
4
5
105 160 160 160 160 105
图1 跨中横截面
485
485
485
485
§4.5 横隔梁内力计算

《桥规》规定:
受弯构件预拱度: (1)钢筋混凝土受弯构件 当由荷载短期效应组合并考虑荷载长期效应影响产生 的长期挠度不超过跨径的1/600时,可不设预拱度; 当不符合上述规定时应设预拱度,且其值应按结构自 重和1/2可变荷载频遇值计算的长期挠度值之和采用。 (2)预应力混凝土受弯构件 当预加应力产生的长期反拱值大于按荷载短期效应组 合计算的长期挠度时,可不设预拱度; 反之应设预拱度,其值应按该项荷载的挠度值与预加 应力长期反拱值之差采用。
§4.4 横隔梁内力计算方法
说明: 横隔梁内力计算方法应与主梁计算方法一致 中横隔梁受力最大,故可偏安全地依据中横隔 梁的弯矩和剪力进行配筋和强度验算 偏压法(或刚性横梁法)计算横隔梁内力
4.4.1 横隔梁内力影响线
力学模型: 将桥梁的中横隔梁近似地视作竖向支承在多根 弹性主梁上的多跨弹性支承连续梁。 可由平衡条件求解连续梁
a 1 η11 Βιβλιοθήκη + 1 2 n 2 ∑ ai
2
1 a η16 = + 1 2 n 2∑ ai
2
aa 1 η21 = + 1 2 2 n 2 ∑ ai aa 1 η31 = + 1 3 2 n 2 ∑ ai
η 26 =
1 aa + 1 22 n 2∑ ai
η36 =
M 63
aa 1 + 1 32 n 2∑ ai
《桥规》规定:
对于钢筋混凝土及预应力混凝土受弯构件,在使用阶 段的长期挠度值,在消除结构自重产生的长期挠度后 梁式桥主梁的最大挠度处不应超过计算跨径的 1/600,梁式桥主梁的悬臂端不应超过悬臂长度的 1/300。此挠度为不计冲击力时的值。
《桥规》6.5.1 钢筋混凝土和预应力混凝土受弯 构件,在正常使用极限状态下的挠度,可根据给 定的构件刚度用结构力学的方法计算。 6.5.2 受弯构件的刚度可按下式计算: 1.钢筋混凝土构件
《主梁内力计算》PPT课件

2
4
24
4
(81.4)
(595.0)
x=1/2
00:16
Q=0 (0)
M 1 16.0619.52 763.4 8
(793.3)
1 活载内力计算方法
•活载内力计算方法
计算步骤 求横向分布系数m; 应用主梁内力影响线,将荷载乘m后,在纵向按 最不利位置布载,求得主梁最大活载内力。
计算方法
4 主梁内力计算例题
简支梁基频的简化计算公式:
f
EIc 2l 2 mc
mc G g
单根主梁:
A 0.3902m2 , Ic 0.066146m4 ,
G 0.3902 25 9.76N / m
G g 9.76 9.81 0.995103 NS 3 m2
C30混凝土
E 1010 N m2
3.4主梁内力计算
00:16
主梁内力计算
•计算截面的确定
小跨径简支梁:
计算跨中截面的
、支M点m截ax面和跨中截面的剪力;
剪力:支点、跨中按直线变化;
弯矩:支点、跨中按二次抛物线变化
Mx
4Mmax x(l x) l2
大跨径简支梁:
还应计算 截L面、截面变化处等的弯矩和剪力。 4
00:16
1 恒载内力计算
S 867.72
73.1
13.39 74.68
88.07
3.75
00:16
4 主梁内力计算例题
计算车道荷载、人群荷载的支点截面剪力
m变化区荷载重心处的内力影响线坐标为:
y 1(19.5 1 4.9) 19.5 0.916 3
车道荷载支点截面剪力:
S
(1
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M r
左
Ribi
左
e
Qr
Ribi 1
(2)荷载P=1,在
r 的右侧:
M r 左 Ribi
左
Qr
Ri bi
4、不利荷载布置,求截面内力(组合)
2.3.4 结构挠度与预拱度计算
桥梁的挠度产生的原因: 恒载挠度、活载挠度
恒载挠度:不表征结构的刚度特性,可 通过施工时预设的反向挠度或称预拱度 来加以抵消,使竣工后的桥梁达到理想 的线型。
l / 600
预拱度(指跨中的反向挠度):为了消 除恒载挠度而设置
其值取等于全部恒载和一半可变荷载频 遇值所产生的竖向挠度值,
(2)均部荷载布载法:——汽车和人群荷载 a、当计算简支梁各截面的Mmax和跨中Qmax
时,采用不变的mc
一般公式: s 1 mc k
b、支点截面剪力或靠近支点截面Q(m有变化)
均布荷载
QA
Q
' A
QA
QA
a 2
m0
mc p
y
(三)计算示例:
已知:五梁式桥,荷载:公路—Ⅱ级,人群 pr=3.0kN/m2 求:跨中最大弯矩和最大剪力,支点截面最大剪力
三、内力组合
承载能力极限状态 正常使用极限状态
四、内力包络图
沿梁轴的各个截面处的控制设计内力值的连线
横隔梁内力计算方法
横梁的作用与受力特点作用: • • 加强结构的横向联系 • 保证全结构的整体性
偏压法计算横隔梁内力 1、力学模型:
将桥梁的中横隔梁近似地视作竖向支承在多根弹性 主梁上的多跨弹性支承连续梁。 可由平衡条件求解连续梁
第十讲主梁内力横隔梁内力计算演示文稿
(优选)第十讲主梁内力横隔梁内力计算
3、例题
已知:五梁式桥,计算跨径19.50m ,每侧栏杆 及人行道重5kN/m。求:边主梁恒载内力
步骤: 1、恒载集度(均布荷载) 2、恒载内力(材料力学方法)
想一想: 中梁与边梁的横载计算有何区别?
二、主梁活载内力计算
左
Qr R1 R2 1 Ri 1
2. 荷载 P=1 位于截面 r 的右侧时
左
M r R1 b1 R2 b2 Ri bi
左
Qr R1 R2 Ri
(二)作用在横隔梁上的计算荷载 按杠杆原理法求得影响线 ====〉加载求截面内力
汽车
Pk qk
人群
2la pr
横隔梁上计算荷载的计算图式
活载挠度:使梁引起反复变形,变形的 幅度(即挠度)愈大,可能发生的冲击 和振动作用也愈强烈,对行车的影响也 愈大。
在桥梁设计中需要通过验算活载挠度来 体现结构的刚度特性。
《公路桥规》规定: 钢筋混凝土及预应力混凝土梁式桥:
➢ 结构不记入自重,汽车荷载(不计冲击 力),此时计算的上部结构跨中最大竖 向挠度时采用可变荷载的频遇值产生的 跨中长期挠度,不应超过
Pk qk
纵向一列车道荷载轮重分布给该横隔梁 的计算荷载为:
Poq
1 2
qk
pk
y1
1 2
qk
la
1 2
pk
y1
人群荷载分布给该横隔梁的计算荷载为:
P0r p0r r
(三)横隔梁内力计算
说明: (1)汽车荷载计冲击和车道折减 (2)横隔梁和普通的连续梁一样,在其跨中位置 承受最大正弯矩,支点截面存在负弯矩和较大的 剪力,因此,设计时应加以分析计算。
2 、计算方法:
鉴于各主梁的荷载横向影响线(即弹性支承力 影响线)已求得,故连续梁(横隔梁)可用静 力平衡条件求解。因桥上荷载横向移动,通常 也用横隔梁内力影响线方法计算。并偏安全地 计算跨中的横隔梁。
(一)横隔梁的内力影响线
横隔梁计算图式
1. 荷载 P=1 位于截面 r 的左侧时
左
M r R1 b1 R2 b2 1 e Ri bi e
1、主梁活载内力计算分两步
(1)求某一根主梁的最不利荷载横向分布系数m;
(2)应用主梁内力影响线,给荷载乘以横向分布
系数,即 ,在纵向最不利位置在内力影响线下
加载,使得miPi
为最大,相应求得主梁最大活
载内力。
mi Pi yi
2、活载内力计算方法
(1)集中荷载布载法:
s 1 miPi yi
(四)计算举例 例用偏压法计算中横隔梁 已知:荷载:公路—Ⅱ级 求:M2-3,Q1右
步骤: 1、确定计算荷载 2、求各主梁横向分布影响线
(偏心压力法)
7.875kN/m
178.5kN
公路-Ⅱ级
4.85
4.85
4.85
4.85
跨中横隔梁的受载图式Байду номын сангаас
3、绘制中横隔梁内力影响线
(1)荷载P=1,在
r
的左侧:
