山东省聊城市第一中学2015届高三10月阶段性检测数学(文)(附答案)
2015-2016学年山东省聊城一中高三(上)期中数学试卷和答案(文科)

2015-2016学年山东省聊城一中高三(上)期中数学试卷(文科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知全集U={1,2,3,4,5,6},集合A={1,2,5},∁U B={4,5,6},则集合A∩B=()A.{1,2}B.{5}C.{1,2,3}D.{3,4,6}2.(5分)已知a,b,c∈R,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是()A.若a+b+c≠3,则a2+b2+c2<3 B.若a+b+c=3,则a2+b2+c2<3C.若a+b+c≠3,则a2+b2+c2≥3 D.若a2+b2+c2≥3,则a+b+c=33.(5分)函数f(x)=的定义域为()A.(﹣1,+∞)B.[﹣1,+∞)C.(﹣1,1)∪(1,+∞) D.[﹣1,1)∪(1,+∞)4.(5分)曲线y=x3﹣2x在点(1,﹣1)处的切线方程是()A.x﹣y﹣2=0 B.x﹣y+2=0 C.x+y+2=0 D.x+y﹣2=05.(5分)设a=20.1,b=ln,c=log3,则a,b,c的大小关系是()A.a>b>c B.a>c>b C.b>a>c D.b>c>a6.(5分)已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是()A.若α⊥γ,β⊥γ,则α∥βB.若m⊥α,n⊥α,则m∥nC.若m∥α,n∥α,则m∥n D.若m∥α,m∥β,则α∥β7.(5分)函数f(x)是定义在(﹣2,2)上的奇函数,当x∈(0,2)时,f (x)=2x﹣1,则f(log2)的值为()A.﹣2 B.﹣ C.7 D.﹣18.(5分)函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,为了得到函数y=cos (2x+)的图象,只需将y=f(x)的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向心平移个单位9.(5分)函数f(x)=2x﹣tanx在(﹣,)上的图象大致是()A.B.C.D.10.(5分)已知e是自然对数的底数,函数f(x)=e x+x﹣2的零点为a,函数g (x)=lnx+x﹣2的零点为b,则下列不等式中成立的是()A.f(a)<f(1)<f(b) B.f(a)<f(b)<f(1) C.f(1)<f(a)<f (b)D.f(b)<f(1)<f(a)二、填空题(本大题共5小题,每小题5分,共25分).11.(5分)已知||=1,||=6,•(﹣)=2,则向量与的夹角为.12.(5分)设等差数列{a n}的前n项为S n,已知a1=﹣11,a3+a7=﹣6,当S n取最小值时,n=.13.(5分)观察下列式子:,…,根据上述规律,第n个不等式应该为.14.(5分)已知a>0,x,y满足约束条件,若z=2x+y的最小值为1,则a=.15.(5分)已知f(x)=|log3x|,若f(a)=f(b)且a≠b.则的取值范围是.三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤).16.(12分)已知等差数列{a n}的前n项和为S n,公差d≠0,且S3=9,a1,a3,a7成等比数列.(1)求数列{a n}的通项公式;(2)设b n=2,求数列{b n}的前n项和T n.17.(12分)已知向量(ω>0),函数f(x)=,若函数f(x)的图象的两个相邻对称中心的距离为.(Ⅰ)求函数f(x)的单调增区间;(Ⅱ)若将函数f(x)的图象先向左平移个单位,然后纵坐标不变,横坐标缩短为原来的倍,得到函数g(x)的图象,当时,求函数g(x)的值域.18.(12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.(Ⅰ)求证:a,b,c成等比数列;(Ⅱ)若a=1,c=2,求△ABC的面积S.19.(13分)已知四棱锥A﹣BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.(Ⅰ)求证:EF∥面ABC;(Ⅱ)求证:平面ADE⊥平面ACD;(Ⅲ)求四棱锥A﹣BCDE的体积.20.(12分)设数列{a n}的前n项和为S n,且a1=1,a n+1=2S n+1,数列{b n}满足a1=b1,点P(b n,b n)在直线x﹣y+2=0上,n∈N*.+1(1)求数列{a n},{b n}的通项公式;(2)设,求数列{c n}的前n项和T n.21.(14分)设函数f(x)=xlnx(x>0):(1)求函数f(x)的单调区间;(2)设F(x)=ax2+f′(x)(a∈R),F(x)是否存在极值,若存在,请求出极值;若不存在,请说明理由;(3)当x>0时,证明:e x>f′(x)+1.2015-2016学年山东省聊城一中高三(上)期中数学试卷(文科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知全集U={1,2,3,4,5,6},集合A={1,2,5},∁U B={4,5,6},则集合A∩B=()A.{1,2}B.{5}C.{1,2,3}D.{3,4,6}【解答】解:∵全集U={1,2,3,4,5,6},又∵∁U B={4,5,6},∴B={1,2,3},∵A={1,2,5},∴A∩B={1,2},故选:A.2.(5分)已知a,b,c∈R,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是()A.若a+b+c≠3,则a2+b2+c2<3 B.若a+b+c=3,则a2+b2+c2<3C.若a+b+c≠3,则a2+b2+c2≥3 D.若a2+b2+c2≥3,则a+b+c=3【解答】解:根据四种命题的定义,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是“若a+b+c≠3,则a2+b2+c2<3”故选:A.3.(5分)函数f(x)=的定义域为()A.(﹣1,+∞)B.[﹣1,+∞)C.(﹣1,1)∪(1,+∞) D.[﹣1,1)∪(1,+∞)【解答】解:要使函数有意义需,解得x>﹣1且x≠1.∴函数的定义域是(﹣1,1)∪(1,+∞).故选:C.4.(5分)曲线y=x3﹣2x在点(1,﹣1)处的切线方程是()A.x﹣y﹣2=0 B.x﹣y+2=0 C.x+y+2=0 D.x+y﹣2=0【解答】解:由题意得,y′=3x2﹣2,∴在点(1,﹣1)处的切线斜率是1,∴在点(1,﹣1)处的切线方程是:y+1=x﹣1,即x﹣y﹣2=0,故选:A.5.(5分)设a=20.1,b=ln,c=log3,则a,b,c的大小关系是()A.a>b>c B.a>c>b C.b>a>c D.b>c>a【解答】解:∵a=20.1>20=10=ln1<b=ln<lne=1c=<log31=0∴a>b>c故选:A.6.(5分)已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是()A.若α⊥γ,β⊥γ,则α∥βB.若m⊥α,n⊥α,则m∥nC.若m∥α,n∥α,则m∥n D.若m∥α,m∥β,则α∥β【解答】解:若α⊥γ,β⊥γ,则α与β相交或平行,故A错误;若m⊥α,n⊥α,则由直线与平面垂直的性质得m∥n,故B正确;若m∥α,n∥α,则m与n相交、平行或异面,故C错误;若m∥α,m∥β,则α与β相交或平行,故D错误.故选:B.7.(5分)函数f(x)是定义在(﹣2,2)上的奇函数,当x∈(0,2)时,f (x)=2x﹣1,则f(log2)的值为()A.﹣2 B.﹣ C.7 D.﹣1【解答】解:由题意得,f(log2)=f(﹣log23)=﹣f(log23)=﹣(﹣1)=﹣(3﹣1)=﹣2.故选:A.8.(5分)函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,为了得到函数y=cos (2x+)的图象,只需将y=f(x)的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向心平移个单位【解答】解:依题意,f(x)=sin(ωx+ϕ)(ω>0)的周期T=2×(﹣)=π=,∴ω=2,又2×+φ=π,∴φ=.∴f(x)=sin(2x+)=cos[﹣(2x+)]=cos(﹣2x)=cos(2x﹣);∴f(x+)=cos[2(x+)﹣]=cos(2x+);∴为了得到函数y=cos(2x+)的图象,只需将y=f(x)的图象向左平移个单位.故选:C.9.(5分)函数f(x)=2x﹣tanx在(﹣,)上的图象大致是()A.B.C.D.【解答】解:定义域(﹣,)关于原点对称,因为f(﹣x)=﹣2x+tanx=﹣(2x﹣tanx)=﹣f(x),所以函数f(x)为定义域内的奇函数,可排除B,C;因为f()=﹣tan>0,而f()=﹣tan()=﹣(2+)<0,可排除A.故选:D.10.(5分)已知e是自然对数的底数,函数f(x)=e x+x﹣2的零点为a,函数g (x)=lnx+x﹣2的零点为b,则下列不等式中成立的是()A.f(a)<f(1)<f(b) B.f(a)<f(b)<f(1) C.f(1)<f(a)<f (b)D.f(b)<f(1)<f(a)【解答】解:∵函数f(x)=e x+x﹣2的零点为a,f(0)=﹣1<0,f(1)=e﹣1>0,∴0<a<1.∵函数g(x)=lnx+x﹣2的零点为b,g(1)=﹣1<0,g(2)=ln2>0,∴1<b <2.综上可得,0<a<1<b<2.再由函数f(x)=e x+x﹣2在(0,+∞)上是增函数,可得f(a)<f(1)<f(b),故选:A.二、填空题(本大题共5小题,每小题5分,共25分).11.(5分)已知||=1,||=6,•(﹣)=2,则向量与的夹角为.【解答】解:由•(﹣)=2,得﹣=2,即=3,cos<,>==,所以<>=,故答案为:.12.(5分)设等差数列{a n}的前n项为S n,已知a1=﹣11,a3+a7=﹣6,当S n取最小值时,n=6.【解答】解:∵等差数列{a n}的前n项为S n,a1=﹣11,a3+a7=﹣6,∴﹣11+2d﹣11+6d=﹣6,解得d=2,∴S n=﹣11n+=n2﹣12n=(n﹣6)2﹣36,∴当S n取最小值﹣36时,n=6.故答案为:6.13.(5分)观察下列式子:,…,根据上述规律,第n个不等式应该为1+++…+<.【解答】解:根据规律,不等式的左边是n+1个自然数倒数的平方的和,右边分母是以2为首项,1为公差的等差数列,分子是以3为首项,2为公差的等差数列,所以第n个不等式应该为1+++…+<故答案为:1+++…+<14.(5分)已知a>0,x,y满足约束条件,若z=2x+y的最小值为1,则a=.【解答】解:先根据约束条件画出可行域,设z=2x+y,将最大值转化为y轴上的截距,当直线z=2x+y经过点B时,z最小,由得:,代入直线y=a(x﹣3)得,a=;故答案为:15.(5分)已知f(x)=|log3x|,若f(a)=f(b)且a≠b.则的取值范围是[2,+∞).【解答】解:根据题意,对于f(x)=|log3x|,有x>0,若f(a)=f(b),则|log3a|=|log3b|,又由a≠b,则有log3a=﹣log3b,即log3a+log3b=log3ab=0,则ab=1,又由a、b>0且a≠b,∴=b+≥2,当且仅当b=取等号,即的取值范围是[2,+∞);故答案为:三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤).16.(12分)已知等差数列{a n}的前n项和为S n,公差d≠0,且S3=9,a1,a3,a7成等比数列.(1)求数列{a n}的通项公式;(2)设b n=2,求数列{b n}的前n项和T n.【解答】解:(1)∵a1,a3,a7成等比数列.∴a32=a1a7,即(a1+2d)2=a1(a1+6d),化简得d=a1,d=0(舍去).∴S3=3a1+=a1=9,得a1=2,d=1.∴a n=a1+(n﹣1)d=2+(n﹣1)=n+1,即a n=n+1.(2)∵b n=2a n=2n+1,∴b1=4,.∴{b n}是以4为首项,2为公比的等比数列,∴T n==2n+2﹣4.17.(12分)已知向量(ω>0),函数f(x)=,若函数f(x)的图象的两个相邻对称中心的距离为.(Ⅰ)求函数f(x)的单调增区间;(Ⅱ)若将函数f(x)的图象先向左平移个单位,然后纵坐标不变,横坐标缩短为原来的倍,得到函数g(x)的图象,当时,求函数g(x)的值域.【解答】解:(1)f(x))==2cosωx(si nωx﹣cosωx)﹣2+3=sin2ωx﹣cos2ωx=,∵,∴.令,求得f(x)的增区间为.(2)将函数f(x)的图象先向左平移个单位,得到y=sin[2(x+)﹣]=sin(2x+)的图象;然后纵坐标不变,横坐标缩短为原来的倍,得到函数g(x)=sin(4x+)的图象,故,∵,、∴,故函数g(x)的值域是.18.(12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.(Ⅰ)求证:a,b,c成等比数列;(Ⅱ)若a=1,c=2,求△ABC的面积S.【解答】(I)证明:∵sinB(tanA+tanC)=tanAtanC∴sinB()=∴sinB•=∴sinB(sinAcosC+sinCcosA)=sinAsinc∴sinBsin(A+C)=sinAsinC,∵A+B+C=π∴sin(A+C)=sinB即sin2B=sinAsinC,由正弦定理可得:b2=ac,所以a,b,c成等比数列.(II)若a=1,c=2,则b2=ac=2,∴,∵0<B<π∴sinB=∴△ABC的面积.19.(13分)已知四棱锥A﹣BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.(Ⅰ)求证:EF∥面ABC;(Ⅱ)求证:平面ADE⊥平面ACD;(Ⅲ)求四棱锥A﹣BCDE的体积.【解答】证明:(Ⅰ)取AC中点G,连接FG、BG,∵F,G分别是AD,AC的中点∴FG∥CD,且FG=DC=1.∵BE∥CD∴FG与BE平行且相等∴EF∥BG.EF⊄面ABC,BG⊂面ABC∴EF∥面ABC…(4分)(Ⅱ)∵△ABC为等边三角形∴BG⊥AC又∵DC⊥面ABC,BG⊂面ABC∴DC⊥BG∴BG垂直于面ADC的两条相交直线AC,DC,∴BG⊥面ADC.…(6分)∵EF∥BG∴EF⊥面ADC∵EF⊂面ADE,∴面ADE⊥面ADC.…(8分)解:(Ⅲ)方法一:连接EC,该四棱锥分为两个三棱锥E﹣ABC和E﹣ADC..…(12分)方法二:取BC的中点为O,连接AO,则AO⊥BC,又CD⊥平面ABC,∴CD⊥AO,BC∩CD=C,∴AO⊥平面BCDE,∴AO为V A的高,,∴﹣BCDE.20.(12分)设数列{a n}的前n项和为S n,且a1=1,a n+1=2S n+1,数列{b n}满足a1=b1,)在直线x﹣y+2=0上,n∈N*.点P(b n,b n+1(1)求数列{a n},{b n}的通项公式;(2)设,求数列{c n}的前n项和T n.=2S n+1可得a n=2S n﹣1+1(n≥2),【解答】解:(1)由a n+1﹣a n=2a n,两式相减得a n+1a n+1=3a n(n≥2).又a2=2S1+1=3,所以a2=3a1.故{a n}是首项为1,公比为3的等比数列.所以a n=3n﹣1.由点P(b n,b n+1)在直线x﹣y+2=0上,所以b n+1﹣b n=2.则数列{b n}是首项为1,公差为2的等差数列.则b n=1+(n﹣1)•2=2n﹣1(2)因为,所以.则,两式相减得:.所以=.21.(14分)设函数f(x)=xlnx(x>0):(1)求函数f(x)的单调区间;(2)设F(x)=ax2+f′(x)(a∈R),F(x)是否存在极值,若存在,请求出极值;若不存在,请说明理由;(3)当x>0时,证明:e x>f′(x)+1.【解答】解:(1)函数的定义域为(0,+∞)求导函数,可得f′(x)=1+lnx令f′(x)=1+lnx=0,可得x=∴0<x<时,f′(x)<0,x>时,f′(x)>0∴函数f(x)在(0,)上单调递减,在(,+∞)单调递增,(2)∴F(x)=ax2+f′(x)(x>0),∴F′(x)=2ax+=(x>0).当a≥0时,F′(x)>0恒成立,∴F(x)在(0,+∞)上为增函数,∴F(x)在(0,+∞)上无极值.当a<0时,令F′(x)=0得x=或x=﹣(舍).∴当0<x<时,F′(x)>0,当x>时,F′(x)<0,∴F(x)在(0,)上单调递增,在(,+∞)上单调递减,∴当x=时,F(x)取得极大值F()=+ln,无极小值,综上:当a≥0时,F(x)无极值,当a<0时,F(x)有极大值+ln,无极小值,(Ⅲ)证明:设g(x)=e x﹣lnx,x>0,则即证g(x)>2,只要证g(x)min>2,∵g′(x)=e x﹣,设h(x)=e x﹣,∴h′(x)=e x+>0恒成立,∴h(x)在(0,+∞)上单调递增,∵h(0.5)=﹣2<1.7﹣2<0,h(1)=e﹣1>0,∴方程h(x)=0有唯一的实根x=t,且t∈(0.5,1)∵当t∈(0.5,1)时,h(x)<h(t)=0,当t∈(t,+∞)时,h(x)>h(t)=0,∴当x=t时,g(x)min=e t﹣lnt,∵h(t)=0,即e t=,则t=e﹣t,∴g(x)min=﹣ln=e﹣t=+t>2=2,∴e x>f′(x)+1.。
山东省聊城第一中学高三数学10月第一次阶段性测试试题
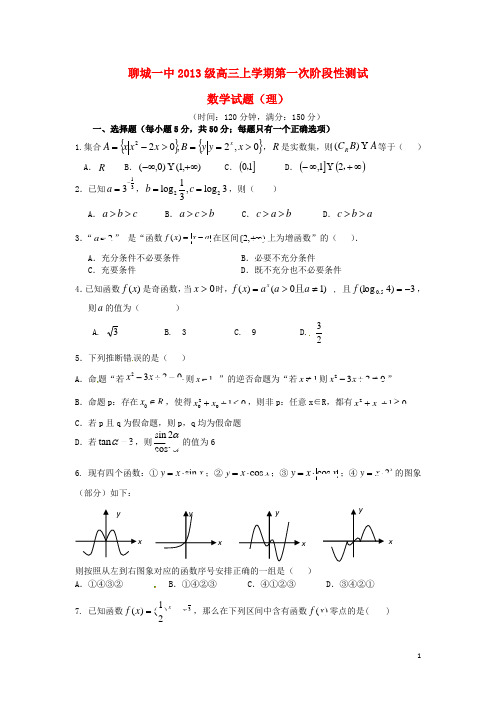
聊城一中2013级高三上学期第一次阶段性测试数学试题(理)(时间:120分钟,满分:150分)一、选择题(每小题5分,共50分;每题只有一个正确选项)1.集合{}{}0,2,022>==>-=x y y B x x x A x ,R 是实数集,则A B C R Y )(等于( )A .RB .),1()0,(+∞-∞YC .(]10,D .(]()∞+∞-,21,Y 2.已知133a -=,221log ,log 33b c ==,则( ) A .a b c >> B .a c b >> C .c a b >> D .c b a >> 3.“2a =” 是“函数()f x x a =-在区间[2,)+∞上为增函数”的( ). A .充分条件不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知函数)(x f 是奇函数,当0>x 时,)10()(≠>=a a a x f x且 , 且3)4(log 5.0-=f ,则a 的值为( )A. 3B. 3C. 9D. 235.下列推断错误的是( )A .命题“若2320,x x -+=则1x = ”的逆否命题为“若1x ≠则2320x x -+≠” B .命题p :存在0x R ∈,使得20010x x ++<,则非p :任意x ∈R ,都有210x x ++≥C .若p 且q 为假命题,则p ,q 均为假命题D .若tan 3α=,则2sin 2cos αα的值为66. 现有四个函数:①sin y x x =⋅;②cos y x x =⋅;③cos y x x =⋅;④2xy x =⋅的图象(部分)如下:则按照从左到右图象对应的函数序号安排正确的一组是( )A .①④③②B .①④②③C .④①②③D .③④②①7. 已知函数31)21()(x x f x-=,那么在下列区间中含有函数)(x f 零点的是( )o Xxxyxyyx yxy O1211-A.)31,0( B.)21,31( C. )32,21( D. )1,32( 8. 函数()sin()(0)f x x ωϕω=+>,)(0<ϕ<π-的一段图象如图所示,则=ϕ( )A .4π-B .2πC . 4π D .2π-9.已知函数①x x y cos sin +=,②x x y cos sin 22=,则下列结论正确的是( ) A.两个函数的图象均关于点(,0)4π-成中心对称 B.函数①的图像可由函数②的图像上所有点的横坐标缩短为原来的21,再向左平移4π个单位长度得到 C.两个函数在区间(,)44ππ-上都是单调递增函数 D.两个函数的最小正周期相同 10. 我们常用以下方法求形如)()(x g x f y =的函数的导数:先两边同取自然对数得:)(ln )(ln x f x g y =,再两边同时求导得到:)(')(1)()(ln )('1'x f x f x g x f x g y y ⋅⋅+=⋅,于是得到:)](')(1)()(ln )('[)(')(x f x f x g x f x g x f y x g ⋅⋅+=,运用此方法求得函数xx y 1=的一个单调递增区间是( )A.(e ,4)B.(3,6) C (0,e ) D.(2,3)二、填空题(本大题共5小题,每小题5分,共25分,把答案填在答卷纸的相应位置上)11. 已知角α终边上一点P(-4,3),则cos ⎝ ⎛⎭⎪⎫π2+αsin (-π-α)cos ⎝ ⎛⎭⎪⎫11π2-αsin ⎝ ⎛⎭⎪⎫9π2+α的值为 .12. 用}{max ,a b 表示,a b 两个数中的最大数,设}{2()max ,f x x x = (14x ≥),那么由函数()y f x =的图象、x 轴、直线14x =和2x =所围成的封闭图形的面积是 . 13. 已知函数3,0,()ln(1),>0.x x f x x x ⎧≤=⎨+⎩ 若f (2-x 2)>f (x ),则实数x 的取值范围是 .14.已知函数()f x ∞∞是(-,+)上的奇函数,且()(2)f x f x =-,当[1,0]x ∈-时,1()12xf x ⎛⎫=- ⎪⎝⎭,则=+)2016()2015(f f __.15.已知()f x =⎪⎩⎪⎨⎧≥<---)0()0(2|1|2x e x x x a x ,且函数()1y f x =-恰有3个不同的零点,则实数a 的取值范围是_______.三、解答题(本大题6小题,其中第16-19题每题12分,第20题13分,第21题14分,解答应写出文字说明、证明过程或演算步骤,并把解答写在答卷纸的相应位置上) 16. (1)已知集合{}{}x y x B x A x x 6log 21,122-==<=-,求B A I ;(2)计算:41log 50.50532527()()24ln lg 200lg 2168e π-+-+-+-17. 已知:在函数x mx x f -=3)(的图象上,以),1(n N 为切点的切线的倾斜角为.4π(Ⅰ)求n m ,的值;(Ⅱ)是否存在最小的正整数k ,使得不等式]3,1[2001)(-∈-≤x k x f 对于恒成立?如果存在,请求出最小的正整数k ,如果不存在,请说明理由.18. 已知函数2()23sin cos 2sin f x x x x =-,x ∈R . (Ⅰ)求函数()f x 的最小正周期与单调增区间; (Ⅱ)求函数()f x 在0,4π⎡⎤⎢⎥⎣⎦上的最大值与最小值.19. 如图所示,将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ,要求M 在AB 的延长线上,N 在AD 的延长线上,且对角线MN 过C 点.已知AB=3米,AD=2米. (Ⅰ)设x AN =(单位:米),要使花坛AMPN 的面积大于32平方米,求x 的取值范围; (Ⅱ)若)4,3[∈x (单位:米),则当AM ,AN 的长度分别是多少时,花坛AMPN 的面积最大?并求出最大面积.20. 对于函数12(),(),()f x f x h x ,如果存在实数,a b 使得12()()()h x a f x b f x =⋅+⋅,那么称()h x 为12(),()f x f x 的生成函数.(Ⅰ)下面给出两组函数,()h x 是否分别为12(),()f x f x 的生成函数?并说明理由; 第一组:12()sin ,()cos ,()sin()3f x x f x x h x x π===+;第二组:1)(,1)(,)(22221+-=++=-=x x x h x x x f x x x f ;(Ⅱ)设12212()log ,()log ,2,1f x x f x x a b ====,生成函数()h x .若不等式23()2()0h x h x t ++<在[2,4]x ∈上有解,求实数t 的取值范围;(Ⅲ)设121(),()(110)f x x f x x x==≤≤,取1,0a b =>,生成函数()h x 使 ()h x b ≥ 恒成立,求b 的取值范围.21.已知函数1()ln ln 22e f x x x =-+,32()()2x g x f x x=--. (1)求()f x 的单调区间;(2)设函数2()4h x x mx =-+,若存在1(0,1]x ∈,对任意的2[1,2]x ∈,总有12()()g x h x ≥成立,求实数m 的取值范围.高三第一次阶段性测试数学试题(理)参考答案 一、选择题:共10小题,每小题5分,共计50分题 号12345678910选 项 D C A A C B BD C C二、填空题:本大题共4小题,每小题4分,满分16分. 11.43-12.123513.(2,1)- 14.1- 15. ()0,1 三、解答题: 16.解:(1)由10212202>⇔<-⇔=<-x x x x x 或0<x ,得),1()0,(+∞⋃-∞=A …2分由0log 216≥-x , 得:60≤<x …4分∴(]6,0=B …5分 ∴(]6,1=⋂B A …6分 (2)120.53(-)353-25-52lg 2-lg 242⨯⨯⎛⎫⎛⎫=++++ ⎪⎪⎝⎭⎝⎭原式12233245=+=…12分 17.解:(I ),13)(2-='mx x f依题意,得.32,113,4tan)1(==-='m m f 即π因为.31,)1(-==n n f 所以…4分(Ⅱ)令.22,012)(2±==-='x x x f 得 当;012)(,2212>-='-<<-x x f x 时 当;012)(,22222<-='<<-x x f x 时 当;012)(,3222>-='<<x x f x 时又.15)3(,32)22(,32)22(,31)1(=-==-=-f f f f 因此, 当.15)(32,]3,1[≤≤--∈x f x 时…8分 要使得不等式]3,1[2001)(-∈-≤x k x f 对于恒成立,则.2016200115=+≥k …10分 所以,存在最小的正整数.2016=k 使得不等式]3,1[2001)(-∈-≤x k x f 对于恒成立. …12分.18.()3sin 2cos21f x x x =+-312(sin 2cos2)122x x =+-π2sin(2)16x =+-.…2分 (Ⅰ)()f x 的最小正周期为2ππ.2T ==…3分 令222,262k x k k πππππ-+≤+≤+∈Z ,解得36k x k ππππ-+≤≤+,所以函数()f x 的单调增区间为[,],36k k k ππππ-+∈Z . …6分(Ⅱ)∵04x π≤≤,∴22663x πππ≤+≤,∴1sin(2x )126π≤+≤ ,于是 12sin(2)26x π≤+≤ ,所以0()1f x ≤≤. …10分当且仅当0x =时,()f x 取最小值min ()(0)0f x f ==. 当且仅当262x ππ+=,即6x π=时最大值max ()()16f x f π==.…12分19.解:解:由于,AMDC AN DN =则AM =32xx - 故S AMPN =AN•AM=232x x - )2(>x …2分(I )由S AMPN > 32 得 232x x - > 32 ,因为x >2,所以2332640x x -+>,即(3x -8)(x -8)> 0从而8283x x <<> 或 即AN 长的取值范围是8(2)(8)3∞U ,,+ …6分 (II )令y =232x x -,则y ′=2226(2)334)(2)(2)x x x x x x x ---=--( …8分 因为当[3,4)x ∈时,y ′< 0,所以函数y =232x x -在[3,4)上为单调递减函数,从而当x =3时y =232x x -取得最大值,即花坛AMPN 的面积最大27平方米,…10分此时AN =3米,AM=9米. …12分 20.(Ⅰ)① 设sin cos sin()3a xb x x π+=+,即13sin cos sin cos 22a x b x x x +=+, 取13,22a b ==,所以()h x 是12(),()f x f x 的生成函数.…2分 ② 设222()(1)1a x x b x x x x -+++=-+,即22()()1a b x a b x b x x +--+=-+,则111a b a b b +=⎧⎪-+=-⎨⎪=⎩,该方程组无解.所以()h x 不是12(),()f x f x 的生成函数.…4分 (Ⅱ)122122()2()()2log log log h x f x f x x x x =+=+= …5分若不等式23()2()0h x h x t ++<在[2,4]x ∈上有解,23()2()0h x h x t ++<,即22223()2()3log 2log t h x h x x x <--=-- 设2log s x =,则[1,2]s ∈,22223log 2log 32y x x s s =--=--,max 5y =-,故,5t <-.…8分(Ⅲ)由题意,得()(110)bh x x x x=+≤≤ 1︒ 若(1,10)b ∈,则)(x h 在1[,b )上递减,在10(b ,]上递增,则min()2h h b b ==,∴1102b b b⎧<<⎪⎨≥⎪⎩,得14b <≤ …10分 2︒ 若1b ≤,则)(x h 在]10,1[上递增,则min (1)1h h b ==+,所以11b b b⎧≤⎪⎨+≥⎪⎩,得01b <≤. …11分3︒ 若10b ≥,则)(x h 在]10,1[上递减,则min (10)1010bh h ==+, 故101010b b b⎧≥⎪⎨+≥⎪⎩,无解 …12分综上可知,0 4.b <≤ …13分 (注:本题也可以分离参数) 21、解:(1) 1()ln ln (0,)22e f x x x x =-+∈+∞,(此处若不写定义域,可适当扣分)故112()22xf x x x-'=-=.∴当02x <<时,()0f x '>;当2x >时,()0f x '<.∴()f x 的单调增区间为(0,2),单调减区间为(2,)+∞ …6分(2)2()2ln ln 2eg x x x x =---,则2221222()2x x g x x x x -+'=-+=,而22115222()048x x x -+=-+>,故在(0,1]上()0g x '>,即函数()g x 在(0,1]上单调递增,∴max ()(1)ln 21g x g ==- …9分而“存在1(0,1]x ∈,对任意的2[1,2]x ∈,总有12()()g x h x ≥成立”等价于“()g x 在(0,1]上的最大值不小于()h x 在[1,2]上的最大值” …10分而()h x 在[1,2]上的最大值为(1),(2)h h 中的最大者,记为max{(1),(2)}h h .所以有(1)ln 21(1)(1)ln 21(2)g h g h =-≥⎧⎨=-≥⎩,(1)ln 215(1)ln 2182g mg m=-≥-⎧∴⎨=-≥-⎩,6ln 2,6ln 21(9ln 2)2m m m ≥-⎧⎪∴∴≥-⎨≥-⎪⎩. 故实数m 的取值范围为[6ln 2,)-+∞ …14分。
2015年山东省聊城市高考一模数学试卷【解析版】

2015年山东省聊城市高考数学一模试卷一、选择题(本大题共10小题,每小题5分,共50分)1.(5分)设集合M={x|x2﹣x<0},N={x|﹣2<x<2},则()A.M∩N=∅B.M∩N=M C.M∪N=M D.M∪N=R 2.(5分)在复平面内,复数的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)下列命题中的假命题是()A.∃x0∈R,lnx0<0B.∃x0∈R,sin x0<0C.∀x∈R,x3>0D.∀x∈R,2x>04.(5分)已知等轴双曲线C与椭圆+=1有相同的焦点,则双曲线C的方程为()A.2x2﹣2y2=1B.﹣=1C.x2﹣y2=1D.﹣=15.(5分)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为()A.B.C.3D.6.(5分)设S n是等差数列{a n}的前n项和,已知a2=3,a6=11,则S7等于()A.13B.49C.35D.637.(5分)某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的等腰直角三角形,该几何体体积是()A.1B.2C.D.8.(5分)“a=b”是“直线y=x+2与圆(x﹣a)2+(y﹣b)2=2相切”的()A.充分必要条件B.必要不充分条件C.充分不必要条件D.既不充分又不必要条件9.(5分)已知实数x,y满足条件,则目标函数z=+的取值范围为()A.[2,]B.[,]C.[2,]D.[,2] 10.(5分)已知函数f(x)=,若关于x的方程f(x)﹣mx=0恰有3个不同的实数根,则实数m的取值范围为()A.(﹣∞,)B.(,+∞)C.(0,)D.(1,+∞)二、填空题(本大题共5个小题,每小题5分,共25分)11.(5分)已知两个单位向量,满足|+2|=,则,的夹角为.12.(5分)将函数f(x)=sin(ωx+φ)(ω>0,﹣≤φ<)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y =sin x的图象,则f()=.13.(5分)从区间(0,10)内任取一个实数x,执行如图所示的程序框图后,输出的结果大于55的概率为.14.(5分)设O是坐标原点,AB是圆锥曲线的一条不经过点O且不垂直于坐标轴的弦,M是弦AB的中点,k ab,k cm分别表示直线AB,OM的斜率,在圆x2+y2=r2中,k ab•k cm=﹣1,在椭圆+=1(a>b>0)中,类比上述结论可得.15.(5分)我们把函数y=f(x)图象上的点到坐标原点距离的最小值叫做函数y=f(x)的“中心距离”,已知函数g(x)=x+(a>0)的“中心距离”不小于,则实数a的取值范围为.三、解答题(本大题共6小题,共75分)16.(12分)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且a=,b=7,函数f(x)=sin2x cos A﹣sin A sin2x(x∈R),且f(x)的最大值为.(Ⅰ)求函数f(x)的单调递增区间;(Ⅱ)求△ABC的面积.17.(12分)为了了解某班同学喜爱打篮球是否与性别有关,对该班全体同学进行了问卷调查,统计调查结果得到如下列联表已知从该班全体同学中随机抽取1人,抽到喜爱打篮球的学生的概率为.(Ⅰ)求列联表中m,n的值;(Ⅱ)用分层抽样的方法在喜欢打篮球的同学中抽取6名同学,然后再从这6名同学中任取2名同学,求所选2名同学中至少有1名女生的概率.18.(12分)在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,BD⊥DC,侧面P AB⊥底面ABCD,P A=AD=AB,点M是PB的中点.(Ⅰ)求证:AM∥平面PDC(Ⅱ)求证:平面PDC⊥平面PBC.19.(12分)已知等差数列{a n}是递增数列,a3=7,且a2,a4,a9成等比数列.(Ⅰ)求数列{a n}的通项公式(Ⅱ)设b n=a n cos nπ(n∈N*),求数列{b n}的前n项和S n.20.(13分)已知动圆M经过定点A(2,0),且在y轴上截得的弦长为4(Ⅰ)求动圆圆心M的轨迹C的方程(Ⅱ)设N(x0,0)是x轴上的定点,BD是经过N点的轨迹C的任意一条弦,若∠BAD恒为钝角,求x0的取值范围.21.(14分)已知函数f(x)=(x2﹣2x+k)e x(e=2.71828…是自然对数的底数)(Ⅰ)若曲线y=f(x)在x=0处的切线与直线x+y=0平行,求k的值(Ⅱ)求函数f(x)的单调区间(Ⅲ)求函数f(x)在[0,2]上的最小值.2015年山东省聊城市高考数学一模试卷参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分)1.(5分)设集合M={x|x2﹣x<0},N={x|﹣2<x<2},则()A.M∩N=∅B.M∩N=M C.M∪N=M D.M∪N=R 【解答】解:集合M={x|x2﹣x<0}=(0,1),N={x|﹣2<x<2}=(﹣2,2),∴M∩N=(0,1)=M,M∪N=(﹣2,2)=N,故选:B.2.(5分)在复平面内,复数的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:=∴复数的共轭复数是1+i故选:A.3.(5分)下列命题中的假命题是()A.∃x0∈R,lnx0<0B.∃x0∈R,sin x0<0C.∀x∈R,x3>0D.∀x∈R,2x>0【解答】解:A.取,则=﹣1<0,因此是真命题;B.取x0=,则=﹣<0,因此是真命题;C.取x≤0,则x3≤0,因此是假命题;D.∀x∈R,2x>0,是真命题.故选:C.4.(5分)已知等轴双曲线C与椭圆+=1有相同的焦点,则双曲线C的方程为()A.2x2﹣2y2=1B.﹣=1C.x2﹣y2=1D.﹣=1【解答】解:椭圆的焦点坐标为(﹣1,0),(1,0),所以双曲线的焦点坐标为(﹣1,0),(1,0),满足c2=1=a2+b2的只有A,故选A.5.(5分)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为()A.B.C.3D.【解答】解:∵,∴==,.故选:B.6.(5分)设S n是等差数列{a n}的前n项和,已知a2=3,a6=11,则S7等于()A.13B.49C.35D.63【解答】解:等差数列{a n}中,设首项为a1,公差为d,,解得:d=2,a1=1,所以:故选:B.7.(5分)某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的等腰直角三角形,该几何体体积是()A.1B.2C.D.【解答】解:由三视图知几何体为四棱锥,其直观图如图:则AS=AB=,四棱锥的高为,底面为直角梯形的面积S=(1+2)×=,∴几何体的体积V=××=.故选:D.8.(5分)“a=b”是“直线y=x+2与圆(x﹣a)2+(y﹣b)2=2相切”的()A.充分必要条件B.必要不充分条件C.充分不必要条件D.既不充分又不必要条件【解答】解:若直线y=x+2与圆(x﹣a)2+(y﹣b)2=2相切,则圆心(a,b)到直线的距离d=,即|a﹣b+2|=2,即a﹣b+2=2或a﹣b+2=﹣2,则a﹣b=0或a﹣b﹣4=0,则a=b”是“直线y=x+2与圆(x﹣a)2+(y﹣b)2=2相切”的充分不必要条件,故选:C.9.(5分)已知实数x,y满足条件,则目标函数z=+的取值范围为()A.[2,]B.[,]C.[2,]D.[,2]【解答】解:由约束条件作出可行域如图,联立,解得:,则A(3,1),联立,解得:,则B(1,2),由图可知,的最小值为,最大值为2.令t=∈[],f(t)=,则当t=1时,t+有最小值为2;又,f(2)=2+=,∴z=+的取值范围是[2,].故选:C.10.(5分)已知函数f(x)=,若关于x的方程f(x)﹣mx=0恰有3个不同的实数根,则实数m的取值范围为()A.(﹣∞,)B.(,+∞)C.(0,)D.(1,+∞)【解答】解:画出分段函数y=f(x)的图象和直线y=mx,关于x的方程f(x)﹣mx=0恰有3个不同的实数根,即为y=f(x)和直线y=mx有三个不同的交点.当直线与y=f(x)(x<0)的图象相切时,直线与y=f(x)(x∈R)恰有两个交点.联立y=mx和y=﹣1﹣x2(x<0),可得x2+mx+1=0,由判别式m2﹣2=0,可得m=(﹣舍去),通过图象观察,当直线的斜率大于时,直线与y=f(x)(x∈R)都有三个交点.则实数m的取值范围为(,+∞).故选:B.二、填空题(本大题共5个小题,每小题5分,共25分)11.(5分)已知两个单位向量,满足|+2|=,则,的夹角为.【解答】解:因为|+2|=,所以|+2|2==()2,又,是两个单位向量,所以,∴=﹣,又,所以cos=,,的夹角为.故答案为.12.(5分)将函数f(x)=sin(ωx+φ)(ω>0,﹣≤φ<)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sin x的图象,则f()=.【解答】解:函数f(x)=sin(ωx+φ)(ω>0,﹣≤φ<)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,可得函数y=sin(2ωx+φ)的图象.再把所得图象再向右平移个单位长度得到函数y=sin[2ω(x﹣)+φ)]=sin(2ωx+φ﹣ω)=sin x的图象,∴2ω=1,且φ﹣ω=2kπ,k∈Z,∴ω=,φ=+2kπ,∴f(x)=sin(x+),∴f()=sin(+)=sin=.故答案为:.13.(5分)从区间(0,10)内任取一个实数x,执行如图所示的程序框图后,输出的结果大于55的概率为.【解答】解:设实数x∈[0,10],经过第一次循环得到x=2x+1,n=2经过第二循环得到x=2(2x+1)+1,n=3经过第三次循环得到x=2[2(2x+1)+1]+1,n=4此时输出x输出的值为8x+7令8x+7≥55,得x≥6由几何概型得到输出的x大于55的概率为==.故答案为:.14.(5分)设O是坐标原点,AB是圆锥曲线的一条不经过点O且不垂直于坐标轴的弦,M是弦AB的中点,k ab,k cm分别表示直线AB,OM的斜率,在圆x2+y2=r2中,k ab•k cm=﹣1,在椭圆+=1(a>b>0)中,类比上述结论可得若AB是圆锥曲线的一条不经过点O且不垂直于坐标轴的弦,M是弦AB的中点,则k AB•k OM=﹣.【解答】解:定理:如果圆x2+y2=r2(r>0)上异于一条直径两个端点的任意一点与这条直径两个端点连线的都斜率存在,则这两条直线的斜率乘积为定值﹣1,即k AB•k OM=﹣1.运用类比推理,写出该定理在椭圆+=1中的推广:若AB是圆锥曲线的一条不经过点O且不垂直于坐标轴的弦,M是弦AB的中点,则k AB•k OM=﹣故答案为:若AB是圆锥曲线的一条不经过点O且不垂直于坐标轴的弦,M是弦AB的中点,则k AB•k OM=﹣.15.(5分)我们把函数y=f(x)图象上的点到坐标原点距离的最小值叫做函数y=f(x)的“中心距离”,已知函数g(x)=x+(a>0)的“中心距离”不小于,则实数a的取值范围为[﹣1,+∞).【解答】解:由题意任取函数g(x)=x+(a>0)图象上的一点P(x,x+),由两点间的距离公式可得P到原点的距离|OP|==≥=,当且仅当2x2=即x=±时取等号,∵“中心距离”不小于,∴≥,解得a≥﹣1,∴实数a的取值范围为:[﹣1,+∞)故答案为:[﹣1,+∞)三、解答题(本大题共6小题,共75分)16.(12分)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且a=,b=7,函数f(x)=sin2x cos A﹣sin A sin2x(x∈R),且f(x)的最大值为.(Ⅰ)求函数f(x)的单调递增区间;(Ⅱ)求△ABC的面积.【解答】解:(I)f(x)=sin2x cos A﹣sin A=(sin2x cos A+sin A cos2x)﹣sin A=sin(2x+A)﹣sin A,∵f(x)的最大值为,∴=,化为sin A=,∵△ABC是锐角三角形,∴,∴f(x)=sin(2x+)﹣,由,(k∈Z),解得≤x≤k(k∈Z).∴函数f(x)的单调递增区间为(k∈Z).(II)由余弦定理可得:a2=b2+c2﹣2bc cos A,∴,化为=0,解得c=或4.经过检验可得:不符合题意,舍去.∴c=4.===7.∴S△ABC17.(12分)为了了解某班同学喜爱打篮球是否与性别有关,对该班全体同学进行了问卷调查,统计调查结果得到如下列联表已知从该班全体同学中随机抽取1人,抽到喜爱打篮球的学生的概率为.(Ⅰ)求列联表中m,n的值;(Ⅱ)用分层抽样的方法在喜欢打篮球的同学中抽取6名同学,然后再从这6名同学中任取2名同学,求所选2名同学中至少有1名女生的概率.【解答】解:(Ⅰ)由于在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为,则喜爱打篮球的学生人数为30,故m=20,又由学生共有50人,则n=50﹣30﹣5=15,故列联表中m,n的值分别为20,15;(Ⅱ)用分层抽样的方法得到喜欢打篮球的同学中抽取6名同学中男生为6×=4人,女生为6﹣4=2人,从这6名同学中任取2名同学,共有=15种情况,其中至少有1名女生有=9种情况,故所选2名同学中至少有1名女生的概率为=.18.(12分)在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,BD⊥DC,侧面P AB⊥底面ABCD,P A=AD=AB,点M是PB的中点.(Ⅰ)求证:AM∥平面PDC(Ⅱ)求证:平面PDC⊥平面PBC.【解答】证明:(Ⅰ)取PC的中点N,连接MN,ND,在Rt△ABD中,∵AB=AD=P A,∴BD=,∠ABD=45°,又∠ABC=90°,∴∠DBC=45°,又∠BDC=90°,∴BC=2…2分∵M,N分别是PB,PC的中点,∴MN,又∵AD=,∴MN∥AD,MN=AD,…4分∴AM∥ND,又∵AM⊄平面PDC,DN⊂平面PDC,∴AM∥平面PDC…5分(Ⅱ)∵侧面P AB⊥底面ABCD,交线为AB,在底面ABCD中,BC⊥AB,∴BC⊥侧面P AB,又AM⊂侧面P AB,∴BC⊥AM…8分在△P AB中,P A=AB,且M是PB的中点,∴AM⊥PB,又PB,BC⊂平面PBC,且PB∩BC=B,∴AM⊥平面PBC…10分由(Ⅰ)知AM∥DN,∴DN⊥平面PBC,又DN⊂平面PDC,∴平面PDC⊥平面PBC…12分19.(12分)已知等差数列{a n}是递增数列,a3=7,且a2,a4,a9成等比数列.(Ⅰ)求数列{a n}的通项公式(Ⅱ)设b n=a n cos nπ(n∈N*),求数列{b n}的前n项和S n.【解答】解:(I)设等差数列{a n}的公差为d>0,由a2,a4,a9成等比数列,可得,∴,化为d=3a1.由a3=7,可得a1+2d=7,联立,解得,∴a n=1+3(n﹣1)=3n﹣2.(II)数列{a n}的前n项和T n==.b n=,∴数列{b n}的前n项和S n=﹣++…+.当n为偶数时,S n=﹣++…+=(a2﹣a1)(a2+a1)+(a4﹣a3)(a4+a3)+…+(a n﹣a n﹣1)(a n+a n﹣1)=3(a1+a2+…+a n)=3S n=.+b n=﹣(3n﹣2)2=.当n为奇数时,S n=S n﹣1综上可得:S n=.20.(13分)已知动圆M经过定点A(2,0),且在y轴上截得的弦长为4(Ⅰ)求动圆圆心M的轨迹C的方程(Ⅱ)设N(x0,0)是x轴上的定点,BD是经过N点的轨迹C的任意一条弦,若∠BAD恒为钝角,求x0的取值范围.【解答】解:(Ⅰ)设动圆圆心M(x,y),则点M到y轴的距离为d=|x|,圆M 的半径r=,∵圆M在y轴上截得的弦长为4,得,即,化简得轨迹C的方程为:y2=4x;(Ⅱ)设经过点N的抛物线y2=4x的任意一条弦为BD的方程为x=my+x0,由消去x得y2﹣4my﹣4x0=0,设B(x1,y1),D(x2,y2),则y1+y2=4m,y1y2=﹣4x0,=(x1﹣2,y1),=(x2﹣2,y2),•=(x1﹣2,y1)•(x2﹣2,y2)=(x1﹣2)(x2﹣2)+y1y2=(my1+x0﹣2)(my2+x0﹣2)+y1y2=(m2+1)y1y2+m(x0﹣2)(y1+y2)+==,因为∠BAD恒为钝角,所以对于任意的m∈R都有,即<0在R上恒成立,所以<0,解得,又因为当x0=2时,∠BAD=180°不合题意,因此x 0的取值范围为:,且x0≠2.21.(14分)已知函数f(x)=(x2﹣2x+k)e x(e=2.71828…是自然对数的底数)(Ⅰ)若曲线y=f(x)在x=0处的切线与直线x+y=0平行,求k的值(Ⅱ)求函数f(x)的单调区间(Ⅲ)求函数f(x)在[0,2]上的最小值.【解答】解:(Ⅰ)∵f(x)=(x2﹣2x+k)e x(e=2.71828…是自然对数的底数),∴f′(x)=(2x﹣2)e x+(x2﹣2x+k)e x=(x2+k﹣2)e x,又∵曲线y=f(x)在x=0处的切线与直线x+y=0平行,∴f′(0)=(02+k﹣2)e0=﹣1;故k=1;(Ⅱ)∵f′(x)=(x2+k﹣2)e x,∴①当k﹣2≥0时,f′(x)≥0,故f(x)在定义域R上是增函数;②当k﹣2<0时,x∈(﹣,)时,f′(x)<0,x∈(﹣∞,﹣)∪(,+∞)时,f′(x)>0;故f(x)在(﹣∞,﹣)上是增函数,在(﹣,)上是减函数,在(,+∞)上是增函数;(Ⅲ)当k≥2时,函数f(x)在[0,2]上单调递增,故f(x)min=f(0)=k;当0<<2,即﹣2<k<2时,函数f(x)在[0,)上是减函数,在(,2]上是增函数;故f(x)min=f()=(2﹣2);当≥2,即k≤﹣2时,函数f(x)在[0,2]上是减函数,故f(x)min=f(2)=k•e2.。
山东省聊城市2015届高考数学二模试卷(文科) 含解析

2015年山东省聊城市高考数学二模试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知复数(i为虚数单位),则z在复平面内对应的点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限2.设集合A={x|x2﹣2x﹣3<0},B={x|y=lnx},则A∩B=()A.(0,3)B.(0,2) C.(0,1) D.(1,2)3.下列函数中,满足f(xy)=f(x)f(y)的单调递增函数是()A.f(x)=x3B.f(x)=﹣x﹣1C.f(x)=log2x D.f(x)=2x4.已知两条不同的直线l,m和两个不同的平面α,β,有如下命题:①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α⊥β,l⊥β,则l∥α,其中正确命题的个数是()A.3 B.2 C.1 D.05.函数的图象的大致形状是()A.B.C.D.6.利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为()A.46 B.48 C.50 D.527.已知函数则=()A.B.1 C.D.﹣18.已知直线ax+y﹣1=0与圆C:(x﹣1)2+(y+a)2=1相交于A,B两点,且△ABC为等腰直角三角形,则实数a的值为()A.B.﹣1 C.1或﹣1 D.19.a1,a2,a3,a4是各项不为零的等差数列,且公差d≠0,若将此数列删去a2,得到的数列a1,a3,a4是等比数列,则的值为()A.1 B.﹣4 C.﹣1 D.410.已知M是△ABC内一点,且,若△MBC,△MCA,△MAB 的面积分别为,则xy的最大值是()A.B.C.D.二、填空题(本大题共5个小题,每小题5分,共25分.)11.△ABC中,已知,则cosC=.12.已知双曲线=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为.13.执行如图所示的程序框图,若输入的T=1,a=2,则输出的T的值为.14.记集合,构成的平面区域分别为M,N,现随机地向M中抛一粒豆子(大小忽略不计),则该豆子落入N中的概率为.15.已知函数f(x)=Msin(ωx+φ),(M>0,ω>0,)的部分图象如图所示,其中A,B两点之间的距离为5,那么f(﹣1)=.三、解答题(本大题共6小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤.) 16.一个小商店从某食品有限公司购进10袋白糖,称池内各袋白糖的重量(单位:g),如茎叶图所示,其中有一个数据被污损.(Ⅰ)若已知这些白糖重量的平均数为497g,求污损处的数据a;(Ⅱ)现从重量不低于498g的所购各袋白糖中随机抽取2袋,求重量是508g的那袋被抽中的概率.17.设△ABC的内角A,B,C的对边分别是a,b,c,已知A=,a=bcosC.(Ⅰ)求角C的大小;(Ⅱ)如图,在△ABC的外角∠ACD内取一点P,使PC=2,过点P作PM⊥CA于M,PN⊥CD 于N,设线段PM,PN的长分别为m,n,∠PCM=x,且,求f(x)=mn的最大值及相应x的值.18.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,,Q是AD的中点.(Ⅰ)求证:平面PQ⊥底面ABCD;(Ⅱ)求三棱锥C﹣PBD的体积.19.在公比为2的等比数列{a n}中,a2+1是a1与a3的等差中项.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)记数列{a n}前n项的和为S n,若数列{b n}满足b n=a n log2(S n+2),试求数列{b n}前n项的和T n.20.已知函数f(x)=alnx+..(Ⅰ)当a=2时,求f(x)的单调区间;(Ⅱ)若f(x)在区间(1,2)上不具有单调性,求a的取值范围.21.已知椭圆E的中心在坐标原点O,它的长轴长,短轴长分别为,右焦点F(c,0),直线l:cx﹣a2=0与x轴相交于点,过点A的直线m与椭圆E交于P,Q两点.(Ⅰ)求椭圆E的方程;(Ⅱ)若,求直线m的方程;(Ⅲ)过点P且平行于直线l的直线与椭圆E相交于另一点M,求证:Q,F,M三点共线.2015年山东省聊城市高考数学二模试卷(文科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知复数(i为虚数单位),则z在复平面内对应的点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】复数代数形式的乘除运算.【专题】数系的扩充和复数.【分析】直接利用复数代数形式的乘除运算化简,求得z的坐标得答案.【解答】解:由=,∴z在复平面内对应的点的坐标为(),在第三象限角.故选:C.【点评】本题考查了复数代数形式的乘除运算,是基础的计算题.2.设集合A={x|x2﹣2x﹣3<0},B={x|y=lnx},则A∩B=()A.(0,3)B.(0,2) C.(0,1) D.(1,2)【考点】交集及其运算.【专题】集合.【分析】求出A中不等式的解集确定出A,求出B中x的范围确定出B,找出A与B的交集即可.【解答】解:由A中不等式变形得:(x﹣3)(x+1)<0,解得:﹣1<x<3,即A=(﹣1,3),由B中y=lnx,得到x>0,即B=(0,+∞),则A∩B=(0,3),故选:A.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.3.下列函数中,满足f(xy)=f(x)f(y)的单调递增函数是()A.f(x)=x3B.f(x)=﹣x﹣1C.f(x)=log2x D.f(x)=2x【考点】抽象函数及其应用.【专题】函数的性质及应用.【分析】根据抽象函数的关系式分别进行判断即可.【解答】解:A.f(x)f(y)=x3y3=(xy)3=f(xy),且函数f(x)为增函数,满足条件.B.f(x)f(y)=﹣x﹣1(﹣y﹣1)=(xy)﹣1,f(xy)=﹣(xy)﹣1,则f(xy)=f(x)f(y)不成立.C.f(xy)=log2xy=log2x+log2y=f(x)+f(y),则f(xy)=f(x)f(y)不成立.D.f(xy)═2xy,f(x)f(y)=2x+2y,f(xy)=f(x)f(y)不成立.故选:A【点评】本题主要考查抽象函数的应用,根据条件进行验证是解决本题的关键.比较基础.4.已知两条不同的直线l,m和两个不同的平面α,β,有如下命题:①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α⊥β,l⊥β,则l∥α,其中正确命题的个数是()A.3 B.2 C.1 D.0【考点】空间中直线与平面之间的位置关系.【专题】空间位置关系与距离.【分析】利用线面平行的性质定理和判定定理对三个命题分别分析解答.【解答】解:对于①,若l⊂α,m⊂α,l∥β,m∥β,则α与β可能相交;故①错误;对于②,若l⊂α,l∥β,α∩β=m,满足线面平行的性质定理,故l∥m;故②正确;对于③,若α⊥β,l⊥β,如果l⊂α,则l⊥α;故③错误;故选C.【点评】本题考查了线面平行的性质定理和判定定理的运用,关键是正确运用定理进行分析解答.5.函数的图象的大致形状是()A.B.C.D.【考点】函数的图象.【专题】数形结合.【分析】先利用绝对值的概念去掉绝对值符号,将原函数化成分段函数的形式,再结合分段函数分析位于y轴左右两侧所表示的图象即可选出正确答案.【解答】解:∵y==当x>0时,其图象是指数函数y=a x在y轴右侧的部分,因为a>1,所以是增函数的形状,当x<0时,其图象是函数y=﹣a x在y轴左侧的部分,因为a>1,所以是减函数的形状,比较各选项中的图象知,C符合题意故选C.【点评】本题考查了绝对值、分段函数、函数的图象与图象的变换,培养学生画图的能力,属于基础题.6.利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为()A.46 B.48 C.50 D.52【考点】频率分布直方图.【专题】计算题;概率与统计.【分析】根据频率分布直方图,利用频率、频数与样本容量的关系进行解答即可.【解答】解:这些用户中,用电量落在区间[150,250]内的频率为1﹣(0.0024+0。
《解析》山东省聊城市2015届高三上学期期末数学试卷(文科)Word版含解析

山东省聊城市2015届高三上学期期末数学试卷(文科)一、选择题(本题共共10小题,每小题5分,共50分.在每小题给出的4个选项中,只有一项符合题目要求)1.已知全集U={0,1,2,3,4,5,6},集合A={1,2},B={0,2,5},则集合(∁U A)∩B=( )A.{3,4,6} B.{3,5} C.{0,5} D.{0,2,4}考点:交、并、补集的混合运算.专题:计算题.分析:直接利用补集和交集的运算进行求解,即可得到答案.解答:解:由∪={0,1,2,3,4,5,6},集合A={1,2},∴∁U A={0,3,4,5,6},又B={0,2,5},∴(∁U A)∩B={0,3,4,5,6}∩{0,2,5}={0,5}.故选C.点评:本题考查了交、并、补集的混合运算,是基础的题.2.复数(1﹣4i)2的虚部为( )A.﹣4i B.﹣4 C.﹣8i D.﹣8考点:复数的代数表示法及其几何意义.专题:数系的扩充和复数.分析:利用复数的运算法则、虚部的定义即可得出.解答:解:复数(1﹣4i)2=1﹣16﹣8i=﹣15﹣8i,其虚部为﹣8.故选:D.点评:本题考查了复数的运算法则、虚部的定义,属于基础题.3.函数y=的定义域为( )A.(﹣1,0)∪(0,1]B.(﹣1,1]C.(﹣4,﹣1]D.(﹣4,0)∪(0,1]考点:函数的定义域及其求法.专题:集合.分析:要使函数表达式有意义只需分母不为零、被开方数为非负数、对数的真数大于零即可,计算即得结论.解答:解:由题意可知,∴,即﹣1<x<0或0<x≤1,故选:A.点评:本题考查求函数的定义域,注意解题方法的积累,属于基础题.4.根据如下样本数据:( )x 3 4 5 6 7 8y ﹣3.0 ﹣2.0 0.5 ﹣0.5 2.5 4.0得到的回归方程为=x+,则.A.a>0,b>0 B.a<0,b<0 C.a>0,b<0 D.a<0,b>0考点:线性回归方程.专题:计算题;概率与统计.分析:利用公式求出b,a,即可得出结论.解答:解:样本平均数=5.5,=0.25,∴=23.75,=17.5,∴b≈1.4>0,∴a=0.25﹣1.4•5.5<0,故选:D.点评:本题考查线性回归方程的求法,考查最小二乘法,属于基础题.5.已知双曲线﹣=1(a>0,b>0)的离心率为,则双曲线的渐近线方程为( )A.y=±2x B.y=±x C.y=±x D.y=±x考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:运用离心率公式,再由双曲线的a,b,c的关系,可得a,b的关系,再由渐近线方程即可得到.解答:解:由双曲线的离心率为,则e==,即c=a,b===a,由双曲线的渐近线方程为y=x,即有y=x.故选D.点评:本题考查双曲线的方程和性质,考查离心率公式和渐近线方程的求法,属于基础题.6.要得到函数y=cos(2x+1)的图象,可以将函数y=cos(2x﹣1)的图象( )A.向左平移1个单位 B.向右平移1个单位C.向左平移2个单位 D.向右平移2个单位考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.解答:解:将函数y=cos(2x﹣1)的图象向左平移1个单位,可得函数y=cos[2(x+1)﹣1]=cos(2x+1)的图象,故选:A.点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.7.已知命题p:∃x0∈(﹣∞,0),2<3,命题q:∀x∈[﹣1,1],cosx>,则下列命题为真命题的是( )A.p∧q B.p∨(¬q)C.(¬p)∧q D.p∧(¬q)考点:复合命题的真假.专题:简易逻辑.分析:由指数函数y=2x与y=3x的图象易知x∈(﹣∞,0)时,2x>3x,则p是假命题;由余弦函数y=cosx的值域易知x∈[﹣1,1]时,cosx>,则q是真命题,然后根据复合命题的真假关系即可作出判断解答:解:命题p:∃x0∈(﹣∞,0),2<3,为假命题,则¬p为真命题,命题q:∀x∈[﹣1,1],cosx>,为真命题,则¬q为假命题,所以p∧q为假命题,p∨(¬q)为假命题,¬p∧q为真命题,p∧(¬q)为假命题.故选:C.点评:本题主要考查复合命题的真假关系,同时考查指数函数的图象与余弦函数的值域.8.设变量x,y满足约束条件,则目标函数z=的最大值为( )A.2 B.C.D.考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.解答:解:作出不等式组对应的平面区域如图:(阴影部分).z=的几何意义为区域内的动点(x,y)到定点D(﹣1,﹣1)的斜率,由图象知,AD的斜率最大,由得,即A(1,2),此时AD的斜率z==,即z的最大值为.故选:B.点评:本题主要考查线性规划以及直线斜率的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法.9.已知数列{a n}满足a n+12﹣2a n+1a n﹣3a n2=0,a2=1,且a n+1>a n,n∈N*,则{a n}的前10项和等于( )A.6(310﹣1)B.(310﹣1)C.6(1﹣310)D.(1﹣310)考点:数列递推式.专题:等差数列与等比数列.分析:数列{a n}满足a n+12﹣2a n+1a n﹣3a n2=0,因式分解为:(a n+1﹣3a n)(a n+1+a n)=0,且a n+1>a n,n∈N*,可得a n+1=3a n,利用等比数列的通项公式及其前n项和公式即可得出.解答:解:∵数列{a n}满足a n+12﹣2a n+1a n﹣3a n2=0,∴(a n+1﹣3a n)(a n+1+a n)=0,且a n+1>a n,n∈N*,∴a n+1=3a n,又a2=1,∴a1=.∴数列{a n}是等比数列,首项为,公比为3.∴{a n}的前10项和==.故选:B.点评:本题考查了等比数列的通项公式及其前n项和公式、因式分解方法,考查了推理能力与计算能力,属于中档题.10.设二次函数f(x)=x2+bx+c(b,c∈R)的导函数为f′(x),关于x的方程f(x)=f′(x)有两个相等实根,则的最大值为( )A.2﹣2 B.2+2 C.D.1考点:导数的运算.专题:导数的综合应用.分析:由f(x)=f′(x)化为:x2+(b﹣2)x+c﹣b=0,由于关于x的方程f(x)=f′(x)有两个相等实数根,可得△=0,可得,代入,再利用基本不等式的性质即可得出.解答:解:f′(x)=2x+b,f(x)=f′(x)化为:x2+(b﹣2)x+c﹣b=0,∵关于x的方程f(x)=f′(x)有两个相等实数根,∴△=(b﹣2)2﹣4(c﹣b)=0,化为,∴==≤=2﹣2,当且仅当b2=4,c=+1时取等号.∴的最大值为﹣2.故选:A.点评:本题考查了导数的运算法则、一元二次方程有实数根与判别式的关系、基本不等式的性质,考查了推理能力与计算能力,属于中档题.二、填空题(本题共5小题,每小题5分,共25分)11.如图给出的是计算1++++的值的一个程序框图,其中判断框内正整数α的值为5.考点:程序框图.专题:图表型;算法和程序框图.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值.解答:解:程序运行过程中,各变量值如下表所示:第一圈:S=1,n=3,i=2,第二圈:S=1+,n=5,i=3,第三圈:S=1++,n=7,i=4,…依此类推,第5圈:S=1++++,n=9,i=5退出循环其中判断框内应填入的条件是:i>5,故答案为:5.点评:算法是新课程中的新增加的内容,也必然是新2015届高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.12.已知点M,N分别是直线x+y+1=0与圆(x﹣1)2+(y﹣1)2=2上的动点,则|MN|的最小值为.考点:两点间的距离公式;直线与圆的位置关系.专题:直线与圆.分析:|MN|的最小值为圆心到直线的距离减去圆的半径,由距离公式可得.解答:解:由题意可得|MN|的最小值为圆心(1,1)到直线的距离d减去圆的半径,由点到直线的距离公式可得d==,∴所求最小值为﹣=点评:本题考查直线和圆的位置关系,涉及点到直线的距离公式,属基础题.13.在边长为2的正方形ABCD中,E为CD的中点,F在边BC上,若•=2,则•=0.考点:平面向量数量积的运算.专题:平面向量及应用.分析:以AB 所在的直线为x轴,以AD所在的直线为y轴,建立直角坐标系,可得A、B、C、D、E点的坐标,设F (2,b),由•=2,故b的值,可得F的坐标,从而求得•的值.解答:解:如图所示:以AB 所在的直线为x轴,以AD所在的直线为y轴,建立直角坐标系,则由题意可得A (0,0)、B(2,0)、C(2,2)、D(0,2)、E(1,2),设F (2,b).由于•=(0,2)•(2,b)=2b=2,故b=1,故F(2,1),=(﹣1,2),则•=(2,1)•(﹣1,2)=﹣2+2=0,故答案为:0.点评:本题主要考查两个向量坐标形式的运算,两个向量的数量积公式的应用,属于基础题.14.一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为.考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:根据几何体的三视图,得出该几何体是棱长为1的正方体,去掉两个相同的小三棱锥;再根据图中数据球场它的体积.解答:解:根据几何体的三视图,得,该几何体是棱长为1的正方体,在两个顶点处各去掉一个相同的小三棱锥;∴该几何体的体积为V正方体﹣2V小三棱锥=13﹣2××××=.故答案为:.点评:本题考查了利用空间几何体的三视图求几何体的体积的应用问题,解题时应根据三视图得出几何体的结构特征是什么.15.已知符号函数sgn(x)=,则函数f(x)=sgn(lnx)﹣|lnx|的零点个数为2.考点:根的存在性及根的个数判断.专题:计算题;函数的性质及应用.分析:化简f(x)=sgn(lnx)﹣|lnx|=,从而求出函数的零点即可.解答:解:由题意,f(x)=sgn(lnx)﹣|lnx|=,显然x=1是函数f(x)的零点,当x>1时,令1﹣lnx=0得,x=e;则x=e是函数f(x)的零点;当0<x<1时,﹣1+lnx<0,故没有零点;故函数f(x)=sgn(lnx)﹣|lnx|的零点个数为2;故答案为:2.点评:本题考查了分段函数的应用及函数的零点与方程的根的关系应用,属于基础题.三、解答题(本题共6个小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤))16.某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.(1)求应从小学、中学、大学中分别抽取的学校数目.(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率.考点:古典概型及其概率计算公式;分层抽样方法.专题:概率与统计.分析:(1)先求出每个个体被抽到的概率,再用各个层的个体数乘以此概率,即得应从小学、中学、大学中分别抽取的学校数目.(2)根据所有的抽法共有=15种,其中抽取的2所学校均为小学的方法有=3种,由此求得抽取的2所学校均为小学的概率.解答:解:(1)每个个体被抽到的概率等于=,故从小学、中学、大学中分别抽取的学校数目为21×=3,14×=2,7×=1.…(2)所有的抽法共有=15种,其中抽取的2所学校均为小学的方法有=3种,故抽取的2所学校均为小学的概率等于=.点评:本题主要考查分层抽样的定义和方法,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数,属于基础题.17.设函数f(x)=sin(ωx﹣)﹣2cos2+1(ω>0),直线y=与函数f(x)图象相邻两公共点的距离为π(Ⅰ)求ω的值;(Ⅱ)在△ABC中,角A,B,C所对的边分别是a,b,c,若点(,0)是函数y=f(x)图象的一个对称中心,且b=3,sinA=3sinC,求a,c的值.考点:三角函数中的恒等变换应用;正弦函数的图象.专题:三角函数的图像与性质.分析:(Ⅰ)利用两角和差的正弦公式以及三角函数的倍角公式将函数进行化简,结合函数的周期公式即可求ω的值;(Ⅱ)根据条件求出B,利用正弦定理和余弦定理进行求解即可.解答:解:(Ⅰ)f(x)=sin(ωx﹣)﹣2cos2+1=sinωxcos﹣cosωxsin﹣cosωx=sinωx﹣cosωx=(sinωx﹣cosωx)=sin(ωx﹣).∵直线y=与函数f(x)图象相邻两公共点的距离为π∴函数f(x)的周期T=2π=,解得ω=1;(Ⅱ)∵ω=1,∴f(x)=sin(x﹣).∵点(,0)是函数y=f(x)图象的一个对称中心,∴﹣=kπ,即B=2kπ+,则当k=0时,B=,∵sinA=3sinC,∴由正弦定理得a=3c,∵b=3,∴b2=a2+c2﹣2accos,即9=9c2+c2+2×3c×=13c2,即c2=,解得c=,a=.点评:本题主要考查三角函数的图象和性质以及正弦定理和余弦函数的应用,考查学生的运算能力.18.已知等差数列{a n}的前n项和为S n,且a2=,S10=40.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=(﹣1)n+1a n a n+1(n∈N*),求数列{b n}的前2n项的和T2n.考点:数列的求和.专题:等差数列与等比数列.分析:(Ⅰ)通过a2=,S10=40计算即得结论;(Ⅱ)通过b n=(﹣1)n+1a n a n+1(n∈N*)写出T2n的表达式,利用相邻两项的差为定值提取公因式计算即得结论.解答:解:(Ⅰ)设等差数列{a n}的公差为d,则,解得,故a n=1+(n﹣1)=n+;(Ⅱ)T2n=a1a2﹣a2a3+a3a4﹣a4a5+…+a2n a2n+1=a2(a1﹣a3)+a4(a3﹣a5)+…+a2n(a2n﹣1a2n+1)=﹣(a2+a4+a6+…+a2n)=﹣(2n2+3n).点评:本题考查求数列的通项、前n项和,注意解题方法的积累,属于中档题.19.如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE 的中点.(1)求证:DF∥平面ABC;(2)求证:平面ADF⊥平面ABE.考点:平面与平面垂直的判定;直线与平面平行的判定.专题:空间位置关系与距离.分析:(1)根据线面平行的判定定理证明FD∥CG即可证明DF∥平面ABC;(2)根据面面垂直的判定定理即即可证明平面ADF⊥平面ABE解答:(1)证明:如图所示,取AB中点G,连CG、FG.∵F为BE的中点.∴EF=FB,AG=GB,∴FG∥EA且FG=EA.又DC∥EA,CD=EA,∴GF∥DC且GF=DC.∴四边形CDFG为平行四边形,∴FD∥CG.∵DF⊄平面ABC,CG⊂平面ABC,∴DF∥平面ABC.(2)证明:△ABC中,CA=CB.G是AB的中点,∴CG⊥AB∵EA⊥平面ABC,CG⊂平面ABC,∴AE⊥CG.∵AB∩EA=A,AB⊂平面AEB,EA⊂平面AEB∴CG⊥平面AEB.又∵DF∥CG,∴DF⊥平面AEB.DF⊂平面BDE∴平面ADF⊥平面ABE.点评:本题主要考查空间面面垂直以及线面平行的判定,根据相应的判定定理是解决本题的关键.20.已知椭圆C:+=1(a>b>1)过点P(﹣1,﹣1),c为椭圆的半焦距,且c=b.(Ⅰ)求椭圆C的标准方程;(Ⅱ)过点P作两条相互垂直的直线l1,l2与椭圆C分别交于另两点M,N,若线段MN的中点在x轴上,求此时直线MN的方程.考点:直线与圆锥曲线的综合问题;椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)由已知条件推导出,且c=b,由此能求出a,b,然后求解椭圆方程.(Ⅱ)设M(x1,y1),N(x2,y2),利用点差法,求出直线MN的方程.解答:解:(Ⅰ)由c=b,可得a2=3b2,椭圆C:+=1(a>b>1)过点P(﹣1,﹣1),可得,解得a2=4,b2=,所以椭圆的方程为:..…(Ⅱ)设M(x1,y1),N(x2,y2),则,两式相减得(x1+x2)(x1﹣x2)+3(y1+y2)(y1﹣y2)=0,因为线段MN的中点在x轴上,所以y1+y2=0,从而可得(x1+x2)(x1﹣x2)=0.…若x1+x2=0,则N(﹣x1,﹣y1).因为过点P作两条相互垂直的直线l1,l2,所以PM⊥PN,所以,得x12+y12=2.又因为x12+3y12=4,所以解得x1=±1,所以M(﹣1,1),N(1,﹣1)或M(1,﹣1),N(﹣1,1).所以直线MN的方程为y=﹣x.…若x1﹣x2=0,则N(x1,﹣y1),因为PM⊥PN,所以,得y12=(x1+1)2+1.又因为x12+3y12=4,所以解得x1=﹣或﹣1,经检验:x=﹣满足条件,x=﹣1不满足条件.综上,直线MN的方程为x+y=0或x=﹣.….点评:本题考查椭圆方程的求法,直线与椭圆方程的综合应用,考查分析问题解决问题的能力,解题时要认真审题,注意点差法的合理运用.21.已知函数f(x)=x3+bx2+cx(b,c∈R)的图象在点x=1处的切线方程为6x﹣2y﹣1=0,f′(x)为f(x)的导函数.(Ⅰ)求b,c的值;(Ⅱ)设g(x)=ae x(a∈R)(e=2.71828…是自然对数的底数),若存在x0∈[0,2],使g(x0)=f′(x0)成立,求a的取值范围.考点:利用导数研究曲线上某点切线方程.专题:综合题;导数的综合应用.分析:(Ⅰ)由f′(x)=3x2+2bx+c,知f(x)在x=1处的切线方程为y=(3+2b+c)x﹣2﹣b,故,由此能求出f(x).(Ⅱ)若存在x0∈(0,2]使g(x0)=f′(x0)成立,即方程g(x)=f′(x)在(0,2]上有解,故a=,令h(x)=,则h′(x)=,由此能求出a的取值范围.解答:解:(Ⅰ)∵f′(x)=3x2+2bx+c,∴f(x)在x=1处的切线方程为y﹣(1+b+c)=(3+2b+c)(x﹣1),即y=(3+2b+c)x﹣2﹣b,∴,即b=﹣,c=3.(Ⅱ)若存在x0∈(0,2]使g(x0)=f′(x0)成立,即方程g(x)=f′(x)在(0,2]上有解,∴a•e x=3x2﹣3x+3,∴a=,令h(x)=,∴h′(x)=,令h′(x)=0,得x1=1,x2=2,列表讨论:x (0,1) 1 (1,2) 2h′(x)﹣0 + 0h(x)↓极小值↑极大值∴h(x)有极小值h(1)=,h(x)有极大值h(2)=,且当x→0时,h(x)→3>,∴a的取值范围是[,3).点评:本题考查实数值和实数取值范围的求法,具体涉及到导数的应用、函数极值的求法和应用、切线方程的求法和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.。
山东省聊城市第一中学2015届高三10月阶段性检测语文试卷.pdf

高三上学期第一次阶段性测试 语文试题 第Ⅰ卷(共36分) 一、(15分,每小题3分) 1.下列加点字的读音完全正确的一组是 A.笞刑(chī) 粗糙(cāo) 虫豸(zhì) 铁镐(hāo)下列各句中,加点的词语使用恰当的一句是A.逐步推广使用清洁的可再生能源,减少使用污染环境的能源,是遏止环境恶化的正确选择。
B.4月以来的多轮强降水使鄱阳湖水体面积由668平方公里扩至2370平方公里,以致极大地改善了江豚等珍稀水生动物的生存环境。
C.国际田联专家诊断,男子110米栏项目仍是和罗伯斯的天下,的竞技状态与日俱增,而罗伯斯则稍欠稳定且实力有所下滑。
D.电视评论的犀利和深刻是主持人思想创造性的外化,主持人只有具备思想的创造性,才能将观点转化为鞭辟入里、发人深省的评说。
阅读下面的文字,完成6~8题。
孔子对民生问题是重视的,但语焉不详。
孟子则把孔子的仁学落实到政治的措施上,要求社会统治者和管理者在解决民生基本问题上体现仁民爱物的思想感情,中国近代的民生主义即发源于此。
首先,要“制民之产”,使百姓丰衣足食。
仁政最核心的内容便是解决好民众的吃穿问题,使他们的物质生活有起码的保障。
其次,“省刑罚薄税收”,人民的负担要有一个限度,过此即有灾难,所以要省刑罚,必须薄税敛。
第三,救济社会上孤苦无援者。
第四,加强教育,德化民俗。
孟子认为要在富民的同时,“谨庠序之教,申之以孝悌之义”,使民去恶从善,形成礼义之风。
这样,社会才有秩序,人民才会有真正的安宁寿福。
在早期儒家代表人物中,没有哪一位比孟子更重视民众的社会作用和历史地位。
孔子讲过“民无信不立”的话。
孟子则大大前进了一步,他提出“得天下有道,得斯民斯得天下矣;得其民有道,得其心斯得民矣;得其心有道,所欲与之聚之,所恶勿施,尔也”,这就是民为邦本的思想。
孟子相信天命,但他把天命化为民意,认为这两者是一致的,这实际上是用民本思想重新解释了传统的天命论,大大提高了民众的地位。
2015年高考文科数学山东卷(含详细答案)

数学试卷 第1页(共33页)数学试卷 第2页(共33页)数学试卷 第3页(共33页)绝密★启用前2015年普通高等学校招生全国统一考试(山东卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|24}A x x =<<,{|(1)(3)0}B x x x =--<,则AB = ( )A .1,3()B .1,4()C .2,3()D .2,4()2.若复数z 满足z1i-=i ,其中i 为虚数单位,则z=( )A .1i -B .1i +C .1i --D .1i -+ 3.设0.60.6a =, 1.50.6b =,0.61.5c =,则a ,b ,c 的大小关系是( )A .a <b <cB .a <c <bC .b <a <cD .b <c <a4.要得到函数πsin(4)3y x =-的图象,只需要将函数sin 4y x =的图象( )A .向左平移π12个单位 B .向右平移π12个单位 C .向左平移π3个单位D .向右平移π3个单位5.若m ∈R ,命题“若0m >,则方程20x x m +-=有实根”的逆否命题是 ( )A .若方程20x x m +-=有实根,则0m >B .若方程20x x m +-=有实根,则0m ≤C .若方程20x x m +-=没有实根,则0m > D .若方程20x x m +-=没有实根,则0m ≤6.为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的.考虑以下结论:①甲地该月14时的平均气温低于乙地该月14时的平均气温; ②甲地该月14时的平均气温高于乙地该月14时的平均气温; ③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差. 其中根据茎叶图能得到的统计结论的编号为( )A .①③B .①④C .②③D .②④7.在区间[0,2]上随机地取一个数x ,则事件“1211log ()12x -+≤≤”发生的概率为( )A .34 B .23 C .13D .148.若函数21()2x x f x a+=-是奇函数,则使()3f x >成立的x 的取值范围为( )A .(,1)-∞-B .0,1-()C .01,()D .(1,)+∞9.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为()AB C .D .10.设函数3, 1,()2, 1.x x b x f x x -⎧=⎨⎩<≥若5(())46f f =,则b =( )A .1B .78C .34D .12第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上. 11.执行如图所示的程序框图,若输入的x 的值为1,则输出的y 的值是_________.12.若x ,y满足约束条件131y x x y y -⎧⎪+⎨⎪⎩≤,≤,≥,则z =x +3y 的最大值为_______.13.过点(1P 作圆221x y +=的两条切线,切点分别为A ,B ,则PA PB =________.14.定义运算“⊗”:22(,,0)x y x y x y xy xy-⊗=∈≠R .当0x >,0y >时,(2)x y y x ⊗+⊗的最小值为__________.15.过双曲线2222:1(0,0)x y C a b a b-=>>的右焦点作一条与其渐近线平行的直线,交C 于点P .若点P 的横坐标为2a ,则C 的离心率为___________.---------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共33页)数学试卷 第5页(共33页)数学试卷 第6页(共33页)三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤. 16.(本小题满分12分)某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单(Ⅰ)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;(Ⅱ)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学1A ,2A ,3A ,4A ,5A ,3名女同学1B ,2B ,3B .现从这5名男同学和3名女同学中各随机选1人,求1A 被选中且1B 未被选中的概率.17.(本小题满分12分)ABC △中,角A ,B ,C 所对的边分别为a ,b ,c .已知cos B =,sin()A B +=,ac =sin A 和c 的值.18.(本小题满分12分)如图,三棱台DEF —ABC 中,AB =2DE ,G ,H 分别为AC ,BC 的中点. (Ⅰ)求证:BD ∥平面FGH ;(Ⅱ)若CF ⊥BC ,AB ⊥BC ,求证:平面BCD ⊥平面EGH .19.(本小题满分12分)已知数列{}n a 是首项为正数的等差数列,数列11{} n n a a +的前n 项和为21nn +.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设()1 2n a n n b a =+,求数列{}n b 的前n 项和n T .20.(本小题满分13分)设函数()()ln f x x a x =+,2()x x g x e=,已知曲线()y f x =在点(1,(1))f 处的切线与直线20x y -=平行. (Ⅰ)求a 的值;(Ⅱ)是否存在自然数k ,使得方程()()f x g x =在(k ,k +1)内存在唯一的根?如果存在,求出k ;如果不存在,请说明理由;(Ⅲ)设函数()min{()()}(min{},m x f x g x p q p q =,,表示中的较小值),求m (x )的最大值.21.(本小题满分14分)平面直角坐标系xOy 中,已知椭圆22221(0)x y a b a b C +=>>:的离心率为,且点1)2在椭圆C 上.(Ⅰ)求椭圆C 的方程;(Ⅱ)设椭圆2222144E x y a b+=:,P 为椭圆C 上任意一点,过点P 的直线y kx m =+交椭圆E 于A ,B 两点,射线PO 交椭圆E 于点Q .(i )求||||OQ OP 的值;(ii )求ABQ △面积的最大值.2015年普通高等学校招生全国统一考试(山东卷)数学(文科)答案解析第Ⅰ卷{2|A B x=3 / 11数学试卷 第10页(共33页) 数学试卷 第11页(共33页)数学试卷 第12页(共33页)1log -≤.02x ≤≤∴所求的概率为:【解析】2()2f x =22x a a =-22xxa a =-,21()21x x f x +=>-【提示】由5 / 11【解析】如图为等腰直角三角形旋转而成的旋转体.242π3h=数学试卷 第16页(共33页) 数学试卷 第17页(共33页)数学试卷 第18页(共33页)7.30OPA ∴∠=,260BPA ∠=,1||||cos60322PA PB PA PB ∴==+=2,然后代入向量数量积的定义可求PA PB .】xx y⊗=由0x>,222x≥⨯2,故答案为7 / 11数学试卷 第22页(共33页) 数学试卷 第23页(共33页)数学试卷 第24页(共33页)G F M =四边形CFDG FGH ,BD ∴∥,G ,H 分别为,AB BC ⊥HC ,EF HE ∥,CF BC ⊥平面EGH ,HE GH H =,又BC ⊂平面BCD EGH .H F H =,BD ⊂平面(Ⅰ)证法一:如图所示,连接CDGF M =由已知可得四边形CFDG利用三角形的中位线定理可得:MH ∥BD ,可得的中点,可得四边形1n n a +,则c9 / 11又数列1n n a +⎬⎭的前(Ⅰ)知21(1)2(2n 11)24n n n n b a n -==-+=,12114244n n T b n ∴=++++…,2311424(1)44n n n n ++++-+…,两式相减,得1143443n n n T +-=+-,1(31)449n n +-+. (Ⅰ)通过对1n n c a +分离分母,并项相加并利用数列1n n a +⎬⎭的前4nn ,写出T 【考点】数列的求和数学试卷 第28页(共33页) 数学试卷 第29页(共33页)数学试卷 第30页(共33页)22004x y +②设1(,A x 212414m x -=+122222222|4164|14(16414||14x x k m k k m k m k -+-++-+⎫⎪+⎭,,将y kx m =+,又24m <+时取得最大值2理、三角形面积公式及换元法,计算即可.【考点】直线与圆锥曲线的综合问题,椭圆的标准方程11 / 11。
山东省聊城市第一中学2015届高三10月阶段性检测历史试题(附答案)

高三上学期第一次阶段性测试历史试题本试题卷分选择题和非选择题两部分,共12页。
考试时间90分钟,满分100分。
第Ⅰ卷选择题(共60分)注:本大题共50小题,1-40小题每题1分,41-50小题每题2分,共60分。
在每小题列出的四个选项中,只有一项是符合题目要求的。
1.“宗”是一个会意字。
在甲骨文中,宗字作“”,“”像宫室屋宇之形,“”可能表示A.祖先牌位B.皇帝宝座C.青铜兵器D.铁制农具2.从秦至清的两千多年中,许多皇帝或由于年幼庸弱,或由于当时形势和力量对比的变化,因而受制于母后、外戚、宦官、权臣、地方割据势力等,导致权力的萎缩或丧失。
这种现象实质上是A.君主专制被颠覆B.中央集权体制遭到破坏C.君权至上的后果D.君主权力受到制约3.中国古代有这样一类官员,他们充当皇帝私人顾问,其权力来自与皇帝的私人关系。
属于这类官员的有A.秦朝御史大夫B.汉朝丞相C.唐朝六部尚书D.明朝内阁大学士4.古希腊城邦雅典的公共墓地主要用于埋葬牺牲的战士,城邦为他们树立墓碑,刻上所有牺牲者的名字,但并不写明他们的家世。
这旨在强调A.城邦公民的平等B.军事对城邦的重要性C.共同的宗教信仰D.血缘对城邦维系的作用5.第一次世界大战结束之际,意大利企业家阿格涅利提出,欧洲要想和平、强大,就必须借鉴美国的成功经验和失败教训,超越邦联阶段,建立联邦制的“欧洲合众国”。
能够佐证上述观点的美国历史事实是①邦联政治结构松散,无力平息社会动荡②联邦剥夺了各州的自主权,稳定了统治秩序③邦联没有统一的关税,严重阻碍了经济发展④联邦统一发行货币,促进了经济的有序发展A.①②③B.①②④C.②③④D.①③④6.法国政治思想家托克维尔在《论美国的民主》中说:“美国的联邦宪法,好像能工巧匠创造的一件只能使发明人成名发财,而落到他人之手就变成一无用处的美丽艺术品。
”这句话着重强调美国联邦宪法A.创造了新的宪法体制B.不具有普适性C.促进了资本主义发展D.具有借鉴意义7.1895年,一位中国外交官对当时四个欧美国家的政体分别作了如下评述,其中对德国的评述是A.“举国听于议院,势太偏重”B.“君主能以事下会议而不能独断”C.“议院主议法,政府主行法,察院主断法”D.“上议院主用世爵,参以选举,君权仍重”8.下面是清道光帝给参与谈判大臣所下达谕旨的部分内容,该谕旨A.颁发于第二次鸦片战争期间B.隐含着天朝上国的外交观念C.导致了社会性质的根本改变D.坚决捍卫国家领土主权完整9.下图所示为1917年山西某县教育会副会长的一则日记。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三上学期第一次阶段性测试数学(文科)试题一、选择题(本题共有10个小题,每小题5分,共50分) 1.若集合{}}{2,0A x x x B x x x ===->,则AB =A .[0,1]B .(,0)-∞C .(1,)+∞D .(,1)-∞- 2.等比数列{}n a 中 13a =,424a =,则345a a a ++=( ) A . 33 B . 72 C . 84 D . 189 3. 122a e e =+, 1234b e e =-,且12,e e 共线,则a 与b A.共线 B.不共线 C.可能共线也可能不共线 D.不能确定 4.设()4x f x e x =+-,则函数()f x 的零点位于区间( ) A .(-1,0)B .(0,1)C .(1,2)D .(2,3)5.设12log 3a =,0.313b ⎛⎫= ⎪⎝⎭,ln c π=,则 ( )A.a b c <<B.a c b <<C.c a b <<D.b a c << 6.已知等差数列{}n a 的前13项之和为134π,则678tan()a a a ++等于( )A .—1B C .3D .17. 已知向量(1,),(1,)a n b n ==-,若b a +2与b 垂直,则a =( )A .1 BC .3D .48.已知数列}2{nn +,欲使它的前n 项的乘积大于36,则n 的最小值为 A .7 B .8 C .9 D .109. 若平面向量=a )2,1(-与b 的夹角是︒180,且︱b ︱53=,则b 的坐标为( )A .)6,3(-B .)6,3(-C .)3,6(-D .)3,6(-10.设()f x 是定义在R 上的周期为3的周期函数,如图表示该函数在区间(2,1]-上的图像,则(2013)f +(2014)f = ( ) (A )3 (B )2 (C )1 (D) 0二、填空题(本大题共5小题,每小题5分,共25分)11.函数x xxx f ln 21)(+-=的导函数是)(x f ',则=')1(f ; 12. 已知数列{}n a 中,),2()1(,1*111N n n a a a a n n n n ∈≥-+==--,则53a a的值是__ _.13.已知ABC ∆的三个内角,,A B C 成等差数列,且1,4,AB BC == 则边BC 上的中线AD 的长为 ;14.已知函数()()()()12314,0log 0a x a x f x f x x ⎧-+<⎪=⎛⎫⎨≥ ⎪⎪⎝⎭⎩ , 若()41f >,则实数a 的取值范围是__. 15.以下四个命题:①在△ABC 中,内角A,B,C 的对边分别为,,a b c ,且B a A b cos sin =,则4π=B ;②设b a ,是两个非零向量且a b a b ⋅=,则存在实数λ,使得a b λ=; ③方程0sin =-x x 在实数范围内的解有且仅有一个;④,a b R ∈且3333a b b a ->-,则a b >;其中正确的命题序号为 。
三、解答题:本大题共6小题,满分75分,解答应写出文字说明、证明过程或演算步骤 16.(本小题满分12分)已知向量(sin ,1)a x =-,1(3cos ,)2b x =-,函数()()2f x a b a =+⋅-.(1)求函数()f x 的最小正周期T 与值域;(2)已知a ,b ,c 分别为ABC ∆内角A , B ,C 的对边,其中A 为锐角,a =4c =,且()1f A =,求A ,b 和ABC ∆的面积S .17.(本小题满分12分)在等差数列{a n }中,n S 为其前n 项和)(*∈N n ,且.9,533==S a (1)求数列{a n }的通项公式; (2)设11+=n n n a a b ,求数列{}n b 的前n 项和n T .18.(本小题满分12分)设两个向量12,e e ,满足12121,1,,e e e e ==满足向量1212,a ke e b e ke =+=-,若1e 与2e 的数量积用含有k 的代数式()f k 表示. 若3a b =. (1)求()f k ;(2)若1e 与2e 的夹角为600,求k 值; (3)若a 与b 的垂直,求实数k 的值.19.(本小题满分12分)在等比数列{}n a 中, 53512),1,0(),(,0a a a a q N n a n +∈∈>*且公比+,2582=a a又3a 和5a .2的等比中项为(1)求数列{}n a 的通项公式(2)设{}n n n b a b 数列,log 2=的前n 项和为n S ,求数列{}n S 的通项公式. (3)当ns s s s n +⋅⋅⋅+++321321最大时,求n 的值.20.(本小题满分13分)已知等差数列{n a },3125,4a a a =+=.数列{n b }的前n 项和为n S ,且112n n S b =-. (1)求数列{n a }、{n b }的通项公式; (2)记12n n n c a b =,求数列{}n c 的前项和n T .21.(本小题满分14分)已知二次函数()f x 的最小值为4,-且关于x 的不等式()0f x ≤的解集为{}13,R x x x -≤≤∈, (1)求函数()f x 的解析式;(2)求函数()()4ln f x g x x x=-的零点个数.参考答案一.选择题(每题5分,共50分) 1-5: CCACA, 6-10: ACBBC 二.填空题(每题5分,共25分) 11.21, 12. 43, 13. 3, 14. 21<a , 15. ①②③④ 三.解答题(共75分) 16. (满分12分)解:(Ⅰ) 2()()22f x a b a a a b =+⋅-=+⋅- 21sin 1cos 22x x x =+++- ……2分1cos 212222x x -=+-12cos 222x x =- sin(2)6x π=-………………4分因为2ω=,所以22T ππ==值域为 ]1,1[-………………6分 (Ⅱ) ()sin(2)16f A A π=-=.因为5(0,),2(,)2666A A ππππ∈-∈-,所以262A ππ-=,3A π=. ……8分由2222cos a b c bc A =+-,得211216242b b =+-⨯⨯,即2440b b -+=.解得2b = ………………10分故11sin 24sin 602322S bc A ==⨯⨯⨯=………………12分 17. 解: (1)由已知条件得⎩⎨⎧=+=+,963,5211d a d a …………………2分解得,2,11==d a …………………………………………4分 ∴12-=n a n .…………………………………6分(2)由(Ⅰ)知,12-=n a n , ∴)121121(21)12)(12(111+--=+-==+n n n n a a b n n n ……………9分∴⎥⎦⎤⎢⎣⎡+--++-+-=+++=)121121()5131()311(2121n n b b b S n n 12)1211(21+=+-=n nn . …………………………12分18.解:222222212*********221212(1)()3(),2363182,()(0).4ke e e ke k e ke e e ke e k e k ke e k e e f k k k+=-++=-++=+∴==≠…4分(2)20121211160()242k e e e e f k k +===与的夹角为,则,,k=1;…………8分21212122212,()()0,0;1()0,0, 1.4a b ke e e ke k e e k e e f k k k k⊥+-==+==≠∴==±(3)若则(1-)1-…………12分19. 解:(1)∵a 1a 5+2a 3a 5+a 2a 8 =25,∴a 32 +2a 3a 5 +a 52 =25又a n >0, ∴a 3+a 5=5 …………1分又a 3与a 5的等比中项为2, ∴a 3a 5=4 …………2分 而1,4,),1,0(5353==∴>∴∈a a a a q ………………3分.16,211==∴a q …………4分n n n a --=⎪⎭⎫⎝⎛⨯=∴5122116 …………5分(2)1,5log 12-=-∴-==+n n n n b b n a b …………7分{}2)9(,1,41n n S b b n n -=∴-=∴为公差的等差数列为首项是以 ……9分 (3)312928,0;9,0;9,089,.123n n n n n S n n S S Sn n n n n nSS S S n n -=∴≤>==><∴=+++⋅⋅⋅+当时当时当时当或时最大…………12分20. 解:(1) 设等差数列{n a }公差为d 由a 3=5,a 1+a 2=4,从而a 1=1、d =2 ……(4分)∴a n =a 1+(n -1)d =2n -1 ……(5分)又当n =1时,有b 1=S 1=1-12 b 1,∴b 1=23……(6分)当n≥2时,有b n =S n -S n-1=12(b n -1-b n )∴b n b n -1=13(n≥2) ……(8分)∴数列{b n }是等比数列,且b 1=23,q =13 ∴b n =b 1q n -1=23n ;……(10分)(2)由(1)知:12123n n n n n c a b -==,……(11分) ∴1223135213333n n nn T c c c -=+++=++++∴231113213333n n n T +-=+++……(12分) ∴23121222321333333n n n n n T +--=++++- 12121333n n n +-=--……(2分)∴113n n n T +=-……(13分)21. 解:(1)()f x 是二次函数, 且关于x 的不等式()0f x ≤的解集为{}13,R x x x -≤≤∈,()2(1)(3)23f x a x x ax ax a ∴=+-=--, 且0a >. ……4分()20,(1)44a f x a x ⎡⎤>=--≥-⎣⎦,且()14f a =-,min ()44, 1.f x a a ∴=-=-= ················································· 6分 故函数()f x 的解析式为()22 3.f x x x =--(2)2233()4ln 4ln 2(0)x x g x x x x x x x--=-=--->,2234(1)(3)()1x x g x x x x --'∴=+-=. ………………8分 ,(),()x g x g x '的取值变化情况如下:………………11分当03x <≤时, ()()140g x g ≤=-<; ························································ 12分 又()55553ee202212290eg =--->--=>. ·············································· 13分 故函数()g x 只有1个零点,且零点50(3,e ).x ∈ ················································· 14分。
