NUAA材料力学课件_13章
合集下载
材料力学课后习题答案13章

= 7.44 × 10− 2 m = 74.4mm
而
2 × 0.050 Fd = (300 N ) 1 1 + + 2.22 × 10 − 2
= 1.004 × 10 3 N
M max = 1.004 ×10 3 N (1.00m ) = 1.004 ×10 3 N ⋅ m
设压杆微弯平衡时的挠曲轴方程为
πx w = f sin l
式中,f 为压杆中点的挠度即最大挠度。
题 13-8 图 解:由题设可知,
w = f sin
πx , l
6
w′ =
πf πx cos l l
据此可得
λ (x ) =
q cr 所作之功为
1 x 2 * 1 ( w′) dx = 2 0 2
∫
∫
x 0
(也可通过左侧题号书签直接查找题目与解)
13-2
比为 8:3。
图示圆截面简支梁,直径为 d,承受均布载荷 q 作用,弹性模量 E 与切变模量 G 之
(1)若同时考虑弯矩与剪力的作用,试计算梁的最大挠度与最大转角; (2)当 l/d =10 与 l/d =5 时,试计算剪切变形在总变形(最大挠度与最大转角)中所占百分比。
(2)被冲击面(弹簧顶面)的静位移为
∆st =
最大冲击载荷为
Pl P 500 + = 1.516 × 10 − 5 m + m = 2.52 × 10 − 3 m 3 EI k 200 × 10
2h + + Fd = P 1 1 ∆ st
于是,杆内横截面上最大的正应力为
Fl 3 ∆= 48EI
得刚度系数
0.030 4 48 × 200 × 10 × F 48 EI 12 N = 6.48 × 10 5 N k= = 3 = 3 ∆ m m l 1.00
材料力学(12)第十三章-1

t 2
dx
M ( x )d 2 M ( x ) dx 2 EI
Page26
2
dW
dW
BUAA
MECHANICS OF MATERIALS
3、通过计算微体的应变能: 最一般的方法,适用于任意形状、任意受力的情况
dz
三向应力状态下的应变能:
2 1
dV 1 2
dy
1 1 2 2 3 3 dxdydz
线弹性体上作用有多个广义力时:
广义位移可以用叠加法求解
外力功一般不可以用叠加法求解 特殊情况:
T F T F
一种载荷在另一种载荷引起的位移上不做功 一种载荷不在另一种载荷方向上引起相应位移
Page22
BUAA
MECHANICS OF MATERIALS
例题:
悬臂梁承受集中力与集中力偶作用,计算外力所做之总 功。弯曲刚度为EI。
夹层刚度远高于芯材 2、面板厚度远小于芯材厚度
工程简化计算:
1、弯曲正应力由面板承受,芯材不承受弯矩,没有弯曲正 应力 2、弯曲切应力由芯材承受,面板不承受剪力 3、弯曲切应力沿芯材均匀分布
Page3
BUAA
MECHANICS OF MATERIALS
§12-5
R / c 10
R——曲梁轴线的曲率半径
c ——截面形心至截面内侧边缘的距离
Page10
BUAA
MECHANICS OF MATERIALS
第十三章
能量法
§13-1 外力功与应变能与克拉比隆定理
Page11
BUAA
MECHANICS OF MATERIALS
引 言
解析法与能量法的比较
dx
M ( x )d 2 M ( x ) dx 2 EI
Page26
2
dW
dW
BUAA
MECHANICS OF MATERIALS
3、通过计算微体的应变能: 最一般的方法,适用于任意形状、任意受力的情况
dz
三向应力状态下的应变能:
2 1
dV 1 2
dy
1 1 2 2 3 3 dxdydz
线弹性体上作用有多个广义力时:
广义位移可以用叠加法求解
外力功一般不可以用叠加法求解 特殊情况:
T F T F
一种载荷在另一种载荷引起的位移上不做功 一种载荷不在另一种载荷方向上引起相应位移
Page22
BUAA
MECHANICS OF MATERIALS
例题:
悬臂梁承受集中力与集中力偶作用,计算外力所做之总 功。弯曲刚度为EI。
夹层刚度远高于芯材 2、面板厚度远小于芯材厚度
工程简化计算:
1、弯曲正应力由面板承受,芯材不承受弯矩,没有弯曲正 应力 2、弯曲切应力由芯材承受,面板不承受剪力 3、弯曲切应力沿芯材均匀分布
Page3
BUAA
MECHANICS OF MATERIALS
§12-5
R / c 10
R——曲梁轴线的曲率半径
c ——截面形心至截面内侧边缘的距离
Page10
BUAA
MECHANICS OF MATERIALS
第十三章
能量法
§13-1 外力功与应变能与克拉比隆定理
Page11
BUAA
MECHANICS OF MATERIALS
引 言
解析法与能量法的比较
材料力学课件PPT

梁的剪力与弯矩
1
梁的剪力
解析剪力对梁的影响和剪切应力。
2
梁的弯曲
讨论梁的弯曲行为和弯曲应力。
3
横截面性能
探索截面形状对梁的强度和刚度的影响。
梁的挠度
1 挠度与刚度
2 梁的支撑条件
3 挠度计算
研究梁的弯曲变形和挠度。
解释梁的不同支撑条件对 挠度的影响。
介绍计算梁挠度的工程方 法。
杆件的稳定性
1
稳定性概念
材料力学课件PPT
材料力学课件PPT是一个全面的教学工具,涵盖了力学基础、应力与变形、杆 件的轴向受力、梁的剪力与弯矩、梁的挠度、杆件的稳定性以及结构稳定裂 解和破坏形态。
力学基础
1
牛顿力学原理
解释物体运动和力的相互作用。
2
力的向量和标量
了解力量的方向和大小。
3
运动和加速度
讨论物体的运动和加速度。
应力与变形
应力
探讨物体所受力的影响。
塑性变形
讲解材料在超出弹性范围时的塑性行为。
弹性变形
解析材料的弹性性质和应变量。
断裂
探索材料的破裂过程和强度。
杆件的轴向受力
拉力
描述由拉力引起的变形和破坏。
压力
研究由压力引起的压缩变形和破坏。
剪力
解释由剪切力引起的变形和破坏。
扭矩
探讨由扭转力引起的变形和破坏。
介绍杆件的稳定性和失稳行为。
2
纯压杆件
研究纯压杆件的稳定性和临界长度。
பைடு நூலகம்
3
压弯杆件
探讨压弯杆件的稳定性和稳定方程。
结构稳定裂解和破坏形态
稳定性裂解
解释结构在突然失去稳定性时的裂解过程。
材料力学课件大学本科专用

详细描述
建筑结构材料如混凝土、钢材等,在设计和施工过程中,必须考虑材料的应力、 应变、强度、刚度等力学性能。材料力学为建筑设计提供了理论支持,确保建筑 结构的安全性和稳定性。
机械工程材料
总结词
机械工程材料的选择和应用,需要基于 材料力学的理论和实践。
VS
详细描述
在机械工程中,各种零部件的材料选择和 设计,如齿轮、轴承、弹簧等,都需要通 过材料力学进行应力分析、疲劳寿命预测 等。这有助于确保机械设备的可靠性和耐 久性。
材料的破坏
脆性破坏
材料在没有明显塑性变形的情况下突 然发生的破坏。
韧性破坏
材料在发生较大塑性变形后发生的破 坏。
03
材料的力学分析
静力学分析
01
静力学分析是研究物体在静止状态下受到的力,以及这些力如 何影响物体的平衡状态。
02
静力学分析主要关注物体在力的作用下不发生运动状态改变的
平衡状态。
静力学分析的基本原理包括力的平衡、力矩平衡和虚功原理等
05
材料力学的实验研究
实验设备与实验方法
实验设备
材料力学实验中常用的设备包括万能材料试 验机、硬度计、冲击试验机等,这些设备用 于测试材料的力学性能,如拉伸、压缩、弯 曲、硬度等。
实验方法
在材料力学实验中,通常采用的标准方法包 括拉伸实验、压缩实验、弯曲实验、硬度实 验等。这些实验方法可以对材料的力学性能 进行定量测量,从而评估材料的性能和可靠
性。
实验数据处理与分析
要点一
数据处理
在材料力学实验中,采集到的原始数据需要进行处理,包 括数据清洗、数据转换和数据计算等。数据处理是实验过 程中非常重要的一环,它能够将原始数据转化为可分析的 统计结果。
建筑结构材料如混凝土、钢材等,在设计和施工过程中,必须考虑材料的应力、 应变、强度、刚度等力学性能。材料力学为建筑设计提供了理论支持,确保建筑 结构的安全性和稳定性。
机械工程材料
总结词
机械工程材料的选择和应用,需要基于 材料力学的理论和实践。
VS
详细描述
在机械工程中,各种零部件的材料选择和 设计,如齿轮、轴承、弹簧等,都需要通 过材料力学进行应力分析、疲劳寿命预测 等。这有助于确保机械设备的可靠性和耐 久性。
材料的破坏
脆性破坏
材料在没有明显塑性变形的情况下突 然发生的破坏。
韧性破坏
材料在发生较大塑性变形后发生的破 坏。
03
材料的力学分析
静力学分析
01
静力学分析是研究物体在静止状态下受到的力,以及这些力如 何影响物体的平衡状态。
02
静力学分析主要关注物体在力的作用下不发生运动状态改变的
平衡状态。
静力学分析的基本原理包括力的平衡、力矩平衡和虚功原理等
05
材料力学的实验研究
实验设备与实验方法
实验设备
材料力学实验中常用的设备包括万能材料试 验机、硬度计、冲击试验机等,这些设备用 于测试材料的力学性能,如拉伸、压缩、弯 曲、硬度等。
实验方法
在材料力学实验中,通常采用的标准方法包 括拉伸实验、压缩实验、弯曲实验、硬度实 验等。这些实验方法可以对材料的力学性能 进行定量测量,从而评估材料的性能和可靠
性。
实验数据处理与分析
要点一
数据处理
在材料力学实验中,采集到的原始数据需要进行处理,包 括数据清洗、数据转换和数据计算等。数据处理是实验过 程中非常重要的一环,它能够将原始数据转化为可分析的 统计结果。
材料力学课件 (14)第十三章-4

R
M PA B
R
1 AB
<1>
解: 同时加上力P和力偶M
R
用单位载荷法计算A/B和A/B
M P
M() M PR(1 cos) M1( ) 1
R
AB
1 EI
2
[M PR(1 cos )] 1 Rd
0
1A B
<2>
2 R (M PR)
EI
Page6
BUAA
R
M PA B
R
( f A l2 )N 2 ( f A sina l1 cos a l3 )N 3 0
N2, N3为独立变量
f A l2 0 f A sina l1 cos a l3 0
能量法方程等价于几何方程
同理,若几何方程满足
能量法方程等价于平衡方程
Page13
BUAA
MECHANICS OF MATERIALS
§13-7 梁的横向剪切变形效应
前一章在计算变形能时,忽略了剪切变形的影响
➢ 考虑剪切效应时梁的应变能
y h/2 dy
z
dy dx
y
b
M(x) y
Iz
FS ( x) SZ FS ( x) ( h2 y2 )
Iz b
2Iz 4
Page14
BUAA
➢ 应变能表达式:
MECHANICS OF MATERIALS
BUAA
MECHANICS OF MATERIALS
本讲内容
单位载荷法例题 §13-7 梁的横向剪切变形效应
Page1
BUAA
W dWid Wi W dWer We
MECHANICS OF MATERIALS
工程力学M-第13章

FAx
A
FBx
FAy
F=45kN BC FBy
3m
A 30°
1m F=45kN BC
FN图 /kN
104
+
D
危险截面为B点左侧截面
M图
45
/kN·m
-
危险点为B点左侧截面上边缘各点
smax=FAN
+Mzmax Wz
=416.60ck4m N 2+435k2cN 5m m 3 =16.90MP<a1.05[σ]=168MPa AC杆是安全的
叠加后(F、q共同作用)A点正应力
s = s' + s"
=
FN A
+ (-
Mz (x)y )
Iz
叠加以后应力分布可能是
a b σ′
+
c d
b σ〞 a
中性轴
c
=
d
b a
中性轴
或
c
d
b a
或
c
d
b a
c d
F
固定端截面为危险截面,危险点的应力为
smax
=
FN A
+
Mzmax Wz
危险点为单向应力状态
1. 外力分解
Fy = Fcosj Fz = Fsinj
2. x截面的内力(不计剪力)
Mz =Fy(l-x)=F(l-x)cosj My =Fz(l-x)=F(l-x)sinj
x
l
3. x截面任一点处正应力
Fy引起的正应力 Fz引起的正应力
s' = - Mz y
Iz
s" = My z
Iy
工程力学材料力学课件
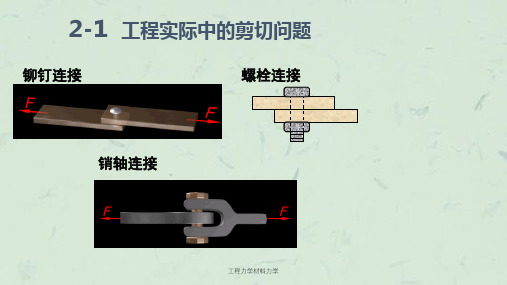
整个接头是安全的
工程力学材料力学
工程力学材料力学
工程力学材料力学
工程力学材料力学
n FS n
b
l
O
FbsAbs bs
Me
(b)
0.5h n FS n
(c)
工程力学材料力学
目录
§2-13 剪切和挤压的实用计算
解:(1)校核键的剪切强度
Fs Abl
由平衡方程 Mo 0 得
Fs d2bld2Me
2 b M l d e 2 0 1 2 0 0 2 0 7 0 0 0 1 0 9 2 8 . 6 1 0 6 P a 2 8 . 6 M P a []
b s A F b s F t4 d14 M 1 P ba s
(3)校核钢板的拉伸强度
F/4
F/4
F/4
F/4
挤压面
F/4 剪切面
F
3F/4
F
F/4
+
工程力学材料力学
2
1
F/4
F/4
F/4
F
F/4
2
1
1 -1F A N 1 1(b F d)t1M 07 Pa
2 -2F A N 2 2(b 3 F 2 d 4 )t 9.3 9 MPa
对错动或错动趋势。
剪床剪钢板
铆钉连接
剪切面
F
F
m
m
工程力学材料力学
F
F
剪切受力特点:作用在构件两侧面上的外力合力大小相
等、方向相反且作用线相距很近。
变形特点:构件沿两力作用线之间的某一截面产生相 对错动或错动趋势。
铆钉连接
F
F
F
m
m
F
工程力学第13章3-讲义修改稿

若略去翼缘上这部分切应力,则腹板内的平均切应力可 近似计算为
m
FS bh
(13.19)
此外,翼缘上还存在平行于翼缘宽度 B 方向的切应力分 量。但与腹板内的切应力比较,一般也是次要的,可以不计。
翼缘的全部面积都位于远离中性轴处,其上各点都有较 大的弯曲正应力,因而翼缘承担了截面上的大部分弯矩。
10
13.5.3 圆形截面梁 圆环形截面梁
max
在相邻截面上如果剪力相同,则截面的翘曲程度也相同,此时弯
矩引起的纤维纵向变形不受剪切变形的影响,所以按照平面假定推导
出的弯曲正应力公式 (13.6) 仍成立。 至于剪力在不同的截面上有变化的情形(如有分布载荷作用的梁
段),则弯曲正应力会受到影响。
弹性力学的精确分析表明,只要梁是细长的,例如梁的跨长 l 与
max
K
FS
z
max
K'
P y
(4) 若假定该弦上各点切应力的 y 分量 y 是相等的,
则
y
(13.14)
FSS
* z
Izb
(13.20)
b —— 弦 KK' 的长度
Sz* —— 弦 KK' 以外的横截面面积 z 轴的静矩 11
(5) 在中性轴上,切应力方向都为铅垂方向,且切应力 数值最大
b 2R
(1) 在圆形截面梁的横截面上,中 性轴上各点切应力与剪力 FS 平行, 其他各点的切应力不平行于 FS 。
(2) 在截面边缘各点处,由于切应 力互等定理的要求,其切应力方向必 与圆周相切。
(3) 由于对称性,截面的铅垂对称 轴上各点切应力为铅垂方向,因而可 设任意一弦 KK'上的各点切应力作用 线相交于 y 轴上某点 P 。
m
FS bh
(13.19)
此外,翼缘上还存在平行于翼缘宽度 B 方向的切应力分 量。但与腹板内的切应力比较,一般也是次要的,可以不计。
翼缘的全部面积都位于远离中性轴处,其上各点都有较 大的弯曲正应力,因而翼缘承担了截面上的大部分弯矩。
10
13.5.3 圆形截面梁 圆环形截面梁
max
在相邻截面上如果剪力相同,则截面的翘曲程度也相同,此时弯
矩引起的纤维纵向变形不受剪切变形的影响,所以按照平面假定推导
出的弯曲正应力公式 (13.6) 仍成立。 至于剪力在不同的截面上有变化的情形(如有分布载荷作用的梁
段),则弯曲正应力会受到影响。
弹性力学的精确分析表明,只要梁是细长的,例如梁的跨长 l 与
max
K
FS
z
max
K'
P y
(4) 若假定该弦上各点切应力的 y 分量 y 是相等的,
则
y
(13.14)
FSS
* z
Izb
(13.20)
b —— 弦 KK' 的长度
Sz* —— 弦 KK' 以外的横截面面积 z 轴的静矩 11
(5) 在中性轴上,切应力方向都为铅垂方向,且切应力 数值最大
b 2R
(1) 在圆形截面梁的横截面上,中 性轴上各点切应力与剪力 FS 平行, 其他各点的切应力不平行于 FS 。
(2) 在截面边缘各点处,由于切应 力互等定理的要求,其切应力方向必 与圆周相切。
(3) 由于对称性,截面的铅垂对称 轴上各点切应力为铅垂方向,因而可 设任意一弦 KK'上的各点切应力作用 线相交于 y 轴上某点 P 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(0 ≺ x ≺ l / 2) 弯矩方程 M ( x) = ( P / 2) x, (0 ≤ x ≤ l / 2) 2 3 l/2 1 P 2 Pl 弯曲变形能 U1 = 2 ∫ ( x) d x = 0 2 EI 2 96 EI
18
1 P 2 Pl 弯曲变形能 U1 = 2 ∫ ( x) d x = 0 2 EI 2 96 EI 2 l/2 k P 2 kP l 剪切变形能 U 2 = 2 ∫ ( ) dx = 0 2GA 2 8GA U 2 12 EIk 两种变形能之比 = 2 U1 GAl 2 对矩形截面 k = 6 / 5, I / A = h / 12 E G= 又: 2(1 + μ ) U 2 12 h 2 = (1 + μ )( ) 19 U1 5 l
记为 k
Q ( x) U2 = ∫ k dx l 2GA
2
其中的系数
A k= 2 I
(S ) ∫A b d A
* 2 z 2
薄壁 k =2 对矩形截面 k = 6 / 5, 圆截面 k = 10 / 9, 圆环 17
例 3 (书例10.3) 已知: 矩形截面简支 梁。 求:比较弯曲和剪切 变形能的大小。 解: 由于对称性,只需计算一半梁中的变形能。 剪力方程 Q ( x) = P / 2,
4 弯曲 纯弯曲时 转角
T ( x) d x U =∫ l 2GI p
2
dθ m = d x EI
6
4 弯曲 纯弯曲时 转角
dθ m = d x EI m dθ = dx EI m θ =∫ dx 0 EI
l
纯弯曲时各截面的弯矩相等,m为常数。
变形能
ml θ= EI 2 1 ml U = W = mθ = 2 2EI
l/2
2 3
U 2 12 EIk 两种变形能之比 = 2 U1 GAl 2 对矩形截面 k = 6 / 5, I / A = h / 12 E G= 又: 2(1 + μ ) U 2 12 h 2 = (1 + μ )( ) U1 5 l 取 μ =0.3 当 h/l = 1/5 时: U 2 / U1 = 0.125
材 料 力 学
第十三章 能 量 方 法
南京航空航天大学 陶秋帆等
1
第十三章 能量方法
本章内容: 1 概述 2 杆件变形能的计算 3 变形能的普遍表达式 4 互等定理 5 卡氏定理 6 虚功原理 7 单位载荷法 莫尔积分 8 计算莫尔积分的图乘法
2
§13. 1 概述
能量原理 与功和能有关的定理,统称为能量原理。 运用能量原理求解问题的方法称为能量法。 功能原理 外力的功等于变形能:
7
m θ =∫ dx 0 EI
l
变形能
横力弯曲时 对细长梁,剪力引起的变形能与弯矩引起的变 形能相比很小,通常可忽略不计。 横力弯曲时,弯矩是x的函数。
ml θ= EI 2 1 ml U = W = mθ = 2 2EI
M ( x) d x dU = 2EI 2 M ( x) d x U =∫ l 2EI
, β Pn
21
β 时广义力的大小为: β P1 ,
β 时广义力的大小为: β P1 , , β Pn 当β 有dβ 时, 位移的增量为:
δ1 d β ,
, δn d β + βPn ⋅ δ n d β
1
则功的增量为:
d W = βP ⋅ δ 1 d β + 1
力的总功为:
W = ( P ⋅ δ 1 + + Pn ⋅ δ n ) ∫ β d β 1 0 1 1 = P ⋅ δ 1 + + Pn ⋅ δ n 1 2 2
23
1 U = W = P ⋅ δ1 + 1 2
1 + Pn ⋅ δ n 2
2 组合变形时的变形能 取一微段为研究对象 由变形能的普遍表达 式,有:
1 1 1 d U = N ( x) d(Δl ) + M ( x) d θ + T ( x) d φ 2 2 2 2 2 2 N ( x) d x M ( x) d x T ( x) d x + = + 2GI p 2 EA 2 EI
积分可得杆的总变形能
T ( x) d x N ( x) d x M ( x) d x +∫ +∫ U =∫ l l l 2EI 2GI p 2 EA
2
2
2
24
积分可得杆的总变形能
T ( x) d x N ( x) d x M ( x) d x +∫ +∫ U =∫ l l l 2EI 2GI p 2 EA
15
剪切应变能密度
Q ( x)(S ) u2 = 2GI b
2
* 2 z 2 2
剪切变形能
Q ( x)(S ) U2 = ∫ dV V 2GI b 2 * 2 ⎡ Q ( x) ( S z ) ⎤ = ∫⎢ d A⎥ d x 2 ∫A 2 l 2GI b ⎣ ⎦
2 * 2 z 2 2
⎡ Q ( x) A = ∫⎢ ⋅ 2 l ⎣ 2GA I
u1 =
σ
2
2E
,
u2 =
τ
2
2G
* z
13
M ( x) y y处应力 σ = , I
Q( x) S τ= Ib
解: 应变能密度为
2G 2E * M ( x) y Q( x) S z y处应力 σ = , τ= I Ib 2 2 2 * 2 M ( x) y Q ( x)(S z ) , u2 = u1 = 2 2 2 2 EI 2GI b
2
8
M ( x) d x dU = 2EI
2
M ( x) d x U =∫ l 2EI
2
5 用广义力和广义位移表示变形能
1 1 可将 U = PΔl , U = mφ , 2 2
统一写为
1 U = mθ 2
1 U = W = Pδ 2
δ1 ε1
6 非线性弹性材料的变形能
U = W = ∫ P dδ , u = ∫ σ dε
0 0
9
例 1 (书例10.1) 已知: 圆截面半圆 曲杆,P , R, EI, GIp 。 求:A点的垂直位 移。 解:1 求内力 截面mn, 取左段
M
T
M = PR sin ϕ ,
2 变形能
T = PR (1 − cos ϕ ) 2 T 2 (ϕ ) R d ϕ M (ϕ ) R d ϕ + dU = 2GI p 2EI
总的功为三项之和:
1 1 U 2 = Q1δ Q1 + + Qnδ Qn 2 2 1 1 + Pδ P1 + + Pmδ Pm 1 2 2 ′ ′ + Q1δ Q1 + + Qnδ Qn
变形能与加载次序无关,所以:
U1 = U 2
30
变形能与加载次序无关,所以: U1 = U 2
1 U1 = Pδ P1 + 1 2 ′ + Pδ P1 + 1
1 1 + Pmδ Pm + Q1δ Q1 + 2 2 ′ + Pmδ Pm 1 1 + Qnδ Qn + Pδ P1 + 1 2 2 ′ + Qnδ Qn
1 + Qnδ Qn 2 1 + Pmδ Pm 2
1 U 2 = Q1δ Q1 + 2 ′ + Q1δ Q1 +
′ Pδ P1 + 1
2
Δl
4
l
2 纯剪切
N ( x) d x U =∫ l 2 EA 2 σ 1 应变能密度 u = σε = 2E 2
2
τ 1 应变能密度 u = τγ = 2G 2
2
3 扭转
1 ml U = W = mφ = 2 2GI p
2
5
3 扭转
1 ml U = W = mφ = 2 2GI p
2
扭矩T是x的函数时
26
1) 先加第一组,再加第二组 加完第一组力时的功为:
1 Pδ P1 + 1 2
1 + Pmδ Pm 2
加完第二组力时,第二 组力的功为:
1 Q1δ Q1 + 2
1 + Qnδ Qn 2
加第二组力时,第一组 ′ ′ 力的功为: Pδ P1 + + Pmδ Pm 1 总的功为三项之和:
27
加第二组力时,第一组 力的功为:
10
1 求内力 截面mn, 取左段
M = PR sin ϕ , T = PR (1 − cos ϕ )
2 变形能
M
2
T
M (ϕ ) R d ϕ T (ϕ ) R d ϕ + dU = 2GI p 2EI
2
P R sin ϕ d ϕ P R (1 − cosϕ ) d ϕ + = 2GI p 2EI
U =W §13. 2 杆件变形能的计算
1 轴向拉伸或压缩
Pl 1 U = W = PΔl = 2EA 2
2
Δl
3
P
l
§13. 2 杆件变形能的计算
1 轴向拉伸或压缩
Pl 1 U = W = PΔl = 2EA 2 2 N ( x) d x 轴力N是x的函数时 dU = P 2EA 2 N ( x) d x U =∫ l 2 EA 2 σ 1 应变能密度 u = σε = 2E 2
2
⎤ (S ) ∫A b d A⎥ d x ⎦
* 2 z 2
记为 k
16
⎡ Q ( x) ( S ) ⎤ = ∫⎢ d A⎥ d x 2 ∫A l 2GI b ⎣ ⎦ * ⎡ Q 2 ( x) A ( S z ) 2 ⎤ = ∫⎢ ⋅ 2∫ d A⎥ d x 2 l 2GA I A b ⎣ ⎦
