高中数学:4.1.2 极坐标系(1))课件(新人教选修4-4)
合集下载
人教版高中数学选修4-4 第一讲 坐标系 二 极坐标系 (共34张PPT)教育课件

A. y 1
sin t
1
x t2
C.
1
yt 2
x cos t
B. y 1
cos t
x tan t
D. y 1
tan t
7.极坐标方程
2
arcsin化(为 直0)角坐标方程的形
式是 ( )
A. x2 y2 x 0
B.y x(1 x)
C. 2x 1 4y2 1 D..y (x 1)
2.极坐标(,)与(ρ,2kπ+θ)( k )表z 示 同一个点.即一点的极坐标的统一的表达式 为(ρ,2kπ+θ)
3.如果规定ρ>0,0≤θ<2π,那么除 极 点外,平面内的点和极坐标就可以一一对 应了。
我们学了直角坐标,也学了极坐 标,那么这两种坐标有什么关系呢? 已知点的直角坐标为,如何用极坐标 表示这个点呢?
M (, )
0
x
2
4
5
6
C
1.如图,在极坐标系中,写出点 AF(,6B, ,4C3 ,)D的, G极(坐5, 标53,所) 并在标的出位E置( 72 , ) ,
E D BA
O
X
4 F
3
G 5
3
解:如图可得A,B,C,D的坐标分别为
(4,0)
(2, )
(3, )
(1, 5 )
4
2
6
点E,F,G的位置如图所示
1
4.极坐标方程ρ=cosθ与ρcosθ= 的2 图形是( ) B
A
B
C
D
解x=:12把,ρc故os排θ=除A,、12 化D;为又直圆角ρ坐=c程os,θ显得然: 过点 (0,1),又排除C,故选B。
5、若A、B的两点极坐标为A(4,
高中数学第一章坐标系2极坐标系课件新人教A版选修4-4

2.将点的极坐标(ρ,θ)化为点的直角坐标(x,y)时,运用到求角 θ 的正弦值 和余弦值,熟练掌握特殊角的三角函数值,灵活运用三角恒等变换公式是关键.
将点的直角坐标化为极坐标
分别把下列点的直角坐标化为极坐标(限定 ρ≥0,0≤θ<2π): (1)(-2,2 3);(2)( 6,- 2);(3)32π,32π. 【思路探究】 利用公式 ρ2=x2+y2,tan θ=yx(x≠0),但求角 θ 时,要注意 点所在的象限.
图 1-2-1
2.互化),极坐标是(ρ,
θ),于是极坐标与直角坐标的互化公式如表:
点M
直角坐标(x,y)
极坐标(ρ,θ)
互化公式
x= ρcos θ y= ρsin θ
ρ2= x2+y2 , tan θ= x2+y2
[小组合作型] 将点的极坐标化为直角坐标
我还有这些不足: (1) ________________________________________________________ (2) ________________________________________________________ 我的课下提升方案: (1) ________________________________________________________ (2) ________________________________________________________
写出下列各点的直角坐标,并判断所表示的点在第几象限.
(1)2,43π;(2)2,23π;(3)2,-π3;(4)(2,-2).
【思路探究】
点的极坐标(ρ,θ)―→xy= =ρρcsions
θ θ
―→点的直角坐标(x,y)―→
将点的直角坐标化为极坐标
分别把下列点的直角坐标化为极坐标(限定 ρ≥0,0≤θ<2π): (1)(-2,2 3);(2)( 6,- 2);(3)32π,32π. 【思路探究】 利用公式 ρ2=x2+y2,tan θ=yx(x≠0),但求角 θ 时,要注意 点所在的象限.
图 1-2-1
2.互化),极坐标是(ρ,
θ),于是极坐标与直角坐标的互化公式如表:
点M
直角坐标(x,y)
极坐标(ρ,θ)
互化公式
x= ρcos θ y= ρsin θ
ρ2= x2+y2 , tan θ= x2+y2
[小组合作型] 将点的极坐标化为直角坐标
我还有这些不足: (1) ________________________________________________________ (2) ________________________________________________________ 我的课下提升方案: (1) ________________________________________________________ (2) ________________________________________________________
写出下列各点的直角坐标,并判断所表示的点在第几象限.
(1)2,43π;(2)2,23π;(3)2,-π3;(4)(2,-2).
【思路探究】
点的极坐标(ρ,θ)―→xy= =ρρcsions
θ θ
―→点的直角坐标(x,y)―→
1.2 极坐标系 课件-高中数学人教A版选修4-4 (共17张PPT)
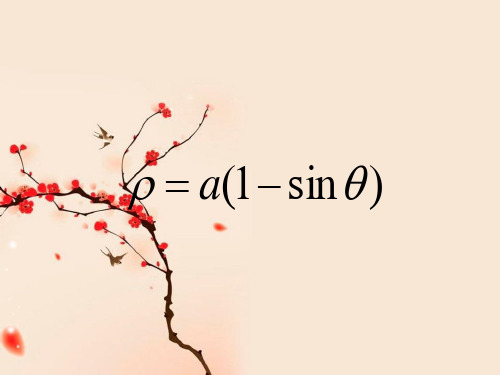
问题3:已知角 终边上有一点 P(1, 3) 如何 求角 的大小及点P到原点距离?
1.互化条件
(1)极点就是坐标原点; (2)极轴为x的正半轴;
(3)具有相同的单位长度.
M(x,y)
2.互化公式
M(,)
. x
y
cos (为极径,为极角) sin
极坐标
直角坐标 O x
x2 y2
y
X
tan y (x 0)
极点;极轴;长度单位; 角度单位和它的正方向。
[2] 点的直角坐标与极坐标互化?
x y
cos (为极径,为极角) sin
极坐标
直角坐标
x2 y2 tan y (x 0)
x
谢谢各位老师的 聆听!
O
X
这样就建立了一个极坐标系
问题1:类比直角坐标系确定点只需知 道横纵坐标, 那么在极坐标中如何确定一点的位置?
引入距离和方位角
x
二、极坐标的表示方法
(1)极径:对于极坐标平面上任意点M到极点O
的距离|OM|叫点M的极径,用表示,=|OM|
(;2)以极轴为始边旋转到射线OM的角 MOX叫点M的极角,记为MOX,= ;
a(1 sin )
极坐标系
如何确定以下两船 的位置关系呢?
(1)距离: 12海里 (2)方向:
发生故障!!!
拯救船
20º
O
x
云南大学北门
银杏大道
从这往南走100米!
一、极坐标系的建立
(1)在平面内取一个定点O,叫做极点。
(2)从极点O引一条射线OX,叫做极轴。
(3)选定一个长度单位和角度单位及 它的正方向(以逆时针方向旋转为 正角)
(3)有序数对(,)就叫做M的极坐标
1.互化条件
(1)极点就是坐标原点; (2)极轴为x的正半轴;
(3)具有相同的单位长度.
M(x,y)
2.互化公式
M(,)
. x
y
cos (为极径,为极角) sin
极坐标
直角坐标 O x
x2 y2
y
X
tan y (x 0)
极点;极轴;长度单位; 角度单位和它的正方向。
[2] 点的直角坐标与极坐标互化?
x y
cos (为极径,为极角) sin
极坐标
直角坐标
x2 y2 tan y (x 0)
x
谢谢各位老师的 聆听!
O
X
这样就建立了一个极坐标系
问题1:类比直角坐标系确定点只需知 道横纵坐标, 那么在极坐标中如何确定一点的位置?
引入距离和方位角
x
二、极坐标的表示方法
(1)极径:对于极坐标平面上任意点M到极点O
的距离|OM|叫点M的极径,用表示,=|OM|
(;2)以极轴为始边旋转到射线OM的角 MOX叫点M的极角,记为MOX,= ;
a(1 sin )
极坐标系
如何确定以下两船 的位置关系呢?
(1)距离: 12海里 (2)方向:
发生故障!!!
拯救船
20º
O
x
云南大学北门
银杏大道
从这往南走100米!
一、极坐标系的建立
(1)在平面内取一个定点O,叫做极点。
(2)从极点O引一条射线OX,叫做极轴。
(3)选定一个长度单位和角度单位及 它的正方向(以逆时针方向旋转为 正角)
(3)有序数对(,)就叫做M的极坐标
选修4-4 1.2 极坐标系

从这向北 2000米。
请问:去菜 市场怎么走?
请分析上面这句话,他告诉了问路人 什么? 从 这 向 北 走 2 0 0 0 米 !
出发点
方向
距离
在生活中人们经常用方向和距离来 表示一点的位置。这种用方向和距离表 示平面上一点的位置的思想,就是极坐 标的基本思想。
一、极坐标系的建立:
在平面内取一个定点O,叫做极点。 引一条射线OX,叫做极轴。 再选定一个长度单位 和角度单位及它的正 方向(通常取逆时针 O 方向)。
[1]给定(,),就可以在极坐 标平面内确定唯一的一点M。 [2]给定平面上一点M,但却 有无数个极坐标与之对应。
原因在于:极角有无数个。
如果限定ρ>0,0≤θ<2π 那么除极点外,平面内的点和极坐标就可以一一 对应了.
M O (ρ,θ)… X
极坐标和直角坐标的互化
平面内的一个点的直角坐标是(1, 3 )
C (5,0) E ( 3,3)
ห้องสมุดไป่ตู้
D (0,2)
π),(3, ) π 例3 已知两点(2,
求两点间的距离.
用余弦定理求 AB的长即可.
3
π 解:∠AOB =
6
B
A
2
推广: 在极坐标下,任意两点P ( 1 ,1 ), P2 ( 2 , 2 ) 1
o
x
之间的距离可总结如下:
2 PP2 12 2 2 1 2 cos(1 2 ) 1
y x y , tan ( x 0) x
2 2 2
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合; 2. 极轴与直角坐标系的x轴的正半
轴重合; 3. 两种坐标系的单位长度相同.
请问:去菜 市场怎么走?
请分析上面这句话,他告诉了问路人 什么? 从 这 向 北 走 2 0 0 0 米 !
出发点
方向
距离
在生活中人们经常用方向和距离来 表示一点的位置。这种用方向和距离表 示平面上一点的位置的思想,就是极坐 标的基本思想。
一、极坐标系的建立:
在平面内取一个定点O,叫做极点。 引一条射线OX,叫做极轴。 再选定一个长度单位 和角度单位及它的正 方向(通常取逆时针 O 方向)。
[1]给定(,),就可以在极坐 标平面内确定唯一的一点M。 [2]给定平面上一点M,但却 有无数个极坐标与之对应。
原因在于:极角有无数个。
如果限定ρ>0,0≤θ<2π 那么除极点外,平面内的点和极坐标就可以一一 对应了.
M O (ρ,θ)… X
极坐标和直角坐标的互化
平面内的一个点的直角坐标是(1, 3 )
C (5,0) E ( 3,3)
ห้องสมุดไป่ตู้
D (0,2)
π),(3, ) π 例3 已知两点(2,
求两点间的距离.
用余弦定理求 AB的长即可.
3
π 解:∠AOB =
6
B
A
2
推广: 在极坐标下,任意两点P ( 1 ,1 ), P2 ( 2 , 2 ) 1
o
x
之间的距离可总结如下:
2 PP2 12 2 2 1 2 cos(1 2 ) 1
y x y , tan ( x 0) x
2 2 2
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合; 2. 极轴与直角坐标系的x轴的正半
轴重合; 3. 两种坐标系的单位长度相同.
1.2.1《极坐标系的概念》课件(新人教选修4-4).

6
C(3, )
2
F (4, )
第15页,共43页。
2
4
5
6
C E
F
A O
B X
4
D
3
G 5
3
第16页,共43页。
要求写出各点: [1]最小正极角的极坐标 [2]最大负极角的极坐标
[3]点的极坐标的统一表达式。
第17页,共43页。
本节课总结:
[1]极坐标系的建立需确定几条?
极点;极径;长度单位和角度正方向。
根据极径定义,极径是距离,当然是正的。 现在所说的“负极径”中的“负”到底是什么 意思?
有比较才能有鉴别!
把负极径时点的确定过程,与正极径时点的确 定过程相比较,看看有什么相同,有什么不同?
第21页,共43页。
五、4、正、负极径时,点的确定过程比较
画出点 (3,/4) 和(-3,/4)
M
[1]作射线OP,使XOP= /4
想一想?
极点(0,)( R) 即极点有无数个极坐标
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法? ③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
第13页,共43页。
三、点的极坐标的表达式的研究
如图:OM的长度为4,
请说出点M的极坐标的其他 4
表达式。
O 思:这些极坐标之间有何异同?
就叫做M的极坐标。
O X
特别强调:表示线段OM的长度,既点M到极 点O的距离;表示从OX到OM的角度,既以OX (极轴)为始边,OM 为终边的角。
第11页,共43页。
题组一:说出下图中各点的极坐标
2
4
5
6
C(3, )
2
F (4, )
第15页,共43页。
2
4
5
6
C E
F
A O
B X
4
D
3
G 5
3
第16页,共43页。
要求写出各点: [1]最小正极角的极坐标 [2]最大负极角的极坐标
[3]点的极坐标的统一表达式。
第17页,共43页。
本节课总结:
[1]极坐标系的建立需确定几条?
极点;极径;长度单位和角度正方向。
根据极径定义,极径是距离,当然是正的。 现在所说的“负极径”中的“负”到底是什么 意思?
有比较才能有鉴别!
把负极径时点的确定过程,与正极径时点的确 定过程相比较,看看有什么相同,有什么不同?
第21页,共43页。
五、4、正、负极径时,点的确定过程比较
画出点 (3,/4) 和(-3,/4)
M
[1]作射线OP,使XOP= /4
想一想?
极点(0,)( R) 即极点有无数个极坐标
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法? ③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
第13页,共43页。
三、点的极坐标的表达式的研究
如图:OM的长度为4,
请说出点M的极坐标的其他 4
表达式。
O 思:这些极坐标之间有何异同?
就叫做M的极坐标。
O X
特别强调:表示线段OM的长度,既点M到极 点O的距离;表示从OX到OM的角度,既以OX (极轴)为始边,OM 为终边的角。
第11页,共43页。
题组一:说出下图中各点的极坐标
2
4
5
6
人教版高二数学选修4《极坐标系的概念》课件(共27张PPT)

新课标人教版课件系列选修4-4
极坐标系的概念
余集高中数学组
唐汝照
Page 1
教学目标
1、理解极坐标的概念,弄清极坐标系的 结构( 建立极坐标系的四要素); 2、理解广义极坐标系下点的极坐标(ρ, θ)与点之间的多对一的对应关系; 3、已知一点的极坐标会在极坐标系中描 点,以及已知点能写出它的极坐标。
极点;极轴;长度单位;计算角度的正方向.
[2]极坐标系内一点的极坐标有多少种表达式?
无数,极角有无数个. [3]一点的极坐标有否统一的表达式? 有。(ρ ,2kπ +θ )
Page 24
课后作业 思考: 极坐标系中, 点M的坐标为 (-10, 3 ), 则下列各 坐标中, 不是M点 的坐标的是( ) 4 ) (A) (10, 3 ) (B) (-10, - 5 3 2 2 (C) (10, - 3 ) (D)(10, 3 )
点M:在角终边的反向延长线上, 且|OM|=|| 5 ° M(-2, ) O 5
6 ° O 6 • •M(-x 2, 5) M (, ) 6
5、关于负极径
x
Page 20
小结: 从比较来看, 负极径比正极径 多了一个操作, 将射线OP“反向延
练习:写出下列各点的负极径的极坐标
Page 25
Page 2
β=α+2kπ,k∈Z 与角α终边相同的角:
平面直角坐标系中的点P与坐标 y 一一 对应的. (a ,b)是 _____ P(a,b)
平面直角坐标系是最 a O x 简单最常用的一种坐标 系,但不是唯一的一种 坐标系. 有时用别的坐 标系比较方便. 还有什么坐标系呢?
Page 3
(, 2k+)
极坐标系的概念
余集高中数学组
唐汝照
Page 1
教学目标
1、理解极坐标的概念,弄清极坐标系的 结构( 建立极坐标系的四要素); 2、理解广义极坐标系下点的极坐标(ρ, θ)与点之间的多对一的对应关系; 3、已知一点的极坐标会在极坐标系中描 点,以及已知点能写出它的极坐标。
极点;极轴;长度单位;计算角度的正方向.
[2]极坐标系内一点的极坐标有多少种表达式?
无数,极角有无数个. [3]一点的极坐标有否统一的表达式? 有。(ρ ,2kπ +θ )
Page 24
课后作业 思考: 极坐标系中, 点M的坐标为 (-10, 3 ), 则下列各 坐标中, 不是M点 的坐标的是( ) 4 ) (A) (10, 3 ) (B) (-10, - 5 3 2 2 (C) (10, - 3 ) (D)(10, 3 )
点M:在角终边的反向延长线上, 且|OM|=|| 5 ° M(-2, ) O 5
6 ° O 6 • •M(-x 2, 5) M (, ) 6
5、关于负极径
x
Page 20
小结: 从比较来看, 负极径比正极径 多了一个操作, 将射线OP“反向延
练习:写出下列各点的负极径的极坐标
Page 25
Page 2
β=α+2kπ,k∈Z 与角α终边相同的角:
平面直角坐标系中的点P与坐标 y 一一 对应的. (a ,b)是 _____ P(a,b)
平面直角坐标系是最 a O x 简单最常用的一种坐标 系,但不是唯一的一种 坐标系. 有时用别的坐 标系比较方便. 还有什么坐标系呢?
Page 3
(, 2k+)
高中数学第一章坐标系1.2极坐标系课件新人教B版选修4_4
对于这类问题的解决方法,可以直接用极坐标内两点间的
2 距离公式 d= ρ2 1+ρ2-2ρ1ρ2cosθ1-θ2求得;也可以把 A, B
两点由极坐标化为直角坐标,利用直角坐标中两点间的距离公 式 d= x1-x22+y1-y22求得, 极坐标与直角坐标的互化体现 了化归的解题思想;还可以考虑其对称性,根据对称性求得.
C(-2,2 3),求它们的极坐标,其中极角 θ∈[0,2π).
解:(1)根据 x=ρcos θ,y=ρsin θ 得 B(-1,-
3),C -
2 2
3 2 3 2 A ,- , 2 2
3 ,0,D(0,-4). 2
2
11π y (2) 根据 ρ = x + y , tan θ = x 得 A 2 3, 6 , B 2π 5 π , ,C4, 3 . 3 2
中两点间的距离公式.解答此题可直接利用极坐标系中两点间的 距离公式求解,也可以先将极坐标化为直角坐标,然后利用两点 间的距离公式求解.
[精解详析] 4π 5π π 7π 5π π ∠AOB= - = ,∠BOC= - = ,∠ 3 6 2 6 6 3
4π 7π π COA= - = .(O 为极点) 3 6 6 (1)∵|AB|= |OA|2+|OB|2= 42+62=2 13. |BC|= |OB|2+|OC|2-2|OB|· |OC|cos∠BOC=2 13, |AC|= |OA|2+|OC|2-2|OA|· |OC|cos∠AOC=4 5-2 3. ∴△ABC 是等腰三角形.
11π 答案:(1)3, 6
7π (2)3, 6
5π (3)3, 6
点的极坐标和直角坐标的互化
高中数学第一讲坐标系1.2极坐标系课件新人教A版选修4_4

D典例透析 IANLI TOUXI
3.极坐标和直角坐标的互化
(1)互化的前提条件
①极坐标系中的极点与直角坐标系中的原点重合;②极轴与x轴
的正半轴重合;③在两种坐标系中取相同的长度单位.
(2)互化公式
①极坐标化为直角坐标
������ = ������cos������, ������ = ������sin������;
法等.
2.在通常情况下,由 tan θ 确定角 θ 时,应根据点 P 所在象限取最
小正角.在这里要注意:当
x≠0
时,角
θ
才能由
tan
θ=
������ ������
按上述方法确定.当 x=0 时,又分三种情况:(1)当 x=0,y=0 时,θ 可取
任何值;(2)当
x=0,y>0
时,可取
θ=
π 2
;
(3)当x=0,y<0
������2 = ������2 + ������2,
②直角坐标化为极坐标
tan������
=
������ ������
(������
≠
0).
M 目标导航 UBIAODAOHANG
Z 知识梳理 HISHI SHULI
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
名师点拨1.极坐标与直角坐标的互化,常用方法有代入法、平方
①因为 yx=
2·cos
π 4
=
1,
������
=
2·sin
π 4
=
1,
所以点
2,
π 4
的直角坐标为(1,1).
②因为 x=6·cos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
π F(6, 4π) 3 π G(7, 5π ) 3
[变式训练 ] 在课本P6的图上描下列点: 变式训练1 的图上描下列点: 变式训练 的图上描下列点
A(3, 0) 4π D (5, ) 3 5π G (6, ) 3
B ( 6 , 2π ) 5π E (3, ) 6
C (3,
π
2
)
F (4,π )
[小结 小结] 小结 由极坐标描点的步骤: 由极坐标描点的步骤: (1) 先按极角找到点所在射线; 先按极角找到点所在射线; 极角找到点所在射线 (2) 在此射线上按极径描点 在此射线上按极径描点. 极径描点
思考: 平面上一点的极坐标是否唯一?若不唯一, 思考 ①平面上一点的极坐标是否唯一?若不唯一 那有多少种表示方法? 那有多少种表示方法? ② 不同的极坐标是否可以写 出统一表达式? 出统一表达式? 3、点的极坐标的表达式的研究 、 π 如图: 的长度为4, 如图:OM的长度为 , = 的长度为 θ 请说出点M的极坐标的其他表达式 请说出点 的极坐标的其他表达式 思考:这些极坐标之间有何异同? 思考:这些极坐标之间有何异同? 极径相同, 极径相同,不同的是极角 思考:这些极角有何关系? 思考:些极角有何关系? 这些极角的始边相同,终边也相同。 这些极角的始边相同,终边也相同。也就是说它们 是终边相同的角。 是终边相同的角。 π 2 4, kπ+ 4 本题点M的极坐标统一表达式 的极坐标统一表达式: 本题点 的极坐标统一表达式: O
5、关于负极径 、
在一般情况下,极径都是取正值。 在一般情况下,极径都是取正值。但在某些必要的 情况下,也允许取负值 负值( 情况下,也允许取负值 ρ<0): 对应的点的位置? 时如何规定 θ θ)对应的点的位置? <0时,点M(ρ (ρ 的位置规定: 当ρ<0时如何规定, ρ,)的位置规定: 时 ρ 点M:在角θ终边的反向延长线上,且|OM|=|ρ| :在角θ终边的反向延长线上, ρ 5π π 6 ° O π M(-2, 5π) 6 x π • M(-2, 5π) 6 • ρ M (ρ, θ) ° O
情境2:请问到深大附中怎么走? 情境 :请问到深大附中怎么走? 从这向南走200米. 从这向南走 米 请分析上面这句话,他告诉了问路人什么? 请分析上面这句话,他告诉了问路人什么? 从 这 向 南 走 2 0 0 米 !
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的 位置。这种用方向 距离表示平面上一点的位置的 方向和 位置。这种用方向和距离表示平面上一点的位置的 思想,就是极坐标的基本思想。 思想,就是极坐标的基本思想。
二、新知学习
1、极坐标系的建立: 、极坐标系的建立: 极点. 在平面内取一个定点O,叫做极点 在平面内取一个定点 ,叫做极点 引一条射线OX,叫做极轴。 ,叫做极轴。 引一条射线 极轴 再选定一个长度单位和角度单位及它 再选定一个长度单位和角度单位及 角度单位 的正方向(通常取逆时针方向) 的正方向(通常取逆时针方向). O 这样就建立了一个极坐标系 极坐标系. 这样就建立了一个极坐标系 X
在极坐标系中, 例2. 在极坐标系中 (1) 已知两点 P 5,π), (2 4π) 求线段 的长度; 的长度; ( Q , ,求线段PQ的长度 3 3 ρ∈R, (2) 已知点 的极坐标为 ρ, π), ρ∈ 说明满足上述 已知点M的极坐标为 的极坐标为( 4 条件的点M的位置 的位置. 条件的点 的位置
4
ρ θ
M
X
4、极坐标系下点与它的极坐标的对应情况
M
P (ρ,θ)
[1]给定(ρ,θ),就可以在极坐标平 [1]给定( 就可以在极坐标平 给定 极坐标 面内确定唯一的一点M 面内确定唯一的一点M
O
X
[2]给定平面上一点M 但却有无数个极坐标与之对应。 [2]给定平面上一点M,但却有无数个极坐标与之对应。 给定平面上一点 原因在于:极角有无数个。 原因在于:极角有无数个。 如果限定ρ 0,0≤θ< 如果限定ρ>0,0≤θ<2π 限定 除极点外 平面内的点和极坐标就可以一一对应 一一对应了 那么除极点 那么除极点外,平面内的点和极坐标就可以一一对应了.
教学目标: 教学目标 1. 理解极坐标的概念 2. 学会用极坐标表示平面上的点 教学重点: 教学重点 1. 理解极坐标的意义 2. 能够在极坐标系中用极坐标确定点位置
一、问题情境
情境1:军舰巡逻在海面上,发现前方有一群水雷, 情境 :军舰巡逻在海面上,发现前方有一群水雷, 如何确定它们的位置以便将它们引爆? 如何确定它们的位置以便将它们引爆? 情境2:请问到深大附中怎么走? 情境 :请问到深大附中怎么走? 从这向南走200米。 从这向南走 米 问题1:为了简便地表示上述问题中点的位置, 问题 :为了简便地表示上述问题中点的位置, 应创建怎样的坐标系呢? 应创建怎样的坐标系呢? 问题2:如何刻画这些点的位置? 问题 :如何刻画这些点的位置?
三、小
结
[1]建立一个极坐标系需要哪些要素 [1]建立一个极坐标系需要哪些要素 极点;极轴;长度单位;角度单位和它的正方向. 极点;极轴;长度单位;角度单位和它的正方向. [2]极坐标系内一点的极坐标有多少种表达式 极坐标系内一点的极坐标有多少种表达式? [2]极坐标系内一点的极坐标有多少种表达式? 无数,极角有无数个. 无数,极角有无数个. [3]一点的极坐标有否统一的表达式 一点的极坐标有否统一的表达式? [3]一点的极坐标有否统一的表达式? 。(ρ π+θ) 有。(ρ,2kπ+θ) 四、课后作业 教材P14-15页5,8,9,10,11 教材 页 , , , , π 思考: 极坐标系中, 的坐标为(-10, ), 则下列各 思考 极坐标系中 点M的坐标为 的坐标为 3 坐标中, 不是M点的坐标的是 坐标中 不是 点的坐标的是( ) 点的坐标的是 π π π) π (A) (10, 4π) (B) (-10, - 5π) (C) (10, - 2π (D)(10, 2π) 3 3 3 3
2、极坐标系内一点的极坐标的规定 、 对于平面上任意一点M,用 表示线段OM的长度, 对于平面上任意一点M,用ρ表示线段OM的长度, M, OM的长度 表示以射线OX为始边,射线OM OX为始边 OM为终边所成的 用θ表示以射线OX为始边,射线OM为终边所成的 叫做点M 极径, 叫做点M 极角, 角,ρ叫做点M的极径, θ叫做点M的极角,有序数对 就叫做M的极坐标。 (ρ,θ)就叫做M的极坐标。 思考: 对比直角坐标系, 思考 对比直角坐标系,比较异同 极点、极轴、长度单位、 (1) 要素:____________________ 、 要素: 极点、极轴、长度单位 角度单位和正方向 ; ____________________; ρ 表示. (2) 平面内点的极坐标用 (ρ, θ)表示 平面内点的极坐标用_____表示 可为任意值. 极点的极坐标为 (0, θ), θ可为任意值 极点的极坐标为_________________ 的极坐标为
M ρ θ O X
如图,写出各点的极坐标: 例1. 如图,写出各点的极坐标: π 2 A(4,0) π 4 5π π B(3, π ) 4 6 π D C(2, 2 ) • C • • B 5π π E A D(5, 6 ) 。 • • π x O E(4.5, π) F 4π π 3
•
G
•
5π π 3
•
E
5π π 3 (-ρ, θ+π)
11π π 6
A(-4,0) 5π π B(3, ) 6 π C(-2, 2 ) π D(-1, 5π) 3 E(3,- π ) 6 (-4,- π) F 3
(ρ, 2kπ+θ) ρ θ
[-ρ, θ+(2k+1)π]
都是同一点的 都是同一点的 极坐标. 极坐标
已知点Q ρ 分别按下列条件求出点P的坐标 的坐标: 例3. 已知点 (ρ, θ),分别按下列条件求出点 的坐标: (1) P是点 关于极点 的对称点; 是点Q关于极点 的对称点; 是点 关于极点O的对称点 π (2) P是点 关于直线θ = 的对称点 是点Q关于直线 的对称点. 是点 2 (3) P是点 关于极轴的对称点。 是点Q关于极轴的对称点 是点 关于极轴的对称点。 ω 注意点M的极坐标具有多值性 注意点 的极坐标具有多值性. 的极坐标具有多值性
θ
x
小结: 从比较来看, 负极径比正极径多了一个操作, 小结: 从比较来看 负极径比正极径多了一个操作 将射线OP“反向延长”. 反向延长” 将射线 反向延长
5π π 6
2π F π 3 • B
π 2
π 4
•
• • πA
D 。 O x
•
5π π 4 [小结 (ρ, θ) 小结] ρ 小结 C 3π π 2
