1999年上海市中学生业余数学学校预备年级招生试题解答 (1)
上海市中学生业余数学学校招生试题 含答案
2017年上海市中学生业余数学学校预备年级招生考试试题（10月21日上午8:30~9:30）得分评分复核本卷满分100分（10’×10=100’）1、计算：（1）2017 × 20162016 - 2016 × 20172017=________（2）13312155132642586538++++++=________2、有一个四位正整数，在它的某位数字前加上一个小数点，再与这个四位数相加，得到数2037、17，则这个四位数是________3、已知一列数：2017，2016，1，2015，2014，1，2013，2012，1，…，3，2，1，则这一列数中，从左向右数，第2017个数是________4、五年级某班有26名男生、在一次考试中，该班有30人得分超过85分，则这次考试中，该班女生中得分超过85分的人数比男生中得分没有超过85分的人数多________人5、某人工作一月（按30天计算）的酬金是1800元加一台自动洗衣机、实际上，他做了12天，得到60元和一台自动洗衣机，则这台自动洗衣机的价值为________元6、如图，在四边形ABCD中，已知AB=BC=a cm，AD=DC=b cm（a，b 为整数），∠DAB=∠BCD=90°，且四边形ABCD的面积为385cm2，则四边形ABCD周长的最小值是________cm7、有三堆棋子，每堆棋子一样多，且都由黑白两色棋子组成、已知第一堆的黑棋和第二堆的白棋数目相等，第三堆的黑棋占三堆全部黑棋的25、若把三堆棋子并成一堆，则在这一堆棋子中，白棋占全部棋子的________（填一个分数）8、如图，由12条线段搭成一个空间框架、框架中两条没有公共端点的线段是不相交的，例如AC与BD是一对不相交的线段（这里AC，BD没有次序之分），则这个框架的12条线段中，不相交的线段有________对9、在如图的10个小方格里分别填上1，2，3，4，5，11，12，13，14，15十个数，使三个2×2的正方形中的四个数的和都相等，则这个和的最大值是________10、有64个1×1×1的小正方体，其中34个是白色的，30个是黑色的、现将它们拼成一个4×4×4的大正方体，则大正方体表面黑色部分面积的最小是________2017年上海市中学生业余数学学校招生试题答案 预备年级1、（1）0;（2）242、20173、6734、45、11006、927、948、36 9、33 10、22。
2019年上海市中学生业余数学学校招生预备试题
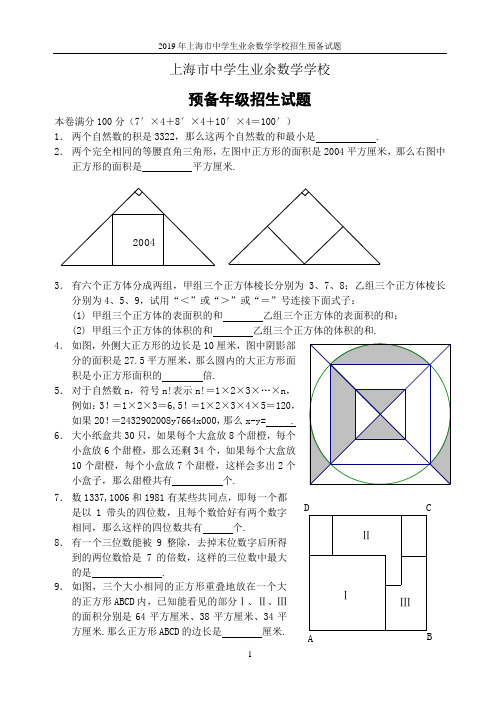
上海市中学生业余数学学校预备年级招生试题本卷满分100分（7′×4＋8′×4＋10′×4＝100′）1． 两个自然数的积是3322，那么这两个自然数的和最小是 .2． 两个完全相同的等腰直角三角形，左图中正方形的面积是2004平方厘米，那么右图中正方形的面积是 平方厘米.20043． 有六个正方体分成两组，甲组三个正方体棱长分别为3、7、8；乙组三个正方体棱长分别为4、5、9，试用“＜”或“＞”或“＝”号连接下面式子：(1) 甲组三个正方体的表面积的和 乙组三个正方体的表面积的和； (2) 甲组三个正方体的体积的和 乙组三个正方体的体积的和. 4． 如图，外侧大正方形的边长是10厘米，图中阴影部分的面积是27.5平方厘米，那么圆内的大正方形面积是小正方形面积的 倍.5． 对于自然数n ，符号n!表示n!＝1×2×3×…×n ，例如：3！＝1×2×3＝6,5！＝1×2×3×4×5＝120，如果20！＝2432902008y7664x000，那么x-y= . 6． 大小纸盒共30只，如果每个大盒放8个甜橙，每个小盒放6个甜橙，那么还剩34个，如果每个大盒放10个甜橙，每个小盒放7个甜橙，这样会多出2个小盒子，那么甜橙共有 个. 7． 数1337,1006和1981有某些共同点，即每一个都是以1带头的四位数，且每个数恰好有两个数字相同，那么这样的四位数共有 个.8． 有一个三位数能被9整除，去掉末位数字后所得到的两位数恰是7的倍数，这样的三位数中最大的是 .9． 如图，三个大小相同的正方形重叠地放在一个大的正方形ABCD 内，已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形ABCD 的边长是 厘米.ⅢⅡⅠBD CA10.两个整数相加的和是两个数字相同的二位数aa ，并且它们的积是三个数字相同的三位数bbb ，写出所有满足条件的两个整数是 .11.如图，三角形ABC 被分成三角形BEF 和四边形AEFC 两部分，那么三角形BEF 面积和四边形AEFC 面积的比是 .5463BE CF A12.把1、2、3、…、10这十个数字分别填入下列十个空格内，每格一个数字，分别记为1210,,,a a a ，并且相邻三个数字的和不超过16，那么12345678910a a a a a a a a a a --+--+--+＝ .答案：1．1732．2254.53．(1) = (2) < 4．55．-16．2507．4328．9819．12.510. 37和18、74和311. 4:2312.13。
2010年上海市中学生业余数学学校预备年级招生试题解答
2010年上海市中学生业余数学学校预备年级招生考试1、若分数51的分子、分母各加X ，分数变成32，则X 的值是 7 。
解：（1+X ）/（5+X ）=2/3 =>3（1+X ）=2（5+X ）=>X=72、数30可以写成3个不同正整数的平方和：30=12+22+52，试将数42、46也写成3个不同正整数的平方和：42 = 52+42+12 、46 = 62+32+12 。
解：由大到小试数62=36、52=25、42=16、32=9、22=4、12=1则42 =52+42+12、46 =62+32+123、如图x ’, y ’, z ’和x, y, z 分别是三角形的三个外角和三个内角, 若x ’：y ’：z ’ =4：5：6，则x ：y ：z= 7：5：3 。
解：内角和x+y+z=180°=>(180°- x ’)+ (180°- y ’)+ (180°- z ’)=180°=> x ’+y ’+z ’=360°而x ’：y ’：z ’ = 4：5：6=> x ’=360°×4/(4+5+6)= 96°、y ’=120°、z ’=144°=> x=180°-96= 84°、y=60°、z=36°=>x ：y ：z=7：5：34、如图，一个U 形的道路，道路的宽都是3m 、周长是86m ，则它面积是 120 m 2。
解：设中间凹陷部分底宽为Y 、两边高各为X 。
则2Y+4X+18=86 => 2X+Y=34而面积S=3X+3X+3(Y+6)=3(2X+Y+6)=3×(34+6)=1205、从1到2010这2010个正整数中，能被8整除，且不能被9整除的正整数有 224 个。
解：设1到2010这2010个正整数中，能被8整除的为k 个。
上海中学生业余数学学校历年初中招生试题汇编(含答案)
上海市中学生业余数学学校历年初中招生试题汇编（含参考答案）目录01．1987年初一年级招生试题 ------------------------------------ 03 02．1988年初一年级招生试题------------------------------------- 05 03．1989年初一年级招生试题------------------------------------- 07 04．1990年初一年级招生试题--------------------------------------09 05．1991年初一年级招生试题------------------------------------- 1106．1992年初一年级招生试题------------------------------------- 13 07．1993年初一年级招生试题------------------------------------- 15 08．1994年初一年级招生试题------------------------------------- 17 09．1995年初一年级招生试题------------------------------------- 19 10．1996年初一年级招生试题------------------------------------- 21 11．1997年初中预备年级招生试题--------------------------------- 23 12．1997年初一年级招生试题------------------------------------- 25 13．1998年初中预备年级招生试题--------------------------------- 2714．1998年初一年级招生试题------------------------------------- 29 15．1999年初中预备年级招生试题--------------------------------- 3116．2000年初中预备年级招生试题--------------------------------- 3317．2001年初中预备年级招生试题--------------------------------- 3518．2002年初中预备年级招生试题--------------------------------- 3719．2003年初中预备年级招生试题--------------------------------- 3920．2004年初中预备年级招生试题--------------------------------- 4121．2005年初中预备年级招生试题--------------------------------- 4322．2006年初中预备年级招生试题--------------------------------- 4523．2007年初中预备年级招生试题--------------------------------- 4724．2008年初中预备年级招生试题--------------------------------- 4925．参考答案---------------------------------------------------- 512005年上海市中学生业余数学学校预备年级招生试题本卷满分100分（7/×4+8/×4+10/×4 =100/）1、 在平面上画一个长方形能把平面分成两个部分，如果画三个长方形，那么最多能把平面分成部分。
1999年数学一真题及答案详解
1999年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (1)2011lim()tan x x x x→-=_____________. (2)20sin()xd x t dt dx -⎰=_____________. (3)24e x y y ''-=的通解为y =_____________.(4)设n 阶矩阵A 的元素全为1,则A 的n 个特征值是 _____________.(5)设两两相互独立的三事件,A B 和C 满足条件:1,()()(),2ABC P A P B P C =∅==< 且已知9(),16P A B C =则()P A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x 是连续函数,()F x 是()f x 的原函数,则 (A)当()f x 是奇函数时,()F x 必是偶函数(B)当()f x 是偶函数时,()F x 必是奇函数(C)当()f x 是周期函数时,()F x 必是周期函数 (D)当()f x 是单调增函数时,()F x 必是单调增函数(2)设21cos 0()() 0xx f x xx g x x -⎧>⎪=⎨⎪≤⎩,其中()g x 是有界函数,则()f x 在0x =处 (A)极限不存在(B)极限存在,但不连续(C)连续,但不可导(D)可导(3)设 01()122 12x x f x x x ≤≤⎧⎪=⎨-<<⎪⎩,01()cos ,,2n n a S x a n x x π∞==+-∞<<+∞∑ 其中12()cos n a f x n xdx π=⎰ (0,1,2,)n = ,则5()2S -等于 (A)12(B)12-(C)34(D)34-(4)设A 是m n ⨯矩阵,B 是n m ⨯矩阵,则(A)当m n >时,必有行列式||0≠AB(B)当m n >时,必有行列式||0=AB(C)当n m >时,必有行列式||0≠AB(D)当n m >时,必有行列式||0=AB(5)设两个相互独立的随机变量X 和Y 分别服从正态分布(0,1)N 和(1,1)N ,则(A)1{0}2P X Y +≤= (B)1{1}2P X Y +≤=(C)1{0}2P X Y -≤=(D)1{1}2P X Y -≤=三、(本题满分6分)设(),()y y x z z x ==是由方程()z xf x y =+和(,,)0F x y z =所确定的函数,其中f 和F 分别具有一阶连续导数和一阶连续偏导数,求.dz dx四、(本题满分5分)求(e sin ())(e cos ),x x LI y b x y dx y ax dy =-++-⎰其中,a b 为正的常数,L 为从点(2,0)A a 沿曲线22y ax x =-到点(0,0)O 的弧.五、(本题满分6分)设函数()(0)y x x ≥二阶可导且()0,(0) 1.y x y '>=过曲线()y y x =上任意一点(,)P x y 作该曲线的切线及x 轴的垂线,上述两直线与x 轴所围成的三角形的面积记为1S ,区间[0,]x 上以()y y x =为曲线的曲边梯形面积记为2S ,并设122S S -恒为1,求曲线()y y x =的方程.六、(本题满分7分)论证:当0x >时,22(1)ln (1).x x x -≥-七、(本题满分6分)为清除井底的淤泥,用缆绳将抓斗放入井底,抓起污泥后提出井口(见图).已知井深30m,抓斗自重400N,缆绳每米重50N,抓斗抓起的污泥重2000N,提升速度为3m/s,在提升过程中,污泥以20N/s 的速率从抓斗缝隙中漏掉.现将抓起污泥的抓斗提升至井口,问克服重力需作多少焦耳的功?(说明:①1N ⨯1m=1Jm,N,s,J 分别表示米,牛,秒,焦.②抓斗的高度及位于井口上方的缆绳长度忽略不计.)八、(本题满分7分)设S 为椭球面222122x y z ++=的上半部分,点(,,),P x y z S π∈为S 在点P 处的切平面,(,,)x y z ρ为点(0,0,0)O 到平面π的距离,求.(,,)SzdS x y z ρ⎰⎰九、(本题满分7分)设4tan :n n a xdx π=⎰(1)求211()n n n a a n ∞+=+∑的值. (2)试证:对任意的常数0,λ>级数1nn a nλ∞=∑收敛. 十、(本题满分8分)设矩阵153,10ac b c a -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦A 其行列式||1,=-A 又A 的伴随矩阵*A 有一个特征值0λ,属于0λ的一个特征向量为(1,1,1),T =--α求,,a b c 和0λ的值.十一、(本题满分6分)设A 为m 阶实对称矩阵且正定,B 为m n ⨯实矩阵,T B 为B 的转置矩阵,试证TB AB 为正定矩阵的充分必要条件是B 的秩().r n =B十二、(本题满分8分)设随机变量X 与Y 相互独立,下表列出了二维随机变量(,)X Y 联合分布率及关于X 和关于Y 的边缘分布率中的部分数值,试将其余数值填入表中的空白处. X Y1y2y 3y()i i P X x p ∙==1x182x18 ()i j P Y y p ∙==161十三、(本题满分6分)设X 的概率密度为36() 0< ()0 其它xx x f x θθθ⎧-<⎪=⎨⎪⎩,12,,,n X X X 是取自总体X 的简单随机样本(1)求θ的矩估计量ˆθ.(2)求ˆθ的方差ˆ().D θ1999年全国硕士研究生入学统一考试数学(一)答案详解一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1) 【答】31 【详解1】 302020t a n l i m t a n t a n l i m t a n 11l i m x x x x x x x x x x x x x -=-=⎪⎭⎫⎝⎛-→→→ 313t a n l i m l i m22031s e c 022===→-→x x x xx x 【详解2】 302020c o s s i n lim sin cos sin lim tan 11lim x x x x x x x x x x x x x x x -=-=⎪⎭⎫⎝⎛-→→→ 313sin lim 3sin cos cos lim 020==+-=→→x x x x x x x x x (2)【答】 2sin x【详解】 ⎰⎰-=--x x du u dx d u t x dt t x dx d 0022)sin ()sin( 202s i n s i n x du u dx d x==⎰ 故本题应填2sin x (3)【答】 xx e x C e C y 222141⎪⎭⎫ ⎝⎛++=-，其中21,C C 为任意常数. 【详解】 特征方程为：042=-λ，解得2-,22,1==λλ.故04"=-y y 的通解为x xe C eC y 22211+=-，由于非齐次项为2,)(2==a e x f x 为特征方程的单根，因此原方程的特解可设为xAxe y 2=*，代入原方程求得41=A , 故所求解为x x x xee C e C y y y 22221141++=+=-* 故本题应填xx e x C e C y 222141⎪⎭⎫ ⎝⎛++=-，其中21,C C 为任意常数. (4)【答】10,,0,-n n【详解】 因为111111111111111---------=---------=-λλλλλλλλλn n n A E λλλ00111)(---=n 故矩阵A 的n 个特征值是n 和0（n-1重）因此本题应填10,,0,-n n(5) 【答】41 【详解】 根据加法式有())()()()()()()(ABC P BC P AB P AC P C P B P A P C B A P +---++=⋃⋃ 由题A,B 和C 两两相互独立，21)()()(,<===C P B P A P ABC φ,因此有 ),()()()(2A P BC P AC P AB P === 0)()(==φP ABC P , 从而 ()169)(3)(32=-=⋃⋃A P A P C B A P 解得 41)(,43)(==A P A P 又根据题设 41)(,21)(=<A P A P 故二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)（1）【答】 应选（A ）【详解】 )(x f 的原函数)(x F 可以表示为C dt t f x F x+=⎰)()(，于是.)()()()(0C u d u f t u C dt t f x F xx+---=+=-⎰⎰-当)(x f 为奇函数时，),()(u f u f -=-从而有)()()()(0x F C dt t f C du u f x F xx=+=+=-⎰⎰即 )(x F 为偶函数.故（A ）为正确选项，至于（B ）、（C ）、（D ）可分别举反例如下：2)(x x f =是偶函数，但其原函数131)(3+=x x F 不是奇函数，可排除（B ）； x x f 2cos )(=是周期函数，但其原函数x x x F 2sin 4121)(+=不是周期函数，可排除（C ）；x x f =)(在区间()∞∞-,内是单调增函数，但其原函数221)(x x F =在区间()∞∞-,内非单调增函数，可排除（D ）。
24621_1999年上海市高中.doc
上海市高中数学班理科班招生测试数学卷一、填空题（本大题满分80分，每小题8分）1、 已知方程ax 2+bx+c=0的两根之积为-6，bx 2+cx+a=0的两根之积为8,则cx 2+ax+b=0的两根之积为2、 图1是由一些边长是1的正方形构成，那么，此图中边长为整数的正方形共有 个3、 如图2如示，正方形BDEF 和正方形PQRS 都是等腰直角△ABC 的内接正方形，则=BDEFPQRS S S4、 已知9919+=x 是方程x 4+bx 2+c=0的根,则整数b 、c 的和b+c=5、 已知正实数x 、y 、z 满足⎪⎩⎪⎨⎧=++=++=++35158zx x z yz z y xy y x 则x+y+z+xyz=6、 如图3如示，直角△ABC 中，∠BAC=90°,M 、N 是BC上的点，BM ＝MN ＝NC ，如果AM ＝4，AN ＝3，则MN ＝ 7、 已知二次函数()c bx ax x f ++=2的系数a 、b 、c 都是整数，并且1999)99()19(==f f 1000<c ，则c ＝8、 已知实数x 、y 满足()()11122=++++y y x x ，则x+y=9、 已知质数p 既可以表示为两个质数之和,也可以表示成两个质数之差，则p= 10、 如图4如示，点D 是等腰直角△ABC 的斜边BC 上的一点，BC ＝3BD ，CE ⊥AD ，则＝CEAE二、解答题（本大题满分70分） 11、 （本题满分14分）若实数a 满足()33333421112+--a＝，试求a 的值。
图1图2图3图412、 （本题满分16分）{}n x x x ,,,21 表示一个由n 个不同的数组成的集合，仅数的排列顺序不同的集合被认为是同一个集合，例如{}{}1323,2,1，，与是同一个集合，若{}{}zx yz xy x ，，与z ,y ,是同一个集合，试证明：x 、y 、z 的乘积为1。
年上海市中学生业余数学学校预备年级招生考试及参考答案
2010年上海市中学生业余数学学校预备年级招生考试2010年上海市中学生业余数学学校预备年级招生考试【第1题】若分数15的分子、分母各加X ，分数变成23，则X 的值是_______。
【分析与解】（方法一）()()125331257X X X X X +=++=+=即X 的值是7。
（方法二）约分之前，分母比分子大514-=；分数15的分子、分母各加X ，分数的分子为()43228÷-⨯=，分母为()432312÷-⨯=；即18512X X +=+； 故X 的值是7。
【第2题】数30可以写成三个不同正整数的平方和：22230125=++试将数42，46也写成三个不同正整数的平方和： 42_____________=；46_____________=。
【分析与解】211=，224=，239=，2416=，2525=，2636=； 先考虑最大的整数的平方；经尝试，22242145=++，22246136=++。
2010年上海市中学生业余数学学校预备年级招生考试【第3题】如图，'x ，'y ，'z 和x ，y ，z 分别是三角形的三个外角和三个内角，若':':'4:5:6x y z =，则::_______x y z =。
z' y'x'yx z【分析与解】因为':':'4:5:6x y z =；所以设'4x k = ，'5y k = ，'6z k = （0k ≠）；则()180'1804x x k =-=-，()180'1805y y k =-=-，()180'1806z z k =-=-； 三角形内角和等于180 ；()()()180418051806180k k k -+-+-=； 三角形外角和等于360 ；456360k k k ++=； 24k =；84x = ，60y = ，36z = ； ::84:60:367:5:3x y z == 。
1999年全国高考上海卷数学(理工农医类)试题及答案
1999年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分.满分150分.考试时间120分钟.第I 卷（选择题共60分）一、选择题：本大题共14小题；第1～10题每小题4分，第11～14题每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的1.如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是 ( )(A) （M ∩P ）∩S (B) （M ∩P ）∪S (C) （M ∩P ）∩S(D) （M ∩P ）∪S2.已知映射f ：B A →，其中，集合{},4,3,2,1,1,2,3---=A 集合B 中的元素都是A 中元素在映射f 下的象，且对任意的,A a ∈在B 中和它对应的元素是a ，则集合B 中元素的个数是( )(A) 4(B) 5(C) 6(D) 73. 若函数()x f y =的反函数是()()0,,≠==ab b a f x g y ，则()b g 等于 ( ) (A) a(B) 1-a(C) b(D) 1-b4.函数()()()0s i n >+=ωϕωx M x f 在区间[]b a ,上是增函数，且()(),,M b f M x f =-=则函数()()ϕω+=x M x g cos 在[]b a ,上( )(A) 是增函数(B) 是减函数(C) 可以取得最大值M(D) 可以取得最小值M -5.若()x x f sin 是周期为π的奇函数，则()x f 可以是( )(A) x sin (B) x cos (C) x 2sin (D) x 2cos6.在极坐标系中，曲线⎪⎭⎫⎝⎛-=3sin 4πθρ关于 ( )(A) 直线3πθ=轴对称(B) 直线πθ65=轴对称 (C) 点⎪⎭⎫⎝⎛3,2π中心对称(D) 极点中心对称7.若干毫升水倒入底面半径为cm 2的圆柱形器皿中，量得水面的高度为cm 6，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是( )(A) cm 36 (B) cm 6(C) cm 3182(D) cm 31238.若(),32443322104x a x a x a x a a x ++++=+则()()2312420a a a a a +-++的值为( )(A) 1(B) －1(C) 0(D) 29.直线0323=-+y x 截圆422=+y x 得的劣弧所对的圆心角为 ( )(A)6π (B)4π (C)3π (D)2π 10.如图，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，EF ∥AB ，EF 23=，EF 与面AC 的距离为2，则该多面体的体积为( )(A)29 (B) 5 (C) 6 (D)215 11.若,22sin ⎪⎭⎫ ⎝⎛<<->>παπαααctg tg 则∈α( )(A) ⎪⎭⎫⎝⎛--4,2ππ (B) ⎪⎭⎫⎝⎛-0,4π (C) ⎪⎭⎫⎝⎛4,0π (D) ⎪⎭⎫⎝⎛2,4ππ 12.如果圆台的上底面半径为5，下底面半径为R ，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1：2，那么R =( )(A) 10(B) 15(C) 20(D) 2513.已知两点,45,4,45,1⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛N M 给出下列曲线方程：①0124=-+y x ②322=+y x ③1222=+y x ④1222=-y x 在曲线上存在点P 满足|MP |=|NP |的所有曲线方程是 ( )(A) ①③(B) ②④(C) ①②③(D) ②③④14.某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有( )(A) 5种(B) 6种(C) 7种(D) 8种第II 卷（非选择题共90分）二．填空题：本大题共4小题；每小题4分，共16分，把答案填在题中横线上.15.设椭圆()012222>>=+b a by a x 的右焦点为1F ，右准线为1l ，若过1F 且垂直于x 轴的弦长等于点1F 到1l 的距离，则椭圆的率心率是_____16.在一块并排10垄的田地中，选择2垄分别种植A 、B 两种作物，每种作物种植一垄，为有利于作物生长，要求A 、B 两种作物的间隔不小于6垄，则不同的选垄方法共有___________种（用数字作答）17.若正数a 、b 满足,3++=b a ab 则ab 的取值范围是______________18.α、β 是两个不同的平面，m 、n 是平面α及β 之外的两条不同直线，给出四个论断：①m ⊥n②α⊥β③n ⊥β④m ⊥α以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个．．命题：________________________________三、解答题：本大题共6小题；共74分，解答应写出文字说明、证明过程或演算步骤.19.（本小题满分10分）解不等式()1,01log 22log 3≠>-<-a a x x a a20.（本小题满分12分）设复数.sin 2cos 3θθ⋅+=i z 求函数⎪⎭⎫ ⎝⎛<<-=20arg πθθz y 的最大值以及对应的θ值.21.（本小题满分12分）如图，已知正四棱柱1111D C B A ABCD -，点E 在棱D D 1上，截面EAC ∥B D 1，且面EAC 与底面ABCD 所成的角为.,45a AB =Ⅰ.求截面EAC 的面积；Ⅱ.求异面直线11B A 与AC 之间的距离； Ⅲ.求三棱锥EAC B -1的体积. 22.（本小题满分12分）右图为一台冷轧机的示意图.冷轧机由若干对轧辊组成，带钢从一端输入，经过各对轧辊逐步减薄后输出.Ⅰ.输入带钢的厚度为α，输出带钢的厚度为β，若每对轧辊的减薄率不超过0r .问冷轧机至少需要安装多少对轧辊？（一对轧辊减薄率输入该对的带钢厚度从该对输出的带钢厚度输入该对的带钢厚度-=）Ⅱ.已知一台冷轧机共有4对减薄率为20%的轧辊，所有轧辊周长均为1600.mm 若第k 对轧辊有缺陷，每滚动一周在带钢上压出一个疵点，在冷轧机输出的带钢上，疵点的间距为.k L 为了便于检修，请计算1L 、2L 、3L 并填入下表（轧钢过程中，带钢宽度不变，且不考虑损耗）.23.（本小题满分14分）已知函数()x f y =的图像是自原点出发的一条折线，当(),2,1,01=+≤≤n n y n时，该图像是斜率为nb 的线段（其中正常数1≠b ），设数列n x 由()(),2,1==n n x f n 定义.Ⅰ.求1x 、2x 和n x 的表达式；Ⅱ.求()x f 的表达式，并写出其定义域；Ⅲ.证明：()x f y =的图像与x y =的图像没有横坐标大于1的交点. 24.（本小题满分14分）如图，给出定点()()00,>a a A 和直线B x l .1:-=是直线l 上的动点，BOA ∠的角平分线交AB 于点C .求点C 的轨迹方程，并讨论方程表示的曲线类型与a 值的关系.1999年普通高等学校招生全国统一考试数学试题（理工农医类）参考解答一、选择题（本题考查基础知识和基础运算）.1. C2. A3. A4. C5. B6. B7. B8. A9. C10. D 11.B12. D13.D14. C二、填空题（本题考查基本知识和基本运算）.15.2116. 12 17. [)+∞,9 18. n m n m ⊥⇒⊥⊥⊥βαβα,,或βαβα⊥⇒⊥⊥⊥n m n m ,,三、解答题19. 本小题主要考查对数函数的性质、对数不等式、无理不等式解法等基础知识，考查分类讨论的思想.解：原不等式等价于()⎪⎩⎪⎨⎧>--<-≥-.01log 2,1log 22log 3,02log 32x x x x a a a a 由①得,32log ≥x a 由②得,43log <x a 或1log >x a ， 由③得.21log >x a由此得,43log 32<≤x a 或.1log >x a当1>a 时得所求的解是{}a x x a x a x >⎭⎬⎫⎩⎨⎧≤≤||4332 ； 当10<<a 时得所求的解是① ② ③{}.0||3243a x x a x a x <<⋃⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤< 20.本小题主要考查复数的基本概念、三角公式和不等式等基础知识，考查综合运用所学数学知识解决问题的能力.解：由20πθ<<得.0>θtg由θθsin 2cos 3i z +=得2arg 0π<<z 及().32cos 3sin 2arg θθθtg tg ==z故 ()z y arg -=θtg tgθθθ232132tg tg tg +-= ,231θθtg tg +=因为,6223≥+θθtg tg 所以.126231≤+θθtg tg 当且仅当⎪⎭⎫ ⎝⎛<<=2023πθθθtg tg 时，即26=θtg 时，上式取等号. 所以当26arctg=θ时，函数y tg 取得最大值.126由z y arg -=θ得.2,2⎪⎭⎫ ⎝⎛-∈ππy 由于在⎪⎭⎫⎝⎛-2,2ππ内正切函数是递增函数，函数y也取最大值.126arctg21.本小题主要考查空间线面关系、二面角和距离的概念，逻辑思维能力、空间想象能力及运算能力.Ⅰ. 解：如图，连结BD 交AC 于O ，连结EO 因为底面ABCD 是正方形， 所以DO ⊥AC又因为ED ⊥底面AC ， 因为EO ⊥AC所以∠EOD 是面EAC 与底面AC 所成二面角的平面角. 所以， 45=∠EOD.45sec 22,2,22a a EO a AC a DO =⋅===故.222a S EAC =∆ II. 解：由题设1111D C B A ABCD -是正四棱柱，得A A 1⊥底面AC ，A A 1⊥AC ， 又A A 1⊥,11B A所以A A 1是异面直线11B A 与AC 间的公垂线. 因为11B D ∥面EAC ，且面BD D 1与面EAC 交线为EO 所以11B D ∥EO 又O 是DB 的中点，所以E 是D D 1的中点，11B D =2EO =2a 所以D D 1.2221a DB B D =-=异面直线11B A 与AC 间的距离为.2a Ⅲ. 解法一：如图，连结11B D 因为D D 1=DB =.2a 所以11B BDD 是正方形，连结D B 1交B D 1于P ，交EO 于Q 因为D B 1⊥B D 1，EO ∥B D 1， 所以D B 1⊥EO 又AC ⊥EO ，AC ⊥ED 所以AC ⊥面11B BDD ， 所以D B 1⊥AC ， 所以D B 1⊥面EAC .所以Q B 1是三棱锥EAC B -1的高. 由DQ =PQ ，得.234311a D B Q B == 所以.42232231321a a a V EAC B =⋅⋅=- 所以三棱锥EAC B -1的体积是.423a 解法二：连结O B 1，则112EO B A EAC B V V --= 因为AO ⊥面11B BDD ，所以AO 是三棱锥1EOB A -的高，AO .22a =在正方形11B BDD 中，E 、O 分别是D D 1、DB 的中点（如右图），则.4321a S EOB =∆ ∴.422243312321a a a V EAC B =⋅⋅⋅=- 所以三棱锥EAC B -1的体积是.423a 22. 本小题主要考查等比数列、对数计算等基本知识，考查综合运用数学知识和方法解决实际问题的能力.Ⅰ.解：厚度为α的带钢经过减薄率均为0r 的n 对轧辊后厚度为().10nr a -为使输出带钢的厚度不超过β，冷轧机的轧辊数（以对为单位）应满足()β≤-nr a 01即().10ar nβ≤- 由于(),0,010>>-ar nβ对比上式两端取对数，得().lg1lg 0ar n β≤-由于(),01lg 0<-r 所以().1lg lg lg 0r an --≥β因此，至少需要安装不小于()01lg lg lg r a--β的整数对轧辊.Ⅱ. 解法一：第k 对轧辊出口处疵点间距离为轧辊周长，在此处出口的两疵点间带钢体积为()⋅-⋅kr a 11600宽度(),%20=r 其中而在冷轧机出口处两疵点间带钢的体积为()⋅-⋅41r a L k 宽度.因宽度相等，且无损耗，由体积相等得()=-⋅kr a 11600()41r a L k -⋅ (),%20=r即.8.016004-⋅=k k L由此得(),20003mm L = (),25002mm L = ()mm L 31251= 填表如下 轧锟序号k1234疵点间距k L （单位：mm ）3125 2500 2000 1600解法二：第3对轧辊出口处疵点间距为轧辊周长，在此处出口的两疵点间带钢体积与冷轧机出口处两疵点间带钢体积相等，因宽度不变，有(),2.0116003-⋅=L所以().20008.016003mm L == 同理(),25008.032mm LL ==().31258.021mm LL ==填表如下 轧锟序号k1 2 3 4 疵点间距k L （单位：mm ）312525002000160023.本小题主要考查函数的基本概念、等比数列、数列极限的基础知识，考查归纳、推理和综合的能力.Ⅰ.解：依题意()00=f ，又由()11=x f ，当10≤≤y 时，函数()x f y =的图像是斜率为10=b 的线段，故由()()10011=--x f x f 得.11=x又由()22=x f ，当21≤≤y 时，函数()x f y =的图像是斜率为b 的线段，故由()()b x x x f x f =--1212，即b x x 112=-得.112b x += 记.00=x 由函数()x f y =图像中第n 段线段的斜率为1-n b，故得()().111---=--n n n n n b x x x f x f 又()()1,1-==-n x f n x f n n ； 所以 .2,1,111=⎪⎭⎫ ⎝⎛=---n b x x n n n由此知数列{}1--n n x x 为等比数列，其首项为1，公比为.1b因,1≠b 得(),111111111-⎪⎭⎫ ⎝⎛-=+++=-=--=-∑b b b b b x x x n n nk k k n即.111-⎪⎭⎫⎝⎛-=-b b b x n nⅡ. 解：当10≤≤y ，从Ⅰ可知,x y =当10≤≤x 时，().x x f = 当1+≤≤n y n 时，即当1+≤≤n n x x x 时，由Ⅰ可知()()().3,2,1,1 =≤≤-+=+n x x x x x b n x f n n n n为求函数()x f 的定义域，须对() ,3,2,1111=-⎪⎭⎫ ⎝⎛-=-n b b b x n n 进行讨论.当1>b 时，111limlim 1-=-⎪⎭⎫ ⎝⎛-=-∞→∞→b bb b b x n n n n ； 当10<<b 时，n x n ,∞→也趋向于无穷大. 综上，当1>b 时，()x f y =的定义域为⎪⎭⎫⎢⎣⎡-1,0b b ； 当10<<b 时，()x f y =的定义域为[)+∞,0. Ⅲ. 证法一：首先证明当1>b ，11-<<b bx 时，恒有()x x f >成立. 用数学归纳法证明：（ⅰ）由Ⅱ知当1=n 时,在(]2,1x 上, ()(),11-+==x b x f y 所以()()()011>--=-b x x x f 成立（ⅱ）假设k n =时在(]1,+k k x x 上恒有()x x f >成立. 可得 (),111++>+=k k x k x f在(]21,++k k x x 上,()().111++-++=k k x x b k x f 所以 ()()x x x b k x x f k k --++=-++111()()()011111>-++--=+++k k k x k x x b 也成立.由(ⅰ)与(ⅱ)知,对所有自然数n 在(]1,+n n x x 上都有()x x f >成立. 即 11-<<b bx 时,恒有()x x f >. 其次，当1<b ,仿上述证明,可知当1>x 时,恒有()x x f <成立. 故函数()x f y =的图像与x y =的图像没有横坐标大于1的交点. 证法二:首先证明当1>b ,11-<<b bx 时,恒有()x x f >成立. 对任意的,1,1⎪⎭⎫ ⎝⎛-∈b b x 存在n x ,使1+≤<n n x x x ，此时有()()()(),10≥->-=-n x x x x b x f x f n n n所以()().n n x x f x x f ->- 又(),1111n n n x bb n x f =+++>=- 所以()0>-n n x x f ，所以()()0>->-n n x x f x x f ， 即有()x x f >成立.其次，当1<b ，仿上述证明，可知当1>x 时，恒有()x x f <成立. 故函数()x f 的图像与x y =的图像没有横坐标大于1的交点.24. 本小题主要考查曲线与方程，直线和圆锥曲线等基础知识，以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力.解法一：依题意，记()(),,1R ∈-b b B 则直线OA 和OB 的方程分别为0=y 和.bx y -=设点()y x C ,，则有a x <≤0，由OC 平分∠AOB ，知点C 到OA 、OB 距离相等.根据点到直线的距离公式得.12bbx y y ++=①依题设，点C 在直线AB 上，故有().1a x aby -+-= 由0≠-a x ，得().1ax y a b -+-= ②将②式代入①式得()()(),11122222⎥⎦⎤⎢⎣⎡-+-=⎥⎦⎤⎢⎣⎡-++a x xy a y a x y a y 整理得()()[].0121222=++--y a ax x a y 若0≠y ，则()()()a x y a ax x a <<=++--0012122；若0=y ，则π=∠=AOB b ,0，点C 的坐标为（0，0），满足上式. 综上得点C 的轨迹方程为()()()a x y a ax x a <≤=++--0012122（ⅰ）当1=a 时，轨迹方程化为().102<≤=x x y ③此时，方程③表示抛物线弧段； （ⅱ）当1≠a 时，轨迹方程化为()a x a a y a a a a x <≤=-+⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛--0111122222④ 所以，当10<<a 时，方程④表示椭圆弧段； 当1>a 时，方程④表示双曲线一支的弧段.解法二：如图，设D 是l 与x 轴的交点，过点C 作CE ⊥x 轴，E 是垂足. （ⅰ）当| BD |≠0时，设点C （x ，y ），则.0,0≠<<y a x由CE ∥BD 得().1a xa y EADA CE BD +-=⋅=因为∠COA =∠COB=∠COD －∠BOD =π－∠COA －∠BOD ，所以2∠COA =π－∠BOD 所以(),1222COACOACOA ∠-∠=∠tg tg tg()BOD BOD ∠-=∠-tg tg π因为,xy COA =∠tg().1a xa y ODBD BOD +-==∠tg所以(),11222a x a y xy x y+--=-⋅整理得()()().0012122a x y a ax x a <<=++--（ⅱ）当| BD | = 0时，∠BOA =π，则点C 的坐标为（0，0），满足上式. 综合（ⅰ），（ⅱ），得点C 的轨迹方程为()()().0012122a x y a ax x a <≤=++--以下同解法一.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 1 1 2
2 3
2
2 3 4
1 是 48 6
14、某同学买某种铅笔， 当他买了 a 支， 付了 b 元(a、 b 都是整数)。 6 营业员说： “你要再多买 10 支，我就总共收你 2 元钱，这样相 当于每买 30 支，你就节省 2 元钱” 。那么 a= 5 支，b= 1 元 解：∵a、b 都是整数，∴b=1 D 由题意得：
分母为 24 的正的既约真分数一共有 7、 一个长方体，表面全部涂上红色后，被分割成若干个体积都等于 1 立方厘米的小正方体，如果在这 些小正方体中，不带红色的小正方体的个数等于 7，那么两面带红色的小正方体的个数等于 36 解：不带红色的小正方体的个数等于 7，说明这个长方体是 3×3×9 的长方体 那么两面带红色的小正方体的个数等于 28+4+4=36 8、 从 100 到 999 这 900 个自然数中， 使得每一数中的一个数码是另外两个数码的平均数， 那么这样的 三位数共有 112 解：因为一个数码是另外两个数码的平均数，则这三个数码可分类如下： 0、2、1；0、4、2；0、6、3；0、8、4；1、3、2；1、5、3；1、7、4；1、9、5 2、4、3；2、6、4；2、8、5；3、5、4；3、7、5；3、9、6； 4、6、5；4、8、6；5、7、6；5、9、7；6、8、7；7、9、8。 那么这样的三位数共有：16×6+4×4=112 个 9、 图中的四边形 ABCD 被 AC 和 BD 分成甲、乙、丙、丁四个三角形，如果 AE=80，BE=60，CE=40， DE=30，那么丙、丁二个三角形面积和是甲、乙二个三角形面积和的 解：S 甲：S 丁=80：40=2：1；S 乙：S 丁=60：30=2：1 ∴S 甲=2 S 丁，S 乙=2 S 丁 S 丙：S 甲=60：30=2：1 ∴S 丙=2S 甲=4 S 丁
4、 在 5、6、7、8、9、10 这六个数字之间分别填上加减乘除四则运算符号，并允许添括号，但不改变 数的顺序，使最后结果为 2000，这样的算式可以是 5×[6×(7×8+9)+10]=2000 5、 边长分别是 6、7、9、10、11、14 的等角六边形 ABCDEF，内接于一个边长为 30 的等边三角形中， 如图所示，同样，这个等角六边形也能内接于另一个边长为 n 的等边三角形中，n≠30，那么 n= 27 解：如图，这个等角六边形也能 9 内接于另一个边长为 27 的等边三 B A 7 角形。 7
F 11 14 9
14
C 10 E 6 D 6 10
11
6、 8 个互不相等的分数，其中每 7 个的和都是分母为 24 的正的既约真分数(分子与分母的最大公约数 是 1 的真分数)，那么这 8 个分数的和是
4 7
解：设 8 个互不相等的分数分别是 a1、a2、a 3、a 4、a 5、a 6、a 7、a 8
3、 如果正整数 n，使得 整数 n 有 解： 8
n + 17 也是正整数，那么这样的正 n−7
个。
24 n + 17 n − 7 + 24 = = 1+ n−7 n−7 n−7 n + 17 也是正整数，则 n-7 必须是 24 的约数，即 n-7=1、2、3、4、6、8、12、24，共 8 个 要使 n−7
1 5 7 11 13 17 19 23 , , , , , , , 8个 24 24 24 24 24 24 24 24 1 5 7 11 13 17 19 23 96 则 7×(a1+a2+a 3+a 4+a 5+a 6+a 7+a 8)= + + + + + + + = =4 24 24 24 24 24 24 24 24 24 4 a1+a2+a 3+a 4+a 5+a 6+a 7+a 8= ∴ 7
12
16
C
b 2 1 1 + a ) 2，即 − × (10= + a) 2 − × (10= a 30 a 15
可得：a=5 15、 游客在 10 时 15 分由码头划船出游， 要求在当天不迟于 13 时返回， 已知河水流速为 1.4 千米/小时， 且水流是流向码头的，船在静水中的速度为 3 千米/小时，如果他每划 30 分钟就休息 15 分钟，中途不 改变方向，且只能在某次休息后往回划，那么他最多能划离码头 1.7 千米。
2、 ABCD 是一个正方形，它是由 4 个小正方形所组成的， E 和 F 分别是 AD 和 AB 的中点，如果△EFC 的面积是 54，那么 AB= 12 解：设小正方形面积是 S，则大正方形面积是 4S △EFC 的面积是 4S-2 S-0.5 S=1.5 S ∴ 1.5 S=54，∴ S=36 ∴ 4S=36×4=144 从而 AB=12
10 x + y 9x = 1+ x+ y x+ y
因为求最大可能的余数，所以从最大的 99÷18 开始 算，也即 81÷18 开始算 81÷18 余数是 9，81÷17 余数是 13，72÷17 余数是 4，72÷16 余数是 8，81÷16 余数是 1 63÷16 余数是 15 往下就不要算了， 所以所得的最大可能 B A 的余数是 15。 13、一个矩形 ABCD 被分割成九个小矩形，且这些小矩形的面积 如图所示，那么矩形 ABCD 的面积
1999 年上海市中学生业余数学学校预备年级招生试题解答
1、 数列
1 1 1 1 a + + +L + + L 的前 60 项的和是 ，其中 a 和 b 是互质的正 2 × 3 3× 4 4 × 5 b ( n + 1) × ( n + 2 )
46
整数，那么 a+b=
1 1 1 1 1 1 1 1 1 1 1 1 解： + + +L + = − + − + − +L + − 2 × 3 3× 4 4 × 5 61× 62 2 3 3 4 4 5 61 62 1 1 30 15 ∴ a+b=46 = − = = 2 62 62 31
5 4
D 30 甲 80
倍。
C 丁 E 丙 40 乙 60
S 丙+ S 丁=4 S 丁+ S 丁=5 S 丁 S 甲+ S 乙=2 S 丁+2 S 丁=4 S 丁 ∴丙、 丁二个三角形面积和是甲、 乙二个三角形面 5 积和的 4
10、数 1919 19 除以 6 所得的余数是 14 2L43
100 个19
而 19 除以 6 所得的余数也是 1，∴ 1919 19 除以 6 所得的余数是 1。 14 2L43
100 个19
11、从 0，1，2，…依次一直写到 1000000，那么这些数的所有数码的和是 27000001
解： 12、如果一个两位数除以它的各位数字的和，那么所得的最大的余数可能是 解：设这个两位数为 10x+y，则 15
A
B
1
解： 1919 19 = 19 × 1 + 102 + 104 + L + 102×99 14 2L43
100 个19
(
)
∵ 10 、 10 、 L 、得的余数都是 4
2×99
∴ 1 + 10 + 10 + L + 10
除以 6 所得的余数就是 1+4×99=397 除以 6 所得的余数，是 1