耦合连续BVP振子中的分支现象
基于新耦合Duffing振子系统的微弱信号检测

基于新耦合Duffing振子系统的微弱信号检测
陈大全;贾美美;李娜
【期刊名称】《内蒙古工业大学学报:自然科学版》
【年(卷),期】2022(41)2
【摘要】为解决传统Duffing振子随机共振微弱信号检测效果较差的问题,提出新耦合Duffing振子随机共振微弱信号检测方法,通过构造一个新颖的非线性耦合形式将两个传统Duffing振子耦合在一起,并且以输出信噪比作为随机共振检测效果的评价指标,研究了各参数对输出信噪比的影响。
在输出信噪比最大时确定了参数选取的范围,然后把相关参数代入该随机共振模型中进行微弱信号检测。
同时将轴承外圈故障信号分别输入到传统Duffing振子随机共振和耦合Duffing振子随机共振模型中,通过对比发现,新耦合Duffing振子随机共振模型对轴承外圈故障信号的检测效果更优,为新耦合Duffing振子随机共振模型在实际工程中的应用提供了参考和依据。
【总页数】9页(P150-158)
【作者】陈大全;贾美美;李娜
【作者单位】内蒙古工业大学电力学院;内蒙古自治区机电控制重点实验室
【正文语种】中文
【中图分类】TN911.23
【相关文献】
1.基于耦合Duffing振子和Van der pol振子系统的微弱信号检测研究
2.基于耦合Duffing振子的微弱故障信号检测
3.基于耦合Duffing振子和Vanderpol振子系统的微弱信号检测研究
4.基于强耦合Duffing振子的微弱脉冲\r信号检测与参数估计
5.基于改进双耦合Duffing振子的微弱信号检测方法
因版权原因,仅展示原文概要,查看原文内容请购买。
【国家自然科学基金】_耦合不动点_基金支持热词逐年推荐_【万方软件创新助手】_20140729
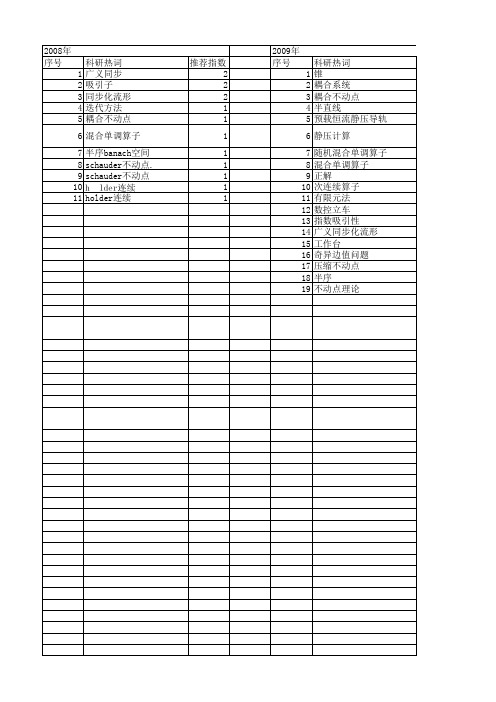
科研热词 推荐指数 迭代算法 2 稳定性 2 收敛性 2 可解性 2 sonnier-christov格式 2 非线性耦合schr(o)dinger方程 1 非线性耦合 1 非线性动力学模型 1 非定常流动 1 自由边界问题 1 肿瘤生长 1 耦合运动 1 耦合不动点 1 正解 1 格混合单调算子 1 整体解 1 向量格 1 动稳定性 1 凹函数 1 全局亚迭代 1 不动点指数 1 1 n阶常微分方程组 1 jensen不等式 1
科研热词 锥 耦合系统 耦合不动点 半直线 预载恒流静压导轨 静压计算 随机混合单调算子 混合单调算子 正解 次连续算子 有限元法 数控立车 指数吸引性 广义同步化流形 工作台 奇异边值问题 压缩不动点 半序 不动点理论
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
2011年 科研热词 推荐指数 离散 2 混沌 2 驱动系统 1 非线性系统 1 随机动力系统 1 重要课题 1 讨论系统 1 耦合离散bvp振子 1 耦合不动点 1 耦合 1 第二类不动点 1 稳定平衡 1 离散耦合logistic模型 1 混沌跟踪控制 1 数值模拟 1 振子 1 弱压缩多值映射 1 广义同步 1 子电路模型 1 周期解 1 单向耦合 1 半正 1 分支图 1 分支 1 共生作用 1 偏序完备度量空间 1 不动点问题 1 不动点 1 一阶非自治奇异耦合方程组 1 schauder不动点定理 1 schauder 1 lyapunov指数 1
南京大学物化实验系列BZ振荡反应

K1 [BrO3-][ H+]。 K2
BrO3- + HBrO2 + H+
K3
2BrO2 + H2O (3) Ce4+ (K4=快速) (4)
(K3 = 1×10 4mol-2.L6.s-1 , 250C ) BrO2 + Ce3+ + H+ 2HBrO2
K5 K4
HBrO2 +
BrO3- + HOBr + H+ (5)
K3 - [BrO3-] = 5×10 6 [BrO3-] K2
K6
Br-的再生可通过下列步骤实现:
4Ce4+ + BrCH(COOH)2 +H2O + HOBr
该体系的总反应是:
2 Br- + 4 Ce3+ + 3CO2 + 6 H+
(6)
2H+ + 2 BrO3- + 3CH2(COOH)2
2 BrCH(COOH)2 + 3CO2 +4 H2O
曾经提出过不少模型来研究化学振荡的反应机理,下面介绍洛特卡(Lotka)-沃尔特 拉(Voltella)的自催化模型。
2X (1) A+X 2Y (2) X+Y E (3) Y
k3 k2
k1
d [ A] =k1[A][X] dt d[ X ] r2=- =k2[X][Y] dt d[E] r3= = k3[Y] dt
r1=-
E。对这一组微分方程求解得: 其净反应是 A
k2[X]-k3ln[X]+ k2[Y]+ k1[A]ln[Y]=常数 这一方程的具体解可用两种方法表示,一种是用[X]和[Y]对 t 作图,如图 1,其浓度随时间 呈周期性变化;另一种是以[X]对[Y],得反应轨迹曲线,如图 2,为一封闭椭圆曲线。反应 轨迹曲线为封闭曲线,则 X 和 Y 的浓度就能沿曲线稳定地周期变化,反应变呈振荡现象。
热连轧机耦合振动现象特征研究

某 2050热连轧机在轧制薄规格、高强钢等难 度较大成品时,F2/F3轧机振动表现强烈。实际 生产中曾尝试采用延长在炉时间、提高烧钢温度、 精轧段减少开水、投用轧制润滑、增加换辊频次等 措施,对轧机振动有所缓解,但无法在根源上消除 振动。为了更加准确描述轧机振动现象,研制了 热连轧机耦合振动在线监测系统,以准确捕捉轧
采用 Solidworks三维建模软件对 2050热连轧 机 F1-F3轧机主传动系统和垂直系统进行三维 建模,将其导入到 ANSYSWorkbench有限元仿真 平台中,采用模态叠加法对模型进行模态分析与 谐响应分析,从而求解得到热连轧机固有动力学 特性,获得的热连轧 F1-F3轧机的主传动的固有 频率如表 2所示。
① 作者简介:王成镇,男,1973年生,高级工程师,北京科技大学控制工程专业,邮箱:wcz007_2022@163.com
— 8—
王成镇等:热连轧机耦合振动现象特征研究
2024年 2月第 1期
机耦合振动状态,为理论研究轧机振动机理提供 科学数据。 2 2050热连轧产线简介
某公司 2050mm热连轧机,引进 SMS机械工艺 和 TMEIC自动化技术,于 2017年投产,工艺布置如 图 1所示,主要由加热炉、除鳞机、调宽压力机、一 架二辊可逆粗轧机 R1、一架四辊可逆粗轧机 R2、七 机架四辊精轧连轧机组 F1~F7、超快冷 +层流冷 却系统、热 轧 卷 取 机 和 平 整 机 等 设 备 组 成。采 用 SMS公 司 PCFC板 形 控 制 系 统 CVC辊 形,液 压 AGC控制、液压弯辊及液压活套等控制技术,精轧 F1~F2、F3~F4和 F5~F7分别采用不用的工作辊 CVC辊形曲线。主要产品厚度范围为 2.5mm~ 25mm,主要宽度范围为 1050mm~1900mm,主要产 品为供冷轧材 DC系列深冲钢品种、强度为 235MPa ~980MPa热轧碳素结构钢和高强钢板等,2050mm 热连轧产线是该基地重要生命线。
复旦大学模拟电路二级运放实例

udan
专用集成电路与系统国家重点实验室
RFIC
整理者
版本号 1.0
日期 2007.10.10
说明 详细介绍二级运放原理和设计仿真, 供新手 入门参考
尹睿
版权所有,不得侵犯!传播与修改请保留版权信息。
目录
1 2 引言 ..................................................................................................................... 1 电路分析 .............................................................................................................. 2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 3 3.1 3.2 3.3 3.4 电路结构 ....................................................................................................... 2 电路描述 ....................................................................................................... 2 静态特性 ....................................................................................................... 3 频率特性 ....................................................................................................... 5 相位补偿 ....................................................................................................... 7 调零电阻 ....................................................................................................... 7 偏置电路 ..................................................................................................... 10 共模输入范围 .............................................................................................. 13 输出动态范围 .............................................................................................. 13 单位增益带宽(GBW) .............................................................................. 14 输入失调电压 .............................................................................................. 14
压电振子特性与支撑方式分析知识分享

压电振子特性与支撑方式分析压电振子特性与支撑方式分析压电振子的振动模式压电振子[X50-52}是压电驱动器的核心部件,起着将电能转换为机械能的作用。
某一几何尺寸的振子在特定条件(按所需方向极化、激励和设置电极等)下,其用以完成机械能和电能相互转换的振动方式多种多样,通常把这种振动方式称为振动模态。
此外,各种振动模态之间还存在着相互影响或藕合作用。
因此在设计压电振子时,除了选择合适的压电陶瓷材料外,还要选择合适的振子及其振动模态。
通常将压电陶瓷激发的振动分成以下四类,如上图所示。
(a)垂直于电场方向的伸缩振动(长度方向),用LE模表示;(b)平行于电场方向的伸缩振动(厚度方向),用TE模表示;(c)垂直于电场平面内的剪切振动(表面),用FS模表示;(d)平行于电场平面内的剪切振动(厚度),用TS模表示。
当这些振动模式作用到压电振子上时,将能产生弯曲振动、伸缩振动和扭转振动。
压电驱动器为了形成所需运动形式,通常使用这四种振动形式中的两种或一种,使两个以上方向的振动加以组合以达到目的。
按照所加电场与弹性波传播方向之间的关系,压电振动又可分为纵向效应和横向效应两大类。
当弹性波的传播方向平行于电场方向时称为纵向效应;当弹性波的传播方向垂直于电场方向时称为横向效应。
骨传导所采用的复合压电振子的振动模态为LE伸缩振动。
压电振子的谐振特性将施加到压电振子上电信号的频率从低频慢J漫地升到高频时,可以发现,通过压电振子的电流随电信号频率的变化而变化[[53-54]。
当电信号频率为某一频率时,电流出现极大值;当电信号频率变化到另一频率时,电流出现极小值。
压电振子的电流随频率而变化这一事实,也表明压电振子的等效阻抗Z随频率也发生变化,如图2.6所示。
图中,IZI代表阻抗的绝对值。
当电信号频率等于几时,压电振子的电流最大而阻抗最小;当电信号频率等于fn时,压电振子电流最小而阻抗最大。
因此,通常称fm为最小阻抗频率或最大导纳频率(导纳=1}阻抗);,fn称为最大阻抗频率或最小导纳频率。
工程振动测试技术_天津大学中国大学mooc课后章节答案期末考试题库2023年

工程振动测试技术_天津大学中国大学mooc课后章节答案期末考试题库2023年1.阻抗头的主要用途是测。
参考答案:原点传递函数2.关于主振型矩阵和正则振型矩阵的关系是()。
参考答案:将主振型矩阵的各列除以其对应主质量矩阵元素的平方根,得到的振型就是正则振型3.一般来说,对于同一个振动系统来说,工程振动的特点是( )。
参考答案:振动频率低,振幅较大。
振动频率高,振幅较小4.机械振动是指物体在其稳定的平衡位置附近所做的()运动。
参考答案:往复5.在做模态实验时,只需要测得传递函数的就可以获得全部模态信息。
参考答案:一行或一列6.在实验过程中,已知振动信号中的频率信号分别为15Hz、30Hz、60Hz、130Hz、180Hz利用小波变换将其进行分解,若选取采样频率为400Hz,两个频率信号无法分开。
参考答案:130Hz和180Hz7.微分电路中RC的应用范围为。
(其中T为输入电压的时间周期)参考答案:小于0.1T8.关于压电式加速度传感器的频率特性,以下说法正确的是。
参考答案:其灵敏度在固有频率附近会发生急剧变化9.振动系统按运动微分方程形式分为线性和()两种形式。
参考答案:非线性10.关于多自由度系统振动问题的求解方法,下列说法错误的是()。
参考答案:根据单自由度系统的求解理论和方法,求得用主坐标和正则坐标表示的响应就结束了11.在建立单自由度弹簧—质量系统的运动微分方程时,当选择物块的静平衡位置为坐标原点,假设x轴方向垂直向下,则物块的位移、速度和加速度方向如何确定()。
参考答案:都垂直向下12.在有阻尼系统的衰减振动中,【图片】黏性阻尼系数,【图片】为系统的固有圆频率,【图片】为系统的质量,【图片】,其中【图片】称为衰减系数,下面关于【图片】和【图片】的说法错误的是()。
参考答案:时,称系统处于小阻尼的情形,此时物块在平衡位置附近做往复运动,具有振动的性质,振幅仍然是常数13.一般的多自由度振动系统(正定系统)中,n个固有频率互不相等,其中第一阶固有圆频率的含义是()。
离散的改进型BVP振子混沌行为研究

{ (b 【1 .y 夕 -x ) :(7p c 口2 =-+ 一 ) 0 y - f
其 中 厂 z 是 的三 次多项式 , , n b均为 常数. () l , , D
( … 1 )
( 2 ) ( 3 )
J 专。 z 。
【一 (一z b) 9 p口 — v
综合 以上 两个模 型 , 通过对 z的三次 项进 行重构 可得 改进 型 B VP模 型如 下
J
l 一 I Ⅱ z一 6 D 一 ( )
按 E lr ue 方法 将系统 离散 化 , 通过理 论分 析后 , 现存在 复杂 的动 力学 行 为 , 发 如周 期轨 ( 周期 轨 ) 拟 , 倍周 期分 岔 , rt Maot 沌 的存 在 , o混 并利 用 Malb进行 数值 模拟 , 出 了分 岔图 、 图和 L a u o t a 画 相 y p n v指 数 图 , 证 了理论分 析 的结果 , 验 并且 从直 观上 展现模 型 的复杂 的动 力学行 为 .
( )F( ) a S mS;b 任 意 X, () y∈S 且 X≠y, l u X) y)> 0 ( ) 意 y∈S和 方程 , 有 i p F ( 一F ( ms ;c任
"一 x)
( ) 任意一 个周 期点 Z, l u I ” Z 一P ( l ; 4的 有 i pF ( ) ms y) >0
图 1 所示 . 1 a 是在 ∈( . 6 10 的分岔 图 , 过部分 的放 大可 以得 到 图( ) 图 () 0 7 ,. ) 通 1 b和图 1 c . 1 b是 () 图( ) 在 ∈( . 2 0 8 ) 0 8 ,. 4 的放 大 图 , 1 c 是 在 ∈( . 0 ,. 6 ) 图 () 0 9 59 0 9 14 的放 大 图.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
) 一
l ), —2 () 1
2一 。
-
)+ , ; ),
= )+ 一 一, ( 2 3 6( 2 )— x
2= 2一 2+ .
冥 中 ,参 数 k 0, 0 8 0, ∈R. > > , >
1 平衡 点 的存在 性 . 1
设 统) 衡 z-,), = 古 一( 告, ( 平 点 为 系 ( 平 点 ) , 令 )1 ) ] 系 1 衡 分 1 的 , , p ( 一 , : ) + ) + 统) 的
摘
要 :对有 阻尼 的耦合的连续 B P振 子, V 利用 平衡 点理论和分 支定理 , 分析 系统 平衡 点 的存在和稳 定性以及存
在 的分支现象, 通过 ma a t b程序对振子数值模 拟 , 出图像并验证理论结果 . l 给 关键词 :B P振子; 平衡点 ;分 支 V
中图 分 类 号 :O 152 7 . 9 文献标识码:A
两类 , 一类 z , 第 , ) 其 中 是映射 p 的不动 点, 二类 z , , 第 : , 2, p ) 旦 ) 其 , 中 X 是 映射 p ) 2 的二周 期点 . 为 了叙 述方 便 , 出下列 3个 记号 给
垒 23 k ,
V
/ 3 + k3 里, 4 k
.
且 一y 1 /= ) = ( 0 是系统 () 3 1 的音叉 分支 曲线 , ± = n是 系统 () 1 的鞍 结分 支 曲线
当 k > , < 时, y l I n 关于第二类平衡点的存在性有下面 2 卢I 个定理
1
一
1 1
垒
±
.
, 39
收 稿 日期 : 20 — 6 0 080— 2
基 金项 目 :河 南 省 软 科 学基 金 资助 项 目(5 3 1 1) 0 10 1 0 1
作者简介: 饶明贵 (9 5 ) 男, 16 一 , 河南光山人, 讲师 , 从事微分方程研究和教学工作 .
了大 约三十 年 , 且成为 展示 典型 非线 性性 现象 的经 典模 型 .T t si ea‘ 并 e uh tp】 了含 有饱 和特 性项 的 B P s U 9 构造 V 振子 , 中非线 性项 是 由场 效 应 晶体管 (E ) 其 F T 实验 测 量得 到 的 . 本文 把非线 性项 近似 为这 样 一个 负饱和 函数 g v = a b 一1 (v 3 . () 一 Ev 6 )]
维普资讯
—
—
11 — 0 8—
河
南
科
学
第2 卷 第9 6 期
D如果 > 1
2
>’ n 或
, 方程 () 1 第一 类平 衡 点 1有 个
, , ) 其 ’Βιβλιοθήκη ) 2个第 一类 平衡 点 有
I
I
,
, l ̄ 丁+ ) x/
,
, , , - - V
j
因为 由场效 应管 实验 测量得 到 的数 据绘 制 的 (—) v 图像 和 该近 似 函数 的图像 在原 点 附近 基本 一致 , 以 所
这种近 似 是合理 的 .
1 耦合 B VP振 子的性质
我 们把 两个 B VP振 子利用 电阻 R耦 合在 一起 , 到 的方程 为 得
互 = l ( l + 一1
线 性项 的 B P方程 进行 了拓 扑和 定 性 的分析 .K t i a ] 究 了相 同 的模 型 并 且给 出 了平衡 点的分 叉 图 V ij t am 4 也研
像 . 由于 B P方 程是 一个 简 单 的 二维 模 型 , 于耦 合 系统 来 说 它也 是 一个 很 好 的单 位 振 子 .H q e1 V 对 ou 1 5 对有 阻尼 的耦合 B P振 子 的 同步 性进 行讨 论 ,ay 也研 究 了它们 的分 叉结 构 .直到 现在 ,V V Ppt  ̄ B P振 子 已经被 研 究
‘。n方程( 有 3 卢 <’ 1 ) 个第一类平衡点z I-+ l V廿 :
- -
I
: +
- -
, - T
z , ,学 中= 3学 , :
. .
m + +
m: 一 ,
.
) : ,学 ) 'I , Z, , 2学 m + m 一m + 礼 一 .
学) ,
其 中
3如果
I /专,_ ̄ 1 号、 xl/ / 7 1 . ' v 一 _
_, ) 2 n方 有 个第一类平衡觚 - , - - 7 - T - )
,
z , ,学 ) 2学 , ,
其 中
4如
号V I2 i /  ̄ l ・ 告 v . /
在文献10中作者把霍普分支理论和矩阵理论相结合提出一种新的利用系统特征方程的各项系数来研究霍普分支存在的条件此处我们将利用这个方法来推导霍普分支存在的条件
维普资讯
第2 6卷 第 9期
20 0 8年 9月
河
南
科
学
V0 . No9 1 26 . S p.2 8 e 00
HENAN SCI ENCE
文 章 编号 :0 4 3 1 (0 8 0 - 0 7 0 10 — 9 8 20 ) 9 1 1 — 4
耦合连续 B P振子 中的分支现象 V
饶 明贵 冯 广庆 ,
(. 南 工 程 学 院 , 州 1河 郑 4 19 ; 2 北 京 航 空 航 天 大 学 , 京 5 11 . 北 10 8 ) 0 0 3
B P B h f r a e o V (o o e V nd r D方程 是 由 Ft gt N gmo ̄究 H d i H xe ( 为 HH 模 型得 到 的, f- P i Huh】 au t z 和 2 1 o kn u ly简记 . ) 他
们通过研 究 HH模 型的动力特性 , 四维系 统降为二维 , 将 这个系统 被称 为 B P模型或 Ft g.au 模型 . V iHuhN gmo z 事 实上 , V B P方 程可 以通 过含 有简 单无 源元 件和 一个 非线性 电导 的 电路 来 得 到 .B ui[ at n】 有三 次 非 对含
