KMP算法的介绍
KMP讲解

有了覆盖函数,那么实现kmp算法就是很简单的了,我们的原则还是从左向右匹配,但是当失配发生时,我们不用把target_index向回移动,target_index前面已经匹配过的部分在pattern自身就能体现出来,只要动pattern_index就可以了。
当发生在j长度失配时,只要把pattern向右移动j-overlay(j)长度就可以了。
说了这么半天那么这种方法是什么呢,这种方法是就大名鼎鼎的确定的有限自动机(Deterministic finite state automaton DFA),DFA可识别的文法是3型文法,又叫正规文法或是正则文法,既然可以识别正则文法,那么识别确定的字串肯定不是问题(确定字串是正则式的一个子集)。对于如何构造DFA,是有一个完整的算法,这里不做介绍了。在识别确定的字串时使用DFA实在是大材小用,DFA可以识别更加通用的正则表达式,而用通用的构建DFA的方法来识别确定的字串,那这个overhead就显得太大了。
{
index = overlay_value[index];
}
if(pattern[index+1]==pattern[i])
{
overlay_value[i] = index +1;
KMP 算法可在O(n+m)时间内完成全部的串的模式匹配工作。
ok,最后给出KMP算法实现的c++代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int kmp_find(const string& target,const string& pattern)
kmp

2 KMP算法:KMP算法是由D.E.Knuth(克努特),J.H.Morris(莫里斯),V.R.Pratt(普拉特)等人共同提出的,该算法主要消除了主串指针(i指针)的回溯,利用已经得到的部分匹配结果将模式串右滑尽可能远的一段距离再继续比较,从而使算法效率有某种程度的提高,O(n+m)。
先从例子入手(p82):按Brute-Force算法i=i-j+2=2-2+2=2,j=1按Brute-Force算法i=i-j+2=2-1+2=3,j=1按Brute-Force算法i=i-j+2=8-6+2=4,j=1,但从已匹配的情况看,模式串在t[6]即“c”前的字符都是匹配的,再看已匹配的串“abaab”,t[1]t[2]与t[4]t[5]相同,那么,因为t[4]t[5]与原串s[6]s[7]匹配,所以t[1]t[2]必然与原串s[6]s[7]匹配,因此说t[3]可以直接与s[8]匹配,按KMP 算法i=8,j=3匹配成功。
从上例看出在匹配不成功时,主串指针i不动,j指针也不回到第一个位置,而是回到一个恰当的位置,如果这时让j指针回到第一个位置,就可能错过有效的匹配,所以在主串指针i不动的前提下,j指针回到哪个位置是问题的关键,既不能将j右移太大,而错过有效的匹配,另一方面,又要利用成功的匹配,将j右移尽可能地大,而提高匹配的效率,因此问题的关键是寻找模式串自身的规律。
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////。
和直接比较若不满足和直接比较所以:满足:,设1i i 12112111112121s ),2(;s )1(""")"2(""")"1(""""t t j k t t t t t t t t s s t t t t s s s s k j k j k j k j i j i m n <<====-+-+----+-////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////设s=” s 1 s 2 ... s n ”, t=” t 1 t 2 ... t m ”,在匹配过程中,当s i ≠ t j (1≤i ≤n-m+1,1≤j ≤m)时,存在(前面的j-1个字符已匹配):” s i-j+1 ... s i-1 ” =” t 1 t 2 ... t j-1 ” (1) 若模式中存在可互相重叠的最长的真子串,满足: ” t 1 t 2 ... t k-1 ”=”t j-k+1 t j-k+2 ... t j-1 ” (2) 其中真子串最短可以是t 1 ,即 t 1。
实验04:串应用KMP算法PPT课件

在生物信息学中的应用
在生物信息学中,KMP算法被广泛应用于基因序列的比对和拼接,以及蛋白质序列 的匹配和比对。
通过构建基因序列或蛋白质序列的索引表,KMP算法可以在O(n+m)的时间复杂度 内完成序列的比对和拼接,提高了比对和拼接的准确性和效率。
KMP算法在生物信息学中的应用有助于深入了解基因和蛋白质的结构和功能,为生 物医学研究和疾病诊断提供了有力支持。
06 实验总结与展望
KMP算法的优缺点
优点
高效:KMP算法在匹配失败时能跳过 尽可能多的字符,减少比较次数,从
而提高匹配效率。
适用范围广:KMP算法适用于各种模 式串匹配问题,不受模式串长度的限 制。
缺点
计算量大:KMP算法需要计算和存储 部分匹配表,对于较长的模式串,计 算量较大。
不适合处理大量数据:KMP算法在处 理大量数据时可能会占用较多内存, 导致性能下降。
匹配失败的处理
当模式串中的某个字符与主串中的对应字符不匹配时,模式串向右 滑动,与主串的下一个字符重新对齐,继续比较
next[ j]表示当模式串中第j个字符与主 串中的对应字符不匹配时,模式串需 要向右滑动的位置。
next数组的构建
next数组的作用
在匹配过程中,通过next数组可以快 速确定模式串需要滑动到哪个位置, 从而提高了匹配效率。
通过已知的next值,递推计算出next 数组中其他位置的值。
KMP算法的时间复杂度
01
02
03
04
时间复杂度分析
KMP算法的时间复杂度取决 于模式串在主串中出现的次数 以及每次匹配所花费的时间。
最佳情况
当模式串在主串中连续出现时 ,KMP算法的时间复杂度为
KMP算法计算next值和nextVal值
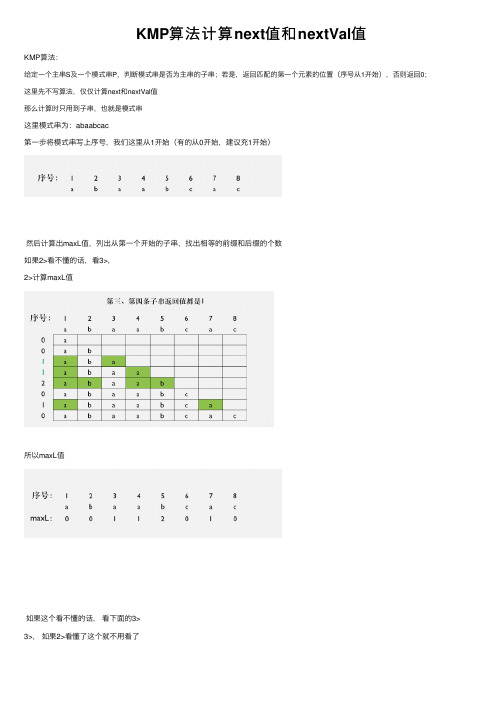
KMP算法计算next值和nextVal值
KMP算法:
给定⼀个主串S及⼀个模式串P,判断模式串是否为主串的⼦串;若是,返回匹配的第⼀个元素的位置(序号从1开始),否则返回0;这⾥先不写算法,仅仅计算next和nextVal值
那么计算时只⽤到⼦串,也就是模式串
这⾥模式串为:abaabcac
第⼀步将模式串写上序号,我们这⾥从1开始(有的从0开始,建议充1开始)
然后计算出maxL值,列出从第⼀个开始的⼦串,找出相等的前缀和后缀的个数
如果2>看不懂的话,看3>,
2>计算maxL值
所以maxL值
如果这个看不懂的话,看下⾯的3>
3>,如果2>看懂了这个就不⽤看了
依次类推4>计算next值
接下来将maxL复制⼀⾏,去掉最后⼀个数,在开头添加⼀个-1,向右平移⼀个格,然后每个值在加1的到next值
5>计算nextVal值,⾸先将第⼀个为0,然后看next和maxL是否相等(先计算不相等的)
当next和maxL不相等时,将next的值填⼊
当next和maxL相等时,填⼊对应序号为next值得nextVal值
所以整个nextVal值为:。
kmp算法概念

kmp算法概念KMP算法概念KMP算法是一种字符串匹配算法,它的全称是Knuth-Morris-Pratt 算法。
该算法通过预处理模式串,使得在匹配过程中避免重复比较已经比较过的字符,从而提高了匹配效率。
一、基本思想KMP算法的基本思想是:当模式串与文本串不匹配时,不需要回溯到文本串中已经比较过的位置重新开始匹配,而是利用已知信息跳过这些位置继续匹配。
这个已知信息就是模式串自身的特点。
二、next数组1.定义next数组是KMP算法中最核心的概念之一。
它表示在模式串中当前字符之前的子串中,有多大长度的相同前缀后缀。
2.求解方法通过观察模式串可以发现,在每个位置上出现了相同前缀和后缀。
例如,在模式串“ABCDABD”中,第一个字符“A”没有任何前缀和后缀;第二个字符“B”的前缀为空,后缀为“A”;第三个字符“C”的前缀为“AB”,后缀为“B”;第四个字符“D”的前缀为“ABC”,后缀为“AB”;第五个字符“A”的前缀为“ABCD”,后缀为“ABC”;第六个字符“B”的前缀为“ABCDA”,后缀为“ABCD”;第七个字符“D”的前缀为“ABCDAB”,后缀为“ABCDA”。
根据上述观察结果,可以得到一个求解next数组的方法:(1)next[0]=-1,next[1]=0。
(2)对于i=2,3,...,m-1,求解next[i]。
①如果p[j]=p[next[j]],则next[i]=next[j]+1。
②如果p[j]≠p[next[j]],则令j=next[j],继续比较p[i]和p[j]。
③重复执行步骤①和步骤②,直到找到满足条件的j或者j=-1。
(3)通过上述方法求解出所有的next值。
三、匹配过程在匹配过程中,文本串从左往右依次与模式串进行比较。
如果当前字符匹配成功,那么继续比较下一个字符;否则利用已知信息跳过一些位置继续进行匹配。
具体地:(1)如果当前字符匹配成功,则i和j都加1。
(2)如果当前字符匹配失败,则令j=next[j]。
KMP算法(改进的模式匹配算法)——next函数

KMP算法(改进的模式匹配算法)——next函数KMP算法简介KMP算法是在基础的模式匹配算法的基础上进⾏改进得到的算法,改进之处在于:每当匹配过程中出现相⽐较的字符不相等时,不需要回退主串的字符位置指针,⽽是利⽤已经得到的部分匹配结果将模式串向右“滑动”尽可能远的距离,再继续进⾏⽐较。
在KMP算法中,依据模式串的next函数值实现字串的滑动,本随笔介绍next函数值如何求解。
next[ j ]求解将 j-1 对应的串与next[ j-1 ]对应的串进⾏⽐较,若相等,则next[ j ]=next[ j-1 ]+1;若不相等,则将 j-1 对应的串与next[ next[ j-1 ]]对应的串进⾏⽐较,⼀直重复直到相等,若都不相等则为其他情况题1在字符串的KMP模式匹配算法中,需先求解模式串的函数值,期定义如下式所⽰,j表⽰模式串中字符的序号(从1开始)。
若模式串p 为“abaac”,则其next函数值为()。
解:j=1,由式⼦得出next[1]=0;j=2,由式⼦可知1<k<2,不存在k,所以为其他情况即next[2]=1;j=3,j-1=2 对应的串为b,next[2]=1,对应的串为a,b≠a,那么将与next[next[2]]=0对应的串进⾏⽐较,0没有对应的串,所以为其他情况,也即next[3]=1;j=4,j-1=3 对应的串为a,next[3]=1,对应的串为a,a=a,所以next[4]=next[3]+1=2;j=5,j-1=4 对应的串为a,next[4]=2,对应的串为b,a≠b,那么将与next[next[4]]=1对应的串进⾏⽐较,1对应的串为a,a=a,所以next[5]=next[2]+1=2;综上,next函数值为 01122。
题2在字符串的KMP模式匹配算法中,需先求解模式串的函数值,期定义如下式所⽰,j表⽰模式串中字符的序号(从1开始)。
若模式串p为“tttfttt”,则其next函数值为()。
KMP算法详解

KMP算法详解KMP 算法详解KMP 算法是⼀个⼗分⾼效的字符串查找算法,⽬的是在⼀个字符串 s 中,查询 s 是否包含⼦字符串 p,若包含,则返回 p 在 s 中起点的下标。
KMP 算法全称为 Knuth-Morris-Pratt 算法,由 Knuth 和 Pratt 在1974年构思,同年 Morris 也独⽴地设计出该算法,最终由三⼈于1977年联合发表。
举⼀个简单的例⼦,在字符串 s = ababcabababca 中查找⼦字符串 p = abababca,如果暴⼒查找,我们会遍历 s 中的每⼀个字符,若 s[i] = p[0],则向后查询p.length() 位是否都相等。
这种朴素的暴⼒的算法复杂度为O(m×n),其中m和n分别是 p 和 s 的长度。
KMP 算法可以⽅便地简化这⼀查询的时间复杂度,达到O(m+n)。
1. PMT 序列PMT 序列是 KMP 算法的核⼼,即 Partial Match Table(部分匹配表)。
举个例⼦:char a b a b a b c aindex01234567PMT00123401PMT 的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
PMT[0] = 0: 字符串 a 既没有前缀,也没有后缀;PMT[1] = 0: 字符串 ab 前缀集合为 {a},后缀集合为 {b},没有交集;PMT[2] = 1: 字符串 aba 前缀集合为 {a, ab},后缀集合为 {ba, a},交集为 {a},交集元素的最长长度为1;PMT[3] = 2: 字符串 abab 前缀集合为 {a, ab, aba},后缀集合为 {bab, ab, b},交集为 {ab},交集元素的最长长度为2;…… 以此类推。
2. 算法主体现在我们已经知道了 PMT 序列的含义,那么假设在 PMT 序列已经给定的情况下,如何加速字符串匹配算法?tar 存储 s 的下标,从 0 开始,若 tar > s.length() - 1,代表匹配失败;pos 存储 p 的下标,从 0 开始,若 s[tar] != p[pos],则 pos ⾛到下⼀个可能匹配的位置。
数据结构kmp算法例题

数据结构kmp算法例题KMP算法(Knuth-Morris-Pratt算法)是一种用于在一个主文本字符串S内查找一个模式字符串P的高效算法。
它利用了模式字符串内部的信息来避免在主字符串中不必要的回溯。
这种算法的关键在于构建一个部分匹配表,用于指示模式字符串中出现不匹配时的下一步匹配位置。
让我们来看一个KMP算法的例题:假设我们有一个主文本字符串S为,"ABC ABCDAB ABCDABCDABDE",模式字符串P为,"ABCDABD"。
我们要在主文本字符串S中查找模式字符串P的出现位置。
首先,我们需要构建模式字符串P的部分匹配表。
部分匹配表是一个数组,用于存储模式字符串中每个位置的最长相同前缀后缀的长度。
模式字符串P,"ABCDABD"部分匹配表:A B C D A B D.0 0 0 0 1 2 0。
接下来,我们使用KMP算法来在主文本字符串S中查找模式字符串P的出现位置。
算法的关键步骤如下:1. 初始化两个指针i和j,分别指向主文本字符串S和模式字符串P的起始位置。
2. 逐个比较S[i]和P[j],如果相等,则继续比较下一个字符;如果不相等,则根据部分匹配表调整j的位置。
3. 如果j达到了模式字符串P的末尾,则说明找到了一个匹配,记录匹配位置,并根据部分匹配表调整j的位置。
4. 继续比较直到遍历完主文本字符串S。
根据上述步骤,我们可以在主文本字符串S中找到模式字符串P的所有出现位置。
总结来说,KMP算法通过构建部分匹配表和利用匹配失败时的信息来避免不必要的回溯,从而实现了高效的字符串匹配。
希望这个例题能帮助你更好地理解KMP算法的原理和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
KMP算法的介绍
by sqybi
Chapter 1:KMP算法摘要
首先看一下KMP算法的程序:
Procedure KMP(p, t: String);
Begin
k := 0;
prefix[1] := 0;
For i:=2 To m Do Begin
While (k > 0) And (p[k+1] <> p[i]) Do
k := prefix[k];
If p[k+1] = p[i] Then Inc(k);
prefix[i] := k;
End;
//以上为自身匹配
q := 0;
For i:=1 To n Do Begin
While (q > 0) And (p[q+1] <> t[i]) Do
q := prefix[q];
If p[q+1] = t[i] Then
q := q + 1;
If q = m Then Begin
WriteLn(i-m);
Exit;
End;
End;
End;
从这一段代码,我们可以发现KMP算法的理论基础,即先进行自身匹配,这样再次在主串中查找模式串的话就会节省一些不必要的时间。
首先,模式串自身匹配时需要的时间复杂度是O(m),而在主串中查找的时间复杂度是O(n),这样KMP 算法就可以在O(m+n)的复杂度内完成字符串的匹配,而不是普通查找的O(m*n)的复杂度,可以大大增加程序的速度。
现在大家通过一个简单的例子来看看KMP在进行模式串查找时的方法。
假设在abacabbc中查找acab,这时候先将模式串进行自身匹配,即prefix[3]=1。
当查找的时候,初始状态是这样的,这时q=0。
a b a c a b b c
a c a b
这时我们先比对主串的第一个位置,相同,这时q=1,i=1。
a b a c a b b c
a c a b
再比对第二个位置,不同,此时q=0,i=2。
a b a c a b b c
a c a b
继续对比第三个位置,这次比较不进入语句①,进入语句②,此时q=1,i=3。
a b a c a b b c
a c a b
接下来是第四个位置,对比结束后q=2,i=4。
a b a c a b b c
a c a b
然后是第五个位置,q=3,i=5。
a b a c a b b c
a c a b
最后是第六个位置,q=4,i=6,退出循环。
a b a c a b b c
a c a b
Chapter 2:KMP算法和朴素的匹配算法对比
从上面的分析,我们可以看出KMP算法会比普通算法快很多。
但是有的同学不放心,问道:会不会出现KMP算法比普通算法慢的情况呢?让我们来做个测试吧。
测试机器的配置是Core Duo T2050,1GB内存,80GB PATA 硬盘,GeForce Go 7300显卡。
为了不让硬盘速度影响到程序执行速度,我特意用WinMount软件Mount了一个内存虚拟的磁盘作为程序评测用。
由于Delphi不支持,所以没有使用inline,不过这应该不会影响到程序的速度。
以下是测试结果:
KMP:
comp-0(comp1.in)∷用时 = 0.02s∷空间 = 57.83M
comp-1(comp2.in)∷用时 = 0.02s∷空间 = 57.83M
comp-2(comp3.in)∷用时 = 0.03s∷空间 = 57.83M
comp-3(comp4.in)∷用时 = 0.03s∷空间 = 57.83M
comp-4(comp5.in)∷用时 = 0.05s∷空间 = 57.83M
comp-5(comp6.in)∷用时 = 0.06s∷空间 = 57.83M
comp-6(comp7.in)∷用时 = 0.06s∷空间 = 57.83M
comp-7(comp8.in)∷用时 = 0.36s∷空间 = 57.83M
comp-8(comp9.in)∷用时 = 0.41s∷空间 = 57.83M
comp-9(comp10.in)∷用时 = 0.02s∷空间 = 57.83M
朴素:
comp-0(comp1.in)∷用时 = 0.02s∷空间 = 19.61M
comp-1(comp2.in)∷用时 = 0.02s∷空间 = 19.61M
comp-2(comp3.in)∷用时 = 0.02s∷空间 = 19.61M
comp-3(comp4.in)∷用时 = 0.02s∷空间 = 19.61M
comp-4(comp5.in)∷用时 = 0.06s∷空间 = 19.61M
comp-5(comp6.in)∷用时 = 0.06s∷空间 = 19.61M
comp-6(comp7.in)∷用时 = 0.06s∷空间 = 19.61M
comp-7(comp8.in)∷用时 = 0.47s∷空间 = 19.61M
comp-8(comp9.in)∷用时 = TLE∷空间 = 19.61M
comp-9(comp10.in)∷用时 = 0.28s∷空间 = 19.61M
其中comp-0到comp-7是随机生成的测试数据,主串最长10000000,模式串最长1000000.可以
发现在这些数据中,KMP的优势并不明显,甚至会比朴素的算法慢。
这是因为KMP使用了自身匹配的思想,需要在自身有很多重复的情况下才能很好的体现它的价值。
可以看一下最后两个数据。
这两个数据都是模式串为一长串a加一个b,而主串是一串a。
其中comp-8主串长度为10000000,模式串100000,而comp-9主串长100000,模式串1000。
可以明显发现KMP的速度优势极大,特别是comp-8,KMP 在0.5sec之内就解决了,而朴素的算法在10sec的时限下最后还是TLE了。
这时我们就可以看出KMP最主要的一个优点——稳定。
Chapter 3:学习KMP的好处
可能有的同学会说:Pascal中提供了一个Pos函数,它就是KMP算法写出来的,为什么要学习KMP 呢?
第一点理由,就是Pos函数不能提供所有形式的KMP查找。
比如如果输入的数字范围是maxLongint 的话,Pos函数就无用武之地了。
虽然可以通过转换到antistring进行Pos,但是那样的效率很低。
这时,学会KMP算法就显得很必要了。
但这不是最主要的。
第二点理由,也是最主要的理由,那就是我们可以学会一种思想。
自身匹配是一种很重要的思想,它可以解决很多和KMP看似无关的问题。
我们学习一个算法,学习的不是它的一串代码,而是它的想法。
从而,可以由此衍生出很多其它的想法,也就可以促进其它算法的学习。
这样,我们才能达到学习KMP 的真正目的。
