面面平行的判定定理最新版
面面平行的判定与性质
2,面面平行的判定： 平面与平面平行的判定定理：
一个平面内有两条相交直线与另一个平面平行,则这两个平面平行.
即：a b
a
Abຫໍສະໝຸດ αa∩ b=Ab// β
a// β
//β β
线不在多，重在相交
简述为：线面平行面面平行
推论：如果一个平面内的两条相交直线分别与另一个平面内的两条直线平行， 那么这两个平面平行。
α β
a b
c d
３，两个平面平行的性质：
（１）两个平面平行，其中一个平面内的直线 必平行于另一个平面
面面平行，则线面平行
注意：这两个平面内的所有直线并 不一定互相平行，它们可能是平行 直线也可能是异面直线，但不可能 是相交直线. 为什么？
这个结论可作为两个 平面平行的性质
（２）两个平面平行的性质定理
如果两个平行平面同时和第三个平面相交， 那么它们的交线平行．
如图α//β，α ∩γ=a， β ∩γ=b， 求证：a//b
β
b
α
a
面面平行，则线线平行 r
练习：
判断下列命题的正误： １．分别在两个平行平面内的两条直线 都平行 ２．如果一个平面内的两条直线平行于 另一个平面，那么这两个平面平行 ３．如果一个平面内的任何一条直线都 平行于另一个平面，那么这两个平面平行
两个平面平行的判定和性质
空间两 条直线
空间直线和平面
空间两个平面
1,两个平面的位置关系
(1)、两个平面平行 ——没有公共点；
(2)、两个平面相交 ——有一条公共直线（至少有一个公共点）．
画两个平行平面的要点是：
表示平面的平行四边形的对应边相互平行．
面面平行定理和判定定理
温馨小提示：本文主要介绍的是关于面面平行定理和判定定理的文章，文章是由本店铺通过查阅资料，经过精心整理撰写而成。
文章的内容不一定符合大家的期望需求，还请各位根据自己的需求进行下载。
本文档下载后可以根据自己的实际情况进行任意改写，从而已达到各位的需求。
愿本篇面面平行定理和判定定理能真实确切的帮助各位。
本店铺将会继续努力、改进、创新，给大家提供更加优质符合大家需求的文档。
感谢支持！(Thank you fordownloading and checking it out!)面面平行定理和判定定理一、面面平行定理面面平行定理的定义：面面平行定理是立体几何中的一个重要定理，它描述了空间中两个平面之间的平行关系。
具体来说，面面平行定理是指，如果一个平面同时与两个平行平面相交，那么它与这两个平行平面的交线也是平行的。
面面平行定理的表述：面面平行定理可以表述为：在空间中，如果平面α与平面β平行，并且平面α与平面γ相交于一条直线l，那么平面β与平面γ也平行，且它们的交线m也与直线l平行。
面面平行定理的证明方法：面面平行定理的证明通常采用反证法。
首先假设平面β与平面γ不平行，那么它们必须相交于一条直线n。
根据平面与直线的位置关系，直线l与直线n 都在平面α内，因此直线l与直线n平行。
但是这与假设直线l与直线n不平行相矛盾。
因此，假设不成立，平面β与平面γ必须平行。
同理，可以证明平面β与平面γ的交线m也与直线l平行。
这样，面面平行定理得证。
二、判定定理面面平行定理和判定定理是空间几何中的重要理论，其中判定定理包括线线平行定理、线面平行定理和面面平行定理。
这些定理在空间几何图形的判定和空间几何问题的求解中具有广泛的应用。
判定定理的种类线线平行定理是指，如果两条直线在同一平面内，且它们的交线与第三条直线平行，则这两条直线平行。
线面平行定理是指，如果一条直线与一个平面平行，那么这条直线上的所有点都与这个平面平行。
面面平行定理是指，如果两个平面上的对应线段平行，则这两个平面平行。
面面平行的性质定理ppt课件.pptx
小结 空间线面间平行关系转化示意图
判定
线线平行
判定 性质
线面平行
知识回顾——线面平行的判定及其性质
线面平行判定定理 线面平行性质定理 面面平行判定定理
新知探究——平面与平面平行的性质
探究一
如果两个平面平行，那么一个平面内的直线 与另一个平面具有什么位置关系？
α
l
β
结论：如果两个平面平行，那么一个平面 内的直线与另一个平面平行.
新知探究——平面与平面平行的性质
AB / / DC 过AB，CD可作平面
AC
BD
/ /
BD∥AC
AB∥CD
ABCD为平行四边形 AB CD
A
β Bγ
C D
夹在两个平行 平面间的所有 平行线段相等.
例3. 如图，设平面α∥平面β，AB、CD是两异面直线，
M、N分别是AB、CD的中点，且A、C∈α，B、
D∈β. 求证：MN∥α.
判定 性质
面面平行
性质
例题2（书P60例6）
求证：夹在两个平行平面间的平行线段相等.
讨论:解决这个问题的基本步骤是什么?
第一步:结合图形，将原题改写成数学符号语言;
已知：如图，α∥β，AB∥CD，A∈α，
C∈α,B∈β，D∈β， 求证:AB=CD
A
C
第二步:分析,作出辅助线；
β Bγ
D
例题2
第三步:书写证明过程.
(完整版)线面、面面平行和垂直的八大定理
线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行，那么这条直线与这个平面平行.符合表示：βββ////a b a b a ⇒⎪⎭⎪⎬⎫⊂⊄2、性质定理：如果一条直线与平面平行,经过这条直线的平面和这个平面相交，那么这条直线和交线平行。
符号表示: b a b a a a ////⇒⎪⎪⎭⎪⎪⎬⎫=⊂⊄βαβαα二、面面平行。
1、判定定理：如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。
符号表示： βα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==N n m M b a a m bn 2、性质定理：如果两个平面平行同时与第三个平面相交，那它们的交线平行。
符号表示： d l d l ////⇒⎪⎭⎪⎬⎫==γβγαβα （更加实用的性质：一个平面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面.符号表示： α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a $:三垂线定理：（经常考到这种逻辑）在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。
符号表示：PA a A oA a po oA a ⊥⇒⎪⎪⎭⎪⎪⎬⎫=⊥⊥⊂⊂ααα 2、性质定理：垂直同一平面的两条直线互相平行。
（更加实用的性质是：一个平面的垂线垂直于该平面内任一直线.)四、面面垂直.1、判定定理：经过一个平面的垂线的平面与该平面垂直。
βααβ⊥⇒⊂⊥a a ,2、性质定理:已知两个平面垂直，在一个平面内垂直于交线的直线垂直于另一个平面。
βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,，。
4空间几何体中平行、垂直相关定理
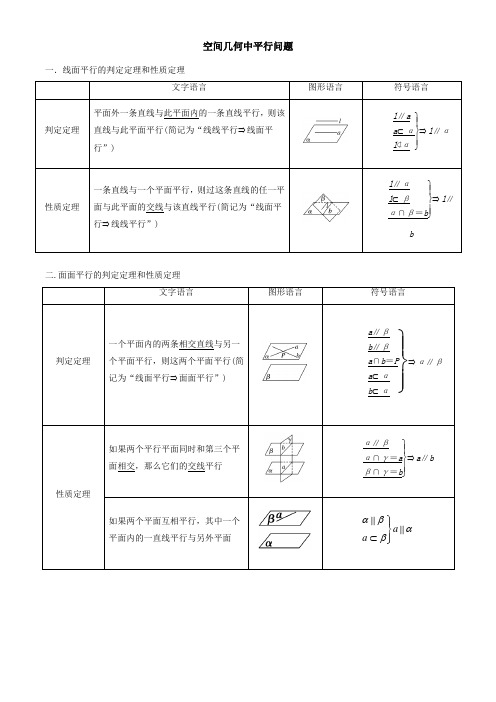
空间几何中平行问题
一．线面平行的判定定理和性质定理
二.面面平行的判定定理和性质定理
a βαβ⎫⎪
⎬⊂⎪⎭
9.5 空间几何中垂直问题
一．直线与平面垂直
1.定义：如果直线l与平面α内的任意一条直线都垂直，则直线l与平面α互相垂直，记作l⊥α，直线l 叫做平面α的垂线，平面α叫做直线l的垂面．
2.判定定理与性质定理
二．平面与平面垂直
1.二面角的有关概念
①二面角：从一条直线出发的两个半平面所组成的图形叫做二面角；
②二面角的平面角：在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的两条射线，这两条射线所构成的角叫做二面角的平面角．
2.平面和平面垂直的定义
两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．
3.平面与平面垂直的判定定理与性质定理。
两个平面平行的判定定理
1、一个平面内的两条相交直线平行于另一个平面，则这两平面平行；
2、垂直于同一直线的两平面平行；
3、一个平面内的两条相交直线与另一个平面内的两条相交直线平行，则这两个平面平行。
两平面平行简介
两平面平行是两平面间的一种位置关系，如果两个平面没有公共点，则称这两
个平面有平行位置关系，简称两平面相互平行，一个平面称为另一个平面的平行平面。
平面与平面平行的性质定理
如果两个平行平面都和第三个平面相交，那么它们的交线平行，由两个平面平行，我们还有：
1、如果两个平面平行，那么其中一个平面内的直线平行于另一个平面；
2、和两个平行平面同时垂直的直线，叫做这两个平行平面的公垂线。
它夹在
这两个平行平面间的部分叫这两个平行平面的公垂线段。
公垂线段的长度叫做两个平行平面的距离。
注意：①两个平面平行，其中一个平面内的直线必平行于另一个平面。
但这两
个平面内的所有直线并不一定相互平行。
它们可能是平行直线，也可能是异面直线，但不可能是相交直线。
②两个平面平行的性质定理指出两个平面平行时所具有的性质：如果两个平面
平行同时与第三个平面相交，那么它们的交线平行。
③一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。
线面、面面平行的性质定理
• (4)相似三角形的周长比等于相似比. • (5)相似三角形的面积比等于相似比的平方. 相似 三角形的传递性，即如果： △ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,那么 △ABC∽A2B2C2
必修2
第二章
点、直线、平面之间的位置关系
3.平行四边形的判定定理
必修2
第二章
点、直线、平面之间的位置关系
定理的应用
例3、 如图：a∥α，A是α另一侧的点，B、C、D 是a 上的点 ，线段AB、AC、AD交于E、F、G点，若BD=4， CF=4，AF=5，求EG.
∵点A为直线a线外一点 ∴点A与直线a确定一个平面，平 面ABD 又∵a∥α ，α ∩平面ABD=EG ∴BD∥EG ∴<AGE= <ADB 又∵<A=<A ∴△AGE∽△ADB ∴EG/BD=AF/AC即 EG/BD=AF/AF+CF ∴EG/4=5/9 ∴EG=20/9
必修2 第二章 点、直线、平面之间的位置关系
D
3．夹在两个平面间的三条线段，它们平行且 相等，则两平面的位置关系为________． 解析： 平行或相交，如图
答案：
平行或相交
第二章 点、直线、平面之间的位置关系
必修2
定理的应用
例1、求证：夹在两个平行平面间的两条平行 线段相等
D
α
A
C
β
B
必修2
第二章
必修2 第二章 点、直线、平面之间的位置关系
巩固练习:
3、棱长为a的正方体AC1中,设M、N、E、F分别为 棱A1B1、A1D1、 C1D1、 B1C1的中点. (1)求证：E、F、B、D四点共面； (2)求证：面AMN∥面EFBD.
面面平行的判定
面面平行的判定
【典型例题】
（ ∴ 又 同2GD理）E1GG=解22G=12 由3A23=C（D13，E1A）∴.B知，GG1GPP1G G2D=13=13 13
PG2 PE
AC. BC.
2, 3
∴△ G1G2 G3∽△CAB，其相似比
为1∶3，
∴S△ G 1 G 2 G 3 ∶S△ABC =1∶9.
面面平行的判定
【典型例题】
已知P为△ABC所在平面外一点，G1、G2、G3 分别是△PAB、△PCB、△PAC的重心. （1）求证：平面G1G2G3∥平面ABC； （2）求S△ G 1 G 2 G ∶3 S△ABC. （1）证明 如图所示，连接PG1、PG2、PG3并 延长分别与边AB、BC、AC交于点D、E、F， 连接DE、EF、FD，则有PG1∶PD=2∶3， PG2∶PE=2∶3，∴G1G2∥DE. 又G1G2不在平面ABC内， ∴ G1G2 ∥平面ABC.同理G2G3∥平面ABC. 又因为G1G2 ∩G2G3=G2， ∴平面G1G2 G3∥平面ABC.
面面平行的判定
【变式训练】 （则∴2四O）E边取/形/ B12ODDE的CG，中D又点1是DO平1G，行/连/ 四12接D边EC形O，，，∴D1OOE ，/ / D 1 G ， ∴GE∥D1O.
又D1O 平面BB1D1D，∴EG∥平面BB1D1D.
（3）由（1）知D1H∥BF，又BD∥B1D1， B1D1 、
面面平行的判定
【变式训练】 如图所示，在正方体ABCD—A1B1C1D1中，E、 F、G、H分别是BC、CC1、C1D1、A1A的中点. 求证： （1）BF∥HD1； （2）EG∥平面BB1D1D； （3）平面BDF∥平面B1D1H.
平面与平面平行的判定定理
面面平行判定定理的应用：要证面面平行，只要证线面平行，而要证线面平行，只要证线线平行。在立体几何中，往往通过线线、线面、面面间的位置关系的转化使问题得到解决。
01
02
03
小结：
面面平行的定义；
01
面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行；
复习回顾：
平面外一条直线与此平面内的一条直线平行，则 该直线与此平面平行．
（2）直线与平面平行的判定定理：
（1）定义法；
线线平行
线面平行
1. 到现在为止,我们一共学习过几种判断直线与平面平行的方法呢?
（1）平行
相交 α∥β 怎样判定平面与平面平行呢？ 问题： 面与平面有几种位置关系？分别是什么？
P
Q
如果平面β内的两条直线是相交的直线，两个平面会不会一定平行？
新课讲授：
一个平面内的两条相交直线与另一个平面平行，则这两个平面平行
两个平面平行的判定定理：
线不在多，重在相交
符号表示：
ａ，ｂ，ａｂ＝Ｐ，ａ，ｂ
图形表示：
a
b
P
平面平行的判定定理的证明
已知：在平面内，有两条直线 、 相交且和平面平行．
探究：
平面内有一条直线与平面平行，，平行吗？
平面内有两条直线与平面平行，，平行吗？
结论：
中的平面α，β不一定平行。如图，借助长方体模型，平面ABCD中直线AD平行平面BCC'B'，但平面ABCD与平面BCC'B'不平行。
结论：
（2）分两种情况讨论：
如果平面β内的两条直线是平行直线，平面α与平面β不一定平行。如图，AD∥PQ，AD∥平面BCC’B’，PQ∥BCC’B’，但平面ABCD与平面BCC’B’不平行。
立体几何9-4线面、面面平行的判定与性质
则另一条也垂直于这个平面，故选B. 答案：B
15
[例2] (文)在四面体ABCD中，CB＝CD， AD⊥BD，且E，F分别是AB，BD的中 点．求证：
为线段CE的中点，所以PN綊12DC.
19
又四边形ABCD是矩形，点M为线段AB的中点，
所以AM綊12DC.所以PN綊AM.
故四边形AMNP是平行四边形．所以 MN∥AP，
而AP⊂平面DAE，MN⊄平面DAE，所以 MN∥DAE.
证法二：取BE中点G，连结GM、GN，
∵GN∥BC，BC∥DA，∴GN∥DA，又
(1)直线EF∥平面ACD； (2)平面EFC⊥平面BCD.
16
解析：(1)在△ABD中，因为E、F分别是AB、 BD的中点，所以EF∥AD.
又AD⊂平面ACD，EF⊄平面ACD， 所以直线EF∥平面ACD. (2)在△ABD中，因为AD⊥BD，EF∥AD，
所以EF⊥BD. 在△BCD中，因为CD＝CB，F为BD的中点，
的中点，求证：MN∥平面DAE.
18
证明：(1)因为BC⊥平面ABE，AE⊂平面 ABE，
所以AE⊥BC. 又BF⊥平面ACE，AE⊂平面ACE， 所以AE⊥BF. 又BF∩BC＝B， 所以AE⊥平面BCE. 又(2B)证E⊂法平一：面取BDCEE的，中所点P以，A连E结⊥PAB，EP.N，因为点N
1
2
重点难点 重点：线面、面面平行的判定定理与性质定
理及应用 难点：定理的灵活运用
3
知识归纳
一、直线与平面平行
面面平行的判定定理FF
1．证明直线与平面平行旳措施：
（1）利用定义: 直线与平面没有公共点
（2）利用鉴定定理．
线线平行
线面平行
关键：找平行线
a
面内
条件:
面外
b
平行
1．证明直线与平面平行旳措施：
（1）利用定义:
（2）利用鉴定定理． 线线平行
线面平行
符号语言
a
b
a
//
a // b
a b
二、两个平面平行旳鉴定
同理可证EG // 平面PAB
线线平行 线面平行
又 EF 平面EFG，EG 平面EFG面面平行
且EF EG E
线面平行
平面PAB // 平面EFG
又 FG 面EFG， FG // 面PAB
课堂练习1 温故而知新
如图.M,N分别是AB,PC旳中点,底面
ABCD是平行四边形
P
求证：MN//面PAD
题型二 平面与平面平行的判定 【例 2】 如图所示，在三棱柱 ABC-A1B1C1 中，点 D，E 分别是 BC 与 B1C1 的中点．求证：平面 A1EB∥平面 ADC1.
[思路探索] 要证平面 A1EB∥平面 ADC1，只需证平面 A1EB 内 有两条相交直线平行于平面 ADC1 即可．
线面平行与面面平行旳小结： 1、证明线面平行时，注意有三个条件
求证:平面MNG//平面ACD
证明:连接AN,交BD于点E 由已知得点E是边BD旳中点 连接CE,则CE必经过点G ∵点N、G分别是△ABD和
△BCD旳重心， ∴NE：NA=1：2
GE：GC=1：2 ∴NG//AC
又NG 平面ACD
AC 平面ACD
∴NG//平面ACD
面面平行的判定定理
行； ×
（5）过已知平面外一条直线，必能作出与已知平面平
行的平面． ×
2021
10
例1 、已知正方体ABCD-A1B1C1D1，求证：平 面AB1D1//平面C1BD 证明：
∵ABCD－A1B1C1D1为正方体， ∴D1C1∥AB，D1C1＝AB， ∴D1C1BA是平行四边形， ∴D1A∥C1B， 又D1A 平面C1BD, C1B 平面C1BD.
2.面面平行判定定理的应用：要证面面平行，需要证线面 平行，而要证线面平行，一定要证线线平行。 在立体几何中，证明线线平行，有时需要添加辅助线，但 是做题要按照先找后作的原则，找不到两条相交直线的时 候再作，并且辅助线一般通过找三角形的中位线，或者按 平行四边形的平行关系来完成。
2021
15
2021
6
如果平面β内的两条直线是相交的直线，两 个平面是不是一定平行？
如图，AC与BD相交，AC∥平面A’B’ C’D’ ， BD∥平面A’B’C’D’，在平面A’B’ C’D’上可以找 到两个相交直线A’C’和B’D’与AC和BD分别平 行，显然平面ABCD与平面A’B’ C’D’平行。
两条相交直线才是关键
2021
7
总结归纳：
两个平面平行的判定定理：
如果一个平面内有两条相交直线都平行 于另一个平面，那么这两个平面平行
图形表示：
bP
符号表示：
a
线不在多 重在相交
ａä，ｂä，ａｂ＝Ｐ，ａ，ｂ
线面平行 面面平行
2021
8
思考:由直线与平面平行的判定定理， “a∥β,b∥β” ，又可用什么条件替 代？由此可得什么推论？
2.2.2
如何证面面平行的判定定理
如何证面面平行的判定定理一、引言平行是几何学中一个重要的概念，它描述了两条直线或两个平面在空间中永远不会相交的关系。
在解决几何问题时，判定两条直线或两个平面是否平行是非常关键的一步。
本文将介绍如何通过证明来判定两个平面是否平行。
二、定义和定理在开始介绍证明过程之前，我们先来回顾一下与本文相关的定义和定理。
定义：•平行：两条直线或两个平面如果在空间中没有交点，则它们被称为平行。
定理：•面面平行的判定定理：如果一条直线与一个平面垂直相交，则这条直线上的任意一点到该垂线上任意一点所作的垂线都与该平面垂直相交。
三、证明过程下面我们将通过详细的步骤来证明“面面平行的判定定理”。
步骤1：假设有一个平面A和另外一个与A垂直相交的直线L。
步骤2：取L上任意一点P，并以P为圆心作一个小圆C1，使得C1与A相交于一点M。
步骤3：连接M与P，并延长直线MP，使其与平面A相交于一点N。
步骤4：取MP上任意一点Q，并以Q为圆心作一个小圆C2，使得C2与A相交于一点S。
步骤5：连接S与Q，并延长直线SQ，使其与平面A相交于一点R。
步骤6：根据构造的方式可知，MQ是垂直于平面A的直线。
同时，由于S、Q、R三点共线，则SR也是垂直于平面A的直线。
步骤7：根据步骤6可知，对于MP上任意一点Q所作的垂线SQ都与平面A垂直相交。
步骤8：由于P是L上任意一点，因此对L上任意一点P所作的垂线都与平面A垂直相交。
综上所述，我们证明了“如果一条直线与一个平面垂直相交，则这条直线上的任意一点到该垂线上任意一点所作的垂线都与该平面垂直相交”的定理。
四、应用举例例1：已知平面A和B分别由以下方程确定：•平面A: 2x + 3y - z = 4•平面B: x + 2y - 3z = 5求证平面A和平面B是平行的。
证明过程：根据定理，我们只需要找到一条直线与两个平面垂直相交即可判定它们是平行的。
以平面A为例，令x = t, y = 0, z = -4t + 4，其中t为参数。
面面平行的判定定理(1)
PQ∥ A1B A1B ∥CD1 故PQ∥CD1 同理可得，……
P
R Q
小结：
1.证明面面平行的方法 （1）面面平行的定义，（两个平面没有公共点） （2）面面平行的判定定理，（一个平面内两条相交直线与另一 个平面分别平行） （3）面面平行判定定理的推论，（一个平面的两条相交直线与 另一个平面的两条直线平行）
如果平面β内的两条直线是相交的直线，两 个平面是不是一定平行？
如图，AC与BD相交，AC∥平面A’B’ C’D’ ， BD∥平面A’B’C’D’，在平面A’B’ C’D’上可以找 到两个相交直线A’C’和B’D’与AC和BD分别平 行，显然平面ABCD与平面A’B’ C’D’平行。
两条相交直线才是关键
a
b
α
β
小试：
判断下列命题是否正确，并说明理由．
（1）若平面 内的两条直线分别与平面 平行，则
与 平行； ×
（2）若平面 内有无数条直线分别与平面 平行，则
与 平行；× （3）平行于同一直线的两个平面平行； ×
（4）两个平面分别经过两条平行直线，这两个平面平
行； ×
（5）过已知平面外一条直线，必能作出与已知平面平
（1）中的平面α，β不一定平行。如图， 借助长方体模型，平面ABCD中直线AD平行 平面BCC’B’ ，但平面 ABCD与平面BCC’B’ 不 平行。
（２）平面内有两条直线与平 面平行，，平行吗？
（2）分两种情况讨论：
Q
P
如果平面β内的两条直线是平行直线，平面 α与平面β不一定平行。如图，AD∥PQ， AD∥平面BCC’B’，PQ∥平面BCC’B’，但平面 ABCD与平面BCC’B’不平行。
变式、正方体ABCD——A1B1 C1D1中，E、F 、 G
面面平行的判定定理
D1
F
· C1
B1G
同理GE ∥平面BDD1B1
∵FG∩GE＝G
D
故得面EFG//平面BDD1B1 A
C E B
三.课堂过关 2.
证明： E、F分别为PC、PD的中点，
EF为PCD的中位线
EF // CD 又 AB // CD
EF // AB
而EF 平面PAB，AB 平面PAB 线线平行
今天学习的内容有： 1.空间两平面的位置关系有几种 2.面面平行的判定定理需要什么条件 3.应用判定定理判定面面平行的关键 是什么 找平行线
方法一：三角形的中位线定理； 方法二：平行四边形的平行关系,
4.思想方法：化归：
1、完成作业：课本34页A第5、6题 2、完成平面关系的性质
一.预习检测; 二.知识点归纳,
如果一个平面内有两条相交直线分别平 行于另一个平面,那么这两个平面平行
有两条怎么样的直线呢
a// β
α
b// β
a
a// b
b
a// β
b// β
b
α
Pa
β
β
c
平面与平面平行的判定定理：
一个平面内有两条相交直线与另一个平面平 行,则这两个平面平行.
符号语言：
a b a∩ b=A
图形语言：
a α Ab
A'
C' B'
又 BC ' 平面 AB ' D ' AD ' 平面 AB ' D '
BC '// 平面 AB ' D ' 同理： C ' D // 平面 AB ' D '
BC ' C ' D C '
两平面平行的判定定理公式
两平面平行的判定定理公式在数学中，两平面平行的判定定理公式用来表达两平面之间的关系是否是平行的。
它提供了一种快速测试两个平面是否平行的方法。
因此，这个定理的公式可以说是一个极其重要的数学定理，它的准确性决定着后续计算的准确度。
两平面平行的判定定理公式一般用来判断两个三维空间中的平面是否具有平行关系。
其具体运算过程是，令两个平面的法线向量分别为a=(a1，a2，a3)和b=(b1，b2，b3)，则两平面以向量a、b的夹角θ表示，如果a=b，那么θ=0，则两平面平行；如果a≠b，而且ab≠0，则可以推出θ，即两平面存在夹角，说明它们不是平行的；如果a≠b，而且ab=0，则可以推出θ=π，即两平面垂直，但不是平行的。
两平面平行的判定定理公式的计算公式可表示为：ab=|a||b|cosθ其中，a、b分别表示两平面法向量，|a|表示a的模，|b|表示b 的模，cosθ表示a、b之间的夹角，由此可以测算出两平面之间夹角大小。
两个平面平行或非平行时，如何计算得出其夹角？利用两平面平行的判定定理，计算方法如下：1、计算两平面的法线向量a、b；2、将a、b的模的乘积(||a|| ||b||)代入公式ab=|a||b|cosθ，得出ab的值；3、由公式ab=|a||b|cosθ，推出cosθ=ab/|a||b|；4、因为cosθ的值在-1到1之间，当cosθ的值大于0，则可以推出θ，即两平面彼此之间存在夹角，说明它们不是平行的，当cos θ=0时，可以推出θ=π，即两平面垂直，但不是平行的。
从以上可以看出，利用两平面平行的判定定理可以轻松地测算出两平面之间的夹角以及其是否平行的关系。
可见，这个定理的公式是一个非常重要的数学定理，它的准确性决定着后续计算的准确度。
在实际应用中，两平面平行的判定定理公式还可以用于求解几何问题、物理解释等，是一个非常重要的数学工具。
例如，在几何问题中，两个三角形的平行判断就可以利用它来轻松判断；在电磁学中，可以应用它来求解电磁场相互作用时的相对位置，从而获得更精确的结果；在电力学中，可以用它来判断两个永磁转子的角度差，从而实现不同的操作行为；在力学中，它也可以用来判断静力学或动力学模型中受力物体之间的关系。
面面平行的判定定理ppt课件.pptx
EF // 平面PAB 同理可证EG // 平面PAB
线面平行 面面平行
又 EF 平面EFG，EG 平面EFG
且EF EG E
平面PAB // 平面EFG
三.能力提升
分析：连结EF， 证明B1E // FC，AF // DE 进而证明B1E // 平面ACF，
DE // 平面ACF， 从而平面DEB1 // 平面ACF，
今天学习的内容有： 1.空间两平面的位置关系有几种？ 2.面面平行的判定定理需要什么条件？ 3.应用判定定理判定面面平行的关键 是什么? 找平行线
方法一：三角形的中位线定理； 方法二：平行四边形的平行关系。
4.思想方法：化归：
1、完成作业：课本34页A第5、6题 2、完成平面关系的性质
一.预习检测; 二.知识点归纳。
//β
β
a// β
线不在多，重在相交
b// β
简述为：线面平行面面平行
【例1】如图，在长方体 ABCD A' B 'C ' D ' 中， 求证：平面 C ' DB // 平面 AB ' D '.
证明： AB // DC // D 'C '
ABC ' D '是平行四边形
D'
BC '// AD '
一.学习目标
1.了解两个平面之间的位置关系； 2.理解和掌握两个平面平行的判定 定理及其简单运用.
一.预习检测
1. 如果平面α内有一条直线a平 行于平面β，那么α∥β （×）
a βቤተ መጻሕፍቲ ባይዱ
α
一.预习检测
2. 如果平面α内有无数条直线都 平行于平面β，那么α∥β. （×）
线面、面面平行的判定与性质
线面、面面平行的判定与性质一、线线、线面、面面平行间的相互转化（1）平行公理:平行于同一直线的两直线平行（线线平行的传递性）（2）线面平行的判定定理：如果平面外的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行（线线平行→线面平行）（3）面面平行的判定定理：一个平面内的两条相交直线分别平行于另一个平面，这两个平面平行（线面平行→面面平行）（4）线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行（线面平行→线线平行）（5）面面平行的性质定理：两个平面平行，其中一个平面内的直线必平行于另一个平面（面面平行→线面平行）（6）面面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行（面面平行→线线平行）三、证明线线平行的方法：（1）线线平行的传递性； （2）三角形中位线； （3）平行四边形对边平行； （4）三角形中对应边成比例； （5）线面平行的性质定理. 三、典型例题例：已知四棱锥ABCD P ,E 是PD 的中点.证明：ACE PB 面//E P DBAC变式1：已知四棱锥ABCD P -,E 是AD 的中点，F 是PB 的中点.证明：ACE PB 面//.变式2：已知四棱锥ABCD P -,BC EF //,EFHG 平面与ABCD 平面相交于HG ，PB HI //,证明:PBC IG 面//.四、巩固训练1.三棱柱111ABC A B C -中，D 为AB 边的中点.求证：1AC ∥平面1CDB .PD BACE FEPDBACF GHIBACA 1B 1C 1D2.【2014高考北京卷 节选】如图，在三棱柱111ABC A B C -中，侧棱垂直于底面，AB BC ⊥，12AA AC ==，E 、F 分别为11A C 、BC 的中点.，求证：1//C F 平面ABE .3.【2013年辽宁卷 节选】如图,AB 是圆O 的直径，PA 垂直圆O 所在的平面，C 是圆O 上的点， Q 为PA 的中点，C 是圆O 上的点，G 为AOC ∆的重心.求证：PBC QG 平面//4.【2013年陕西卷】如图，四棱柱1111D C B A ABCD -的底面ABCD 是正方形，O 是底面中心，O A 1⊥底面ABCD ，211==B AA AB .（1）证明：B CD BD A 11//平面平面；（2）求三棱柱111D B A ABD -的体积．C 1B 1A 1F ECBA5.【2014高考陕西卷】四面体ABCD 及其三视图如图所示，平行于棱BC AD ,的平面分别交四面 体的棱CA DC BD AB ,,,于点H G F E ,,,.（1）求四面体ABCD 的体积；（2）证明：四边形EFGH 是矩形.２２１俯视图左视图 主视图ABCDEFGH6. 【珠海市2015届高三9月摸底考试】如图的多面体中，四边形11ABB A 和11ACC A 都为矩形. （1）若AC BC ⊥，证明：直线BC ⊥平面11ACC A ；（2）是否存在过1A C 的平面α，使得直线1//BC α平行，若存在请作出平面α并证明，若不存在请说明理由.1AA。
面面平行定理
面面平行定理
在几何学中，面面平行定理是一种重要的定理，它宣称在任意四边形中，如果对角线相交，则其任意两条对角线的交点分别位于其他两条边的中点上。
本文将对这一定理进行详细阐述，介绍它的几何形式和推导过程，及其在几何中的重要性。
定理的近义词：
面面平行定理也被称为“垂直平分线”，“垂直中位线”，“垂直交线”，“平行平分线”，“平行中位线”，“平行交线”，等等。
它涉及到四边形中两条对角线的位置关系，及其余两条边的位置关系。
定理的形式：
面面平行定理可以用以下形式表示：在任意四边形中，如果对角线相交，则其任意两条对角线的交点分别位于其他两条边的中点上。
如果能证明这个结论是正确的，那么它的说明就象以下这样：（1）对角线相交时，相交点位于其他两条边的中点。
（2）其余两条边的中点位于相交点上。
在图形上可以很直观地看出这种位置关系，但是要证明这一定理也需要进行精确的推导。
定理的推导：
在几何中，证明面面平行定理的推导步骤如下：
首先，我们考虑一边形ABCD，两条对角线AC和BD相交于点O，试证明：点O位于边AB的中点M上，点O位于边CD的中点N上。
第一步的证明：将点O移动到点A，点M移动到点C，从而得到
两个三角形AOM和COM，由于它们处于对称位置，所以，角AOM和角COM是相等的，因此，AM=MC，因此，点O位于边AB的中点M上。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
.
1、完成作业：课本45页第10题 2、完成平面与平面平行的性质学案：
一.知识点归纳;二.预习检测。
.
当水平仪的气泡居 中时，水平仪所在 的直线就是水平线。
.
辅加练习
1 如图所示，平面ABCD∩平面EFCD = CD，
M、N、H 分别是 DC、CF、CB 的中点，
D1
F
C1
G
B1
同理GE ∥平面BDD1B1
∵FG∩GE＝G
D
故得面EFG//平面BDD1B1 A
.
C E B
三.课堂过关 2.
.
证明 E、 ： F分别 P、 C 为 PD 的中点， EF为PC的 D 中位线
EF//CD 又AB//CD
EF//AB
而 E F 平 P面 ， A AB B 平 P面 A 线线平B 行
求证 平面 MNH // 平面 DBF
D
E
A M
CN
H
F
B.
课堂小结
.
两平面平行 没有公共点
α∥β
两平面相交 有一条公共直线
α∩β=a
图形表示
.
(二).两平面平行的判定
b
Aa
地面
.
平面与平面平行的判定定理：
一个平面内有两条相交直线与另一个平面平
行,则这两个平面平行.
即：a b
a α Ab
a∩ b=A a// β b// β
//β 线不在多β，重在相交
简述为：线面平行面面平行
EF//平面 PAB 同理E可 G //平 证P 面 AB
线面平行 面面平行
又 E F 平 E面 ， F E G G 平 E面 FG
且 EF EG E
平P 面 A//平 B E 面 FG .
三.课堂过关
分析：E连F， 结 证明 B1E//FC，AF//DE 进而B1证 E//平 明 A 面 C ， F
DE//平面 AC， F 从而 D平 1 E //平 B 面 A面 C ， F
.
变式1：如图，在长方体 A B C D A 'B 'C 'D '中， 求证：平面 C'DB//平面 AB' D.'
证明：Q AB / / D C / / D ' C '
ABC'D'是平行四边形
D'
BC'//AD'
求证：平面PQR∥平面CB1D1.
分析：连结A1B， PQ∥ A1B A1B ∥CD1 故PQ∥CD1 同理可得，……
P
R Q
.
今天学习的内容有： 1.空间两平面的位置关系有几种？ 2.面面平行的判定定理需要什么条件？ 3.应用判定定理判定面面平行的关键
是什么? 找平行线
方法一：三角形的中位线定理；
a β
α
.
一.预习检测
4.(3)如果平面α内有无数条直线 都平行于平面β，那么α∥β（. ×）
α
β
.
一.预习检测
4.(4)若两个平面分别经过两条平行直线，
则这两个平面平行。
（a /b /,a ,b //（） ×）
a
β
αb
.
二.知识点归纳 (一)两个平面的位置关系
位置关系 公共点 符号表示
问题 怎样使用水平仪来检测桌面是否水平?
地面
思考
工人师傅常将水平仪 在桌面上交叉放置两 次，如果水平仪的气 泡两次都在中央,就 能判断桌面与地面 平行.
为什么工人师傅只检查两次且交叉放置呢?
.
.
一.学习目标 1.了解两个平面之间的位置关系； 2.理解和掌握两个平面平行的判定 定理及其简单运用.
.
如何正确理解两个平面平行的判定定理:
1.两个平面平行需要多少个条件? 5个条件
2.两个平面平行时为什么只需要其中一个平 面内的两条相交直线与另一个平面平行,而 不是一条或更多条直线?
(公理3的推论2:两条相交直线确定一个平面)
3.两个平面平行时为什么不用其中一个平面 内的两条平行直线与另一个平面平行?
A'
C' B'
又 QBC' 平面 AB' D' AD' 平面 AB' D'
BC'// 平面 AB' D' 同理： C ' D // 平面 AB' D'
D A
C B
QB C'IC'DC'
平面C'DB// 平面 AB' D'
.
变式2、已知正方体ABCD-A1B1C1D1，P,Q, R, 分别为A1A,AB,AD的中点 。
.
一.预习检测
2．如果平面 //平面 ，直线a ，那
么直线 a和平面 的位置关系是__a__/_/___
αa
β
.
一.预习检测
3．如果平面 //平面 ，直线a，直
线 b ，那么直线 a和 b的位置关系是
__平__行_或__异__面______
a α
b
β
a α
b
β
.
一.预习检测
4.(2)如果平面α内有一条直线a 平行于平面β，那么α∥β（×）
.
3.两个平面平行时为什么不用其中一个平面 内的两条平行直线与另一个平面平行?
a
b
α
ห้องสมุดไป่ตู้
β
.
三.课堂过关
1.如图，在正方体ABCD——A1B1C1D1中， E、F、G分别是棱BC、C1D1、 B1C1的中点。 求证：面EFG//平面BDD1B1.
分析：由FG∥B1D1 易得FG∥平面BDD1B1 A1