高级中学高一数学竞赛班选拔考试试题第一卷
数学竞赛试题高一及答案

数学竞赛试题高一及答案一、选择题(每题5分,共20分)1. 若函数f(x) = 2x^2 + 3x + 1的图像关于直线x = -1/2对称,则下列哪个函数的图像也关于直线x = -1/2对称?A. g(x) = x^2 + 2x + 3B. h(x) = -x^2 + 2x - 3C. i(x) = x^2 - 2x + 3D. j(x) = -x^2 - 2x - 3答案:B2. 已知集合A = {1, 2, 3},集合B = {2, 3, 4},则A∪B等于:A. {1, 2, 3, 4}B. {1, 2, 3}C. {2, 3}D. {1, 3, 4}答案:A3. 若方程x^2 - 5x + 6 = 0的两个根为α和β,则α + β的值为:A. 1B. 2C. 3D. 5答案:C4. 函数y = |x - 2| + 3的图像与x轴交点的个数是:A. 0B. 1C. 2D. 3答案:B二、填空题(每题5分,共20分)1. 已知等差数列的前三项依次为2, 5, 8,则该数列的第五项为________。
答案:112. 圆的方程为x^2 + y^2 - 6x - 8y + 25 = 0,则圆心坐标为________。
答案:(3, 4)3. 函数y = sin(x)在区间[0, π]上的最大值为________。
答案:14. 已知三角形的三边长分别为3, 4, 5,则该三角形的面积为________。
答案:6三、解答题(每题15分,共30分)1. 证明:若一个三角形的两边长分别为a和b,且满足a^2 + b^2 =c^2(c为第三边长),则该三角形为直角三角形。
证明:根据勾股定理,若三角形的两边长为a和b,且满足a^2 + b^2 = c^2,则第三边c所对的角θ为直角,即θ = 90°。
因此,该三角形为直角三角形。
2. 解方程:2x^2 - 3x - 2 = 0。
解:首先,我们计算判别式Δ = b^2 - 4ac = (-3)^2 - 4*2*(-2) = 9 + 16 = 25。
高一数学竞赛试题参考答案

高一数学竞赛试题参考答案一、选择题:(本题共10小题,每题4分,共40分。
在每小题给出的四个选项中,只有一项符合题目要求的。
)1.[答案] B[解析] 当a ≤0时,B =∅,满足B ⊆A ;当a >0时,欲使B ⊆A ,则⎩⎪⎨⎪⎧3-a ≥-43+a ≤4⇒a ≤1.故选B.2.[答案] C[解析] 由已知ax 2+ax -3≠0恒成立, 当a =0时,-3≠0成立; 当a ≠0时,Δ<0,∴a 2+12a <0, ∴-12<a <0,综上所述,a ∈(-12,0].3.C 【解析】 依题意,函数y =x 2-ax +12存在大于0的最小值,则a >1且a 2-2<0,解得a∈(1,2),选择C.4.B 【解析】 ∵2=log 24>log 23>log 22=1,故f (log 23)=f (1+log 23)=f (2+log 23)=f (3+log 23)=⎝ ⎛⎭⎪⎫123+log 23=124 5.C 【解析】 由f (x -1)=f (x +1)知f (x )是周期为2的偶函数,因为x ∈[0,1]时,f (x )=x 2,故当x ∈[-1,0],-x ∈[0,1]时,f (x )=f (-x )=(-x )2=x 2,由周期为2可以画出图象,结合y =⎝⎛⎭⎫110x的图象可知,方程f (x )=⎝⎛⎭⎫110x在x ∈⎣⎡⎦⎤0,103上有三个根,要注意在x ∈⎝⎛⎦⎤3,103内无解. 6.[答案] D[解析] 由题意,DE ⊥平面AGA ′, ∴A ,B ,C 正确,故选D. 7.[答案] B[解析] 设f (x )=2x -3-x ,因为2x ,-3-x 均为R 上的增函数,所以f (x )=2x -3-x 是R 上的增函数.又由2x -3-x >2-y -3y =2-y -3-(-y ),即f (x )>f (-y ),∴x >-y ,即x +y >0.8.[答案] A[解析] m =x -1-x ,令t =1-x ≥0,则x =1-t 2,∴m =1-t 2-t =-(t +12)2+54≤1,故选A.9.[答案] B[解析] 将f (x )=x 2+(a -4)x +4-2a 看作是a 的一次函数,记为g (a )=(x -2)a +x 2-4x +4. 当a ∈[-1,1]时恒有g (a )>0,只需满足条件⎩⎪⎨⎪⎧ g (1)>0,g (-1)>0,即⎩⎪⎨⎪⎧x 2-3x +2>0,x 2-5x +6>0,解之得x <1或x >3. 10.[答案] B[解析] 由已知得f (x )=⎩⎨⎧x 2-2(-1≤x ≤32),x -x 2(x <-1或x >32),如图,要使y =f (x )-c 与x 轴恰有两个公共点,则-1<c <-34或c ≤-2,应选B.二、填空题(本大题共4小题,每小题4分,共16分。
高级中学高一数学竞赛班选拔考试试题第一卷
高级中学高一数学竞赛班选拔考试试题第一卷(第一轮考试时间100分钟,满分100分)一.选择题:(每题6分,共36分)1.若非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},则能使A⊆(A B)成立的所有a的集合是( )(1998年高中数学联赛一试第二题6分)(A){a|1≤a≤9} (B){a|6≤a≤9} (C){a|a≤9} (D)Φ2.根据图中骰子的三种不同状态显示的数字,推出?处的数字是()A.1 B.2 C.3 D.63.已知有理数x、y、z两两不等,则,,x y y z z xy z z x x y------中负数的个数是( )A.1个B.2个C.3个D.0个或2个4.有A、B、C、D、E共5位同学一起比赛象棋,每两人之间只比赛1盘,比赛过程中统计比赛的盘数知:A赛了4盘,B赛了3盘,C赛了2盘,D赛了1盘,则同学E赛了()盘A.1 B.2 C.3 D.45.一椭圆形地块,打算分A、B、C、D四个区域栽种观赏植物,要求同一区域种同一种植物,相邻的两块种不同的植物,现有4那么有()种栽种方案.A.60B.68C. 78D.846.甲乙两人轮流在黑板上写下不超过10的正整数,规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字()时有必胜的策略A .10 B.9 C.8 D.6二.填空题:(每小题6分,共42分)1.当整数m =_________时,代数式13m 6-的值是整数. 2.已知:a 、b 、c 都不等于0,且|abc |abc |c |c |b |b |a |a +++的最大值为m ,最小值为n ,则 (m+n) 2004=_________.3.若n 是正整数,定义n !=n ×(n-1)×(n-2)×…×3×2×1,设 m =1!+2!+3!+4!+…+2003!+2004!,则m 的末两位数字之和为4.不等式|x |3-2x 2-4|x |+3<0的解集是__________5. 小华、小亮、小红3位同学分别发出新年贺卡x 、y 、z 张,如果已知x 、y 、z 的最小公倍数是60;x 、y 的最大公约数是4;y 、z 的最大公约数是3,已知小华至少发出了5张贺卡,那么,小华发出的新年贺卡是 张.6.小敏购买4种数学用品:计算器、圆规、三角板、量角器的件数和用钱总数列下表:则7. 已知a 为给定的实数,那么集合M ={x ∈R| x 2-3x-a 2+2=0}的子集的个数是三.解答题:(每小题各11分,共22分,写出必要的解答过程)1、甲、乙两人到物价商店购买商品,商品里每件商品的单价只有8元和9元两种.已知两人购买商品的件数相同,且两人购买商品一共花费了172元,求两人共购买了两种商品各几件?2、 长方形四边的长度都是小于10的整数(单位:厘米),这四个长度数可以构成一个四位数,这个四位数的千位数字与百位数字相同,并且这个四位数是一个完全平方数,求这个长方形的面积.参考解答一、选择题1.B 2.D 3. B 4.B 5.D 6. D二、填空题1.0或1 2.0 3.4 4. 由原不等式分解可得(|x|-3)(x 2+|x|-1)<0,由此得所求不等式的解集为5. 20 6.58 7. 4三、解答题:1、解:设每人购买了n 件商品,两人共购买了单价为8元的x 件,单价为9元的有y 件.则 ⎩⎨⎧=+=+.17298,2y x n y x 解之,得⎩⎨⎧-=-=.16172,17218n y n x 因为0,0≥≥y x ,所以4310959≤≤n . 所以整数10=n .故⎩⎨⎧==.12,8y x2.解: 设长方形的边长为xcm 、ycm ,则四位数N=1000x+100x+10y+y=1100x+11y=11(100x+y )=11(99x+x+y ) ∵N 是一个完全平方数,11为质数,∴x+y 能被11整除,又∵1≤x ≤9,1≤y ≤9 ∴2 ≤x+y ≤18,得x+y=11∴N=11(99x+x+y )=112(9x+1) ∴9x+1是一个完全平方数, 经试算知当x=7时满足条件,故y=4,从而长方形的面积=7×4=28cm 2.。
数学竞赛高一试题及答案

数学竞赛高一试题及答案一、选择题(每题5分,共10分)1. 已知函数\( f(x) = 2x^2 - 3x + 1 \),求\( f(-1) \)的值。
A. 4B. 6C. 8D. 102. 一个圆的半径为5,求其面积。
A. 25πB. 50πC. 75πD. 100π二、填空题(每题5分,共10分)3. 已知\( a \)、\( b \)、\( c \)为三角形的三边长,且\( a^2 + b^2 = c^2 \),这个三角形是________。
4. 将\( 1 \)、\( 2 \)、\( 3 \)三个数字排列成三位数,所有可能的组合数是________。
三、解答题(每题15分,共30分)5. 已知数列\( \{a_n\} \)满足\( a_1 = 1 \),\( a_{n+1} = a_n + 2n \),求\( a_5 \)。
6. 一个直角三角形的斜边长为\( 5 \),一条直角边长为\( 3 \),求另一条直角边长。
四、证明题(每题15分,共30分)7. 证明:对于任意正整数\( n \),\( 1^3 + 2^3 + ... + n^3 = (1 + 2 + ... + n)^2 \)。
8. 证明:若\( a \)、\( b \)、\( c \)是三角形的三边长,且\( a^2 + b^2 = c^2 \),则这个三角形是直角三角形。
五、综合题(每题15分,共20分)9. 一个工厂计划在一年内生产\( x \)个产品,已知生产每个产品的成本是\( 10 \)元,销售每个产品的价格是\( 20 \)元。
如果工厂希望获得的利润不少于\( 10000 \)元,求\( x \)的最小值。
10. 已知函数\( g(x) = x^3 - 6x^2 + 11x - 6 \),求\( g(x) \)的极值点。
答案:一、选择题1. 答案:B. 6(计算方法:\( f(-1) = 2(-1)^2 - 3(-1) + 1 = 2 + 3 + 1 = 6 \))2. 答案:B. 50π(计算方法:圆面积公式为\( πr^2 \),代入\( r = 5 \))二、填空题3. 答案:直角三角形4. 答案:6(排列组合方法:\( 3 \times 2 \times 1 = 6 \))三、解答题5. 答案:\( a_5 = 1 + 2(1) + 2(2) + 2(3) + 2(4) = 1 + 2 + 4 +6 + 8 = 21 \)6. 答案:根据勾股定理,另一条直角边长为\( 4 \)(计算方法:\( 5^2 - 3^2 = 4^2 \))四、证明题7. 证明:根据等差数列求和公式,\( 1 + 2 + ... + n =\frac{n(n+1)}{2} \),立方后得到\( \left(\frac{n(n+1)}{2}\right)^2 \),展开后即为\( 1^3 + 2^3 + ... + n^3 \)。
高一竞赛数学试卷1

高一竞赛数学试卷一、选择题(每小题5分,共30分)1)A 、2B 、3C 、4D 、52、已知设函数,则的最大值为( )A 、1B 、2C 、D 、4 3、设[]x 是不超过x 的最大整数,则[][][]=+++500log 2log 1log 333 ( ) A 、2014 B 、2026 C 、2032 D 、21424、定义在R 上的偶函数()f x 满足:对任意的[)()1212,0,,x x x x ∈+∞≠均有()()()()12120f x f x x x --<,则满足:()1213f x f ⎛⎫-> ⎪⎝⎭的x 的取值范围是( )A 、12,33⎛⎫ ⎪⎝⎭B 、12,33⎡⎤⎢⎥⎣⎦ C 、12,23⎛⎫⎪⎝⎭ D 、12,23⎡⎤⎢⎥⎣⎦5、一个三棱锥的四个面所在的平面把空间分成的部分数为( ) A 、 9 B 、 11 C 、13 D 、156、到两互相垂直的异面直线的距离相等的点有( )A 、1个B 、3个C 、4个D 、无穷多个二、填空题(每小题5分,共40分)7、设集合{[]}{}22,2A x x x B x =-==<,其中[]x 表示不大于x 的最大整数,则A B = 。
8、函数2log ()341xf x x -=--的值域是 。
9、若直线y x b =+与曲线y =有且只有1个公共点, 则b 的取值范围是____________。
10、正方体的截平面不可能是 :⑴钝角三角形;⑵直角三角形;⑶菱形;⑷正五边形;⑸正六变形。
11、设方程310x x ++=与10x =的根分别是,αβ, 则αβ+=__________。
12、方程1112011x y +=有 组正整数解。
()sin 1θ-()1,()2,()6,xf x xg xh x x =+==-+()min{(),(),()}F x f x g x h x =()F x 7214、正方体1111ABCD A B C D -的棱长为1,P 是面对角线1BC 上的一动点,Q 是底面ABCD 上的一动点,则1D P PQ +的最小值等于 。
高一上学期数学竞赛选拔试卷

当 时, ;当 时, 。所以当 时, 。
从而 ,此时 ,经检验 是原方程的解
16.解:如图,设L、N分别是PB、PC的中点,
连结MD,ME,ML,MN,DL和EN
则ML∥PC,且ML=PC;MN∥PB,且MN=PB
又由∠PDB=∠PEC=90°知DL=PB,EN=PC
因此DL=MN①ML=EN②
A.m>-1 B.m≥0 C.-1<m<0 D.-1<m<1
4.下列三数 的大小关系正确的是
A. B.
C. D.
5.设函数 的定义域是 时,a的取值范围为集合M;它的值域是R时,a的取值范围为集合N,则下列表达式中正确的是
A. B. C. D.
6.已知函数 的图象与函数 ( 且 )的图象关于直线 对称,记 .若 在区间 上是增函数,则实数 的取值范围是
并且PLMN为平行四边形
于是∠PLM=∠PNM
∠DLP=2∠PBA=2∠PCA=∠ENP
故∠DLM=∠DLP+∠PLM=∠ENP+∠PNM=∠ENM③
因而由①②③知△DML≌△MEN
故DM=EM,从而BC的中点M在DE的垂直平分线上
即DE的垂直平分线必经过BC的中点M.
16、(本题满分20分)
函数 的定义域为 ,且满足:
①对于任意的 , ;
② 在区间 上单调递增.
(1)求 和 的值;
(2)求不等式 的解集.
参考答案
1.C解: ; 。要使 ,则
,即 。所以数对 共有30
2.C;3. A
4.解:因为 , 。
令 ,则 。又因为 ,所以 。
再令 ,则 ,而 ,所以 。
综上所述,有 。因此选(C)。
高一数学竞赛班选拔考试试卷
重点中学高一数学竞赛班选拔考试试卷1.{}{}0,1A x x =⊆,用列举法表示集合A=___________。
2.新高一某班的50名学生中,参加数学竞赛辅导的有22人,参加物理竞赛辅导的有20人,参加化学竞赛辅导的有19人,既参加数学又参加物理的有15人,既参加数学又参加化学的有12人,既参加物理又参加化学的有10人,三科都没参加的有20人,则三科都参加的有_____________人。
3.在小于100的正整数n 中,能使分数1(332)(41)n n ++化为有限小数的n 的所有可能值为___________。
4.在一个圆形时钟的表面,OA 表示秒针,OB 表示分针(O 为两针的旋转中心)。
若现在时间恰好是12点整,则经过_______秒后,OAB ∆面积第一次达到最大。
(用分数表示) 5.已知a 、b 、c 为整数,且2006,2005a b c a +=-=,若a b <,则a b c ++的最大值为________. b=2013-a>a 则a<1006.5 a 最大为1006 c=2005+a 所以a+b+c=2006+2005+a=a+4011所以最大值是1006+4011=50176.如果两个一元二次方程20x x m ++=与210mx x ++=都有两个不相等的实数根,并且其中有一个公共的实根0x ,那么0x =_________。
7.如果一个两位数5x 与一个三位数3yz 的积是29400,那么,x y z ++=____。
29400/400>73, 29400/300=98x 只能为7或8或929400/75=392只有这个是整数。
所以x+y+z=7+9+2=18因为29400=75*392所以x=7、y=9,z=2所以x+y+z=7+9+2=188.一名模型赛车手遥控一辆赛车。
先前进1米,然后原地逆时针方向旋转角0(0180)αα<<,被称为一次操作。
高中数学高一级第一学期数学竞赛试题(word文档有答案)
高中数学高一级第一学期数学竞赛试题班级 姓名 学号 评分一. 选择题(10*4=40)1.设},0)()({,}0)({,}0)({=⋅=Φ≠==Φ≠==x g x f x P x g x N x f x M 则集合P 恒满足的关系为( ) A.N M P ⋃= B.N M P ⋃⊆ C.Φ≠P D.N M P ⋂=2.ABC ∆中,c b a ,,分别是角C B A ,,的对边,==-=+B C A b c a 则,3,2π( )A.839arccos B.45 C.60 D.839arcsin3.设⎪⎩⎪⎨⎧=为无理数为有理数x x x f 01)( ,对于所有x 均满足)()(x g x xf ≤的函数)(x g 是( )A.x x g sin )(=B.x x g =)(C.2)(x x g =D.x x g =)(4.已知,都是长度小于1的向量,对于任意非负实数,,b a 下列结论正确的是( )A.b a u a +≤+B.b a u a +≥+C.b a u a +=+D.不能确定b a u a ++的大小关系5.设ABC ∆的三个内角C B A ,,成等差数列,其外接圆半径为1,且有+-C A sin sin ,22)cos(22=-C A 则此三角形的面积为 ( ) A.433 B.43 C.43或433 D.43或533 6.函数)cos(3)sin()(θθ-++=x x x f 的图象关于y 轴对称,则=θ( )A.)(6Z k k ∈-ππ B.)(3Z k k ∈-ππ C.)(62Z k k ∈-ππ D.)(32Z k k ∈-ππ7.数列}{n a 中,11=a 且411++=+n n n a a a ,则=99a ( ) A.412550 B.2500 C.412450 D.24018.设函数22)(2+-=x ax x f 对于满足41<<x 的一切0)(>x f ,则a 的取值范围是( )A.1>aB.1-<aC.11<<-aD.1-≥a9.设函数xxx y +-+=11arctan arctan ,则它的值域为( ) A.]4,43[ππ-- B.}43,4{ππ- C.)4,43(ππ-- D. )4,43(ππ-10.函数8422)(22+-++-=x x x x x f 的最小值是( )A.23B.15+C.10D.22+二. 填空题(4*5=20)11.ABC ∆中,36=∠A ,F E ,分别在边AC AB ,上,且CF BE =,N M ,分别是线段CE BF ,的中点,则直线MN 与直线AB 所成的较小的角的大小为 。
高一数学《函数与方程》竞赛试题与答案
高一数学《函数与方程》竞赛试题第I 卷(选择题)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2021·福建·厦门一中高一竞赛)若函数y =f (x )图象上存在不同的两点A ,B 关于y 轴对称,则称点对[A ,B ]是函数y =f (x )的一对“黄金点对”(注:点对[A ,B ]与[B ,A ]可看作同一对“黄金点对”)已知函数2229,0()4,041232,4x x f x x x x x x x +<⎧⎪=-+≤≤⎨⎪-+>⎩,则此函数的“黄金点对”有()A .0对B .1对C .2对D .3对2.(2021·黑龙江·鸡西实验中学高一竞赛)已知函数()lg ,010=11,10x x f x x x ⎧<≤⎨-+>⎩,若,,a b c 互不相等,且()()()f a f b f c ==,则abc 的取值范围是()A .()1,10B .()111,C .()1011,D .()10+∞,3.(2022安徽·高一竞赛)已知单调函数()f x 的定义域为(0,)+∞,对于定义域内任意x ,[]2()log 3f f x x -=,则函数()()9g x f x x =+-的零点所在的区间为A .(1,2)B .(2,3)C .(3,4)D .(4,5)4.(2022浙江温州·高一竞赛)已知函数32log ,0()41,0x x f x x x x ⎧>=⎨++≤⎩,函数()()F x f x b =-有四个不同的零点1x ,2x ,3x ,4x ,且满足:1234x x x x <<<,则1234x x x x +的值是().A .-4B .-3C .-2D .-15.(2022广东潮州·高一竞赛)已知()()20f x ax bx c a =++>,分析该函数图像的特征,若方程()0f x =一根大于3,另一根小于2,则下列推理不一定成立的是()A .232ba<-<B .240ac b -≤C .()20f <D .()30f <6.(2022湖南·衡阳市八中高一竞赛)设()f x 是定义在R 上的偶函数,对任意的x ∈R ,都有()()22f x f x -=+,且当[]2,0x ∈-时,()122xf x ⎛⎫=- ⎪⎝⎭,若在区间(]2,6-内关于x 的方程()()log 20(01)a f x x a -+=<<恰有三个不同的实数根,则实数a 的取值范围是()A.1,42⎛⎫⎪ ⎪⎝⎭B.4⎛ ⎝⎭C .10,2⎛⎫⎪⎝⎭D .1,12⎛⎫ ⎪⎝⎭7.(2022陕西渭南·高二竞赛)已知定义在R 上的函数()f x 满足:(](]222,1,0()2,0,1x x f x x x ⎧--∈-⎪=⎨-∈⎪⎩且(2)()f x f x +=,52()2xg x x -=-,则方程()()f x g x =在区间[]37-,上的所有实根之和为()A .14B .12C .11D .78.(2022河南·高三竞赛(理))已知函数lg ,0,()2,0,x x x f x x ⎧>⎪=⎨≤⎪⎩若关于x 的方程2()()10f x af x -+=有且只有3个不同的根,则实数a 的值为A .2-B .1C .2D .3二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.9.(2021·福建·厦门一中高一竞赛)已知定义在R 上的偶函数f (x ),满足f (x +2)=-f (x )+f (1),且在区间[0,2]上是增函数,下列命题中正确的是()A .函数()f x 的一个周期为4B .直线4x =-是函数()f x 图象的一条对称轴C .函数()f x 在[6,5)--上单调递增,在[5,4)--上单调递减D .方程()0f x =在[0,2021]内有1010个根10.(2022·湖南衡阳·高二竞赛)已知函数()22,0log ,0x x f x x x +≤⎧=⎨>⎩,若()f x a =有三个不等实根123,,x x x ,且123x x x <<,则()A .()f x 的单调递减区间为()0,1B .a 的取值范围是()0,2C .123x x x 的取值范围是(]2,0-D .函数()()()g x f f x =有4个零点11.(2022·山东德州·高二竞赛)对x ∀∈R ,[]x 表示不超过x 的最大整数.十八世纪,[]y x =被“数学王子”高斯采用,因此得名为高斯函数.人们更习惯称之为“取整函数”,例如:[]3.54-=-,[]2.12=,则下列命题中的真命题是()A .[1,0]x ∀∈-,[]1x =-B .x ∀∈R ,[]1x x <+C .函数[]y x x =-的值域为[0,1)D .方程22022[]20230x x --=有两个实数根12.(2022·辽宁高二竞赛)已知函数()221,0log ,0xx f x x x ⎧+≤⎪=⎨>⎪⎩,()()()222g x f x mf x =-+,下列说法正确的是()A .()y f x =只有一个零点()1,0B .若()y f x a =-有两个零点,则2a >C .若()y f x a =-有两个零点1x ,()212x x x ≠,则121=x x D .若()g x 有四个零点,则32m >第II 卷(非选择题)三、填空题:本题共4个小题,每小题5分,共20分.13.(2021·浙江省杭州学军中学高一竞赛)已知函数()11||f x x x x +=-++,则方程()()21f x f x -=所有根的和是___________.14.(2022浙江高三竞赛)已知()f x 是偶函数,0x ≤时,()[]f x x x =-(符号[]x 表示不超过x 的最大整数),若关于x 的方程()() 0f x kx k k =+>恰有三个不相等的实根,则实数k 的取值范围为__________.15.(2021·浙江省杭州学军中学高一竞赛)已知函数222101,()2 1,x mx x f x mx x ⎧+-≤≤=⎨+>⎩,,,若()f x 在区间[)0,+∞上有且只有2个零点,则实数m 的取值范围是_________.16.(2021·浙江省杭州学军中学高一竞赛)已知函数22log (2),20()21,0x x f x x x x +-<≤⎧=⎨-+>⎩,若函数[]2()(())(1)(())()g x f f x a f f x R a a =-++∈恰有8个不同零点,则实数a 的取值范围是____________.四、解答题:本大题共5小题,17题共10分,其余各题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤.17.(2022湖南·高三竞赛)已知二次函数2()163f x x x p =-++.(1)若函数在区间[1,1]-上存在零点,求实数p 的取值范围;(2)问是否存在常数(0)q q ≥,使得当[,10]x q ∈时,()f x 的值域为区间D ,且D 的长度为12q -.(注:区间[,]a b ()a b <的长度为b a -).18.(2022浙江高二竞赛)已知函数()2,,f x x ax b a b =++∈R ,(1)0f =.(1)若函数()y f x =在[0,1]上是减函数,求实数a 的取值范围;(2)设()()()21212x xF x f a =-+--,若函数()F x 有三个不同的零点,求实数a 的取值范围;19.(2022四川高一竞赛))已知函数()21log f x x =+,()2xg x =.(1)若()()()()()F x f g x g f x =⋅,求函数()F x 在[]1,4x ∈的值域;(2)若()H x 求证()()11H x H x +-=.求12320212022202220222022H H H H ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值;(3)令()()1h x f x =-,则()()()()24G x h x k f x =+-,已知函数()G x 在区间[]1,4有零点,求实数k 的取值范围.20.(2022广东高一竞赛)已知函数21()log 4(1)22x xf x k k k ⎡⎤=⋅--++⎢⎣⎦.(1)当2k =时,求函数()f x 在[0,)+∞的值域;(2)已知01k <<,若存在两个不同的正数a ,b ,当函数()f x 的定义域为[],a b 时,()f x 的值域为[1,1]a b ++,求实数k 的取值范围.21.(2022·山西运城高二竞赛)已知函数()()44log 41log 2x x f x =+-,()142log 23x g x a a -⎛⎫=⋅- ⎪⎝⎭.(1)若1x ∀∈R ,对[]21,1x ∃∈-,使得()221420x xf x m +≥-成立,求实数m 的取值范围;(2)若函数()f x 与()g x 的图象有且只有一个公共点,求实数a 的取值范围.22.(2022江苏盐城高一竞赛)若定义域为(0,)+∞的函数()f x 满足()0a f x f x ⎛⎫+= ⎪⎝⎭,则称()f x 为“a 型”弱对称函数.(1)若函数sin ()ln 1x mf x x x +=-+为“1型”弱对称函数,求m 的值;(2)已知函数()f x 为“2型”弱对称函数,且函数()f x 恰有101个零点(1,2,...,101)i x i =,若1011i i x =∑>λ对任意满足条件函数()f x 的恒成立,求λ的最大值.高一数学《函数与方程》竞赛试题答案一、单选题:本题共8小题,每小题5分,共40分。
高一新生数学竞赛选拔试题
数学竞赛选拔测试一、选择题1、设集合,,若,则实数的取值范围是()A. C. D.2、设函数,函数的定义域为,则 ( )A.B. C D.3、若,,则一定有A. B. C. D.4、函数的零点个数为( )A.1 B.2 C.3 D.45、若函数是奇函数,则实数的取值范围是()A. B.C. D.6、关于恒成立,则实数的取值范围是()C.7、设,,则( )A B.C D.8、某市生产总值连续两年持续增加,第一年的增长率为,第二年的增长率为,则该市这两年生产总值的年平均增长率为( )A. B.C. D9A D10、设表示不超过的最大整数.若存在实数,使得=1,,…,同时成立,则正整数的最大值是A.3B.4C.5D.6二、填空题11、设一元二次方程有整数根的充要条件是____________________.12、已知常数,函数的图像经过点、,,则___________.13、能说明“若对任意的都成立,则在上是增函数”为假命题的一个函数是__________________.14、已知函数在时取得最小值,则_______________.15、已知,函数,当时,不等式的解集是________________;若函数恰有2个零点,则的取值范围是_________________.三、解答题16,解关于.17、解关于的不等式.18、已知函数是奇函数,且,.(I)求的值;(II)判断并证明的单调性.19、已知,函数.(Ⅰ)当时,解不等式;(Ⅱ)若关于的方程的解集中恰好有一个元素,求的取值范围;(Ⅲ)设,若对任意,函数在区间上的最大值与最小值的差不超过,求的取值范围.20、已知集合.(I)设,,,试判断与的关系;(II)任取,与的关系;(III)能否找到,使得,且.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高级中学高一数学竞赛班选拔考试试题第一卷
(第一轮考试时间100分钟,满分100分)
一.选择题:(每题6分,共36分)
1.若非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},则能使A⊆(A B)成立的所有a的集合是( )(1998年高中数学联赛一试第二题6分)
(A){a|1≤a≤9} (B){a|6≤a≤9} (C){a|a≤9} (D)Φ
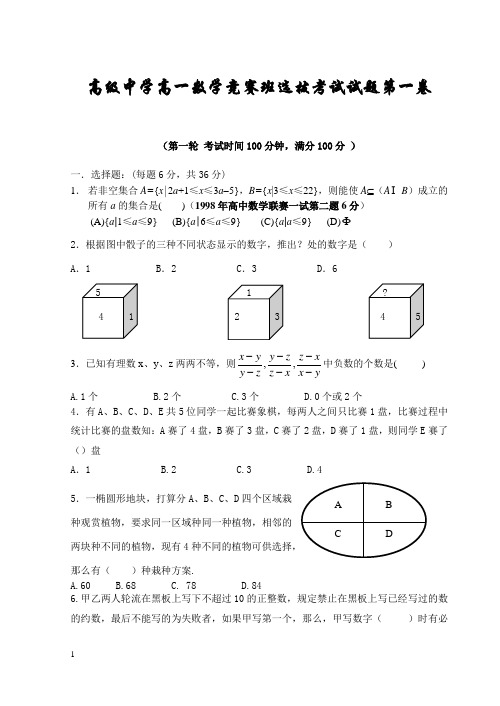
2.根据图中骰子的三种不同状态显示的数字,推出?处的数字是()
A.1 B.2 C.3 D.6
3.已知有理数x、y、z两两不等,则,,
x y y z z x
y z z x x y
---
---
中负数的个数是( )
A.1个
B.2个
C.3个
D.0个或2个
4.有A、B、C、D、E共5位同学一起比赛象棋,每两人之间只比赛1盘,比赛过程中统计比赛的盘数知:A赛了4盘,B赛了3盘,C赛了2盘,D赛了1盘,则同学E赛了()盘
A.1 B.2 C.3 D.4
5.一椭圆形地块,打算分A、B、C、D四个区域栽
种观赏植物,要求同一区域种同一种植物,相邻的
两块种不同的植物,现有4
那么有()种栽种方案.
A.60
B.68
C. 78
D.84
6.甲乙两人轮流在黑板上写下不超过10的正整数,规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字()时有必
胜的策略
A .10 B.9 C.8 D.6
二.填空题:(每小题6分,共42分)
1.当整数m =_________时,代数式
1
3m 6-的值是整数. 2.已知:a 、b 、c 都不等于0,且|abc |abc |c |c |b |b |a |a +++的最大值为m ,最小值为n ,则 (m+n) 2004=_________.
3.若n 是正整数,定义n !=n ×(n-1)×(n-2)×…×3×2×1,设 m =1!+2!+3!+4!+…+2003!+2004!,则m 的末两位数字之和为
4.不等式|x |3-2x 2-4|x |+3<0的解集是__________
5. 小华、小亮、小红3位同学分别发出新年贺卡x 、y 、z 张,如果已知x 、y 、z 的最小公倍数是60;x 、y 的最大公约数是4;y 、z 的最大公约数是3,已知小华至少发出了5张贺卡,那么,小华发出的新年贺卡是 张.
6.小敏购买4种数学用品:计算器、圆规、三角板、量角器的件数和用钱总数列下表:
则7. 已知a 为给定的实数,那么集合M ={x ∈R| x 2
-3x-a 2+2=0}的子集的个数
是
三.解答题:(每小题各11分,共22分,写出必要的解答过程)
1、甲、乙两人到物价商店购买商品,商品里每件商品的单价只有8元和9元两种.已知两人购买商品的件数相同,且两人购买商品一共花费了172元,求两人共购买了两种商品各几件?
2、 长方形四边的长度都是小于10的整数(单位:厘米),这四个长度数可以构成一个四位数,这个四位数的千位数字与百位数字相同,并且这个四位数是一个完全平方数,求这个长方形的面积.
参考解答
一、选择题
1.B 2.D 3. B 4.B 5.D 6. D
二、填空题
1.0或1 2.0 3.4 4. 由原不等式分解可得(|x|-3)(x 2+|x|-1)<0,
由此得所求不等式的解集为5. 20 6.58 7. 4
三、解答题:
1、解:设每人购买了n 件商品,两人共购买了单价为8元的x 件,单价为9元的有y 件.则 ⎩⎨⎧=+=+.17298,2y x n y x 解之,得⎩⎨⎧-=-=.
16172,17218n y n x 因为0,0≥≥y x ,所以4
310959≤≤n . 所以整数10=n .
故⎩
⎨⎧==.12,8y x
2.解: 设长方形的边长为xcm 、ycm ,
则四位数N=1000x+100x+10y+y=1100x+11y=11(100x+y )=11(99x+x+y ) ∵N 是一个完全平方数,11为质数,∴x+y 能被11整除,
又∵1≤x ≤9,1≤y ≤9 ∴2 ≤x+y ≤18,得x+y=11
∴N=11(99x+x+y )=112(9x+1) ∴9x+1是一个完全平方数, 经试算知当x=7时满足条件,故y=4,从而长方形的面积=7×4=28cm 2.。
