苏教版小学数学六年级上册长方体正方体知识点分析
苏教版六年级数学上册全部知识点汇总
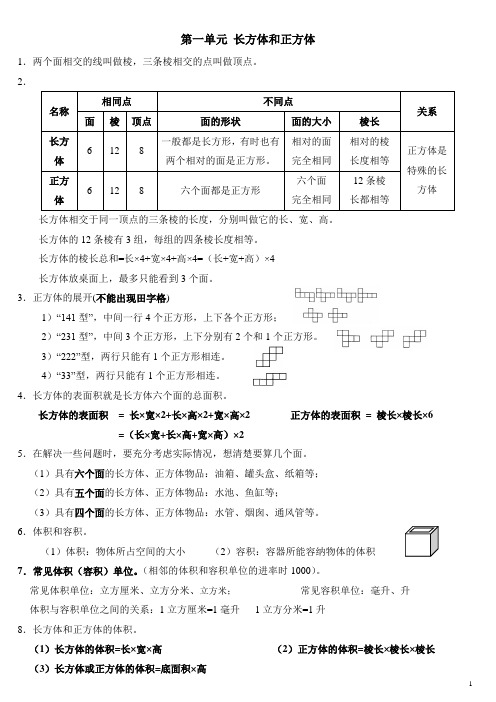
第一单元长方体和正方体1.两个面相交的线叫做棱,三条棱相交的点叫做顶点。
2.名称相同点不同点关系面棱顶点面的形状面的大小棱长长方体6 12 8一般都是长方形,有时也有两个相对的面是正方形。
相对的面完全相同相对的棱长度相等正方体是特殊的长方体正方体6 12 8 六个面都是正方形六个面完全相同12条棱长都相等长方体相交于同一顶点的三条棱的长度,分别叫做它的长、宽、高。
长方体的12条棱有3组,每组的四条棱长度相等。
长方体的棱长总和=长×4+宽×4+高×4=(长+宽+高)×4长方体放桌面上,最多只能看到3个面。
3.正方体的展开(不能出现田字格)1)“141型”,中间一行4个正方形,上下各个正方形;2)“231型”,中间3个正方形,上下分别有2个和1个正方形。
3)“222”型,两行只能有1个正方形相连。
4)“33”型,两行只能有1个正方形相连。
4.长方体的表面积就是长方体六个面的总面积。
长方体的表面积= 长×宽×2+长×高×2+宽×高×2 正方体的表面积= 棱长×棱长×6 =(长×宽+长×高+宽×高)×25.在解决一些问题时,要充分考虑实际情况,想清楚要算几个面。
(1)具有六个面的长方体、正方体物品:油箱、罐头盒、纸箱等;(2)具有五个面的长方体、正方体物品:水池、鱼缸等;(3)具有四个面的长方体、正方体物品:水管、烟囱、通风管等。
6.体积和容积。
(1)体积:物体所占空间的大小(2)容积:容器所能容纳物体的体积7.常见体积(容积)单位。
(相邻的体积和容积单位的进率时1000)。
常见体积单位:立方厘米、立方分米、立方米;常见容积单位:毫升、升体积与容积单位之间的关系:1立方厘米=1毫升1立方分米=1升8.长方体和正方体的体积。
(1)长方体的体积=长×宽×高(2)正方体的体积=棱长×棱长×棱长(3)长方体或正方体的体积=底面积×高第二单元 分数乘法1.分数和整数相乘:用分数的分子和整数相乘的积做分子,分母不变;能约分的要先约分。
苏教版六年级上册长方体和正方体(教师版)(知识梳理+典例分析+举一反三+巩固提升)

第1讲长方体和正方体一、知识梳理知识点一:长方体和正方体的认识1.长方体的特征长方体是由6个长方形(也可能有2个相对的面是正方形)围成的立体图形,有6个面、12条棱和8个顶点,相对的面完全相同、相对的棱长度相等。
2. 长方体的长、宽、高的含义长方体相交于同一顶点的三条棱的长度,分别叫作它的长、宽、高。
知识点二:长方体和正方体的展开图1.沿着正方体(或长方体)的棱将其剪开,可以把正方体(或长方体)展开成一个平面图形,这个平面图形就是正方体(或长方体)的展开图。
2.正方体(或长方体)的展开图的特点:在展开图中,正方体的6个面完全相同(长方体相对的面完全相同),相对的面完全隔开。
3. 一个表面涂色的正方体,把每条棱平均分成相等的若干份,然后切成同样大的小正方体。
(1)3面涂色的小正方体有8个。
(2)如果用n表示把正方体的棱平均分成的份数(n为大于或等于2的自然数),用a、b分别表示2面涂色和1面涂色的小正方体的个数,那么a=(n-2)×12,b=(n-2)2×6。
知识点三:长方体、正方体的表面积计算1.意义长方体(或正方体)6个面的总面积。
2.计算方法(1)长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2。
(2)正方体的表面积=棱长×棱长×6。
知识点四:体积与体积单位1.体积的意义:物体所占空间的大小叫作物体的体积。
2.容积的意义:容器所能容纳物体的体积叫作容器的容积。
常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3和m3。
计量液体的体积,通常用升或毫升作单位。
1立方分米 = 1升,1立方厘米 = 1毫升知识点五:长方体和正方体的体积1.长方体的体积=长×宽×高,字母公式为V=abh。
2.正方体的体积=棱长×棱长×棱长,字母公式为V=a3。
苏教版六年级数学(上册)长方体和正方体知识点汇总

长方体和正方体一、长方体和正方体的认识<一个长方体至少可以有两个面是正方形,最多可以有6各面是正方形,但不会存在3个、4个、5个面是正方形!练习:(1)判断并改正:1、长方体的六个面一定是长方形; ( )2、正方体的六个面面积一定相等; ( )3、一个长方体(非正方体) 最多有四个面面积相等; ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )~8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
( )11、有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( )12、长方体和正方体最多可以看到3个面。
( )13、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( )14、长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( )15、一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )(2)填空:\1、一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
2、一个长方体的底面是一个正方形,则它的4个侧面是( )形。
3、正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
4、把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)×4 长+宽+高=棱长和÷4)正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的,因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
前和后面的彩带长度=高的长度;左和右面的彩带长度=高的长度;上和下面的彩带长度=长的长度。
苏教版六年级数学(上册)长方体和正方体知识点汇总

长方体和正方体一、长方体和正方体的认识面是正方形!练习:(1)判断并改正:1、长方体的六个面一定是长方形; ( )2、正方体的六个面面积一定相等; ( )3、一个长方体(非正方体) 最多有四个面面积相等; ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
( )11、有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( )12、长方体和正方体最多可以看到3个面。
( )13、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( )14、长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( )15、一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )(2)填空:1、一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
2、一个长方体的底面是一个正方形,则它的4个侧面是( )形。
3、正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
4、把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)×4 长+宽+高=棱长和÷4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的, 因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
前和后面的彩带长度=高的长度;左和右面的彩带长度=高的长度;上和下面的彩带长度=长的长度。
需要彩带的长度=高×4+长×2+宽×2+打结部分长度20×4+30×2+10=150cm练习:(1)有一个长方体的鱼缸,长50厘米,宽30厘米,高30厘米,需要在用铝合金包裹玻璃连接处,需要( )米的铝合金。
苏教版小学六年级数学上册知识点(最新最全)

苏教版小学六年级数学上册知识点(最新最全)苏教版数学六年级上册知识点第一单元:长方体和正方体长方体和正方体是几何体的两种常见形式。
长方体有6个面,其中4个面是长方形,另外2个面是正方形。
正方体有8个面,全部都是正方形。
它们的面、棱和顶点都有特定的特征。
表面积是指长方体或正方体6个面的总面积。
计算长方体表面积的公式是2×(长×宽+长×高+宽×高),计算正方体表面积的公式是6×(棱长的平方)。
体积是指物体所占空间的大小,容积是指所能容纳其他物体的体积。
计算长方体和正方体的体积可以使用公式V=长×宽×高和V=棱长的立方,单位可以是立方米、立方厘米等等。
第二单元:分数乘法分数乘法可以用来表示相加的和或者一个数的几分之几。
与整数相乘时,可以将整数与分数的分子相乘,分数的分母作为分母,最后约分成最简分数。
与分数相乘时,可以用分子相乘的积作为分子,用分母相乘的积作为分母,最后约分成最简分数。
分数连乘可以用分子连乘的积作为分母,分母连乘的积作为分母,计算过程中能约分的先约分,可以使计算简便。
倒数是指乘积为1的两个数互为倒数。
任何整数都可以看作为分母是1的分数。
求一个数的倒数,只要将这个数的分子与分母交换位置。
1的倒数是1.假分数的倒数都小于或等于1(或者说不大于1);真分数的倒数都大于1.第三单元:分数除法分数除法的计算法则是甲数除以乙数(不为0)等于甲数乘乙数的倒数。
分数连除或乘除混合计算可以从左向右依次计算,但一般是遇到除以一个数,把它改写成乘这个数的倒数来计算。
除数大于1时,商小于被除数;除数小于1时,商大于被除数;除数等于1时,商等于被除数。
1.百分数表示一个数是另一个数的百分之几,也称为百分比或百分率。
2.百分数的读法是先写分子,再加上百分号。
注意,百分数后面不带单位。
3.百分数可以与小数互化,方法是去掉百分号并将小数点向左移动两位,或者将小数点向右移动两位并在后面加上百分号。
苏教版六年级上册长方体正方体必会知识点

长方体和正方体必会知识点总结一、算棱长总和1、用两根同样长的铁丝,一根围成一个棱长为4厘米的正方体,另一根围成一个长方体,这个长方体长5厘米,宽4厘米,它的高是多少厘米?2、把棱长是2厘米的3个小正方体拼成一个长方体,这个长方体的棱长和是多少?3、一个由两个正方体拼成的长方体,长方体的棱长和是64厘米,求长方体的宽。
4、一个长方体的底面是正方形,棱长和是120厘米,宽是5厘米,求它的高。
5、一个长方体的食品盒长宽高分别是40厘米、20厘米和15厘米,售货员用红色的塑料绳,如图那样进行了捆扎,接口部分用了30厘米,捆扎用的塑料绳全长多少厘米?二、展开图1、如图是一个长方体中的四个面,请你画出其余两个面,使它成为一个完整的展开图,并算出围这个长方体框架要用多少厘米长的铁丝。
2、如图是一张长方形的硬纸板,请你沿着图中的虚线把这张硬纸板剪成三块,使每块都可以折成一个无盖的正方体。
该怎样剪?(在图中画出来)三、表面涂色的正方体1、将棱长是8厘米的正方体切成整厘米数的小正方体且没有剩余,最多能切多少个?最少能切多少个?2、一个棱长是5分米的正方体木块的表面涂满了红色,把它锯成棱长都是1分米的小正方体木块。
(1)三个面涂有红色的小正方体有多少个?(2)两个面涂有红色的小正方体有多少个?(3)一个面涂有红色的小正方体有多少个?(4)一个面都没有红色的小正方体有多少个?3、把若干个体积相同的小正方体堆成一个大的正方体,然后在大正方体的表面涂上颜色。
已知两个面被涂上颜色的小正方体共有24个,那么这些小正方体一共有多少个?四、算表面积(读题时先看单位,然后考虑几个面,复杂题型前后、左右、上下分组考虑,不要遗漏,无效面积记得减掉)1、一个长方体的无盖玻璃鱼缸,它的长是90厘米,宽是30厘米,高是60厘米,制作这个鱼缸至少需要多大面积的玻璃?2、一节排气管道长1米,它的横截面是一个正方形,边长是2厘米,做一节这样的排气管至少需要多少平方米的铁皮?3、粉刷一间长5米、宽4米、高3米的房间,房间门窗面积是8平方米,这间房的粉刷面积是多少?4、健身中心建一个游泳池,该游泳池的长50米,是宽的2倍,深2·5米,要在池的四周和底面都贴上瓷砖,共需要多少平方米的瓷砖?1、一个长方体的底面积是20平方厘米,高是8厘米,长方体的体积是多少?2、将一个长12 厘米,宽10厘米,高5厘米的长方体截成一个体积最大的正方体,这个正方体的体积是多少?3、一根2米长的长方体木块,平均截成两段后表面积增加了0·6平方米,求原来长方体木块的体积?4、用水泵往一个长50米、宽30米的游泳池中注水,如果这个水泵每时能注水200平方米的水,多少时间才能使水深达2·4米?5、挖一个长10m、宽8m、深5m的长方体蓄水池。
苏教版数学六年级上册各单元知识点整理(重点归纳)

苏教版数学六年级上册知识点第一单元:长方体和正方体1、长方体和正方体的特征发现:相对的2个面在展开图中不能相邻。
正方体展开图:(11种)6种:中间四个一连串,两边各一随便放。
简称“一四一”型3种:二三紧连错一个,三一相连一随便,简称“二三一”型1种:两两相连各错一,简称“二二二”型1种:三个两排一对齐简称“三三”型要求:理解并掌握这些情况,能找准哪2个面是相对的面。
3、表面积概念及计算s=(ab+ah+bh)×2=2ab+2ah+2bh正方体表面积= 棱长×棱长×6s= 6×a×a=6a2注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
4、体积概念及计算5、相关例题:(1)已知长方体a=20cm,b=5cm,h=6cm,求体积。
V=abh=20×5×6=600(cm3)(2) 已知长方体S底=100cm2,h=6cm,求体积。
V=S底×h=100×6=600(cm3)(3) 已知长方体S侧=30cm2,a=20cm,求体积。
V=S侧×长=30×20=600(cm3)(4) 已知正方体的棱长是6cm,求表面积和体积。
S表=6a2=6×6×6=216 cm2;V= a3=6×6×6=216 cm3发现:棱长是6厘米的正方体体积和表面积相等。
(×)原因:虽然数值相等,但单位名称不一样。
(5)测P9(5)一张长40厘米、宽30厘米的长方形铁皮,四角各剪去一个边长5厘米的正方形,做成一个深5厘米的无盖长方体铁盒,这个铁盒的容积是多少?30-5-5=20(厘米)40-5-5=30(厘米) 30×20×5=3000(立方厘米)(6)测P11(4)长方体的长是12厘米,高8厘米,阴影部分两个面的面积和是180平方厘米,这个长方体的体积是多少立方厘米?180÷(12+8)=9(厘米) 12×9×8=864(立方厘米)(7)测P16(8)一个密封的长方体玻璃罐,长30厘米,宽18厘米,高12厘米。
苏教版六年级上册数学第一单元——长方体和正方体基础知识梳理

长方体和正方体基础知识梳理一、长方体和正方体的特征二、正方体的展开图(1)141型:(2)231型:(3)222型:(4)33型:三、长方体和正方体的棱长总和(1)长方体的棱长总和=长×4+宽×4+高×4=(长+宽+高)×4 转化:高=棱长总和÷4-长-宽(2)正方体的棱长总和=棱长×12转化:棱长=棱长总和÷12四、长方体和正方体的表面积(1)长方体的侧面积=底面周长×高(2)长方体的底面积=长×宽(3)长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2=(长+宽)×2×高+长×宽×2(4)正方体的表面积=棱长×棱长×6=棱长²×6五、长方体和正方体的体积(1)长方体的体积=长×宽×高(2)正方体的体积=棱长×棱长×棱长=棱长³(3)长方体(正方体)的体积=底面积×高(4)体积单位: 1m³=1000dm³ 1dm³=1000cm³ 1m³=1000000cm ³1L=1dm³ 1mL=1cm³六、物体浸没问题(1)完全浸没①物体的体积=容器底面积×水面上升(下降)的高度②水面上升(下降)的高度=物体的体积÷容器底面积③容器底面积=物体的体积÷水面上升(下降)的高度④水面现在的高度=水面原来的高度+水面上升的高度=水面原来的高度-水面下降的高度(2)不完全浸没①水的体积=容器底面积×水面原来的高度②水面现在的高度=水的体积÷(容器底面积-物体底面积)③水面上升的高度=水面现在的高度-水面原来的高度④水的体积=(容器底面积-物体底面积)×水面现在的高度七、表面涂色的正方体一个表面涂色的大正方体,棱长被平均分成n份,变成了若干个小正方体,那么:小正方体的个数:n³3面涂色的个数:82面涂色的个数:12(n-2)1面涂色的个数:6(n-2)²没有涂色的个数:(n-2)³八、表面涂色的长方体一个表面涂色的长方体,长、宽、高分别被平均分成a、b、h份,变成了若干个小正方体,那么:小正方体的个数:a×b×h3面涂色的个数:82面涂色的个数:4(a-2)+4(b-2)+4(h-2)1面涂色的个数:2(a-2)(b-2)+2(a-2)(h-2)+2(b-2)(h-2)没有涂色的个数:(a-2)(b-2)(h-2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏教版小学数学六年级上册长方体正方体知识点分析
长方体、正方体相关易混点总结:
1、棱的长度:注意是计算长度,长度单位:厘米、分米、米。
不能和表面积、体积混淆。
计算长度就是看清那几个棱,相加就行。
如测验卷中的纸盒用绳子捆扎。
用铁丝焊一个长方体框架。
这种就是求长度的。
注意到计算长度,看清了,都能做对的。
2、面积(表面积)——面积单位:平方厘米、平方分米、平方米,相邻单位的进率是100。
一般比如讲需要多少纸板、需要多少玻璃、粉刷面积、贴磁砖等就是计算面积。
(1)纸盒:完整的是6个面。
不完整的:比如书本16页饼干盒的侧面一圈是4个面。
无盖的纸盒、长方体的拎袋,就是没有“上面”,共5个面。
17页的影集套,少一个“左面”。
(四个侧面)(没有上面)(没有左侧面)
(2)游泳池、玻璃鱼缸,5个面,少一个“上面”。
(3)粉刷油漆教室、房间的墙面,要看清有没有天花板(顶),地面要不要粉刷油漆(一般地面是不粉刷的),再确定是5个面还是4个面,另外要注意扣除门窗的面积。
(4)贴磁砖:卫生间贴磁砖,地面和墙要贴磁砖的,看清顶上要不要贴。
游泳池贴磁砖,那就是5个面,最上面是空的没地方贴的。
书本18页的综合题,就是要看清是哪几个面,比如第7题昆虫箱,木板和纱网分别计算。
第10题火柴盒,内盒和外盒要分别计算,内盒少一个“上面”,只有5个面,而外盒是少二个“侧面”,只有4个面。
书本18页最后一个思考题,像这种题目,就是不规则形体,各个面要分别计算,或者要对不同的面进行分类,比如朝向我们的面(正面)一共有一个,“上面”一共有几个,“左面”一共有几个,“右面”一共有几个等等,分类清楚后就好算了。
以上这些是单纯计算表面积的。
测验练习中还有像切开某个长方体,增加多少个面,增加多少面积,这种题目,就是要看清它是从哪个位置来切的,切开以后新增加出来的面是什么样子的,长多少宽多少,注意到这点就能计算出来了。
(这些是书本36页表面积的变化引申出来的题目)
3、体积(容积)
体积单位是立方厘米、立方分米、立方米。
容积单位:升、毫升。
相邻单位的进率是1000,因为是3个10相乘出来的。
体积一般是指最外面的大小,就是一个整体的体积。
容积一般是指放多少东西,是指盒子里面的。
当然一般计算时会忽略盒子的厚度的。
体积的计算方法:长X宽X高或者底面积X高横截面面积X长
书本29页思考题:典型的综合题目:
一个长方体,如果高增加2厘米,就变成一个正方体,这时表面积比原来增加56平方厘米。
原来长方体的体积是多少立方厘米?
这个题目,粗看比较困难,既讲表面积,又求体积。
但是只要分析它的变化情况,就能找到关键。
题目中隐藏了条件,比如,(1)高增加后就变成正方体,而正方体的各条棱是相等的,那说明原来长方体的长和宽是相等的,因为它们都没有增加也能成正方体,说明原来就相等。
(2)表面积比原来增加,看这个图,原来长方体的表面有6个面,现在是正方体了,也是6个面,哪些部分发生了变化呢?注意最上面这个面,不是增加出来的,是原来就有的,和它没有关系,现在增加出来的,只是高增加了2厘米的部分,那它增加的面,是4个小的侧面,这4个小的侧面竟然是一样大的,因为上面说到原来的长方体的长和宽是相等的。
所以,从上面(1)和(2)分析出来,表面积增加了56平方厘米,是4个小侧面增加造成的,那一个小侧面是56÷4=14平方厘米,小侧面的高是2厘米,那小侧面的长是7厘米,也就是原来这个长方体的长和宽都是7厘米,原来的长方体的高是5厘米。
这样就可以计算出原来长方体的体积是245立方厘米。
P32,练习七第9题,
一个花坛,底面是边长1.2米正方形,四周用木条围成,高0.9米。
(1)这个花坛占地多少平方米?(2)用泥土填满这个花坛,大约需要多少立方米泥土?(3)做这样一个花坛,四周大约需要多少平方米的木条?
这个题目,要弄清几个概念,
(1)占地多少平方米?是求占地面积,这个占地面积,其实只有一个底面占地了,所以只要求一个底面的面积就行了。
这个可不是求表面积哟。
(2)需要多少立方米泥土?那这个求容积。
用底面积X高就可以计算了。
(3)四周需要多少平方米的木条?这是求表面积了,注意它只说了四周,那只要算四个侧面就行了。
四个侧面是一样大的,仔细看它的二个棱分别是多少,就好算了。
这题还要注意,这是计算小数乘法,注意小数点。
面积、体积的概念不要混。
P34,6,正方的工艺蜡烛,棱长6厘米,求(1)体积是多少立方厘米?(2)做这个蜡烛盒至少要用多少玻璃?【想想这个蜡烛盒是用几个面做成的?要是6个面的话,蜡烛怎么点呢?】
P34,7,公园入口处12根长方体立柱,每根长2.4米,宽0.8米,高11.5米。
(1)12根立柱一共占地多少平方米?【占地,是指占据地面,那只有最下面是占地的】(2)12根所占的空间有多大?【占据空间的大小叫体积】
(3)在每根立柱的四周和上面贴大理石,每根贴的面积至少是多少平方米?【注意:每根,四周和上面】
后面是学:分数乘法
从计算方面讲,主要是计算时掌握计算的方法,要灵活的就是怎样合理约分,计算灵活。
仔细算应该没问题的。
从应用题方面讲,典型的是求“谁的几分之几”是多少,这样就要注意这个“谁”,它是一个标准,以它为标准来计算的。
做应用题时要看清“谁”和“几分之几”是能放在一起计算的,就是“谁”和“几分之几”不能混错到别的东西或别的分数上去。
