《材料力学》学习资料
材料力学讲义
第一章 绪论及基本概念§1−1 材料力学的任务要想使结构物或机械正常地工作，必须保证每一构件在荷载作用下能够安全、正常地工作。
因此，在力学上对构件有一定的要求：1． 强度，即材料或构件抵抗破坏的能力； 2． 刚度，即抵抗变性的能力；3． 稳定性，承受荷载时，构件在其原有形态下的平衡应保持为稳定平衡§1−2 可变性固体的性质及基本假设可变性固体：理学弹性体、小变性 基本假设：1． 连续、均匀性； 2． 各项同性假设。
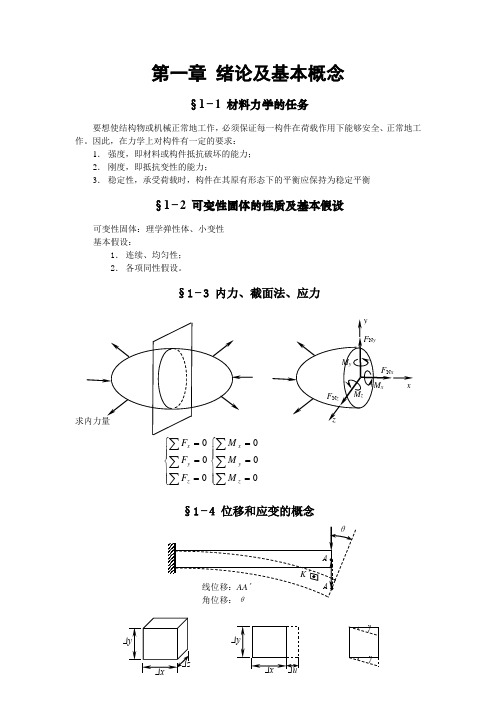
§1−3 内力、截面法、应力⎪⎪⎩⎪⎪⎨⎧===∑∑000z y x F F F ⎪⎪⎩⎪⎪⎨⎧===∑∑000z y xM M M§1−4 位移和应变的概念x u x x ∆∆=→∆0limε称为K 点处沿x 方向的线应变 直角的改变量γ称为切应变。
§1−5 杆件变性的基本形式1．轴向拉伸或轴向压缩2．剪切3．扭转4．弯曲第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸，此时杆被2−1虚线)；若作用力F 压缩杆件(图(图2−2工程中许多构件，(图2−3)、各类(图2−4)等，这类结构的构2−1和图2−2。
§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。
按截面法求解步骤有：可在此截面处假想将杆截断，保留左部分或右部分为脱离体，移去部分对保留部分的作用，用内力来代替，其合力F N ，如图2−5b 或图2−5c 所示。
对于留下部分Ⅰ来说，截面m −m 上的内力F N 就成为外力。
由于原直杆处于平衡状态，故截开后各部分仍应维持平衡。
根据保留部分的平衡条件得 mF N F N （a ）（b ） （c ）图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0(2−1)式中，F N 为杆件任一截面m −m 上的内力，其作用线也与杆的轴线重合，即垂直于横截面并通过其形心，故称这种内力为轴力，用符号F N 表示。
材料力学总复习
一、基本变形
外力
拉伸与压缩
扭转
弯曲
内力
FN F
应力 强度条件
变形
FN
A
max [ ]
l FNl EA
刚度条件
T Me
T
IP
max [ ]
Mnl
GI P
FS 外力
M 外力对形心之矩
My
,
FS
S
* z
Iz
bI z
, max [ ] max [ ]
1、积分法
2、叠加法
∑Fix＝ 0， FN1 cos30°＋FN2＝0 (1)
（2）画节点A的位移图（见图c） （3）建立变形方程
△L1＝△L2cos30°
（4）建立补充方程
△L1＝△LN1＋△LT，
即杆①的伸长△l1由两部份组成，△l N1表示由轴力FN1引起的变形， △lT表示温度升高引起的变形，因为△T 升温，故△lT 是正值。
因为AB 杆受的是拉力，所以沿AB 延
长线量取BB1等于△L1；同理，CB 杆受
的也是拉力，所以沿杆CB 的延长线量取
BB2 等于△L。
分别在点B1 和B2 处作BB1 和BB2 的垂
线，两垂线的交点B′为结构变形后节点
B应有的新位置。即结构变形后成为
ABˊC 的形状。图c称为结构的变形图。
为了求节点B的位置，也可以单独作出节点B的位移图。位移图的作 法和结构变形图的作法相似，如图d所示。
C1 5、求应力并校核强度:
A1
1
FN 1 A
66 .7 MPa ,
2
FN 2 A
133 .2MPa ,
剪切
F AB A1
F BC A2
材料力学知识点总结
三、应力 1.定义 (Definition)：由外力引起的内力的集度 2. 应力 ①平均应力
pm
=
ΔF ΔA
②全应力（总应力）
p lim ΔF dF ΔA0 ΔA dA
③全应力分解为 垂直于截面的应力称为“正应力”
lim ΔFN dFN ΔA0 ΔA dA
位于截面内的应力称为“切应力”
·§3-3 薄壁圆筒的扭转
1 10 r0
姚小宝
薄壁圆筒：壁厚
（r0—圆筒的平均半径）
3.推论 （1）横截面上无正应力，只有切应力；
（2）切应力方向垂直半径或 与圆周相切.
圆周各点处切应力的方向于圆周相切,且数值相等,近似的认为沿壁厚方向各点处
切应力的数值无变化.
4.推导
此式为薄壁圆筒扭转时横截面上切应力的计算公式. 薄壁筒扭转时横截面上的切应力均匀分布,与半径垂直,指向与扭矩的转向一致.
固定铰支座
固定端
5.静定梁的基本形式：
·§4-2 梁的剪力和弯矩
一、内力计算
简支梁 外伸梁
悬臂梁
求内力——截面法
姚小宝
二、内力的符号规定 1.剪力符号
2.弯矩符号
当 dx 微段的弯曲下凸（即该段的下 半部受拉 ）时,横截面 m-m 上的弯矩为 正；
当 dx 微段的弯曲上凸（即该段的下半 部受压）时,横截面 m-m 上的弯矩为负.
2.平面假设
变形前为平面的横截面 ,变形后仍保持为平面.
3.几何关系 倾角 是横截面圆周上任一点 A 处的切应变, d 是 b-b 截面相对于 a-
a 截面象刚性平面一样绕杆的轴线转动的一个角度.
tan
材料力学的基本知识与积累
材料力学的基本知识与积累材料力学是研究材料在受力下的力学性能和变形行为的学科，是工程学中的重要基础学科之一。
它涉及到材料的强度、刚度、韧性、疲劳寿命等方面的问题，对于工程设计和材料选择具有重要的指导意义。
一、材料的力学性能材料的力学性能是指材料在受力下表现出的各种力学特性。
其中，强度是指材料在受力下能够承受的最大应力值，是衡量材料抗拉、抗压能力的指标。
刚度是指材料在受力下的变形程度，是衡量材料抗变形能力的指标。
韧性是指材料在受力下的断裂性能，是衡量材料抗断裂能力的指标。
疲劳寿命是指材料在长期受到交变应力作用下的寿命，是衡量材料抗疲劳性能的指标。
二、材料的力学行为材料在受力下的变形行为可以分为弹性变形和塑性变形两种。
弹性变形是指材料在受力下发生的可恢复的变形，即当外力作用消失时，材料能够恢复到原来的形状。
塑性变形是指材料在受力下发生的不可恢复的变形，即当外力作用消失时，材料无法完全恢复到原来的形状。
材料的弹性模量是衡量材料抗变形能力的指标，塑性变形的程度则取决于材料的屈服强度。
三、材料的屈服与断裂材料的屈服是指材料在受力下发生的从弹性变形到塑性变形的转变。
当材料受到的应力超过其屈服强度时，材料开始发生塑性变形。
而材料的断裂是指材料在受力下发生的从塑性变形到断裂的转变。
当材料受到的应力超过其抗拉强度时，材料发生断裂。
因此，对于工程设计和材料选择来说，需要考虑材料的屈服强度和抗拉强度，以保证材料的安全可靠性。
四、材料的疲劳寿命材料的疲劳寿命是指材料在长期受到交变应力作用下的寿命。
疲劳寿命的长短取决于材料的疲劳强度和疲劳寿命曲线。
疲劳强度是指材料在一定的应力水平下能够承受的循环应力次数，疲劳寿命曲线则是描述材料在不同应力水平下的疲劳寿命的函数关系。
对于工程设计来说，需要选择具有较长疲劳寿命的材料，以保证工程结构的使用寿命。
五、材料力学的积累材料力学的积累是指通过实验和理论研究，对材料的力学性能和变形行为进行总结和归纳的过程。
材料力学知识点总结免费版
材料力学知识点总结材料力学是研究物质内部力学行为以及材料的变形和破坏的学科。
它是工程领域中非常重要的基础学科，涉及材料的结构、性能和应用等方面。
本文将从基本概念、力学性质、变形与破坏等方面对材料力学的知识点进行总结。
1.弹性力学弹性力学是材料力学的基础，研究材料在外力作用下的变形与恢复过程。
弹性力学主要关注材料的弹性性质，即材料在外力作用下是否能够发生恢复性变形。
弹性力学的基本理论包括胡克定律、泊松比等。
2.塑性力学塑性力学研究材料的塑性行为，即材料在外力作用下会发生永久性变形的能力。
塑性力学主要关注材料的塑性应变、塑性流动规律等。
常见的塑性变形方式包括屈服、硬化、流变等。
3.破裂力学破裂力学研究材料的破裂行为，即材料在外力作用下发生破裂的过程。
破裂力学主要关注材料的断裂韧性、断口形貌等。
常见的破裂失效方式包括断裂、断裂韧性减小、疲劳等。
4.疲劳力学疲劳力学研究材料在交变应力作用下的疲劳失效行为。
疲劳力学主要关注材料的疲劳寿命、疲劳强度等。
材料在交变应力作用下会逐渐积累微小损伤，最终导致疲劳失效。
5.断裂力学断裂力学研究材料在应力集中区域的破裂行为。
断裂力学主要关注材料的应力集中系数、应力集中因子等。
在材料中存在裂纹等缺陷时，应力集中会导致裂纹扩展，最终引发断裂失效。
6.成形加工力学成形加工力学研究材料在加工过程中的变形行为。
成形加工力学主要关注材料的流变性质、加工硬化等。
常见的成形加工方式包括挤压、拉伸、压缩等。
7.热力学力学热力学力学研究材料在高温条件下的力学行为。
热力学力学主要关注材料的热膨胀、热应力等。
材料在高温条件下，由于热膨胀不均匀等因素，会产生热应力，从而影响材料的力学性能。
通过以上对材料力学的知识点的总结，我们可以了解到材料力学对工程领域的重要性。
在工程实践中，需要根据材料的力学性质来设计和制造材料的结构，以保证其性能和安全性。
因此，掌握材料力学的基本概念和原理对于工程师和科研人员来说是至关重要的。
材料力学复习资料
材料力学一、判断题1.拉杆伸长后，横向会缩短，这是因为杆有横向应力的存在。
( N)2.平行移轴公式表示图形对任意两个相互平行轴的惯性矩和惯性积之间的关。
( N)3.圆截面杆件受扭时，横截面上的最大切应力发生在横截面离圆心最远处。
( Y)4.单元体上最大切应力作用面上必无正应力。
(N)6．未知力个数多于独立的平衡方程数目，则仅由平衡方程无法确定全部未知力,这类问题称为超静定问题。
( Y)7．两梁的材料、长度、截面形状和尺寸完全相同，若它们的挠曲线相同，则受力相同。
( Y )8．主应力是过一点处不同方向截面上正应力的极值。
( Y )10．第四强度理论宜采用于塑性材料的强度计算。
(N )11.拉杆伸长后，横向会缩短，这是因为杆有横向应力的存在。
( N)12.圆截面杆件受扭时，横截面上的最大切应力发生在横截面离圆心最远处。
(Y) 13．细长压杆，若其长度系数增加一倍，临界压力增加到原来的4倍。
(N)14．两梁的材料、长度、截面形状和尺寸完全相同，若它们的挠曲线相同，则受力相同。
(Y )15．主应力是过一点处不同方向截面上正应力的极值。
( Y )16．由切应力互等定理可知：相互垂直平面上的切应力总是大小相等。
(N)17．矩形截面梁横截面上最大切应力τmax出现在中性轴各点。
(Y )18．强度是构件抵抗破坏的能力。
（Y）19．均匀性假设认为，材料内部各点的应变相同。
（N）20．稳定性是构件抵抗变形的能力。
（N）21．对于拉伸曲线上没有屈服平台的合金塑性材料，工程上规定2.0σ作为名义屈服极限，此时相对应的应变为2.0%=ε。
（N）22．任何情况下材料的弹性模量E都等于应力和应变的比值。
（N）23．求解超静定问题,需要综合考察结构的平衡、变形协调和物理三个方面。
（Y ）24．第一强度理论只用于脆性材料的强度计算。
（N）25．有效应力集中因数只与构件外形有关。
（N ）26．工程上将延伸率δ≥10％的材料称为塑性材料。
(完整版)材料力学知识点总结
一、基本变形材料力学总结变形现象： 平面假设： 应变规律： = d ∆l = 常数dx变形现象：平面假设： 应变规律：=d = dx变形现象：平面假设： 应变规律：= y= N =T= T = MyI Z = M max WZ= QS * z I z b = QS max max I bz max W= E （单向应力状态） = G（纯剪应力状态）=⎛ N ⎫≤ []maxA ⎪ ⎝ ⎭max[]=un塑材：u=s 脆材：u =bmax= ⎛ T ⎫ ≤ [] ⎪ ⎝ W t ⎭max弯曲正应力 1． [t ]= [c ]max≤ []2． [t ]≠ [c ] t max ≤ [t ] cmac ≤ [c ]弯曲剪应力=Q max S max ≤ [] max I bz轴向拉压扭转弯曲刚度条=T ⋅180 ≤[]max GIP注意：单位统一ymax≤[y]max≤[]件变形d∆l=N ; ∆L =NLdx EA EAEA—抗拉压刚度=d=Tdx GIZ=TLGIPGI p—抗扭刚度1=M (x)(x) EIy '' =M (x)EIEI—抗弯刚度应用条件应力在比例极限圆截面杆，应力在比例极限小变形，应力在比例极限矩形A=bhbh 3bh 2IZ=12;WZ=6实心圆A= d 24d4d3IP=32;Wt=16d4d3IZ=64;WZ=32空心圆D 2A =(1-2)4d44IP=32(1 -)d 3W =(1 -4)t16d 4I =(1-4)Z64d34WZ=32(1-)其（1）'剪切（1）强度条件：=Q≤[]A—剪切面积A（2）挤压条件：=P bs ≤[]bs A bsJA j—挤压面积矩形：=3Qmax 2 A圆形：=4Qmax 3A环形：= 2Qmax Amax均发生在中性轴上它公（2）GE式2(1 )二、还有：（1）外力偶矩：m = 9549 N (N •m)n（2）薄壁圆管扭转剪应力：=TN—千瓦；n—转/分2r 2t（3）矩形截面杆扭转剪应力：max =Tb2h;=TG b3hDB c AD 'Z ZC c cn n三、截面几何性质（1）平行移轴公式：I =I +a 2A;（2）组合截面：IYZ=IZ Y+abA1.形心：y c∑A i y ci=i =1 ；∑A ii =1∑A i z ciz =i =1∑A ii =12.静矩：S Z =∑A i y ci ；S y =∑A i z ci3.惯性矩：I Z =∑(I Z ) i ；I y =∑(I y ) i四、应力分析：（1）二向应力状态（解析法、图解法）a．解析法： b.应力圆：n σ：拉为“+”，压为“-”xτ：使单元体顺时针转动为“+”x yx y cos 2sin 2α：从x 轴逆时针转到截面的法线为“+”2 2 xx y sin 2cos 22 xtg22xmaxminxx yy2c：适用条件：平衡状态(2)三向应力圆：；； 1 3max 1 min 3 max 2nn2x y22xyxc121223311（3） 广义虎克定律：1(1 (1E 123xE xyz1 ( 1(2E 231yE yzx1(1(3E3 1 2zExy*适用条件：各向同性材料；材料服从虎克定律（4） 常用的二向应力状态 31. 纯剪切应力状态：1，20 ，3x2. 一种常见的二向应力状态：132r 3r 4五、强度理论破坏形式脆性断裂塑性断裂强度理论 第一强度理论（最大拉应力理论）莫尔强度理论 第三强度理论 （最大剪应力理论） 第四强度理论（形状改变比能理论） 破坏主要因素 单元体内的最大拉应力单元体内的最大剪应力单元体内的改变比能破坏条件 1 = bmax =su f = u fs强度条件 1 ≤ [] 1-3≤ []适用条件 脆性材料 脆性材料 塑性材料 塑性材料*相当应力：r，，]r 11r 313r 4222242232r=2+42≤[]=2+32≤[]4r22(M +N ) + 4≤ []r3 =r=(M+N)2+32≤[]WM 2 +T 2r3 =圆截面WM 2 + 0.75T 2r4=(M+N)2 + 4(T)2W Z A W t(M+N)2 + 4(T)2W Z A W t α 中性轴ZMpr3 =≤ []r 4 =≤ []i 2I Z*y =-=-ZAe y e ytg=y=-I ZtgZ I y中性轴Z≤ []Z≤ []A W≤ []P Mmax =±max ±max≤ []sincos( +)W Z W y=max maxM强度条件43=±P ±MA W)I yI Z=M (y c os+z s in公式简图弯扭拉（压）弯扭拉（压）弯斜弯曲类型六、材料的力学性质脆性材料＜5%塑性材料≥5%低碳钢四阶段：（1）弹性阶段（2）屈服阶段（3）强化阶段（4）局部收缩阶段b强度指标s ,b e sα塑性指标,tg E七．组合变形只有σs，无σbb剪断断口垂直轴线拉断断口与轴夹角45ºb45º拉断铸铁断口垂直轴线剪断s b 滑移线与轴线45︒，剪45低碳钢扭压拉八、压杆稳定欧拉公式： P=2EI min，=2E，应用范围：线弹性范围，σ<σ ，λ>λcr(l ) 2cr2crpp柔度：=ul；=E；0 =a -s， σib柔度是一个与杆件长度、约束、截面尺寸、形状有关的数据，λ↑P cr ↓σcr ↓λ>λp ——大柔度杆：cr =2E2临界应力λo <λ<λp ——中柔度杆：σcr=a-b λλ<λ0——小柔度杆：σcr =σsλoλPλ稳定校核：安全系数法： n P c rP I n w ，折减系数法：P []A提高杆件稳定性的措施有： 1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点：应力特征：破坏应力小于静荷强度； 断裂特征：断裂前无显著塑性变形； 断口特征：断口成光滑区和粗糙区。
材料力学复习资料
一基本概念1.工程构件正常工作必须满足强度、刚度和稳定性的要求。
杆件的强度代表了杆件抵抗破坏的能力；杆件的刚度代表了杆件抵抗变形的能力；杆件的稳定性代表了杆件维持原有平衡形态的能力。
2.变形固体的基本假设是连续性假设、均匀性假设、各向同性假设。
连续性假设认为固体所占据的空间被物质连续地充满而毫无空隙；均匀性假设认为材料的力学性能是均匀的；各向同性假设认为材料沿各个方向具有相同的力学性质。
3.截面法的三个步骤是截取、代替和平衡。
4.杆件变形的基本形式有：拉压，扭转，剪切，弯曲。
5.截面上一点处分布内力的集度，称为该截面该点处的应力。
6.截面上的正应力方向垂直于截面，切应力的方向平行于截面。
7.在卸除荷载后能完全消失的变形称为弹性变形，不能消失而残留下来的变形称为塑性变形。
8.低碳钢受拉伸时，变形的四个阶段为弹性阶段、屈服阶段、强化阶段和局部变形阶段。
9.由杆件截面骤然变化而引起的局部应力骤增的现象称为应力集中。
10.衡量材料塑性的两个指标是伸长率和断面收缩率。
11.受扭杆件所受的外力偶矩的作用面与杆轴线垂直。
12.低碳钢圆截面试件受扭转时，沿横截面破坏；铸铁圆截面试件受扭转时，沿45度角截面破坏。
13.梁的支座按其对梁在荷载作用平面的约束情况，可以简化为三种基本形式，即固定端、固定铰支座、可（活）动铰支座。
14.工程上常用的三种基本形式的静定梁是：简支梁、悬臂梁、外伸梁。
15.平面弯曲梁的横截面上有两个内力分量，分别为剪力和弯矩。
16.拉（压）刚度、扭转刚度和弯曲刚度的表达式分别是EA、GI p和EI z。
17.当梁上有横向力作用时，梁横截面上既有剪力又有弯矩，该梁的弯曲称为横力弯曲。
梁横截面上没有剪力（剪力为0），弯矩为常数，该梁的弯曲称为纯弯曲。
18.在弯矩图发生拐折处，梁上必有集中力的作用。
19.在集中力偶作用处，剪力图将不变。
20.梁的最大正应力发生在最大弯矩所在截面上离中性轴最远的点处。
材料力学知识点总结(重、难点部分)
第一章 绪 论一、基本要求（1）了解构件强度、刚度和稳定性的概念，明确材料力学课程的主要任务。
（2）理解变形固体的基本假设、条件及其意义。
（3）明确内力的概念、初步掌握用截面法计算内力的方法。
（4）建立正应力、剪应力、线应变、角应变及单元体的基本概念。
（5）了解杆件变形的受力和变形特点。
二、重点与难点1．外力与内力的概念外力是指施加到构件上的外部载荷（包括支座反力）。
在外力作用下，构件内部两部分间的附加相互作用力称为内力。
内力是成对出现的，大小相等，方向相反，分别作用在构件的两部分上，只有把构件剖开，内力才“暴露”出来。
２．应力，正应力和剪应力在外力作用下，根据连续性假设，构件上任一截面的内力是连续分布的。
截面上任一点内力的密集程度（内力集度），称为该点的应力，用p 表示0lim A P dP p A dA→∆==∆ P ∆为微面积A ∆上的全内力。
一点处的全应力可以分解为两个应力分量。
垂直于截面的分量称为正应力，用符号σ表示；和截面相切的分量称为剪应力，用符号τ表示。
应力单位为Pa 。
1MPa=610Pa, 1GPa=910Pa 。
应力的量纲和压强的量纲相同，但是二者的物理概念不同，压强是单位面积上的外力，而应力是单位面积的内力。
3．截面法截面法是求内力的基本方法，它贯穿于“材料力学”课程的始终。
利用截面法求内力的四字口诀为：切、抛、代、平。
一切：在欲求内力的截面处，假想把构件切为两部分。
二抛：抛去一部分，留下一部分作为研究对象。
至于抛去哪一部分，视计算的简便与否而定。
三代：用内力代替抛去部分队保留部分的作用力。
一般地说，在空间问题中，内力有六个分量，合力的作用点为截面形心。
四平：原来结构在外力作用下处于平衡，则研究的保留部分在外力与内力共同作用也应平衡，可建立平衡方程，由已知外力求出各内力分量。
４．小变形条件在解决材料力学问题时的应用由于大多数材料在受力后变形比较小，即变形的数量远小于构件的原始尺寸。
材料力学知识点归纳总结(完整版)
材料力学知识点归纳总结（完整版）1.材料力学：研究构件（杆件）在外力作用下内力、变形、以及破坏或失效一般规律的科学，为合理设计构件提供有关强度、刚度、稳定性等分析的基本理论和方法。
2.理论力学：研究物体（刚体）受力和机械运动一般规律的科学。
3.构件的承载能力：为保证构件正常工作，构件应具有足够的能力负担所承受的载荷。
构4.件应当满足以下要求：强度要求、刚度要求、稳定性要求5.变形固体的基本假设：材料力学所研究的构件，由各种材料所制成，材料的物质结构和性质虽然各不相同，但都为固体。
任何固体在外力作用下都会发生形状和尺寸的改变——即变形。
因此，这些材料统称为变形固体。
第二章：内力、截面法和应力概念1.内力的概念：材料力学的研究对象是构件，对于所取的研究对象来说，周围的其他物体作用于其上的力均为外力，这些外力包括荷载、约束力、重力等。
按照外力作用方式的不同，外力又可分为分布力和集中力。
2.截面法：截面法是材料力学中求内力的基本方法，是已知构件外力确定内力的普遍方法。
已知杆件在外力作用下处于平衡，求m－m截面上的内力，即求m－m截面左、右两部分的相互作用力。
首先假想地用一截面m－m截面处把杆件裁成两部分，然后取任一部分为研究对象，另一部分对它的作用力，即为m－m截面上的内力N。
因为整个杆件是平衡的，所以每一部分也都平衡，那么，m－m截面上的内力必和相应部分上的外力平衡。
由平衡条件就可以确定内力。
例如在左段杆上由平衡方程N－F＝0 可得N=F3.综上所述，截面法可归纳为以下三个步骤：1、假想截开在需求内力的截面处，假想用一截面把构件截成两部分。
2、任意留取任取一部分为究研对象，将弃去部分对留下部分的作用以截面上的内力N来代替。
3、平衡求力对留下部分建立平衡方程，求解内力。
4.应力的概念：用截面法确定的内力，是截面上分布内力系的合成结果，它没有表明该分布力系的分布规律，所以，为了研究相伴的强度，仅仅知道内力是不够的。
知识资料材料力学(八)(新版)
弯曲变形粱的挠度与转角（一）挠曲线在外力作用下，梁的轴线由直线变为光洁的弹性曲线，梁弯曲后的轴线称为挠曲线。
在平面弯曲下，挠曲线为梁形心主惯性平面内的一条平面曲线v=f(x)(见图5-8-1)。
（二）挠度与转角梁弯曲变形后，梁的每一个横截面都要产生位移，它包括三部分：1. 挠度梁横截面形心在垂直于轴线方向的线位移，称为挠度，记作v。
沿梁轴各横截面挠度的变化规律，即为梁的挠曲线方程。
v=f(x)2．转角横截面相对本来位置绕中性轴所转过的角度，称为转角，记作θ。
小变形情况下，3．此外，横截面形心沿梁轴线方向的位移，小变形条件下可忽略不计。
(三)挠曲线近似微分方程在线弹性范围、小变形条件下，挠曲线近似微分方程为上式是在图5—8—l所示坐标系下建立的。
挠度w向下为正，转角θ顺时针转为正。
积分法计算梁的位移按照挠曲线近似微分方程(5—8—1)，积分两次，即得梁的转角方程和挠度方程，即由第1 页/共6 页式中积分常数C、D，可由梁的边界条件来决定。
当梁的弯矩方程需分段列出时，挠曲线微分方程也需分段建立，分段积分。
于是全梁的积分常数数目将为分段数目的两倍。
为了决定所有积分常数，除利用边界条件外，还需利用分段处挠曲线的延续条件(在分界点处左、右两段梁的转角和挠度均应相等)。
用叠加法求梁的位移（一）叠加原理几个荷载同时作用下梁的任一截面的挠度或转角等于各个荷载单独作用下同一截面挠度或转角的总和。
（二）叠加原理的适用条件叠加原理仅适用于线性函数。
要求挠度、转角为梁上荷载的线性函数，必须满意： 1．材料为线弹性材料；2．梁的变形为小变形；3．结构几何线性。
（三）叠加法的特征1．各荷载同时作用下挠度、转角等于单独作用下挠度、转角的总和，应该是几何和，同一方向的几何和即为代数和。
2．梁在容易荷载作用下的挠度、转角应为已知或可查手册。
3．叠加法相宜于求梁某一指定截面的挠度和转角。
[例 5—8—1] 用积分法求图5—8—3所示各梁的挠曲线方程时，试问应分为几段?将浮上几个积分常数? 并写出各梁的边界条件和延续条件。
理工类专业课复习资料-材料力学基本概念和公式
第一章 绪论第一节 材料力学的任务1、组成机械与结构的各组成部分，统称为构件。
2、保证构件正常或安全工作的基本要求：a)强度，即抵抗破坏的能力；b)刚度，即抵抗变形的能力；c)稳定性，即保持原有平衡状态的能力。
3、材料力学的任务：研究构件在外力作用下的变形与破坏的规律，为合理设计构件提供强度、刚度和稳定性分析的基本理论与计算方法。
第二节 材料力学的基本假设1、连续性假设：材料无空隙地充满整个构件。
2、均匀性假设：构件内每一处的力学性能都相同3、各向同性假设：构件某一处材料沿各个方向的力学性能相同。
木材是各向异性材料。
第三节 内力1、内力：构件内部各部分之间因受力后变形而引起的相互作用力。
2、截面法：用假想的截面把构件分成两部分，以显示并确定内力的方法。
3、截面法求内力的步骤：①用假想截面将杆件切开，一分为二；②取一部分，得到分离体；③对分离体建立平衡方程，求得内力。
4、内力的分类：轴力N F ；剪力S F ；扭矩T ；弯矩M第四节 应力1、一点的应力： 一点处内力的集（中程）度。
全应力0limA Fp A∆→∆=∆；正应力σ；切应力τ；p =2、应力单位：Pa （1Pa=1N/m 2，1MPa=1×106 Pa ，1GPa=1×109 Pa ）第五节 变形与应变1、变形：构件尺寸与形状的变化称为变形。
除特别声明的以外，材料力学所研究的对象均为变形体。
2、弹性变形：外力解除后能消失的变形成为弹性变形。
3、塑性变形：外力解除后不能消失的变形，称为塑性变形或残余变形。
4、小变形条件：材料力学研究的问题限于小变形的情况，其变形和位移远小于构件的最小尺寸。
对构件进行受力分析时可忽略其变形。
5、线应变：ll ∆=ε。
线应变是无量纲量，在同一点不同方向线应变一般不同。
6、切应变：tan γγ≈。
切应变为无量纲量，切应变单位为rad 。
第六节 杆件变形的基本形式1、材料力学的研究对象：等截面直杆。
(完整版)材料力学必备知识点
材料力学必备知识点1、 材料力学的任务：满足强度、刚度和稳定性要求的前提下，为设计既经济又安全的构件，提供必要的理论基础和计算方法。
2、 变形固体的基本假设：连续性假设、均匀性假设、各向同性假设。
3、 杆件变形的基本形式：拉伸或压缩、剪切、扭转、弯曲。
4、 低碳钢：含碳量在0.3%以下的碳素钢。
5、 低碳钢拉伸时的力学性能：弹性阶段、屈服阶段、强化阶段、局部变形阶段 极限：比例极限、弹性极限、屈服极限、强化极限6、 名义（条件）屈服极限：将产生0.2%塑性应变时的应力作为屈服指标7、 延伸率δ是衡量材料的塑性指标塑性材料 随外力解除而消失的变形叫弹性变形；外力解除后不能消失的变形叫塑性变形。
>5%的材料称为塑性材料： <5%的材料称为脆性材料8、 失效：断裂和出现塑性变形统称为失效9、 应变能：弹性固体在外力作用下，因变形而储存的能量10、应力集中：因杆件外形突然变化而引起的局部应力急剧增大的现象11、扭转变形：在杆件的两端各作用一个力偶，其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线，致使杆件的任意两个横截面都发生绕轴线的相对转动。
12、翘曲：变形后杆的横截面已不再保持为平面；自由扭转：等直杆两端受扭转力偶作用且翘曲不受任何限制；约束扭转：横截面上除切应力外还有正应力13、三种形式的梁：简支梁、外伸梁、悬臂梁14、组合变形：由两种或两种以上基本变形组合的变形15、截面核心：对每一个截面，环绕形心都有一个封闭区域，当压力作用于这一封闭区域内时，截面上只有压应力。
16、根据强度条件 可以进行（强度校核、设计截面、确定许可载荷）三方面的强度计算。
17、低碳钢材料由于冷作硬化，会使（比例极限）提高，而使（塑性）降低。
18、积分法求梁的挠曲线方程时，通常用到边界条件和连续性条件；因杆件外形突然变化引起的局部应力急剧增大的现象称为应力集中；轴向受压直杆丧失其直线平衡形态的现象称为失稳19、圆杆扭转时，根据（切应力互等定理），其纵向截面上也存在切应力。
材料力学 知识要点
第一章绪论一、基本概念：强度：构件抵抗破环的能力1.构件应满足的三个要求：刚度：构件抵抗变形的能力稳定性：构件保持原有平衡的能力连续性假设：固体物质不留空隙的空满固体所占的空间2.变形固体的三个基本假设均匀性假设：固体内各处有相同的力学性能各向同性假设：在任一方向，固体的力学性能都相同注：各向同性材料：金属等各向异性材料：木材，胶合材料，复合材料3，两个限制条件：线弹性：材料变形处于线弹性阶段。
？小变形：变形及变形引起的位移，都远小于物体的最小尺寸4，原始尺寸原理：小变形条件下，常用变形前构件的尺寸代替变形后的构件尺寸来计算，即不考虑变形带来的影响。
（一处例外：压杆稳定）5，圣维南原理：如用与外力系静力等效的合力来代替原力系，则除在原力系作用区域内有明显,差别外，在离外力作用区域略远处，这种代替带来的误差很小，可以不计。
6，材力中的力：表面力集中力分布载荷作用方式：体积力外力按种类分内力：在外力作用下，构件因反抗或阻止变形而产生于物体内部的相互作用力按作用方式分静载荷交变载荷动载荷冲击载荷1，截（取）：用假象面把构件分成两部分7，研究内力的基本方法----截面法2，代（替）：用内力代替截去的部分的作用3，平（衡方程）：列静力平衡方程，求解未知内力8，应力-----内力的集度（任一应力应指明两个要素：哪一点，哪个方向上）（1）平均应力定义：单位面积上的内力 定义式：A Fp m = （ 注意：m p 是一个矢量，有方向）（2） 应力定义：平均应力的极限定义式：dA dFm p = )0dA (→单位：MPa ，矢量性：是矢量，有大小，方向。
正应力： 定义：应力垂直于截面的分量（F ∆垂直于截面的分量N F ∆在截面上的应力） 定义式： )0(→=dA dA dF N σ切应力： 定义：应力平行于截面的分量（F ∆平行于截面的分量S F ∆在截面上的应力） 定义式： ()0d →=dA AdFs τ9，变形与应变变形：在外力作用下，构件尺寸、形状发生变化的现象。
(完整版)材料力学知识点总结
材料力学总结一、基本变形二、还有：（1）外力偶矩：)(9549m N nNm •= N —千瓦；n —转/分 （2）薄壁圆管扭转剪应力：tr T22πτ=（3）矩形截面杆扭转剪应力：hb G Th b T 32max ;βϕατ==三、截面几何性质（1）平行移轴公式：;2A a I I ZC Z += abA I I c c Y Z YZ += （2）组合截面： 1．形 心：∑∑===ni ini cii c AyA y 11； ∑∑===ni ini cii c AzA z 112．静 矩：∑=ci i Z y A S ； ∑=ci i y z A S 3. 惯性矩：∑=i Z Z I I )( ；∑=i y y I I )(四、应力分析：（1）二向应力状态（解析法、图解法）a ． 解析法： b.应力圆：σ：拉为“+”，压为“-” τ：使单元体顺时针转动为“+”α：从x 轴逆时针转到截面的 法线为“+”ατασσσσσα2sin 2cos 22x yx yx --++=ατασστα2cos 2sin 2x yx +-=yx xtg σστα--=220 22minmax 22x y x yx τσσσσσ+⎪⎪⎭⎫⎝⎛-±+=c ：适用条件：平衡状态(2)三向应力圆：1max σσ=； 3min σσ=；231max σστ-=x（3）广义虎克定律：[])(13211σσνσε+-=E [])(1z y x x E σσνσε+-=[])(11322σσνσε+-=E [])(1x z y y E σσνσε+-=[])(12133σσνσε+-=E [])(1y x z z E σσνσε+-=*适用条件：各向同性材料；材料服从虎克定律（4）常用的二向应力状态 1．纯剪切应力状态：τσ=1 ，02=σ，τσ-=32．一种常见的二向应力状态：223122τσσσ+⎪⎭⎫⎝⎛±=2234τσσ+=r2243τσσ+=r五、强度理论*相当应力：r σ11σσ=r ，313σσσ-=r ，()()()][212132322214σσσσσσσ-+-+-=r σxσ六、材料的力学性质脆性材料 δ＜5% 塑性材料 δ≥5%低碳钢四阶段： （1）弹性阶段（2）屈服阶段 （3）强化阶段 （4）局部收缩阶段 强度指标 σσb s ,塑性指标 δψ,E tg ==σα七．组合变形ε八、压杆稳定欧拉公式：2min2)(l EI P cr μπ=，22λπσE cr =，应用范围：线弹性范围，σcr <σp ，λ>λp柔度：iul =λ；ρρσπλE=；ba s σλ-=0，柔度是一个与杆件长度、约束、截面尺寸、 形状有关的数据，λ↑P cr ↓σcr ↓λ>λp ——大柔度杆：22λπσE cr =λo <λ<λp ——中柔度杆：σcr=a-b λλ<λ0——小柔度杆：σcr =σs稳定校核：安全系数法：w I cr n P P n ≥=，折减系数法：][σϕσ≤=AP提高杆件稳定性的措施有：1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点：应力特征：破坏应力小于静荷强度； 断裂特征：断裂前无显著塑性变形； 断口特征：断口成光滑区和粗糙区。
材料力学复习资料
选择题1.危险截面是_______所在的截面。
A.最大面积B.最小面积C.最大应力D.最大内力2．图示矩形截面，Z轴过形心C，则该截面关于Z、Z1及Z2轴的惯性矩关系为_______。
A. Iz > Iz1> Iz2B. Iz2> Iz1> IzC. Iz2 > Iz> Iz1D. Iz1> Iz> Iz23．偏心拉伸（压缩）实质上是_______的组合变形。
A.两个平面弯曲B.轴向拉伸（压缩）与平面弯曲C.轴向拉伸（压缩）与剪切D.平面弯曲与扭转4．几何尺寸、支承条件及受力完全相同，但材料不同的二梁，其_______。
A. 应力相同,变形不同B. 应力不同,变形相同C. 应力与变形均相同D. 应力与变形均不同5．一铸铁梁，截面最大弯矩为负，其合理截面应为_______。
A．工字形 B.“T”字形 C.倒“T”字形 D.“L”形6.在图示受扭圆轴横截面上的切应力分布图中，正确的结果是_______。
7．梁的正应力公式是在“平面弯曲”前提下推导得到的，“平面弯曲”即_______。
A．梁在平面力系作用下产生的弯曲B．梁的内力只有弯矩没有剪力的弯曲C．梁的横截面变形后仍为平面的弯曲D．梁的轴线弯曲变形后仍为（受力平面内）平面曲线的弯曲8．工程中一般是以哪个指标来区分塑性材料和脆性材料的？_______。
A．弹性模量 B.强度极限 C.比例极限 D.延伸率9．今有两种压杆，一为中长杆，另一为细长杆，在计算临界力时，如中长杆误用细长杆的公式，而细长杆误用中长杆的公式，其后果是_______。
A．两杆都安全 B.两杆都不安全C．中长杆不安全，细长杆安全 D.中长杆安全，细长杆不安全10．对于没有明显屈服阶段的塑性材料，通常以产生0.2%的_______所对应的应力作为屈服极限，用σ0.2表示。
A.应力B.残余应力C.引伸率D.塑性应变11.低碳钢拉伸经过冷作硬化后，以下四种指标中哪种得到提高_______。
材料力学知识
第一章材料力学大体知识§大体概念：理论力学------研究物体（刚体）受力和机械运动一样规律的科学。
材料力学------研究构件（杆件）在外力作用下内力、变形、和破坏或失效一样规律的科学，为合理设计构件提供有关强度、刚度、稳固性等分析的大体理论和方式。
4．1 构件的承载能力为保证构件正常工作，构件应具有足够的能力负担所经受的载荷。
因此，构件应当知足以下要求：一、强度要求：即构件在外力作用下应具有足够的抗击破坏的能力。
在规定的载荷作用下构件固然不该破坏，包括断裂和发生较大的塑性变形。
例如，冲床曲轴不可折断；建筑物的梁和板不该发生较大塑性变形。
强度要求确实是指构件在规定的利用条件下不发生意外断裂或显著塑性变形。
二、刚度要求：即构件在外力作用下应具有足够的抗击变形的能力。
在载荷作用下，构件即便有足够的强度，但假设变形过大，仍不能正常工作。
例如，机床主轴的变形过大，将阻碍加工精度；齿轮轴变形过大将造成齿轮和轴承的不均匀磨损，引发噪音。
刚度要求确实是指构件在规定的事业条件下不发生较大的变形。
3、稳固性要求：即构件在外力作用下能维持原有直线平稳状态的能力。
经受压力作用的细长杆，如千斤顶的螺杆、内燃机的挺杆等应始终维持原有的直线平稳状态，保证不被压弯。
稳固性要求确实是指构件在规定的利用条件下不产生丧失稳固性破坏。
若是构件的横截面尺寸不足或形状不合理，或材料选用不妥，不能知足上述要求，将不能保证工程结构或机械的平安工作。
相反，若是不适当的加大构件横截面尺寸或选用高强材料，这虽知足了上述要求，却利用了更多的材料和增加了本钱，造成浪费。
咱们能够作出以下结论：材料力学是研究各类构件（主若是杆件）的强度、刚度和稳固性的学科，它提供了有关的大体理论、计算方式和实验技术，使咱们能合理地确信构件的材料和形状尺寸，以达到平安与经济的设计要求。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
00习题要求：1．将题目转化为Microsoft Word文档；2．解题过程用Microsoft Word文档，公式用公式编辑器，只交电子文档作业；3．期末考试前必须作对所有所给题目，否则不能参加期末考试，请于指定时间前交作业。
第一题（2010年3月5日前交该题作业）星期五1.21 Determine the smallest allowable cross-sectional areas of members BD, BE, and CE of the truss shown. The working stresses are 20 000 psi in tension and 12 000 psi in compression. (A reduced stress in compression is specified to reduce the danger of buckling.)SolutionThe free-body diagram of homogeneous BC in Fig.(b). The equilibrium equation are0243616,0=-⨯=∑Ay FP M, P=24(kips)=24000(lb)The free-body diagram of truss in Fig.(c). The equilibrium equation are0368)166488166448(316,0=⨯-+⨯++⨯+⨯=∑BD Ay E P P M ,P BD =－8.944(kips) (Compression)088,0=-=∑CE Ay BP P MP CE =24(kips) (Tension )01664436707.0,0=++--=∑BD BE Ay y P P P FP BE =-11.32(kN) (Compression)The normal stress of a member CE, DE and DF is)./(1200089442in lb A lbA P BDBD BD BD ≤==σ (Compression) A BD =0.745(in.2))./(12000113202in lb A lbA P BEBE BE BE ≤==σ (Compression)A BE =0.943(in.2))(2000024000psi A lbA P CECE CE CE ≤==σ (Tension ) A BE =1.2(in.2)1 .37 Compute the maximum force P that can be applied to the foot pedal. The l/4-in.-diameter pin at B is in single shear, and its working shear stress is 4000 psi. The cable attached at C has a diameter of 1/8 in. and a working normal stress of 20 000 psi.SolutionThe free-body diagram of bracket in Fig.(b). The equilibrium equation are010sin 26,0=-=∑οT P M B , P=0.05788T (a) 010cos ,0=+=∑οT P F Bx x , P Bx =-0.9848T 010sin ,0=--=∑οT P P FBy y, P By =0.2315TAccording to the normal stresses formula, we have )./(20000.125.0422in lb in T≤⨯=πσ T=245.4(lb) According to the shear stresses formula, we have)./(4000.25.02315.09848.04422222222in lb in T d P P A V By Bx ≤⨯+=+==ππτ T=194.1(lb)According to formula (a), we getP=0.05788T=0.05788×194.1=11.2(lb)第二题（2010年3月10日前交该题作业）星期三2.37 An initially rectangular element of a material is deformed into the shape shown in the figure. Find εx , εy , and γ for the element.SolutionAccording to the definition of the axial strain, we have:004.02.02.01992.0-=-=x ε 01.015.015.01515.0=-=y ε0157.09.07.156.16==-=οοογ2.69（g ） The bars AB, AC and AD are pinned together as shown in the figure. Calculate the axial force in the strut caused by the 10-kip load. For each steel bar. A = 0.3 in.2 and E = 29 x 106 psi. For the aluminum bar, A = 0.6 in.2 and E = 10 x 106 psi.Solution Equilibrium:)(101020cos 40cos 3lb P P P AD AC AB ⨯=⨯++⨯οοοο20sin 40sin ⨯=⨯AD AB P PCompatibilityAB x y δδδ=⨯-⨯οο40sin 40cosAD x y δδδ=⨯+⨯οο20sin 20cos y AC δδ=Hooke ’s law:)/.(1020.)(6.0)./(1010.)(12106226lb in P in in lb in P AC AC AC -⨯=⨯⨯⨯⨯=δ )/.(1001.18.)(3.0)./(102940cos /.)(12106226lb in P in in lb in P AB AB AB -⨯=⨯⨯⨯⨯=οδ )/.(1068.14.)(3.0)./(102920cos /.)(12106226lb in P in in lb in P AD AD AD-⨯=⨯⨯⨯⨯=οδ we getAB x AC P P 01.1840sin 40cos 20=⨯-⨯⨯οοδAD x AC P P 68.1420sin 20cos 20=⨯+⨯⨯οοδwe obtainAD AB AC P P P 436.9160.632.17+= and)(101020cos 40cos 3lb P P P AD AC AB ⨯=⨯++⨯οοοο20sin 40sin ⨯=⨯AD AB P P AD AB P P 5321.0=AD AD AC P P P 436.95321.0160.632.17+⨯=AD P 71.12=AC AD P P 362.1= 5321.0436.9160.632.17÷+=AB AB AC P P P AB P 89.23= AC AB P P 7249.0=So we obtainP AC =3.53×103 (lb) P AB =2.56×103 (lb) P AD =4.80×103 (lb)第三题（2010年3月15日前交该题作业）星期一3.27 The compound shaft, composed of steel, aluminum, and bronze segments, carries the two torques shown in the figure. If T C = 250 lb.ft, determine the maximum shear stress developed in each material. The moduli of rigidity for steel, aluminum, and bronze are 12 x 106 psi, 4 x 106 psi, and 6 x 106 psi, respectively.SolutionAccording to the angle of twist formula, we have032)500(32)750(32444=+-+-BroBro B DB AluAlu B CD SteSte B AC d G T L d G T L d G T L πππ016324)500(4112)750(6444=⨯⨯+⨯-⨯+⨯-⨯BB B T T T 0.5（T B -750）+0.0625(T B -500)+0.5T B =0 T B =382.4(lb.ft)According to the torsion formula, we have)(22466112)7504.382(163max psi Ste =⨯-⨯=πτ)(4.898212)5004.382(163max psi Alu =⨯-⨯=πτ )(233701124.382163max psi Ste =⨯⨯=πτ第四题（2010年3月19日前交该题作业的剪力图、弯矩图部分）星期五第四题（2010年3月24日前交该题作业的应力部分）星期三5.35 Determine the maximum tensile and compressive bending stresses in the beam shown.Solution ：1） FBD(support reactions at A and B)2） Shear-Moment Diagrams 3） Section Modulus Moment of inertiaI ＝100×106 (mm)44） Maximum Bending StressAt the top of section C it is in compression46610100130.105.12mmmmmm N I c M topC c ⨯⨯⨯==σ＝16.25 （Mpa ） At the bottom of section C it is in tension46610100200.105.12mmmmmm N I c M bot C t ⨯⨯⨯==σ＝25 （Mpa ） At the top of section B it is in tension46610100130.1012mmmmmm N I c M topB c ⨯⨯⨯==σ＝15.6 （Mpa ） At the bottom of section C it is in compression46610100200.1012mmmmmm N I c M bot B t ⨯⨯⨯==σ＝24 （Mpa ） So we get46610100130.105.12mmmmmm N I c M topC c ⨯⨯⨯==σ＝16.25 （Mpa ）46610100200.1012mmmmmm N I c M bot B t ⨯⨯⨯==σ＝24 （Mpa ）第五题（2010年3月29日前交该题作业）星期一5.68 For the beam shown, compute the shear stress at 1.0-in. vertical intervals on the cross section that carries the maximum shear force. Plot the results.Solution ：1)FBD(support reactions at B and C)2)Shear-Moment Diagrams 3)Section Modulus Moment of inertiaI ＝97.0in.4The first moment of this area at 1.0-in. vertical intervals on the cross section3112314in Q =⨯⨯=＝12 in.3 or3125.1525.115.2314in Q =⨯⨯+⨯⨯==15.125 in 3 4)Maximum shear Stresspsi in in in b I Q V 8.350.0.1.97.125.15225043max max =⨯⨯==τ=350.8psi Shear Stress at 1.0-in. vertical intervals on the cross sectionpsi in in in b I Q V 4.278.0.1.97.122250431max =⨯⨯==τ=278.4psi第六题（2010年4月12日前交该题作业）星期一6.72 Compute the value of EI δ at the overhanging end A of the beam, by superposition.According to deflection formulas for beams, we knowEIm N m EI m m m N L a LEI a w BC BwBC).(600)422()4(24)2()/(400)2(24222222=⨯-⨯⨯=-=θEIm N m BwBC AMBC ).(120023=⨯=θδ EI a M EI a M B B BMB 323)2(==θ EI m N m EI m m N m BMB AMB ).(213323)4().(80023=⨯⨯=⨯=θδ EIm N EI m m N EI a w AB AwAB ).(8008)2()/(4008344=⨯==δ EIm N AwABAMB AwBC A ).(17333=--=δδδδ7.44 The beam ABCD has four equally spaced supports. Find all the support reactions.SolutionAccording to slope formulas for beams, we know])())(3(2)3[(24)(3230L L L L EI L w B +⨯-⨯⨯-=δ ])2()()3[()3(6))(2(222L L L EI L L L R B --⨯⨯+0])()()3[()3(6))((222=--⨯⨯+L L L EIL L L R C])2()2)(3(2)3[(24)2(3230L L L L EI L w C +⨯-⨯⨯-=δ ])2(])2()3[(2)2(23[)3(6)2(3223L L L L L L LL EI L L R B --+-⨯⨯+ 0])()2()3[()3(6)2)((222=--⨯⨯+L L L EIL L L R C018718824220=++-C B R R L w 018818724220=++-C B R R L w30330Lw R R C B ==According to the equilibrium equation and according to symmetry ，A 、D supports have the same magnitude ， )3(0L w R R R R D C B A ⨯=+++ D A R R = we have30330L w R R C B ==, 520Lw R R D A ==第七题（2010年4月16日前交该题作业）星期五8.27 The cross sections of the members of the pin-jointed structure are 200-mm square. Find the maximum compressive stress in member BDE.SolutionThe maximum compressive stress in member BDE )(95.682.02.010001.582.02.010009062max MPa C =⨯⨯+⨯⨯⨯=σ第八题（2010年4月26日前交该题作业）星期一8.49 For the state of stress shown, determine the principal stresses and the principal directions. Show the results on a sketch of an element aligned with the principal directions.SolutionThe principal stresses222122xy yx y x τσσσσσσ+⎪⎪⎭⎫ ⎝⎛-±+=⎭⎬⎫ 228264264+⎪⎭⎫ ⎝⎛--±+-=which yields)(4.101ksi =σ )(4.82ksi -=σ The principal directions 6.158648222tan -=-=--⨯=-=yx xyσστθ The two solution areο99.572-=θ and οοο01.12218099.57=+- ο0.29-=θ and ο0.61Determine the angles 1θ (associated with 1σ) and the angles 2θ (associated with 2σ) θτθσσσσσ2sin 2cos 22'xy yx yx x +-++=)292sin(8)292cos(264264οο⨯-+⨯---++-=)(4.8ksi -=and θτθσσσσσ2sin 2cos 22'xy yx yx y ---+=)292sin(8)292cos(264264οο⨯--⨯----+-=)(4.10ksi =Therefore we conclude the angles 1θ=61.0o (associated with 1σ) and the angles ο292-=θ (associated with 2σ)第九题（2010年4月30日前交该题作业）星期五8.108 A shaft carries the loads shown in the figure. If the working shear stress is τw = 80 MPa, determine the smallest allowable diameter of the shaft. Neglect the weights of the pulleys and the shaft as well as the stress due to the transverse shear force.SolutionAccording the support, we know there is the largest bending moment occurs at C, the largest torque occurs in segment BC. Show in the figure.At C section, we haveM max =2.5kN ×0.6m=1.5(kN.m) T BC =0.3(kN.m)Therefore, the stress at the bottom of the section are3363max max )().(105.13232mm d mm N d M S M ⨯⨯⨯===ππσ 3363)().(103.01616mm d mm N d T J r T BC BC ⨯⨯⨯===ππτ Draw the Mohr ’s circleAppend(2)Figure (a) shows a reinforced concrete beam, where the cross-sectional area of the steel reinforcement is 19600 mm2. Using n = E st/E co= 8 and the working stresses of 12 MPa for concrete and 140 MPa for steel, determine the largest bending moment that the beam can carry.SolutionSuppose the tensile stress is zero and compressive stress is not zero in the concrete, the first moment of the transformed cross section about the neutral axis is zero. According to the maximum compressive stress in concrete and tensile stress in steel, the neutral axis is0)(2)()(221211=-⨯--⨯--⨯h d nA h h b b hhb st (b) 0)1670(1960082)280()9009820(2982022=-⨯⨯--⨯--⨯h h h 061152000026544004502=-+h h 013589337.58982=-+h h )(0.222mm h =The moment of inertia about the neutral axis221312131)(3))((3h h h nA h h b b h b I st -++---= (c) 23)2221670(19600832229820-⨯⨯+⨯=I49)(10)8.32881.35(mm I ⨯+=49)(106.364mm ⨯=The moment)(12106.3642229max MPa Mco ≤⨯⨯=σ ).(19708m kN M ≤)(140106.364)2221670(89MPa M st ≤⨯-⨯=σ).(4.4406m kN M ≤The beam carries a uniformly distributed load of intensity w o on a simply supported span 24 ft long. Determine the largest allowable value of w o2081l w M =20)30(814.4406⨯=w )/(16.390m kN w =)/(00.40m t w =第十题（2010年5月7日前交该题作业）星期五AppendThe 9-m-long concrete column is built in at its base and stayed by two beam at the top. Determine the largest axial load that can be carried. Use E =25 GPa and yp σ=20 MPa for concrete.SolutionDetermine the moment of inertia of the cross-sectional area about the z-axis and y-axis44123)(8432.1)(108432.112)2400(1600m mm mm mm I z =⨯=⨯=8192.0)(108192.012)1600(2400423=⨯=⨯=imm mm mm I yThe slenderness ratio of a 1600mm x 2400mm rectangle The least radius of gyration with z-axis)(48.0)(4.26.1)(8432.124m m m A I r z z =⨯== 5.3748.092=⨯=mmC zC The least radius of gyration with y-axis )(2133.0)(4.26.1)(8192.024m m m A I r yy =⨯==5.292133.097.0=⨯=mmC yCThe slenderness ratio157201000252222=⨯⨯==πσπypC ECFor the slenderness ratio zC yC C C , is less than C C , so that the concrete column is of intermediate length. These equations yield the factor of safety755.115785.3715785.37335883353333=⨯-⨯⨯+=-+=C zC C zC z C C C C N 736.115785.2915785.29335883353333=⨯-⨯⨯+=-+=C yC C yC y C C C C N and the working stress)(07.11755.12015725.371212222MPa N C C yp C zC zw =⨯⎥⎦⎤⎢⎣⎡⨯-=⎥⎥⎦⎤⎢⎢⎣⎡-=σσ )(32.11736.12015725.291212222MPa N C C yp C yC yw =⨯⎥⎦⎤⎢⎣⎡⨯-=⎥⎥⎦⎤⎢⎢⎣⎡-=σσ The largest allowable axial load thus becomes)(4338)(42512)(10512.424.26.11007.1166t kN N A P zw z ==⨯=⨯⨯⨯==σ )(4435)(43459)(10459.434.26.11032.1166t kN N A P yw y ==⨯=⨯⨯⨯==σ So we obtain axial load P )(4338t P P z ==。