高考数学模拟小练习6
高考数学倒计时模拟卷6理 试题

2021高考数学〔理〕倒计时模拟卷〔6〕1、集合{|(1)0},{1}U x x x A =-≤=,那么UA =( )A. [0,1]B. [0,1)C. (0,1)D. (,0](1,)-∞⋃+∞2、在ABC △中,45A ∠=︒,4AB AC ==,D 是ABC △所在平面上的一点,假设3BC DC =,那么DB AD ⋅=( )A.16232- B. 16232+ C. 162 D. 329-3、复数z 满足1i 4i ()z +=-,那么z =( ) A .22i +B .12i +C .12i -D .22i -4、具有线性相关关系的变量 ,x y ,满足一组数据如表所示,假设y 与x 的回归直线方程为ˆˆ332yx =-,那么 m 的值是( )x1 2 3y1- 1m8A. 4B.92C. 5D. 65、函数()ln sin f x x x =+ (x ππ-≤≤且0x ≠)的图象大致是( )A.B.C.D.6、一几何体的三视图如图,该几何体的顶点都在球O 的球面上,球O 的外表积是〔 〕A .2πB .4πC .8πD .16π 7、 3353sin 5cos 1414ααππ⎛⎫⎛⎫+=-+ ⎪ ⎪⎝⎭⎝⎭,那么5tan 14απ⎛⎫+= ⎪⎝⎭( )A. 5 3-B. 35-C. 35D. 538、数列{}n a 的前n 项和为n S ,且222(1),an n n nS a n b S -=-=,那么数列{}n b 的最小项为( )A.第3项B.第4项C.第5项D.第6项9、,?a b 是两条不重合的直线, ,αβ是两个不重合的平面,那么以下命题中正确的选项是( )A. //,//a b b α,那么//a αB. ,,//a b αβαβ⊂⊂,那么//a bC. //,a b a α⊥,那么b α⊥a α⊂,且b α⊄时,假设//b α,那么//a b10、如图,平行四边形ABCD 的四个顶点在双曲线()2222:10,0x y C a b a b-=>>上,直线AB 的斜率11k =,直线AD 的斜率212k =,那么双曲线的离心率是( )A.3B.62C.31+D.611、函数()()sin ,0,2f x x x R πωϕωϕ⎛⎫=+∈>< ⎪⎝⎭的局部图象如下图,假如1223x x π+=,那么()()12f x f x += ( )3 B. 3-C. 0D.1212、()0,xx xe a f x e a>=+,假设() f x 的最小值为1?-,那么a = ( )A. 21eB. 1eC. eD. 2e13、二项式2(nx 的二项式系数之和为1024,那么展开式中的常数项是__________ 14、()2,1M -,设()0,1N x ,假设22:1O x y +=上存在点P ,使得60MNP ∠=︒,那么0x 的取值范围是__________.15、假设函数2log y x =的图象上存在点(,)x y ,满足约束条件30220x y x y y m +-≤⎧⎪-+≥⎨⎪≥⎩,那么实数m 的最大值为______.16、过抛物线22y x =焦点F 的直线交该抛物线于,?A B 两点,假设2AF FB =,那么AF =__________17、ABC △的内角,,A B C 的对边分别为,,,a bc a =)(sin sin )()sin b A B c b C -=-.1.求角A 的大小;2.求ABC △的面积的最大值.18、如图,在四面体ABCD 中, 90,ABC ADC BC BD ∠=∠=︒==.1.求证: AD BD ⊥AB 与平面BCD 所成的角为60,点E 是AC 的中点,求二面角C BD E --的大小.19、某品牌经销商在一随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控〞,否那么称其为“非微信控〞,调查结果如下: 微信控 非微信控 合计男性 26 24 50 女性 302050合计56 441001. 根据以上数据,能否有95%的把握认为“微信控〞与“性别〞有关?5人,再随机抽取3人赠送礼品,记这3人中“微信控〞的人数为X ,试求X 的分布列和数学期望.参考公式: ()()()()()22n ad bc k a b c d a c b d -=++++,其中n a b c d =+++.参考数据:()20P K k ≥0.50 0.40 0.25 0.15 0.10 0.05 0.0250k 0.455 0.708 1.323 2.072 2.706? 3.841?5.02420、设直线:(1)(0)l y x k =+≠与椭圆2224(0)x y m m +=>相交于,?A B 两个不同的点,与 x 轴相交于点,C O 为坐标原点.1.证明: 222414k m k >+;3AC CB =,求△OAB 的面积获得最大值时椭圆的方程.21、函数()1x f x ae lnx =--.2x =是()f x 的极值点,求a ,并求()f x 的单调区间;()0f x ≥,求a 的取值范围,22、在平面直角坐标系xOy 中,直线l 的参数方程为1212x t y ⎧=⎪⎪⎨⎪=-⎪⎩ (t 为参数).以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为2sin p θ=l 与圆C 的交点个数C 与直线l 交于,A B 两点,求线段AB 的长度23、选修4-5:不等式选讲 函数()53f x x x =--+.x 的不等式()1f x x ≥+;f ()x 的最大值为m ,假设0,0,a b >>44a b ab m e e e -⋅=,求ab 的最小值. 答案1.B2.A解析:由题可知,22()33DB CB AB AC ==-212()333AD AB BD AB AB AC AB AC =+=--=+所以22212242()()333999DB AD AB AC AB AC AB AC AB AC ⋅=-⋅+=-+⋅24232161616cos 459999=⨯-⨯+⨯⨯︒=应选A 3.D解析:(1i 4)z +=,422i 1iz ==-+. 4.A 5.C 6.C 7.A解析:335553sin 3sin 23sin 5cos 14141414ααααππππ⎛⎫⎛⎫⎛⎫⎛⎫+=π++=+=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,那么55tan 143απ⎛⎫+=- ⎪⎝⎭,应选:A8.A解析:∵1(1)n n n a S S n -=->,∴1n n n S a S --=,那么21(1)n S n -=-,即2*(N )n S n n =∈, ∴22(1)21n a n n n =--=-.易知0n b >,∵2121244144222,()(1)1n n n n n n b b n b n n -++====++,当11n >+时, 1n >,∴当13n ≤<时, 1n n b b +>,当3n ≥时, 1n n b b +<,又23132,281b b ==,∴当3n =时, n b 由最小值.9.C解析:在A 中,有可能a α⊂,也可能a α⊄,故A 错;在B 中,直线,?a b 可能平行,也可能异面,故B 错;在C 中, //,a b a α⊥,那么由线面垂直的性质定理得b α⊥,故C 正确; 在D 中,直线,?a b 也可能异面,故D 错. 应选:C .在A 中,有可能a α⊂,也可能a α⊄;在B 中,直线,?a b 可能平行,也可能异面;在C 中,由线面垂直的性质定理得b α⊥;在D 中,直线,?a b 也可能异面.此题考察命题真假的判断,考察空间中线线、线面、面面间的位置关系等根底知识,考察运算求解才能,是中档题. 10.B解析:由双曲线的对称性可知,,B D 关于原点对称,设()00,A x y ,()11,B x y ,()11,D x y --,01101y y k x x -=-,01201y y k x x +=+,把,A B 两点的坐标分别代入双曲线C 的方程22221x y a b -=中,并相减,整理得2220122201y y b x x a -=-.∴2220101011222201010112y y y y y y b k k x x x x x x a -+-⋅=⋅===-+-.∴()222222a b c a ==-,∴e =. 11.C解析:由所给图像可得,该函数的图象关于点,03π⎛⎫⎪⎝⎭对称, 所以,当1223x x π+=时, ()()12f x f x =-,即()()120f x f x +=. 12.A解析:由()xx xe f x e a =+,得()()()()()()22'x x x x x x x x x e xe e a xe e e e ax a f x e a e a ++-⋅++==++,令()x g x e ax a =++,那么()'0x g x e a =+>,那么()g x 在(),-∞+∞上为增函数,又()110g e-=>, ∴存在01x <-,使()00g x =,即()00f x '=,000x e ax a ∴++=,①函数() f x 在0(,)x -∞上为减函数,在()0,x +∞上为增函数,那么() f x 的最小值为()00001x x x e f x e a==-+,即000x x x e e a =--,②联立①②可得02x =-,把02x =-代入①,可得21a e =,应选A. 13.1152014.3,3⎡⎤-⎢⎥⎣ 15.1解析:作出约束条件30220x y x y y m +-≤⎧⎪-+≥⎨⎪≥⎩表示的平面区域,得到如图的三角形,再作出对数函数2log y x =的图象,可得该图象与直线30x y +-=交于点(2,1)M , 当该点在区域内时,图象上存在点(,)x y 满足不等式组,且此时m 到达最大值, 即m 的最大值为1 故答案为:1.作出不等式组表示的平面区域,得到如图的三角形,观察图形可得函数2log y x =的图象与直线30x y +-=交于点(2,1),当该点在区域内时,图象上存在点(,)x y 满足不等式组,且此时m 到达最大值,由此即可得到m 的最大值.此题给出二元一次不等式组,求能使不等式成立的m 的最大值,着重考察了二元一次不等式组表示的平面区域和函数图象的作法等知识,属于中档题 16.38解析:2,1cos 1cos p p θθ=⋅--可得1cos 3θ=,故31cos 8p AF θ==-17.1.在ABC △的内角,,A B C 的对边分别为,,,a b c 23a =(23)(sin sin )()sin b A B c b C -=-.整理得:()(sin sin )()sin a b A B c b C +-=-, 利用正弦定理得:222a b c bc -=-,即:2221cos 22b c a A bc +-==,由于:0πA <<, 解得:π3A =. 2.由于π23,3a A ==, 所以:2222cos a b c bc A =+-,整理得:22122b c bc bc bc bc =+-≥-=, 所以:113sin 123322ABC S bc A =≤⋅=△. 18.1. 由得222BC BD CD += BD BC ∴⊥又,AB BC BD AB B ⊥⋂=BC ∴⊥平面ABD又CD AD ⊥,BC CD C ⋂=AD ∴⊥平面BCDAD BD ∴⊥C BD E --的大小为60.19.()()()()()()22210026203024500.649 3.8415050564477n ad bc k a b c d a c b d -⨯⨯-⨯===≈<++++⨯⨯⨯ 所以没有95%的把握认为“微信控〞与“性别〞有关. 2. 3319123105105EX =⨯+⨯+⨯= 2k X 的可能取值,计算对应的概率值,即可求出X 的分布列与数学期望值.20.1.依题意,直线l 显然不平行于坐标轴,故(1)y k x =+可化为11x y k =-. 将11x y k =-代入2224x y m +=,消去 x ,得2222(14)2(1)0k y ky k m +-+-=,①由直线l 与椭圆相交于两个不同的点,222244(1)(14)0k k m k ∆=--+>,整理得222414k m k >+1122(,),(,)A x y B x y .由①,得122214k y y k +=+, 因为3AC CB =,得12y 3y =-,代入上式,得2214k y k -=+. 于是,△OAB 的面积11222211221442k k S OC y y y k k =⋅-==≤=+, 其中,上式取等号的条件是241k =,即12k =±. 由2214k y k -=+,可得214y =±. 将211,24k y ==-及211,24k y =-= 这两组值分别代入①,均可解出252m =.所以,△OAB 的面积获得最大值时椭圆的方程是2228155x y +=. 21.1. ()f x 定义域为()0,+∞,()1'x f x ae x =-∵2x =是()f x 极值点∴()21'202f ae =-=,∴212a e = ∴()()22111ln 1,'22x x f x e x f x e e e x =--=- 设()()21102x g x e x e x -->,那么()2211'02x g x e e x--> 所以()g x 在()0,+∞上单调递增又()22112022g e e =⨯-= 所以当()0,2x ∈时, ()0g x <即()'0f x <所以()f x 单调递减当时()2,x ∈+∞,()0g x >即()'0f x >所以()f x 单调递增 综上212a e=,()f x 的单调递增区间为()2,+∞,单调递减区间为()0,2 2.∵()f x 定义域为()0,+∞,0x e >∴()0f x ≥恒成立ln 1x x a e +⇔≥在()0,+∞恒成立 令()()ln 10xx g x x e +=>,只需()max a g x ≥ ()()()21ln 1ln 1'x x x x e x e x x x g x e e -+⋅--== 令()()1ln 10u x x x x =-->,那么()211'0u x x x=--< ∴()u x 在()0,+∞上单调递减而()10u =,∴当()0,1x ∈时, ()0u x >即()'0g x >,()g x 单调递增当()1,x ∈+∞时, ()0u x <即()'0g x <,()g x 单调递减所以()()max 11g x g e=-, ∴1a e ≥,故a 的取值范围是1,e ⎡⎤+∞⎢⎥⎣⎦22.1.∵直线l的参数方程为121x t y ⎧=⎪⎪⎨⎪=⎪⎩ (t 为参数).∴消去参数t 得直线l10y +-=,∵圆C 的极坐标方程为2sin p θ=,即22sin p p θ=,∴由222,sin p x y p y θ=+=,得圆C 的直角坐标方程为2220x y y +-=.∵圆心()0,1在直线l 上,∴直线l 与圆C 的交点个数为21知圆心()0,1在直线l 上,∴AB 为圆C 的直径,∵圆C 的直角坐标方程为2220x y y +-=.∴圆C的半径1r ==, ∴圆C 的直径为2,2AB ∴=23.3x ≤-时,由531x x x -++≥+,得7x ≤,所以3x ≤-;当35x -<<时,由531x x x ---≥+,得13x ≤,所以133x -<≤;当5x ≥时,由531x x x ---≥+, 得9x ≤-,无解.综上可知, 13x ≤,即不等式()1f x x ≥+的解集为1,3⎛⎤-∞ ⎥⎝⎦53538x x x x --+≤---=,所以函数f ()x 的最大值8m =.应为448a b ab e e e -⋅=,所以448a b ab +=+.又0,0a b >>,所以4a b +≥=,所以有20ab -≥,0>,2>,4ab ≥,即ab 的最小值为4四季寄语情感寄语在纷繁的人群中/牵手走过岁月/就像走过夏季/拥挤的海滩在我居住的江南/已是春暖花开季节/采几片云彩/轻捧一掬清泉/飘送几片绿叶/用我的心/盛着寄给/北国的你不要想摆脱冬季/看/冰雪覆盖的世界/美好的这样完整/如我对你的祝福/完整地这样美好挡也挡不住的春意/像挡也挡不住的/想你的心情/它总在杨柳枝头/泄露我的秘密往事的怀念/爬上琴弦/化作绵绵秋雨/零零落落我诚挚的情怀/如夏日老树下的绿荫/斑斑驳驳虽只是一个小小的祝福/却化做了/夏季夜空/万点星辰中的一颗对你的思念/温暖了/我这些个漫长的/冬日从春到夏,从秋到冬......只要你的帘轻动,就是我的思念在你窗上走过.在那个无花果成熟的季节,我才真正领悟了你不能表达的缄默.我又错过了一个花期/只要你知道无花也是春天/我是你三月芳草地燕子声声里,相思又一年朋友,愿你心中,没有秋寒.一到冬天,就想起/那年我们一起去吃的糖葫芦/那味道又酸又甜/就像......爱情.谢谢你/在我孤独时刻/拜访我这冬日陋室只要有个窗子/就拥有了四季/拥有了世界愿你:俏丽如三春之桃,清素若九秋之菊没有你在身边,我的生活永远是冬天!让我们穿越秋天/一起去领略那收获的喜悦!在冬天里,心中要装着春天;而在春天,却不能忘记冬天的寒冷.落红不是无情物,化作春泥更护花.愿是只燕,衔着春光,翩翩向你窗.请紧紧把握现在/让我们把一种期翼/或者是一种愿望/种进大地/明春/它就会萌生绿色的叶片.此刻又是久违的秋季/又是你钟爱的季节/于是/秋风秋雨秋云秋月/都化作你的笑颜身影/在我的心底落落起起.此刻已是秋季/你可体验到/收获怀念的感觉/和秋雨一样真实动人.一条柳枝/愿是你生活的主题/常绿常新/在每一个春季雨声蝉鸣叶落风啸/又一个匆匆四季/在这冬末春初/向遥远的你/问安!又是夏季/时常有暴雨雷鸣/此刻/你可以把我当作大雨伞/直至雨过天晴/留给你一个/彩虹的夏季!。
高考数学模拟试题含答案详解

高考数学模拟试题含答案详解一、选择题1. 已知函数 $ f(x) = x^2 4x + 3 $,求 $ f(2) $ 的值。
答案:将 $ x = 2 $ 代入函数 $ f(x) $,得 $ f(2) = 2^2 4\times 2 + 3 = 1 $。
2. 已知等差数列 $\{a_n\}$ 的首项为 $a_1 = 3$,公差为 $d = 2$,求第 $n$ 项 $a_n$ 的表达式。
答案:等差数列的通项公式为 $a_n = a_1 + (n 1)d$,代入$a_1 = 3$ 和 $d = 2$,得 $a_n = 3 + (n 1) \times 2 = 2n + 1$。
3. 已知等比数列 $\{b_n\}$ 的首项为 $b_1 = 2$,公比为 $q = 3$,求第 $n$ 项 $b_n$ 的表达式。
答案:等比数列的通项公式为 $b_n = b_1 \times q^{n1}$,代入 $b_1 = 2$ 和 $q = 3$,得 $b_n = 2 \times 3^{n1}$。
4. 已知三角形的两边长分别为 $a = 5$ 和 $b = 8$,夹角为$60^\circ$,求第三边长 $c$。
答案:利用余弦定理 $c^2 = a^2 + b^2 2ab \cos C$,代入 $a = 5$,$b = 8$,$C = 60^\circ$,得 $c^2 = 5^2 + 8^2 2 \times5 \times 8 \times \cos 60^\circ = 49$,所以 $c = 7$。
5. 已知函数 $ g(x) = \frac{1}{x} $,求 $ g(x) $ 的定义域。
答案:由于 $x$ 不能为 $0$,所以 $g(x)$ 的定义域为 $x \neq 0$。
二、填空题1. 已知函数 $ h(x) = \sqrt{4 x^2} $,求 $ h(x) $ 的定义域。
答案:由于根号内的值不能为负,所以 $4 x^2 \geq 0$,解得$2 \leq x \leq 2$。
高考模拟试题(六)数学(后附参考答案解析)

绝密★启用前高考模拟试题(六)数学时间:120分钟分值:150分注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题:“012<+-∈∃ax x R x ,”的否定为()01.2≥+-∈∃ax x R x A ,01.2≥+-∈∀ax x R x B ,01.2<+-∈∀ax x R x C ,01.2>+-∈∃ax x R x D ,2.抛物线x y 22=的准线方程是()1.-=x A 1.=x B 21.-=x C 21.=x D 3.若点2,2(在幂函数αx x f =)(的图像上,则=)41(f ()21.A 1.B 2.C 4.D 4.在10)(a x +的展开式中,7x 的系数为15,则=a ()21.-A 21.B 1.-C 1.D 5.已知函数4(sin 31)(2π+-=x x f ,则)(x f 的最小正周期为()2.πA π.B 23.πC π2.D 6.已知点C 在直线AB 上运动,O 为平面上任意一点,且)(4+∈+=R y x OB y OA x OC ,,则y x ⋅的最大值是()41.A 81.B 161.C 321.D 7.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金杖,长5尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,其重量为M ,现将该金杖截成长度相等的10段,记第i 段的重量为)10,,2,1(⋅⋅⋅=i a i ,且⋅⋅⋅<<21a a 10a <,若M a i 548=,则=i ()4.A 5.B 6.C 7.D 8.在ABC △中,角C B A ,,的对应边分别为c b a ,,,已知222==c b ,,且4π=C ,则ABC △的面积为()31.+A 431.+B 62.+C 462.+D 9.设椭圆1222=+y x 的右焦点是F ,右准线为L ,点L A ∈,线段AF 交C 于点F .若FB FA 3=,=()2.A 3.B 2.C 3.D 10.将函数)32sin()(π+=x x f 向右平移32π个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数)(x g y =的图象,则函数)(x g y =与x x x ,32ππ=-=轴围成的图形面积为为()21.A 23.B 231.+C 231.-D 11.已知直三棱柱111C B A ABC -的各棱长均为1,棱1BB 所在直线上的动点M 满足1BB BM λ=,AM 与侧面C C BB 11所成的角为θ,若]2,22[∈λ,则θ的取值范围是()]6,12[.ππA 4,6[.ππB 3,4[.ππC ]125,3[.ππB 12.已知x a y =(0>a 且1≠a )是定义在R 上的单调递减函数,记a 的所有可能取值构成集合A ;),(y x P 是椭圆191622=+y x 上一动点,点),(111y x P 与点P 关于直线1+=x y 对称,记411-y 的所有可能取值构成集合B ,若随机地从集合B A ,中分别抽出一个元素1λ,2λ,则21λλ>的概率是()21.A 31.B 32.C 43.D 第Ⅱ卷(非选择题共100分)二、填空题:把答案填在相应题号后的横线上(本大题共4小题,每小题5分,共20分).13.已知iibi a R b a 21711--=+∈,,(i 是虚数单位),则=+b a ________.14.已知双曲线经过点22,1(,其一条渐近线方程为x y 2=,则该双曲线的标准方程为________.15.如框图所示,若13)(2-=x x f ,取1.0=ε,则输出的值为_______.16.已知{}]4,3[sin 2)(|上是增函数在ππ-==ax x f a M ,}013|{|1|有实数解方程=+-=--b b N x 有实数,设N M D =,且定义在R 上的奇函数mx nx x f ++=2)(在D 内没有最小值,则m 的取值范围是________.三、解答题:共70分。
高三数学小练(附答案)

高三数学小练一. 选择题 1. {}{}S x x T x x x S T =+>=-+<⋂213102||,,则等于( ) A B C D R .()().()..-∞⋃+∞-,-,,2121φ2. αβ、均为锐角,cos cos αβαβ==+115CO 、,则等于( ) A B C D ....ππππππ434434323或或3. 等边∆ABC 顶点顺时针方向排列,若点A 、B 分别对应复数-+1231i 和,则顶点C 对应复数为( ) A B C D i ....-----32332234. 函数y x x =-cos 的部分图象是( )5. 一个等差数列共3n 个项,其前2n 个项之和为100,后2n 个项之和为200,那么其中间n 个项之和为( )A. 150B. 125C. 75D. 506. 以原点为顶点、椭圆C :x y 22431+=的左准线为准线的抛物线交椭圆C 右准线于P 、Q 两点,则|PQ|等于( )A. 2B. 4C. 8D. 167. 直线y x =+cos α1的倾斜角的取值范围是( )(其中α∈R ) A B C D .[0].[0).[].[0][),,,,,πππππππ246434-⋃8. 圆台的上、下底面半径分别为r 与R ,高为h ,且r :R :h =1:4:4,那么此圆台侧面展开图扇环的圆心角的大小等于( )A B C D ....56654554ππππ二. 填空题 9. 若抛物线的焦点为F(2,1),准线L 的方程为20x y +=,则其顶点M 的坐标为__________。
10. 已知x ,y 为正实数,且x a a y ,,,12依次成等差数列,x b b y ,,,12依次成等比数列,那么()a a b b 12212+的取值范围是___________________。
三. 解答题11. 设数列{}a n 的前n 项和为S n ,若{}S n 是各项均为正数的等比数列,试比较a a a n n n +++212与的大小,并加以证明。
2021年高考数学模拟试题(六)(含解析)

选项C. 若 , ,则 ,又 ,所以 ,故C正确
选项D. 若 , ,则 或 ,故D不正确.
故选:BC
【点睛】本题考查平面与平面的平行垂直的判断,直线与平面的平行与垂直的判断,属于基础题.
10.已知抛物线 的焦点为 ,过点 的直线 交抛物线于 、 两点,以线段 为直径的圆交 轴于 、 两点,设线段 的中点为 ,则( )
A.
B. 若 ,则直线 的斜率为
C. 若抛物线上存在一点 到焦点 的距离等于 ,则抛物线的方程为
D. 若点 到抛物线准线的距离为 ,则 的最小值为
【答案】ACD
【解析】
【分析】
通过设直线 ,与抛物线方程联立,得到根与系数的关系 , ,选项 均可转化为坐标的运算,代入根与系数的关系,得到结果,C选项可直接根据焦半径公式,计算并判断.
【详解】解: , ,设切点为 ,则 ,
, .
原式 ,当且仅当 ,即 时等号成立,
即 .
故选:C.
【点睛】本题考查了导数的几何意义,考查了基本不等式.切线问题,一般设出切点,由切点处的导数值为切线的斜率以及切点既在切线上又在函数图像上,可列出方程组.运用基本不等式求最值时注意一正二定三相等.
8.已知双曲线 的右焦点为 ,过点 的直线交双曲线的右支于 、 两点,且 ,点 关于坐标原点的对称点为 ,且 ,则双曲线的离心率为( )
【详解】设 , ,
设直线 ,与抛物线方程联立
, , , ,
A. ,
故A正确;
B.根据焦半径公式可知 , ,
【详解】 可变形为 ,
所以 且 ,解之得: ,
所以由“ ”不能推出“ ”,
但“ ”可以推出“ ”,
高三数学模拟试题及答案

高三数学模拟试题及答案一、选择题1. 已知集合A={x | x² - 1 = 0},则A的元素个数为()A. 1B. 2C. 3D. 4答案:B2. 若a > 0,b < 0,则a与b的和的符号为()A. 正B. 负C. 零D. 无法确定答案:D3. 设函数f(x) = √(x²-2x+1),则f(3)的值为()A. 0B. 1C. 2D. 3答案:B4. 在△ABC中,角A = 60°,边AC = 5cm,边BC = 4cm,则边AB 的长度为()A. 3.5cmB. 4cmC. 4.5cmD. 5cm答案:C5. 某商店对现金支付的商品提供10%的折扣,小明购买了一件原价500元的商品,他需要支付多少元?()A. 45元B. 50元C. 450元D. 500元答案:C二、计算题1. 已知函数f(x) = |x - 3| + 2,求f(5)的值。
解:当x = 5时,f(x) = |5 - 3| + 2 = 4答案:42. 解方程:3x + 5 = 2(x - 1) + 7解:展开得:3x + 5 = 2x - 2 + 7移项得:3x + 5 = 2x + 5化简得:x = 0答案:03. 已知函数f(x) = x² - 4x + 5,求f(3)的值。
解:当x = 3时,f(x) = 3² - 4 × 3 + 5 = 9 - 12 + 5 = 2答案:24. 某商品在经过两次10%的折扣后,售价为270元,求其原价。
解:设原价为x元,则经过第一次折扣后为0.9x元,经过第二次折扣后为0.9 × 0.9x元。
根据题意,0.9 × 0.9x = 270,解方程得:x = 300答案:300三、应用题1. 一辆自行车上午以每小时20公里的速度向南骑行,下午以每小时15公里的速度向北骑行。
如果来回共耗时8小时,求行程的总长度。
高考数学必考点专项第6练 函数与方程(练习及答案)(全国通用)(新高考专用)

高考数学必考点专项第6练函数与方程习题精选一、单选题1. 函数2()=2+log ||x f x x 的零点个数为( ) A. 0 B. 1 C. 2 D. 32. 已知函数若()g x 存在2个零点,则a的取值范围是( )A. [1,)-+∞B. [0,)+∞C. [1,0)-D. [1,)+∞3. 若过点(,)a b 可以作曲线x y e =的两条切线,则( ) A. b e a <B. a e b <C. 0b a e <<D. 0a b e <<4. 已知()f x 是定义在R 上的奇函数,且满足,当时,,则函数在区间上所有零点个数为( )A. 0B. 2C. 4D. 65. 已知函数2()()x f x e ax x R =-∈有三个不同的零点,则实数a 的取值范围是( )A.B.C.D.6. 设a ,b R ∈,函数若函数()y f x ax b =--恰有3个零点,则( )[6,6]-A. 1a <-,0b <B. 1a <-,0b >C. 1a >-,0b <D. 1a >-,0b > 7. 已知函数的零点为,函数()f x 的最小值为0y ,且则函数的零点个数是( )A. 3B. 4C. 3或4D. 2或38. 已知函数,若函数()()g x x f x a =⋅-的零点个数恰为2个,则( )A.2837a <<或1a =- B. 7382a <<C.7382a <<或1a =- D. 7382a <<或54a =-9. 已知函数2,0()ln ,0kx x f x x x +⎧=⎨->⎩,则下列关于[()]2y f f x =-的零点个数判别正确的是( )A. 当0k =时,有无数个零点B. 当0k <时,有3个零点C. 当0k >时,有3个零点D. 无论k 取何值,都有4个零点二、多选题10. 若关于x 的方程23--=02x x k 在(1,1)-上有实根,则( )A. k 的最大值为52B. k 的最小值为916-C. 95[-,)162k ∈D. 95(,]162k ∈-11. 已知函数,().g x kx =若方程()()f x g x =有实根,则实数k的取值可以是( )012[,),y x x ∈A.12B. 1-C. 1D. (2,+)∞上的任意一个数12. 已知定义域为R 的奇函数()f x ,当0x >时,21,01()1,121x x x f x x x ⎧-+<⎪=⎨>⎪-⎩,下列说法中正确的是( )A. 当121122x x -<<<时,恒有12()()f x f x >B. 若当(0,]x m ∈时,()f x 的最小值为34,则m 的取值范围为17[,]26C. 不存在实数k ,使函数()()F x f x kx =-有5个不相等的零点D. 若关于x 的方程3[()][()]04f x f x a --=所有实数根之和为0,则34a =-13. 已知函数,若方程()0f x a -=有两个不相等的实根,则实数a 的取值范围可以是( )A.B.C.D.14. 已知函数,则方程22()2()10f x f x a -+-=的根的个数可能为( )A. 2B. 6C. 5D. 4三、填空题15. 用二分法求函数()=34x f x x --的一个零点,其参考数据如下:(2,)+∞根据此数据,可得方程34=0x --的一个近似解(精确度0.01)为__________.16. 方程103x e x =-的解(,1),x k k k Z ∈+∈,则k =__________. 17. 已知()|lg |2f x x kx =--,给出下列四个结论:(1)若0k =,则()f x 有两个零点; (2)0k ∃<,使得()f x 有一个零点;(3)0k ∃<,使得()f x 有三个零点;(4)0k ∃>,使得()f x 有三个零点;以上正确结论的序号是__________. 四、解答题18. 已知二次函数2()2(,).f x x bx c b c R =++∈(1)若函数()y f x =的零点为1-和1,求实数b ,c 的值;(2)若()f x 满足(1)0f =,且关于x 的方程()0f x x b ++=的两个实数根分别在区间(3,2)--,(0,1)内,求实数b 的取值范围.19. 已知函数2()22(0)f x ax ax b a=-++>在区间[2,0]-上有最小值1,最大值9.(1)求a b+的值;(2)设()()f xg xx=,若不等式在区间[2,4]上恒成立,求实数k的取值范围;(3)设,若函数()F x有三个零点,求实数λ的取值范围.答案和解析1.【答案】C .【解答】解:函数2()2log ||xf x x =+的零点个数,即为函数2xy =-的图象和函数2log ||y x =的图象的交点个数,作出函数的图象如下:数形结合可得,函数2xy =-的图象和函数2log ||y x =的图象的交点个数为2. 故选.C2.【答案】A解:函数()()g x f x x a =++存在2个零点, 即关于x 的方程()f x x a =--有2个不同的实根, 即函数()f x 的图象与直线y x a =--有2个交点. 作出直线y x a =--与函数()f x 的图象,如图所示,由图可知,1a -,解得1a -, 故选.A3.【答案】D解:函数xy e =是增函数,0xy e '=>恒成立, 函数的图象如图,0y >,即取得坐标在x 轴上方,如果(,)a b 在x 轴下方,连线的斜率小于0,不成立.点(,)a b 在x 轴或下方时,只有一条切线. 如果(,)a b 在曲线上,只有一条切线;(,)a b 在曲线上侧,没有切线;由图象可知(,)a b 在图象的下方,并且在x 轴上方时,有两条切线,可知0.a b e <<故选:.D4.【答案】D解:由,得,故,故函数是周期为4的周期函数.又因为()f x 是定义在R 上的奇函数,所以,所以,故1x =是函数()f x 的对称轴.当时,,由此画出()f x 的大致图象如下图所示,令()()10g x xf x =-=,注意到(0)0g ≠,故上述方程可化为,画出1y x=的图象, 由图可知与1y x=图象都关于点(0,0)对称,它们两个函数图象的6个交点A 与F ,B 与E ,C 与D , 所以函数在区间[6,6]-上所有零点个数为6.故选.D5.【答案】C解:0x =时,(0)10f =≠,令2()0xf x e ax =-=,得2xe a x=,令2()x e g x x =,则问题转化为y a =与2()xe g x x=有三个交点,3(2)()xx e g x x -'=,令()0g x '=,解得2x =,()f x∴当0x <或2x >时,()0g x '>,()g x 在(,0)-∞,(2,)+∞单调递增,当02x <<时,()0g x '<,()g x 在(0,2)单调递减,()g x 在2x =处取极小值,2(2)4e g =,作出()g x 的图象如下:要使直线y a =与曲线2()x e g x x =有三个交点,则24e a >,故实数a 的取值范围是2e (,).4+∞故选.C6.【答案】C解:当0x <时,()(1)0y f x ax b x ax b a x b =--=--=--=,()y f x ax b =--最多一个零点;当0x 时,3211()(1)32y f x ax b x a x ax ax b =--=-++-- 3211(1)32x a x b =-+-, 2(1)y x a x '=-+,当10a +,即1a -时,0y ',()y f x ax b =--在[0,)+∞上递增,()y f x ax b=--最多一个零点,不合题意; 当10a +>,即1a >-时,令0y '>得[1,),x a ∈++∞函数递增,令0y '<得[0,1),x a ∈+函数递减,函数最多有2个零点; 根据题意函数()y f x ax b =--恰有3个零点,所以函数()y f x ax b =--在(,0)-∞上有一个零点,在[0,)+∞上有2个零点, 如右图:01ba∴<-且,解得0b <,10a ->,31(1)6b a >-+,31(1)06a b ∴-+<<,11a -<<,故选:.C7.【答案】D解:如图所示,函数2()(0)f x ax bx c a =++>的零点为1x ,212()x x x <,令2()0f x ax bx c =++=, 240.b ac ∴∆=->由2(())()()0f f x af x bf x c =++=,0∆>,1()f x x ∴=或2().f x x =函数()f x 的最小值为0y ,且012[,),y x x ∈画出直线2y x =,1.y x =则直线2.y x =与()y f x =必有两个交点,此时2().f x x =有2个实数根,即函数(())y f f x =有两个零点.直线1y x =与()y f x =可能有一个交点或无交点,此时1()f x x =有一个实数根2b x a=-或无实数根. 综上可知:函数(())y f f x =的零点有2个或3个.故选.D8.【答案】D解:如图,可得()f x 的图象.令()0g x =,当0x =时,不符合题意;当0x ≠时,令()0g x =,得()a f x x =, ()g x 零点个数为2个,则函数()f x 与a y x =有两个交点. 易知0a =不符合题意.若0a >,则满足,可得73;82a << 若0a <,因左支已交于一点,则右支必然只能交于一点,故,此时无解;或,解得54a =- 综上,a 的取值范围内为7382a <<或5.4a =- 故选.D9.【答案】A解:设()f x t =,对于A ,当0k =时,函数()f x 对应的图象如下图:当0t 时,由()2f t =得22=此时方程恒成立了,即[()]2y f f x =-有无数个零点,故A 正确,D 错误.对于B ,当0k <时,对应的图象如下图:当0t >时,由()2f t =,此时ln 2t -=,得2(0,1)t e -=∈,当0t 时,由()2f t =得0t =,由2()(0,1)t f x e -==∈,此时x 有一个解,由()0t f x ==,此时x 有一个解,综上[()]2y f f x =-的零点个数为2个,故B 错误, C .当0k >时,对应的图象如下图:当0t >时,由()2f t =,此时ln 2t -=,得2(0,1)t e -=∈,当0t 时,由()2f t =得0t =,由2()(0,1)t f x e -==∈,此时x 有2个解,由()0t f x ==,此时x 有2个解,综上[()]2y f f x =-的零点个数为4个,故C 错误,故选.A10.【答案】BC 解:22339()2416k x x x =-=--,(1,1)x ∈-, 函数239()416y x =--的图象开口向上,对称轴为34x =, 当34x =时,min 916y =-,当1x =-时,max 52y =, (1,1)x ∈-,95[,).162k ∴∈- 故选.BC11.【答案】ACD解:由题意,可得函数()f x 的图象和函数()g x 的图象有交点,如图所示:(2,1)A ,12OA k =, ∴函数()f x 的图象和函数()g x 的图象有交点,数形结合可得12k或1k <-, 故选.ACD12.【答案】BC解:根据定义域为R 的奇函数()f x ,当0x >时,21,01()1,121x x x f x x x ⎧-+<⎪=⎨>⎪-⎩, 如图所示:对于A :当121122x x -<<<时,根据函数的图象12()()f x f x >不一定成立,故A 错误; 对于B :当(0,]x m ∈时,要使()f x 的最小值为34,令13214x =-,解得76x =,故m 的取值范围为17[,]26,故B 正确;对于C :令()f x kx =,故21x x kx -+=,整理得2(1)10x k x -++=,由于2(1)40k =+->,解得1k >,或3(k <-舍)若0k <,则当(0,1]x ∈时,0()()0y kx f x F x =<<⇒>,故3k <-舍去.又当1k >时,设1x 是方程()0F x =的较大根11x =>= 故1k >也不合题意.考虑y kx =与21y x x =-+有一个交点与121y x =-也有一个交点的情况, 因为y kx =与21y x x =-+有一个交点,故22(1)4230k k k ∆=+-=+-=,解得1k =或3(k =-舍)又当(0,)x ∈+∞时,y x =与121y x =-只有一个交点(1,1),与y x =和21y x x =-+的交点重合综上所述不存在实数k ,使得()F x 有5个不相等的零点, C 正确;对于D :3()04f x -=,解得112x =,276x =,所以1253x x +=, 令53x =-,则553()()337f f -=-=- 由于当23133[1,0),()()4247x f x x ∈-=---<-<-故37a =-也满足题意,D 不正确。
2021年高考数学模拟训练卷 (6)(含答案解析)
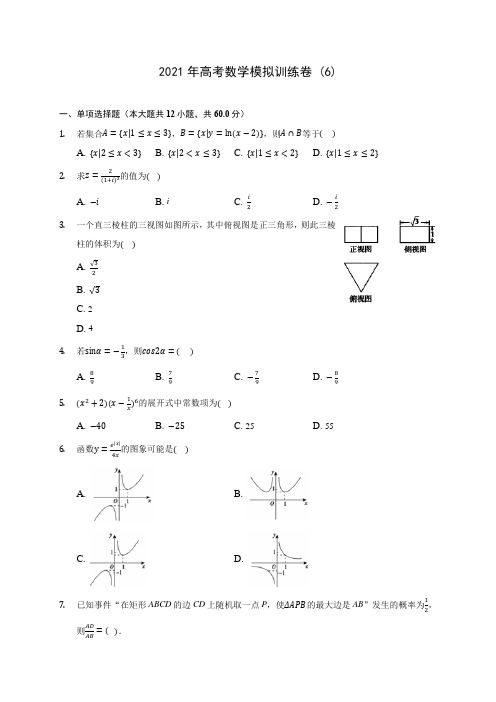
2021年高考数学模拟训练卷 (6)一、单项选择题(本大题共12小题,共60.0分)1.若集合A={x|1≤x≤3},B={x|y=ln(x−2)},则A∩B等于()A. {x|2≤x<3}B. {x|2<x≤3}C. {x|1≤x<2}D. {x|1≤x≤2}2.求z=2(1+i)2的值为()A. −iB. iC. i2D. −i23.一个直三棱柱的三视图如图所示,其中俯视图是正三角形,则此三棱柱的体积为()A. √32B. √3C. 2D. 44.若sinα=−13,则cos2α=()A. 89B. 79C. −79D. −895.(x2+2)(x−1x)6的展开式中常数项为()A. −40B. −25C. 25D. 556.函数y=e|x|4x的图象可能是()A. B.C. D.7.已知事件“在矩形ABCD的边CD上随机取一点P,使ΔAPB的最大边是AB”发生的概率为12,则ADAB=().A. 12B. 14C. √32D. √748. 圆x 2+y 2+4x −4y =0和圆x 2+y 2+2x −8=0相交于M ,N 两点,则|MN|= ( )A. 4B. 3√55C. 12√55D. 6√559. 在△ABC 中,内角A ,B ,C 的对边长分别为a ,b ,c ,已知a 2−c 2=b ,且sin(A −C)=2cosAsinC ,则b =( )A. 6B. 4C. 2D. 110. 已知直三棱柱ABC −A 1B 1C 1的顶点都在球O 上,且AB =4,AA 1=6,∠ACB =30°,则此直三棱柱的外接球O 的表面积是( )A. 25πB. 50πC. 100πD.500π311. 己知A 、F 分别为双曲线C 的左顶点和右焦点,点D 在C 上,△AFD 是等腰直角三角形,且∠AFD =90°,则C 的离心率为( )A. √2B. √3C. 2D. √2+112. 已知函数f(x)=(x −m)2+(ae x −3m)2(m ∈R)的最小值为910,则正实数a =( )A. 3B. 3e −2C. 3e 2D. 3或3e −2二、填空题(本大题共4小题,共20.0分)13. 设PA ⃗⃗⃗⃗⃗ =(k , 12),PB ⃗⃗⃗⃗⃗ =(4 , 5),PC ⃗⃗⃗⃗⃗ =(10 , k),则k = ______ 时,点A ,B ,C 共线. 14. 若x ,y 满足{x ≥1y ≥−1x +y ≥3,则z =x +2y 的最小值为______.15. 函数f(x)=Asin(ωx +φ)(其中A >0,ω>0,|φ|<π2)的图象如图所示,则,f(0)=______.16. 已知直线y =x +b(b ≠0)与抛物线y =12x 2交于A ,B 两点,O 为抛物线的顶点.若OA ⊥OB ,则实数b 的值为________.三、解答题(本大题共7小题,共84.0分)17.已知数列{a n}的前n项和为S n,a1=2,且满足a n+1=S n+2n+1(n∈N∗).}为等差数列;(Ⅰ)证明数列{S n2n(Ⅱ)求S1+S2+⋯+S n.18.某水产品经销商销售某种鲜鱼,售价为每千克20元,成本为每千克15元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失3元.根据以往的市场调查,将市场日需求量(单位:千克)按[50,150),[150,250),[250,350),[350,450),[450,550)进行分组,得到如图的频率分布直方图.(Ⅰ)未来连续三天内,连续两天该种鲜鱼的日需求量不低于350千克,而另一天的日需求量低于350千克的概率;(Ⅱ)在频率分布直方图的日需求量分组中,以各组区间的中点值代表该组的各个值,并以日需求量落入该区间的频率作为日需求量取该区间中点值的概率.若经销商每日进货400千克,记经销商每日利润为X(单位:元),求X的分布列和数学期望.19. 如图,在四棱锥P −ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA =PD =√2,底面ABCD 为直角梯形,其中BC//AD ,AB ⊥AD ,AD =2AB =2BC =2,O 为AD 中点.(1)求证:PO ⊥平面ABCD ;(2)求异面直线PB 与CD 所成角的余弦值.20. 已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,设A(0,b),B(a,0),F 1,F 2,分别是椭圆的左右焦点,且S △ABF 2=√32(1)求椭圆C 的方程;(2)过F 1的直线与以F 2为焦点,顶点在坐标原点的抛物线交于P ,Q 两点,设F 1P ⃗⃗⃗⃗⃗⃗⃗ =λF 1Q ⃗⃗⃗⃗⃗⃗⃗ ,若λ∈[2,3],求△F 2PQ 面积的取值范围.21.已知函数f(x)=13x3−x2+ax(其中a为常数).(1)若x=−1是f(x)的极值点,求函数f(x)的减区间;(2)若f(x)在(−2,+∞)上是增函数,求a的取值范围.22.在平面直角坐标系中,曲线C的参数方程为{x=3+5cosθy=−4+5sinθ(θ为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴建立极坐标系.(1)求曲线C的极坐标方程;(2)过点P(2,0),倾斜角为π4的直线l与曲线C相交于M,N两点,求1|PM|+1|PN|的值.23.已知函数f(x)=|2x−a|+|2x+3|,g(x)=|3x−2|.(1)解不等式g(x)<|2x+1|;(2)若对任意的x1∈R,任意的x2∈[0,1],使得f(x1)≥g(x2)成立,求实数a的取值范围.【答案与解析】1.答案:B解析:解:∵B={x|y=ln(x−2)}={x|x−2>0}={x|x>2},∴A∩B={x|2<x≤3},故选:B根据集合的交集运算进行求解.本题主要考查集合的基本运算,比较基础.2.答案:A解析:解:z=2(1+i)2=22i=1i=−i−i2=−i,则z的值为:−i.故选:A.利用复数代数形式的乘除运算化简复数z,则答案可求.本题考查了复数代数形式的乘除运算,是基础题.3.答案:B解析:解:由三视图还原原几何体如图,原几何体是正三棱柱,底面边长为2,高为1.∴底面积为S=√3,体积V=√3×1=√3.故选:B.由三视图还原原几何体,可知原几何体是正三棱柱,底面边长为2,高为1,然后由棱柱体积公式求解.本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.4.答案:B解析:本题考查了二倍角公式的应用,利用公式可以将所求cos2α应用已知的sinα表示,属于基础题型.解:sinα=−13,cos2α=1−2sin2α=1−2×(−13)2=79.故选B.5.答案:B解析:本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.利用展开式的通项公式即可得出.解:因为(x−1x )6的展开式的通项公式为:T r+1=C6r x6−r(−1x)r=(−1)r C6r x6−2r,所以(x2+2)(x−1x)6的展开式中常数项为:x2(−1)4C64x−2+2×(−1)3C63x0=15−40=−25.故选B.6.答案:C解析:解:函数为奇函数,图象关于原点对称,排除B,当x=1时,y=e4<1,排除A;当x→+∞时,e|x|4x→+∞,排除D.故选:C.判断函数的奇偶性和对称性,利用特殊值和极限思想进行排除.本题主要考查函数图象的识别和判断,判断函数的奇偶性以及利用排除法是解决本题的关键.7.答案:D解析:如图所示,设CD上的P1,P2两点刚好满足P1B=P2A=AB,那么,当P在P1P2之间时,就满足“ΔAPB的最大边是AB”,根据几何概型P1P2=12CD,DP1=14CD,设CD=4,AD=x,则DP2=3⇒AP 2=√7=AB ,故选D .8.答案:C解析:本题考查直线与圆、圆与圆的位置关系,涉及直线与圆相交的性质以及弦长的计算,属于中档题. 首先求出直线MN ,根据弦心距和半径和弦长之间的关系求出|MN |解:∵两圆的方程分别为x 2+y 2+4x −4y =0,x 2+y 2+2x −8=0,两式相减可得x −2y +4=0, ∴两圆的公共弦所在直线的方程是x −2y +4=0.∵圆x 2+y 2+4x −4y =0的圆心坐标为(−2,2),半径为2√2, ∴圆心到公共弦的距离,∴|MN|=2√(2√2)2−(2√55)2=12√55,故选C .9.答案:C解析:本题主要考查正弦定理和余弦定理的应用,属于基础题.由条件利用正弦定理和余弦定理求得2(a 2−c 2)=b 2,再根据已知条件,求得b 的值. 解:在△ABC 中,∵sin(A −C)=sinAcosC −cosAsinC =2cosAsinC , ∴sinAcosC =3cosAsinC , ∴a ⋅a 2+b 2−c 22ab=3c ⋅b 2+c 2−a 22bc,∴2(a 2−c 2)=b 2.又已知a 2−c 2=b ,∴b =2, 故选:C .10.答案:C解析:本题考查球的表面积公式,利用正弦定理求三角形外接圆半径,属于基础题.首先利用三棱柱和球的关系求出球的半径,进一步利用球的表面积公式求出结果.解:根据直三棱柱ABC−A1B1C1的顶点都在球O上,且AB=4,AA1=6,∠ACB=30°,在△ABC中,ABsin30∘=8=d(d为△ABC外接圆的直径),设外接球的半径为R,所以R=√(d2)2+(AA12)2=5,所以S球=4π⋅52=100π,故选:C.11.答案:C解析:解:由题意,|AF|=|DF|∴c+a=b2a,∴e2−e−2=0,∵e>1,∴e=2,故选:C.由题意,|AF|=|DF|,可得c+a=b2a,即可求出C的离心率.本题考查双曲线C的离心率,考查学生的计算能力,比较基础.12.答案:A解析:解:(x−m)2+(ae x−3m)2表示点A(x,ae x)与点B(m,3m)的距离的平方,点A在曲线y=ae x上,点B在曲线y=3x上,如图,可得a>0,设与y=3x平行的直线与曲线y=ae x相切于点P(x0,ae x0).∵y′=ae x,∴ae x0=3,…①。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年高考数学模拟小练习6
一、选择题:
1、已知向量a = (cos θ,sin θ),向量b =(3,-1) , 则 |2a -b | 的最大值、最小值分别是 (
)
A.42,0
B.4,22
C.16,0
D.4,0
2、设f (x ), g (x )分别是定义在R 上的奇函数和偶函数,当x <0时,f ′(x )g (x )+f (x )g ′(x )>0,且g (-3)=0, 则不等式f (x )g (x )<0的解集是 ( ) A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞)
D.(-∞,-3)∪(0,3)
3、函数b kx y +=,其中k ,b )0(≠k 是常数,其图象是一条直线,称这个函数为线性函数,对于非线性可导函数)(x f ,在点x 0附近一点x 的函数值)(x f ,可以用如下方法求其近似代替值:)(x f ))(()(000x x x f x f -'+≈,利用这一方法,998.3=m 的近似代替值
A .大于m
B .小于m
C .等于m
D .与m 的大小关系无法确定
二、填空题:
4、已知命题P :.10<<C ,:Q 不等式 12>-+c x x 的解集为R .如果P 和Q 有且仅有一个正确,
则c 的取值范围是 .答().,,+∞⎥⎦
⎤ ⎝⎛1210
5、已知函数f (x)的定义域为(- ∞,2],部分对应值如下表. f ′ (x)为f (x)的导函数,函数y = f ′ (x)的图象如图所示. 若两正实数a ,b 满足|f (a +b)|<1,则b + 1
a - 1 的取值范围是 .
6、一个与球心距离为2的平面截球所得的圆面面积为π,则球的表面积为 三、解答题:
7、已知ABC △
1
,且sin sin A B C +=. (I )求边AB 的长;
F
D
C
P
B
A
(II )若ABC △的面积为1
sin 6
C ,求角C 的度数.
8、已知:四棱锥P —ABCD ,PA ⊥平面ABCD ,底面ABCD 是直角梯形,∠A = 90°,且AB //
CD ,AB = 1
2CD ,点F 在线段PC 上运动. (1)当F 为PC 的中点时,求证:BF//平面PAD ; (2)设PF
FC = λ,求当λ为何值时有BF ⊥CD.
9、在一次小测验中共有3道选择题和2道填空题,每答对一道题得20分,答错或不答得0分。
某同学答对每道选择题的概率均为0.8,答对每道填空题的概率均为0.5,各道题答对与否互不影响.
(1)求该同学恰好答对2道选择题和1道填空题的概率;
(2)求该同学至多答对4道题的概率;
(3)若该同学已经答对了两道填空题,把这次测验的得分记为ξ,求ξ的概率分布列及数学期望
10、已知函数)(1)(2
3
R x ax x x f ∈++= (1)若函数在点3
1
=
x 处取得极值,求实数a 的值;
(2)求满足01
)(≥-x
x f 的x 的集合
四、6答案
1、【解答】 如图,点A (cos θ,sin θ)在圆122=+y x 上运动时,延OA 到C ,使
||=||2OA =2a , 求||-的最值,显然2||||==.当1OC 与
反向时有最大值4,2OC 与同向时有最小值0. ∴选D.
2、【解答】 设F (x )= f (x )g (x ), 当x <0时,∵F ′(x )= f ′(x )g (x )+f (x )g ′(x )>0. ∴F (x )在R 上为增函数.
∵F (-x )= f (-x )g (-x )=-f (x )·g (x ).=-F (x ).
故F (x )为(-∞,0)∪(0,+∞)上的奇函数. ∴F (x )在R +
上亦为增函数. 已知g (-3)=0,必有F (-3)=F (3)=0. 构造如图的F (x )的图象,可知
F (x )<0的解集为x ∈(-∞,-3)∪(0,3).
3、【解答】A
4、【解答】若P 和Q 都正确,则由P ,有10<<c .由Q ,有12>-+c x x 的解集为R . 用函数认识不等式,只需()c x x x f 2-+=的最小值()=0f 2.c ,c 2
1
1>>此时
12
1
<<c .
若P 和Q 都不正确,则由P ,有1>c .由Q ,有,c 2
1
0≤<其交集为空集,此时c 不存在.
由题设知,10≠>c ,c ,用补集思想,所求c 的取值范围为().,,+∞⎥⎦
⎤
⎝⎛1210
5、【解答】(- ∞,- 1)∪(1,+∞)
6、
【解答】20π
7、【解答】(I )由题意及正弦定理,得1AB BC AC ++=,
BC AC +=,两式相减,得1AB =.
(II )由ABC △的面积
11sin sin 26BC AC C C =,得1
3
BC AC =, 由余弦定理,得222cos 2AC BC AB C AC BC +-=
22()21
22
AC BC AC BC AB AC BC +--==, 所以60C =.
8、【解答】(1)取CD 中点E ,连结EF ,BE. ∵F 是PC 中点,∴EF//PD .
∵EF ⊄平面PAD ,PD ⊆平面PAD ,∴EF//平面PAD. ∵AB = 12CD ,AB//CD ,∴DE=//
AB ,∴BE//AD.
∵BE ⊄平面PAD ,AD ⊆平面PAD ,∴BE//平面PAD.
∵EF ⊆平面BEF ,BE ⊆平面BEF ,EF ∩BE = E ,∴平面BEF//平面PAD. 而BF ⊆平面BEF ,∴BF//平面PAD .
(2)当λ = 1,即F 为PC 中点时有BF ⊥CD.
∵PA ⊥平面ABCD ,CD ⊆平面ABCD ,∴PA ⊥CD. ∵∠A = 90°,AB//CD ,∴CD ⊥AD.
∵PA ⊆平面PAD ,AD ⊆平面PAD ,PA ∩AD = A , ∴CD ⊥平面PAD.
由(1)知平面PAD//平面BEF ,∴CD ⊥平面BEF. ∵BF ⊆平面BEF ,∴CD ⊥BF. 9、【解答】(1) 各道题答对与否互不影响,是独立事件:
. 25.022.064.03)5.0(2.0)8.0(2
12223⨯⨯⨯⨯=⋅⋅C C =0.192. (2) “至多答对4道题”与“5道题全答对”是对立事件, 即 872.0128.01)5.0()8.0(12
3
=-=- (3) 依题意:ξ=40、60、80、100.
008.0)2.0()40(3===ξP ; 096.0)2.0)(8.0()60(21
3===C P ξ 384.0)2.0()8.0()80(223===C P ξ; 512.0)8.0()100(333===C P ξ
因ξ满足二项分布,故4.28.03=⨯==np E ξ 10、(1).23)(2ax x x f +=' ,03231)31
(=+=
'a f .2
1-=∴a (2),01)(2
3≥+=-x ax x x x f ⎩⎨⎧≥+≠∴.
0,02ax x x 当,0,0>-≤>x a x a 或 当,0,0≠=x a 当,0,0a x x a -≥<<或。
