7数上册三视图的作业题
三视图习题50道(含答案)
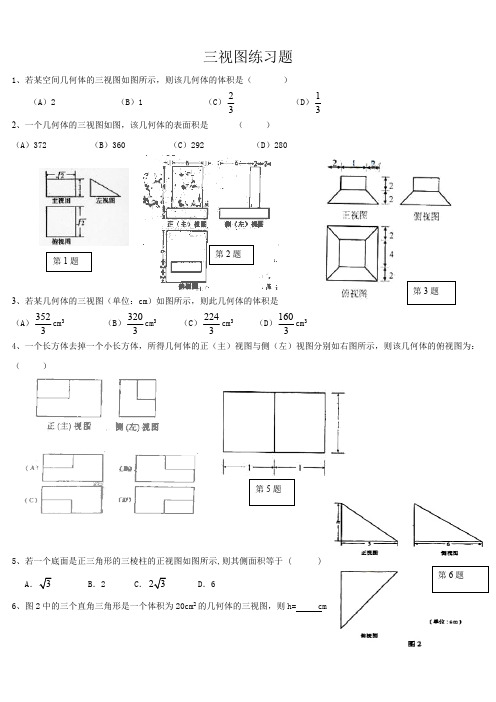
三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是()(A)2(B)1(C)23(D)132、一个几何体的三视图如图,该几何体的表面积是()(A)372 (B)360 (C)292 (D)2803、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是(A)3523cm3(B)3203cm3 (C)2243cm3(D)1603cm34、一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为:()5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB.2 C..66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为 。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图)是( )10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .B .C .D .9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为 ()(A )(B )(C )(D )13、若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 3cm .14、设某几何体的三视图如上图所示。
七上数学每日一练:简单几何体的三视图练习题及答案_2020年单选题版

七上数学每日一练:简单几何体的三视图练习题及答案_2020年单选题版答案答案答案答案答案2020年七上数学:图形的变换_投影与视图_简单几何体的三视图练习题~~第1题~~(2020安图.七上期末) 如图所示的几何体,从上面看得到的图形是( ) A . B . C . D .考点: 简单几何体的三视图;~~第2题~~(2020浦北.七上期末) 如图所示的几何体,从上面看到的平面图形是( )A . 正方形B . 长方形C . 圆D . 圆柱考点: 简单几何体的三视图;~~第3题~~(2020顺城.七上期末) 如图是某会展中心展出的一只紫砂壶,你认为是从上面看到的效果图是( ) A . B . C . D .考点: 简单几何体的三视图;~~第4题~~(2018沙洋.七上期末) 如图所示的圆柱体从正面看得到的图形可能是( ) A . B . C . D .考点: 简单几何体的三视图;~~第5题~~(2019大东.七上期末) (2019·宁波模拟) 下列几何体中,俯视图是三角形的几何体是( )A .B .C .D .考点: 简单几何体的三视图;答案答案答案答案答案(2019萝北.七上期末) 如图中几何体由一些完全相同的小立方体组成,从上面看到图形的形状是( ) A . B . C . D .考点: 简单几何体的三视图;~~第7题~~(2020咸阳.七上期中) 由4个相同的小立方体搭成的几何体如图所示,则它的主视图是( ) A . B . C . D .考点: 简单几何体的三视图;~~第8题~~(2019牡丹江.七上期末) 下列基本几何体中,从正面、上面、左面观察都是相同图形的是( )A . 圆柱B . 三棱柱C . 球D . 长方体考点: 简单几何体的三视图;~~第9题~~(2019下陆.七上期末) 下列四个图形中,是三棱柱的平面展开图的是A .B .C .D .考点:简单几何体的三视图;~~第10题~~(2019云浮.七上期末) 第14届中国(深圳)国际茶产业博览会在深圳会展中心展出一只如图所示的紫砂壶,从不同方向看这只紫砂壶,你认为是从上面看到的效果图是( )A .B .C .D .考点: 简单几何体的三视图;2020年七上数学:图形的变换_投影与视图_简单几何体的三视图练习题答案2.答案:C3.答案:C4.答案:B5.答案:C6.答案:C7.答案:A8.答案:C9.答案:C10.答案:C。
七上数学每日一练:由三视图判断几何体练习题及答案_2020年综合题版

七上数学每日一练:由三视图判断几何体练习题及答案_2020年综合题版答案解析答案解析答案解析2020年七上数学:图形的变换_投影与视图_由三视图判断几何体练习题1.(2017扬州.七上期末) 如图 1,是由一些棱长为单位 1 的相同的小正方体组合成的简单几何体.(1)请在图 2 方格纸中分别画出几何体的主视图、左视图和俯视图.(2)如果在其表面涂漆,则要涂平方单位.(几何体放在地上,底面无法涂上漆)(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加个小正方体.考点: 简单组合体的三视图;由三视图判断几何体;作图﹣三视图;2.(2017扬州.七上期末) 由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.(1) 请画出它的主视图和左视图;(2) 给这个几何体喷上颜色(底面不喷色),需要喷色的面积为(3) 在不改变主视图和俯视图的情况下,最多可添加块小正方体.考点: 由三视图判断几何体;作图﹣三视图;3.(2016江苏.七上期末) 在平整的地面上,有若干个完全相同的棱长的小正方体堆成一个几何体(如图所示).(1) 这个几何体由个小正方体组成,请画出这个几何体的三视图;(2) 如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色(注:该几何体与地面重合的部分不喷漆).考点: 简单组合体的三视图;由三视图判断几何体;作图﹣三视图;4.答案解析答案解析(2016秦淮.七上期末) 一个几何体的三个视图如图所示(单位:cm ).(1) 写出这个几何体的名称:;(2) 若其俯视图为正方形,根据图中数据计算这个几何体的表面积.考点: 几何体的表面积;由三视图判断几何体;5.(2016句容.七上期末) 解答(1) 由大小相同的小立方块搭成的几何体如图1,请在图2的方格中画出该几何体的俯视图和左视图.(2) 用小立方体搭一个几何体,使得它的俯视图和左视图与你在方格中所画的一致,则这样的几何体最少要个小立方块,最多要个小立方块.考点: 由三视图判断几何体;作图﹣三视图;2020年七上数学:图形的变换_投影与视图_由三视图判断几何体练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
七年级数学上册专题提分精练判断几何体的三视图(解析版)
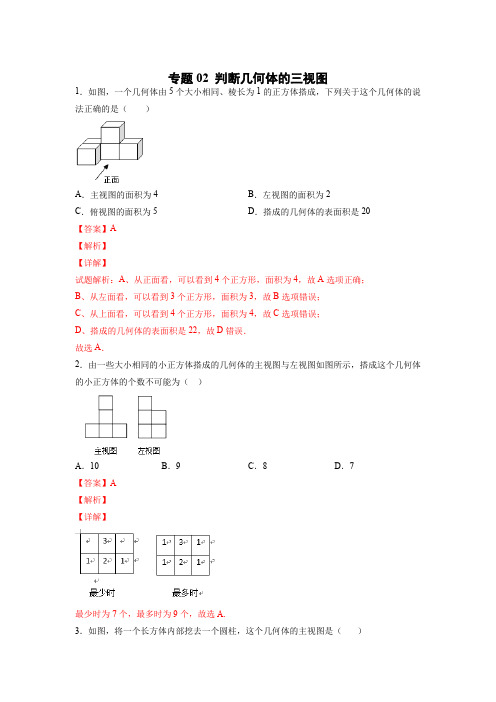
专题02 判断几何体的三视图1.如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是()A.主视图的面积为4B.左视图的面积为2C.俯视图的面积为5D.搭成的几何体的表面积是20【答案】A【解析】【详解】试题解析:A、从正面看,可以看到4个正方形,面积为4,故A选项正确;B、从左面看,可以看到3个正方形,面积为3,故B选项错误;C、从上面看,可以看到4个正方形,面积为4,故C选项错误;D、搭成的几何体的表面积是22,故D错误.故选A.2.由一些大小相同的小正方体搭成的几何体的主视图与左视图如图所示,搭成这个几何体的小正方体的个数不可能为()A.10B.9C.8D.7【答案】A【解析】【详解】最少时为7个,最多时为9个,故选A.3.如图,将一个长方体内部挖去一个圆柱,这个几何体的主视图是()A.B.C.D.【答案】A【解析】【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【详解】解:从正面看易得主视图为长方形,中间有两条垂直地面的虚线.故选:A.【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.4.如图所示是一个放在水平面上的几何体,它的主视图是()A.B.C.D.【答案】B【解析】【分析】根据主视图是从正面看到的图形,可得答案.【详解】从正面看是一个上下平行,左右大肚子的图形,故排除A、D;由于几何体中部是空的,主视图需要画虚线.故选:B.【点睛】本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图.5.从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是()A.B.C.D.【答案】C【解析】【详解】左视图就是从物体的左边往右边看.小正方形应该在右上角,故B错误,看不到的线要用虚线,故A错误,大立方体的边长为3cm,挖去的小立方体边长为1cm,所以小正方形的边长应该是大正方形13,故D错误,所以C正确.故此题选C.6.如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是()A.3个或4个或5个B.4个或5个C.5个或6个D.6个或7个【答案】A【解析】【详解】根据主视图,左视图,画出俯视图可能情况.所以选A.7.在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的最少个数为m,最多个数为n,下列正确的是()A.m=5,n=13B.m=8,n=10C.m=10,n=13D.m=5,n=10【答案】A【解析】【详解】由主视图和左视图可以确定:正方体堆成的几何体由两层组成,其底面最多有9个相同的正方体组成,恰好构成了边长为3个小正方体棱长的正方形,上面一层最多在这个正方形的4个顶点处各放1个相同的正方体.因此最多有正方体n=9+4=13个;底层正方体最少的个数应是3个,第二层正方体最少的个数应该是2个,因此这个几何体最少有m=2+3=5个小正方体组成.故选:A.点睛:当一个几何体已知两个视图时,它的形状不能确定.应分为最多和最少各有多少,来判断,解题关键是利用“主视图”疯狂盖,利用“左视图”拆违章,找到正方体的个数,比较复杂,求最少时容易出错,应该吧中间的向后移一行,最右边向后移2行即可.8.如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中左视图相同的是___.【答案】甲和乙【解析】【分析】根据三个俯视图分别判断出几何体的左视图,即可得答案.【详解】解:由已知条件可知,甲的左视图有2列,每列小正方数形数目分别为2,2;乙的左视图有2列,每列小正方数形数目分别为2,2;丙的主视图有2列,每列小正方数形数目分别为2,1.∴左视图相同的是:甲和乙.故答案为:甲和乙.【点睛】本题考查几何体的三视图画法.解题的关键是掌握由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.9.如图,三棱柱的上下底面均为周长为12cm 的等边三角形,现要从中截取一个上下底面均为等边三角形且底面周长为3cm 的小三棱柱.(1)请写出截面的形状______;(2)若小三棱柱的高为6cm ,则截去小三棱柱后,剩下的几何体的棱长总和是多少?【答案】(1)长方形;(2)46【解析】【分析】(1)依据大正三棱柱的底面周长为10,截取一个底面周长为3的小正三棱柱,即可得到截面的形状;(2)依据△ADE 是周长为3的等边三角形,△ABC 是周长为10的等边三角形,即可得到四边形DECB 的周长,再计算棱长总和.【详解】解:(1)由题意可知,截面是长方形,故填:长方形;(2)1cm DE =,3cm BD CE ==,4cm BC =()1334246222446+++⨯+⨯=+=(cm ). 【点睛】本题主要考查了截一个几何体,截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形.10.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)【答案】(1)主,俯;(2)207.36cm2【解析】【分析】(1)根据三视图的定义解答即可;(2)所求组合几何体的表面积=长方体的表面积+圆柱的侧面积,据此代入数据计算即可.【详解】解:(1)如图所示:;故答案为:主,俯;(2)组合几何体的表面积=2×(8×5+8×2+5×2)+4×π×6=2×66+24×3.14=207.36(cm2).【点睛】本题考查了几何体的三视图和几何体表面积的计算,正确理解题意、熟练掌握基本知识是关键.11.如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图.(1)当组成这个几何体的小正方体的个数为8个时,几何体有多种形状.请画出其中两种几何体的左视图;(2)若组成这个几何体的小正方体的个数为n,请写出n的最小值和最大值;(3)主视图和俯视图为下面两图的几何体有若干个,请你画出其中一个几何体.【答案】(1)画图见解析;(2) n最小为8,最大为11;(3)画图见解析.【解析】【分析】(1)由俯视图可得该几何体有2行,则左视图应有2列,由主视图可得共有3层,那么其中一列必为3个正方形,另一列最少是1个,最多是3个;(2)由俯视图可得该组合几何体有3列,2行,以及最底层正方体的个数及摆放形状,由主视图结合俯视图可得从左边数第二列第二层最少有1个正方体,最多有2个正方体,第3列第2层,最少有1个正方体,最多有2个正方体,第3层最少有1个正方体,最多有2个正方体,分别相加得到组成组合几何体的最少个数及最多个数即可得到n的可能的值.(3)根据三视图画出符合条件的一个几何体即可.【详解】(1)如图所示;下图中的任意两个即可.(2)∵俯视图有5个正方形,∴最底层有5个正方体,由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;由主视图可得第2层最多有4个正方体,第3层最多有2个正方体;∴该组合几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,∴n的最小值为8,最大值为11.(3)如图所示.【点睛】本题考查对三视图的理解应用及空间想象能力.可从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,综合上述分析数出小立方块的个数.12.下图是一个机器零件的毛坯,请将这个机器零件的三视图补充完整.【答案】图形见解析.【解析】【详解】试题分析:根据三视图的定义补全视图即可.试题解析:如图所示.13.用若干大小相同的小立方块搭一个几何体,使得从上面和左面看到的这个几何体的形状图如图所示.请你画出从正面看到的几何体的形状图.(画出两种即可)【答案】作图见解析【解析】【分析】结合左视图和俯视图即可画出主视图.【详解】解:作图如下:【点睛】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.14.用小立方块搭一个几何体,使它从正面和从上面看的形状图如图所示.从上面看的形状图中,小方形中的字母表示该位置小立方块的个数,试回答下列问题.(1) x ,z 各表示多少?(2) y 可能是多少?这个几何体最少由几个小立方块搭成?最多呢?【答案】(1)1x =AB 2AC =,3z =AB 2AC =;(2)y 可能是1 或 2.【解析】【详解】 试题分析:(1)利用从正面看得到的形状图,可以得到小正方体的层数,也就可以得到相应值.(2)因为y 在中间,所以小于2层,值是1,或者2,然后分类讨论.试题解析:(1)1x =,3z =.(2) y 可能是 1 或 2,321121111++++++=,321221112++++++= .这个几何体最少由 11 个立方体搭成,最多由12 个立方体搭成.点睛:一般先由各视图想象从各方向看到的几何体形状,然后综合起来确定几何体(或实物原型)的形状,再根据三个视图“长对正”,“高平齐”,“宽相等”确定轮廓线的位置,以及各个方向的尺寸.15.用小立方块搭一个几何体,主视图与左视图如下图,它最少要多少个立方块?最多要多少个立方块?画出这个几何体最多、最少两种情况下的俯视图,并用数字表示在该位置的小立方体的个数.【答案】3,5【解析】【详解】试题分析:根据几何体的主视图和左视图,判断出高度,然后确定俯视图中显示的正方体的个数,计算最多和最少的个数即可.试题解析:根据题意可知:俯视图,最少的情况:3块;俯视图,最多的情况:5块16.用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示.(1)它最多需要多少个小立方体?它最少需要多少个小立方体?(2)请你画出这两种情况下的从左面看到的形状图.【答案】(1)10;8(2)图形见解析【解析】【详解】试题分析:(1)利用左视图以及主视图可以得出这几个几何体最多的块数,以及最少块数;(2)画出这两种情况下从左面看到的形状.试题解析:(1)它最多需要2×5=10个小立方体,它最少需要2×3+2=8个小立方体.(2)小立方体最多时的左视图有2列,从左往右依次为2,2个正方形;小立方体最少时的左视图有2种情况:①有2列,从左往右依次为1,2个正方形;②有2列,从左往右依次为2,2个正方形;如图所示:17.如图,在平整地面上,若干个完全相同的棱长为10cm的小正方体堆成一个几何体.(1)这个几何体由______个小正方体组成.(2)在下面网格中画出左视图和俯视图.(3)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.【答案】(1)10;(2)作图见解析;(3)3200cm2.【解析】【详解】试题分析:(1)从左往右三列小正方体的个数依次为:6,2,2,相加即可;(2)由已知条件可知,左视图有3列,每列小正方形数目分别为3,2,1;俯视图有3列,每列小正方数形数目分别为3,2,1.据此可画出图形;(3)根据露出的小正方体的面数,可得几何体的表面积.试题解析:解:(1)这个几何体由6+2+2=10个小正方体组成,故答案为10;(2)如图所示:(3)露出表面的面一共有32个,则这个几何体喷漆的面积为3200cm2.。
三视图练习题

三视图练习题一、基本概念题1. 请简述三视图的概念及其作用。
2. 三视图包括哪三个视图?分别表示物体的哪些信息?3. 在三视图中,主视图、俯视图和左视图之间的位置关系是怎样的?二、识图题(1)正方体(2)长方体(3)圆柱体(1)球体(2)圆锥体(3)圆环体(1)三棱柱(2)四棱锥(3)六棱柱三、绘图题(1)一个长方体,长、宽、高分别为10cm、6cm、4cm。
(2)一个圆柱体,底面直径为8cm,高为10cm。
(3)一个圆锥体,底面直径为6cm,高为8cm。
(1)一把直尺(2)一个手机(3)一个茶壶四、分析题(1)主视图为矩形,俯视图为圆形,左视图为矩形。
(2)主视图为三角形,俯视图为矩形,左视图为三角形。
(1)主视图、俯视图和左视图均为正方形。
(2)主视图、俯视图和左视图均为圆形。
五、应用题(1)主视图为长方形,长、宽、高分别为10cm、6cm、4cm。
(2)主视图为圆形,直径为8cm,高为10cm。
(1)一个长方体木箱,长、宽、高分别为60cm、40cm、20cm。
(2)一个圆柱形水桶,底面直径为40cm,高为50cm。
六、综合题(1)一个长方体上放置一个正方体。
(2)一个圆柱体和一个圆锥体组合在一起。
(1)一个长方体挖去一个圆柱体形成的组合体,长方体的长、宽、高分别为20cm、10cm、5cm,圆柱体直径为5cm,高为10cm。
(2)一个正方体和一个四棱锥组合在一起,正方体边长为8cm,四棱锥底面边长为6cm,高为4cm。
七、判断题1. 三视图中,主视图和俯视图的长度方向一定相同。
()2. 在三视图中,左视图的宽度方向与主视图的高度方向一致。
()3. 任何物体的三视图都可以通过旋转和翻转得到。
()八、选择题A. 主视图B. 俯视图C. 正视图D. 左视图A. 主视图B. 俯视图C. 左视图D. 所有视图A. 主视图反映了物体的长度和高度B. 俯视图反映了物体的长度和宽度C. 左视图反映了物体的宽度和高度D. 三视图中的每个视图都包含了物体的所有尺寸信息九、填空题1. 三视图是用于表达物体______、______和______三个方向尺寸的图样。
七上数学每日一练:由三视图判断几何体练习题及答案_2020年填空题版
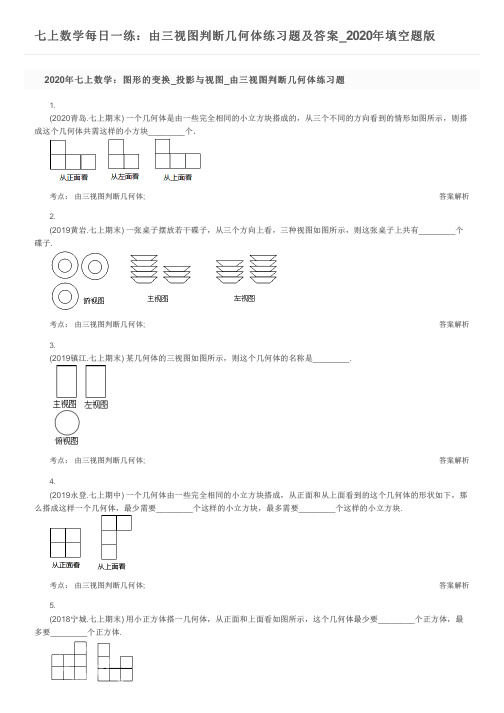
七上数学每日一练:由三视图判断几何体练习题及答案_2020年填空题版答案解析答案解析答案解析答案解析2020年七上数学:图形的变换_投影与视图_由三视图判断几何体练习题1.(2020青岛.七上期末) 一个几何体是由一些完全相同的小立方块搭成的,从三个不同的方向看到的情形如图所示,则搭成这个几何体共需这样的小方块________个.考点: 由三视图判断几何体;2.(2019黄岩.七上期末) 一张桌子摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上共有________个碟子.考点: 由三视图判断几何体;3.(2019镇江.七上期末) 某几何体的三视图如图所示,则这个几何体的名称是________.考点: 由三视图判断几何体;4.(2019永登.七上期中) 一个几何体由一些完全相同的小立方块搭成,从正面和从上面看到的这个几何体的形状如下,那么搭成这样一个几何体,最少需要________个这样的小立方块,最多需要________个这样的小立方块.考点: 由三视图判断几何体;5.(2018宁城.七上期末)用小正方体搭一几何体,从正面和上面看如图所示,这个几何体最少要________个正方体,最多要________个正方体.答案解析答案解析答案解析答案解析答案解析答案解析正面 上面考点: 由三视图判断几何体;6.(2018辽阳.七上期末) 如图所示是由四个相同的小立方体组成的几何体分别从正面和左面看到的图形,那么原几何体可能是________.(把图中正确的立体图形的序号都填在横线上)考点: 由三视图判断几何体;7.(2018孟津.七上期末) 由n 个相同的小正方形堆成的几何体,其视图如图所示,则n 的最大值是________,最小值是________.考点: 由三视图判断几何体;8.(2018辉.七上期末) 用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体最少需要正方体________个。
三视图习题50道(含答案).

三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是( (A2 (B1 (C23(D132、一个几何体的三视图如图,该几何体的表面积是((A372 (B360 (C292 (D2803、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是(A3523cm3(B3203cm3 (C2243cm3(D1603cm34、一个长方体去掉一个小长方体,所得几何体的正(主视图与侧(左视图分别如右图所示,则该几何体的俯视图为: (5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积...等于 (A.2 C..66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图是(10、一空间几何体的三视图如图所示,则该几何体的体积为( .A.2π+B. 4π+C. 2π+D. 4π 11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A .9πB .10πC .11πD .12π第7题侧(左视图正(主视图俯视图俯视图正(主视图侧(左视图12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c2m为((A(B(C(D13、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是3cm.14、设某几何体的三视图如上图所示。
则该几何体的体积为3m15、已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm,可得这个几何体的体积是(A.3 4000 cm3B.3 8000 cm3C.3 2000cmD.34000cm16、一个几何体的三视图如上图所示,其中正视图与侧视图都是边长为2的正三角形,则这个几何体的侧面积为(A.33π B.2πC.3π D.4π第14题正视图侧视图俯视图第17题17、如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为(A .32πB .16πC .12πD .8π18、下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10πC.11π D .12π19、右图是一个多面体的三视图,则其全面积为( AB6C6 D4 20、如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为(A .2πB .52πC .4πD .5π21、一个几何体的三视图及其尺寸(单位:cm如图所示,则该几何体的侧面积为_ ______cm 2.22、如果一个几何体的三视图如图所示(单位长度: cm, 则此几何体的表面积是(A. 2(20cm + B.212cmC. 2(24cm + D. 242cm俯视图左视图俯视图图2723. 如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为A .π3 B .π2 C .π23D .π424. 如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
初中数学三视图练习题

初中数学三视图练习题初中数学三视图练习题数学是一门重要的学科,它不仅培养了我们的逻辑思维能力,还帮助我们解决实际生活中的问题。
在初中数学中,三视图是一个重要的概念,它能够帮助我们理解和描述三维物体的形状。
在本文中,我将介绍一些初中数学三视图练习题,并探讨其解题方法。
第一题:一个长方体的三视图如下图所示,请你画出这个长方体的展开图。
这道题要求我们根据给定的三视图来画出长方体的展开图。
展开图是将一个三维物体展开成一个平面图形,以便我们更好地理解其形状。
要解决这道题,我们可以先观察三视图,找出它们之间的关系。
在这个例子中,我们可以发现,底视图和正视图是一样的,而侧视图则是将底视图旋转了90度。
因此,我们可以根据这个关系来画出长方体的展开图。
第二题:一个正方体的三视图如下图所示,请你计算这个正方体的表面积和体积。
这道题要求我们根据给定的三视图来计算正方体的表面积和体积。
表面积是指正方体的所有面的总面积,而体积则是指正方体的内部空间的大小。
要解决这道题,我们可以先观察三视图,找出它们之间的关系。
在这个例子中,我们可以发现,正视图和侧视图是一样的,而顶视图则是将正视图旋转了90度。
因此,我们可以根据这个关系来计算正方体的表面积和体积。
在计算表面积时,我们可以将正方体分解成六个面,然后计算每个面的面积,最后将它们相加。
在计算体积时,我们可以利用正方体的边长来计算,即体积等于边长的立方。
通过解决这些练习题,我们可以加深对三视图的理解,并提高解决实际问题的能力。
三视图是一个重要的数学概念,它不仅在数学中有着广泛的应用,还在许多其他领域中起着重要作用,如工程、建筑等。
因此,我们应该认真学习和掌握三视图的相关知识。
总结起来,初中数学三视图练习题是一个有趣且具有挑战性的练习,它能够帮助我们提高数学思维能力和解决实际问题的能力。
通过反复练习和探索,我们可以更好地理解和应用三视图的知识。
希望大家能够喜欢并享受这个过程,并在学习中取得好成绩!。
