2013年四年级走美杯答案详解

合集下载

2013年走美杯试题及答案

第十一届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示注意事项：1.考生要按要求在密封线内填好考生的有关信息。

2.不允许使用计算器。

小学四年级试卷（B卷）一、填空题I（每题8分，共40分）1.4026×125×4+317＝2.规定A※B＝（A+3）×（B-2）.1 2※17＝3.小宇春看一本故事书，每天看15页，24天刚好看完；如果每天多看3页，___天可以看完；4.如图；一张桌子坐6人，两张桌子并起来可以坐10人，三张桌子并起来可以坐14人，照这样10张桌子排成两排，每排5张桌子，可以坐____人。

5.一瓶可乐2.5元，3个空瓶可以再换一瓶可乐，有30元，最多可以喝到_____瓶可乐。

二、填空题II（每题10分，共50分）6.三个连续的偶数，它们的平均数能被三个不同的质数整除，这三个偶数中最小的数最小是______。

7.甲、乙看一本120页的书，10月1日开始，甲每天读8页；乙每天读13页，但是他每读天就停一天。

10月7日长假结束时，甲、乙二人乙比甲读得多。

多_____页。

8.一个数介于2013至2156之间，它除以5、11、13这三个数所得的余数相同，这个余数最大是_____。

9.右面的算式是由1-9九个数字组成的，其中“7”已填好，请将其余各数填入□，使得等式成立。

÷= -= -710.一天，奇奇到动物园，他看到猴子，熊猫和狮子三种动物，这三种动物总数量在26—32之间，猴子和狮子的总数量比熊猫的数量多。

熊猫和狮子的总数量比猴子数量的2倍多，猴子和熊猫的总数量比狮子的3倍还要多。

熊猫的数量比狮子的数量的1倍少。

熊猫有____只。

三、填空题III （每题12分，共60分）11.如图，在△ABC 中，M 是边AB 的中点，N 是边AC 上的三等分点，CM 是BN 相交于点K 。

若△BCK 的面积等于1，则△ABC 的面积等于_____。

12.甲、乙二人分别从A 、B 两地同时出发匀速相向而行，8小时两人相遇，若两人每小时都多走2千米，则6小时两人就相遇在距离AB 中点3千米的地点，已知甲比乙行得快，那么甲原来每小时行______千米。

2013年第十一届走美杯初赛小学五年级B卷(含解析)

第十一届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学五年级试卷（B 卷）一、填空题Ⅰ（每题8分，共40分）1．算式143214372⨯⨯⨯⨯的计算结果是_________．2．2012年第一季度某省出口总额为80．7亿美元，比进口总额的1．5倍还多11．1亿美元，这季度该省进口总额为_________亿美元．3．200到220之间有唯一的质数，它是_________．4．3将0~5这六个数字中的4个数字填入由图的圆圈中，每条线段两端的数字作差（大或小），可以得到5个差，这5个差恰好为1~5．在所有满足条件的填法中，四位数ABCD 的最大值是_________．5．蕾蕾去买方便面，递给老板1张面值100元的纸币，老板找完钱后对她说：“你才给我1张钱，我却给了你16张钱，还有价值5元的方便面，你真是太赚了啊！”，如果老板找给蕾蕾的钱要么是面值10元的，要么是面值5元的，那么这16张钱中有_________张是面值10元的．二、填空题Ⅱ（每题10分，共50分）6．将数字1~9填入右图竖式的9个方格中，每个数字只能用一次，那么和的最大值为_________．7．魔地上有一块魔石，不断向上均匀生长，为避免它把天捅破，仙界长老决定派出植物战士吸食魔石，抑制它的生长，每名植物战士每天吸食的量相同，如果派出14名植物战士，16天后魔石就会把天捅破；如果派出15名植物战士，24天后魔石就会把天捅破，至少派出_________名植物战士，才能保证天不会被捅破．8．有10个小伙子，他们的体重和身高各不相同；对于任意两个小伙子A 和B ，如果A 比B 重，或者A 比B 高，则称“A 不比B 差”；如果一个小伙子不比其它9个人差，就称这个小伙子是“棒小伙”，那么，这10个人中最多有个“棒小伙”_________．9．军区食堂晚饭需用1000斤大米和200斤小米，军需员到米店后发现米店正在促销，“大米1元1斤，每购10斤送1斤小米（不足10斤部分不送）；小米2元一斤，每购5斤送2斤大米（不足5斤部分不送）．”军需员至少要付_________元钱才能买够晚饭需用的米．10．如图，正方形ABCD 中，等腰直角三角形AEF 的面积是1，长方形EFGH 的面积是10，那么，正方形DC BA3201+ABCD 的面积是_________．三、填空题Ⅲ（每题12分，共60分）11．定义(2)(2)2a b a b =++-，算式135791113(1357911)⨯⨯⨯⨯⨯⨯-的计算结果是_________．12．一个正整数恰有8个约数，它的最小的3个约数的和为15，且这个四位数的一个质因数减去另一个质因数的5倍等于第三个质因数的2倍，这个数是_________．13．甲从A 地出发前往B 地，乙、丙两人从B 地出发前往A 地，甲行了50千米后，乙和丙才同时从B 地出发，结果甲和乙相遇在C 地，甲和丙相遇在D 地，已知甲的速度是丙的3倍，甲的速度是乙的1．5倍，C 、D 两地之间的距离是12千米．那么A 、B 两地之间的距离是_________千米．14．小俊掷骰子游戏，刚开始他站在起点格（如图），如果他掷出1至5点，掷出几点就前进几格，如果他掷出6点或某次前进后超出终点格，则立即返回起点格；若小俊掷了三次恰好到达终点格，掷骰子的顺序有_________种可能．起123456789终15．老师让同学们计算..AB C D E +时，马小虎把.D E 中的小数点看漏了，得到错误结果39.6；而马大虎把加号看成了乘号，得到错误结果36.9，那么，正确的计算结果应该是_________．HGFEDCBA第十一届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学五年级试卷（B 卷）参考答案1 2 3 4 5 6 7 8 888888 46．4 211 5304 3 3972 17 10 9 10 11 12 13 14 15116824．522013或12211302126.1参考解析一、填空题Ⅰ（每题8分，共40分）1．算式143214372⨯⨯⨯⨯的计算结果是_________．【考点】速算巧算【难度】☆☆ 【答案】888888【解析】原式(1113)(37)4372=⨯⨯⨯⨯⨯⨯(71113)(337)(42)=⨯⨯⨯⨯⨯⨯10011118888888=⨯⨯=．2．2012年第一季度某省出口总额为80．7亿美元，比进口总额的1．5倍还多11．1亿美元，这季度该省进口总额为_________亿美元．【考点】差倍问题【难度】☆☆【答案】46.4【解析】进口总额为：(80.711.1) 1.569.6 1.546.4-÷=÷=亿美元．3．200到220之间有唯一的质数，它是_________．【考点】质数合数【难度】☆☆【答案】211【解析】范围内的偶数全为合数；201、207、213、219都是3的倍数；205、215都是5的倍数；203、217都是7的倍数；209是11的倍数；只有211是质数．4．将0~5这六个数字中的4个数字填入由图的圆圈中，每条线段两端的数字作差（大或小），可以得到5个差，这5个差恰好为1~5．在所有满足条件的填法中，四位数ABCD 的最大值是_________．【考点】数字谜【难度】☆☆【答案】5304【解析】共有6个差，故5和0必须存在，为使ABCD 最大，需要5A =，并且B 和C 中有一个为0；B 作为百位数字应尽量大，若4B =，则0C =，但此时D 已无法填出，故B 最大为3；3B =时，0C =，此时有4D =，最大值为5304．DC BA5．蕾蕾去买方便面，递给老板1张面值100元的纸币，老板找完钱后对她说：“你才给我1张钱，我却给了你16张钱，还有价值5元的方便面，你真是太赚了啊！”，如果老板找给蕾蕾的钱要么是面值10元的，要么是面值5元的，那么这16张钱中有_________张是面值10元的．【考点】鸡兔同笼问题【难度】☆☆【答案】3【解析】假设全是5元的，那么16张钱共51680⨯=元，比实际情况的100595-=元少了958015-=元，故有10元钱15(105)3÷-=张．方程方法：设有x 张10元，则有方程：105(16)1005x x +-=-，解得3x =．二、填空题Ⅱ（每题10分，共50分）6．将数字1~9填入右图竖式的9个方格中，每个数字只能用一次，那么和的最大值为_________．【考点】数字谜【难度】☆☆☆【答案】3972【解析】让和最大，则和的百位为9，若和的十位不为8，那么第二个加数百位最大为7，但是十位无法提供进位；所以和的十位最大为7．此时第二个加数百位为8．第三个加数千位为3，剩下1、2、4、5、6．若个位没有进位，只能是2125++=，那么十位无法凑出和为7．故而个位有进位，满足要求的最大的和为1280431563972++=．7．魔地上有一块魔石，不断向上均匀生长，为避免它把天捅破，仙界长老决定派出植物战士吸食魔石，抑制它的生长，每名植物战士每天吸食的量相同，如果派出14名植物战士，16天后魔石就会把天捅破；如果派出15名植物战士，24天后魔石就会把天捅破，至少派出_________名植物战士，才能保证天不会被捅破．【考点】应用题——牛吃草【难度】☆☆☆【答案】17【解析】这是一个反生长型的牛吃草问题；设一名战士一天的吸食量是“1”，设魔石每天的增长量为x ，捅破天所需的魔石量为y ，那么有方程组：161416241524y x y x =-⨯⎧⎨=-⨯⎩，解得17x =，故应至少派17名战士来抑制生长．8．有10个小伙子，他们的体重和身高各不相同；对于任意两个小伙子A 和B ，如果A 比B 重，或者A 比B 高，则称“A 不比B 差”；如果一个小伙子不比其它9个人差，就称这个小伙子是“棒小伙”，那么，这10个人中最多有个“棒小伙”_________．【考点】极端思想、构造【难度】☆☆【答案】10【解析】令最高的人体重排第10，第二高的人体重排第9，第三高的人体重排第8，……，最矮的人最重，这样10个人都是“棒小伙”．3201+9．军区食堂晚饭需用1000斤大米和200斤小米，军需员到米店后发现米店正在促销，“大米1元1斤，每购10斤送1斤小米（不足10斤部分不送）；小米2元一斤，每购5斤送2斤大米（不足5斤部分不送）．”军需员至少要付_________元钱才能买够晚饭需用的米．【考点】列方程解应用题、估算【难度】☆☆☆☆【答案】1168【解析】仔细观察两种米的促销方法，会发现其折扣本质是相同的（如果把“10斤大米”和“5斤小米”看做一份促销品的话，那么10元钱能买到的折扣都是15份促销品），故不存在多买大米好还是多买小米好的问题，只需凑足所需重量，就一定是最省的方法；设买大米x 斤，小米y 斤，列方程组：210005120010x y x y ⎧+≤⎪⎪⎨⎪+≤⎪⎩来估算大米与小米应买多少斤；得到大致重量：大米买950斤，小米买105斤，此时花了1160元，已有992斤大米和200斤小米，再用8元买8斤大米即可，最少用1168元（构造方法不唯一）．10．如图，正方形ABCD 中，等腰直角三角形AEF 的面积是1，长方形EFGH 的面积是10，那么，正方形ABCD 的面积是_________．【考点】三角形面积【难度】☆☆☆【答案】24.5【解析】241AEF S EF =÷=△，故2EF =；故1025FG =÷=，254 6.25BFG DEH S S ==÷=△△；故12 6.2521024.5ABCD S =⨯+⨯+=．三、填空题Ⅲ（每题12分，共60分）11．定义(2)(2)2a b a b =++-，算式135791113(1357911)⨯⨯⨯⨯⨯⨯-的计算结果是_________．【考点】定义新运算【难度】☆☆☆【答案】2【解析】本题可以算出答案，但用递推推出答案会使过程更简单，由定义式可推得：13352=⨯-，135=(13522)7213572⨯⨯-+⨯-=⨯⨯⨯-……以此类推，1357911=1357911132⨯⨯⨯⨯⨯⨯-，故原式答案为2．12．一个正整数恰有8个约数，它的最小的3个约数的和为15，且这个四位数的一个质因数减去另一个质因数的5倍等于第三个质因数的2倍，这个数是_________．【考点】约数与倍数、质数【难度】☆☆☆ 【答案】2013或1221HGFEDCBA【解析】这个正整数有8个约数，还至少有3个质因数，故由约数个数定理可知此数应恰有3个不同的质因数；和为15的3个最小约数只能是：（1、3、11），故这个正整数至少含有质因数3、11；由于6111532-⨯=⨯，3735112-⨯=⨯，故本题答案为：31161=2013⨯⨯或31137=1221⨯⨯．13．甲从A 地出发前往B 地，乙、丙两人从B 地出发前往A 地，甲行了50千米后，乙和丙才同时从B 地出发，结果甲和乙相遇在C 地，甲和丙相遇在D 地，已知甲的速度是丙的3倍，甲的速度是乙的1．5倍，C 、D 两地之间的距离是12千米．那么A 、B 两地之间的距离是_________千米．【考点】行程问题、量率对应【难度】☆☆☆ 【答案】130【解析】设距A 地50千米处为E 地，则由于甲速:乙速 1.5:13:2==，故25BC BE =；甲速:丙速3:1=，故14BD BE =；故213125420CD BE BE BE =-==千米，求得80BE =千米，全长5080130+=千米．14．小俊掷骰子游戏，刚开始他站在起点格（如图），如果他掷出1至5点，掷出几点就前进几格，如果他掷出6点或某次前进后超出终点格，则立即返回起点格；若小俊掷了三次恰好到达终点格，掷骰子的顺序有_________种可能．起1 2 3 4 5 6 7 8 9 终【考点】分类枚举【难度】☆☆☆【答案】21【解析】走到终点的方式分两种：要么前进3次，要么先投出6点，再前进2次；前一种情况有（1、2、5）（1、3、4）（1、4、3）（1、5、2）（2、1、5）（2、2、4）（2、3、3）（2、4、2）（2、5、1）（3、1、4）（3、2、3）（3、3、2）（3、4、1）（4、1、3）（4、2、2）（4、3、1）（5、1、2）（5、2、1）共18种，后一种情况有：（6、3、5）（6、4、4）（6、5、3）共3种，总走法为21种．15．老师让同学们计算..AB C D E +时，马小虎把.D E 中的小数点看漏了，得到错误结果39.6；而马大虎把加号看成了乘号，得到错误结果36.9，那么，正确的计算结果应该是_________．【考点】逻辑推理、位值原理【难度】☆☆☆☆【答案】26.1【解析】.39.6AB C DE +=，故6C =；又.6.36.9A B D E ⨯=，故5E =；再利用加法式：.6539.6AB D +=，得4B =；再利用乘法式： 4.6.536.9A D ⨯=，做数字谜可由乘积中的9推出D ；3(6D +的个位数)9=，故1D =或6；但由于加法式的结果不足40，故D 只能为1； 4.61539.6A +=，故2A =；所以原结果为24.6 1.526.1+=．。

2013年第十一届走美杯小学四年级试卷C详解

11届走美小学四年级试卷（C 卷）一、填空题Ⅰ（每题8分，共40分）1、12345×11 = 。

【分析】原式135795=2、罗马数字I 、V 、X 、L 、C 、D 、M 分别表示1、5、10、50、100、500、1000，2×M+5×L+7×X+9×I = 。

【分析】原式21000550710912329=⨯+⨯+⨯+⨯=3、一位老师带着十二名学生去植树，树苗共有44棵。

老师扛6棵树苗，男生每人扛4棵树苗，女生每人扛2棵树苗。

女生有人。

【分析】12名学生共扛了38棵树苗，若12名学生都是男生，可以扛48棵树苗，比实际多10棵，下面开始替换，将1名男生换成女生，少扛2棵树苗，现共需少10棵树苗，因此，女生有1025÷=人。

4、一排座位20个，已坐了一些人。

再坐一人就会有两人座位相邻。

已就坐的至少人【分析】如下图，1个人做多可以排除3个座位，20362÷= ，因此至少需要617+=人。

5、5名裁判员给一名体操运动员打分，若去掉一个最高分，平均得分9分；若去掉一个最低分，平均得分9.2；那么最高分与最低分相差分．【分析】去掉一个最高分，总分为36分，去掉一个最低分，总分为36.8分，因此，最高分比最低分多36.8360.8-=分。

二、填空题Ⅱ（每题10分，共50分）6、平行四边形的面积是60平方厘米，E 是CD 的中点。

阴影部分的面积是平方厘米。

B【分析】1302ABE ABCD S S ∆==，1154AOB ABCD S S ∆==，15ABE AOB S S S ∆∆=-=阴影平方厘米。

7、四个不同的自然数，有一个是偶数质数，任意两个的和是2的倍数，任意三个的和是3的倍数，这四个数的和又恰是4的倍数。

这4个数的和最小等于。

【分析】有一个是偶数质数，而偶数质数只有2由于任意2个数的和是2的倍数，即偶数，因此其余三个数都是偶数由于任意3个数的和是3的倍数，因此除了2以外，另外三个数的和是3的倍数，因此四个数的和除以3余2，由于任意3个数的和是四个数的和减去剩下的一个数，因此任意一个数除以3的余数都是2因此，由同余定理，任意两个数的差既是2的倍数，又是3的倍数，即任意两数之差都是6的倍数此时，这四个数最小是2、8、14、20，四个数的和未44，是4的倍数，于是4个数的和最小等于44。

走美杯四年级试题和答案

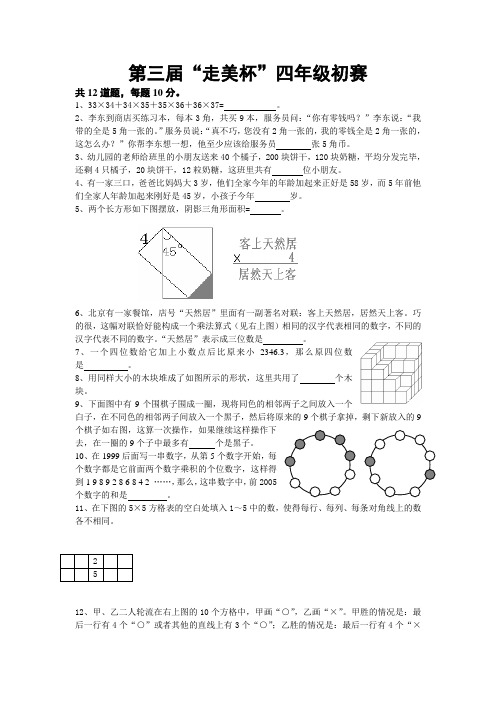
第三届“走美杯”四年级初赛共12道题，每题10分。

1、33×34＋34×35＋35×36＋36×37= 。

2、李东到商店买练习本，每本3角，共买9本，服务员问：“你有零钱吗？”李东说：“我带的全是5角一张的。

”服务员说：“真不巧，您没有2角一张的，我的零钱全是2角一张的，这怎么办？”你帮李东想一想，他至少应该给服务员张5角币。

3、幼儿园的老师给班里的小朋友送来40个橘子，200块饼干，120块奶糖，平均分发完毕，还剩4只橘子，20块饼干，12粒奶糖，这班里共有位小朋友。

4、有一家三口，爸爸比妈妈大3岁，他们全家今年的年龄加起来正好是58岁，而5年前他们全家人年龄加起来刚好是45岁，小孩子今年岁。

5、两个长方形如下图摆放，阴影三角形面积= 。

6、北京有一家餐馆，店号“天然居”里面有一副著名对联：客上天然居，居然天上客。

巧的很，这幅对联恰好能构成一个乘法算式（见右上图）相同的汉字代表相同的数字，不同的汉字代表不同的数字。

“天然居”表示成三位数是。

7、一个四位数给它加上小数点后比原来小2346.3，那么原四位数是。

8、用同样大小的木块堆成了如图所示的形状，这里共用了个木块。

9、下面图中有9个围棋子围成一圈，现将同色的相邻两子之间放入一个白子，在不同色的相邻两子间放入一个黑子，然后将原来的9个棋子拿掉，剩下新放入的9个棋子如右图，这算一次操作，如果继续这样操作下去，在一圈的9个子中最多有个是黑子。

10、在1999后面写一串数字，从第5个数字开始，每个数字都是它前面两个数字乘积的个位数字，这样得到1 9 8 9 2 8 6 8 4 2 ……，那么，这串数字中，前2005个数字的和是。

11、在下图的5×5方格表的空白处填入1～5中的数，使得每行、每列、每条对角线上的数各不相同。

12、甲、乙二人轮流在右上图的10个方格中，甲画“○”，乙画“×”。

第十二届“走美杯”数学解题技能初赛试题及答案(四年级)

第十二届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛注意事项:1．请在密封线内填好有关信息. 总分2．不允许使用手机、计算器等电子设备.小学四年级试卷（A 卷）填空题I（每题8 分，共40 分）1. 计算：47167×61×7=。

2. 4 个人排成一排，有种不同的排法。

3. 我们知道0,1,2,3，……叫做自然数。

只能被1 和自身整除的大于1 的自然数叫做质数或者素数，比如2,3,5,7,11 等。

按照从小到大的顺序，第10 个质数是.4. 吴宇写好了三封信和三个信封，要将每封信放入相应的信封中，一个信封只放入一封信，三封信中至少有一封信被装错的所有可能情形有种.5. “24 点游戏”是很多人熟悉的数学游戏，游戏过程如下：任意从52 张扑克牌（不包括大小王）中抽取4 张，用这4 张扑克牌上的数字（A=1，J=11，Q=12，K=13）通过加减乘除四则运算得出24，先找到算法者获胜。

游戏规定4 张牌扑克都要用到，而且每张牌只能用1 次，比如 2,3,4，Q，则可以由算法（2×Q）×（4-3）得到 24.如果在一次游戏中恰好抽到了9,7,3,2，则你的算法是。

填空题II（每题10 分，共50 分）6. 将一个正方形纸片按照下图所示方式折叠两次后再对折，沿对折线剪开，得到个小正方形纸片。

7. 将一根长 80 厘米的细绳对折一次后，用剪刀在中点处剪开，取其中长度最长的与最短的各一段，这两段绳的绳长之和是厘米。

8. 下图中有个平行四边形。

9、古希腊的数学家们将自然数按照以下方式与多边形联系起来，定义了多边形数：三角形数：1,3,6,10,15…… 四边形数：1,4,9,16,25…… 五边形数：1,5,12,22,35……六边形数：1,6,15,28,45…………则按照上面的顺序，第6 个五边形数为。

10. 用 180°与四边形的每一个内角作差，所得到的值叫做这个内角的角亏。

第十四届走美杯决赛解析四年级

新
舟教
育
竞赛
升学部

家门口的中小学辅导专家
走美杯
———————————————————————————————————————————————— 难度系数：☆☆☆ ———————————————————————————————————————————————— 第二种情况：最少可以划分为 4 个本原格点三角形。最少如图：
解析：整除 988000 49 20163......13 所以，满足要求的数分别是 49 的 1 20163 倍，共 20163 个。 ———————————————————————————————————————————————— 难度系数：☆ ———————————————————————————————————————————————— 3. 只能被 1 与其自身整除的大于 1 的自然数称为素数或质数，比如 2,3,5,7,11,13 等，大于 1 的自然数如果不是素数，则称为合数。除唯一的偶素数 2 之外，相邻的两个素数之间至少间隔一个合数，比如 3, 5； 5,7； 7,11 等。两个连续的素数之间间隔的合数个数称为这两个连续素数的间隔数，间隔数为 1 的两个素数称为孪生素数，比如 3,5；。 5,7 ；而 7,11 的间隔数为 3 ，那么 100 以内的连续素数的最大间隔数为解析：质数与合数 100 以内共有 25 个素数，如下图，经观察：间隔最大的一组连续素数是 89 、 97 ，间隔数为 7 。
新
舟教
育
竞赛
升学部

家门口的中小学辅导专家
走美杯
2, 3, 5 , 7 11, 13， 15， 17, 19 23, 29, 31, 37, 41, 43, 47 53, 59 61, 67, 71, 73, 79 83, 89 97 ————————————————————————————————————————————————

走美杯四年级试题及答案

走美杯四年级试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项是正确的？A. 地球是平的B. 太阳是宇宙的中心C. 地球围绕太阳转D. 月亮是地球的卫星答案：C2. 哪个国家被称为“千岛之国”？A. 中国B. 日本C. 印度尼西亚D. 印度答案：C3. 下列哪个选项是数学中的“奇数”？A. 2B. 4C. 5D. 8答案：C4. 以下哪种动物是哺乳动物？A. 蛇B. 鳄鱼C. 鲸鱼D. 乌龟答案：C5. 世界上最高的山峰是？A. 珠穆朗玛峰B. 乞力马扎罗山C. 富士山D. 阿尔卑斯山答案：A二、填空题（每题2分，共10分）1. 一年有______个季节。

答案：四2. 地球上最大的陆地动物是______。

答案：非洲象3. 光年是长度单位，表示光在一年内通过的距离，大约是______公里。

答案：9.46万亿4. 人体最大的器官是______。

答案：皮肤5. 世界上最大的海洋是______。

答案：太平洋三、简答题（每题5分，共20分）1. 简述地球的自转和公转。

答案：地球的自转是指地球围绕自己的轴线旋转，周期约为24小时，导致了昼夜交替。

地球的公转是指地球围绕太阳的轨道运动，周期约为365.25天，导致了季节更替。

2. 请解释什么是生态系统。

答案：生态系统是由生物群落和其所在的非生物环境相互作用而形成的一个统一整体，包括了生产者、消费者和分解者等生物组成部分以及水、土壤、空气等非生物组成部分。

3. 请列举三种常见的哺乳动物。

答案：猫、狗、牛4. 描述一下水循环的过程。

答案：水循环是指地球上水分子在大气、陆地和海洋之间不断循环的过程，包括蒸发、凝结、降水和径流等环节。

四、计算题（每题10分，共20分）1. 如果一个长方形的长是8米，宽是5米，求其面积。

答案：面积 = 长× 宽 = 8米× 5米 = 40平方米2. 一个班级有40名学生，如果每名学生需要2本练习册，那么总共需要多少本练习册？答案：总练习册数 = 学生数× 每人练习册数= 40 × 2 = 80本五、阅读理解题（每题5分，共10分）阅读以下短文，回答后面的问题。

5-1-2-2 乘除法数字谜(一).教师版

5-1-2-2.乘除法数字谜（一）
教学目标
数字谜是杯赛中非常重要的一块，特别是迎春杯，数字谜是必考的，一般学生在做数字谜的时候都采用尝试的方式，但是这样会在考试中浪费很多时间．本模块主要讲乘除竖式数字谜的解题方法，学会通过找突
1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式．
模块一、乘法数字谜
是一个残缺的乘法竖式，其中
【难度】2星【题型】填空
所以b≥6，从而d≥6．由22□÷c≥60和c＞2知c=3，
de=
76
30 000，所以．再由乘积不小于30000
下面残缺的算式中，只写出了3个数字1，其余的数字都不是
【难度】2星【题型】填空
了说明的方便，这个算式中的关键数字用英文字母表示．很明显e= 0三数之一，两位数应是（100+f ）的因数．101，103，102=17×6，则C 只能取3，，ab 317=⨯，，53ab =
【题型】填空
⨯=
．510)2161080
【答案】。

第七届“走美杯”数学解题技能展示大赛初赛(四年级)

第七届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛初赛一、填空题I（每题8分，共40分）1.37×37+2×63×37+63×63= ．2.3.价4.C5.60券价值为_____________．二、填空题Ⅱ（每题10分，共50分）6.（09年走美三、四、五年级都考）A,B都是整数，A大于B，且A×B=2009，那么A-B的最大值为______，最小值为_____．7.（09年走美三、四、五年级都考）一天，红太狼和灰太狼同时从“野猪林”出发，到“天堂镇”。

红太狼一半路程溜达，一半路程奔跑。

灰太狼一半时间溜达，一半时间奔跑。

如果它们溜达的速度相同，奔跑的速度也相同，则先到“天堂镇”是_______．8.柯南家2008年一年用电10200千瓦时，上半年的月平均用电比下半年的月平均用电少100千瓦时。

柯南家下半年月平均用电为______千瓦时．9.某校A、B、C三名同学参加“走进美妙的数学花园”，其指导教师赛前预测“A获金牌，B不会获金牌，C不会获铜牌”。

结果出来后，三人之中，一人获金牌，一人获银牌，一人获铜牌，指导教师的预测只有一个人与结果相符。

由此可以推论：_______获得银牌．10.从1、2、3、4、5、6这些数中，任取两个数，使其和不能被3整除，则有_____种取法．三、填空题Ⅲ（每题12分，共60分）11.“走美商场”开业了！门口有规律地堆放了一些同样的礼品盒供顾客领取。

每一礼品盒宽9厘米，长18厘米。

摆好后其上面四层的正面图如右图所示，共摆十层，则一共有___个礼品盒，整个图形的周长为____厘米．12.（四年级、五年级题类似）乒乓球从高空落下，到达地面后弹起的高度是落下高度的一半，如果乒乓球从8米的高度落下，那么弹起后再落下，则弹起第___次时它的弹起高度不足1米。

13.在一个长方形的面积为169平方厘米。

在这个长方形内任取一点P，则点P到长方形四边的距离之和最小值为_____厘米14.下图是5×5的方格纸，小方格为边长1厘米的正方形，图中共有____个正方形，所有这些正方形有面积之和为_______．在时候有两位贩卖家畜的商人把他们共有一群牛卖掉，每头牛买得的钱数正好等于牛的头数。

2013年第十一届走美杯小学四年级试卷A详解

11届走美小学四年级试卷（A卷）一、填空题Ⅰ（每题 8分，共 40分）1、4026譢ul025譢ul02= 。

【分析】原式 2013 2 25 2 2013002、规定 A ※ B = (A+3)譢u-248?B-2）。

1 2※ 17 = 。

【分析】原式 (12 3) (17 2)2253、小宇春看一本故事书，每天看 15页，24天刚好看完；如果每天多看 3页，天可以看完。

【分析】该书有15 24 360页，每天多看 3页，则每天看 18页，需 360 18 20 天看完。

4、一瓶可乐 2.5元，3个空瓶可以再换一瓶可乐。

有 30元，最多可以喝到瓶可乐。

【注意】该题有歧义，这题中能否问别人借一个瓶子，若能，则答案应为 18，若不能，则答案为 17。

【分析】一、可以问别人借瓶子由题意，3 个空瓶=1 瓶可乐+1 个空瓶那么实际上，2 个空瓶=1 瓶可乐也就是说，花 5 元钱，买 2 瓶可乐，实际上可以喝到 3 瓶可乐（喝完 2 瓶，剩 2个空瓶，借来 1 个空瓶，换1 瓶可乐，喝掉可乐，把空瓶还掉）于是，30 元钱最多能喝到瓶可乐30 5318二、不能问别人借瓶子30 元钱可以买瓶可乐12 个空瓶可以换瓶可乐30 2.5 124 个空瓶可以换 1 瓶可乐12最后喝了瓶可乐，还剩 2 个空瓶。

3 412 4 1 175、某公司每天上班时间由上午8：30至下午5：30。

在这段间内时钟的时针和分针会重叠次。

【分析】法一：8：30分时，时针指在 8、9之间，分针指着 6，在 9点时，时针指在 9，分针指在 12，分针超过了时针，于是，在 8：30到 9：00之间，分针与时针重合一次同理、9：00到 10：00，10：00到 11：00之间，分针与时针各重合一次注意到，11：00到 12：00之间，分针与时针是在 12：00整重合的，而 12：00到1：00之间，分针与时针也是在 12：00整重合的，于是又是 1次接下来，1：00到 2：00，2：00到 3：00，3：00到 4：00，4：00到 5：00之间，分针与时针各重合一次5：00时，时针指在 5，分针指在 12，5：30分，时针指在 5、6之间，分针指着 6，分针超过了时针，于是，在 5：00到 5：30之间，分针与时针重合一次综上，共重合 9次法二：环形跑道从 8：30到 5：30，共经过 9小时，这 9小时中，分针跑了 9圈，时针跑了 9 12 0.75圈，分针比时针多跑 8.25圈一开始，在 8：30分时，时针指在 8、9之间，分针指着 6，分针落后时针75 360 0.25 圈，于是分针必时针多跑的 0.25圈内，会追上时针一次，以后，每比时针多跑 1圈，多追上 1次，于是，多跑 8.25圈，追上了 9次，即分针与时针重合 9次二、填空题Ⅱ（每题 10分，共 50分）6、如图所示，它是由六个正方形组成的平面硬纸片，由它可以折叠成一个正方体，点“L”将与点重合。

2013年第十一届走美杯初赛小学三年级B卷(含解析)

第十一届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学三年级试卷（B卷）一、填空题Ⅰ（每题8分，共40分）1．1357197199++++++=_________．2．用运算符号将1、4、7、7组成一个算式，使结果等于24．3．将1、2、3、4、5、6这6个数字填入下左图的6个圆圈中，使每条线上三个数字之和都等于10．4．如下图，四个一样的长方形拼成一个边长为10厘米的大正方形，中间形成了一个小正方形，每个长方形的周长是_____厘米．5．将10000000000减去101011后所得的答案中，数字9共出现______次．二、填空题Ⅱ（每题10分，共50分）6．伟伟今年8岁，爸爸34岁．再过______年，爸爸的年龄是伟伟的三倍．7．红色水笔5元一支，蓝色水笔7元一支，花102元共买了16支，蓝色水笔买了_____支．8．五个连续偶数的和是7的倍数，这五个数之和最小等于________．9．甲、乙、丙、丁四人进行乒乓球比赛（没有平局）．每两人都要赛一场，比赛结束后统计成绩，甲胜了2场，乙胜了1场，丙最多胜______场．10．将黑、白各一粒围棋子放在下图方格的格点上，但两粒棋子不能在同一条线上．有______种不同放法．（旋转后位置相同的算同一种）三、填空题Ⅲ（每题12分，共60分）11．A、B两地相距1200米，大成从A地出发6分钟后，小功从B地出发，又过了12分钟两人相遇，大成每分钟比小功多走20米，小功每分钟走______米．12．200位数M由200个1组成，2013M⨯，积的数学和是______．13．一瓶可乐2元，两个空瓶可以再换一瓶可乐，有30元，最多可以喝到______瓶可乐．14．44⨯的方格中应有30个正方形，下图已去掉了4个点，最少再去掉______个点，才能使图中恰好只剩一个正方形．15．有6个边长为2厘米的等边三角形，2个边长为2厘米的正方形，请你选取其中的一些或全部，拼出一个八边形，在方框中画出多边形的拼法．第十一届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学三年级试卷（B卷）参考答案1 2 3 4 5 6 7 810000 (17)(74)24+⨯-=答案不唯一20 7 5 11 709 10 11 12 13 14 153 9 28 1200 304 答案不唯一参考解析一、填空题Ⅰ（每题8分，共40分）1．1357197199++++++=_________．【考点】等差数列求和【难度】☆【答案】10000【解析】项数：(1991)21100+⨯÷=．-÷+=，求和：(1199)1002100002．用运算符号将1、4、7、7组成一个算式，使结果等于24．【考点】24点游戏【难度】☆【答案】(17)(74)24+⨯-=【解析】24点游戏主要考虑哪些最后能得到24，例如：38=24⨯．⨯、46=243．将1、2、3、4、5、6这6个数字填入下左图的6个圆圈中，使每条线上三个数字之和都等于10．【考点】数阵图【难度】☆☆【答案】【解析】12345621+++++=，31021=9⨯-，说明三个顶点上填的三个数之和为9，=++=++=++，只有1、3、5可以位于顶点位置，把数补充完整即可．91351262344．如下图，四个一样的长方形拼成一个边长为10厘米的大正方形，中间形成了一个小正方形，每个长方形的周长是_____厘米．【考点】巧求周长【难度】☆【答案】20【解析】长方形的长+宽10⨯（厘米）=，所以周长是102=205．将10000000000减去101011后所得的答案中，数字9共出现______次．【考点】多位数计算【难度】☆【答案】7【解析】100000000001010119999898989-=，出现7次．二、填空题Ⅱ（每题10分，共50分）6．伟伟今年8岁，爸爸34岁．再过______年，爸爸的年龄是伟伟的三倍．【考点】年龄问题中的差倍【难度】☆☆【答案】5【解析】差倍问题．(348)(31)13-÷-=（岁），138=5-（岁）．7．红色水笔5元一支，蓝色水笔7元一支，花102元共买了16支，蓝色水笔买了_____支．【考点】应用题——方程【难度】☆☆【答案】11【解析】设蓝色水笔买了x支，那么红色水笔(16)x⨯-+=，解得11-支，根据题意可得5(16)7102x xx=．8．五个连续偶数的和是7的倍数，这五个数之和最小等于________．【考点】等差数列【难度】☆☆【答案】70【解析】五个连续偶数的和一定是中间数的5倍，又是7的倍数，还是偶数，那么最小是70，此时这5个数分别是10，12，14，16，18．9．甲、乙、丙、丁四人进行乒乓球比赛（没有平局）．每两人都要赛一场，比赛结束后统计成绩，甲胜了2场，乙胜了1场，丙最多胜______场．【考点】体育比赛中的逻辑推理【难度】☆☆【答案】3【解析】一共要比3+2+1=6（场），那么丙最多赢3场，胜负情况可进行如下安排：甲、乙、丙均胜丁，甲胜乙，丙胜甲，丙胜乙．10．将黑、白各一粒围棋子放在下图方格的格点上，但两粒棋子不能在同一条线上．有______种不同放法．（旋转后位置相同的算同一种）【考点】计数问题【难度】☆☆☆ 【答案】9【解析】如下图所示：三、填空题Ⅲ（每题12分，共60分）11．A 、B 两地相距1200米，大成从A 地出发6分钟后，小功从B 地出发，又过了12分钟两人相遇，大成每分钟比小功多走20米，小功每分钟走______米．【考点】行程问题【难度】☆☆☆【答案】28【解析】如果把小功走的12分钟换成大成来走，多走1220240⨯=（米），6121230++=（分），12002401440+=（米），大成速度144030=48÷（米/分），小功速度4820=28-（米/分）．12．200位数M 由200个1组成，2013M ⨯，积的数学和是______．【考点】进位与数字和问题【难度】☆☆☆【答案】1200【解析】多位数计算．200120012003200211120132220001110+333⨯=+个个个个，如果列竖式相加，不会发生进位，所以和的数字和等于各个加数的数字和相加，200220020031200⨯++⨯=．13．一瓶可乐2元，两个空瓶可以再换一瓶可乐，有30元，最多可以喝到______瓶可乐．【考点】最值问题【难度】☆☆【答案】30【解析】方法一：302=15÷（瓶），不断用空瓶换可乐，152=71÷，(71)24+÷=（瓶），42=2÷（瓶），22=1÷（瓶），此时已经喝了15742129++++=（瓶）可乐，且剩余一个空瓶，可以向店主借一个空瓶，换一瓶可乐，喝完后再把瓶子还给店主．方法二：一瓶可乐价值2元，可认为可乐值1元，瓶子值1元，在不浪费的情况下，30元最多可以喝到30瓶可乐．14．44的方格中应有30个正方形，下图已去掉了4个点，最少再去掉______个点，才能使图中恰好只剩一个正方形．【考点】图形中的最值【难度】☆☆☆【答案】4【解析】现在共有9个正方形，每去1个点，最多去掉两个正方形(只有去掉点A去掉三个正方形)，最有所以最少要去掉4个点，经试验得如下图所示：．15．有6个边长为2厘米的等边三角形，2个边长为2厘米的正方形，请你选取其中的一些或全部，拼出一个八边形，在方框中画出多边形的拼法．【考点】图形的拼接【难度】☆☆☆【答案】【解析】拼出八边形即可．。

05年第三届至13年第十一届走美杯试题答案 (1)

目录第三届“走美杯”答案 (2)第四届“走美杯”答案 (3)第五届“走美杯”答案 (4)第六届走美杯三年级初赛试题参考答案 (6)第六届走美杯三年级决赛试题参考答案 (9)第七届走美杯三年级初赛试题参考答案 (10)第八届走美杯三年级初赛试题参考答案 (11)第九届走美杯三年级A卷初赛试题参考答案 (13)第十届走美杯三年级B卷试题及答案详解 (14)第三届走美杯四年级试题参考答案 (18)第四届走美杯四年级试题参考答案 (19)第六届走美杯四年级初赛试题参考答案 (20)第六届走美杯四年级决赛试题参考答案 (24)第七届走美杯四年级初赛试题参考答案 (24)第八届走美杯四年级初赛试题参考答案 (25)第九届走美杯四年级A卷初赛参考答案 (27)第九届走美杯四年级B卷初赛参考答案 (28)第三届走美杯五年级试题参考答案 (33)第四届走美杯五年级试题参考答案 (34)第五届走美杯五年级初赛试题参考答案 (35)第六届走美杯五年级初赛试题参考答案 (39)第六届走美杯五年级决赛试题参考答案 (42)第七届走美杯五年级初赛试题参考答案 (43)第八届走美杯五年级初赛试题参考答案 (46)第九届走美杯五年级初赛试题参考答案 (48)第九届走美杯五年级B卷初赛试题参考答案 (52)第三届走美杯六年级试题参考答案 (52)第四届走美杯六年级试题参考答案 (53)第五届走美杯六年级试题参考答案 (54)第六届走美杯六年级决赛试题参考答案 (58)第七届走美杯六年级初赛试题参考答案 (59)第八届走美杯六年级初赛试题参考答案 (62)第九届走美杯六年级A卷初赛试题参考答案 (65)第十届2012走美杯六年级试题及答案详 (66)第六届走美杯三年级初赛试题参考答案1.22222.861；574；5733.604.155.4；36.90÷15=34－28=67.10；28.169.22210.3711.略12.361.【答案】100012.【答案】100003.【答案】404.【答案】11705.【答案】MT79366.【答案】2008；87.【答案】38.【答案】49.【答案】灰太狼10.【答案】711.【答案】105 ；312.【答案】7； 213.【答案】55；540 14.【答案】4或315.【答案】1、2 、4 、8 .第八届走美杯三年级初赛试题参考答案第九届走美杯三年级A卷初赛试题参考答案第十届走美杯三年级B卷试题及答案详解1、49042、73、364、35、46、9787、2607或23708、509、810、1203111、12、5，2，6 1 2 3 4 5 4 5 1 2 3 2 3 4 5 1 5 1 2 3 4 3 4 5 1 2第六届走美杯四年级初赛试题参考答案1.20082.64；15625（64×15625）3.2或54.155.906.200000077.168.1；2；2；39.5610.3011.147张，15块12.2100第七届走美杯四年级初赛试题参考答案1. 100002. 403. 丙；甲4. 3 、1 、25. 156. 2008；87. 灰太狼8. 9009. C.10. 1011. 55；54012. 413. 2614.55 ；259平方厘米15.21、555502、1043、254、445、19；5176、97、388、79、100010、126311、6412、328213、814、415、1176答案：1、2010012 2、19 3、0。

【试卷】2013年第11届“走美杯”小学数学竞赛试卷(六年级初赛B卷)_c958b7

2013年第11届“走美杯”小学数学竞赛试卷（六年级初赛B卷）一、填空题I（每题8分，共40分）1．（8分）183×279×361﹣182×278×360的计算结果是（）A．217017 B．207217 C．207216 D．2170162．（8分）假设地球是个均匀的球体（半径6378千米），围绕地球赤道正上方上有一圈铁丝，铁丝的周长比地球赤道长1米，在赤道和铁丝之间会有一个缝隙，下列动物中，有种可以安全通过铁丝．①蚂蚁；②蜜蜂；③青蛙；④老鼠；⑤猫；⑥成年奶牛；⑦大象．3．（8分）将0﹣5这六个数字中的4个数字填入图的圆圈中，没条线段两端的数字作差（大或小），可以得到5个差，这5个查恰好为1﹣5．在所有满足条件的填法中，四位数ABCD （首位不能为0）的最小值是．4．（8分）一次考试中，总人数的又3人得了3分，总人数的又4人得了4分，总人数的又5得了5分，其余人都得2分．已知得2分的人数和得5分的人数一样多，则有人得了4分．5．（8分）在一个长20米、宽8米、深1.6米的长方体游泳池的四壁及地面贴磁砖，磁砖是边长为0.2米的正方形，共需磁砖块．二、填空题II（每题10分，共50分）6．（10分）如图，正方形的边长是20厘米，阴影部分面积为平方厘米．（π取3.14）7．（10分）两个相同的玻璃杯，都装满了糖水，糖与水的质量比分别是1：7和1：9，现将这两杯糖水混合，混合后糖水的含糖率是%．8．（10分）一个游戏需要8人参加，分成红、黄两队，每队各4人，一对兄弟来参加这个游戏，他们俩很想被分在同一队，但是谁被编入哪个队是完全随机的，那么这对兄弟被分进同一队的可能性是．9．（10分）将数字1～9填入如图竖式的9个方格中，每个数字只能用一次，那么和的最大值为．10．（10分）军区食堂晚饭需用1000斤大米和200斤小米，军需员到米店后发现米店正在促销，“大米1元1斤，每购10斤送1斤小米（不足10斤部分不送）；小米2元一斤，每购5斤送2斤大米（不足5斤部分不送）．”军需员至少要付元钱才能买够晚饭需用的米．三、填空题III（每题12分，共60分）11．（12分）定义a□b=（a+2）（b+2）﹣2：算式1×3×5×7×9×11×13﹣（1□3□5□7□9□11）的计算结果是．12．（12分）如图中共能数出个三角形．13．（12分）甲乙两船从一条和的A、B两个码头同时出发，相向而行，甲船的静水速度比乙船的静水速度快20%，水速为乙船静水速度的10%，两船在距离中点10千米处相遇．A、B两个码头间的距离为千米．14．（12分）一个四位数，他最小的8个约数的和是43，那么这个四位回文数是．（回文数例如：1111、4334、3210123）15．（12分）小俊掷骰子游戏，刚开始他站在起点格（如表），如果他掷出1至5点，掷出几点就前进几格，如果他掷出6点或某次前进后超出终点格，则立即返回起点格；若小俊掷2013年第11届“走美杯”小学数学竞赛试卷（六年级初赛B卷）参考答案与试题解析一、填空题I（每题8分，共40分）1．（8分）183×279×361﹣182×278×360的计算结果是（）A．217017 B．207217 C．207216 D．217016【解答】解：183×279×361﹣182×278×360=（182+1）×（278+1）×（360+1）﹣182×278×360=182×（278+1）×（360+1）﹣182×278×360+279×361=（182×278+182）×（360+1）﹣182×278×360+279×361=182×278×360+182×278+182×360+182﹣182×278×360+279×361=182×278+182×360+182+279×361=182×（278+360+1）+279×361=182×278+182×361+279×361=50596+（182+279）×361=50596+461×361=50596+166421=217017．故选：A2．（8分）假设地球是个均匀的球体（半径6378千米），围绕地球赤道正上方上有一圈铁丝，铁丝的周长比地球赤道长1米，在赤道和铁丝之间会有一个缝隙，下列动物中，有5种可以安全通过铁丝．①蚂蚁；②蜜蜂；③青蛙；④老鼠；⑤猫；⑥成年奶牛；⑦大象．【解答】解：铁丝与赤道的缝隙宽度为：1÷2÷3.14≈0.16（米）=16（厘米），所以宽度为16厘米的缝隙，可以通过的动物有：蚂蚁、蜜蜂、青蛙、老鼠、猫，而成年奶牛和大象则不能通过．故答案为：5．3．（8分）将0﹣5这六个数字中的4个数字填入图的圆圈中，没条线段两端的数字作差（大或小），可以得到5个差，这5个查恰好为1﹣5．在所有满足条件的填法中，四位数ABCD （首位不能为0）的最小值是1052．【解答】解：因为四位数ABCD最小，因此A为1，B为0；又因为必须有一个差为5，故CD中有一个为5，若C为5，那么D只能为2或3；若D为5，那么C无解；因此，最小值为1052．故答案为：1052．4．（8分）一次考试中，总人数的又3人得了3分，总人数的又4人得了4分，总人数的又5得了5分，其余人都得2分．已知得2分的人数和得5分的人数一样多，则有259人得了4分．【解答】解：设总人数为60份，那么3分的是20份+3人，4分的是15份加4人，5分的是12份加5人，剩下2分的是13份﹣12人，5分和2分的一样多，即：13份﹣12人=12份+5人即1份=17人所以4分：15×17+4=255+4=259（人）；答：则有259人得了4分．故答案为：259．5．（8分）在一个长20米、宽8米、深1.6米的长方体游泳池的四壁及地面贴磁砖，磁砖是边长为0.2米的正方形，共需磁砖6240块．【解答】解：（20×8+20×1.6×2+8×1.6×2）÷（0.2×0.2）=（160+64+25.6）÷0.04=249.6÷0.04=6240（块）；答：共需磁砖6240块．故答案为：6240．二、填空题II（每题10分，共50分）6．（10分）如图，正方形的边长是20厘米，阴影部分面积为400平方厘米．（π取3.14）【解答】解：3.14×（20÷2）2×2﹣（3.14×202×2÷4﹣20×20）=628﹣（628﹣400）=628﹣228=400（平方厘米）故答案为：400．7．（10分）两个相同的玻璃杯，都装满了糖水，糖与水的质量比分别是1：7和1：9，现将这两杯糖水混合，混合后糖水的含糖率是11.25%．【解答】解：（+）÷2×100%=××100%=11.25%答：混合后糖水的含糖率是11.25%；故答案为：11.25．8．（10分）一个游戏需要8人参加，分成红、黄两队，每队各4人，一对兄弟来参加这个游戏，他们俩很想被分在同一队，但是谁被编入哪个队是完全随机的，那么这对兄弟被分进同一队的可能性是．【解答】解：兄弟二人分法如下：哥哥分到红队、弟弟分到黄队，哥哥分到黄队、弟弟分到红队，哥哥和弟弟都分到黄队，哥哥和弟弟都分到红队，共有4种可能；其中他们俩被分在同一队有：哥哥和弟弟都分到黄队，哥哥和弟弟都分到红队，共2种可能，所以2=；故答案为：．9．（10分）将数字1～9填入如图竖式的9个方格中，每个数字只能用一次，那么和的最大值为3972．【解答】解：根据题干分析可得：答：和的最大值是3972．故答案为：3972．10．（10分）军区食堂晚饭需用1000斤大米和200斤小米，军需员到米店后发现米店正在促销，“大米1元1斤，每购10斤送1斤小米（不足10斤部分不送）；小米2元一斤，每购5斤送2斤大米（不足5斤部分不送）．”军需员至少要付1168元钱才能买够晚饭需用的米．【解答】解：设买大米x斤，小米y斤，列方程组：，得到大致重量：大米买950斤，小米买105斤，此时花了1160元，已有992斤大米和200斤小米，再用8元买8斤大米即可，最少用1168元；答：军需员至少要付1168元钱才能买够晚饭需用的米．故答案为：1168．三、填空题III（每题12分，共60分）11．（12分）定义a□b=（a+2）（b+2）﹣2：算式1×3×5×7×9×11×13﹣（1□3□5□7□9□11）的计算结果是2．【解答】解：1□3□5□7□9□=[（1+2）×（3+2）﹣2]□5□7□9=13□5□7□□911=[（13+2）（5+2）﹣2]□7□9□11=103□7□9□11=[（103+2）（7+2）﹣2]□9□11=943□9□11=[（943+2）（9+2）﹣2]□11=10393□11=（10393+2）（11+2）﹣2=135135﹣2=135133；1×3×5×7×9×11×13﹣（1□3□5□7□9□11）=135135﹣135133=2；故答案为：2．12．（12分）如图中共能数出72个三角形．【解答】解：24+22+12+10+2+2=72（个）故答案为：72．13．（12分）甲乙两船从一条和的A、B两个码头同时出发，相向而行，甲船的静水速度比乙船的静水速度快20%，水速为乙船静水速度的10%，两船在距离中点10千米处相遇．A、B两个码头间的距离为110千米．【解答】解：水速为“1”，则乙船静水速度为10，甲船静水速度为12，若乙顺水、甲逆水，则两船在中点相遇，不符合要求．因此甲船顺水，甲的速度是13，乙的速度是9，若全程为22份，相遇时甲走了13份，因此，2份为10千米，全程为：10÷2×22=5×22=110（千米）答：A、B两个码头间的距离为110千米．故答案为：110．14．（12分）一个四位数，他最小的8个约数的和是43，那么这个四位回文数是2772．（回文数例如：1111、4334、3210123）【解答】解：由分析可知：约数首先为自然数，首先该有1和2，不该有5和10，而1+2+3+4+6+7+8+9=40不够43，而回文数必然是11的倍数，所以11也是这8个约数之一，把11考虑进去，则有：1+2+3+4+6+7+9+11=43，以上数的最小公倍数为：4×7×9×11=2772，正好满足要求；答：这个四位回文数是2772；故答案为：2772．15．（12分）小俊掷骰子游戏，刚开始他站在起点格（如表），如果他掷出1至5点，掷出几点就前进几格，如果他掷出6点或某次前进后超出终点格，则立即返回起点格；若小俊掷①1+1+3+5=10，考虑加数的位置，有12种可能；②1+1+4+4=10，考虑加数的位置，有6种可能；③1+2+2+5=10，考虑加数的位置，有12种可能；④1+2+3+4=10，考虑加数的位置，有24种可能；⑤1+3+3+3=10，考虑加数的位置，有4种可能；⑥2+2+3+3=10，考虑加数的位置，有6种可能；⑦2+2+2+4=10，考虑加数的位置，有4种可能；一共有12+6+12+24+4+6+4=68种可能；情况二，第一次就掷出了6，剩下3个数的和是10；①1+5+4=10，考虑加数的位置，有6种可能；②2+5+3=10，考虑加数的位置，有6种可能；③2+4+4=10，考虑加数的位置，有3种可能；④3+4+3=10，考虑加数的位置，有3种可能；一共有6+6+3+3=18种可能；第三种情况第二次掷出6，第三次和第四次都掷出5；那么第一次可以是1～6，就有6种可能；68+18+6=92（种）答：掷骰子的顺序有92种可能．故答案为：92．参与本试卷答题和审题的老师有：齐敬孝；pyzq；春暖花开；姜运堂；张召伟；旭日芳草；xiaosh；忘忧草；TGT；ZGR（排名不分先后）菁优网2016年4月22日。

word完整版四年级第十三届走美杯真题和答案与解析四年级

第十三届“走进美好的数学花园”青少年展现沟通活动兴趣数学解题技术展现大赛初赛小学四年级试卷（ B 卷）2015 年 3 月 8 日南京填空题I （每题8 分，共40 分）1 计算 5×13×31×73×137=__________________【分析】：此题考察多位数乘法的计算。

直接列式子计算。

2、用 1 个 1、 2 个 2、 2 个 3构成一些 4位数，则能够构成的不一样 4 位数一共有 __________ 个。

【分析】：此题考察摆列组合。

1,2,2,3,3五个数字取出 4 个。

相当于 5 个拿走一个，只好拿走1 或 2 或 3。

有① 2233 ② 1223 ③ 1233这三种组合。

剖析第①种，当两个 2 连在一同， 2233 3223 3322 两个 2 中间隔一个数， 23233232 两个 2 中间隔两个数 2332. 这样第一种小状况有6种。

第② 种，相同剖析，可是 1 和 3能够交换一次，因此有6×2=12 种。

第③种，把22 和 33 交换，用换位思虑的方法，同第② 种。

因此一共有6+12+12 得 30 种3、整除凡因数，20152015的数称为2015 的因数， 1 和还有一些非平庸因数，那么2015 明显整除2015 ，称为 20152015 的全部非平庸因数之和为的平庸因数，除了平______________【分析】：考察因数观点和分解质因数方法。

2015 分解质因数 2015=5 ×13×31，每两个因数两两组合，得 5+403+13+155+31+65=672 。

注明：分解质因数的方法， 2015÷50=403 ，对于403 的列举量很大，很难分解，这里需要知道一个方法，只需试到这个数的开方数以下的质数。

20×20=400 ，因此只需把 403 除以 20 之内的质数就能够试出来。

SH四年级走美杯初赛汇总

第七届走美杯四年级初赛一、填空题Ⅰ（每题8分，共40分）1、 3737263376363⨯+⨯⨯+⨯=______2、下边的一排方格中，除9、8外，每个方格中的字都表示一个数（不同的字可以表示相同的数字），已知其中任何3个连续的方格中的数相加起来都为22，则“走”+“进”+“数”+“学”+“花”+“园”3、 “走美”商场有下列几种瓶装蜂蜜出售：甲，净重3kg ,售价33.99元;乙，净重2kg ，售价22.99元;丙，净重500g ,售价5.99元，那么，_____种蜂蜜最贵，____种蜂蜜最便宜。

4、一个数学玩具的包装盒是正方体，其表面展开图如下。

现在每方格内都填上相应的数字。

已知将这个表面展开图沿虚线折成正方体后，相对面的两数之和为“3”，则填在A 、B 、C 内的三个数字依次是________。

5、某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划：该球拍每只售价为人民币60元，同时购买者可获赠1张奖券，积累3张奖券可兑换1只球拍。

由此可见，1张奖券价值为________元。

二、填空题Ⅱ（第题10分，共50分）6、 A ,B 都是整数，A 大于B ，且2009A B ⨯=，那么A B -的最大值为________，最小值为________。

7、一天，红太狼和灰太狼同时从“野猪林”出发，到“天堂镇”。

红太狼一半路程溜达，一半路程奔跑。

灰太狼一半时间溜达，一半时间奔跑。

如果它们溜达的速度相同，奔跑的速度也相同，则先到“天堂镇”是___________。

8、柯南家2008年一年用电10200千瓦时，上半年的月平均用电比下半年的月平均用电少100千瓦时。

柯南家下半年月平均用电为___________千瓦时。

9、某校A 、B 、C 三名同学参加“走进美妙的数学花园”，其指导教师赛前预测“A 获金牌，B 不会获金牌，C 不会获铜牌”。

结果出来后，三人之中，一人获金牌，一人获银牌，一人获铜牌，指导教师的预测只有一个人与结果相符。