专题16 几何体的几何特征与点线面关系【解析版】
几何形的点线和平面关系

几何形的点线和平面关系在几何学中,点、线和平面是最基本的几何概念,它们相互之间存在着密切的关系。
本文将探讨几何形的点线和平面之间的关系,从而进一步理解几何学的基本原理。
一、点和线的关系点是几何形的最简单元素,可以看成是没有长度、宽度和高度的,仅有位置而无大小的几何实体。
线是由无数个点按照一定的规律连在一起形成的,它具有长度但没有宽度和高度。
点与线之间的关系主要体现在以下几个方面。
1. 线上的任意两点确定一条唯一的直线。
这是几何学中的著名定理,也是点和线之间最基本的关系之一。
通过两个点可以描绘一条直线,而且这条直线是唯一确定的。
2. 点可以在线上任意移动,但不会改变线的性质。
无论点在线的哪个位置,线依然是直线,具有一维的性质。
点的位置可以改变,但并不会影响线本身。
3. 线段是由两个端点围成的部分。
线段是线上的一小段,它的两个端点是线上的两个点。
线段是线的一种特殊情况,有着特定的长度。
二、点、线与平面的关系点和线是平面上的基本构成要素,通过它们可以形成更复杂的几何形状。
点、线与平面之间的关系可以从以下几个方面来理解。
1. 平面可以通过点和线来确定。
在平面上任取三个不共线的点,这三个点就可以确定一个平面。
另外,通过一条直线和一点外的另一条直线,可以确定一个平面。
2. 平面可以包含无数个点和线。
在平面上,可以找到无数个点和线,并且这些点和线都在这个平面上。
平面是一个二维的几何对象,可以容纳无数个点和线。
3. 点在平面上可以自由移动,但不会改变平面的性质。
无论点在平面的任何位置,平面仍然是二维的,具有无限大的面积。
点的位置可以改变,但并不会影响平面本身。
4. 线可以在平面上自由延伸和移动。
平面上的线可以无限延伸,可以增加或减小它的长度,但不会离开平面。
线可以在平面上自由移动,但始终保持在平面内部。
5. 平面可以与平面相交,形成新的几何形状。
两个平面可以相交,相交的区域形成一条线,或者是一个点。
通过不同的相交关系,我们可以得到不同的几何形状。
空间几何的基本概念点线与面的关系

空间几何的基本概念点线与面的关系空间几何的基本概念:点、线与面的关系空间几何是研究三维空间中点、线和面之间的关系的数学分支。
点、线和面是空间几何中最基本的概念,它们之间的关系是建立在欧几里得几何基础上的。
本文将介绍空间几何中点、线和面的定义及其之间的关系。
一、点点是空间几何中最基本的对象,它是没有长度、宽度和高度的,仅有一个位置。
点通常用字母标记,如A、B、C等。
在空间中,任意两点可以确定一条线段,而三个非共线的点可以确定一个平面。
二、线线是空间几何中由无数个点组成的集合,它只有长度没有宽度和高度。
线通常用字母表示,如l、m、n等。
线可以分为直线和曲线两种。
直线是在空间中两点之间连续延伸的路径,它有无限个点。
而曲线则是非直线的线,它的形状可以是弯曲或蜿蜒的。
三、面面是空间几何中由无数个直线组成的集合,它有长度和宽度,没有高度。
面通常用字母表示,如α、β、γ等。
面可以分为平面和曲面两种。
平面是由无数个共面的点和一条穿过其中的直线组成的,它没有弯曲的部分。
而曲面则不是平的,它可以弯曲或扭曲。
点、线和面的关系是空间几何中重要的内容。
在空间中,点是构成线和面的基础。
在两个点之间,可以画一条直线,它是连接两个点的最短路径。
多个点可以连成一条折线,折线也是一种线。
线可以在平面内运动、延伸或相交,形成不同的几何形状,而面是由无数条线构成的,它们共面并围成了一个封闭的区域。
点线面之间的关系可以通过以下几个方面进行描述:1. 点与线的关系:一条直线上的任意两点可以确定一条线段,反之,一条线段也可以看作是两个端点之间的直线。
点也可以在一条直线上移动,形成线段的延伸或缩短。
两条相交的直线可以在交点处确定一个新的点。
2. 点与面的关系:一个点可以在平面内,平面也可以通过一个点来确定。
在一个平面上,可以找到无数个点。
3. 线与面的关系:一条线可以在平面内或平面上延伸,两条相交的直线可以确定平面上的一条直线。
一个平面上可以有多条直线,它们可以平行、相交或重合。
初一下册几何点线面体,讲解

初一下册几何点线面体,讲解点、线、面、体是几何学中的基本概念,它们之间的关系可以用来描述空间中的形状和结构。
●点:点是几何学中最基本的元素之一。
它没有大小,也没有方向。
在空间中,点的位置由其坐标确定。
通过在二维空间中放置一个点,可以形成一个有序数对,其中第一个数表示该点在x轴上的位置,第二个数表示该点在y轴上的位置。
在三维空间中,需要三个数来确定点的位置,即x、y和z坐标。
●线:线是由无数个点组成的集合。
在二维空间中,线是由所有有序数对组成的集合,其中第一个数是x坐标,第二个数是y坐标。
线有起点和终点,并且可以无限延伸。
在三维空间中,线是所有有序数对组成的集合,其中除了x和y坐标外,还有一个z坐标。
●面:面是由无数条线组成的集合。
在二维空间中,面是由所有有序数对组成的集合,其中第一个数是x坐标,第二个数是y坐标。
面有边界,并且可以无限延伸。
在三维空间中,面是由所有有序数对组成的集合,其中除了x和y坐标外,还有一个z坐标。
●体:体是由无数个面组成的集合。
在三维空间中,体是由所有有序数对组成的集合,其中除了x、y和z坐标外,还有一个表示高度的参数。
体有边界和内部空间。
●点、线、面、体的关系可以通过几何图形来演示。
例如,一个正方形可以由一个点、四条线和四个面组成。
通过将点移动到不同的位置,可以形成不同的几何图形。
总之,点、线、面、体是几何学中的基本概念,它们之间的关系可以用来描述空间中的形状和结构。
通过学习和理解这些概念和关系,我们可以更好地理解和掌握几何学的基础知识。
点线面的关系

点线面的关系在几何学中,点、线和面构成了基本的几何要素,它们之间存在着紧密的关系。
点是最基本的元素,它是没有长度、宽度和高度的,只有位置。
线是由一系列相邻点组成的,它具有长度但没有宽度和高度。
面由若干条线段相交形成的封闭区域,它具有长度和宽度但没有高度。
点、线和面之间的关系可以通过以下几个方面来描述。
1. 点与线的关系点与线之间的关系比较简单。
一条线段由两个端点组成,而一个点可以是一条线段的一个端点。
点可以在线上或者线的延长线上,也可以不在线上。
点的位置相对于线的位置有多种可能:在线的中间、在线的一端或者在线的外部。
点和线之间的关系可以通过点是否在线上来判断。
2. 点与面的关系点和面之间的关系也比较简单。
点可以在面上、在面的边界上或者在面的外部。
如果一个点在面上,则称该点在该面内。
点和面之间的关系可以通过点是否在面上来判断。
3. 线与线的关系线与线之间的关系有多种情况。
两条线可以相交,也可以平行或重合。
线与线之间的关系可以通过它们的位置关系来描述:如果两条线没有任何交点,则它们平行;如果两条线有且仅有一个交点,则它们相交;如果两条线的所有点都重合,则它们重合。
4. 线与面的关系线和面之间的关系也有多种情况。
线可以位于面内、跨越面或者位于面的边界上。
当一条线既在面内又与面相交时,它被称为切线。
线和面之间的关系可以通过它们的位置关系来判断。
5. 面与面的关系面与面之间的关系也有多种情况。
两个面可以平行,也可以相交。
两个相交的面可以有共线的边,也可以没有共线的边。
两个面之间的关系可以通过它们的位置关系来描述。
综上所述,点、线和面之间存在着丰富的关系。
它们相互作用和相互影响,形成了几何学中复杂而有趣的结构。
通过研究点、线和面之间的关系,我们可以深入理解几何学的基本原理,并将其应用于实际问题的解决中。
几何学作为数学的一部分,对于我们认识和探索世界具有重要的意义。
因此,我们应该充分理解和运用点、线和面之间的关系,以拓宽我们的视野和思维方式。
点线与面的几何关系

点线与面的几何关系点、线和面是几何学中基本的几何要素,它们之间存在着密切的几何关系。
在本文中,我们将探讨点、线和面之间的几何关系,以及它们在三维空间中的特殊性质和应用。
一、点与线的关系点是几何学中最基本的要素,它是没有任何维度的,只有位置信息。
而线则是由无数个点组成的,它具有一维的性质,可以看作是一维的延伸。
点和线之间的几何关系主要包括以下几个方面:1.1 点在直线上当一个点处于一条直线上时,我们可以说该点在直线上。
直线是由无数个点组成的,其中的任意一个点都可以被称为直线上的点。
1.2 点与线的相对位置一个点相对于一条直线可以有三种位置关系:点在直线上、点在直线的左侧或点在直线的右侧。
这是由点与直线的几何关系所决定的。
1.3 点的投影通过将垂直于直线的线段与直线相交,我们可以找到点在直线上的垂直投影。
这个投影点是点与直线之间的最短距离所在的点。
1.4 点到直线的距离点到直线的距离是指点到直线的最短距离。
我们可以通过求解该点到直线的垂直投影来计算得到。
二、点与面的关系面是由无数个点和线组成的,它具有二维的性质。
点、线与面之间的几何关系如下所示:2.1 点在平面上当一个点处于一个平面上时,我们可以说该点在平面上。
平面是由无数个点组成的,其中的任意一个点都可以被称为平面上的点。
2.2 点与平面的相对位置一个点相对于一个平面可以有四种位置关系:点在平面上、点在平面的上方、点在平面的下方或点在平面的内部。
这是由点与平面的几何关系所决定的。
2.3 点到平面的距离点到平面的距离是指点到平面的最短距离。
我们可以通过求解该点到平面的垂直投影来计算得到。
三、线与面的关系线是由无数个点组成的,面是由无数个点和线组成的,因此线与面之间的几何关系也是十分重要的。
线与面的关系如下所示:3.1 线在平面上当一条线处于一个平面上时,我们可以说该线在平面上。
这条线可以与平面内的任意一条线相交或平行。
3.2 线与平面的相对位置一条线相对于一个平面可以有三种位置关系:线在平面内、线与平面平行或线与平面相交。
点线面与体点线面与体的基本概念与特征

点线面与体点线面与体的基本概念与特征点线面与体是几何学中的基本概念,它们是描述和构建几何图形和空间的基本要素。
本文将介绍点线面与体的基本概念与特征,并讨论它们在几何学中的重要性。
一、点的概念与特征点是几何学中最基本的概念之一,它没有长度、宽度和高度,只有位置。
点可以表示为一个具体的坐标或一种抽象的符号,如(x, y, z)或A。
无论如何表示,点都是几何空间中的一个具体位置。
点有以下几个特征:1. 点是零维的,没有尺寸和形状。
2. 点没有方向,可以在空间中移动,但它的位置始终不变。
3. 两个不同点之间可以通过直线连接。
二、线的概念与特征线是由一系列点连接而成的几何对象,它有长度但没有宽度和高度。
线是由无数个点构成的,可以通过这些点的连续性来描述一个曲线或直线。
线有以下几个特征:1. 线是一维的,有长度但没有宽度和高度。
2. 线无论怎样延长都没有尽头,可以无限延伸。
3. 线可以是直线或曲线,直线是两个点之间的最短路径,而曲线则不是。
三、面的概念与特征面是由一系列线连接而成的几何对象,它有长度和宽度但没有高度。
面可以看作由无数个点和线组成的一个平坦的二维区域。
面有以下几个特征:1. 面是二维的,有长度和宽度但没有高度。
2. 面可以是平面或曲面,平面可以由至少三个相互连接的点所确定,而曲面则不是。
3. 面可以被划分为许多小区域,每个小区域都可以表示为一个点、线或面。
四、体的概念与特征体是由一系列面连接而成的几何对象,它有长度、宽度和高度。
体是空间中的一个三维区域,可以看作由无数个点、线和面组成的一个立体物体。
体有以下几个特征:1. 体是三维的,在长度、宽度和高度上都有尺寸。
2. 体是由至少四个面连接而成的,每个面都可以表示为一个点、线或面。
3. 体可以是正体或曲体,正体的面都是平面,而曲体则不是。
点线面与体在几何学中起着重要的作用。
它们是描述和构建几何图形和空间的基本要素,为我们研究和应用几何学提供了基础。
立体几何讲空间点线面的位置关系课件

线与面的关系
总结词
线与面的关系是空间几何中 复杂的关系之一
详细描述
线与面的关系有多种形式, 如线在面上、线与面相交、 线与面平行等。这些关系可 以通过几何定理进行证明和 推导,如线面平行的判定定 理和性质定理等。
总结词
线与面的关系是空间几何中 复杂的关系之一
详细描述
线与面的关系有多种形式, 如线在面上、线与面相交、 线与面平行等。这些关系可 以通过几何定理进行证明和 推导,如线面平行的判定定 理和性质定理等。
空间面的定义与性质
总结词
几何中的面是由一组线围成的闭合空间。
详细描述
面是由一组线围成的闭合空间,表示一个二维的空间区域。根据定义,面有一定的厚度和大小。面的性质包括封 闭性和延展性,即面是封闭的边界,可以延展成一定的大小和形状。同时,面也可以由三个不同的点确定一个唯 一的平面。
03
点线面的位置关系
点与面的关系
总结词
详细描述
总结词
详细描述
点与面的关系是决定面形状的 关键
一个点可以确定一个平面,当 这个点位于平面上时,它与平 面的关系是固定的。此外,当 多个点位于同一平面时,它们 共同确定了该平面的形状和大 小。
点与面的关系是决定面形状的 关键
一个点可以确定一个平面,当 这个点位于平面上时,它与平 面的关系是固定的。此外,当 多个点位于同一平面时,它们 共同确定了该平面的形状和大 小。
详细描述
在几何学中,点被视为最基本的元素,表示一个具体的空间 位置。它没有大小和形状,只有位置。点的性质包括唯一性 和无限可重复性,即任意两个不同的点都可以确定一条直线 ,且同一直线上可以有无数个点。
空间线的定义与性质
总结词
几何中的线是点的集合,表示一个连续的空间路径。
立体几何 点线面位置关系+线面位置关系 定理+图
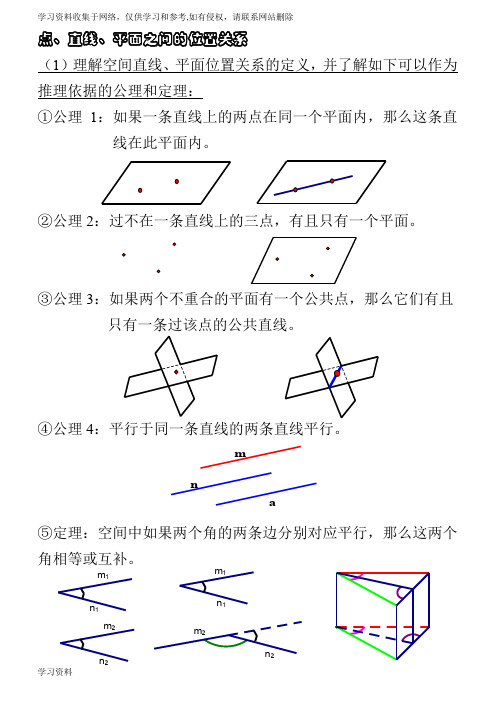
点、直线、平面之间的位置关系
(1)理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理:
①公理1:如果一条直线上的两点在同一个平面内,那么这条直
线在此平面内。
②公理2:过不在一条直线上的三点,有且只有一个平面。
③公理3:如果两个不重合的平面有一个公共点,那么它们有且
只有一条过该点的公共直线。
④公理4:平行于同一条直线的两条直线平行。
⑤定理:空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补。
n m a m 1n 1m 2n 2m 1n 1
m 2n
2
(2)以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理。
理解以下判定定理:
①平面外一条直线与此平面内的一条直线平行,则该直线与此
平面平行。
②一个平面内的两条相交直线与另一个平面平行,则这两个平
面平行。
③一条直线与一个平面内的两条相交直线垂直,则该直线与此
平面垂直。
④一个平面过另一个平面的垂线,则两个平面垂直。
理解以下性质定理,并能够证明:
①如果一条直线与一个平面平行,那么过该直线的任一个平面与
此平面的交线和该直线平行。
②两个平面平行,则任意一个平面与这两个平面相交所得的交线相互平行。
③垂直于同一个平面的两条直线平行。
④两个平面垂直,则一个平面内垂直于交线的直线与另一个平
面垂直。
(3)能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章立体几何专题16 几何体的几何特征与点线面关系【压轴综述】在立体几何中,判定和证明空间的线线、线面以及面面之间的位置关系(主要是平行与垂直的位置关系),计算空间图形中的几何量(主要是角与距离)是两类基本问题.正确揭示空间图形与平面图形的联系,并有效地实施空间图形与平面图形的转换是分析和解决这两类问题的关键.要善于将空间问题转化为平面问题:这一步要求我们具备较强的空间想象能力,对几何体的结构特征要牢牢抓住.立体几何压轴题多以选择题、填空题形式出现,往往与不等式、导数、三角函数等相结合,具有一定的综合性.其中折叠问题、几何体的切接及截面问题、角的计算问题等比较多见.一.折叠问题最重要的是找到折叠之前与折叠之后不变量,这是两个图形的桥梁,再结合新图形的新特征处理.二.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角.三.几何体的切接、截面问题:(1)求解与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径等.通过作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.这样才能进一步将空间问题转化为平面内的问题;(2)转化后如何算?因为已经是平面内的问题,那么方法就比较多了,如三角函数法、均值不等式、坐标法,甚至导数都是可以考虑使用的工具.四.角的计算问题1. 二面角的平面角及其求法有:定义法、三垂线定理及其逆定理、找公垂面法、射影公式、向量法等,依据题目选择方法求出结果.2.求异面直线所成角的步骤:一平移,将两条异面直线平移成相交直线.二定角,根据异面直线所成角的定义找出所成角.三求角,在三角形中用余弦定理或正弦定理或三角函数求角.四结论.3.线面角的计算:(1)利用几何法:原则上先利用图形“找线面角”或者遵循“一做----二证----三计算”. (2)利用向量法求线面角的方法(i 分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角); (ii)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角(钝角时取其补角),取其余角就是斜线和平面所成的角.下面通过例题说明应对这类问题的方法与技巧.【压轴典例】例1. (2019·安徽高三月考(理))在长方体1111ABCD A B C D -中,11BC CC ==,13AD B π∠=,则直线1AB 与1BC 所成角的余弦值为( )A .3B .6C .7D .14【答案】D 【解析】长方体中,11BC CC ==,1BC =11AD BC =13AD B π∠=,知AB =,又∵11BC AD P ,∴11B AD ∠是1AB 与1BC 所成的角.∴在11AB D ∆中,111AB B D ==11cos 14B AD ∠==.选D.例2. (2019·陕西高三月考(理))已知正方体1111ABCD A B C D -的体积为点P 在正方形1111D C B A上,且1,A C 到P 的距离分别为2,,则直线CP 与平面11BDD B 所成角的正切值为( )A.2B.3C.12D.13【答案】A 【解析】易知AB =1C P ,在直角1CC P ∆中,可计算12C P ==;又1112,4A P A C ==,所以点P 是11A C 的中点;连接AC 与BD 交于点O ,易证AC ⊥平面11BDD B ,直线CP 在平面11BDD B 内的射影是OP ,所以CPO ∠就是直线CP 与平面11BDD B 所成的角,在直角CPO ∆中,tan 2CO CPO PO ∠==例3.(2019·浙江高考真题)设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P AC B --的平面角为γ,则( ) A .,βγαγ<< B .,βαβγ<< C .,βαγα<< D .,αβγβ<<【答案】B 【解析】方法1:如图G 为AC 中点,V 在底面ABC 的投影为O ,则P 在底面投影D 在线段AO 上,过D 作DE 垂直AE ,易得//PE VG ,过P 作//PF AC 交VG 于F ,过D 作//DH AC ,交BG 于H ,则,,BPF PBD PED α=∠β=∠γ=∠,则cos cos PF EG DH BDPB PB PB PBα===<=β,即αβ>,tan tan PD PDED BDγ=>=β,即y >β,综上所述,答案为B.方法2:由最小角定理βα<,记V AB C --的平面角为γ'(显然γ'=γ) 由最大角定理β<γ'=γ,故选B.-为正四面体,P为VA中点,易得方法3:(特殊位置)取V ABCα=⇒α=β=γ=,故选B.cos sin sin33例4. (浙江省诸暨市2018届5月适应)如图,矩形中,,是线段(不含点)上一动点,把沿折起得到,使得平面平面,分别记,与平面所成角为,平面与平面所成锐角为,则()A. B. C. D.【答案】A【解析】如图,过作,在中,由,可得.由等积法可得,则∵平面平面,且,可得平面,则.过作,垂足为,连接,则为平面与平面所成的锐角.∵到的距离即.故选:A.例5.(黑龙江省哈尔滨市第六中学2018届押题卷(一))如图, 在正方体中, , 过直线的平面平面,则平面截该正方体所得截面的面积为()A. B. C. D.【答案】D【解析】如图所示,连接交于,取中点,连接、、和,易得,,;,为平面截该正方体所得截面,且;,,,;,即平面截该正方体所得截面的面积为.故选D.例6.(2018年理新课标I卷)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为()A. B. C. D.【答案】A【解析】根据相互平行的直线与平面所成的角是相等的,所以在正方体中,平面与线所成的角是相等的,所以平面与正方体的每条棱所在的直线所成角都是相等的,同理平面也满足与正方体的每条棱所在的直线所成角都是相等,要求截面面积最大,则截面的位置为夹在两个面与中间的,且过棱的中点的正六边形,且边长为,所以其面积为,故选A.例7. (黑龙江省哈尔滨市第六中学2018届押题卷(二))在中,分别为三边中点,将分别沿向上折起,使重合,记为,则三棱锥的外接球面积的最小值为________________. 【答案】9【解析】例8.(2017·全国高考真题(理))a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC 所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;②当直线AB与a成60°角时,AB与b成60°角;③直线AB与a所成角的最小值为45°;④直线AB与a所成角的最大值为60°.其中正确的是________.(填写所有正确结论的编号)【答案】②③【解析】由题意知,a 、b 、AC 三条直线两两相互垂直,画出图形如图, 不妨设图中所示正方体边长为1, 故|AC |=1,|AB|=斜边AB 以直线AC 为旋转轴,则A 点保持不变,B 点的运动轨迹是以C 为圆心,1为半径的圆,以C 坐标原点,以CD 为x 轴,CB 为y 轴,CA 为z 轴,建立空间直角坐标系, 则D (1,0,0),A (0,0,1),直线a 的方向单位向量a =(0,1,0),|a |=1, 直线b 的方向单位向量b =(1,0,0),|b |=1,设B 点在运动过程中的坐标中的坐标B ′(cos θ,sin θ,0), 其中θ为B ′C 与CD 的夹角,θ∈[0,2π),∴AB ′在运动过程中的向量,'AB =(cos θ,sin θ,﹣1),|'AB|=设'AB 与a 所成夹角为α∈[0,2π], 则cos α()()10102'cos sin a AB θθ--⋅==⋅,,,,|sin θ, ∴α∈[4π,2π],∴③正确,④错误. 设'AB 与b 所成夹角为β∈[0,2π],cos β()()'1100''AB b cos sin AB bbAB θθ⋅-⋅===⋅⋅,,,,θ|, 当'AB 与a 夹角为60°时,即α3π=,|sin θ|3πα===, ∵cos 2θ+sin 2θ=1,∴cos β2=|cos θ|12=,∵β∈[0,2π],∴β3π=,此时'AB 与b 的夹角为60°, ∴②正确,①错误. 故答案为:②③.【压轴训练】1.(2018届湖南省郴州市二中第六次月考)已知三棱锥的底面是直角三角形,⊥,,⊥平面,是的中点.若此三棱锥的体积为,则异面直线与所成角的大小为()A.45° B.90° C.60° D.30°【答案】C【解析】∵⊥平面,,∴三棱锥的体积,∴=4,∴,.设的中点为,连接,,如图,则,,,∴△是正三角形,∴∠=60°.∵是的中点,则∥,∴∠是异面直线与所成的角,即异面直线与所成角的大小为60°.故选:C2.(2019·湖北高三月考)如图,E 、F 分别是三棱锥P ABC -的棱AP 、BC 的中点,10PC =,6AB =,7EF =,则异面直线AB 与PC 所成的角为( )A .30°B .60︒C .0︒D .120︒【答案】B 【解析】如图所示:取AC 中点G ,连接,EG FG ,因为E 、F 分别是棱AP 、BC 的中点,且G 为AC 中点,所以GE PC 且152GE PC ==,所以GF AB ∥且132GF AB ==;所以异面直线AB 与PC 所成的角即为EGF ∠或其补角,则2225371cos 2352EGF +-∠==-⨯⨯,所以120EGF ∠=︒,所以异面直线AB 与PC 所成的角即为EGF ∠的补角:60︒. 故选:B.3.(2019·广东广雅中学高三开学考试(文))在正方体1111ABCD A B C D -中,点O 是四边形ABCD 的中心,关于直线1A O,下列说法正确的是( )A .11//AO D CB .1A O BC ⊥ C .1//A O 平面11B CDD .1A O ⊥平面11AB D【答案】C 【解析】如下图所示,设1111A C B D M =I ,则M 为11A C 的中点,在正方体1111ABCD A B C D -中,11//AA CC ,则四边形11AAC C 为平行四边形,11//AC A C ∴. 易知点O 、M 分别为AC 、11A C 的中点,1//A M OC ∴,则四边形1A MCO 为平行四边形,则1//AO CM ,由于过直线外一点有且只有一条直线与已知直线平行,则A 选项中的命题错误;1//A O CM Q ,1AO ⊄平面11B CD ,CM ⊂平面11B CD ,1//AO ∴平面11B CD ,C 选项中的命题正确; 易知BM CM =,则BCM ∆为等腰三角形,且BC 为底,所以,BC 与CM 不垂直,由于1//AO CM ,则1A O 与BC 不垂直,B 选项中的命题错误;四边形1111D C B A 为正方形,则1111B D A C ⊥,在正方体1111ABCD A B C D -中,1CC ⊥平面1111D C B A ,11B D ⊂平面1111D C B A ,111B D CC ∴⊥,1111AC CC C =Q I ,11B D ∴⊥平面11A CC ,1A C ∴⊂平面11A CC ,111AC B D ∴⊥,同理可证11A C AB ⊥,且1111AB B D B =I , 1A C ∴⊥平面11AB D ,则1A O 与平面11AB D 不垂直,D 选项中的命题错误.故选:C.4.(2019·安徽高三开学考试(理))如图,在正方体111ABCD A B C D-中,F 是棱11A D 上动点,下列说法正确的是( )A .对任意动点F ,在平面11ADD A 内不存在...与平面CBF 平行的直线B .对任意动点F ,在平面ABCD 内存在..与平面CBF 垂直的直线C .当点F 从1A 运动到1D 的过程中,FC 与平面ABCD 所成的角变大.. D .当点F 从1A 运动到1D 的过程中,点D 到平面CBF 的距离逐渐变小.. 【答案】C 【解析】对于A 选项,//AD BC ,AD ⊄平面CBF ,BC ⊂平面CBF ,//AD ∴平面CBF ,又AD ⊂平面11ADD A ,所以,A 选项中的命题错误;对于B 选项,反设平面ABCD 内存在直线a 满足a ⊥平面CBF ,a ⊂Q 平面ABCD ,由平面与平面垂直的判定定理可得平面CBF ⊥平面ABCD ,事实上,平面CBF 与平面ABCD 不垂直,假设不存在,所以,B 选项中的命题错误;对于C 选项,由于F 到平面ABCD 的距离d 不变且FC 变小,设直线FC 与平面ABCD 所成的角为θ,则sin dFCθ=,可知θ在逐渐变大,C 选项中的命题正确; 对于D 选项,由于点F 到平面ABCD 的距离不变,BCD ∆的面积不变,则三棱锥F BCD -的体积不变,即三棱锥D BCF -的体积不变,在点F 的运动过程中,BCF ∆的面积不变,由等体积法可知,点D 到平面BCF 的距离不变,D 选项中的命题正确.故选:C. 5.(河北省衡水中学2019届高三第一次摸底)如图,在正方体中,点,分别为棱,的中点,点为上底面的中心,过,,三点的平面把正方体分为两部分,其中含的部分为,不含的部分为,连结和的任一点,设与平面所成角为,则的最大值为( )A. B.C. D.【答案】B【解析】连结.因为平面.所以过的平面与平面的交线一定是过点且与平行的直线.过点作交于点,交于点,则,连结,.则平行四边形即为截面.则五棱柱为,三棱柱为,设点为的任一点,过点作底面的垂线,垂足为,连结,则即为与平面所成的角,所以.因为,要使的正弦值最大,必须最大,最小,当点与点重合时符合题意.故.故选B.6.(福建省莆田第九中学2018届高考模拟)过正方体的顶点的平面与直线垂直,且平面与平面的交线为直线,平面与平面的交线为直线,则直线与直线所成角的大小为()A. B. C. D.【答案】C【解析】如图所示,因为,所以.同理,所以,因为过正方体的顶点的平面与直线垂直,所以,,所以直线与直线所成角就是所成的角,因为△是等边三角形,所以所成的角为,所以直线与直线所成角就是,故答案为:C.7.(浙江省余姚中学2018届模拟卷(二)如图,已知平面,,、是直线上的两点,、是平面内的两点,且,,,,.是平面上的一动点,且直线,与平面所成角相等,则二面角的余弦值的最小值是()A. B. C. D.【答案】B【解析】,,,,同理为直线与平面所成的角,为直线与平面所成的角,又,在平面内,以为轴,以的中垂线为轴建立平面直角坐标系则,设,整理可得:在内的轨迹为为圆心,以为半径的上半圆平面平面,,为二面角的平面角,当与圆相切时,最大,取得最小值此时故选.8.如图,正方体1111ABCD A B C D -的棱长为1,过A 点作平面1A BD 的垂线,垂足为点H ,有下面三个结论:①点H 是1A BD ∆的中心;②AH 垂直于平面11CB D ;③直线1AC 与直线1B C 所成的角是90°.其中正确结论的序号是_______.【答案】①②③ 【解析】对于①,因为AH ⊥平面1A BD ,1AB AD AA ==, 所以1Rt Rt Rt ∆≅∆≅∆ABH ADH AA H , 所以1HB HD HA ==,所以H 是1A BD ∆的外心;又因为1A BD ∆是等边三角形,所以点H 是△1A BD 的中心.故①正确; 对于②,因为1111//,=A B AB A B AB ,//,=CD AB CD AB ,所以11//A B CD ,且11A B CD =,所以四边形11A B CD 是平行四边形,所以11//B C A D . 又因为1A D ⊂平面1A BD ,1B C ⊄平面1A BD ,所以1//B C 平面1A BD . 同理可证11//B D 平面1A BD .又因为1111B C B D B ⋂=,所以平面11//CB D 平面1A BD ;又因为AH 垂直于平面1A BD ,所以AH 垂直于平面11CB D .故②正确; 对于③,连接111,,AC BC AD .因为四边形11BCC B 是正方形,所以11B C BC ⊥.因为AB ⊥平面11BCC B ,1B C ⊂平面11BCC B ,所以1B C AB ⊥. 又因为1BC AB B =,所以1B C ⊥平面11ABC D .又因为1AC ⊂平面11ABC D ,所以11AC B C ⊥, 所以直线1AC 与1B C 所成的角是90°.故答案为①②③9.(2019·全国高三月考(文))《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪.在四棱锥P ABCD - 中,底面ABCD 为邪田,两畔CD AB ,分别为1,3,正广AD 为,PD ⊥ 平面ABCD ,则邪田ABCD 的邪长为_______;邪所在直线与平面PAD 所成角的大小为________. 【答案】4 6π【解析】过点C 作CE AB ⊥,垂足为E ,延长AD BC ,,使得ADBC F =(如图).由题意可得2CE BE ==,则4BC ==由题意知,//AB AD CD AB ⊥,所以13DF CD AF AB ==,所以DF =.因为PD ⊥ 平面ABCD ,所以PD AB ⊥,又AB AD ⊥,所以AB ⊥ 平面PAD ,则AFB ∠ 是直线BC 与平面PAD 所成角的平面角,tan3AB AFB AF ∠===,所以6AFB π∠= 故答案为: 46π10.(湖北省武汉市2018届高中毕业生四月调研)在四面体中,,则四面体体积最大时,它的外接球半径_________.【答案】【解析】 【分析】设AB=2x (0<x <1),则CE=DE=,11.(河北省衡水金卷2018年调研卷(二))如图,将正方形沿着边抬起到一定位置得到正方形,并使得平面与平面所成的二面角为,为正方形内一条直线,则直线与所成角的取值范围为_______.【答案】【解析】不妨设正方形的边长为,作,垂足为,由,得平面,故,又,得平面,故直线在平面内的射影为,易知,则与平面所成的角为与平面内的直线所成的最小角为,而直线与所成角的最大角为(当与重合时,与所成角为的),所以直线与所成角的取值范闱为,故答案为.12.(江苏省南通市2018届最后一卷)已知边长为2的等边三角形中,、分别为、边上的点,且,将沿折成,使平面平面,则几何体的体积的最大值为__________.【答案】.【解析】设的高为,的高为,当平面平面时,由面面垂直的性质定理得平面,以几何体的体积,,当,在时,取得最大值,,故选B.13.(2016浙江)如图,在ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .【答案】12【解析】试题分析: ABC 中,因为2,120AB BC ABC ==∠=,所以30BAD BCA ∠=∠=. 由余弦定理可得2222cos AC AB BC AB BC B =+-⋅ 2222222cos12012=+-⨯⨯=,所以AC =设AD x =,则0x <<DC x =.在ABD ∆中,由余弦定理可得2222cos BD AD AB AD AB A =+-⋅ 22222cos30x x =+-⋅24x =-+.故BD =在PBD ∆中, PD AD x ==, 2PB BA ==.由余弦定理可得()22222224cos 2222x x PD PB BD BPD PD PB x +--++-∠===⋅⋅⋅,所以30BPD ∠=. 由此可得,将ABD 沿BD 翻折后可与PBD 重合,无论点D 在任何位置,只要点D 的位置确定,当平面PBD ⊥平面BDC 时,四面体PBCD 的体积最大(欲求最大值可不考虑不垂直的情况).过P 作直线BD 的垂线,垂足为O .设PO d =,则11sin 22PBDS BD d PD PB BPD =⨯=⋅∠,12sin302d x =⋅,解得d =.而 BCD的面积()()111sin 2sin30222S CD BC BCD x x =⋅∠=⋅=. 当平面PBD⊥平面BDC 时:四面体PBCD的体积()111332BCDV Sd x =⨯=⨯x x=.观察上式,易得()x x ≤,当且仅当x x ,即x 时取等号,同时我们可以发现当x x PBCD的体积最大,为1 . 214.(河南省郑州外国语学校2018届高三调研)在菱形中,,,将沿折起到的位置,若二面角的大小为,三棱锥的外接球心为,则三棱锥的外接球的表面积为__________.【答案】【解析】四边形是菱形,,是等边三角形,过球心O作平面,则为等边的中心,的中点为E,,得,,,在中,由,可得.在中,,即,设三棱锥的外接球的半径为R,即,三棱锥的外接球的表面积为.故答案为:.15.(北京市2019届一轮复习)如图,在矩形中,,,为边的中点.将△沿翻折,得到四棱锥.设线段的中点为,在翻折过程中,有下列三个命题:① 总有平面;② 三棱锥体积的最大值为;③ 存在某个位置,使与所成的角为.其中正确的命题是____.(写出所有..正确命题的序号)【答案】①②【解析】取DC的中点为F,连结FM,FB,可得MF∥A1D,FB∥DE,可得平面MBF∥平面A1DE,所以BM∥平面A1DE,所以①正确;当平面A1DE与底面ABCD垂直时,三棱锥C﹣A1DE体积取得最大值,最大值为:,所以②正确.存在某个位置,使DE与A1C所成的角为90°.因为DE⊥EC,所以DE⊥平面A1EC,可得DE⊥A1E,即AE⊥DE,矛盾,所以③不正确;故答案为:①②16.(湖南省张家界市2018届三模)知三棱锥满足底面,是边长为的等边三角形,是线段上一点,且.球为三棱锥的外接球,过点作球的截面,若所得截面圆的面积的最小值与最大值之和为,则球的表面积为__________.【答案】【解析】将三棱锥P —ABC 补成正三棱柱,且三棱锥和该正三棱柱的外接球都是球O ,记三角形ABC 的中心为,设球的半径为R ,PA=2x ,则球心O 到平面ABC 的距离为x ,即O =x ,连接C ,则C=4,,在三角形ABC 中,取AB 的中点为E ,连接D ,E ,则在直角三角形OD 中,由题意得到当截面与直线OD 垂直时,截面面积最小,设此时截面圆的半径为r,则最小截面圆的面积为,当截面过球心时,截面面积最大为,,如图三,球的表面积为故答案为:100 .17.(2019·全国高三月考(理))已知球内接三棱锥P ABC -中,PA ⊥平面ABC ,ABC △为等边三角形,32π3,则直线PC 与平面PAB 所成角的余弦值为________.【答案】10【解析】 如图:由正弦定理得小圆1O 的半径为:r =1=,则2AD =,又由343233R ππ=,得球的半径R 2=,所以AP ===取AB 的中点E ,连接PE ,CE ,则CPE ∠就是直线PC 与平面PAB 所成的角,又PC ==PE ===所以cosCPE ∠=10=.直线PC 与平面PAB . 18.(2019·河北高三月考(理))如图,在四棱锥P ABCD -中,PD AC ⊥,AB ⊥平面PAD ,底面ABCD 为正方形,且3CD PD +=.若四棱锥P ABCD -的每个顶点都在球O 的球面上,则球O 的表面积的最小值为_____;当四棱锥P ABCD -的体积取得最大值时,二面角A PC D --的正切值为_______.【答案】6π【解析】(1).设()03CD x x =<<,则3PD x =-.∵AB ⊥平面PAD , ∴AB PD ⊥,又PD AC ⊥, ∴PD ⊥平面ABCD ,则四棱锥P ABCD -可补形成一个长方体,球O 的球心为PB 的中点,从而球O 的表面积为()2243126x πππ⎡⎤=-+≥⎣⎦⎝⎭.(2).四棱锥P ABCD -的体积()()213033V x x x =⨯-<<, 则22V x x '=-+,当02x <<时,0V '>;当23x <<时,0V '<. 故()max 2V V =,此时2AD CD ==,1PD =. 过D 作DH PC ⊥于H ,连接AH , 则AHD ∠为二面角A PC D --的平面角.∵5DH ==,∴tan AD AHD DH ∠==。
