拉乌尔定律和亨利定律
亨利定律与拉乌尔定律的区别和联系

尊敬的读者:今天我想和你一起探讨一个有趣且深刻的主题——亨利定律与拉乌尔定律的区别和联系。
这个主题看似简单,但其中蕴含着深刻的内涵,需要我们从多个角度进行思考和剖析。
本文将深入探讨这两个定律,并从多个层面展开讨论,以便让读者更全面地理解这两个概念。
让我们以从简到繁的方式来探讨亨利定律与拉乌尔定律。
亨利定律,又称为90/10定律,指的是在某种现象中,前10%的个体通常会占据整体现象的90%的份额。
这个定律最初被意大利经济学家维尔弗雷多·帕累托(Vilfredo Pareto)提出,并被广泛应用于各个领域。
相比之下,拉乌尔定律则是认为在某个领域,相对强者的数量总是呈现一个拉乌尔分布,即比例越来越大的分布。
这两个定律在描述现象时有着不同的侧重点,亨利定律更注重于个体实力的不平等导致的整体不平等,而拉乌尔定律则更侧重于描述相对强者的数量分布规律。
在深入探讨亨利定律与拉乌尔定律的区别和联系之前,我们需要了解这两个定律的基本概念和应用范围。
亨利定律最初是在经济领域提出的,但后来被扩展到社会学、心理学、生物学等领域,被认为是一种普适的规律。
而拉乌尔定律则更多地应用于社会学、政治学等领域,并且在实际应用中往往伴随着政治、社会等因素的干扰和调整。
从应用范围上来看,亨利定律更具有普适性,而拉乌尔定律更多地受到具体领域和外部因素的影响。
我们还需要从实际应用的角度,分析亨利定律与拉乌尔定律在不同领域的应用情况。
在经济学领域,亨利定律被广泛应用于描述财富分配不均的现象,而拉乌尔定律则更多地被用来解释社会阶层的分布规律。
在实际社会中,这两个定律往往相互交织,相互影响,对于理解社会和经济现象具有重要意义。
在总结和回顾本文的内容时,我们可以看到亨利定律与拉乌尔定律在描述不平等现象时有着不同的侧重点,但在实际应用中又常常相互交织。
而对于我们个人来说,理解这两个定律不仅可以帮助我们更好地认识社会和经济现象,也可以帮助我们更好地规划个人的发展和生活。
2.4 拉乌尔定律、亨利定律
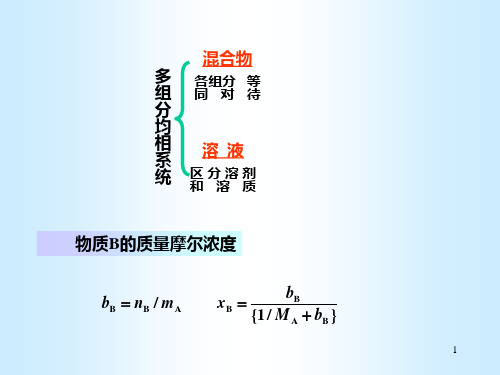
多 组
各组分 等 同对待
分
均
相 系
溶液
统
区分溶剂 和溶质
物质B的质量摩尔浓度
bB nB / mA
xB
{1 /
bB MA
bB }
1
§2-4 拉乌尔定律、亨利定律
1. 液态混合物和溶液的饱和蒸气 压
设由组分A, B, C……组成液态混 合物或溶液, T一定时, 达到气, 液两相 平衡.
此时, 气态混合物的总压力为p, 则 p 即为温度T下该液态混合物或溶液的 饱和蒸气压.
水(A)和乙酸乙酯(B)不完全混溶, 在37.55℃时两液相呈平衡.
一相中含质量分数为w(B) = 0.0675的酯, 另一相中含w(A) =
0.0379的水, 假定拉乌尔定律对每相中的溶剂都能适用, 已知
37.55℃时, 纯乙酸乙酯的蒸气压力是22.13kPa, 纯水的蒸气
压力是6.399kPa, 试计算:
ln p(s) 3133 27.650 11.99 p(s) 160.3k Pa Pa 200K / K
计算结果表明, 所给过程是恒温恒压不可逆相变化过程, 为
此可根据计算所得的液体及固体CO2在200 K的蒸气压数据, 设
计以下可逆过程进行计算:
8
s, 100kPa, 200K
s, 160.3kPa, 200K G2
(1)计算下述过程Gm :
CO2( s, 100kPa, 200K ) →CO2( l, 100kPa, 200K )
(2)判断在100 kPa下, CO2(l)能否稳定存在?
(1) 200 K时液体及固体CO2的饱和蒸气压:
ln p(l) 2013 22.405 12.34 p(l) 228.7kPa Pa 200K / K
拉乌尔定律和亨利定律的区别

拉乌尔定律和亨利定律的区别拉乌尔定律和亨利定律都是热力学中的重要定律,它们分别描述了气体和液体中溶解度与温度、压力之间的关系。
在研究物质的溶解度时,这两个定律都具有重要作用,但它们之间存在着一些明显的区别。
拉乌尔定律是描述气体溶解度与温度之间关系的定律。
它的基本表述是:在一定的压力下,气体的溶解度随着温度的升高而降低。
这个定律主要适用于理想气体,即气体分子之间不存在相互作用力的情况。
在实际情况下,气体分子之间会存在一定的相互作用力,因此拉乌尔定律只能作为近似计算的基础。
亨利定律则是描述气体或液体在溶剂中的溶解度与压力之间关系的定律。
它的基本表述是:在一定的温度下,气体或液体的溶解度随着压力的升高而增加。
这个定律适用于气体和液体的溶解度,但是在气体的溶解度计算中,由于气体分子之间的相互作用力较小,因此亨利定律通常更为准确。
在实际应用中,拉乌尔定律和亨利定律经常被用来计算化学反应中气体的溶解度。
例如,在某些化学反应中,气体的溶解度是反应速率的重要影响因素。
通过应用拉乌尔定律和亨利定律,我们可以计算出在不同温度和压力下气体的溶解度,从而更好地理解反应的动力学过程。
另一方面,拉乌尔定律和亨利定律在环境科学中也具有非常重要的应用。
例如,在海洋环境中,气体的溶解度对海洋生态系统和海洋化学循环过程具有重要影响。
通过应用这些定律,我们可以更好地理解海洋生态系统和化学循环的过程,预测海洋环境的变化和响应措施。
总之,拉乌尔定律和亨利定律都是热力学中非常重要的定律,它们分别描述了气体和液体中溶解度与温度、压力之间的关系。
尽管它们之间存在着一些区别,但在应用中它们经常被一起使用,以便更好地理解物质的溶解过程。
拉乌尔定律与亨利定律

必须考虑60m的水压;水柱高度与Pa的换算。
不要忘了水面上的压力.
或者直接计算压力增加值;因为必 气泡V 4 r 3
须考虑常压时N2的残留即溶解。
3
另外,PV=nRT的应用;P=101.325KPa
经济舱综合症
深静脉血栓形成(DVT(deep vein thrombosis)) 又叫“经济舱综合症(EC S(Economiccabinsyndrome))
第一,要在飞行中尽量多活动,即使不便离 开座位,也要尽量活动脚趾,让血液流通。 其次,要多喝水和不含酒精的饮料,少喝酒。
上网;钓鱼;打牌时也要避免患经济舱综合症
神舟七号飞船,2008年9月25日晚
2008年9月27日翟志刚出舱活动 这是中国人首次漫步太空
16:16 轨道舱第一次泄压完毕,舱内气压由1 个标准大气压降至70千帕。 16:27 轨道舱第二次泄压,气压降至2千帕, 满足出舱条件。航天服内压力为40千帕。
对策:提高氧浓度;用氦(溶解更少)代替氮;
减少气泡:包括预备运动或者药物.
课堂练习题P161,3-4 提示:
P=101325Pa(PN278%),有一个比例或者亨利系数.约 为1.39× 10-5kg(N2)/kg(血液).不用P134例2的系数。
暂不考虑温度对系数的影响。即在体温时仍近似
用上面的系数。
§3.6 拉乌尔定律与亨利定律
PA PA xA
(拉乌尔) Raoult’s Law(1887年):定T下,在稀薄
溶纯液溶中剂的,溶蒸剂气A的压蒸PA气 压PA,等于同温下,
乘以溶液中溶剂的摩尔分数xA Raoult’s Law适用于非电解质的稀薄溶液.
拉乌尔定律和亨利定律的区别

拉乌尔定律和亨利定律的区别
拉乌尔定律和亨利定律都是人口学中的规律,但它们针对的对象不同。
拉乌尔定律是指:在一定时间内,城市人口增加量等于自然增长量与城市外迁入量之和,即ΔP = ΔN + ΔM。
它将城市内部增长与城市间迁移联系在了一起,描述了人口城市化的趋势和现象。
而亨利定律是指:在相同条件下,农村人口增长率高于城市人口增长率,但城市人口总数增加量高于农村人口。
它主要反映出城乡人口比例变化的趋势,表明了城市化进程对农村人口的吸引力。
需要注意的是,以上内容纯属学术探讨,不涉及任何政治话题。
拉乌尔定律和亨利定律

第五节 拉乌尔定律和亨利定律一、亨利定律在一定的温度下,稀溶液中挥发性溶质在气相中的平衡分压与其在溶液中的摩尔分数成正比。
p B =k x x B亨利定律适用于稀溶液中挥发性溶质,是单元操作“吸收”的理论基础。
应用亨利定律应注意以下几点:① 亨利定律只适用于溶质在气相中和液相中分子形式相同的物质;② 气体混合物溶于同一种溶剂时,亨利定律对各种气体分别适用。
其压力为该种气体的分压;③亨利定律除了用摩尔分数表示外,还可以用物质的量浓度c B 、质量摩尔浓度b B 或质量分数w B 等表示,此时,亨利定律的表达式相应为:p B =k c c Bp B =k m b Bp B =k w w B④亨利定律适用于稀溶液中挥发性溶质,溶液越稀,定律越准确。
二、亨利定律的应用亨利定律是化工单元操作----气体吸收的理论基础,气体吸收是利用混合气体中各种气体在溶剂中溶解度的差异,有选择性地将溶解度大的气体吸收,使之从混合气体中分离出来。
若以相同的分压进行比较,则x k 越小,B x 越大,因此,x k 可作为吸收气体所用溶剂的选择依据。
三、二组分液体混合二组分系统F = C -Φ+2。
其中K =2。
故F = 2-Φ+2=4-Φ。
即二组分的最多能以四相平衡共存,最大自由度为3(温度、压力和组成)。
需要用比较复杂的三维坐标系。
但为了讨论的方便,可固定一个自由度(常是温度或压力)。
此时二组分系统的自由度f = 2-Φ+1= 3-Φ。
最大自由度为2,便可以用平面坐标描述。
1. 拉乌尔定律在一定温度下,溶入了非电解质溶质的稀溶液,其溶剂的饱和蒸气压与溶剂的摩尔分数成正比,比例系数为该溶剂在此温度下的饱和蒸气压。
表达式为。
拉乌尔和亨利定律公式

拉乌尔定律(Laval's law)是一种经济学理论,用来描述贸易自由化对于贸易伙伴国家之间贸易顺差(即出口额大于进口额)的影响。
拉乌尔定律的公式为:
贸易顺差=对外直接投资(FDI)+人力资本净流出
其中,对外直接投资(FDI)指的是企业直接投资海外的资金总额,人力资本净流出指的是人力资本(即技能、知识、经验等人才)从国内流向海外的总额。
拉乌尔定律认为,贸易自由化能够促进企业直接投资海外,并且还能促进人力资本的流动,进而提升贸易顺差。
亨利定律(Heckscher-Ohlin theorem)是一种经济学理论,用来解释国家间的贸易为什么会出现顺差或逆差(即出口额大于进口额或出口额小于进口额)。
亨利定律的公式为:
贸易顺差=绝对成本差
其中,绝对成本差指的是生产相同产品的成本在两个国家之间的差异。
根据亨利定律,如果生产相同产品的成本在一个国家更低,那么该国家就会出现贸易顺差,而另一个国家则会出现贸易逆差。
拉乌尔定律和亨利定律是两种经济学理论,用来解释国家间贸易顺差
的原因。
拉乌尔定律认为,贸易自由化能够促进企业直接投资海外,并且还能促进人力资本的流动,从而提升贸易顺差。
而亨利定律则认为,如果生产相同产品的成本在一个国家更低,那么该国家就会出现贸易顺差,而另一个国家则会出现贸易逆差。
这两种理论的公式分别为:
拉乌尔定律:贸易顺差=对外直接投资(FDI)+人力资本净流出
亨利定律:贸易顺差=绝对成本差
这两种理论都是用来解释国家间贸易顺差的原因,但它们所考虑的因素有所不同。
拉乌尔定律认为,贸易自由化和人力资本流动是导致贸易顺差的主要因素,而亨利定律则认为,生产成本差异是导致贸易顺差的主要因素。
拉乌尔定律与亨利定律课件

拉乌尔定律和亨利定律都是描述 气体溶质在液体中的溶解度的规
律。
两个定律都指出,气体的溶解度 与其分压成正比。
两个定律都适用于一定温度和压 力条件下,气体的溶解度与分压
之间的关系。
两个定律的不同之处
拉乌尔定律适用于稀溶液,而亨 利定律适用于任何浓度的溶液。
拉乌尔定律中的比例系数是溶质 的摩尔溶解度,而亨利定律中的
在食品行业
拉乌尔定律可以用来预测在特定温 度和压力条件下,气体在液体食品 中的溶解度,从而控制食品的质量 和口感。
03
亨利定律
亨利定律概述
01
描述气体溶解度与压力之间的关 系
02
由英国物理学家Henry在1803年 发现
亨利定律的物理意义
当气体溶解度在一定温度下保持恒定 时,气体的溶解度与该气体的分压成 正比
拉乌尔定律公式
通常表示为 S = K * P,其中 S 是溶解度,K 是常数,P 是压力。
拉乌尔定律适用范围
适用于描述气体在液体中的溶解度与温度和压力的关系,尤其在高 压和低温条件下。
拉乌尔定律的物理意义
揭示了气体在液体中的溶解度与压力和温度之间的依赖关系。 随着压力的增加,气体的溶解度会增加;随着温度的升高,气体的溶解度会降低。
即当气体的压力增加时,其溶解度也 会相应增加
亨利定律的应用场景
在化工生产中,常常需要将气体溶解在液体中,利用亨利定律可以指导生产过程 中的压力控制,以获得所需的溶解度和产品纯度
在环保领域,亨利定律可以用于计算气体在水中的溶解度,从而评估气体对水生 生态的影响
04
拉乌尔定律与亨利定律的比较
两个定律的相同之处
拉乌尔定律的数学表达式为 S = kPa,其中S为溶解度, k为常数,Pa为压力。亨利 定律的数学表达式为P = kC ,其中P为压力,k为常数, C为浓度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= 0 .244 kg ⋅ mol −1
的摩尔质量为0.122kg⋅mol-1, 故 已知苯甲酸 C6H5COOH 的摩尔质量为 ⋅ 苯甲酸在苯中的分子式为 (C6H5COOH)2 .
00-8-16
4
葡萄糖(C 溶于400g乙醇中 溶液的沸点较纯乙 乙醇中, 例 10g葡萄糖 6H12O6)溶于 葡萄糖 溶于 乙醇中 醇的上升0.1428℃, 另外有 有机物质溶于 有机物质溶于100g乙醇中 此溶 乙醇中, 醇的上升 ℃ 另外有2g有机物质溶于 乙醇中 液的沸点则上升0.1250℃, 求此有机物的相对摩尔质量 液的沸点则上升 ℃ 求此有机物的相对摩尔质量.
溶于苯中达到气液平衡. 例 20℃下HCl溶于苯中达到气液平衡 液相中每 ℃ 溶于苯中达到气液平衡 液相中每100g苯含有 苯含有 1.87g HCl, 气相中苯的摩尔分数为 气相中苯的摩尔分数为0.095. 已知苯与 已知苯与HCl的摩尔质 的摩尔质 量分别为78.11g⋅mol−1与36.46 g⋅mol−1. 20℃苯饱和蒸气压为 量分别为 ⋅ ⋅ ℃ 10.01 kPa. 试计算 ℃时HCl在苯中溶解的亨利系数 试计算20℃ 在苯中溶解的亨利系数. 在苯中溶解的亨利系数
拉乌尔定律和亨利定 律
x ( HCl ) =
1.87 / 36.46 = 0.0385 1.87 / 36.46 + 100 / 78.11 x (C6 H 6 ) = 1 − 0.0385 = 0.9615
溶剂苯服从拉乌尔定律, 并结合分压定律, 有 溶剂苯服从拉乌尔定律, 并结合分压定律,
p( C 6 H 6 ) = p ∗ ( C 6 H 6 ) ⋅ x ( C 6 H 6 ) = p ⋅ y ( C 6 H 6 )
∗ ∗ pA , 2 = 1.7422 × pA ,1 = 1.7422 × 101 .325kPa = 176 .525kPa
沸腾时
00-8-16
∗ ∗ p = pA , 2 x A + pB , 2 (1 − x A ) ∗ p − pB , 2 101 .325 − 76 .198 0.250; x xA = ∗ = = B = 0.75 ∗ pA , 2 − pB , 2 176 .525 − 76 .198
∆ Tf = K f bB = 40 × 0.25063 K = 10.03K
′ ′ mB / M B 5 / 9000 ′ ( 2 ) bB = mol ⋅ kg − 1 = 5.848 × 10 − 3 mol ⋅ kg − 1 = mA 0.095
′ ∆ Tf′ = K f bB = 40 × 5.848 × 10 −3 K = 0.2339 K
理想液态混合物, 用 到K-K方程, 组成
∗ ∗ p A , 2 和 pB , 2 , 则 苯和甲苯的的饱和蒸气压为 在373.1K苯和甲苯的的饱和蒸气压为
∗ pA,2 ln ∗ = − 30726 1 − 1 = 0.5551 pA,1 8.314 373.1 353.3
对题给有机物(C)的乙醇 溶液 对题给有机物 的乙醇(A)溶液 的乙醇
mC / M C 2 × 10 −3 kg −1 ∆ Tb′ 0.1250K bC = kg = = = mA M C × 0.1 Kb 1.0282K ⋅ mol −1 ⋅ kg 0.02 × 1.0282 MC = kg ⋅ mol −1 = 164.5 × 10 −3 kg ⋅ mol −1 0.1250 M r = 164.5
00-8-16 7
渗透压
∏ = cBRT 对稀溶液: 对稀溶液 cB = ρA bB
bB = 0.560K ∆Tf = = 0.301mol ⋅ kg −1 K f 1.86K ⋅ kg ⋅ mol −1
则 cB = 998.2 kg ⋅m−3×0.301 mol⋅kg−1 = 301 mol⋅m−3 ⋅ ⋅
Π = 301.0 mol⋅m−3×8.314 J⋅K−1⋅mol−1×310.2 K ⋅ ⋅
冰点下降
(2)另一溶质相对摩尔质量为 另一溶质相对摩尔质量为9000, 溶于樟脑形成质量百分数 另一溶质相对摩尔质量为 5%的溶液 求凝固点降低多少? 的溶液, 求凝固点降低多少 的溶液
m B / M B 5 / 210 (1) bB = mol ⋅ kg −1 = 0.25063 mol ⋅ kg −1 = mA 0.095
∗ pB,2 ln ∗ = − 31999 1 − 1 = − 0.2850 pB,1 8.314 373 .1 383 .7 ∗ ∗ pB , 2 = 0 .7520 × pB ,1 = 0 .7520 × 101 .325 kPa = 76 .198 kPa
得
p ∗ (C6 H 6 ) ⋅ x (C6 H 6 ) 10.01kPa × 0.9615 p= = = 101.3kPa y (C6 H 6 ) 0.095
p( HCl) p{1 − y(C6 H 6 )} 101.3kPa(1 − 0.095) 故 k ( HCl) = = = x( HCl) x( HCl) 0.0385 = 2381kPa
渗透压
M ( C 12 H 22 O 11 ) = 342.299g ⋅ mol − 1 (1 ) 1000/18.01 5 x ( H 2 O) = = 0 .99641 1000/18.01 5 + 68.4/342.2 99 p ( H 2 O) = p * ( H 2 O) x ( H 2 O)
= 2.339 × 0.99641kPa = 2.3306kPa m 68.4 + 1000 ( 2) V = cm 3 = 1.0434 × 10 3 cm 3 = ρ 1.024 n 68 .4 / 342 .299 c= mol ⋅ dm − 3 = V 1.0434 = 0.1915 mol ⋅ dm − 3 = 0.1915 × 10 3 mol ⋅ m − 3 ∴ π = cRT = 0.1915 × 10 3 × 8.314 × 293.15Pa = 467kPa
00-8-16 3
苯中溶入0.245g苯甲酸 测得凝固点降低 苯甲酸, 例 在25.00g苯中溶入 苯中溶入 苯甲酸 测得凝固点降低0.2048 K.
凝固点降低 试求苯甲酸在苯中的分子式. 试求苯甲酸在苯中的分子式
mB ∆Tf = Kf bB = Kf MBmA
MB =
K f mB 5 .10 ×ቤተ መጻሕፍቲ ባይዱ0 .245 = kg ⋅ mol − 1 ∆ Tf m A 0 .2048 × 25 .00
5
即
00-8-16
人的血浆的凝固点为–0.560℃, 求37.0℃时血浆的渗透 例 人的血浆的凝固点为 ℃ ℃ 已知37 时水的体积质量(密度 密度)为 压. 已知 ℃时水的体积质量 密度 为998.2 kg⋅m−3, 水的凝 ⋅ 固点降低常数K 血浆可视为稀溶液. 固点降低常数 f = 1.86 K⋅kg⋅mol−1 . 血浆可视为稀溶液 ⋅ ⋅
00-8-16 1
已知101.325kPa下 , 纯苯 的正常沸点和蒸发焓分别为 例 已知 下 纯苯(A)的正常沸点和蒸发焓分别为 353.3K和30762J⋅mol−1, 纯甲苯 的正常沸点和蒸发焓分别为 纯甲苯(B)的正常沸点和蒸发焓分别为 和 ⋅ 383.7K和31999J⋅mol−1. 苯和甲苯形成理想液态混合物 若有该 苯和甲苯形成理想液态混合物, 和 ⋅ 种液态混合物在101.325kPa, 373.1K沸腾 计算其组成 沸腾, 种液态混合物在 沸腾 计算其组成.
2
已知樟脑(C 的凝固降低常数K 例 已知樟脑 10H15O)的凝固降低常数 f = 40K⋅mol–1⋅kg , (1) 的凝固降低常数 ⋅ 某一溶质相对摩尔质量为210, 溶于樟脑形成质量百分数 的 溶于樟脑形成质量百分数5%的 某一溶质相对摩尔质量为 溶液, 求凝固点降低多少? 溶液 求凝固点降低多少
= 776 kPa
00-8-16 6
蔗糖(C 溶于1kg的水中 已知 ℃ 的水中,已知 例 在20℃下将 ℃下将68.4g蔗糖 12H22O11)溶于 蔗糖 溶于 的水中 已知20℃ 下此溶液的密度为1.024g⋅cm-3, 纯水饱和蒸气压为 纯水饱和蒸气压为2.339kPa.求: 下此溶液的密度为 ⋅ 求 (1)此溶液的蒸气压 此溶液的蒸气压; 此溶液的蒸气压 (2)此溶液的渗透压 此溶液的渗透压. 此溶液的渗透压
沸点上升
对题给葡萄糖(B)的乙醇 溶液 对题给葡萄糖 的乙醇(A)溶液 的乙醇
m B / M B 10 / 180 bB = mol ⋅ kg −1 = 0.1216mol ⋅ kg −1 = mA 0.4 ∆Tb 0.1428 Kb = K ⋅ mol −1 ⋅ kg = 1.0282K ⋅ mol −1 ⋅ kg = bB 0.1216
