拉乌尔定律和亨利定律的适用范围为稀溶液共102页文档
合集下载
2.4 拉乌尔定律、亨利定律
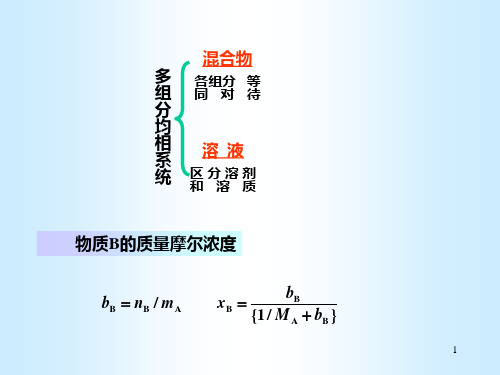
混合物
多 组
各组分 等 同对待
分
均
相 系
溶液
统
区分溶剂 和溶质
物质B的质量摩尔浓度
bB nB / mA
xB
{1 /
bB MA
bB }
1
§2-4 拉乌尔定律、亨利定律
1. 液态混合物和溶液的饱和蒸气 压
设由组分A, B, C……组成液态混 合物或溶液, T一定时, 达到气, 液两相 平衡.
此时, 气态混合物的总压力为p, 则 p 即为温度T下该液态混合物或溶液的 饱和蒸气压.
水(A)和乙酸乙酯(B)不完全混溶, 在37.55℃时两液相呈平衡.
一相中含质量分数为w(B) = 0.0675的酯, 另一相中含w(A) =
0.0379的水, 假定拉乌尔定律对每相中的溶剂都能适用, 已知
37.55℃时, 纯乙酸乙酯的蒸气压力是22.13kPa, 纯水的蒸气
压力是6.399kPa, 试计算:
ln p(s) 3133 27.650 11.99 p(s) 160.3k Pa Pa 200K / K
计算结果表明, 所给过程是恒温恒压不可逆相变化过程, 为
此可根据计算所得的液体及固体CO2在200 K的蒸气压数据, 设
计以下可逆过程进行计算:
8
s, 100kPa, 200K
s, 160.3kPa, 200K G2
(1)计算下述过程Gm :
CO2( s, 100kPa, 200K ) →CO2( l, 100kPa, 200K )
(2)判断在100 kPa下, CO2(l)能否稳定存在?
(1) 200 K时液体及固体CO2的饱和蒸气压:
ln p(l) 2013 22.405 12.34 p(l) 228.7kPa Pa 200K / K
多 组
各组分 等 同对待
分
均
相 系
溶液
统
区分溶剂 和溶质
物质B的质量摩尔浓度
bB nB / mA
xB
{1 /
bB MA
bB }
1
§2-4 拉乌尔定律、亨利定律
1. 液态混合物和溶液的饱和蒸气 压
设由组分A, B, C……组成液态混 合物或溶液, T一定时, 达到气, 液两相 平衡.
此时, 气态混合物的总压力为p, 则 p 即为温度T下该液态混合物或溶液的 饱和蒸气压.
水(A)和乙酸乙酯(B)不完全混溶, 在37.55℃时两液相呈平衡.
一相中含质量分数为w(B) = 0.0675的酯, 另一相中含w(A) =
0.0379的水, 假定拉乌尔定律对每相中的溶剂都能适用, 已知
37.55℃时, 纯乙酸乙酯的蒸气压力是22.13kPa, 纯水的蒸气
压力是6.399kPa, 试计算:
ln p(s) 3133 27.650 11.99 p(s) 160.3k Pa Pa 200K / K
计算结果表明, 所给过程是恒温恒压不可逆相变化过程, 为
此可根据计算所得的液体及固体CO2在200 K的蒸气压数据, 设
计以下可逆过程进行计算:
8
s, 100kPa, 200K
s, 160.3kPa, 200K G2
(1)计算下述过程Gm :
CO2( s, 100kPa, 200K ) →CO2( l, 100kPa, 200K )
(2)判断在100 kPa下, CO2(l)能否稳定存在?
(1) 200 K时液体及固体CO2的饱和蒸气压:
ln p(l) 2013 22.405 12.34 p(l) 228.7kPa Pa 200K / K
《物理化学第4版》第四章4-3 拉乌尔定律和亨利定律ppt课件

12
亨利定律只适用于平衡系统; 对于公式中的 k[%],B 冶金系统广泛应用, 我们称之为百分之一亨利系数。但是,冶 金行业仍称之为亨利系数。
13
三、 拉乌尔定律和亨利定律的应用 1、应用拉乌尔定律测定溶剂的相对蒸 气压下降 2、利用亨利定律求难溶气体的溶解度
3、计算挥发性溶质在平衡气相的组成
14
1、文字叙述:定温下,稀溶液中溶剂的蒸 气压pA等于纯溶剂的蒸气压pA*乘以溶液中 溶剂的摩尔分数xA。 2、数学表达式:
pA pA* xA
2
(1)式中的各量均指平衡状态下的性 质; (2)适用于稀溶液中的溶剂,xA1时 严格适用;一般而言,溶液愈稀愈接近 实际(分压)。
3
(3)对于双组分系统, xA =1 -xB, 则 pA= pA* xA= pA*(1-xB)
1、文字叙述:一定温度 下,微溶气体B在溶液中 的平衡组成xB与该气体在 气相中的平衡分压pB成正 比。即亨利定律。
pB g xB l
7
2、数学表达式:
pB=kx,BxB
式中, xB是挥发性溶质(即所溶解的气 体B) 在溶液中的摩尔分数. pB是平衡时液面上该气体的分压. kx,B 溶质组成用摩尔分数表示时的 亨利系数. 是一个常数,其数值与T、p 及溶剂、溶质的性质有关.
§4-3 拉乌尔定律和亨利定律
研究溶液中组分的热力学, 如化学 势,采用的基本方法仍然是研究与液相 组分呈平衡的气体的化学势. 因此,必须 知道液相组成与平衡气相分压有何关 系?这一关系由两个经验定律来描述.
1
一、拉乌尔定律
(法国化学家F.M.Raoult)
在溶剂中加入非挥发性溶质后,溶剂的 蒸气压降低, 1887年发表了定量关系.
bB (40
亨利定律只适用于平衡系统; 对于公式中的 k[%],B 冶金系统广泛应用, 我们称之为百分之一亨利系数。但是,冶 金行业仍称之为亨利系数。
13
三、 拉乌尔定律和亨利定律的应用 1、应用拉乌尔定律测定溶剂的相对蒸 气压下降 2、利用亨利定律求难溶气体的溶解度
3、计算挥发性溶质在平衡气相的组成
14
1、文字叙述:定温下,稀溶液中溶剂的蒸 气压pA等于纯溶剂的蒸气压pA*乘以溶液中 溶剂的摩尔分数xA。 2、数学表达式:
pA pA* xA
2
(1)式中的各量均指平衡状态下的性 质; (2)适用于稀溶液中的溶剂,xA1时 严格适用;一般而言,溶液愈稀愈接近 实际(分压)。
3
(3)对于双组分系统, xA =1 -xB, 则 pA= pA* xA= pA*(1-xB)
1、文字叙述:一定温度 下,微溶气体B在溶液中 的平衡组成xB与该气体在 气相中的平衡分压pB成正 比。即亨利定律。
pB g xB l
7
2、数学表达式:
pB=kx,BxB
式中, xB是挥发性溶质(即所溶解的气 体B) 在溶液中的摩尔分数. pB是平衡时液面上该气体的分压. kx,B 溶质组成用摩尔分数表示时的 亨利系数. 是一个常数,其数值与T、p 及溶剂、溶质的性质有关.
§4-3 拉乌尔定律和亨利定律
研究溶液中组分的热力学, 如化学 势,采用的基本方法仍然是研究与液相 组分呈平衡的气体的化学势. 因此,必须 知道液相组成与平衡气相分压有何关 系?这一关系由两个经验定律来描述.
1
一、拉乌尔定律
(法国化学家F.M.Raoult)
在溶剂中加入非挥发性溶质后,溶剂的 蒸气压降低, 1887年发表了定量关系.
bB (40
拉乌尔定律与亨利定律

PB = k X,B xB PB = kb,B bB PB = kC,B CB
+
应该注意,气体在液体里的分子状态应该相同 应该注意 气体在液体里的分子状态应该相同. 气体在液体里的分子状态应该相同
HCl ( g ) → H (aq ) + Cl (aq )
定律不适用
问题:对于 气体在H 的溶解 定律是否适用? 的溶解,定律是否适用 问题 对于CO2气体在 2O的溶解 定律是否适用 对于
课堂练习题P161,3-4 课堂练习题
提示: 提示
P=101325Pa(PN278%),有一个比例或者亨利系数 约 有一个比例或者亨利系数.约 有一个比例或者亨利系数 血液).不用 的系数。 为1.39× 10-5kg(N2)/kg(血液 不用 × 血液 不用P134例2的系数。 例 的系数 暂不考虑温度对系数的影响。 暂不考虑温度对系数的影响。即在体温时仍近似 用上面的系数。 用上面的系数。 压力增大, 溶解增加。 压力增大,N2溶解增加。 p = gh
ρ
必须考虑60m的水压;水柱高度与Pa的换算。 的水压;水柱高度与 的换算 的换算。 必须考虑 的水压 不要忘了水面上的压力. 不要忘了水面上的压力 或者直接计算压力增加值;因为必 气泡 V = 4 π r 3 或者直接计算压力增加值 因为必 3 须考虑常压时N 的残留即溶解。 须考虑常压时 2的残留即溶解。 另外, 的应用; 另外,PV=nRT的应用;P=101.325KPa 的应用
水的饱和蒸气压
10 C 1227.8 Pa 20 C 2337.8 Pa ° 30 C 4242.8 Pa
相对湿度(relative humidity)RH(% ) 相对湿度 20℃ ,空气中的 H2O为1568.9 Pa ℃ 空气中的 空气中的P RH=(1568.9/2337.8) ×100% =67.110 % 问题:相对湿度的可能的最大值与最小值分别是 问题 相对湿度的可能的最大值与最小值分别是? 相对湿度的可能的最大值与最小值分别是
第二讲 溶液及胶体——拉乌尔定律、亨利定律

• 开启易拉罐后, 压力减小, CO2气体的溶解度随之减 小, 从液体中释放出来.
• 热玻棒插入碳酸饮料中, 亨利常数随之增大, CO2 5 气体从液体中释放出来 .
4. 亨利定律的其它形式 当溶质的组成用cB , bB 等表示时, 亨利定律可表示成:
pB kc ,B cB kb ,B bB k x ,B xB
注意 : k x ,B , kc ,B , kb ,B的 大小和单位都是不同的 .
5. 几点说明 • 同拉乌尔定律,亨利定律的应用条件与对象是稀溶液(严格 地说是理想稀溶液)中的溶质, 且溶质在两相中的分子形态必 须相同. (氯化氢、氨气溶于水不适用)
• 当有几种气体共存时, 每一种分别适用于亨利定律. • 亨利常数随温度升高而增大. • 亨利常数的大小和单位与采用的组成表示方式有关.
(2) p = pA + pB =(6.306 + 18.56)kPa = 24.86 kPa
3
另外若溶质和溶剂都有挥发性,溶液 仍为理想溶液,拉乌尔定律仍然适用, 可将分别求出溶质及溶剂的蒸气压
4
2. 亨利定律
实验表明:一定温度下, 稀溶液中挥发性溶质B在平衡气相中的 分压力pB与该溶质B在平衡液相中的摩尔分数xB成正比. 亨利定律: 气体的溶解度与气体的分压呈正比 pB = kx, BxB kx, B 亨利常数, 与T 及溶剂, 溶质的性质有 关
k x ,B
p
B
xB
101325Pa 3.61 10
5
2.81GPa
又
故
bB
k b ,B
4.490 10 2 dm 3 kg 1 22.4dm 3 mol 1
拉乌尔定律和亨利定律

第五节 拉乌尔定律和亨利定律一、亨利定律在一定的温度下,稀溶液中挥发性溶质在气相中的平衡分压与其在溶液中的摩尔分数成正比。
p B =k x x B亨利定律适用于稀溶液中挥发性溶质,是单元操作“吸收”的理论基础。
应用亨利定律应注意以下几点:① 亨利定律只适用于溶质在气相中和液相中分子形式相同的物质;② 气体混合物溶于同一种溶剂时,亨利定律对各种气体分别适用。
其压力为该种气体的分压;③亨利定律除了用摩尔分数表示外,还可以用物质的量浓度c B 、质量摩尔浓度b B 或质量分数w B 等表示,此时,亨利定律的表达式相应为:p B =k c c Bp B =k m b Bp B =k w w B④亨利定律适用于稀溶液中挥发性溶质,溶液越稀,定律越准确。
二、亨利定律的应用亨利定律是化工单元操作----气体吸收的理论基础,气体吸收是利用混合气体中各种气体在溶剂中溶解度的差异,有选择性地将溶解度大的气体吸收,使之从混合气体中分离出来。
若以相同的分压进行比较,则x k 越小,B x 越大,因此,x k 可作为吸收气体所用溶剂的选择依据。
三、二组分液体混合二组分系统F = C -Φ+2。
其中K =2。
故F = 2-Φ+2=4-Φ。
即二组分的最多能以四相平衡共存,最大自由度为3(温度、压力和组成)。
需要用比较复杂的三维坐标系。
但为了讨论的方便,可固定一个自由度(常是温度或压力)。
此时二组分系统的自由度f = 2-Φ+1= 3-Φ。
最大自由度为2,便可以用平面坐标描述。
1. 拉乌尔定律在一定温度下,溶入了非电解质溶质的稀溶液,其溶剂的饱和蒸气压与溶剂的摩尔分数成正比,比例系数为该溶剂在此温度下的饱和蒸气压。
表达式为。
稀溶液中的两个经验定律

稀溶液中的两个经验定律
➢ 拉乌尔定律 ➢ 亨利定律
拉乌尔定律(Raoult’s Law)
定温下,在稀溶液中,溶剂的蒸气压等于纯溶 剂的蒸气压乘以溶液中溶剂的摩尔分数。
pA
p
* A
x
A
pA* 代表纯溶剂 A 的蒸气压, xA 代表溶液中A的摩尔分数。
若溶液中仅有A、B两个组分,则: xA xB 1
pA
p
* A
(1
xB )
pB pB*xB
溶剂的蒸气压,因加入溶质而降低。 (溶液中溶剂的蒸气压较纯溶剂的蒸气压低)
双液系:
pA
pቤተ መጻሕፍቲ ባይዱ
* A
x
A
pB pB*xB
亨利定律(Henry’s Law)
在一定温度和平衡状态下,气体在液体里的溶 解度(物质的量分数)和该气体的平衡分压成正比。
p kxx
kx 是一个常数,p是平衡时液面上该气体的压力, x 是挥发性溶质(即所溶解的气体)在溶液中的物质的量 分数。
p kxx p kmmB p kccB
➢ 拉乌尔定律 ➢ 亨利定律
拉乌尔定律(Raoult’s Law)
定温下,在稀溶液中,溶剂的蒸气压等于纯溶 剂的蒸气压乘以溶液中溶剂的摩尔分数。
pA
p
* A
x
A
pA* 代表纯溶剂 A 的蒸气压, xA 代表溶液中A的摩尔分数。
若溶液中仅有A、B两个组分,则: xA xB 1
pA
p
* A
(1
xB )
pB pB*xB
溶剂的蒸气压,因加入溶质而降低。 (溶液中溶剂的蒸气压较纯溶剂的蒸气压低)
双液系:
pA
pቤተ መጻሕፍቲ ባይዱ
* A
x
A
pB pB*xB
亨利定律(Henry’s Law)
在一定温度和平衡状态下,气体在液体里的溶 解度(物质的量分数)和该气体的平衡分压成正比。
p kxx
kx 是一个常数,p是平衡时液面上该气体的压力, x 是挥发性溶质(即所溶解的气体)在溶液中的物质的量 分数。
p kxx p kmmB p kccB
拉乌尔定律适用于稀溶液中的溶剂※克方程

吸附:当气体或液体与某些固体接触时,气体或液体的分子会积聚在固体表面上,这种现 象称之为吸附。它可以被认为是某些固体能将某些物质从气体混合物(或溶液)中凝聚到某 表面上的一种物理化学现象。 -----------放热过程:吸附过程是由流体(气体或液体)与固体构成一个体系,是非均相过程。流体分 子从流体相被吸附到固体表面,其分子的自由焓降低,与未吸附前相比,其分子的熵也降 低了。按照热力学定律,自由焓变化(ΔG)、焓变化(ΔH)及熵变化(ΔS)关系如下: ΔG=ΔH-TΔS 上式中ΔG、ΔS均为负值。故ΔH肯定为负值。因此,吸附过程必然是个放 热过程。 吸附剂的再生:当吸附进行一定时间后,吸附剂的表面就会被吸附物所覆盖,使吸附能力 急剧下降,此时就需将被吸附物脱附,使吸附剂得到再生。 毛细管现象:毛细管凝结现象是指被吸附的蒸气在多孔性的吸附剂孔隙中凝结为液体的现 象。 吸附滞留现象:即在脱附过程中,欲使吸附剂达到与吸附时同样的吸附量,需更低的平衡 压力。这种现象称之为“吸附滞留现象” -----吸收过程中,气体组分在吸收剂中只是单纯的物理溶解过程,因而称为物理吸收。但在有 些情况下,溶解在吸收剂中的组分要与吸收剂中能够参加化学反应而生成化合物,这种吸 收叫做化学吸收。
1、理想溶液定义 液体混合物中的各组分,在全部浓度范围内都遵循拉乌尔定律,则称此溶液为理想溶液。 2、理想溶液所具有的理想特性,主要有: (1)体积的加和性。(2)溶液在混合或稀释时无热效应 (不同组分质点间相互作用力与同一组分质点间相互作用力相差不大,混合时相互吸引力没有变化) (3)同类分子间与异类分子间的相互作用力相等不产生缔合和氢键现象。 (4)在全部浓度范围内,各组分都严格遵循拉乌尔定律。 ---------理想气体-理想溶液(共性,个性) 理想气体中各物质的分子间不存在相互作用力,分子本身的总体积与容器相比忽略不计。理想溶液中各 物质的分子间存在相互作用力,而且各种分子间作用力彼此相等,分子本身的总体积与溶液的体积相比 不但不能忽略,而且所占比重很大,各种分子的本身体积彼此相等。各种物质分子间作用力彼此相等, 各种分子本身的体积也彼此相等,这是理想混合气体与理想溶液微观共性所在。两者的微观个性则表现 在作用力及分子体积的数值上不同。 一句话:理想气体的数值为零,而理想溶液则分别是不为零的常数。微观共性所在。 ---------正偏差: 蒸气压高于理论值,说明两类分子间的相互作用力小,液体分子容易蒸发。由于同名质点的相互作用力 大于异名质点,而相互作用力大的有聚集倾向,因此正偏差的极端情况是液相分层。 负偏差: 蒸气压低于理论值,这表明两类分子间的相互作用力大,阻碍了液体分子的蒸发。两组分有生成化合物 倾向时也属于这种情况。 -------yA>xA 这表明理想溶液中易挥发组分在气相中的含量大于它在液相中的含量。类似地,可以证明不易挥发组分 在液相中的含量比它在气相中的大。
经典稀溶液中的两个定律.ppt

T
f
Tf
T
f
T
f
数学上: x 0 ln(1 x) x
xB
fus Hm R
T
(T
f
)2
xB
fus Hm
R(T
f
)2
T
nB nA nB
nB nA
fus Hm
R(T
f
)2
T
nB mA
fus Hm
R(T
f
)2
T
MA
.....
nB mA
MA
fus Hm
R(T
f
)2
T
mBM A
.....
7
拉乌尔定律和亨利定律
1. 拉乌尔定律 (Roault)
pA p*A xA
2. 亨利定律 (Henry)
pB K x,B xB
pB KB,x xB KB,mmB K c B,c B
K B,x K B,m K B,c 亨利常数
..... K= f ( T,p )
8
§4.7 理想液态混合物
.....
25
2. 凝固点降低 Freezing-point depression
纯溶剂: 溶剂(l) 稀溶液: 溶液(l)
溶剂(s)
Tf
溶剂(s)
Tf
相平衡, 溶剂: A(l) = A*(s) A*(l) + RT ln xA = A*(s)
1
ln xA RT
* A
(
l
)
* A
(
s)
融化
得空气K被B溶,m解(O后2),= p0θ/.241.9pθ×= 1K0B-,m4 (O2)m(O2) 各气K体B的,m分(N压2)= p0θ/.728.3p5θ =×K1B0,m-(4N2)m(N2)
