影院座位设计的数学模型
噶米影院座位设计优化模型

影院座位设计优化模型下图为影院的剖面示意图,座位的满意程度主要取决于视角α和仰角β。
视角α是观众眼睛到屏幕上、下边缘视线的夹角,α越大越好;仰角β是观众眼睛到屏幕上边缘视线与水平线的夹角,β如果太大会使人的头部过分上仰,引起不舒适感,一般要求β不超过30︒。
(1) 地板线倾角θ=10︒,问最佳座位在什么地方。
(2) 求地板线倾角θ(一般不超过20︒),使所有观众的平均满意程度最大。
(3) 地板线设计成什么形状可以进一步提高观众的满意程度。
影院座位设计优化模型吕华军陈霞曹智芳摘要:本文针对影院座位设计问题,利用三角形正切,建立了视角α与仰角β关于地板线倾角θ的数学模型。
并通过Matlab、Lingo、VB等软件,利用求极值的方法解答了问题一,得当倾角θ为10︒时,最佳座位在(6.228,1.4)处。
对于问题二,我们通过泛函分析等方法,将座位分成n排,得出排与排之间的距离是14.5/n,对每排观众的视角α和仰角β进行求和,得出视角α和仰角β的平均值,从而取得平均满意度,再通过求极值的方法算出当θ为15.14︒时,观众的平均满意度最大。
此外,在β角不超过30︒的前提下我们还对地板线的设计进行改进(将第一排座位抬高),通过方程组(7)的解答,可得到最佳的地板线设计,进一步提高观众的满意度。
我们还对模型进行了误差分析,若n越大,模型的精确度就越高。
关键词:座位设计仰角视角平均满意度一、问题的重述下图为影院的剖面示意图,座位的满意程度主要取决于视角α和仰角β。
视角α是观众眼睛到屏幕上、下边缘视线的夹角,α越大越好;仰角β是观众眼睛到屏幕上边缘视线与水平线的夹角,β如果太大会使人的头部过分上仰,引起不舒适感,一般要求β不超过30︒。
(1) 地板线倾角θ=10︒,问最佳座位在什么地方。
(2) 求地板线倾角θ(一般不超过20︒),使所有观众的平均满意程度最大。
(3) 地板线设计成什么形状可以进一步提高观众的满意程度。
电影院座位的排列组合题

电影院座位的排列组合题在电影院中,座位的排列组合是一个常见的问题。
通过不同的排列组合方式,可以实现座位的合理规划和管理,以提供更好的观影体验。
本文将探讨电影院座位的排列组合问题,并提出一种有效的解决方案。
在电影院中,座位的排列方式通常采用矩阵形式。
每个座位可以用行和列的坐标来表示。
假设一个电影院的座位排列为m行n列,即总共有m*n个座位。
首先,我们考虑座位的排列组合方式。
对于每个座位,观众可以选择坐下或离开。
因此,每个座位有两种状态:占用或空闲。
对于m*n个座位来说,一共有2^(m*n)种可能的组合方式。
然而,并不是所有的组合方式都是可行的。
在实际情况中,观众需要一定的间隔来保持舒适的观影环境。
为了满足这一要求,我们可以引入一些限制条件。
首先,由于人的身体大小是有限的,我们需要确保每个座位周围有足够的空间。
通常情况下,至少要保持一个座位的间隔。
这就意味着每个观众所占据的空间实际上是一个2*2的矩阵。
在排座位时,我们可以将这个矩阵看作是一个整体,而不是单独的座位。
其次,为了方便观众的进出,我们可以在每一排中留出通道。
这样,观众可以更轻松地通过通道进入或离开他们所在的排。
为了确保通道的宽度足够,我们可以预留一定数量的座位来构建通道。
在考虑了以上限制条件后,座位的排列组合方式将大大减少。
我们可以使用排列组合的方法进行计算,得到最终的组合方式数。
在实际应用中,可以使用计算机程序来快速计算。
通过合理的座位排列组合,电影院可以提供更好的观影体验。
观众可以更轻松地进入和离开座位,同时享受到更宽敞舒适的观影环境。
此外,通过适当的座位规划,电影院还可以最大限度地提高座位数量,从而增加收益。
总结起来,电影院座位的排列组合是一个重要的问题。
通过合理的座位规划,可以提供更好的观影体验,增加观众的舒适度和满意度。
同时,适当的座位规划也能够增加电影院的经济效益。
在实际应用中,我们可以使用计算机程序来计算最佳的座位排列组合方式,以实现座位的合理规划和管理。
关于最优观影位置选择的数学模型
数理科学科技创新导报 Science and Technology Innovation Herald169当今这个时代,电影是一种喜闻乐见的大众艺术,人们喜欢在闲暇时间走进影院,体验其中的喜怒哀乐。
而同时,作为一种消费,人们总是希望自己能坐在电影院的最佳位置,使得视觉、听觉得到最好的享受。
在设计影院时,已经充分考虑了观众看电影的舒适度,对于影院的地板倾角、前后排椅子之间的距离等都经过了精心的设计,而尽管如此,不同位置看电影肯定也有很大差异。
根据这个想法,该文进行了数学建模。
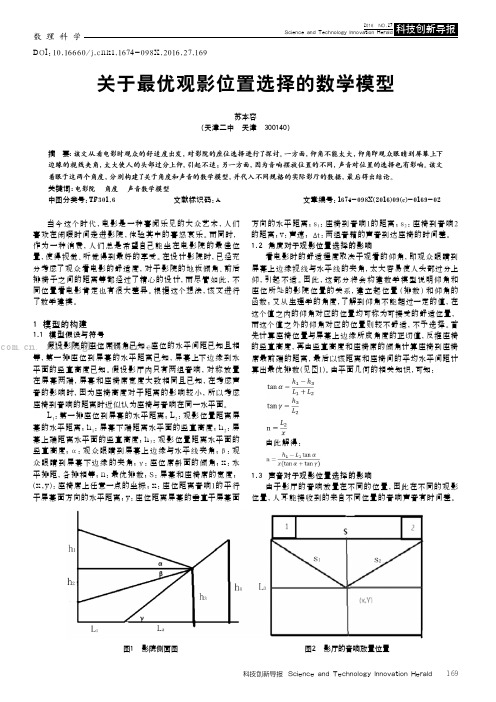
1 模型的构建1.1 模型假设与符号假设影院的座位席倾角已知,座位的水平间距已知且相等,第一排座位到屏幕的水平距离已知,屏幕上下边缘到水平面的竖直高度已知。
假设影厅内只有两组音响,对称放置在屏幕两端,屏幕和座椅席宽度大致相同且已知,在考虑声音的影响时,因为座椅高度对于距离的影响较小,所以考虑座椅到音响的距离时近似认为座椅与音响在同一水平面。
L 1:第一排座位到屏幕的水平距离;L 2:观影位置距离屏幕的水平距离;h 1:屏幕下端距离水平面的竖直高度;h 2:屏幕上端距离水平面的竖直高度;h 3:观影位置距离水平面的竖直高度;α:观众眼睛到屏幕上边缘与水平线夹角;β:观众眼睛到屏幕下边缘的夹角;γ:座位席斜面的倾角;x:水平排距,各排相等;n:最优排数;S:屏幕和座椅席的宽度;(x,y):座椅席上任意一点的坐标;x:座位距离音响1的平行于屏幕面方向的水平距离;y:座位距离屏幕的垂直于屏幕面方向的水平距离;s 1:座椅到音响1的距离;s 2:座椅到音响2的距离;v:声速;:两组音箱的声音到达座椅的时间差。
1.2 角度对于观影位置选择的影响看电影时的舒适程度取决于观看的仰角,即观众眼睛到屏幕上边缘视线与水平线的夹角,太大容易使人头部过分上仰,引起不适。
因此,这部分将会构建数学模型说明仰角和座位所处的影院位置的关系,建立起位置(排数)和仰角的函数;又从生理学的角度,了解到仰角不能超过一定的值,在这个值之内的仰角对应的位置均可称为可接受的舒适位置,而这个值之外的仰角对应的位置则较不舒适,不予选择。
影院座位设计的优化模型

参 考 文 献: [ 1 】周人 忠 . 电影 院建 筑设 计 [ . 京 : 国建 筑 工 业 出 M】 北 中
5 { t ( ̄ . ( )<a 3) no
t =( L —d t ( )+C ) nO a
如图 1
,
( +h > 时为正 ) £
收稿 日期 :0 00 1 2 1.3 9
—
霎 漱
川 拱… … ~ ; 姬
38 6 因此 , 可得 目标 函数 :
( : )
四川理 工 学 院学报 ( 自然科 学版 )
=
21 0 0年 6月
2 .4 9 , 时 =6 9 即最佳 位 置在 中央 一 列 67 2 。 此 . m,
约束 条 件 : 影 院 中每排 据屏 幕 的距 离 可 表示 为 :
=
看电影 的效果都会略有下降 , 出现这一结果的原因主要
是 因 为 在 前 面 3排 时 , 然 视 角 比较 大 , 仰 角也 比较 虽 但 大 并且 还 超过 了 3 。 而 在后 面 几排 , 然 仰 角 较 小 , 0, 虽 但 视 角也 很 小 , 因此效 果也 不 是 很 好 。所 以这 一 结 果对 整
体 效果 来 说是 非 常 合 理 的。 此 模 型 还 可 以 用 于 大 型 场
d+0 8 n一1 n ∈ Z .( )( 且 ≤ n≤ m)
其 中: 表示观众眼睛到水平 面的距离 , 表示影 院中座 n
位 的排 数 。
对 于 这个 多 目标 问 题 , “ 目标优 化 法 ” 用 主 对模 型进
行求解 。进一步分析 , 人们看 电影 时 , 角大时能达 到 视
更 好 的观 看 效 果 , 通 过 调 整 颈 部 的 扭 转 角 度 , 而 只要 角
数学建模-影院角度

数学建模-影院⾓度影院⾓度问题下图为影院的剖⾯⽰意图,座位的满意程度主要取决于视⾓α和仰⾓β。
视⾓α是观众眼睛到屏幕上、下边缘视线的夹⾓,α越⼤越好;仰⾓β是观众眼睛到屏幕上边缘视线与⽔平线的夹⾓,β太⼤使⼈的头部过分上仰,引起不舒服感,⼀般要求β不超过30度。
记影院屏幕⾼h ,上边缘距地⾯⾼ H,地板线倾⾓θ,第⼀排和最后⼀排座位与屏幕⽔平距离分别为 d和 D ,观众平均座⾼为c(指眼睛到地⾯的距离)。
已知参数 h=1.8,d = 4.5 , D=19 ,c =1.1,H=5(单位:m)。
(1)地板线倾⾓θ =10 ,问最佳座位在什么地⽅?(2)求地板线倾⾓(⼀般不超20 ),使所有观众的平均满意程度最⼤。
(3)地板线设计成什么形状可以进⼀步提⾼观众的满意程度。
摘要对于问题1,⾸先根据满意度设置两种求解情况,第⼀种是当仰⾓β<=30时,由于⾓度较⼩,可以粗略的认为只要β<=30,就⽆须再考虑仰⾓对观众的影响。
将视⾓α作为满意度依据,另⼀种当β>30时,同时考虑这两个⾓度对满意度的影响,同时设置α的影响因⼦p,和β的影响因⼦1-p,根据观众实际情况合理的设置p,这⾥拟合了不同的p对满意度的影响。
通过MATLAB求出了距离屏幕6.2274m的距离观众满意度最佳。
对于问题2,将观众离散均匀分布,算出每⼀排距离屏幕的距离xi,然后利⽤问题⼀情况⼆的思路求出每⼀排的满意度Si,最后求和除以总的排数求出S。
同时⽤不同的θ和p来拟合,找出不同p的情形下最⼤S对应的θ。
问题3从提⾼地板线和将地板线设计成折线这两个⽅⾯来提⾼满意度。
关键词:⾮线性规划 MATLAB 三⾓函数⼀,问题提出⼆,模型假设假设题⽬给出的已知参数是合理的。
三,符号说明S 平均满意度Si 第i排的满意度x 到屏幕的⽔平距离xi 第i排到屏幕的⽔平距离p 对α和β影响的权重θ重新设置的地板线⾓度n 总的排数四,模型建⽴与求解4.1问题⼀的分析与求解⾸先根据满意度设置两种求解情况,第⼀种是当仰⾓β<=30时,就将视⾓α作为满意度依据,另⼀种当β>30时,同时考虑这两个⾓度对满意度的影响,同时设置α的影响因⼦p,和β的影响因⼦1-p,根据观众实际情况合理的设置p,此处设置不同的p来拟合数据进⽽分析规律。
数学建模作业:影院座位选择

标准实用影院座位选择摘要看电影是众多大学生所喜爱的业余享受,怎样选择一个好位子观影也是大家所关心的一个问题。
本文针对如何在敬文讲堂选择一个好位子看电影,建立模型进行分析。
由于座位的满意程度主要取决于视角和仰角,视角越大,仰角越小越合适.因此是一个多目标规划问题。
本文先建立了模型1,采用主目标法找出了讲堂最优的一个位子。
而后就"怎样选择一个好位子"的问题,建立模型2,分析了讲堂中央部分座位的满意程度,因为这个问题涉及的目标较多,即要考虑水平和垂直两种情况,相对复杂。
模型 2 作了巧妙的假设,提出了"基本视效"的概念将目标化为单一的一个,运用几何的方法,给出了各个座位的基本视效值,从而基本视效值大的座位满意度高,反之,满意度低。
模型 2 的优点在于避免了其他方法,如权重法的主观性。
因此模型也更加可信。
关键词多目标规划视角仰角几何基本视效m a t l a b一、问题的背景看电影一直是广大学生所偏好的业余活动,将自己隐藏在一片漆黑之中,心随画面变换,感受视听震撼,仿佛置身另一个世界,一时间忘却所有烦恼。
在师范大学,每到周末便可看到各个海报栏贴着电影放映的信息,其中每周敬文讲堂放映的英文电影,因其免费放映、效果良好、寓教于乐,更是成为多年来的保留节目。
每每放映之前,讲堂门口都聚集着众多同学,排着长队,准备争抢观影好地形。
二、问题的提出有效视角是指人的有效视觉范围,一般,双眼正常有效视角大约为水平90°,垂直70°,考虑双眼余光时的视角大约为水平180°,垂直90°。
观影时的视角是观众眼睛到屏幕上、下边缘视线的夹角。
经医学实验得知:10°以内是视力敏锐区,即中心视野,对图像的颜色及细节部分的分辨能力最强。
20°以内能正确识别图形等信息,称为有效视野。
*0°~30°,虽然视力及色辨别能力开始降低,但对活动信息比较敏感,30°之外视力就下降很低了。
数学建模综合题影院座位设计问题讲课讲稿

数学建模综合题影院座位设计问题数学模型张峰华材料学院材料成型及控制工程04班 20123631 刘泽材料学院材料成型及控制工程04班 20123627 杨海鹏材料学院冶金工程03班 20123203一、问题重述影院座位的满意程度主要取决于视角α和仰角β,视角是观众眼睛到屏幕上下边缘的视线的夹角,越大越好;仰角是观众眼睛到屏幕上边缘视线与水平线的夹角,太大使人的头部过分上仰,引起不适,一般要求仰角β不超过030;记影院的屏幕高为h ,上边缘距离地面高为H ,影院的地板线通常与水平线有一个倾角θ,第一排和最后一排与屏幕水平距离分别为,d D ,观众的平均座高为c (指眼睛到地面的距离),已知参数h =1.8. H =5, 4.5,19d D ==,c =1.1(单位m)。
求解以下问题:(1) 地板线的倾角010=θ时,求最佳座位的所在位置。
(2) 地板线的倾角θ一般超过020,求使所有观众的平均满意程度最大时的地板线倾角。
二、问题的分析电影院座位的设计应满足什么要求,是一个非常现实的问题。
根据题意观众对座位的满意程度主要取决于观看时的视角α和仰角β,α越大越好,而β越小越好,最佳位置就是要在这两者之间找到一个契合点,使观众对两者的综合满意程度达到最大。
本文通过对水平视角α和仰角β取权重,建立适当的坐标系,从而建立一个线形型满意度函数。
针对问题一,已知地板线倾角,求最佳座位所在,即将问题转化求综合满意度函数的最大值,建立离散加权的函数模型并利用Matlab 数学软件运算求解;针对问题二,将所有观众视为离散的点,要使所有观众的平均满意程度达到最大,即将问题转化求满意度函数平均值的最大值。
对此利用问题一所建立的满意度函数,将自变量转化为地板线倾角;在问题二的基础上对地板线形状进行优化设计,使观众的平均满意程度可以进一步提高。
本文在满意度呈线性的基础上来建立模型的,为使模型简化,更好地说明问题,文中将作以下假设。
影院座位设计

影院座位设计问题分析 座位的满意程度主要取决于视角α与仰角β,视角α是观众眼睛到屏幕上、下边缘视线的夹角,α越大越好;仰角β是观众眼睛到屏幕上边缘视线与水平线的夹角,β太大使人的头部过分上仰,引起不舒适感,一般要求β不超过030。
模型假设1、β不超过030时,由决β定的满意程度相同;2、α越大,由α决定的满意程度越大;3、同一排的各个座位的满意程度都相同。
模型构成 以屏幕所在直线为y 轴,地面所在直线为x 轴。
建立直角坐标系,如图1所示设某一座位的坐标为(x ,y ),则由三角函数关系式知: xy H -=βtan ……………………(1) xy h H --=-)tan(αβ 又αβαβαβtan tan 1tan tan )tan(+-=- ∴)tan(tan 1)tan(tan tan αββαββα-+--=2()()hx x H y H h y =+--- ……………………(2) 又c d x y +-=θtan )(, 知o x y 图12tan [()tan ][()tan ]()tan tan hx x H x d c H h x d c H x d c x αθθθβ⎧⎫=⎪⎪+-------⎪⎪⎨⎬---⎪⎪=⎪⎪⎩⎭…………………(⊗)模型求解(1)地板线倾角θ=010,问最佳座位在什么地方?由模型假设1知,最佳座位显然要满足0030β<≤ 从而, 3.9( 4.5)tan 0tan x x θβ--<=≤3当θ=010时,⇒ 6.227191.8 1.8tan 43x x x α≤≤⎧⎫⎪⎪⎪⎪⎨⎬≤<⎪⎪⎪⎪⎩⎭易知,x=6.227时,tan α取得最大值,此时y=(6.227—4.5)0tan10+1.1=1.409 即最佳座位处为(6.227,1.409)(2)求地板线倾角θ(一般不超过020),使所有观众的平均满意程度最大。
由(⊗)式知,当x 取某一定值时,θ越大,则α就越大,β就越小,也即观众的满意度就越大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
影院座位设计的数学模型2002级3班 吴小刚【摘要】:本文在平均视角越大越好的前提下,建立了一个简单的数学模型,求出了最佳视角所在位置,提出了进一步提高观众满意程度的地板设计方案。
【关键词】:视角 平均视角 模型 数学建摸问题提出:下图为影院的剖面示意图,座位的满意程度主要取决于视角。
仰角α是观众眼睛到屏幕上边缘视线与水平线的夹角,β是观众眼睛到屏幕下边缘视线与水平线的夹角,视角的大小等于α-β,c 为观众平均坐高。
a=3.9m b=2.1m d=4.5m D=19m c=1.1m(1) 地板倾角θ=10度,问最佳位置在什么地方。
(2) 求地板线倾角 θ(一般不超过20度),使所有观众的平均满意程度最大。
(3) 地板线设计成什么形状可以进一步提高观众的满意程度。
模型假设:1、观众的满意程度主要取决于视角α-β,越大越好。
2、观众眼睛处于同一斜面,可以在斜面的任意位置。
3、如图建立直角坐标系,设某观众的眼睛在此坐标系中的坐标为(x,y )。
模型建立:根据题目,结合模型假设,有Y=xtan θ tan α=tan x d x αθ-+ tan β=tan b x d x θ-+ tan ()βα-=βαβαtan tan 1tan tan +-=xd x x b a ab x d b a +++-++-θθ22tan tan )()(模型求解:(1)令f(x)=(d+x)+xd x x b a ab +++-θθ22tan tan )( )tan(20βαπβα-∴<-< 为增函数要使tan(βα-)最大,即视角βα-最大,只需f(x)最小,为此,我们对f(x)求导f ′(x)=1+2222)()tan tan )(())(tan )(tan 2(x d x x b a ab x d b a x +++--++-θθθθ =1+22222)(tan )(tan )(tan x d ab d b a d d x +-+--+θθθ 令f ′(x)=0x=1tan tan )(tan 222+++=θθθab d b a d (0≤x ≤14.5) 0≤x<1tan tan )(tan 222+++=θθθab d b a d f’(x)>0 1tan tan )(tan 222+++=θθθab d b a d <x ≤14.5 f’(x)<0 因此,tan(βα-)在x=1tan tan )(tan 222+++=θθθab d b a d 处取得最大值。
将 a=3.9,b=4.5,θ=10度代入上式,解得x=3.7m综上,当地板倾角θ=10度时,最佳座位在离屏幕水平距离为4.5+3.7=8.2m 处。
(2)假设相邻两排观众间的水平距离为1 m ,那么观众所在位置的横坐标x 的取值范围为0---14.5,x 为整数。
下面结合模型,利用VB 语言编写程序,分别求出地板倾角θ=1,2,----,20度时的平均视角,从而找出使得平均视角最大的θ的值。
具体程序见附录①,程序运行结果如下:结果分析:从以上数据可看出,随着地板倾角θ的增大,平均视角也在增大。
那么,这是否意味着θ=20度就是所求结果呢?当然不是,我们还得考虑如下问题:处在最后一排的观众的水平视线应该位于屏幕中线以下,否则观众就得低着头看电影了,这与实际不符。
我们可用如下数学语言来描述这个问题:假设最后一排观众所在位置的地板高为h,则由题目数据及以上分析可得h≤5-1.8/2-1.1=3m。
对于此限制条件,可用VB语言描述,具体程序见附录②,程序运行结果如下:结果分析:以上数据就是地板倾角在不同取值时,最后一排所在位置的地板高度,不难看出,当地板倾角θ=12度时,h≈3m ,最符合限制条件。
综上,地板的倾角应为12度。
敏感性分析:由于地板倾角的取值和相邻两排座位间的水平距离都是假设的,因此需要对二者(即t,x)作敏感性分析。
首先我们研究地板倾角在12度附近变化时对平均视角的影响。
假设相邻两排座位间的水平距离x不变,利用VB分别求出地板倾角为11.5、12.6、----、12.4、12.5度时的平均视角,具体程序见附录③,程序运行结果如下:结果分析:从以上数据可知,当地板倾角θ在12度附近变化时,对平均视角并无多大影响,这说明对地板倾角的假设是可用的。
下面我们研究相邻两排座位间的水平距离改变时对平均视角的影响。
结合实际,间距可取为0.7m、0.8m、0.9m.假设地板倾角不变,利用VB求出不同间距所对应的平均视角,具体程序见附录④,程序运行结果如下:结果分析:我们可以挑取某一地板倾角对应的平均视角进行比较,在此以12度为例。
Step( )Step( 1) Step(0.9 ) Step(0.8 ) Step(0.7 ) A(12) 2.904829 2.904831 2.904833 2.65224从以上比较结果可知,相邻两排间的水平间距取0.8m 为宜。
(3)首先证明如下结论:如图所示,随着点A 的下降(点A 位于点C 所在水平线上),α逐渐减小。
证明:cos α=ab c b a 2222-+≥ab c ab 222-=1-abc 22∵随着点A 的下降,a,b 都在增大∴1-abc 22增大,即cos α增大 又∵0〈 α〈90º∴α逐渐减小基于以上结论,我们可以适当升高位于屏幕下边缘所在水平面以下的座位,从而增大视角和平均视角,进一步提高观众的满意程度。
地板可设计如下:值得注意的是,ab 、cd 不能太长,否则位于同一水平面的前排观众会影响后排观众的视线,不符合题目要求。
另外,cd 应该稍低于屏幕下边缘所在水平线,否则后排观众将不能看到屏幕下边缘。
附录①Private Sub Form_Click()Dim x%, t%, f!, y!, a(20)Const pi = 3.14f = 0y = 1.8 / (4.5 + x + (16 - 8.2 * (Tan(pi * t / 180)) + (Tan(pi * t / 180)) ^ 2 * x ^ 2) / (4.5 + x))For t = 0 To 20For x = 0 To 20f = f + yNext xa(t) = f / 21Next tFor t = 0 To 18 Step (3)Print "a("; t; ")"; "="; a(t); "a("; t + 1; ")"; "="; a(t + 1); "a("; t + 2; ")"; "="; a(t + 2)PrintNext tEnd Sub②Private Sub Form_Click()Dim y!, x!, t%, h(20)Const pi = 3.14For t = 0 To 20y = 14.5 * Tan(t * pi / 180)h(t) = yNext tFor t = 0 To 18 Step (3)Print "h("; t; ")"; "="; h(t); "h("; t + 1; ")"; "="; h(t + 1); "h("; t + 2; ")"; "="; h(t + 2)PrintNext tEnd Sub③Private Sub Form_Click()Dim x%, t!, f!, y!, a(20)Const pi = 3.14f = 0y = 1.8 / (4.5 + x + (16 - 8.2 * (Tan(pi * t / 180)) + (Tan(pi * t / 180)) ^ 2 * x ^ 2) / (4.5 + x))For t = 11.5 To 12.5 Step (0.1)For x = 0 To 14f = f + yNext xa(t) = f / 15Next tFor t = 11.5 To 12.5 Step (0.1)Print "a("; t; ")"; "="; a(t)PrintNext tEnd Sub④Private Sub Form_Click()Dim x%, t%, f!, y!, a(20)Const pi = 3.14f = 0y = 1.8 / (4.5 + x + (16 - 8.2 * (Tan(pi * t / 180)) + (Tan(pi * t / 180)) ^ 2 * x ^ 2) / (4.5 + x))For t = 0 To 20For x = 0 To 20f = f + yNext xa(t) = f / 21Next tFor t = 0 To 18 Step (3)Print "a("; t; ")"; "="; a(t); "a("; t + 1; ")"; "="; a(t + 1); "a("; t + 2; ")"; "="; a(t + 2)PrintNext tEnd Sub【参考文献】:【1】姜启源谢金星叶俊《数学模型》高等教育出版社【2】朱道元《数学建模案例精选》科学出版社Mathematical modeling for theater seat designWu Xiaogang【Abstract】A simple mathematical modeling is set up in view of the average angle of view, a best position of viewing is acquired,.Furtherly the floor design programmers for promoting the watchers satisfaction is proposed. 【Key words】Perspective Average perspective Model Mathematical modeling。
