中山纪中三鑫双语学校小学升初中面试(1)

合集下载

初中化学《有机合成材料1》

2、本课题与学生的生活实际紧密联系，让学生通过身边的材料，查阅相关资料等学会归纳总结的学习方法。
•
.
24
四、说教法：
根据本节课的教学内容和知识特点，我主要会采用情憬教学法、讨论式教学法和实验指导等多种教学方法的相互补充来完成本课题的教学
.
25
六、说教学程序
根据教材的特点和学生实际，我主要通过以下程序来完成本单元的教学 1、创设4个教学情景（1）在本课题的引入时，我会用学生看得见、摸得着得生活日常用品：衣服、塑料杯、药匙、笔筒、电脑外壳等引入。让学生对这些材料进行简单归类，从而得出生活中得很多用品都是用有机材料制成的。（2）在对有机物和无机物的概念的形成的教学中，我采取让学生填写课本99面的活动与探究，通过在填表的过程中认识什么叫有机物，什么叫无机物，同时给学生一个交流的机会，指导甲烷、乙醇和葡萄糖的相对分子质量比较小，而淀粉和蛋白质的的相对分子质量很大，从而自然引出有机物中：小分子、和有机高分子的概念。
.
11
现象：塑料碎片加热后变成液态，冷却后变成白色固体。
结论：这类高分子材料可以反复加工，多次使用，能制成薄膜、拉成丝或压制成所需要的各种形状，这种材料具有热塑性。
.
12
讨论交流：
电源插座、电视机外壳能用热塑性塑料吗？你知道这类产品用什么材料做成的吗？
.
13
有机合成材料之二——合成纤维
.
15
阅读下列信息，谈谈你的看法：
塑料是由石油炼制的产品制成的，塑料的制造成本低，而且耐用、防水，大部分塑料的抗腐蚀能力强，不与酸碱反应，一般不导热、不导电，是电的绝缘体，塑料容易被塑制成不同形状的日常用品。有些塑料容易燃烧，并且产生有毒气体，大部分塑料不会腐烂，也不能被细菌分解，容易造成“白色污染”，回收利用废弃塑料时，分类十分困难，而且经济上不合理。

初中数学专题02等腰三角形的存在性问题(原卷版)

专题二等腰三角形的存在性问题【考题研究】近几年各地的中考数学试题中，探索等腰三角形的存在性问题频频出现，这类试题的知识覆盖面较广，综合性较强，题意构思精巧，要求学生要有较高的分析问题的能力和解决问题的能力，这类问题符合课标对学生能力提高的要求。

【解题攻略】在讨论等腰三角形的存在性问题时，一般都要先分类．如果△ABC是等腰三角形，那么存在①AB＝AC，②BA＝BC，③CA＝CB三种情况．解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．几何法一般分三步：分类、画图、计算．哪些题目适合用几何法呢？如果△ABC的∠A（的余弦值）是确定的，夹∠A的两边AB和AC可以用含x的式子表示出来，那么就用几何法．①如图1，如果AB＝AC，直接列方程；②如图2，如果BA＝BC，那么；③如图3，如果CA＝CB，那么．代数法一般也分三步：罗列三边长，分类列方程，解方程并检验．如果三角形的三个角都是不确定的，而三个顶点的坐标可以用含x的式子表示出来，那么根据两点间的距离公式，三边长（的平方）就可以罗列出来．【解题类型及其思路】解题类型：动态类型：1.一动点类型问题；2.双动点或多动点类型问题背景类型：1.几何图形背景；2.平面直角坐标系和几何图形背景解题思路：几何法一般分三步：分类、画图、计算；代数法一般也分三步：罗列三边长，分类列方程，解方程并检验．如果△ABC是等腰三角形，那么存在①AB＝AC，②BA＝BC，③CA＝CB三种情况．已知腰长画等腰三角形用圆规画圆，已知底边画等腰三角形用刻度尺画垂直平分线．解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．【典例指引】类型一【二次函数综合题中根据条件判定三角形的形状】典例指引1．抛物线2y x bx c =++与x 轴交于点A ，点B （1，0），与y 轴交于点C （0，﹣3），点M 是其顶点．（1）求抛物线解析式；（2）第一象限抛物线上有一点D ,满足∠DAB =45°,求点D 的坐标；（3）直线x t = (﹣3＜t ＜﹣1)与x 轴相交于点H ．与线段AC ，AM 和抛物线分别相交于点E ，F ，P ．证明线段HE ，EF ，FP 总能组成等腰三角形.【举一反三】（2020·江西初三期中）如图①，已知抛物线y =ax 2+bx +3（a ≠0）与x 轴交于点A （1，0）和点B （-3，0），与y 轴交于点C ．（1）求抛物线的解析式；（2）设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由；（3）如图②，若点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标．类型二【利用二次函数的性质与等腰三角形的性质确定点的坐标】典例指引2．（2019·山东初三期末）如图1，已知抛物线2()30y ax bx a =++≠与x 轴交于点(1,0)A 和点(3,0)B -，与y 轴交于点C .（l ）求抛物线的表达式；（2）如图l ，若点E 为第二象限抛物线上一动点，连接,BE CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标；（3）如图2，在x 轴上是否存在一点D 使得ACD ∆为等腰三角形？若存在，请求出所有符合条件的点D 的坐标；若不存在，请说明理由.【举一反三】（2019·广东省中山市中山纪念中学三鑫双语学校初三期中）如图，已知抛物线y ＝ax 2+bx +c 的图象与x 轴交于A （2，0），B （﹣8，0）两点，与y 轴交于点C （0，﹣8）．（1）求抛物线的解析式；（2）点F是直线BC下方抛物线上的一点，当△BCF的面积最大时，求出点F的坐标；（3）在（2）的条件下，是否存在这样的点Q（0，m），使得△BFQ为等腰三角形？如果有，请直接写出点Q的坐标；如果没有，请说明理由．类型三【确定满足等腰三角形的动点的运动时间】典例指引3．（2018济南中考）如图1，抛物线平移后过点A（8，,0）和原点，顶点为B，对称轴与轴相交于点C，与原抛物线相交于点D．（1）求平移后抛物线的解析式并直接写出阴影部分的面积；（2）如图2，直线AB与轴相交于点P，点M为线段OA上一动点，为直角，边MN与AP相交于点N，设，试探求：①为何值时为等腰三角形；②为何值时线段PN的长度最小，最小长度是多少．【举一反三】如图所示，抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0）、B（3，0）、C（0，3）三点．点D从C出发，沿线段CO以1个单位/秒的速度向终点O运动，过点D作OC的垂线交BC于点E，作EF∥OC，交抛物线于点F．（1）求此抛物线的解析式；（2）小明在探究点D运动时发现，①当点D与点C重合时，EF长度可看作O；②当点D与点O重合时，EF长度也可以看作O，于是他猜想：设点D运动到OC中点位置时，当线段EF最长，你认为他猜想是否正确，为什么？（3）连接CF、DF，请直接写出△CDF为等腰三角形时所有t的值．【新题训练】1．（2020·江西初三）如图，在平面直角坐标系中，已知点A(﹣2，﹣4)，直线x=﹣2与x轴相交于点B，连接OA，抛物线y=﹣x2从点O沿OA方向平移，与直线x=﹣2交于点P，顶点M到点A时停止移动．（1）线段OA 所在直线的函数解析式是；（2）设平移后抛物线的顶点M 的横坐标为m ，问：当m 为何值时，线段P A 最长？并求出此时P A 的长．（3）若平移后抛物线交y 轴于点Q ，是否存在点Q 使得△OMQ 为等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．2．（2018·山东中考真题）如图，在平面直角坐标系中，二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ，交y 轴于点()0,6C ，在y 轴上有一点()0,2E -，连接AE .（1）求二次函数的表达式；（2）若点D 为抛物线在x 轴负半轴上方的一个动点，求ADE ∆面积的最大值；（3）抛物线对称轴上是否存在点P ，使AEP ∆为等腰三角形，若存在，请直接写出所有P 点的坐标，若不存在请说明理由.3．（2016·广西中考真题）在平面直角坐标系中，抛物线223y x x =--+与x 轴交于A ，B 两点（A 在B 的左侧），与y 轴交于点C ，顶点为D ．（1）请直接写出点A ，C ，D 的坐标；（2）如图（1），在x 轴上找一点E ，使得△CDE 的周长最小，求点E 的坐标；（3）如图（2），F 为直线AC 上的动点，在抛物线上是否存在点P ，使得△AFP 为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由．4．（2019·广东广州市第二中学初三）如图（1），在平面直角坐标系中，矩形ABCO，B点坐标为（4，3），抛物线y＝12-x2＋bx＋c经过矩形ABCO的顶点B、C，D为BC的中点，直线AD与y轴交于E点，与抛物线y＝12-x2＋bx＋c交于第四象限的F点．（1）求该抛物线解析式与F点坐标；（2）如图，动点P从点C出发，沿线段CB以每秒1个单位长度的速度向终点B运动；同时，动点M从点A出发，沿线段AE 13个单位长度的速度向终点E运动．过点P作PH⊥OA，垂足为H，连接MP，MH．设点P的运动时间为t秒．①问EP＋PH＋HF是否有最小值，如果有，求出t的值；如果没有，请说明理由．②若△PMH是等腰三角形，求出此时t的值．5．（2019·湖南中考模拟）如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B与y 轴交于点C（0，3），抛物线的对称轴与x轴交于点D．（1）求二次函数的表达式；（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．6．（2018·山东中考模拟）如图，抛物线y=﹣x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．（1）求抛物线的表达式；（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．7．（2019·山东中考模拟）已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C （﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△P AB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P 使△PDE 为等腰直角三角形？若存在，求出点P 的坐标；若不存在，说明理由．8．（2018·广东中考模拟）如图，在平面直角坐标系xOy 中，二次函数24y ax bx =+-（0a ≠）的图象与x 轴交于A （﹣2，0）、B （8，0）两点，与y 轴交于点B ，其对称轴与x 轴交于点D ．（1）求该二次函数的解析式；（2）如图1，连结BC ，在线段BC 上是否存在点E ，使得△CDE 为等腰三角形？若存在，求出所有符合条件的点E 的坐标；若不存在，请说明理由；（3）如图2，若点P （m ，n ）是该二次函数图象上的一个动点（其中m ＞0，n ＜0），连结PB ，PD ，BD ，求△BDP 面积的最大值及此时点P 的坐标．9．（2019·四川中考模拟）如图，已知二次函数y ＝﹣x 2+bx +c （c ＞0）的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，且OB ＝OC ＝3，顶点为M ．（1）求二次函数的解析式；（2）点P 为线段BM 上的一个动点，过点P 作x 轴的垂线PQ ，垂足为Q ，若OQ ＝m ，四边形ACPQ 的面积为S ，求S 关于m 的函数解析式，并写出m 的取值范围；（3）探索：线段BM 上是否存在点N ，使△NMC 为等腰三角形？如果存在，求出点N 的坐标；如果不存在，请说明理由．10．（2019·甘肃中考模拟）如图，已知二次函数y =ax 2+bx +c 的图象与x 轴相交于A （﹣1，0），B （3，0）两点，与y 轴相交于点C （0，﹣3）．（1）求这个二次函数的表达式；（2）若P 是第四象限内这个二次函数的图象上任意一点，PH ⊥x 轴于点H ，与BC 交于点M ，连接PC ． ①求线段PM 的最大值；②当△PCM 是以PM 为一腰的等腰三角形时，求点P 的坐标．11．（2019·安徽中考模拟）如图，已知直线1y x =+与抛物线2y ax 2x c =++相交于点()1,0A -和点()2,B m 两点.（1）求抛物线的函数表达式；（2）若点P 是位于直线AB 上方抛物线上的一动点，当PAB ∆的面积S 最大时，求此时PAB ∆的面积S 及点P 的坐标；（3）在x 轴上是否存在点Q ，使QAB ∆是等腰三角形？若存在，直接写出Q 点的坐标（不用说理）；若不存在，请说明理由.12．（2018·江苏中考模拟）（2017南宁，第26题，10分）如图，已知抛物线2239y ax ax a =--与坐标轴交于A ，B ，C 三点，其中C （0，3），∠BAC 的平分线AE 交y 轴于点D ，交BC 于点E ，过点D 的直线l 与射线AC ，AB 分别交于点M ，N ．（1）直接写出a的值、点A的坐标及抛物线的对称轴；（2）点P为抛物线的对称轴上一动点，若△P AD为等腰三角形，求出点P的坐标；（3）证明：当直线l绕点D旋转时，11AM AN均为定值，并求出该定值．13．（2019·重庆中考模拟）如图，在平面直角坐标系中，一抛物线的对称轴为直线，与y轴负半轴交于C点，与x轴交于A、B两点，其中B点的坐标为（3，0），且OB＝OC．（1）求此抛物线的解析式；（2）若点G（2，y）是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.（3）若平行于x轴的直线与该抛物线交于M、N两点（其中点M在点N的右侧），在x轴上是否存在点Q，使△MNQ为等腰直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．14．（2019·辽宁中考模拟）抛物线y＝ax2+bx﹣3（a≠0）与直线y＝kx+c（k≠0）相交于A（﹣1，0）、B（2，﹣3）两点，且抛物线与y轴交于点C．（1）求抛物线的解析式；（2）求出C、D两点的坐标（3）在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，求出点P的坐标．15．（2020·浙江初三期末）如图，抛物线y＝﹣12x2+2x+6交x轴于A，B两点（点A在点B的右侧），交y轴于点C，顶点为D，对称轴分別交x轴、线段AC于点E、F．（1）求抛物线的对称轴及点A的坐标；（2）连结AD，CD，求△ACD的面积；（3）设动点P从点D出发，沿线段DE匀速向终点E运动，取△ACD一边的两端点和点P，若以这三点为顶点的三角形是等腰三角形，且P为顶角顶点，求所有满足条件的点P的坐标．16．（2020·湖北初三期末）如图，已知二次函数的图象经过点A（4，4），B（5，0）和原点O，P为二次函数图象上的一个动点，过点P作x轴的垂线，垂足为D（m，0），并与直线OA相较于点C．（1）求出二次函数的解析式；（2）当点P在直线OA的上方时，求线段PC的最大值；（3）当点P在直线OA的上方时，是否存在一点P，使射线OP平分∠AOy，若存在，请求出P点坐标；若不存在．请说明理由；（4）当m＞0时，探索是否存在点P，使得△PCO为等腰三角形，若存在，求出P点的坐标；若不存在，请说明理由．17．（2019·吉林初三）如图1，抛物线与y ＝﹣211433x x ++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，连接AC 、BC ，点D 是线段AB 上一点，且AD ＝CA ，连接CD ．（1）如图2，点P 是直线BC 上方抛物线上的一动点，在线段BC 上有一动点Q ，连接PC 、PD 、PQ ，当△PCD 面积最大时，求PQ +10CQ 的最小值；（2）将过点D 的直线绕点D 旋转，设旋转中的直线l 分别与直线AC 、直线CO 交于点M 、N ，当△CMN 为等腰三角形时，直接写出CM 的长．18．（2020·江苏初三期末）在平面直角坐标系xOy 中，抛物线2y x mx n =-++与x 轴交于点A ,B ( A 在B的左侧)(1)如图1，若抛物线的对称轴为直线3,4x AB =-= .①点A 的坐标为( ， )，点B 的坐标为( ， ); ②求抛物线的函数表达式;(2)如图2，将(1)中的抛物线向右平移若干个单位，再向下平移若干个单位，使平移后的抛物线经过点O ，且与x 正半轴交于点C ，记平移后的抛物线顶点为P ，若OCP ∆是等腰直角三角形，求点P 的坐标.。

2011年中山市中小学教师中级专业技术资格评审通过名单

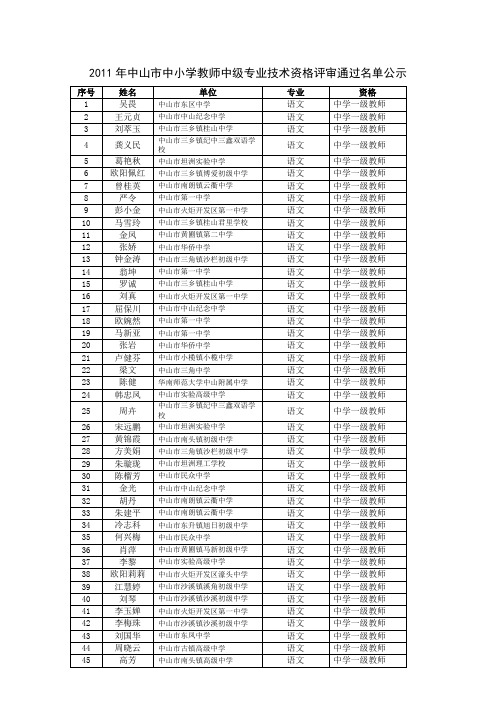
数学英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语英语
中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师中学一级教师
中山市古镇高级中学中山市南头镇高级中学中山市石岐中学中山市石岐北区中学中山市实验高级中学中山市港口中学中山市古镇初级中学中山市三乡镇纪中三鑫双语学校中山市黄圃镇第二中学中山市南朗镇云衢中学中山市民众中学中山市板芙镇初级中学中山市坦洲实验中学中山市南朗镇云衢中学中山市三角镇沙栏初级中学中山市阜沙镇牛角初级中学中山市黄圃镇中学中山市板芙镇初级中学中山市南朗镇云衢中学中山市黄圃镇中学中山市三乡镇理工学校中山市黄圃镇中学中山市华侨中学中山市小榄镇实验高级中学中山市黄圃镇第二中学中山市民众镇浪网中学中山市火炬开发区濠头中学中山市黄圃镇马新初级中学中山市西区初级中学中山市东升镇旭日初级中学中山市坦洲中学中山市石岐杨仙逸中学中山市第一中学中山市东升镇高级中学中山市古镇初级中学中山市东区松苑中学中山市黄圃镇中学中山市坦洲中学中山市小榄镇小榄中学中山市黄圃镇第二中学中山市三乡镇博爱初级中学中山市三角镇沙栏初级中学中山市横栏中学中山市南朗镇云衢中学华南师范大学中山附属中学中山市民众中学中山市三角中学

教学案例_2

关于公布2009年广东省初中语文
读书活动教学专题教研评选结果的通知
各市教育局教研室、广东实验中学：
为推动我省初中语文新课程教学研究工作，我室语文科在2009年秋季学期开展了初中语文读书活动教学专题教研，举行了初中语文读书活动教学案例和教学论文评选活动。

经过各地初评推荐和省组织专家评审，评出了优秀教学案例69名、优秀教学论文97名。

现将评选结果公布如下，请各地做好宣传表彰工作。

附件：2009年广东省初中语文读书活动教学专题教研评选结果
广东省教育厅教研室
二○一○年四月二十六日
附件：
2009年广东省初中语文读书活动教学专题教研评选结果
一、优秀教学案例
二、优秀教学论文。

十博士点评小学生诗歌节获奖作品

116树枝上鸟儿（组诗）方妍（中山市纪中三鑫双语学校六年级）一你的羽毛像京剧戏台上的包龙图一样像一颗星星也没有的夜一样又黑又长你的嘴黄灿灿的好像刚饮下一缕散发光和热的朝阳你的眼睛越过重重绿叶像清早带着微凉露水的风窥探闭合的花蕾一样向巨大的“水泥盒子”中那其中一个窗口好奇地张望二你低头梳着羽毛，光滑柔亮得像舞台幕布十博士点评小学生诗歌节获奖作品广东省小学生诗歌节已经举办五届，有几十万小学生用自己的文字参与了诗歌节，并走出了一些势头不错的诗人与作家，如王芗远、朱夏妮等。

我们更关注的是诗歌节对诗心的培育，在诗歌节的官方网站天空城，我们看到了有关孩子、有关诗歌、有关语文教育、有关审美教育等各种各样的话题。

我们从2014年小学生诗歌节的获奖作品中挑选了十首诗歌，同时邀请了国内十位文学博士对诗歌进行点评、解读，在小学生与大博士的互动中，我们希望能更好地读懂孩子，一起培育一颗颗诗心。

编者语：. All Rights Reserved.你身旁没有伙伴，日子一定过得寂寞孤独如果树的枝丫是五线谱那你就是五线谱上黑色的、唯一一个音符看，谷底太阳破壳而出你也是时候找个伙伴别再整天叫着“苦啊，苦！”快去，快去别再犹豫，把烦恼向它倾诉！快去，快去此时铺满天空的云霞是我对你最诚挚的祝福！三你在树的臂弯中蹦跳身上披着叶翠绿的影你像一个刚从战场凯旋的将军正接收着热烈的欢迎你的尾巴一上一下地翘着像极了公园里的跷跷板一定是你的妈妈教你：“随时保持警惕”瞧你那副小样儿充满狡黠聪颖谁知道你有没有逃过蛇的毒牙有没有甩掉过凶狠的鹰你是那样的活泼既不用背“36π是多少”、“山不在高，有仙则名”也不用背“be动词加动词ing”你是那样的可爱活像淘气小孩儿打碎了花瓶你就这样浑身充满灵气地站在枝头用枝叶遮蔽自己你在偷偷看我，自作聪明以为我看不到你其实我也躲在窗帘背后眨巴着眼睛偷偷看你【点评】张立群（首都师范大学博士）：组诗突出第二人称“你”，让人读起来显得单纯而亲切。

粤教研室[2004]21号

粤教研室[2004]21号广东省2003年中青年初中语文教师阅读教学竞赛
和优秀教学设计、论文、课件评选活动结果公布
各市教育局教研室：
经各地初评推荐和省组织专家评审，广东省2004年中青年初中语文教师阅读教学竞赛和优秀教学设计、论文、课件评选活动已经顺利结束，共评选出阅读教学竞赛一等奖（10名）、二等奖（12名）、三等奖（49名），教学论文一等奖（11名）、二等奖（32名）、三等奖（59名），教学设计一等奖（16名）、二等奖（28名）、三等奖（59名），教学课件一等奖（9名）、二等奖（13名）、三等奖（68名）。

现将评选结果予以公布，望各地认真做好宣传表彰工作。

附件：广东省2004年中青年初中语文教师阅读教学竞赛和优秀教学设计、论文、课件评选活动结果
广东省教育厅教研室
二OO四年六月三日
附件
广东省2003年中青年初中语文教师阅读教学竞赛和优秀教学设计、论文、课件评选活动结果
一、教学竞赛
一等奖（10名）
二等奖（12名）
二、教学论文一等奖（11名）
二等奖（32名）
三等奖（59名）
三、教学设计
三等奖（65名）
四、教学课件
三等奖（68名）。

粤考越高分----初中生必读名著导读

七年级上
高尔基三部曲《童年》反映了小主人公阿廖沙在父亲去世后，随母亲寄住在外祖父家中度过的岁月。其间，他得到外祖母的疼爱、呵护，受到外祖母所讲述的优美童话的熏陶，同时也亲眼目睹两个舅舅为争夺家产争吵打架以及在生活琐事中表现出来的自私、贪婪。这种现实生活中存在的善与恶、爱与恨在他幼小的心灵上留下了深刻的印象。阿廖沙就是在这种“令人窒息的、充满可怕景象的狭小天地里”度过了自己的童年。
八年级下
江奈生斯威夫特
本书主要描写了外科医生格列佛随“羚羊号”出航南太平洋，不幸中途遇险，格列佛死里逃生，从此开始了一系列的奇遇。小说通过格列佛在利立浦特(小人国)、布罗卜丁奈格(大人国)、勒皮他 (飞岛国)和慧骃国的奇遇，反映了18世纪前半期英国社会的一些矛盾，揭露并批判了英国统治阶级的腐败和罪恶及英国资产阶级在资本主义原始积累时期的疯狂掠夺和残酷剥削。
一部名著，一个人生
畅游书海，阅人生难历之事；访遍名川，历百代一瞬之沧桑。读名著是一个从书中汲取营养的过程，一个人任凭经历再丰富，也只能品尝到几种苦辣酸甜，而一本书却能让你看到人生百态，因为一部名著便是一个人生。对于我来说，读书是我生命的一部分。晨光喜微之时，四书、五经伴随着我，让我在神清气爽的晨光中沐浴着儒家经典的古文气息，有的是一种氤氲缭绕、波澜不惊之感，“知之为知之，不知为不知”让我在学习生活中更加实事求是。 “知之者不如好知者，好之者不如乐之者”让我深刻体味了对学习理应持的态度。 “飞龙在天”则深刻揭示了物极必反的自然规律。于是，古文玄妙的哲理，深刻动人的教化让我一天六成长，能“就有道而正”，能“见贤思齐”，“择善而从”。从而一天天修正自己的错漏不足，以趋于贤，以后方可“治国，平天下” 实现自己的伟大抱负。读名著，插上想象的双翼，加以审美的慧眼，再加之动人以情的字字句句，一幕幕悲喜场景便交替上演。读《红楼梦》，我仿佛看到林黛玉“独倚花锄空洒泪”，听闻他想吟“一朝春尽红颜老，花落人亡两不知”。美景、红颜终成一林黄土，多少痴男怨女，只恨情难终，头已白，债难偿。读《高老头》，我隐约看见：高里奥在伏盖公寓的破屋神经质地幻想女儿能来看他，而他最珍爱的女儿却双双在上流社会享受可怜的父亲给予她们的奢华生活。高里奥奋斗一辈子，只因两个女儿和这个巴黎金钱社会，终于沦落到死后拿不出棺材钱的地步。读《三国演义》我仿佛看见魏、蜀、吴兵戈不息，三分天下，运筹帷幄……这些场景至今如在眼前。

中考专项练习之铅垂法

铅垂法一、解答题(共14小题，每小题5分，共70分)1.(2017·毕节市中考真题) 如图，在平面直角坐标系中，二次函数的图象交坐标轴于，，三点，点是直线下方抛物线上一动点．(1)求这个二次函数的解析式；(2)是否存在点，使是以为底边的等腰三角形？若存在，求出点坐标；若不存在，请说明理由；(3)动点运动到什么位置时，面积最大，求出此时点坐标和的最大面积．(5分)2.如图，抛物线与轴交与，两点，(1)求该抛物线的解析式；(2)设中的抛物线交轴与点，在该抛物线的对称轴上是否存在点，使得的周长最小？若存在，求出点的坐标；若不存在，请说明理由．(3)在中的抛物线上的第二象限上是否存在一点，使的面积最大？若存在，求出点的坐标及的面积最大值．若没有，请说明理由．(5分)3.阅读材料：如图，过的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫的“水平宽”，中间的这条直线在内部线段的长度叫的“铅垂高”．我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半．解答下列问题：如图，抛物线顶点坐标为点，交轴于点，交轴于点．(1)求抛物线和直线的解析式；(2)点是抛物线（在第一象限内）上的一个动点，连结，，当点运动到顶点时，求铅垂高及；(3)是否存在一点，使，若存在，求出点的坐标；若不存在，请说明理由．(5分)4.(2015·中山市纪中三鑫双语学校月考)如图，二次函数的图象与轴交于、两点，与轴交于点，已知，且经过点，是第一象限内抛物线上的一个动点，为抛物线的顶点．(1)求抛物线的解析式； (2)求的面积；(3)求的面积的最大值，并求此时点的坐标．(5分)5.(2018·南开实验学校期中考试) 如图所示，抛物线的顶点为，直线与抛物线交于点(1)求抛物线顶点的坐标和点的坐标 (2)求的面积(3)是抛物线上位于直线上方的一点，当点的坐标为多少时，的面积最大？(5分)6.(2015·中山市古镇初级中学期中考试) 如图，在平面直角坐标系中，二次函数的图象与轴交于、两点，点在原点的左侧，点的坐标为，与轴交于点，点是直线下方的抛物线上一动点．(1)求这个二次函数的表达式；(2)当点运动到什么位置时，四边形的面积最大？求出此时点的坐标和四边形的最大面积．(5分)7.(2018·中山市纪中三鑫双语学校中考模拟) 如图，抛物线与轴交于、两点，与轴交于点．(1)求点、、的坐标；(2)在抛物线的对称轴上有一动点，求的值最小时的点的坐标；(3)若点是直线下方抛物线上一动点，求四边形面积的最大值．(5分)8.(2016·中山市期中考试) 如图，二次函数的图象与轴交于、两点，与轴交于点，已知，且经过点，是第一象限内抛物线上的一个动点．(1)求抛物线的解析式；(2)在对称轴上是否存在一点，使得最短？若点存在，求出点的坐标，若点不存在，请说明理由；(3)求面积的最大值，并求出此时点的坐标．(5分)9.抛物线顶点坐标为点，交轴于点，交轴于点．(1)抛物线和直线的解析式；(2)连结、，求的铅垂高及．(5分)10.如图，已知抛物线与轴交于、两点，与轴交于点，为顶点．(1)求；(2)求；(3)若点是第四象限抛物线上一动点，求的最大值．(5分)11.(2016·苏州市昆山市期中考试) 已知抛物线与直线交于点，．(1)求、、的值；(2)直接写出当时，自变量的范围是；(3)已知点是抛物线的顶点，求的面积．(5分)12.(2017·纪雅单元测试) 如图，一次函数的图象与轴交于，与轴交于点，以直线为对称轴的抛物线，经过，两点，与轴正半轴交于点．(1)求一次函数及抛物线的函数表达式；(2)在直线下方的抛物线上，是否存在一点，使得的面积最大，若存在，求出点的坐标，并求出最大面积是多少．(5分)13.如图，抛物线与轴交于、两点，与轴交于点，已知点，点．(1)求抛物线的函数解析式；(2)若点是抛物线位于第一象限上的动点，求面积的最大值及此时点的坐标．(5分)14.(2020·惠州市惠城区月考) 如图，已知二次函数的图象交x 轴于点，交轴于点(1)求这个二次函数的表达式(2)点是直线下方抛物线上的一动点，求面积的最大值(3)直线分别交直线和抛物线于点，当是等腰三角形时，直接写出的值(5分)二、填空题(共1小题，每小题5分，共5分)15.点是抛物线上一个动点，且在直线：上方，当点坐标为时，最大．(5分)。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中山纪中三鑫双语学校小学升初中语文面试（一）
一、基础知识部分（22分）
1、看拼音，写汉字。

（10分）
（bǐng
）告慰（
jiè
）（
jiǎo
）正埋（
zàng
）磅（
bó
）
（róng
）球抵（
yù
）（
kuí
）花舞（
dǎo
）倒（
méi
）
2、用“√”选出下列加横线字的正确意思。

（4分）
（1）疾走：A、疾病（）；B、痛苦（）；C、痛恨（）；D、快速（）
（2）引弓：A、退（）；B、领（）；C、拉（）；D、拿（）
（3）滔滔不绝：A、尽（）；B、断（）；C、少（）D、一定（）
（4）家常便饭：A、简单的（）；B、方便的（）；C、顺利的（）；D、马上的（）3、请判断下列句子是不是病句，如果不是病句，请在题号划“√”；如果是病句，请在原句上修改。

（4分）
（1）经过福楼拜的精心指导，使莫泊桑的作品很快成为有世界影响的名著。

（2）我老远就看到了槐林和灰椋鸟儿们的叫声。

（3）学习能不能取得好成绩，关键在于勤奋。

（4）看到害人的鸦片被销毁，成千上万老百姓的心情激动得跳哇，叫哇，欢呼声响彻底虎门上空。

4、下列各组词中，各有一个错别字，请用“—”标出，并把正确的写在括号里。

（4分）
A、气势汹汹高赡远瞩开诚相见纹丝不动（）
B、完璧归赵情不自禁应接不瑕开卷有益（）
C、爱不失手色彩斑斓前俯后仰水泄不通（）
D、再接再励晶莹剔透斩钉截铁穷途末路（）
二、语文知识积累（共10分）
5、根据语境填写合适的语文常识：（每空1分）
（1）《水浒传》的作者是，该书描写了北宋徽宗时，以为首的108名好汉
在聚义，打家劫舍，杀富济贫的豪举。

（2）请写出《水浒传》中你喜欢的一位好汉的姓名，并写出他的外号，然
后简要概括此外号表现出的人物特征。

6、按课文默写句子：（每空1分，共4分）
王师北定中原日，。

，绝知此事要躬行。

，唯见长江天际流。

，乌蒙磅礴走泥丸。

三、语文能力考核。

（3分）
早在两千多年前，我们的祖先就在南沙群岛的小岛上开垦、种植。

片片岛屿，留下了祖先生息繁衍的烟火。

南沙群岛拥有难以计数的珍贵的海洋生物，蕴藏着极为丰富的矿产资源，贮存了用之不竭的海洋动力。

南沙群岛是镶嵌在南中国海上的一串串珍珠，是祖国沟通世界的重要通道，是祖国领土不可分割的一部分。

7、这段话介绍了我国南沙群岛3个方面的特征，请分别概括。

（每条不超过6个字）
①②③
四、阅读下面的课文，回答文后的问题。

（25分）
“生命桥”
有一个狩猎队，把一群羚羊赶到了悬崖边，准备全部活捉。

几分钟以后，羚羊群分成了两群：老羚羊为一群，年轻羚羊为一群。

一只老羚羊走出羊群，超年轻羚羊群叫了一声，一只年轻羚羊应声跟老羚羊走到了悬崖边。

年轻羚羊向后退了几步，突然奔跑着向悬崖对面跳过去，随即老羚羊紧跟后面也飞跃出去，只是老羚羊跃起的高度要低一些。

当年轻羚羊在空中向下坠时，奇迹出现了：老羚羊的身子刚好出现在年轻羚羊的蹄上，年轻羚羊在老羚羊的背上猛蹬一下，下坠的身体又突然升高并轻巧地落在了对面的悬崖边，而老羚羊就像一只断翅的鸟，笔直地坠入了山涧。

试跳成功紧接着一对对羚羊（A、陵B、凌）空腾起没有拥挤没有争夺秩序井然快速飞跃。

顿时，山涧上空划出了一道道令人眼花缭乱的弧线，那弧线是一（A、坐B、座）以老羚羊的死亡做桥墩的生命桥。

那情景是何等的神圣。

猎人们个个惊得目瞪口呆，不由自主地放下了猎枪。

8、阅读第一自然段，请用三个成语形容羚羊面临绝境的情景。

（3分）
9、阅读第二自然段，对比《船长》一文，无论是动物，还是人类，当灾难来临的时候，他们（它们）作出了几乎相同的选择，请用简洁的语言概括这个选择是什么？这样做的理由又是什么？（4分）
哈尔威船长，站在指挥台上，大声吼道：“全体安静，注意听命令！把救生艇放下去。

妇女儿童先走，其他乘客跟上，船员断后，必须把六十人救出去。

”（《船长》）
他们（它们）的选择是
理由是
10、阅读第三自然段，请给划线的句子加上标点（请在原文上添加）。

（3分）
11、阅读第三自然段，请在文中（）选择正确的汉字，并打“√”。

（2分）
12、阅读全文，说说本文以“生命桥”为题的含义。

（3分）
我的理解
13、第三段末尾“猎人们个个惊得目瞪口呆，不由自主地放下了猎枪”,请你联系上下文，分析猎人们放下猎枪的原因。

（2分）
我的分析：
14、本文课题命名为“生命桥”，请模仿例句，用其它事物作比喻，再写两个句子，写出你对“桥”的感悟。

（4分）
例句：桥是连接死的绝望到生的希望的生命躯体；
桥是演奏陌生到熟悉的友谊乐章……
仿句：桥是
桥是
15、猎人眼睁睁地看着斑羚往下跳，太让人心疼了！请根据你所掌握的比喻、拟人等修辞知识，给“猎人们”写一句保护野生动物的公益广告词，要求至少运用一种修辞手法。

（4分）。