用锐角三角函数概念解题的常见方法(含答案11页)
初三数学锐角三角函数含答案
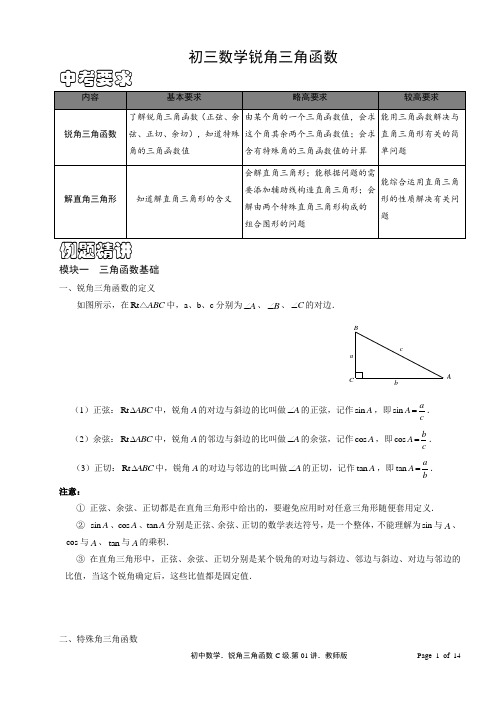
初三数学锐角三角函数中考要求例题精讲模块一 三角函数基础一、锐角三角函数的定义如图所示，在Rt ABC △中，a 、b 、c 分别为A ∠、B ∠、C ∠的对边．（1）正弦：Rt ABC ∆中，锐角A 的对边与斜边的比叫做A ∠的正弦，记作sin A ，即sin aA c=． （2）余弦：Rt ABC ∆中，锐角A 的邻边与斜边的比叫做A ∠的余弦，记作cos A ，即cos b A c =． （3）正切：Rt ABC ∆中，锐角A 的对边与邻边的比叫做A ∠的正切，记作tan A ，即tan a A b=． 注意：① 正弦、余弦、正切都是在直角三角形中给出的，要避免应用时对任意三角形随便套用定义． ② sin A 、cos A 、tan A 分别是正弦、余弦、正切的数学表达符号，是一个整体，不能理解为sin 与A 、cos 与A 、tan 与A 的乘积．③ 在直角三角形中，正弦、余弦、正切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边的比值，当这个锐角确定后，这些比值都是固定值．二、特殊角三角函数a A这些特殊角的三角函数值一定要牢牢记住！ 三、锐角三角函数的取值范围在Rt ABC ∆中，90C ∠=︒，000a b c a c b c >>><<，，，，，又sin a A c =，cos b A c =，tan aA b=，所以 0sin 10cos 1tan 0A A A <<<<>，，． 四、三角函数关系 1．同角三角函数关系： 22sin cos 1A A +=，sin tan cos AA A= 2．互余角三角函数关系：(1) 任意锐角的正弦值等于它的余角的余弦值：()sin cos 90A A =︒-；(2) 任意锐角的余弦值等于它的余角的正弦值：()cos sin 90A A =︒-； (3) 任意锐角的正切值等于它的余角的余切值：()tan cot 90A A =︒-． 3．锐角三角函数值的变化规律：(1)A 、B 是锐角，若A >B ，则sin A >sin B ；若A <B ，则sin A <sin B(2) A 、B 是锐角，若A >B ，则cos A <cos B ；若A <B ，则cos A >cos B (3) A 、B 是锐角，若A >B ，则tan tan A B >；若A <B ，则tan tan A B < 【例1】 已知在ABC △中，A B ∠∠、是锐角，且5sin tan 22913A B AB cm ===，，，则ABC S =△ ． 【解析】过C 作CD AB ⊥于D ，这样由三角函数定义得到线段的比：5sin tan 213CD CDA B AC BD====，， 设5132CD m AC m CD n BD n ====，，，，解题的关键是求出m n 、值．51222CD BD n m AD m ====， 所以529122922AB AD BD m m m =+=+==所以12101452ABC m CD S AB CD ===⋅=，，△ 小结：设ABC △中，a b c 、、为A B C ∠∠∠、、的对边，R 为ABC △外接圆的半径，不难证明：与锐角三角函数相关的几个重要结论：（1）111sin sin sin 222ABC S bc A ac B ab C ===△；（2）2sin sin sin a b c R A B C===． 【答案】145【巩固】如图，点A 在半径为R 的O 上，以A 为圆心，r 为半径作A ，设O 的弦PQ 与A 相切，求证PA QA ⋅为定值．【答案】证明线段乘积为定值，联想到三角形的面积，可以和三角函数联系起来．∵1sin 2APQ S PA QA A =⋅△，12APQ S r PQ =⋅△， ∴sin PA QA A r PQ ⋅⋅=⋅．在APQ △中，sin 2PQ A R =，∴2PQPA QA r PQ R⋅=⋅÷，∴2PA QA Rr ⋅=为定值．【例2】 求tan1tan2tan3tan89︒⋅︒⋅︒⋅⋅︒的值【答案】∵tan cot 1αα=，tan cot(90)αα=︒-∴tan1tan89tan1cot11︒︒=︒︒=，tan2tan88tan2cot 21︒︒=︒︒=， tan44tan46tan44cot 441︒︒=︒︒=，而tan451︒=，∴tan1tan2tan3tan891︒⋅︒⋅︒⋅⋅︒=．【巩固】化简：22sin cos sin 1tan sin cos αααααα++-- 【解析】原式()2222cos sin cos sin cos sin sin cos αααααααα+=+--22cos sin sin cos cos sin αααααα-==--． 【答案】sin cos αα-【例3】已知tan α1）221cos sin cos 1sin cos sin a ααααα-+-+（2090α︒<<︒）．【答案】⑴221cos sin cos 1sin cos sin a ααααα-+-+()()222222sin sin sin sin cos sin sin cos sin cos cos 3cos cos cos sin cos cos cos sin cos sin sin αααααααααααααααααααααα⎛⎫+ ⎪++⎝⎭====+⎛⎫++ ⎪⎝⎭，1sin 2cos αα-=OQPA【巩固】已知tan 2α=，求4sin 2cos 5cos 3sin αααα-+．【答案】4sin 2cos 5cos 3sin αααα-+4sin 24226cos 3sin 532115cos αααα-⨯-===+⨯+．【例4】 已知α为锐角，且22sin 5cos 10αα-+=，求α的度数． 【答案】∵22sin cos 1αα+=∴22(1cos )5cos 10αα--+=，即：22cos 5cos 30αα+-=． ∴(2cos 1)(cos 3)0αα-+=． 解得：cos 3α=-或1cos 2α=． ∵0cos 1α≤≤，∴1cos 2α=，∴60α=︒． 【巩固】若α为锐角，且22cos 7sin 50αα+-=，求α的度数．【答案】由α为锐角，可知0sin 1α<<． 又由22cos 7sin 50αα+-=，22sin cos 1αα+=可知22sin 7sin 30αα-+=，解之得1sin 302αα=⇒=︒． 【例5】已知sin cos αα+（α为锐角），求作以1sin α和1cos α为两根的一元二次方程． 【解析】∵sin cos αα+=，两边平方得：22sin cos 2sin cos 2αααα++=又∵22sin cos 1αα+=，∴1sin cos 2αα⋅=．∴11sin cos sin cos sin cos αααααα++==112sin cos αα⋅= ∴以1sin α和1cos α为两根的一元二次方程为：220x -+=【答案】220x -+=【巩固】若方程222210x ax a -+-=的一个根是sin α，则它的另一个根必是cos α或cos α-． 【答案】不妨设方程的另一根为m ，由一元二次方程的根系关系可知sin m a α+=，21sin 2a m α-=， 故2(sin )1sin 2m m αα+-=，整理可得22sin (sin )1m m αα=+-，即22sin 1m α+=，又22sin cos 1αα+=，故cos m α=±．【巩固】已知：ABC △中，方程2(sin sin )(sin sin )(sin sin )0B A x A C x C B -+-+-=的两根相等，求证60B <︒． 【答案】两根相等则判别式为0，但是观察系数的规律，是否有其他的好办法呢？∵此方程系数之和为0，∴1x =必为此方程的根．又∵此方程两根相等，∴121x x ==，∴12sin sin 1sin sin C Bx x B A-==-．又由正弦定理，有c b b a -=-，∴2c ab +=． 再由余弦定理，有22222222()3()26212cos 22882c a a c c a ba c ca ca ca B caca ca ca ++-+-+--====≥．∴60B ︒≤，且等号不会成立，否则方程就不存在了．【巩固】在ABC △中，60A =︒，最大边与最小边的边长分别是方程2327320x x -+=的两个根，求ABC △的外接圆半径和内切圆的面积．【答案】题目中涉及到边长的关系，以及外接圆半径，这为正弦定理提供了便利条件．∵60A =︒，且显然此三角形有两边不等（即以已知方程为根的两边）， ∴ABC △中，A 既不是最大角也不是最小角，不防设b 为最大边，c 为最小边， 由韦达定理，有3293b c bc +==，， 又由余弦定理，有：2222cos a b c bc A =+-222()3b c bc b c bc =+-=+- 813249=-=．∴7a =（7a =-舍去）又由正弦定理，有2sin aR A===∴7916a b c ++=+=． 1sin 2S bc A P r ==⋅（其中2a b cP ++=，r 为内切圆半径）即132822r =⨯，∴r =∴内切圆面积21ππ3S r ==．【例6】 若0°<θ<30°，且1sin 3km θ=+(k 为常数，且k <0)，则m 的取值范是 ． 【答案】∵0°<θ<30°∴sin 0°<sin θ<sin 30°，即0<sin θ<12∴0<13km +<12，所以1136km -<<，又因为0k <∴1163m k k<<-． 模块二 解直角三角形一、解直角三角形的概念根据直角三角形中已知的量（边、角）来求解未知的量（边、角）的过程就是解直角三角形．二、直角三角形的边角关系如图，直角三角形的边角关系可以从以下几个方面加以归纳： （1）三边之间的关系：222a b c += (勾股定理) （2）锐角之间的关系：90A B ∠+∠=︒（3）边角之间的关系：sin cos ,cos sin ,tan a b aA B A B A c c b=====三、解直角三角形的四种基本类型（1）已知斜边和一直角边(如斜边c ，直角边a )，由sin aA c=求出A ∠，则90B A ∠=︒-∠，b =； （2）已知斜边和一锐角(如斜边c ，锐角A )，求出90B A ∠=︒-∠，sin a c A =，cos b c A =； （3）已知一直角边和一锐角(如a 和锐角A )，求出90B A ∠=︒-∠，tan b a B =，sin ac A=； （4）已知两直角边(如a 和b )，求出c =tan aA b=，得90B A ∠=︒-∠． 具体解题时要善于选用公式及其变式，如sin a A c =可写成sin a c A =，sin a c A=等． 四、解直角三角形的方法解直角三角形的方法可概括为：“有斜(斜边)用弦(正弦，余弦)，无斜用切(正切，余切)，宁乘毋除，取原避中”．这几句话的意思是：当已知或求解中有斜边时，就用正弦或余弦；无斜边时，就用正切或余切； 当所求的元素既可用乘法又可用除法时，则用乘法，不用除法；既可由已知数据又可用中间数据求得时，则用原始数据，尽量避免用中间数据． 五、解直角三角形的技巧及注意点在Rt ABC ∆中，90A B ∠+∠=︒，故sin cos(90)cos A A B =︒-=，cos sin A B =．利用这些关系式，可在解题时进行等量代换，以方便解题． 六、如何解直角三角形的非基本类型的题型对解直角三角形的非基本类型的题型，通常是已知一边长及一锐角三角函数值，可通过解方程(组)来转化为四种基本类型求解；（1）如果有些问题一时难以确定解答方式，可以依据题意画图帮助分析；（2）对有些比较复杂的问题，往往要通过作辅助线构造直角三角形，作辅助线的一般思路是：①作垂线构成直角三角形；②利用图形本身的性质，如等腰三角形顶角平分线垂直于底边等． 七、直角三角形中其他重要概念（1）仰角与俯角：在视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角．如图⑴．（2）坡角与坡度：坡面的垂直高度h 和水平宽度l 的比叫做坡度（或叫做坡比），用字母表示为hi l=，坡面与水平面的夹角记作α，叫做坡角，则tan hi lα==．坡度越大，坡面就越陡．如图⑵． cb aC BA（3）方向角（或方位角）：方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达为北（南）偏东（西）××度．如图⑶．八、解直角三角形应用题的解题步骤及应注意的问题：（1）分析题意，根据已知条件画出它的平面或截面示意图，分清仰角、俯角、坡角、坡度、水平距离、垂直距离等概念的意义；（2）找出要求解的直角三角形．有些图形虽然不是直角三角形，但可添加适当的辅助线，把它们分割成一些直角三角形和矩形（包括正方形）；（3）根据已知条件，选择合适的边角关系式解直角三角形；（4）按照题目中已知数据的精确度进行近似计算，检验是否符合实际，并按题目要求的精确度取近似值，注明单位．【例7】 如图，某高层楼房与上海东方明珠电视塔隔江想望，甲、乙两学生分别在这楼房的A B ，两层，甲在A 层测得电视塔塔顶D 的仰角为α，塔底C 的俯角为β，乙在B 层测得塔顶D 的仰角为θ，由于塔底的视线被挡住，乙无法测得塔底的俯角，已知A B ，之间的高度差为a ，求电视塔高CD （用含a αβθ，，，的代数式表示）【解析】作AE CD ⊥于E ，BF CD ⊥于F ，设DE x = 在Rt ADE ∆中，由tan DE AE α=，得tan tan DE xAE αα==， 在Rt DBF ∆中，由tan DFBFθ=，得 tan tan DF x aBF θθ+==，因为AE BF =， 所以tan tan x x a αθ+=，解得tan tan tan a x αθα⋅=-，从而tan tan aAE θα=- 在Rt AEC ∆中，由tan EC AE β=，得tan tan tan tan a EC AE ββθα=⋅=- 所以()tan tan tan tan tan tan tan tan tan tan a a a CD DE EC αβαβθαθαθα+=+=+=--- 【答案】()tan tan tan tan a αβθα+-【例8】 一座建于若干年前的水库大坝的横断面如图所示，其中背水面的整个坡面是长为90米、宽为5图(3)图(2)图(1)俯角仰角视线视线水平线铅垂线米的矩形． 现需将其整修并进行美化，方案如下：① 将背水坡AB 的坡度由1:0.75改为；② 用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域，依次相间地种草与栽花 ．（1）求整修后背水坡面的面积；（2）如果栽花的成本是每平方米25元，种草的成本是每平方米20元，那么种植花草至少需要多少元？【答案】（1）作AE BC ⊥于E ．∵ 原来的坡度是1:0.75，∴ 140.753AE EB == ． 设4AE k =，3BE k =， ∴ 5AB k =， 又 ∵ 5AB =米， ∴1k =，则4AE =米 ．设整修后的斜坡为AB '，由整修后坡度为，有AE EB ='，∴∠AB E '=30°， ∴ 28AB AE '==米 ． ∴ 整修后背水坡面面积为908720⨯=米2 ． （2）将整修后的背水坡面分为9块相同的矩形，则每一区域的面积为80米2 ．解法一：∵ 要依次相间地种植花草，有两种方案：第一种是种草5块，种花4块，需要20×5×80+25×4×80=16000元； 第二种是种花5块，种草4块，需要20×4×80+25×5×80=16400元 ． ∴ 应选择种草5块、种花4块的方案，需要花费16000元 ．解法二：∵ 要依次相间地种植花草，则必然有一种是5块，有一种是4块，而栽花的成本是每平方米25元，种草的成本是每平方米20元，∴ 两种方案中，选择种草5块、种花4块的方案花费较少 ． 即：需要花费20×5×80+25×4×80=16000元 ．【例9】 如图，在某海域内有三个港口A 、D 、C ．港口C 在港口A 北偏东60︒方向上，港口D 在港口A北偏西60︒方向上．一艘船以每小时25海里的速度沿北偏东30︒的方向驶离A 港口3小时后到达B 点位置处，此时发现船舱漏水，海水以每5分钟4吨的速度渗入船内．当船舱渗入的海水总量超过75吨时，船将沉入海中．同时在B 处测得港口C 在B 处的南偏东75︒方向上．若船上的抽水机每小时可将8吨的海水排出船外，问此船在B 处至少应以怎样的航行速度驶向最近的港口停靠，才能保证船在抵达港口前不会沉没（要求计算结果保留根号）？并指出此时船的航行方向．DCBA【解析】连结AC、AD、BC、BD，延长AT，过B作BT AT⊥于T，AC与BT交于点E．过B作BP AC⊥于点P．由已知得90BAD∠=︒，30BAC∠=︒，32575AB=⨯=（海里），在BEP∆和AET∆中，90BPE ATE∠=∠=︒，AET BEP∠=∠，∴30EBP EAT∠=∠=︒．∵60BAT∠=︒，∴30BAP∠=︒，从而17537.52BP=⨯=（海里）．∵港口C在B处的南偏东75︒方向上，∴45CBP∠=︒．在等腰Rt CBP∆中，BC==，∴BC<AB．BAD∆是Rt∆，∴BD AB>．综上，可得港口C离B点位置最近．∴此船应转向南偏东75︒方向上直接驶向港口C．设由B驶向港口C船的速度为每小时x海里，548)5÷⨯-<7，解不等式，得x>．答：此船应转向沿南偏东75︒的方向向港口C航行，且航行速度至少不低于每小时能保证船在抵达港口前不会沉没．【答案】此船应转向沿南偏东75︒的方向向港口C航行，且航行速度至少不低于每小时证船在抵达港口前不会沉没．【巩固】海面上B处有一货轮正在向正南方向航行，其航行路线是当它到达正南方C时，在驶向正西方的目的地A处，且200CA CB==海里，在AB中点O处有一客轮，其速度为货轮的一半，现在客轮要截住货轮取一件货物，于是选择某一航向行驶去截住货轮，那么当客轮截住客轮时至少航行了多少海里，它所选择了怎样的方向角？（路程保留整数海里，角度精确到度）【解析】如图，由题意可知，ABC∆为等腰直角三角形，假设客轮截住货轮的地点在BC边上时，过OD BC⊥于D，OD为客轮到达BC边的最短距离，即客轮航行的路程为OD，由货轮速度为客轮的2倍可知，货轮航行的距离为2OD BC=，即货轮此时到达了C点，∴客轮截住货轮的地点不可能在BC边上．∴客轮截住货轮的地点在AC 边上．设在AC 边上的F 点两船相遇，设客轮航行的距离为x ，即OE x =，则2BC CE x +=， ∴2200CE x =-，过O 作OF AC ⊥于F ，则11002OF BC ==海里，11002FC AC ==海里， ∴3002EF x =-在Rt DEF ∆中，222OF EF OE +=， 即222100(3002)x x +-=，解得x =1282x ≈，2118x ≈∴141OE OA ≤=∴1282x ≈不符合题意，∴118x ≈ 即当客轮截住货轮时，航行了118海里． 在Rt OEF ∆中，100cos 0.8475118EOF ∠=≈ ∴32EOF ∠=︒∴客轮的航行方向应为南偏东32︒．【答案】客轮的航行方向应为南偏东32︒课堂检测1． （辽宁竞赛）如图，湖心岛上有一凉亭，现欲利用湖岸边的开阔平整地带，测量凉亭顶端到湖面所在平面的高度AB (见示意图)，可供使用的工具有测倾器、皮尺．（1）请你根据现有条件，设计一个测量凉亭顶端到湖面所在平面的高度AB 的方案，画出测量方案的平面示意图，并将测量的数据标注在图形上（所测的距离用m ，n 表示，角用α，β表示，测倾器高度忽略不计）；（2）根据你所测量的数据，计算凉亭到湖面的高度AB (用字母表示)．F EDOC BA【解析】（1）如图所示，在点C 测得ACB α∠=，在点D 测得ADB β∠=，测得DC m =（2）在Rt ABC ∆中，设AB x =，tan x BC α=在Rt ABD ∆中，tan xBD β= BD BC m -=， 即tan tan x xm βα-= 解得tan tan tan tan x m αβαβ⋅=-【答案】（1）DC m =；（2）tan tan tan tan m αβαβ⋅-2． 化简：222tan1tan 2....tan89sin 1sin 2...sin 89︒⋅︒︒︒+︒++︒【解析】tan1tan2....tan89tan451︒⋅︒︒=︒=()()22222222sin 1sin 2...sin 89sin 1cos 1sin 2cos 2...sin 45︒+︒++︒=︒+︒+︒+︒++︒1894422=+=，故原式289=． 【答案】2893． 如图1、图2，是一款家用的垃圾桶，踏板AB （与地面平行）或绕定点P （固定在垃圾桶底部的某一位置）上下转动（转动过程中始终保持''AP A P BP B P ==，）．通过向下踩踏点A 到'A （与地面接触点）使点B 上升到点'B ，与此同时传动杆BH 运动到''B H 的位置，点H 绕固定点D 旋转（DH 为旋转半径）至点'H ，从而使桶盖打开一个张角'HDH ∠．如图3，桶盖打开后，传动杆''H B 所在的直线分别与水平直线AB DH 、垂直，垂足为点M C 、，设''H C B M =．测得6cm 12cm '8cm AP PB DH ===，，．要使桶盖张开的角度'HDH ∠不小于60︒，那么踏板AB 离地面的高度至少等于多少cm ？（结果保留两位有效数字）【解析】过点'A 作'A N AB ⊥垂足为N 点，在Rt 'H CD ∆中， 若'HDH ∠不小于60︒， 则'3sin 60'H C H D ≥︒=， 即3''43H C H D ≥=， ∴''43B M H C =≥， ∵Rt 'Rt 'A NP B MP ∆∆∽ ∴''''A N A PB M B P=， ∴''643'23 3.5cm 'A P B M A N B P ⋅⨯=≥=≈，∴踏板AB 离地面的高度至少等于3.5cm ．【答案】踏板AB 离地面的高度至少等于3.5cm课后作业1． 化简求值：1sin 1sin 1cos 1cos 1sin 1sin 1cos 1cos αααααααα⎛⎫⎛⎫-+-+-- ⎪⎪ ⎪⎪+-+-⎝⎭⎝⎭（090α︒<<︒） 【解析】原式()()()()222222221sin 1sin 1cos 1cos 1sin 1sin 1cos 1cos αααααααα⎡⎤⎡⎤-+-+⎢⎥⎢⎥=-⋅-⎢⎥⎢⎥----⎣⎦⎣⎦由090α︒<<︒可知，0cos 1α<<，0sin 1α<<．故原式1sin 1sin 1cos 1cos cos cos sin sin αααααααα-+-+⎛⎫⎛⎫=-- ⎪⎪⎝⎭⎝⎭2sin 2cos 4cos sin αααα--=⋅=． 图3图2C MAA'P BB'HDH'H'DHB'BPA'A（图1）NCMA'PBB'HDH'【答案】42． 若045α︒<<︒，且sin cos αα=sin α的值． 【解析】方法1：由2263sin cos sin cos 256αααα==，结合22sin cos 1αα+=，可得 2226397sin (1sin )sin 2561616ααα-=⇒=或． 由045α︒<<︒可知221sin sin 452α<︒=，故27sin sin 16αα=⇒=． 方法2：由sin cos 2sin cos αααα=，结合22sin cos 1αα+=，可得sin cos αα+==cos sin αα-=，故sin α．3． （2011甘肃兰州）通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad ）．如图①在ABC △中，AB AC =，顶角A 的正对记作sadA ，这时=BCsadA AB=底边腰．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题： （1）60sad ︒= ．（2）对于0180A ︒<<︒，∠A 的正对值sadA 的取值范围是 ． （3）如图②，已知3sin 5A =，其中A ∠为锐角，试求sadA 的值．【解析】（1）1（2）02sadA <<（3）设53AB a BC a ==，，则4AC a =．在AB 上取4AD AC a ==，作DE AC ⊥于点E ． 则312416164sin 4cos 44555555DE AD A a a AE AD A a a CE a a =⋅=⋅==⋅=⋅==-=，，，CD =图②图①C BAC B A∴CDsadAAC==EDCBA。
锐角三角函数的解题技巧
在矩形中AB=DC=4，
∠2＋∠α=90°
又DE⊥AC，
∠1＋∠2=90°
∴∠1=∠α
点评：注意把条件集中到一起．
例9.如图，点A是一个半径为300米的圆形森林公园的中心，在森林公园附近有B、C两个村庄，现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通，经测得∠ABC=45o，∠ACB=30o，问此公路是否会穿过该森林公园？请通过计算进行说明。
解：如图，设BC=3m，则AB=5m，
(2)如图所示，已知AB是⊙O的直径，CD是弦，且CD⊥AB，BC=6，AC=8，则sin∠ABD的值是（ ）
分析：
因为AB是⊙O的直径，所以∠ACB=90°．因为BC=6，AC=8，所以AB=10．因为∠ABD=∠ACD=∠ABC，所以在Rt△ACB中， 故正确答案为D．
(二)同角的三角函数之间的关系
(1)平方关系：sin2α＋cos2α=1
(2)商数关系：
（三）两角的关系
任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值，任意锐角的正切值与它的余角的正切值的积等于1．即若A+B=90°，则sinA=cosB，cosA=sinB，tanA·tanB=1．
图4
参考数据：
分析：（1）由图可知 是直角三角形，于是由勾股定理可求。
（2）利用三角函数的概念即求。
解：设需要t小时才能追上。
则
（1）在 中， ，
则 （负值舍去）故需要1小时才能追上。
（2）在 中
即巡逻艇沿北偏东 方向追赶。
例20.如图5，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且建筑物周围没有平整地带，该建筑物顶端宽度AD和高度DC都可直接测得，从A、D、C三点可看到塔顶端H，可供使用的测量工具有皮尺，测倾器。
用锐角三角函数解决问题
正弦函数性质
04
05
值域：$\sin\alpha$的 值域为$\{ - 1,0,1\}$
周期性：$\sin(x + 2k\pi) = \sin x,k \in \mathbf{Z}$
余弦函数的定义和性质
余弦函数定义：对于 任意一个锐角 $\alpha$，它的余弦 函数记作 $\cos\alpha$，可以 简称为余弦。
一个角的正切值与余切值的关系式为：$\frac{\tan\alpha}{\tan\beta} = \frac{\sin\alpha}{\cos\beta}$
利用两角和与差的三角函数公式解题
两角和的正弦公式
$\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta$
解析：因为一个三角形的一个锐角为$30^{\circ}$。所 以另外两个角分别为$60^{\circ}$和$90^{\circ}$
解析：因为$\tan B = \frac{b}{a}$。所以$\frac{\sin B}{\cos B} = \frac{b}{a}$
THANKS
谢谢您的观看
05
解题技巧与策略
重视基础，掌握基本题型
掌握特殊角度的三角函数值，如30度、45度和60度的正弦值、余弦值和正切值。 熟悉常见的基本题型，如已知角度求函数值，或者已知函数值求角度。 理解并掌握常见三角函数公式的变形和使用方法，如和差角公式、和差化积公式等。
注意角度的范围，避免出错
牢记角度的范围，避免在解题过程中出现负角或 者大于180度的角。
通过锐角三角函数可判定一个三角形是否为等腰三角形。
判定直角三角形
通过锐角三角函数可判定一个三角形是否为直角三角形。
锐角三角函数的题型及解题技巧
锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础，它应用广泛，解题技巧性强，下面归纳出锐角三角函数的常见题型，并结合例题介绍一些解题技巧。
一、 化简或求值例1 （1）已知tan 2cot 1a a -=，且a 是锐角，求22tan cot 2a a +-的值。
（2）化简()()22sin cos cos sin a b a b a a a a ++-。
分析分析 （1）由已知可以求出tan a 的值，化简22tan cot 2a a +-可用1tan cot a a =×；（2）先把平方展开，再利用22sin cos 1a a +=化简。
化简。
解 （1）由tan 2cot 1a a -=得2tan 2tan a a -=，解关于tan a 的方程得tan 2a =或tan 1a =-。
又a 是锐角，∴tan 2a =。
∴22tan cot 2a a +-＝22tan 2tan cot cot a a a a -×+＝2(tan cot )a a -＝tan cot a a -。
由tan 2a =，得1cot 2a =，∴22tan cot 2a a +-＝tan cot a a -＝13222-=。
（2）()()22sin cos cos sin a b a b a a a a ++-＝2222sin 2sin cos cos a ab b a a a a +××+＋2222cos 2cos sin sin a ab b a a a a -××+＝()()222222sin cos sin cos a b a a a a +++＝22a b +。
说明说明 在化简或求值问题中，经常用到“1”的代换，即22sin cos 1a a +=，tan cot 1a a ×=等。
等。
二、已知三角函数值，求角例2 在△ABC 中，若223cos sin 022A B æö-+-=ç÷ç÷èø(),A B ÐÐ均为锐角，求C Ð的度数。
锐角三角函数应用题的方法与技巧
锐角三角函数应用题的方法与技巧
x
《锐角三角函数应用题的方法与技巧》
一、总体思路
1、识别出三角形所涉及的三角函数，并确定三角函数的参数：根据题干里面提供的线段、角度等长度或角度来初步判断三角形的形状，并由此来计算出三个角度和三条边。
2、判断题目的性质：根据题目要求，判断出是求边长还是求角度。
3、解答：
（1）求边长：利用相应的三角函数关系（正弦定理、余弦定理、正切定理等），求出答案;
（2）求角度：利用相应的三角函数关系，求出角度的三角函数值，再用反三角函数求出角度。
二、技巧总结
1、画图法：根据题干中提供的信息，画出准确的三角形图形，便于计算和判断。
2、直角三角形快速求角度：根据对边比斜边的特点，找出角度所对应的三角函数值，再用反三角函数计算出角度。
3、正弦定理、余弦定理：正弦定理可用于计算夹角的一边的长度，余弦定理可用于求另一边的长度。
4、正切定理：正切定理可以用于求夹角的角度大小。
5、各种三角函数的关系：在计算三个角度的大小时，可以利用三个角度的和为180°；在计算三条边的长度时，可以利用三条边之和的性质。
锐角三角函数的解题技巧
(1)平方关系：sin2α＋cos2α=1
(2)商数关系：
（三）两角的关系
任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值，任意锐角的正切值与它的余角的正切值的积等于1．即若A+B=90°，则sinA=cosB，cosA=sinB，tanA·tanB=1．
答案：D
分析：
(1)要求sinα与cosα的关系的值，而已知tanα的值，故可通过 来求值．
(2)已知tanα的值，也可通过 ，把要求的式子的分子，分母同时除以cos2α转化成关于tanα的关系，这样便可求出结论．
点评：在进行三角函数有关计算时，常利用有关公式进行变换．
2、化简计算
例3、计算
分析：
这是一组有关特殊角三角函数值的计算题，计算中最关键是将它们先化成具体的数值，同时还要应用其它一些知识帮助求值，如(1)注意分母有理化，(2)应掌握整数指数幂的意义．
(5)0＜sinA＜1，0＜cosA＜1
2、同名三角函数值的变化规律
当角α在0°～90°间变化时，它的正切和正弦三角函数值随着角度的增大而增大；余弦三角函数值随着角度的增大而减少．
三、解题方法技巧点拨
1、求锐角三角函数的值
例1、(1)在Rt△ABC中，∠C=90°，若 ，求cosB，tanB的值．
分析：本题主要考查锐角三角函数的定义，结合图形求解可化繁为简，迅速得解．
5、求线段长与面积
例6、如图，在△ABC中，∠A=30°，∠B=45°，AC=4，求BC的长．
分析：
题中有30°，45°特殊角，想把它们放到直角三角形中，利用三角函数来解题．
点评：
（1）在作高线构造直角三角形时，一般不过特殊角的顶点作垂线，这样便于利用特殊角解题．
初中锐角三角函数解题方法
正弦余弦定义
三角形 内角和
正弦 余弦
定义 计算 解题
营销网络
正切定义
1. 正 切 函 数 在 何 种 情 况 下 有 定 义 ： 由 于 正 切 函 数 的 定 义 式 是 tanθ=sinθ/cosθ，所以当θ对应的余弦值为零时，正切函数无定义。 2. 正切函数的周期性：正切函数是奇函数，即f(-θ)=-f(θ)，具有π的周期性， 也就是tan(θ+π)=tanθ。 3. 正切函数的值域：正切函数的值域为实数集R，也就是说，它可以取到任 意实数值。
$[-11]$，而其值域是$[90^\circ90^\circ]$因此，若$a$在$[11]$之间，那么$x$就在$[-90^\circ
02
利用反三角函数解决值域问题
在初中锐角三角函数的中，需要注意以 下几点：
sin、cos函数值域均为[-1, 1]，当角度 为°时取到最小值-1，为90°或270°时取 到最大值1，因此在解题时需要注意根
正弦函数
一、正弦函数是以 y = sinx 形式表达的函数，表示角 x 的正弦值为函数值，其中 x 是以弧度为单位的角。 二、 正弦函数的定义域为实数集，值域为 [-1,1]，且在整个定义域内具有周期性。
正弦函数的解题技巧：
一、 根据三角函数定义和性质进行换元：通过代入不同的变量和角度值，将三角函 数转化为更简单易解的形式。 二、 运用正弦函数的周期性：在解题过程中遇到周期性的问题，可运用正弦函数的 周期性，进行变形和化简，以达到解题的目的。
据题目给出的角度范围进行判断。
03
初中锐角三角函数解题技巧
周期变换
周期的求法和利用
•锐角三角函数的周期是指它们的函数值在一定区间内重复出现的长度。对于正弦函数 和余弦函数来说，它们的周期都是2π。而正切函数和余切函数的周期则是π。学生可 以通过掌握这些基本概念，理解周期的概念和求法。并且，周期的性质在解题中也有 很大的帮助，例如，可以通过周期的知识，将某些三角函数题目转化为相同的函数形 式，从而方便计算和答题。
用锐角三角函数概念解题的常见方法(含答案页)
用锐角三角函数概念解题的常见方法(含答案11页)用锐角三角函数概念解题的常见方法1．锐角三角函数（1）锐角三角函数的定义我们规定：sinA=abab，cosA=，tanA=，cotA=．ccba锐角的正弦、余弦、正切、余切统称为锐角的三角函数．（2）用计算器由已知角求三角函数值或由已知三角函数值求角度对于特殊角的三角函数值我们很容易计算，甚至可以背诵下来，但是对于一般的锐角又怎样求它的三角函数值呢？用计算器可以帮我们解决大问题．①已知角求三角函数值；②已知三角函数值求锐角．2直角三角形中，30°的锐角所对的直角边等于斜边的一半．3．锐角三角函数的性质（1）0<sinα<1，o<cosα<1（0°<α<90°）1（2）tanα·cotα=1或tanα=（3）tanα=1；cot?sin?cos?，cotα=．cos?sin?（4）sinα=cos（90°-α），tanα=cot（90°-α）．有关锐角三角函数的问题，常用下面几种方法：一、设参数例1. 在?ABC中，?C?90?，如果tanA?5，那么sinB的值等于（）12D.12 5A.513B.1213C.512解析：如图1，要求sinB的值，就是求AC5的值，而已知的tanA?，也就是AB12BC5? AC12可设BC?5k，AC?12k则AB?(5k)2?(12k)2?13k?sinB?12k12?，选B 13k13二、巧代换例2. 已知tan??3，求sin??2cos?的值。
5sin??cos?解析：已知是正切值，而所求的是有关正弦、余弦的值，我们可以利用关系式sin??3，作代换sin??3cos?，代入即可达到约分的目的，也可以把所求的cos?分式的分子、分母都除以cos?。
tan??2sin??2sin??2cos? ?cos?sin5sin??cos?5?1cos?再把sin?1?3代入，得：原式? cos?16三、妙估计例3. 若太阳光与地面成37?角，一棵树的影长为10m，则树高h的范围是（取?1.7）A. 3?h?5B. 5?h?10C. 10?h?15D. h?15 解析：如图2，树高h?10tan37?，要确定h的范围，可根据正切函数是增函数，估计tan30??tan37??tan45?即10tan30??10tan37??10tan45??10??h?10 3?5?h?10，故选B四、善转化例4. 在?ABC中，1?A?30?，tanB?BC?，求AB的长。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
用锐角三角函数概念解题的常见方法1．锐角三角函数（1）锐角三角函数的定义我们规定：sinA=ac，cosA=bc，tanA=ab，cotA=ba．锐角的正弦、余弦、正切、余切统称为锐角的三角函数．（2）用计算器由已知角求三角函数值或由已知三角函数值求角度对于特殊角的三角函数值我们很容易计算，甚至可以背诵下来，但是对于一般的锐角又怎样求它的三角函数值呢？用计算器可以帮我们解决大问题．①已知角求三角函数值；②已知三角函数值求锐角．2直角三角形中，30°的锐角所对的直角边等于斜边的一半．3．锐角三角函数的性质（1）0<sinα<1，o<cosα<1（0°<α<90°）（2）tan α·cot α=1或tan α=1cot α； （3）tan α=sin cos αα，cot α=cos sin αα． （4）sin α=cos （90°-α），tan α=cot （90°-α）．有关锐角三角函数的问题，常用下面几种方法： 一、设参数例1. 在ABC ∆中，︒=∠90C ，如果125tan =A ，那么sinB 的值等于（ ） 512.125.1312.135.D C B A 解析：如图1，要求sinB 的值，就是求AB AC 的值，而已知的125tan =A ，也就是125=AC BC 可设k AC k BC 125==， 则k k k AB 13)12()5(22=+=13121312sin ==∴k k B ，选B 二、巧代换例2. 已知3tan =α，求ααααcos sin 5cos 2sin +-的值。
解析：已知是正切值，而所求的是有关正弦、余弦的值，我们可以利用关系式3cos sin tan ==ααα，作代换ααcos 3sin =，代入即可达到约分的目的，也可以把所求的分式的分子、分母都除以αcos 。
图1图21cos sin 52cos sin cos sin 5cos 2sin +-=+-ααααααα 再把3cos sin =αα代入，得：原式161= 三、妙估计例 3. 若太阳光与地面成︒37角，一棵树的影长为10m ，则树高h 的范围是（取7.13=）A. 53≤<hB. 105<<hC. 1510<<hD. 15<h解析：如图2，树高︒=37tan 10h ，要确定h 的范围，可根据正切函数是增函数，估计︒<︒<︒45tan 37tan 30tan即︒<︒<︒45tan 1037tan 1030tan 10103310<<⨯∴h 105<<∴h ，故选B四、善转化 例4. 在ABC ∆中，1031tan 30==︒=∠BC B A ，，求AB 的长。
解析：注意题中所说的ABC ∆并不是直角三角形！如图3，ABC ∆不是直角三角形，为了利用31tan =B ，可以作AB CD ⊥于D ，这样B ∠就是一直角三角形中的一角，A ∠也出现在另一个直角三角形中，设x CD =，则x BD 3= 由222)10()3(=+x x ，得1=x即CD ＝1，BD ＝3再有330cot =︒⋅=CD AD33+=∴AB五、适时构造例5. 不查表，不用计算器，求︒75sin 的值。
解析：我们可以先画ABC Rt ∆，使︒=∠︒=∠9030C A ，，如图4，延长CA 至D ，使AD ＝AB ，连结BD ，则︒=∠=∠15DBA D ，︒=∠∴75DBC图4设BC ＝1，则3232+===CD AC AB ，，426263275sin 26)32(122+=++=︒∴+=++=∴BD六、准确分类例6. “曙光中学”有一块三角形形状的花圃ABC ，现可直接测量到︒=∠30A ，AC＝40米，BC ＝25米，请你求出这块花圃的面积。
图5 图6解析：ABC ∆中，已知两边和其中一边的对角，这时特别注意ABC ∆的形状不惟一！要分两种情况分别求出，如图5、图6，作AB CD ⊥，分出直角三角形后，可求得面积应为：22)1503200()1503200(米或米-+1．在Rt △ABC 中，∠C 为直角，sinA=2，则cosB 的值是（ ）A ．12 B C ．1 D 2．下列各式不成立的是（ ）A ．sin50°<sin89°B ．cos1°<cos88°C ．tan22°<cot45°D ．cos23°>sin23°3．∠A 是锐角，tanA>3，则∠A （ ） A ．小于30° B ．大于30° C ．小于60° D ．大于60° 4．下列各式正确的是（ ）A ．sin30°+sin30°=sin60°B ．tan60°-tan30°=tan30°C ．cos （60°-30°）=cos60°-cos30°D ．3tg30°5．一个人从山下沿30°角的坡路向上攀登，如果在坡面上走了100米，•那么他上升的高度是（ ）A ．100米B ．50米C ．D ．无法确定6．在△ABC 中∠C 为直角，各边长均扩大2倍，则锐角A 的四个三角函数值（ ） A ．都扩大2倍 B ．都缩小2倍C ．没有变化D ．有的扩大2倍，有的缩小2倍 7．cos 60tan 45cot 302cot 45︒-︒︒-︒的值等于（ ）A ．．-12 C D ．8．用计算器求“已知cot α=1.515，求α”时，先计算（ ）A ．1cot α B ．α C D ．9．在Rt △ABC 中，∠C=90°，BC=2，则cosA=______．10．若sin （90°-α）=2，则cos （90°-α）=______． 11．在Rt △ABC 中，∠C=90°，sinA=38，b=6，则c=______． 12．2cos30°-3tan α=0，则锐角α是_____度．13．用不等号连接右面的式子：cos40°_____cos20°，sin37°______sin42°．14°-12cos60°=_______，（sin30°+tan45°）·cos60°=_______． 15．在Rt △ABC 中，∠C 为直角，若sinA=35，则cosB=_______．16．若tan α·tan35°=1，则锐角α的度数等于________．17.△ABC 中，∠C 为直角，∠A 、∠B 、∠C 所对的边分别是a ，b ，c ，已知b=3，•求∠A 的四个三角函数．18. 正方形ABCD 中的正三角形ABP ，•已知正方形的边长为1，•试计算tan•∠PAD ．19.一个等腰三角形的两边是10、12，这个三角形顶角的正弦、余弦、正切、余切．20．如图是一块三角形形状的草坪ABC，经测量：∠B=30°，∠A=45°，BC=25m，请你求出这块花圃的面积．（结果用根号表示）21.△ABC中，││+（sinB-12）2=0，求∠C．答案:1．D [点拨]sinA=2，所以∠A=45°，所以cos∠A=2．2．B [点拨]余弦函数值随角度的增大而减小，所以cos1°<cos88°．3．B [点拨]因为tanA>3，所以tan>tan30°．•又因为正切值随着角度的增大而减小，所以∠A>30°．4．D5．B [点拨]他上升的高度为100×sin30°=50．6．C7．D [点拨] cos60tan45cot302cot45︒-︒︒-︒11-2．8．A9点拨]此题有多种方法，这里例举一种：，cosA=4ACAB==2．10．12[点拨]因为sin（90-α）=2，所以90°-α=60°，所以cos（90°-α）=cos60°=12．11[点拨]tanA=38=6a，a=94，．12．30° [点拨]因为2cos30°-3tanα=0，所以tanα=3，α=30°．13．<，< [点拨]正弦值随着角度的增大而增大，余弦值随着角度的增大而减小．14．34，34[点拨°-12cos60°2-12×12=34；（sin30°+tan45°）·cos60°=（12+1）×12=34．15．35[点拨]因为∠A=90°-∠B，所以sinA=35=sin（90°-∠B）=cosB．16．55° [点拨]因为tan35°·cot35°=1，tanα·tan35°=1，所以tanα=cot35°，α=55°．17．解：根据勾股定理得：所以sinA=4ac==cosA=14bc==；tanA=ab=，．18．解：过点P作PE⊥AD，交BC于点F（如图所示）．显然EF=1，BF=CF=12，AD=ED=12．在直角三角形BFP中，PF=sin60°×BP=2×1=2．pE=EF-PF=1-2=22．在△AEP中，∠AEP=90°，所以tan∠PAD=22PEAE=19．解：如图所示：AB=AC=10，BC=12，作AD⊥BC于点D，作CE⊥AB于点E．∵AB=AC ，AD ⊥BC ，∴BD=CD=6．在直角三角形ABD 中，．又∵S △ABC =12AB ·CE=12BC ·AD ，所以10×CE=12×8，CE=9.6．在直角三角形ACE 中，．所以sin ∠BAC=9.610CE AC ==0.96，cos ∠BAC= 2.810AE AC ==0.28， tan ∠BAC=9.6242.87CE AE ==，cot ∠BAC=724． 20．解：如图，过B 作BD ⊥AC 于点D ．在直角三角形BCD 中，∠B=30°，∠BDC=90° sinB=CDBC，即CD=BC ×sinB=25×sin30°=12.5（米）BD=BC ×cosB=25×2=2（米） 在直角三角形ACD 中，∠A=45° 所以AD=CD=12.5（米）11 所以三角形地ABC 的面积是12AB ·CD=12252=（平方米）答：略．21．解：∵││≥0，（sinB-12）2≥0且│+（sinB-12）2=0∴│cosA-2│=0，（sinB-12）2=0所以cosA-2=0，sinB-12=0，即cosA=2，sinB=12，因此∠A=45°，∠B=30°所以∠C=180°-45°-30°=105°．。